Network Model-Assisted Inference from Respondent-Driven Sampling Data

Summary

Respondent-Driven Sampling is a widely-used method for sampling hard-to-reach human populations by link-tracing over their social networks. Inference from such data requires specialized techniques because the sampling process is both partially beyond the control of the researcher, and partially implicitly defined. Therefore, it is not generally possible to directly compute the sampling weights for traditional design-based inference, and likelihood inference requires modeling the complex sampling process. As an alternative, we introduce a model-assisted approach, resulting in a design-based estimator leveraging a working network model. We derive a new class of estimators for population means and a corresponding bootstrap standard error estimator. We demonstrate improved performance compared to existing estimators, including adjustment for an initial convenience sample. We also apply the method and an extension to the estimation of HIV prevalence in a high-risk population.

1. Introduction

There is much interest in estimating features of hard-to-reach human populations. Such populations are characterized by the lack of a serviceable population sampling frame. In some settings, the target population is well-connected by a network of social relations. Link-tracing sampling strategies such as snowball sampling (Goodman (1961) and others) and respondent-driven sampling (RDS) (Heckathorn, 1997) are often used to leverage those social relations to sample beyond the small subgroup available to researchers. In these settings, subsequent samples are identified and selected based on their social ties with other members of the target population. The statistical literature dealing with such strategies (Frank, 1971; Goodman, 1961; Thompson, 1990; Thompson and Frank, 2000), typically assumes an idealized setting in which the initial sample is assumed to be a probability sample from the target population. The applied literature such as Trow (1957) and Biernacki and Waldorf (1981), has traditionally recognized that this is impractical, and therefore treated link-tracing samples (typically referred to as snowball samples, despite Goodman’s probabilistic framing) as convenience samples for which probability-based inferential methods are unfounded.

The work of Heckathorn and colleagues (Heckathorn, 1997, 2007; Salganik and Heckathorn, 2004; Volz and Heckathorn, 2008) around the RDS specialization of link-tracing sampling is innovative in reducing the number of links followed per respondent, such that many waves of sampling are fostered, decreasing the dependence of the final sample on the initial convenience sample. The second main innovation of the RDS paradigm is in the respondent-driven nature of the sampling process in which subsequent samples are selected by the passing of coupons by current sample members, thus reducing the confidentiality concerns often present in hard-to-reach marginalized populations. While this approach does reduce the dependence of the final sample on the initial sample, it is possible for substantial bias to remain based on the initial sample of seeds, as studied in simulations by Gile and Handcock (2010) and illustrated empirically by Johnston (2010). Current estimation methods (Gile, 2011; Heckathorn, 1997, 2007; Salganik and Heckathorn, 2004; Volz and Heckathorn, 2008), however, do not correct for biases introduced by seed selection. A common feature of networked populations is that social ties are often more likely to occur between people who have similar attributes than those who do not, a tendency called homophily by attributes (Freeman, 1996; Lazarsfeld and Merton, 1954; McPherson et al., 2001). Homophily exacerbates the effects of the initial sample. In this paper we present a novel approach and inferential frame to correct for bias introduced by seed selection in the presence of homophily. In particular, we treat the problem of estimation of the population proportion of a binary nodal covariate in populations with homophily on that covariate, based on a branching link-tracing sample beginning with seeds selected by a convenience mechanism.

There is a varied formal statistical literature on inference from link-tracing network samples. All of this work, however, involves the assumption that the initial sample is a probability sample drawn from a well-defined sampling frame, and that subsequent sampling is adaptive, or dependent on population characteristics only through their observed portions (Thompson and Seber, 1996). In the design-based framework, these works consider cases where sampling probabilities are known for all units in the analysis (Frank, 1971, 2005; Goodman, 1961; Thompson, 1992, 2006). Inference is then made without reference to any superpopulation model. In the likelihood frame, the literature treats cases where the adaptive sampling process is amenable to the model, and therefore the modeling can be conducted without explicit treatment of the sampling process (Handcock and Gile, 2010; Pattison et al., 2012; Thompson and Frank, 2000). The traditional approach to RDS, originally due to Heckathorn (1997), represents an alternative to this paradigm. The assumption of the initial probability sample is replaced by an assumption of sufficient waves of sampling to adequately reduce the dependence of the sample on the initial sample.

In this paper, we concern ourselves with a case in which none of these approaches suffice. The sampling probabilities of the units are not known, making the traditional design-based approaches inadequate. The initial sample is not a probability sample, so the sample is not adaptive or amenable, and any likelihood inference must consider the sampling process as well as the population model. Such a joint modeling approach has been conducted in a few works (Felix-Medina and Monjardin, 2006; Felix-Medina and Thompson, 2004; Frank and Snijders, 1994), but each of these requires an initial probability sample from some frame to allow for modeling of the sampling process. And while in some cases, the waves of sampling may be sufficient to suitably reduce the dependence on the initial sample, this is often not the case (Gile and Handcock, 2010), and we are interested in the cases when there is insufficient sample depth. In particular, we propose a model-assisted design-based approach, using an estimate of network structure (homophily) to reduce bias induced by the initial sample.

We begin in Section 2 by introducing respondent-driven sampling. In Section 3, we then present our Model-Assisted inferential approach. Section 4 presents a simulation study illustrating the removal of bias introduced by the initial convenience sample. An application to HIV prevalence estimation among injecting drug users in the Ukraine can be found in Section 5, and Section 6 presents a discussion and concluding remarks.

2. Respondent-Driven Sampling

2.1. Notation

We assume the target population consists of N people (nodes) with labels 1, …, N. Let the N-vector z represent a binary nodal outcome variable of interest. We refer to this variable as “infection status”, such that

$$z_i=\{\begin{array}{ll}0\hfill & i\text{not}\text{infected}\hfill \\ 1\hfill & i\text{infected}\hfill \end{array}i\in 1\dots N.$$

We assume the target population is connected by a network of mutual relations with N×N adjacency matrix y:

$$y_{ij}=y_{ji}=\{\begin{array}{ll}1\hfill & i\text{and}j\text{connected}\hfill \\ 0\hfill & i\text{and}j\text{not}\text{connected},\hfill \end{array}$$

and that this network forms a single connected component. Denote by d_i = Σ_j y_ij the nodal degree, or number of network ties or alters of node i. Let d = {d₁, …, d_N}. Denote by x_i = Σ_j z_jy_ij the number of network ties node i shares with infected nodes, and let x = {x₁, …, x_N}.

2.2. Sampling Procedure

We consider an RDS procedure of the following form:

• 0An small initial sample is selected from the population members accessible to researchers, typically using a convenience mechanism. These are called the seeds and comprise wave k = 0 of the sample. They are typically 3–12 in number.
• 1Each member of wave k is given a small number (typically 2–3) of uniquely identified coupons to distribute among their alters.
• 2Coupon recipients returning their coupons to the study center are subsequently enrolled in the study. A person previously recruited can not be recruited again. The wave number of a respondent is one more than that of their recruiter.
• 3Steps (1) and (2) are repeated until the desired sample size, n, is attained.

This process has proved effective at recruiting large and diverse samples from many hard-to-reach populations (Abdul-Quader et al., 2006), and has been widely used. It has been heavily used in the monitoring of disease prevalence and risk behaviors among high-risk populations such as sex workers, men who have sex with men, and injecting drug users (Malekinejad et al., 2008), largely in the service of the reporting requirements of UNAIDS for all countries with concentrated HIV epidemics (UNAIDS, 2008). It is also used by the US Centers for Disease Control and Prevention in the behavioral monitoring of injecting drug users and high-risk heterosexuals in 25 large US cities (Lansky et al., 2007), and has also been used in other populations such as unregulated workers (Bernhardt et al., 2009) and jazz musicians (Heckathorn and Jeffri, 2001).

We represent the full sampling mechanism by the random variables:

$$\begin{array}{c}{S}_i^k=\{\begin{array}{ll}1\hfill & \text{person}i\text{is}\text{sampled}\text{in}\text{wave}k\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}i\in 1\dots N,k\in 0,\dots .\\ S_i=\sum _{k=0}^{\infty }{S}_i^k=\{\begin{array}{ll}1\hfill & \text{person}i\text{is}\text{sampled}\hfill \\ 0\hfill & \text{person}i\text{is}\text{not}\text{sampled}\hfill \end{array}i\in 1\dots N,\end{array}$$

and let s^k denote the observed sampling vector corresponding to the people sampled in wave k. Based on the sampling procedure, we exactly observe the elements of z, d and x corresponding to i : s_i = 1. A variant when x cannot be observed directly, as in the application in Section 6, substitutes an estimate of x based on observed referral patterns.

Further we assume each respondent distributes a number of coupons completely at random from among their alters, with the number determined by a common distribution.

2.3. Design-based Inferential Approach

We consider design-based estimators for the population mean $\mu =\frac{1}{N}{\sum }_{i=1}^N{z}_i$. Because the sampling probabilities of the people selected through RDS are almost never explicitly known, we follow Volz and Heckathorn (2008), and Gile (2011) in constructing a model for the sampling process, and estimating sampling probabilities accordingly. We use a generalized ratio estimator of the form:

$$\widehat{\mu }=\frac{{\sum }_{i=1}^N\frac{S_i{z}_i}{{\widehat{\pi }}_i}}{{\sum }_{i=1}^N\frac{S_i}{{\widehat{\pi }}_i}},$$ (1)

where estimated sampling probabilities π̂_i = 𝔼(S_i|𝒮) are computed under an approximation 𝒮 to the true RDS sampling process. If the inclusion probabilities are known this estimator is referred to as the Häjek estimator (Hajek, 1971; Lumley, 2010), and typically performs better than the corresponding Horvitz-Thompson estimator (Särndal et al., 1992). The estimators introduced by Volz and Heckathorn (2008) and Gile (2011) differ, and ours further differs, in their specification of the sampling process 𝒮.

Most inference from RDS data approximates the sampling process as a with-replacement random walk on the space of graph nodes, with transitions along the edges or social relations, and sampling treated as a Markov chain at stationarity (Salganik and Heckathorn, 2004; Volz and Heckathorn, 2008). The resulting inference involves sampling weights proportional to the self-reported degrees. These are the stationary distribution sampling probabilities of a with-replacement random walk on a connected network. While this is a useful first approximation, it has several limitations. First, as highlighted in Gile (2011), this type of inference does not respect the without-replacement nature of the sampling process, which can lead to biased estimates. Gile (2011) presents an approach correcting for this feature by substituting a without-replacement successive sampling approximation to the sampling process. Neither this, nor earlier estimators, however, address the fundamental issue of bias induced by the selection of the initial sample. Such bias is illustrated in Gile and Handcock (2010), as well as in the current paper, and correction for it is a key contribution of the present paper.

As with these earlier approaches, the first requirement of our sampling model is that it account for the different sampling probabilities by nodal degree. Unlike these other approaches, we further require our approach to account for the bias introduced by the selection of seeds in the presence of network homophily in the underlying population. This requires consideration of features of the social network, y, in particular the homophily of the relations.

We make no assumptions about the mechanism for selecting the initial sample and will condition on the seed characteristics throughout the analysis.

If the network y were fully known, we could use simulation to estimate the sampling probability

$${\widehat{\pi }}_{i,\mathbf{y}}=\mathbb{E}(S_i\mid \mathcal{S},\mathbf{y},{\mathbf{s}}^0)$$ (2)

of each node, conditional on the selection of seeds, s⁰. Explicitly, we would repeatedly simulate RDS under sampling model 𝒮 starting from s⁰ each time and compute the π̂_i,y as the proportion of simulated samples containing node i. These could be used in (1) to form an estimator. Unfortunately, y is typically only partially known, and so we apply a model-assisted approach.

3. A Model-Assisted Approach

Our approach is an extension of the model-assisted design-based approaches presented in Särndal et al. (1992). Existing work in this area uses a working model for the variable of interest, conditional on the auxiliary variables to construct estimators that are (approximately) design-unbiased, whether the model holds or not, and have smaller design variance if the model does hold. Our case is slightly different. The sampling process we consider is only locally defined, and originates at a sample with unknown distribution. We therefore model the partially-observed auxiliary variable (the network) directly. We cannot guarantee design-unbiasedness, and use the working model form to recover approximate design-unbiasedness, rather than to improve efficiency. This is necessary because the impact of the seed characteristics on the subsequent sample is mediated by the structure of the underlying social network. We therefore assume a working superpopulation model from which the network was drawn and use it to estimate sampling probabilities conditional on the selection of the initial sample. This approach is also similar in spirit to non-response adjustment using propensity models in survey sampling (e.g., Särndal and Lundström, 2005).

3.1. Network Working Model

The primary structural features of the network influencing RDS are the individual connectedness in the network, the differential connectedness by infection status, the homophily on infection status, and bottlenecks (an extremal form of homophily). These were identified in prior work (Gile, 2011; Gile and Handcock, 2010; Goel and Salganik, 2009).

We consider models of exponential-family random graph model (ERGM) form (Frank and Strauss, 1986; Hunter et al., 2008; Hunter and Handcock, 2006), conditional on the set of nodal degrees (d) and infection statuses (z), and including a single additional parameter representing homophily on z. In particular:

$$P(\mathbf{Y}=\mathbf{y}\mid \mathbf{z},\mathbf{d},\eta )=\frac{exp(\eta g(\mathbf{y},\mathbf{z}))}{c(\eta \mid \mathbf{z},\mathbf{d})}\mathbf{y}\in \mathcal{Y}(\mathbf{z},\mathbf{d}),$$ (3)

where $g(\mathbf{y},\mathbf{z})={\sum }_{i=1}^{N_W}{\sum }_{j=1}^{N_W}{y}_{ij}{z}_i(1-z_j)$ is the number of ties connecting individuals inhomogeneous on infection status. Here c(η|z, d) = Σ_{u∈𝒴(z,d)} exp(ηg(u, z)), and the space 𝒴 (z, d) consists of all binary undirected networks consistent with d and z (the dependence on d and z is suppressed below).

The ERGM captures individual-level connectivity (degree), the overall connectedness of the respective groups (degree counts broken down by group) and homophily on the infection status (the count of cross-group ties). The combined effect of these features controls the level of clustering on infection status within the network. Hence the ERGM represents the structural features of the networked population that prior work indicates are most influential on the sampling process. Note that extreme bottlenecks could be missed. As we do not have direct information on them, they are not modeled explicitly, although some of their effects may be captured by the other terms in the model (e.g., via high homophily on infection status).

Note that this model form, as well as the simulation procedure to follow, requires specification of a population size N_W. Ideally this value will be close to the actual size of the hidden population, N, but in our algorithm it represents a working population size parameter. Inaccuracy in this estimate may degrade the finite population adjustment of the estimator, but will not affect inference when the sample fraction (n/N) is small.

Given this model form, we use the estimator (1) based on sampling weights assumed constant over equivalence classes by degree and infection status and estimated under the model:

$${\widehat{\pi }}_{i,\eta }=\mathbb{E}(S_i\mid \mathcal{S},\mathbf{z},\mathbf{d},\eta ,{\mathbf{s}}^0)=\sum _{\mathbf{y}\in \mathcal{Y}(\mathbf{z},\mathbf{d})}{\widehat{\pi }}_{i,\mathbf{y}}P(\mathbf{Y}=\mathbf{y}\mid \mathbf{z},\mathbf{d},\eta ),$$

with π̂_i,y = 𝔼(S_i|𝒮, y, s⁰), as in (2). Note that to treat these equivalence classes, we condition on the equivalence classes of the seed nodes selected, rather than the unique identities of those nodes.

We also do not know the network working model parameter η. However, the statistic g(y, z) is sufficient for η. Hence P(Y = y|z, d, g(y, z) = g̃, η) = P(Y = y|z, d, g(y, z) = g̃) and is uniform on 𝒴 (z, d, g̃) = {y ∈ 𝒴 (z, d, g) : g(y, z) = g̃}. The estimator is then computed using sampling probabilities based on the network working model conditional on a value of g(y, z) estimated from the data:

$${\widehat{\pi }}_i=\mathbb{E}(S_i\mid \mathcal{S},\mathbf{z},\mathbf{d},\stackrel{\sim }{g},{\mathbf{s}}^0)=\sum _{\mathbf{y}\in \mathcal{Y}(\mathbf{z},\mathbf{d},\stackrel{\sim }{g})}{\pi }_{i,\mathbf{y}}P(\mathbf{Y}=\mathbf{y}\mid \mathbf{z},\mathbf{d},\stackrel{\sim }{g})$$ (4)

These are the estimated probabilities used in our proposed estimator. This requires fitting a network working model to data sampled through RDS, which we address in the next section.

3.2. Fitting the Network Working Model

Thompson and Frank (2000) and Handcock and Gile (2010) provide an approach to fitting models of form similar to (3) to data sampled through link-tracing samples. Unfortunately, these approaches require a sample that is amenable to the model in question (Handcock and Gile, 2010). That is:

$$P(\mathbf{S}\mid \mathbf{y},\mathbf{d},\mathbf{z})=P(\mathbf{S}\mid {\mathbf{y}}_{\mathit{obs}},{\mathbf{d}}_{\mathit{obs}},{\mathbf{z}}_{\mathit{obs}}),$$ (5)

where *_obs represents the observed part of *, and also that the sampling and model parameters are separable. This is equivalent to the conditions for ignorability according to Rubin (1976) and Little and Rubin (2002). Unfortunately, in the case of RDS, condition (5) is violated by the convenience sample of seeds, which may well depend on unobserved characteristics.

Therefore, we require a novel approach to model fitting. As d and z are unknown, we construct design-based estimators of them from estimates of the sampling probabilities π̂_i. Specifically, let T_kl be the number of nodes of degree k and infection status l, k ∈ {1, …, N_W − 1}, l ∈ {0, 1} and $\mathbf{T}={\left\{T_{kl}\right\}}_{k=1;l=0}^{k=N_W-1;l=1}$. We estimate T and g(y, z) by,

$${\stackrel{\sim }{T}}_{kl}=\frac{1}{N_W}\sum _{i=1}^{N_W}\frac{S_i\mathbb{I}(d_i=k,z_i=l)}{{\widehat{\pi }}_i}$$ (6)

$$\stackrel{\sim }{g}(\mathbf{y},\mathbf{x})=\sum _{i=1}^{N_W}\frac{S_i(x_i(1-z_i)+(d_i-x_i)z_i)}{2{\widehat{\pi }}_i}$$ (7)

where 𝕀(*) is the indicator function on *, and π̂_i is assumed constant for all i : d_i = k, z_i = l. Note that this requires the observation of {x_i : S_i = 1, i = 1, …, N_W}, and that (7) is just the Horvitz-Thompson estimator for the number of cross-group ties, based on weighting the number of cross-group ties reported by each respondent. The factor of 2 reflects that each edge in the population could be counted by either incident node. We then estimate the network model conditional on g(y, z) = g̃(y, x) and the joint degree and infection status sequence implied by T̃. Details of this computation are given in the Appendix.

3.3. Algorithm

Note that the value of the network working model parameter, required to estimate π, in turn, depends on the value of π. We therefore apply an approach similar to self-consistency (Lee and Meng, 2007) to find a joint solution to (6) and (7), as well as to the equations:

$${\widehat{\pi }}_i=\mathbb{E}\left(S_i\mid \mathcal{S},\mathbf{z},\mathbf{d},\stackrel{\sim }{\mathbf{T}},\stackrel{\sim }{g}(\mathbf{y},\mathbf{x}),s^0\right)i=1,\dots ,N_W.$$ (8)

This approach iterates between estimating the network working model parameter given values for the sampling probabilities, and then estimating the sampling probabilities given the network working model parameter. Explicitly, it is:

• Estimate π̂_i proportional to degree d_i.

• Iterate the following steps:

  • Compute design-based estimates of statistics T̃_kl and g̃(y, x) using π̂ in (6) and (7).

  • Simulate M networks according to the working ERG model corresponding to T̃ and g̃(y, x).

  • Estimate π̂ by simulated RDS sampling from the simulated networks.

• Use the resulting estimated probabilities, π̂, to form the weighted estimator of the quantity of primary interest:

$${\widehat{\mu }}_{MA}=\frac{{\sum }_{i=1}^{N_W}\frac{S_i{z}_i}{\widehat{\pi }}}{{\sum }_{i=1}^{N_W}\frac{S_i}{\widehat{\pi }}}.$$ (9)

The iterative nature of this procedure is similar to that used for the successive sampling estimator of Gile (2011). This algorithm differs in the core process of estimating the inclusion probabilities. More details of this procedure are provided in the Appendix.

The simulation procedure implicit in this estimation algorithm lends itself to a realistic bootstrap approach to standard error estimation. We present such a bootstrap in the next section.

3.4. Measure of Uncertainty: Bootstrap

Unlike earlier RDS estimators, the estimator given in (9) allows for estimators of uncertainty that account for the estimated network relational structure of the underlying population as well as incorporating several observable features of the sampling process. The former is because of the use of the network working model for the population over which the RDS sampling procedure operates. The latter is because our procedure enables the simulation of complex RDS designs. In particular, if we believe there is seed bias we can incorporate it into the sampler, and if there is measurable sampling bias (as in the application) we can incorporate that also. This allows the procedure to incorporate available information about the population and sampling and greatly improves the accuracy of the representation of the actual sampling process. The accuracy of the bootstrap depends directly on the quality of the approximation to the actual sampling process.

We propose a parametric bootstrap approach to obtaining confidence intervals, according to the following procedure:

1. For b = 1, … B, iterate the following steps:

   1. Simulate a network Y_b from the model given in (2) conditional on g̃(y, x)^h and T^h where h is the final iteration of the algorithm in the Section 3.

   2. Simulate one RDS sample S_Yb with parameter 𝒮 from Y_b.

   3. Compute an estimator μ̂_MA(b) of μ based on the sample S_Yb using the algorithm in the Appendix.

2. Use the empirical distribution 𝒟̂(μ̂_MA) of {μ̂_MA(1), μ̂_MA(2), … μ̂_MA(B)} to estimate the distribution of μ̂_MA under the estimated model form.

The distribution of 𝒟̂(μ̂_MA) may then be used to form confidence intervals for μ which account for the full estimated relational structure as well as observable biases of the sampling process. We use the standard deviation of the resulting population of B bootstrap estimates as an estimate of the standard error of μ̂_MA. B = 500 bootstrapped samples have been sufficient in our simulations. In our simulations, this procedure took about 90 seconds per sample on a single processor when N_W = 1000 and 5 minutes when N_W = 10000. Parallelization is straightforward and dramatically reduces elapsed time. A large additional speedup can be obtained by replacing step (c) with (c′) in which the class-specific inclusion probabilities ${\widehat{\pi }}_i^h$ are not computed but replaced with those π̂_i from the original data. While these estimates of the inclusion probabilities vary from bootstrap sample to sample, their uncertainty is a small part of the overall uncertainty. This reduces the procedure to about 1–3 seconds per sample on a single processor. The simulation study in the next section uses (c′).

4. Comparing the Model-Assisted to Existing Estimators: A Simulation Study

Gile and Handcock (2010) present an extensive simulation study of RDS based, where possible, on a set of realistic characteristics of data from the CDC pilot study of RDS (Abdul-Quader et al., 2006). For comparison purposes, our simulation study uses simulated populations very similar to those in Gile and Handcock (2010). Our simulations consist of 3 sub-studies: a primary study of estimator performance under conditions it is designed to address, a sensitivity analysis to mis-specification of the network model, and a simulation addressing the performance of the bootstrap uncertainty estimator.

4.1. Study Design

Our simulation study includes three levels of simulation:

• The generation of random networks according to specified network features

• The generation of simulated RDS samples from each network

• The estimation of infection prevalence from each set of simulated sample data.

We use variants of the network and sampling parameters to study the behavior of the proposed estimator. Parameter descriptions and levels are listed in Tables 1 and 2. We include the detailed mathematical expressions for the simulation parameters to aid transparency, however the primary study has a 2 × 2 factorial design, so that qualitative results can be systematically compared when the most important sources of bias are introduced.

Table 1.

Parameters of simulated networks. Default parameters given in boldface.

Parameter	Meaning	Values
Number of nodes		10000, 1000
Prevalence	$\mu =\frac{1}{N}{\sum }_i{z}_i$	0.20
Mean degree	$\overline{\mathbf{d}}=\frac{1}{N}{\sum }_{i=1}^N\mathbb{E}(d_i)=\frac{1}{2N}{\sum }_{i,j-1}^N\mathbb{E}(Y_{ij})$	7
Homophily	$\mathrm{H}=\frac{N^1{\overline{d}}^1{N}^0{\overline{d}}^0}{(N^1{\overline{d}}^1+N^0{\overline{d}}^0){\sum }_{i,j}{z}_i(1-z_j)\mathbb{E}(y_{ij})}$	1, 2
(Differential) Activity Ratio	$\text{DA}=\frac{{\overline{d}}^1}{{\overline{d}}^0}$	1, 2
	where N0 = N(1 − μ ), N1 = Nμ ${\overline{d}}^1=\frac{1}{N^1}{\sum }_{i,j}{\mathbf{z}}_i\mathbb{E}(y_{ij}),{\overline{d}}^0=\frac{1}{N^0}{\sum }_{i,j}(1-{\mathbf{z}}_i)\mathbb{E}(y_{ij})$

Table 2.

Parameters of simulated RDS sampling. Default parameters given in boldface.

Parameter	Meaning	Values
Number of Seeds	$n^0={\sum }_i{S}_i^0$	10
Seed Selection	Sequentially with probability proportional to degree from either:	full population, infected nodes
Branching	From each sampled node, up to ncup previously unselected alters are selected completely at random for subsequent sampling. ncup are selected whenever available.	2
Sample Size	Sampling stops when n nodes have been sampled.	500

To allow for comparability across simulation conditions, throughout our simulations, we maintain the same true recoverable prevalence, μ = 0.20, the same sample size n = 500, and the same mean degree d̄ = 7. We consider variations on the population size (hence the sample fraction), the degree of clustering or homophily on infection status, and differential rates of tie formation by infection status (or (differential) activity ratio, DA). The parameter levels considered are summarized in Table 1. Note that this parameterization of homophily corresponds to the factor by which the expected number of cross-group ties is deflated, beyond the expected level absent homophily. A (default) homophily value of 2 here is close to (default) level 5 in the parameterization of Gile and Handcock (2010).

Under each set of network parameters, networks are simulated according to an ERGM with model

$$P(\mathbf{Y}=\mathbf{y}\mid \mathbf{z},\beta )=\frac{exp(\beta g(\mathbf{y},\mathbf{z}))}{c(\beta \mid \mathbf{z})}\mathbf{y}\in \mathcal{Y},$$ (10)

where c(β|z) = Σ_{u ∈ 𝒴}exp(βg(u, z)), and the space 𝒴 consists of all binary undirected networks on N nodes. The sufficient statistics g(y, z) are given by:

$$\begin{array}{l}{g}_1(\mathbf{y})=\sum _{i=1}^N\sum _{j<i}{y}_{ij}{z}_i{z}_j\\ g_2(\mathbf{y})=\sum _{i=1}^N\sum _{j<i}{y}_{ij}(1-z_i)(1-z_j)\\ g_3(\mathbf{y})=\sum _{i=1}^N\sum _{j=1}^N{y}_{ij}{z}_i(1-z_j).\end{array}$$ (11)

These three terms correspond to the unique cells of the 2 × 2 mixing matrix on z, and for a given number of nodes N and prevalence μ, are uniquely defined by d̄, H, and DA. Note that this model is similar to (3), but not identical. In particular, g₃(·) of (11) is very similar to g(·) of (3). While (3) conditions on the fixed degree of each node, model (10) allows for stochastic variability in degrees around mean value parameters given by (11).

From each simulated network, a single RDS sample is drawn according to parameters in Table 2. A fixed number n⁰ of seed nodes are selected with probability proportional to degree (the best case for the earlier estimators), from either the full population or from the infected nodes only (to simulate extreme seed bias). The simulated process treats the case of two coupons distributed by each respondent completely at random among its previously un-sampled alters. Two coupons are chosen for simplicity, and because it represents the sampling process better than either 3 (equating to the return of all coupons in typical practice) or 1 (resulting in non-branching chains).

For each simulation case, we simulate 200 networks with one RDS sample from each, and we compare five estimators, as summarized in Table 3.

Table 3.

Five estimators compared in the simulation study.

Abbreviation	Source	Estimator
Mean	Naive sample mean of zi	μ̂
SH	Salganik and Heckathorn (2004)	μ̂SH
VH	Volz and Heckathorn (2008)	μ̂VH
SS	Gile (2011)	μ̂SS
MA	Proposed Model-Assisted	μ̂MA

4.2. Primary Results

We are especially interested in the performance of the proposed estimator under two forms of bias: finite population bias and bias induced by seed selection. Gile and Handcock (2010) and Gile (2011) show that finite population bias is induced in conditions of large sample fractions and differential activity. Gile and Handcock (2010) show that bias in the initial sample of seeds induces bias in the estimates in the presence of homophily. We therefore consider a 2 × 2 factorial simulation design based on these two features. The simulation conditions correspond to:

1. No finite population bias, No seed bias:

   small sample fraction, no differential activity, no homophily, no seed bias.

2. Finite population bias, No seed bias:

   large sample fraction, differential activity, no homophily, no seed bias.

3. No finite population bias, Seed bias:

   small sample fraction, no differential activity, homophily, seed bias.

4. Finite population bias, Seed bias:

   large sample fraction, differential activity, homophily, seed bias.

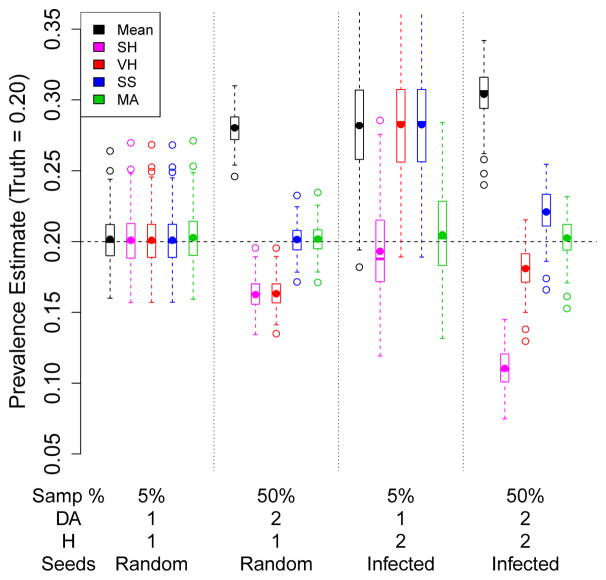
Under the first condition, previous estimators have been found to perform well. In the first part of Figure 1, there is a small sample fraction (5%, N = 10000), no homophily on infection status (H = 1), the ratio of mean degrees by infection (DA) is 1, and seeds are chosen from the full population, so there is no bias induced by seed selection. In this case, none of the estimators considered exhibit bias, and the naive sample mean exhibits the lowest variance, although the variability is similar across estimators.

Fig. 1.

Comparison of performance of five RDS estimators under four conditions. μ̂_SS and μ̂_MA are based on a working population size N. Results from 200 simulations.

The second part of Figure 1 illustrates the case μ̂_SS is designed to address. In this case, the sample fraction is large (about 50%, N = 1000), and infected nodes have mean degree twice than that of uninfected (DA = 2). In this case there is still no homophily (H = 1), and no seed bias. Here, the higher-degree infected nodes are over-represented in the sample, resulting in positive bias in the sample mean. Because of the assumed linear mapping from degree to sampling probability, μ̂_SH and μ̂_VH over-correct for this feature, resulting in negative bias. μ̂_SS and μ̂_MA appropriately adjust for the over-sampling of infected nodes, resulting in unbiased estimators without increased variance.

The third section of Figure 1 considers the case the new estimator, μ̂_MA, is designed to address. There is homophily (H = 2), and all seeds are selected from among the infected nodes. This case treats a small sample fraction (N = 10000) and activity ratio 1 (DA = 1). Here, most of the earlier estimators exhibit substantial bias due to the selection of seeds, while the proposed estimator corrects for the selection of seeds. It is also of interest to note that μ̂_SH also has negligible bias, and what bias there is is in the opposite direction from that of the other estimators.

The final case considers the joint effects of large sample fraction (N = 1000), non-unity activity ratio (DA = 2), homophily (H = 2), and biased selection of seeds (all infected). Here, the sample mean over-represents the higher-degree and initially sampled infected nodes. μ̂_VH exhibits a strong negative bias, similar to that in the second case. The two effects jointly cause tremendous bias in μ̂_SH. μ̂_SS is affected by seed bias, although not by the sample fraction. Here, again, the proposed estimator correctly adjusts for all of these effects. Although in this example the effects of sample fraction/activity ratio are of larger magnitude than those of seed bias/homophily, in practice the relative magnitudes of these will vary across data sets.

4.3. Sensitivity to the network working model

The role of the network working model is to provide a (stochastic) representation of the networked population. This model is the basis of the improved representation of the RDS design leveraged by the proposed estimator. The complexity of real-world social networks is high, so that simple network models only capture a subset of this complexity. In this section, we address this sensitivity by applying the proposed method to simulated networks with more complex structure.

The ERGM in (3) is designed to represent two levels of network structure that are important to RDS. The first is the nodal level individual heterogeneity in the propensity to have social ties, measured by the nodal degrees. The second is at the dyadic level and captures the homophily, or propensity for ties to be between individuals with the same infection status, beyond that implied by the infection prevalence. As infection status is the primary outcome of interest, this homophily is the most important to capture. The model (3) does not capture third level triadic effects, those based on the structure of triads of relations between individuals. While these are tertiary to the monadic and dyadic effects, they can influence the RDS. Unfortunately RDS results in branching tree patterns of observations that limit the empirical information on these triadic effects. Hence the model (3) presumes that the triadic structure is fully produced by the modeled monadic and dyadic components.

The purpose of this section is to assess the sensitivity of the estimator to this misspecification of the triadic effects. Explicitly, we consider networked populations with higher levels of transitivity than specified in the network working model and compare the performance of the estimators. Transitivity is represented by the edgewise shared partner (alter) statistics, denoted EP₀(y), …, EP_NW−2(y), where EP_k(y) is defined as the number of unordered pairs i, j such that y_ij = 1 and i and j have exactly k common alters. It is a measure of the shared “friendliness of friends”. The geometrically weighted edgewise shared partner (GWESP) statistic, conditional on the θ parameter, is

$${\text{gwesp}}_{\theta }(\mathbf{y})\equiv e^{\theta }\sum _{i=1}^{N_W-2}[1-{(1-e^{-\theta })}^i]{\text{EP}}_i(\mathbf{y})\theta \ge 0.$$ (12)

The GWESP is an aggregate measure of local clustering or the overall “inwardness” of ties. The parameter θ controls just how local the clustering needs to be. If θ = 0 an edge with one shared partner counts the same as an edge with two or more shared partners. If θ > 0 an edge with one shared partner counts less than an edge with two or more shared partners. So large values of θ mean that very tight clustering is highly weighted and loose clustering is emphasized less. These terms have been developed for ERGM by Snijders et al. (2006) and Hunter and Handcock (2006).

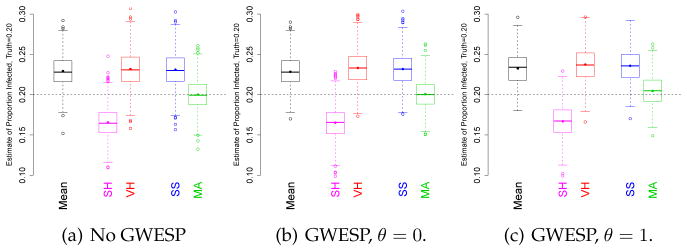
Real-world networked populations over which RDS will be applied may be expected to have higher levels of transitivity than that produced by monadic and dyadic effects. To investigate the relative performance of the estimator in populations with higher transitivity, we generate networks with monadic and dyadic statistics similar to those considered in the primary analysis but with higher transitivity as measured by the GWESP statistic. Because of the computational complexity of GWESP terms on large networks, and to test the correction for seed bias under model misspecification, we consider the populations with (N = N_W = 1000), high homophily (H = 2), activity ratio 1 (DA = 1) and biased selection of seeds (all infected), a condition under which μ̂_MA is approximately unbiased.

We introduce elevated transitivity by inducing increased shared partnerships in the simulated networks. In particular, we add a gwesp_θ(y) term to model (10) to control the rate of shared partnerships of nodes sharing a tie (i.e. nested triangle structures), using sufficient statistic (12). We compute the expected value of this statistic in the original (No GWESP) condition, then inflate that value by a factor of 10. The new population of networks is generated from an ERGM with the resulting set of sufficient statistics: all other statistics are held at their previous values and the GWESP statistic set to the inflated value. In addition, so as to not confound differences in transitivity and differences in degree distribution, we condition the GWESP model on the exact sequences of degrees in the No GWESP networks. The two levels of GWESP considered differ in the θ parameter of (12).

Figure 2 compares the same estimators as in Figure 1. The first panel presents a comparison condition in which GWESP is not elevated. The middle panel consider populations with gwesp₀(y) ten times that in the original. A value of θ = 0 means that the statistic measures the number of pairs of people that are connected both by a direct edge and by a two-path through another person (that is, the number of edges minus the number of edges connected by no two-paths). As can be seen, the performance of μ̂_MA is little effected by the increased transitivity. The right panel compares populations with ten times gwesp₁(y). A value of θ = 1 means that the statistic weighs up the connectedness of edges with more weight on the terms with more shared partners. In this case μ̂_MA has modest positive bias (0.46%) and similar variance compared to the estimators on the original populations.

Fig. 2.

Comparison of performance of five RDS estimators when the network working model mis-specifies the transitivity. The populations in the left panel do not have elevated transitivity. The middle panel networks have GWESP with θ = 0 elevated by a factor of 10, with respect to the left panel while the right increases the GWESP statistic with θ = 1 by a factor of 10. Results from 1000 simulations.

4.4. Evaluation of the Uncertainty Estimator

We illustrate the performance of the proposed bootstrap standard error estimator by comparing five critical cases. We treat the cases in Figure 1, as well as a case in which we expect the estimator to perform poorly. The initial sample can be selected either independent of infection status (denoted “No”in the bias column of Table 1) or all from within the infected subgroup (“Initial” bias). We also introduce referral bias where all infected alters are 20% more likely to be referred than uninfected alters (“Referral” bias). We induce referral bias in the absence of seed bias.

In each case, we use 500 bootstrapped re-samples for each of 200 simulated RDS samples. The parameters of the samples, observed standard errors of simulated estimators, average estimated standard errors, and coverage rates of nominal 95% and 90% confidence intervals based on the quantiles of the Gaussian distribution are given in Table 4.

Table 4.

Observed (simulation) standard errors of estimates, and average bootstrap standard error estimates, along with coverage rates of nominal 95% and 90% confidence intervals for procedure given in Section 3.4 for varying sample proportion, homophily H, and activity ratio DA, and for various biases in the sample selection process. Observed standard errors are based on 200 samples. Bootstrap standard errors are the average bootstrap standard error estimates over the same 200 samples. Nominal confidence intervals are based on quantiles of the Gaussian distribution.

% sample	homoph. H	DA	sample bias	SE observed	SE bootstrap	coverage 95%	coverage 90%
5%	1	1	No	0.0200	0.0194	94.0%	86.1%
50%	1	2	No	0.0100	0.0103	95.4%	91.7%
5%	2	1	Initial	0.0321	0.0298	92.0%	85.5%
50%	2	2	Initial	0.0141	0.0162	98.1%	93.7%
5%	2	1	Referral	0.0388	0.0325	81.5%	69.0%

The magnitudes of the average bootstrap standard error estimates are quite close to the observed values in the first four cases, and the coverage rates in the cases without referral bias are very close to their nominal values. The last row of Table 4 illustrates the poor performance of the estimator in the case of extreme referral bias. In this case, the estimator μ̂ _MA has positive bias (4.23%), leading to lower coverage rates of the nominal intervals.

5. Application to HIV prevalence in Hidden Populations

We apply our estimator to data collected in 2007 among injecting drug users (IDU) in Mykolaiv, Ukraine. The HIV epidemic in the Ukraine is one of the most severe in Europe, and still growing. As of 2009, the adult HIV prevalence was estimated at 0.86% (Ukrainian AIDS Centre, 2009). Ukraine’s epidemic is most severe among injecting drug users and their sexual partners, who account for the majority of new infections (United States Agency for International Development, 2010). The data we consider here were collected as part of a series of studies of IDU across major Ukrainian cities in 2007 (Kruglov et al., 2008). We focus on the data collected in Mykolaiv because the contacts available to the researchers were part of an HIV-based program, and all seeds in this sample were HIV positive.

This study began with 6 seeds and continued until wave 10, with 31 samples from wave 10, and a total of 260 samples. The average wave number was 6.1. The homophily based on HIV status for the population is estimated to be H = 1.98 and the activity ratio is estimated to be 0.72 (estimates computed using the R package RDS, Handcock et al. (2009)).

Although the size of the population was not known precisely, an estimated range of population sizes is available through scale-up and multiplier methods (Kruglov et al., 2008; UNAIDS/WHO, 2003). We chose a population size, N = 4000, near the low end of this range. The variability of population size estimates is quite large, with a point estimate closer to 8000 in 2008 (Berleva et al., 2010)). We used sensitivity analysis to verify that population size 4000 is sufficiently large that our estimates are insensitive to increased population size.

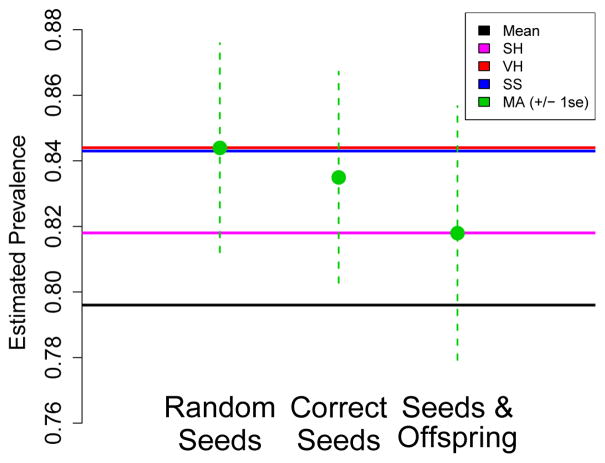
We compare estimates for this application based on the previous estimators (μ̂_SH, μ̂_VH, μ̂_SS) as well as three variants of μ̂_MA, summarized in Figure 3. Because computing μ̂_MA involves simulating RDS with specified characteristics, we can consider different versions of the estimator, based on which features of the observed sampling structure are matched. We therefore compare three estimates based on matching the following features to the observed data:

Fig. 3.

HIV prevalence estimates for injecting drug users in Mykolaiv, Ukraine, 2007. Three versions of μ̂_MA are considered, represented by the points with vertical error bars. Four estimators μ̂_SH, μ̂_VH, μ̂_SS, and the sample mean, are represented as horizontal lines for ease of comparison with all three values of μ̂_MA.

1. Random Seeds: Do not match initial sample distribution. Treat initial sample proportional to degrees.

2. Correct Seeds: Match seeds to observed seeds in the data.

3. Seeds & Offspring: Match seeds to observed seeds in the data. Also, match the numbers of recruits (offspring) by wave and infection status.

The first (a) is used as comparison only, and does not adjust for seed bias. As illustrated in Figure 3, this results in an estimate very close to that given by μ̂_SS and μ̂_VH (μ̂_VH = 0.844, μ̂_SS = 0.843, μ̂_MA = 0.845). Variant (b) is the standard variant developed in this paper, which results in the second estimate in Figure 3, μ̂_MA = 0.837. This adjustment is in the direction we would expect, decreasing the prevalence estimate, corresponding to down-weighting the group over-represented in the seeds. The difference between (1) and (2) shows the impact of adjusting for seed bias in this setting. The modest magnitude of this adjustment can be partially attributed to the larger number of sample waves, relative to the homophily level. Also, in additional simulation studies (not shown here), seed selection biased in favor of the majority group resulted in less bias in estimates than seed selection biased in favor of minority groups. Therefore, the high observed prevalence likely also contributed to the smaller effect, compared to our simulation study.

The third condition (c) highlights the flexibility and possibilities for extensions of μ̂_MA. We note that in these data, infection groups differed in their recruitment behavior. Some differences in recruitment behavior have been referred to as differential recruitment effectiveness in Heckathorn (2007), as well as in Tomas and Gile (2011). This is a pattern in which one group systematically recruits more effectively than another group. In this case, however, the pattern was more complex. On average, infected and uninfected participants did not vary greatly in their recruitment effectiveness. However, uninfected participants in the early waves of the study recruited disproportionately few additional participants, as illustrated in Table 5. Because of the branching nature of the sampling, this resulted in a dramatic under-representation of uninfected IDU in the survey. To correct for this, however, we needed to estimate and replicate offspring distributions varying by both infection status and survey wave.

Table 5.

Average number of successful recruitments per recruiter by wave and infection status of recruiter (with number of recruiters in parentheses). Uninfected recruiters were rare and unsuccessful in early waves, contributing to under-representation of uninfected participants in the sample. There were no uninfected participants in waves 0 (seeds) or 3.

	Recruiter	Recruiter
Wave	Uninfected (N)	Infected (N)
10	0.00 (7)	0.00 (24)
9	0.93 (14)	0.75 (24)
8	1.25 (8)	1.08 (26)
7	1.71 (7)	1.10 (20)
6	0.86 (7)	1.05 (20)
5	1.00 (4)	1.28 (18)
4	0.50 (4)	0.95 (21)
3	− (0)	1.67 (15)
2	0.00 (1)	1.07 (14)
1	0.00 (1)	1.15 (13)
0 (Seeds)	− (0)	2.33 (6)
Total	0.89 (53)	0.99 (217)

We therefore applied a version of μ̂_MA modified to reflect the empirical offspring distribution by wave and infection status. In most cases, this required simply assigning an offspring distribution equal to the empirical offspring distribution by wave and infection status. For uninfected recruiters in wave 3, we used averaged empirical values from waves 2 and 4. For waves 10 and beyond, we replicated the empirical results from wave 9. Whenever a simulated recruiter did not have enough eligible alters to allow for the number of recruits selected from the appropriate distribution, we assigned any unfulfilled recruitments to the next active recruiters of the same infection status with fewer than 3 assigned recruits. This is straight-forward to apply in our model-assisted setting and illustrates how this approach allows the approximation to the sampling design to be improved using available information.

The results of this analysis are illustrated in the third bar of Figure 3. The resulting estimate, 0.817, was substantially lower than the earlier estimates, suggesting the offspring distribution had a substantial impact on the resulting estimates.

6. Discussion

In this article we introduce a new approach to estimation based on RDS data that uses a working model for the underlying networked population to more accurately estimate the inclusion probabilities necessary for design-based inference.

We demonstrate that this approach allows us to correct for features addressed by earlier estimators, as well as features not previously addressed. In particular, differential sampling probabilities based on nodal degrees are addressed by the proposed estimator and also by earlier RDS estimators (Gile, 2011; Heckathorn, 2007; Salganik and Heckathorn, 2004; Volz and Heckathorn, 2008). Finite population effects are addressed by the proposed estimator and also by Gile (2011). In addition, our proposed estimator is able to adjust for the convenience sample of seeds, a feature not accounted for in any previous approach.

We apply this approach to obtain improved estimation of HIV prevalence in an IDU population in the Ukraine. We improve the approximation to the actual RDS process resulting in improved estimates, and compute associated measures of uncertainty. We also show the flexibility of the working model approach. It allows for additional information available in a particular application to be incorporated via the ERGM framework, and leverages recent advances in that area (Handcock et al., 2008; Snijders et al., 2006) to fit the models conditional on z and d.

Note that the finite-population correction of our approach requires the specification of a working population size. If the hidden population size is unknown, but sufficiently large, the estimator is not sensitive to the working population size. This is likely the case for most RDS samples; Gile et al. (2012), for example, do not find appreciable finite population effects in any of several traits across 12 study populations in the Dominican Republic.

Another important assumption is the form of the social network working model. Our estimator relies on a simple model, not because we believe it to be strictly accurate, but because we expect it to capture the network features most important to the sampling process, and because it is feasible to estimate from the available data. Our sensitivity analysis suggests that the approach may still perform reasonably under some forms of working model misspecification, although its performance may be degraded in some cases.

Several extensions of this approach are possible. First, if data on the characteristics of all alters are not available, we may wish to estimate the sum of cross-group ties (g(y, x)) based on referral patterns. Such an estimate is used in the application to HIV prevalence estimation (Section 5).

Our approach can also be extended to include additional measurable features of the network working model or sampling process, such as homophily on neighborhood of residence or bias in the passing of coupons. We illustrate one such extension in Section 5, in which we observe an aberrant pattern of recruitment by infection status, and adapt the estimator to condition on this pattern. Note that the resulting estimate is very close to that given by μ̂_SH. This is consistent with results in Tomas and Gile (2011) indicating that μ̂_SH is not as susceptible to bias induced by differential recruitment effectiveness as μ̂_VH or μ̂_SS.

It is important to note that this estimator does not remove the need for strong assumptions regarding RDS data. One critical assumption is that we are able to measure all the important features of the underlying population and sampling procedure. Consider, for example, the case of biased sampling by an invisible characteristic: if drug users who are interested in quitting are more likely to participate in the study, this status may not be visible to their contacts. Thus recruiters could not be asked their numbers of potential quitter contacts, and the rate of recruitment of this group would be confounded with their number in the target population thwarting valid inference on their population proportion. A more mundane challenge arises from reporting inaccuracy. Gile et al. (2012) show that test-retest variation in degree reporting can induce important differences in estimates. There are also network structures on which this estimator, and all others currently available, may result in very poor estimates. In particular, populations with sub-groups that are disconnected or connected weakly are not conducive to inference based on assuming a random walk on a network. In such a case, the final sample would be (nearly) completely dependent on the composition of the initial convenience sample. If the groups corresponded exactly to a measured characteristic, such as street-based versus venue-based sex workers, a version of the proposed estimator would have an extremely large variance and variance estimate. If the grouping was latent, as in high risk verses low risk MSM, the sample would contain very little information about the relative sizes of the groups and the variance estimate would be a substantial under-estimate. Finally, the network models that may be fit to RDS data as currently collected are limited by the branching structure of the sampling. Ties between participants who do not recruit each other are not observed, making triadic terms such as those in Snijders et al. (2006) impossible to observe or identify in a model.

The strongest contribution of the proposed method is its flexibility. It is able to retain the finite population corrections available in the successive sampling estimator of Gile (2011), and the robustness to differential recruitment effectiveness available in the Salganik-Heckathorn estimator, while reducing bias due to the composition of seeds, and potentially adjusting for other measurable features of the study population or sample.

We intend to make code available for these procedures in the R package RDS on CRAN (Handcock et al., 2009; R Development Core Team, 2012).

Appendix: Estimation Procedure

This appendix details the estimation procedure of Section 3. Specifically, we propose the following algorithm to compute the new estimator μ̂_MA of μ.

1. Estimate the following according to their empirically observed values:

   • Sample size n

   • Number of seeds n^seeds, and degree and infection status of seeds, given by ${\mathbf{T}}^{\mathit{seeds}}=\{{\mathbf{T}}_{ij}^{\mathit{seeds}}\}$, where ${\mathbf{T}}_{ij}^{\mathit{seeds}}$ represents the number of seeds with degree i and infection j, i ∈ 1… N_W − 1, j ∈ {0, 1}.

   • Offspring distributions p^s, where ${\mathbf{p}}_i^s$ = the proportion of the sample with i offspring, i = 0, 1,…, maximum number of coupons.

2. Estimate:

   $${\widehat{\pi }}_i^0=\frac{d_i}{N_W}\sum _{j=1}^{N_W}\frac{S_j}{d_j},i:S_i=1.$$

3. For r = 1… h:

   1. Estimate:

      $$\begin{array}{ll}\hfill {\stackrel{\sim }{T}}_{kl}^r& =\frac{1}{N_W}\sum _{i=1}^{N_W}\frac{S_i\mathbb{I}(d_i=k,z_i=l)}{{\widehat{\pi }}_i^{r-1}}\hfill \\ \hfill \stackrel{\sim }{g}{(\mathbf{y},\mathbf{x})}^r& =\sum _{i=1}^{N_W}\frac{S_i(x_i(1-z_i)+(d_i-x_i)z_i)}{2{\widehat{\pi }}_i^{r-1}}\hfill \end{array}$$

   2. Compute the ERGM parameter η in the model (2) conditional on T̃^r and g̃(y, x)^r (Gile and Handcock, 2013). Denote the estimate by η^r. This step is conducted using the statnet R package (Handcock et al., 2003).

   3. Simulate M₁ networks according to the distribution given by η̂^r, T̃^r, and g̃(y, x)^r (Gile and Handcock, 2013).

   4. Simulate M₂ RDS samples from each of the M₁ networks in the previous step, according to sampling parameter 𝒮 = {n, T^seeds, p^s}. Let $U_{kl}^r$ represent the number of times a node of degree k and infection l is sampled, over all M = M₁ × M₂ samples.

   5. Estimate ${\widehat{\pi }}_i^r\forall i$ : S_i = 1 in a manner similar to Fattorini (2006) and Gile (2011):

      $${\widehat{\pi }}_i^r=\frac{U_{d_i{z}_i}^r+1}{M·T_{d_i{z}_i}^r+1}$$

4. Let ${\widehat{\pi }}_i={\widehat{\pi }}_i^h$

5. Estimate

   $${\widehat{\mu }}_{MA}=\frac{{\sum }_{i=1}^{N_W}\frac{S_i{z}_i}{{\widehat{\pi }}_i}}{{\sum }_{i=1}^{N_W}\frac{S_i}{{\widehat{\pi }}_i}}$$

The simulations in this paper are based on r = 3 iterations, each including M₁ = 25 network samples and M₂ = 20 RDS samples from each network. In general, we recommend at least M₁ = 25, M₂ = 20 and r = 3. Estimation time scales with sample size, population size, and M. In our simulations estimates with N_W = 1000 require about 3 minutes on a personal computer. The estimates with N_W = 10000 require about 10 minutes on a personal computer. In practice, these parameters can be adjusted for desired precision in the solution to (7).