Joint Reconstruction of Multi-channel, Spectral CT Data via Constrained Total Nuclear Variation Minimization

Abstract

We explore the use of the recently proposed “total nuclear variation” (TV_N) as a regularizer for reconstructing multi-channel, spectral CT images. This convex penalty is a natural extension of the total variation (TV) to vector-valued images and has the advantage of encouraging common edge locations and a shared gradient direction among image channels. We show how it can be incorporated into a general, data-constrained reconstruction framework and derive update equations based on the first-order, primal-dual algorithm of Chambolle and Pock. Early simulation studies based on the numerical XCAT phantom indicate that the inter-channel coupling introduced by the TV_N leads to better preservation of image features at high levels of regularization, compared to independent, channel-by-channel TV reconstructions.

1 Introduction

In recent years, great strides have been made in the development of iterative reconstruction algorithms for x-ray CT. Compared to the analytic algorithms that are employed on most clinical scanners, iterative algorithms offer a number of advantages [1, 2, 3, 4], including the ability to incorporate prior knowledge about the object into the reconstruction model [5, 6]. Typically, the “optimal” image is identified as the minimizer of a cost function containing a data-fidelity term and regularization. The latter term can help prevent overfitting to noisy data, select a unique solution to an ill-posed inverse problem, and encourage desired properties in the image (e.g. smoothness).

The total variation is one of the most widely used regularizers in imaging inverse problems. It was originally proposed by Rudin, Osher, and Fatemi for noise removal [7], but it has since been applied to a multitude of other problems, including deblurring [8], demosaicking [9], super-resolution [10], and tomographic reconstruction [11]. The success of the TV is due to several reasons. It was designed with the explicit intention of preserving sharp discontinuities while suppressing noise, and it is one of few convex penalties with this property [12]. Additionally, others have shown that TV regularized reconstruction algorithms can sometimes yield accurate reconstructions from highly undersampled measurement data [11]. This phenomenon may be partially explained in CT by the fact that images tend to be approximately piecewise constant, and the TV promotes sparsity in the image gradients.

A topic that has received more attention recently is how to generalize the total variation to multi-channel images [13, 14, 15, 16]. A multi-channel image may be viewed as a stack of scalar images or as a vector field, where each point in space corresponds to multiple contrast values. This situation arises in many contexts, such as color imaging and spectral CT. The latter will be the focus of this work. The most straightforward way to generalize the total variation to multi-channel images is to sum up the total variation of the individual channels. This technique, which we refer to as “channel-by-channel” TV, has been employed for spectral CT reconstruction previously [6, 17]. A major theoretical disadvantage of this approach is that it penalizes each image channel independently, despite the fact that there are generally large inter-channel correlations. For example, a simple visual inspection of a pair of low and high kVp images from the same phantom sugggests that there is a high degree of similarity (See Figure 1). Contrast changes appear to follow the same pattern, edges are in the same locations, and textures are likely to be similar. If some of these properties could be captured by a generalized, TV-like prior, then perhaps it would be advantageous to reconstruct both channels in tandem.

Figure 1.

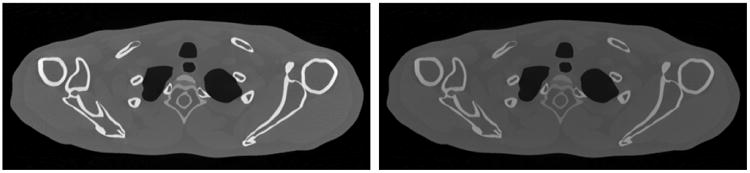
These 80 kVp (left) and 140 kVp (right) reconstructions of the numerical XCAT phantom suggest that images derived from common projection data acquired with different energy spectra are correlated. In particular they appear to have a very similar edge structure.

It turns out that there are many ways to generalize the TV to multi-channel images, but we will focus on a specific choice, which has been referred to as the “total nuclear variation” (TNV) [16]. We had previously suggested the TNV prior [18], unaware that at least two earlier works had already discussed it in the context of color image restoration [15, 16]. The TNV penalty encourages all of the image channels in a multi-channel reconstruction to have common edge locations and for their gradient vectors to point in a common direction. Equivalently, we can say that it has a bias for image channels that have parallel level sets [19]. The notion that multi-channel images should have gradient fields that share a common direction has been discussed in several other works on color image processing [20, 21, 19].

The development of effective regularization strategies is particularly important for spectral CT for a variety of reasons. Since the detected photons are divided into multiple energy bins, the SNR of each channel is immediately reduced in proportion to the square root of the number of energy channels [22]. Further, the multi-energy data is typically used to derive quantitative, basis-material images through a process called basis-material decomposition (BMD), which may occur before [23], during [24], or after [25] the image reconstruction process. The ability to form quantitative images through BMD is perhaps the most compelling advantage of spectral CT. Unfortunately, the decomposition is usually quite ill-conditioned, which results in a substantial amplification of noise. This already poses significant challenges for protocols involving a two-material decomposition and will be even worse when trying to handle three or more basis materials [22]. Therefore, whether the BMD is performed in the sinogram domain or the image domain, it is important to mitigate as much noise as possible during the reconstruction. Several other works have proposed denoising methods which may be applied in the image domain [26] or the sinogram domain [27]. These approaches have the benefit of being fast and plugging into an already existing reconstruction framework, but we believe there will always be some advantages to building noise suppression into the reconstruction model. This allows the greatest flexibility in modeling physical and statistical factors in projection space while simultaneously enforcing priors in image space. Aside from noise suppression, multi-channel generalizations of the total variation may be particularly useful for reconstructing sparse-view photon counting CT data when detector limitations are the bottleneck in acquisition time [6].

In this work, we develop an iterative reconstruction model for jointly reconstructing multi-channel spectral CT data with the proposed TNV prior. Using Chambolle and Pock's primal-dual algorithm (CPPD) [28], we derive update equations for two different optimization programs. The first minimizes the proposed TNV subject to a constraint on the euclidean data-divergence, and the second minimizes the more primitive channel-by-channel TV with the same data constraint. This approach allows us to fairly compare these two generalized TV penalties over a variety of different smoothing levels, by adjusting a single parameter. We believe that in practice there may be good reasons for performing the basis-material decomposition either before or after the image reconstruction process, so we test the TNV in both domains. In the first simulation study, we consider a 5-bin photon counting system and jointly reconstruct the corresponding five logged sinograms. We will refer to the logged energy-bin data hereafter as the “energy basis.” In the second study, we investigate the impact of the TNV in the “material basis.” We simulate dual kVp data and perform a maximum-likelihood material decomposition to obtain a pair of bone and soft-tissue sinograms. We simultaneously reconstruct all four sinograms (low, high, bone, and soft-tissue) using both the channel-by-channel TV and TNV optimization programs. We hypothesize that this hybrid approach of co-reconstructing the dual kVp data with the decomposed sinograms may help control noise in the material images by coupling them to the much higher SNR energy basis images.

2 Theory

2.1 Notation and definitions

In this section, we outline the notation that we will use for the remainder of the document. We adopt a somewhat unconventional set of indexing rules in order to maintain as much clarity as possible in describing algebraic operations on vectors with multiple dimensions of spatial and spectral information.

Single-channel images

Consider a discretized 2D image u ∈ I where I = ℝ^M·N is a finite dimensional vector space equipped with an inner product

$${\langle u,v\rangle }_I=\sum _{i,j}u(i,j)v(i,j),u,v\in I.$$ (1)

We use the convention u(i, j) to refer to a particular pixel, where i and j specify the row and column indices and u(i, j) ∈ ℝ is a discretized version of some continuous image function u(x, y). The quantity ∇u is a vector in the space G = I×I, where the operator ∇u : I ↦ G represents a discrete approximation to the gradient. At each pixel location we define the quantity (∇u)(i, j) ∈ ℝ² as

$$(\nabla u)(i,j)=\left(\begin{array}{c}{(\nabla u)}^x(i,j)\\ {(\nabla u)}^y(i,j)\end{array}\right),$$ (2)

Where

$${(\nabla u)}^x(i,j)=\{\begin{array}{cc}u(i+1,j)-u(i,j)& j<N\\ 0& j=N\end{array}$$ (3)

$${(\nabla u)}^y(i,j)=\{\begin{array}{cc}u(i,j+1)-u(i,j)& i<M\\ 0& i=M\end{array}.$$ (4)

We also define an inner product in G,

$${\langle \mathit{v},\mathbf{z}\rangle }_G=\sum _{i,j}{v}^x(i,j)z^x(i,j)+v^y(i,j)z^y(i,j),\mathit{v},\mathbf{z}\in G.$$ (5)

Note that we use bold font to indicate that each spatial location (i, j) maps to a vector of values. Further, we will need a discrete divergence operator div z : G ↦ I, which is chosen to be the negative transpose of the gradient operator, defined by

$${\langle \nabla u,\mathbf{z}\rangle }_G=-{\langle u,\text{div}\mathbf{z}\rangle }_I.$$ (6)

Lastly, we define the mixed ℓ₁/ℓ₂-norm in G as

$${\Vert \mathbf{z}\Vert }_{1,2}=\sum _{i,j}{\Vert \mathbf{z}(i,j)\Vert }_2\mathbf{z}\in G,$$ (7)

indicating that we take an ℓ₁-norm over the spatial indices (i, j) and an ℓ₂-norm of each 2-vector z(i, j). This mixed-norm notation is often used in the literature on sparse regression and occasionally to compactly define the isotropic total variation [29],

$$\text{TV}(u)={\Vert \nabla u\Vert }_{1,2}.$$ (8)

Multi-channel images

Now, we consider a discrete image u ∈ ℐ with L spectral or information channels,

$$\mathbf{u}(i,j)=\left(\begin{array}{c}{u}_1(i,j)\\ u_2(i,j)\\ ⋮\\ u_L(i,j)\end{array}\right),$$ (9)

where ℐ = ℝ^L·M·N·. The quantity u is a discretized version of some continuous vector field u(x, y), such as an RGB color image. We also define an inner product in ℐ,

$${\langle \mathbf{u},\mathbf{v}\rangle }_{\mathcal{I}}=\sum _{\ell }\sum _{i,j}{u}_{\ell }(i,j)v_{\ell }(i,j)\mathbf{u},\mathbf{v}\in \mathcal{I},$$ (10)

where the subscript ℓ denotes a particular image channel. Since u is the discrete analog of a vector field, we can also define the discrete Jacobian, Ju : ℐ↦𝒢, which generalizes the gradient operator to vector fields. In particular we have

$$(J\mathbf{u})(i,j)=\left(\begin{array}{cc}{(\nabla {\mathbf{u}}_1)}^x(i,j)& {(\nabla {\mathbf{u}}_1)}^y(i,j)\\ {(\nabla {\mathbf{u}}_2)}^x(i,j)& {(\nabla {\mathbf{u}}_2)}^y(i,j)\\ ⋮& \\ {(\nabla {\mathbf{u}}_L)}^x(i,j)& {(\nabla {\mathbf{u}}_L)}^y(i,j)\end{array}\right).$$ (11)

At every pixel (i, j), the sub-matrix (Ju) (i, j) fully characterizes the first-order derivatives of u, with each row consisting of the gradient vector of one of the L image channels. The quantity Ju is in vector space 𝒢=ℐ × ℐ = ℝ^(L×2) (M · N) with an inner product

$${\langle V,Z\rangle }_{\mathcal{G}}=\sum _{\ell }\sum _{i,j}{V}_{\ell }^x(i,j)Z_{\ell }^x(i,j)+V_{\ell }^y(i,j)Z_{\ell }^y(i,j)V,Z\in \mathcal{G}.$$ (12)

A element V ∈ 𝒢 is a discretized version of a tensor field V(x, y), so we use uppercase font to indicate that every spatial location (i, j) maps to a matrix. Again, we need an analog of the divergence operator Div Z : 𝒢 ↦ ℐ that is the negative transpose of J. It is constructed to satisfy

$${\langle J\mathbf{u},Z\mathbf{\rangle }}_{\mathcal{G}}=-{\langle \mathbf{u},\text{Div}Z\rangle }_{\mathcal{I}}.$$ (13)

We define the mixed ℓ₁/nuclear-norm as

$${\Vert Z\Vert }_{1,\ast }=\sum _{i,j}{\Vert Z(i,j)\Vert }_{\ast }Z\in \mathcal{G},$$ (14)

where ‖Z(i, j)‖_⋆ is referred to as the “nuclear norm” of matrix Z(i, j) and is equal to the sum of its singular values.

Linear imaging model

In this work we will assume that the reconstructed image u is related to the data vector g by the linear equation

$$\mathbf{g}=A\mathbf{u},$$ (15)

where g is a vector in the vector space 𝒟 ∈ ℝ^{L · K}, and K represents the total number of line integrals in our sinogram. The quantity g is formed by concatenating the sinograms of each channel, and the operator A : ℐ → 𝒟 is similarly formed by concatenating the projector model of each of the L channels.

$$\mathbf{g}=\left(\begin{array}{c}{A}_1{u}_1\\ A_2{u}_2\\ ⋮\\ A_L{u}_L\end{array}\right).$$ (16)

We define an inner product in 𝒟,

$${\langle \mathbf{g},\mathbf{q}\rangle }_{\mathcal{D}}\sum _{\ell }\sum _k{g}_{\ell }(k)q_{\ell }\mathbf{g},\mathbf{q}\in \mathcal{D}.$$ (17)

Just as with the image domain, we use subscripts to index over spectral channels and the index k in parenthesis to identifies a specific ray in the projection space.

2.2 The Scalar Total Variation

Total variation regularized CT reconstruction algorithms have been studied extensively due to the approximate gradient sparsity of CT images. Several works have demonstrated that such schemes may yield accurate reconstructions from highly undersampled projection data [30, 11, 31, 32, 6]. However, the success of these sparse-view reconstruction methods is highly task-dependent.

The anisotropic TV

The “anisotropic” TV is simply defined as the ℓ₁-norm of the derivative of the image u,

$${\text{TV}}_a(u)={\Vert \nabla u\Vert }_1=\sum _{i,j}{\Vert ({\nabla }_u)(i,j)\Vert }_1,$$ (18)

where it is useful to think of the ‖·‖₁ as a “sparsity-inducing” norm because it is a convex relaxation of ‖·‖₀.

The isotropic TV

Somewhat more common is the “isotropic” TV, which is defined in terms of the gradient-magnitude image,

$$\text{TV}(u)={\Vert \nabla u\Vert }_{1,2}=\sum _{i,j}{\Vert (\nabla u)(i,j)\Vert }_2.$$ (19)

This penalty function has similar properties to the anisotropic TV but is sometimes favored because it is rotationally invariant in the continuous setting. The anisotropic TV tends to favor horizontal and vertical edges [33].

2.3 Vectorial Total Variation

Now, we consider generalizing the TV to the ℳ-channel image u.

The channel-by-channel TV

The simplest way to extend the definition of the TV to this vector-valued image, u, would be to take the summation of the total-variation of each channel. This is given by

$${\text{TV}}_S(\mathbf{u})=\sum _{\ell =1}^L\text{TV}(u_{\ell }).$$ (20)

We will refer to this approach as the “channel-by-channel” TV because it imposes no coupling between image channels.

The Total Nuclear Variation

The proposed multi-channel generalization of the TV induces a tight coupling between image channels through a pixel-wise penalty on the rank of the Jacobian, Ju. This particular form, which we will call the “total nuclear variation” [16] is given by

$${\text{TV}}_N(\mathbf{u})={\Vert J\mathbf{u}\Vert }_{1,\ast }=\sum _{i,j}{\Vert (J\mathbf{u})(i,j)\Vert }_{\ast },$$ (21)

where ‖(Ju)_ℓ‖_⋆ = ‖σ⃗‖, and σ⃗ is a vector of the singular values of Ju. This same form has been independently proposed by at least three different authors since 2013 [15, 16, 18]. These authors have pointed out several nice properties of the TV_N. Similarly to the channel-by-channel TV, it is convex and rotationally invariant when defined on the space of continuous images. Additionally, for a single-channel image, it reduces exactly to the usual isotropic TV.

However, unlike the channel-by-channel TV, the TV_N couples the different image channels by encouraging common edge locations and alignment of their gradient vectors. We also point out the following interesting equivalence: two images have gradient fields that point in the same direction (up to a sign difference) if and only if they share the same set of level curves [19].

This gradient-coupling effect comes from the fact that the nuclear norm encourages rank sparsity in (Ju)_ℓ [34, 35] by. If pixel ℓ lies within a constant-valued region of all of the image channels then this Jacobian matrix will be entirely null-valued, and all of its singular values will be zero. Further, if all of the gradient vectors of the various image channels are parallel or anti-parallel, such as at a common edge, then the Jacobian will be rank one and thus have only one non-zero singular value. This is because parallel or anti-parallel vectors are not linearly independent. The fact that the TV_N treats parallel and anti-parallel vectors the same means that it is robust to contrast inversions. The connection between singular-value sparsity and gradient coupling is illustrated in Figure 2. In spectral CT, there may be edges that exist in some channels and not others, such as when imaging flowing contrast agents. This does not appear to present a problem for the TV_N penalty because it primarily encourages common edge directions and not common edge magnitudes. Therefore, there is no bias toward falsely propagating edges into channels where they do not belong.

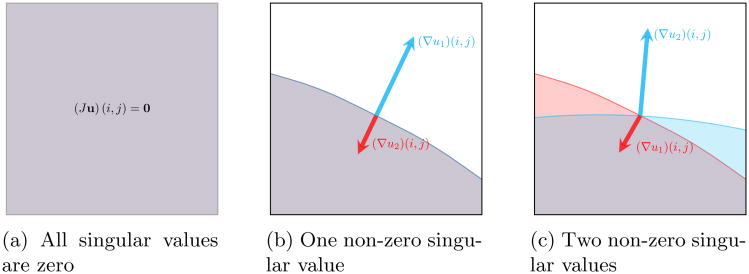
Figure 2.

This illustrates the relationship between the directionality of the gradient vectors of a 2-channel image and the singular values of its Jacobian. When both channels are constant valued, both singular values of the Jacobian are zero (a). If the gradient vectors are parallel or anti-parallel, one singular value is non-zero (b). Both singular values will be nonzero if the gradients have unique directions (c).

Converting to a “noise-balanced” image space

In spectral CT imaging it is often the case that certain channels are significantly noisier than others, and we have found that the total nuclear variation regularization is more effective if a noise-balancing transform is applied prior to reconstruction or denoising. Consider a two-channel image, ǔ, corrupted by zero-mean, Gaussian noise with variances ${\sigma }_1^2$ and ${\sigma }_2^2$ for channels 1 and 2, respectively. A common approach to denoising is to solve the following optimization problem:

$$\underset{\mathbf{u}}{min}\frac{1}{2}{\Vert u_1-{\check{u}}_1/{\sigma }_1\Vert }_2^2+\frac{1}{2}{\Vert (u_2-{\check{u}}_2)/{\sigma }_2\Vert }_2^2+\lambda \text{TV}(\mathbf{u}).$$ (22)

The quantity ǔ is the original noise corrupted image, and u is the denoised image. In the data-fidelity term, each channel is inversely weighted by the standard deviation of the noise. This weighting scheme is statistically motivated because it ensures that as λ approaches zero, the likelihood of the resultant image, ℒ(u|ǔ), is monotonically increasing. We find that it is advantageous when using the TV_N penalty to also incorporate this inverse standard-deviation scaling into the regularization term. Therefore, we can define a new scaled image as u′ = (u₁/σ₁, u₂/σ₂)^T and solve the following optimization problem:

$$\underset{{\mathbf{u}}^{\prime }}{min}\frac{1}{2}{\Vert {\mathbf{u}}^{\prime }-{\check{\mathbf{u}}}^{\prime }\Vert }_2^2+\lambda \text{TV}({\mathbf{u}}^{\prime }).$$ (23)

The scaling ensures that the global noise levels are the same in both image channels, and the modified optimization problem effectively incorporates this scaling into the data-fidelity term as well as the regularization. For image reconstruction, the same type of scaling would be applied to the sinogram data. In general, the projection data will not have a uniform noise level within a single energy channel, so we use some average measure of channel noise to determine the global scale factor. We find that this noise-balancing procedure is an important step, as it improves the noise suppression in multi-spectral images with unequal noise levels. Note we can also write down an equivalent constrained optimization problem,

$$\begin{array}{cc}\underset{{\mathbf{u}}^{\prime }}{min}& {\text{TV}}_N({\mathbf{u}}^{\prime })\\ \mathrm{s}.\mathrm{t}.& {\Vert {\mathbf{u}}^{\prime }-{\check{\mathbf{u}}}^{\prime }\Vert }_2\le \varepsilon ,\end{array}$$ (24)

where some mapping exists between λ and ε such that both schemes yield the same family of solutions.

3 Materials and methods

3.1 General reconstruction model

Assume we have a set of L sinograms, corresponding either to the directly measured energy channels of a spectral CT system or to the basis-material projections. We jointly reconstruct these channels by solving the following data-constrained optimization problem:

$$\begin{array}{cc}\underset{\mathbf{u}}{min}& \text{TV}(\mathbf{u})\\ \mathrm{s}.\mathrm{t}.& {\Vert A\mathbf{u}-\mathbf{g}\Vert }_W\le \epsilon ,\end{array}$$ (25)

where g is the multi-channel projection data related to u by the discrete fan-beam projection operator A. The TV term refers to either the channel-by-channel TV_S or the total nuclear variation TV_N. The norm on the data constraint ‖·‖_W is a weighted ℓ₂ norm, defined by

$${\Vert g\Vert }_W^2={\langle g,W_g\rangle }_{\mathcal{D}}.$$ (26)

This penalized weighted least squares (PWLS) data model is often used in CT reconstruction because when the weights are selected such that $W=K_{\mathbf{g}}^{-1}$, the data fidelity term corresponds to the likelihood function for Gaussian data with covariance K_g. The single adjustable parameter ε controls the balance between data-fidelity and regularity. By fixing ε we can directly compare reconstructions using the naïve channel-by-channel TV_S to our proposed TV_N subject to the same data fidelity constraint.

3.2 The Chambolle Pock Primal Dual Algorithm

In this section, we will provide an overview of the first-order, primal-dual algorithm of Chambolle and Pock [28] and demonstrate how to apply it to our reconstruction model. For a tutorial on how to apply the CPPD algorithm to various CT reconstruction schemes, we refer the reader to Sidky et al [36].

The proximal mapping

In order to describe the CPPD algorithm, we must first introduce the concept of a proximal mapping. For a function f(x), the proximal mapping is defined by

$${\mathbf{\text{prox}}}_f(x)=\underset{u}{argmin}f(u)+\frac{1}{2}{\Vert u-x\Vert }_2^2.$$ (27)

It will also be useful to consider the proximal mapping of the scaled function λf, which can be written as

$${\mathbf{\text{prox}}}_{\lambda f}(x)=\underset{u}{argmin}f(u)+\frac{1}{2\lambda }{\Vert u-x\Vert }_2^2.$$ (28)

The proximal mapping can be interpreted as a generalized projection operator because for the special case that f(x) is an indicator function, then it is a euclidean projection. For an extensive overview of the prox operator and applications, refer to Parikh and Boyd [37].

A general saddle-point problem

Let X and Y be two finite-dimensional, real vector spaces. The CPPD algorithm is designed to solve the saddle-point problem described by

$$\underset{x\in X}{min}\underset{y\in Y}{max}\langle Kx,y\rangle -F(y)+G(x),$$ (29)

where F(y) and G(x) are convex functions with very simple proximal mappings, and K is a general linear operator. In particular, the proximal mappings associated with F and G should have a closed form or be easily solvable to high precision. It turns out that many interesting image processing and reconstruction problems fit this description, including the reconstruction model described in the previous section. The CPPD update equations are summarized by Algorithm 1. The parameters θ,σ,τ can be thought of as step-size parameters that affect convergence speed but not the final solution. In this work, we use θ = 1.0 and $\sigma =\tau =\frac{1}{\Vert K\Vert }$. Though Chambolle and Pock only prove convergence when the strict inequality στ‖K‖² < 1 is satisfied, we find that setting στ‖K‖² = 1 causes no stability problems. A similar observation is made in [36]. The quantity ‖K‖ is the “spectral norm” of the operator K, which is equivalent to its largest singular value. As in [36] we use the power method to iteratively compute ‖K‖, which relies only on matrix-vector multiplications. The CPPD algorithm has close ties with several other popular algorithms, including ADMM, split-bregman, and proximal-point. This is further discussed in [28].

Algorithm 1 CPPD Algorithm
1:	Initialize: θ∈ [−1, 1], στ‖K‖2 < 1, x(0), x̄(0)∈ X, y(0) ∈ Y	▹‖K‖ = σmax(K)
2:	repeat
3:	y(k+1) = proxσF(y(k) + σKx̄(k))
4:	x(k+1) = proxτG(x(k) − τKTy(k+1))
5:	x̄(k+1) = x(k+1) +θ(x(k+1) − x(k))
6:	until x(k+1), y(k+1) = x(k) y(k)	▹ stop when convergence criteria met

Applying the CPPD algorithm to VTV reconstruction

Now we will outline how the CPPD algorithm can be applied to the data-constrained optimization problem of (25). First we rewrite (25) as

$$\underset{\mathbf{u}}{min}\text{TV}(\mathbf{u})+{\delta }_{\epsilon }(A\mathbf{u}-\mathbf{g}),$$ (30)

where the indicator function δ_ε(x) is defined by

$${\delta }_{\epsilon }(x)=\{\begin{array}{cc}0& {\Vert \mathbf{x}\Vert }_W\le \epsilon \\ \infty & {\Vert \mathbf{x}\Vert }_W\le \epsilon \end{array}.$$ (31)

In the subsequent steps we will recast this objective into a saddle-point problem by dualizing the VTV and data-constraint terms. All of the following transformations follow from the definition of the Fenchel conjugate. More details on the Fenchel conjugate, also referred to as the Legendre transform, are in the appendix. First, we introduce an auxiliary variable q and rewrite the data constraint as

$${\delta }_{\epsilon }(A\mathbf{u}-\mathbf{g})=\underset{\mathbf{q}}{max}{\langle \mathbf{q},A\mathbf{u}-\mathbf{g}\rangle }_{\mathcal{D}}-\epsilon {\Vert W^{-1/2}\mathbf{q}\Vert }_2.$$ (32)

Similarly, we can rewrite the TV penalty function as an optimization over another auxiliary variable, z. For the channel-by-channel TV_S, we have

$${\text{TV}}_S(\mathbf{u})=\underset{Z}{max}{\langle J\mathbf{u},Z\rangle }_{\mathcal{G}}-{\delta }_{\mathcal{S}}(Z),$$ (33)

where the definition of the set 𝒮 is given by

$$𝒮=\{Z\in \mathcal{G}:{\Vert Z_{\ell }(i,j)\Vert }_2\le 1\forall i,j,m\}.$$ (34)

The proposed TV_N penalty function can be expressed as:

$${\text{TV}}_N(\mathbf{u})=\underset{Z}{max}{\langle J\mathbf{u},Z\rangle }_{\mathcal{G}}-{\delta }_{\mathcal{N}}(Z),$$ (35)

where the set 𝒩 is defined by

$$\mathcal{N}=\{Z\in \mathcal{G}:{\sigma }_{max}(Z(i,j))\le 1\forall i,j\}.$$ (36)

The quantity Z(i, j) is an L × 2 matrix, with the same dimensions as the Jacobian derivative at pixel (i, j), and σ_max is its largest singular value. These transformations, which are detailed in Appendix A, allow us to write our original VTV reconstruction model as a primal-dual, saddle-point problem,

$$\underset{\mathbf{u}}{min}\underset{Z,\mathbf{q}}{max}{\langle J\mathbf{u},Z\rangle }_{\mathcal{G}}+{\langle \mathbf{q},A\mathbf{u}-\mathbf{g}\rangle }_{\mathcal{D}}-{\delta }_{\mathcal{S}/\mathcal{N}}(Z)-\epsilon {\Vert W^{-1/2}\mathbf{q}\Vert }_2,$$ (37)

where the indicator function is either δ_𝒮 for the channel-by-channel TV_S or δ_𝒩 for the proposed TV_N. We can directly apply the CPPD update equations of Algorithm 1 by making the following assignments.

$$\begin{array}{c}x\to \mathbf{u},y\to \left(\begin{array}{c}\mathbf{q}\\ Z\end{array}\right),K\to \left(\begin{array}{c}A\\ J\end{array}\right)\\ F(\mathbf{q},Z)={\delta }_{\mathcal{S}/\mathcal{N}}(Z)-\epsilon {\Vert W^{-1/2}\mathbf{q}\Vert }_2-\langle \mathbf{q},\mathbf{g}\rangle ,G(\mathbf{u})=0\end{array}$$ (38)

The resulting update equations are given by Algorithm 2. The operator Π_𝒮/𝒩 is a Euclidean projection onto the set 𝒮 or 𝒩, and the Div operator is the negative transpose of the discrete Jacobian operator J. Note that the q-update is written in terms of the proximal map of the function F_q, which we define as F_q = ‖W^(−1/2)q‖₂. While there does not appear to be a closed-form expression for this proximal map, it can be reduced to a very simple scalar optimization problem as long as W is diagonal. This is detailed in the appendix along with an efficient method for performing the Euclidean projection in the primal variable update.

Algorithm 2 Data-constrained VTV Update Equations
1:	Initialize:	$\theta =1,\sigma \tau {\Vert \left(\begin{array}{c}A\\ D\end{array}\right)\Vert }_2^2=1,(\mathbf{u},\overline{\mathbf{u}},\mathbf{q},\mathit{Z})\to \mathbf{0}$
2:	repeat
3:	Z(k+1) = П𝒮/𝒩(Z(k) + σDū(k))
4:	q(k+1) = proxσεFq (q(k)+σ(Aū(k)−g))
5:	u(k +1) = u(k) + τ (Div Z(k +1) − AT q(k +1))
6:	ū(k+1) = u(k+1) + θ (u(k+1) − u(k+1))
7:	until	▹ stop when convergence criteria met

3.3 Simulation studies

To investigate the impact of the proposed vectorial TV regularization, we performed two numerical simulation studies with the computerized XCAT phantom. In the first experiment we simulate an ideal, photon-counting system with 5 energy windows and directly reconstruct images corresponding to the log-normalized bin data. We will refer to this image basis as the “energy” basis because each image channel corresponds directly to the measurements of one energy window.

In the second experiment, we simulate an ideal, dual-kVp scan and perform what we will refer to as a “hybrid” reconstruction. As we will detail later, we first decompose the 80/140 kVp data into a bone/soft-tissue “material” basis and then we co-reconstruct this synthetic data with the raw 80/140 kVp sinograms. The TV_N penalty couples all four image channels so that the relatively noisy basis-material channels may benefit from the higher SNR energy-bin channels.

3.3.1 Data generation

The XCAT shoulder phantom

All simulations used the same 2D pixelized shoulder phantom, which was generated from an axial slice of the XCAT phantom and is pictured in Figure 3. The XCAT software package was used to generated a set of bone and soft-tissue density maps on a 2048 × 2048 pixel grid. These density maps were then used as input to a polyenergetic, distance-driven projector model to generate the simulated raw data that would be inputted to our reconstruction algorithm.

Figure 3.

The 2D XCAT shoulder phantom used for all simulations studies, depicted at 60 keV (a) for reference. The projection data were generated using bone (b) and soft-tissue (c) density maps with the appropriate mass-attenuation curves.

Ideal photon counting model

To generate the 5-bin photon-counting data, we used a realistic 120 kVp simulated x-ray tube spectrum with hard thresholds at 40,60,80,100, and 120 keV. We did not model any physical factors in the detector response, so our bin response functions are perfect rect functions. Our simulated spectrum had virtually no emissions below 20 keV, so we can think of these bins as being evenly spaced. Using a distance-driven projector model, polyenergetic projections were computed with 896 detector elements per view and 400 views, and Poisson noise was added.

Dual kVp hybrid model

The other configuration we looked at was an 80/140 dual kVp acquisition with the same number of detectors and views as the photon counting simulation. We simulated realistic 80 and 140 kVp x-ray tube spectra to generate two sets of consistent projection data. This type of consistent, dual-kVp data can be acquired on many current scanners by performing two back-to-back scans. One could also approximate consistent, dual-kVp data with a fast kV-switching geometry by interpolating the missing views in the low and high kVp sinograms. Gaussian noise was added to approximate a compound Poisson noise model. From the noisy 80 and 140 kVp projection data, we synthesized bone and soft-tissue basis sinograms using a maximum-likelihood material decomposition. Since the material decomposition is performed in the projection space, it is ray-by-ray separable, resulting in a series of small optimization problems that we solve to high precision using Newton's method. In the “hybrid” study, we will co-reconstruct these 4 channels of data, consisting of our log-normalized, dual kVp data (energy basis) and the synthesized, material-basis data.

3.3.2 Preprocessing and reconstruction

Both the 5-channel photon-counting data and the 4-channel dual kVp hybrid data were reconstructed using the reconstruction model outlined in (25). For reconstruction, we used a 512 × 512 grid of 1 mm pixels and a matched projector/backprojector pair based on Joseph's method [38].

Computing data-weights

For the raw-basis projection data, we will use the data-weighting approach described by Bouman [2], which results in a diagonal W matrix, where the diagonal elements equal the pre-logged projection data. This is a quadratic approximation to the log-likelihood. For the synthetic, bone/soft-tissue sinograms, we estimate the variances using the Cramer-Rao lower bound [39] and weight by their inverse. This is similar to the approach described by Schirra [40] and Sawatzky [17], but we ignore the off-diagonal terms in this work for simplicity. The reason for omitting these terms is because the CPPD algorithm relies on the functions F and G in (29) having simple proximal maps, and we require this simplification to meet that criteria. This problem only arises in the data-constrained form of the optimization problem. When solving the equivalent unconstrained optimization problem (as in [40, 17]), including the inter-channel noise correlations is straightforward. Generally, fewer algorithmic tools are available for solving the data-constrained form, but we favor it for this work because it provides a mechanism for fairly comparing the channel-by-channel TV to the TNV.

Tuning the data-constraint parameter

The only parameter that we will vary in our reconstruction model (25) is ε, which controls the trade-off between data fidelity and smoothness. In general, smaller values of ε will result in noisier images, while higher values allow the VTV term to find a smoother solution. At the extreme case of ε = 0, only images with projections that exactly match the measured data are allowed. There is also some finite value ε = ε_max for which the algorithm will return an image of all zeros. In order to determine an interesting range for ε, we first compute a ground truth image u_true by performing FBP on noiseless, non-sparse projection data. Then we define a new parameter ε* which is defined by equation 39,

$${\epsilon }^{\ast }\equiv {\Vert A{\mathbf{u}}_{\text{true}}-\mathbf{g}\Vert }_W$$ (39)

where g are the noisy projection data we wish to reconstruct. In this study we will select values of ε that satisfy ε = αε*, where α ∈ (0,1). We subjectively selected a range of α values that represent a range of solutions from under-smoothed to over-smoothed in order to demonstrate how the TV_N compares to the channel-by-channel TV in various regimes.

As described earlier, the projection data were re-scaled prior to reconstruction, so that the average noise levels were approximately the same in every spectral channel.

4 Results

In the following section, we present the resulting images from our simulation study, comparing directly the channel-by-channel TV and the proposed TNV. In all of our comparisons, we refer to the reference image u_true, which is obtained by performing FBP on noiseless full-view data (1200 views).

4.1 Photon counting study

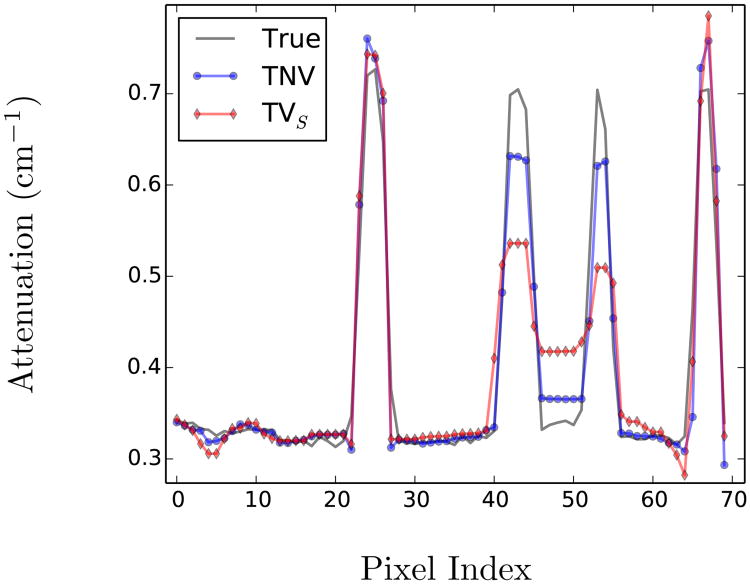
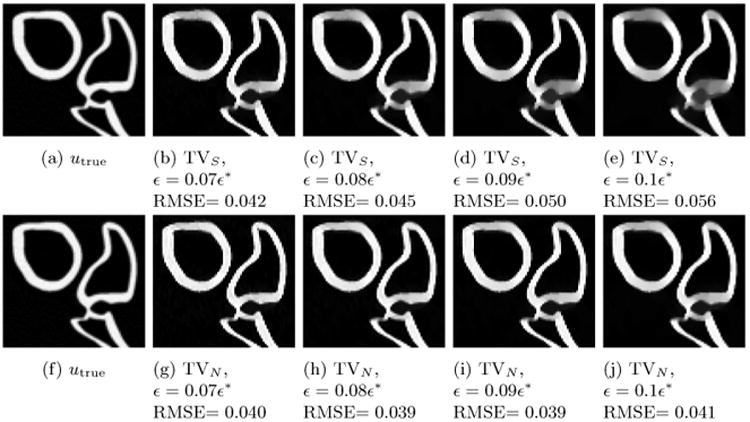
Here we present the results of performing a simultaneous reconstruction of the five photon-counting bins after log-normalization, using both the channel-by-channel TV_S and the proposed TV_N. This is an example of performing a joint reconstruction on data in the energy basis because we did not perform a material decomposition. In this setup, bin 1 (0-40 keV) was the noisiest, due to significant attenuation below 40 keV. We find that the inter-channel coupling introduced by the total nuclear variation has the greatest impact on the noisiest channels, so we present reconstructed images from this energy bin, focusing on the ROI's indicated in Figure 4. The resulting images are depicted in figures 5 through 6. The image window was manually adjusted for each ROI to highlight the relevant structures but is fixed within a particular figure. In general, we find that the images reconstructed with TV_N regularization suffer from less edge blurring as the smoothing parameter ε is increased. The profile plot in Figure 7 gives a closer look at how the TV_N better preserves bony structures in the lowest energy bin image. We confirmed that these profiles were extracted from images of similar noise levels by measuring the sample variance in a nearby, uniform muscle ROI. This is expected because our data-constrained, reconstruction model allows us to select the noise level directly by tuning the ε parameter.

Figure 4.

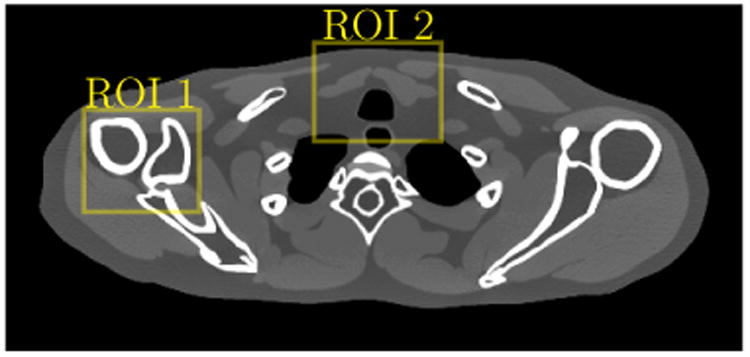
XCAT reference image, with ROI's indicated in yellow

Figure 5.

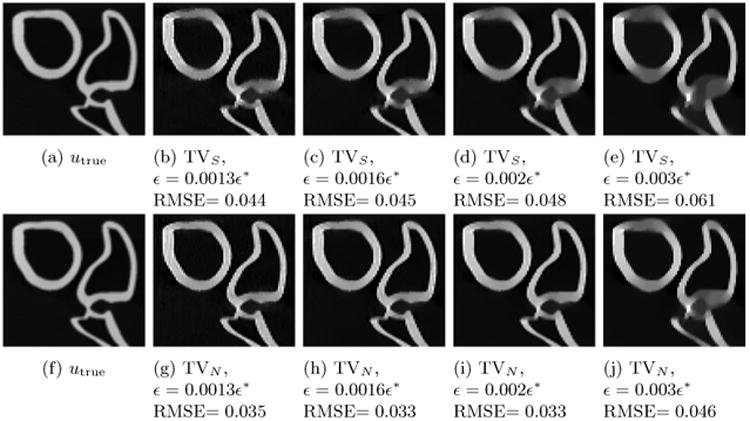
Bin 1 (0-40keV) image, bone ROI/window comparison with channel-by-channel TV (top) and TV_N (bottom). Grayscale window in cm⁻¹ [0.30, 0.85]. The reference image u_true is an FBP reconstruction of the fully sampled (1200 views) noiseless data.

Figure 6.

Bin 1 (0-40keV) image, soft-tissue ROI comparison with channel-by-channel TV (top) and TV_N (bottom). Grayscale window in cm⁻¹ [0.30, 0.35]. The reference image *u_true is an FBP reconstruction of the fully sampled (1200 views) noiseless data.

Figure 7.

This is a vertical profile through the 0-40 keV, bone-ROI image with ε = 0.0016ε*. The TNV regularized reconstruction shows slightly better preservation of bony structures. The noise levels were estimated from a nearby ROI in a uniform muscle region (σ_TVS = 0.0025, σ_TVN =0.0022).

4.2 Dual kVp Hybrid Study

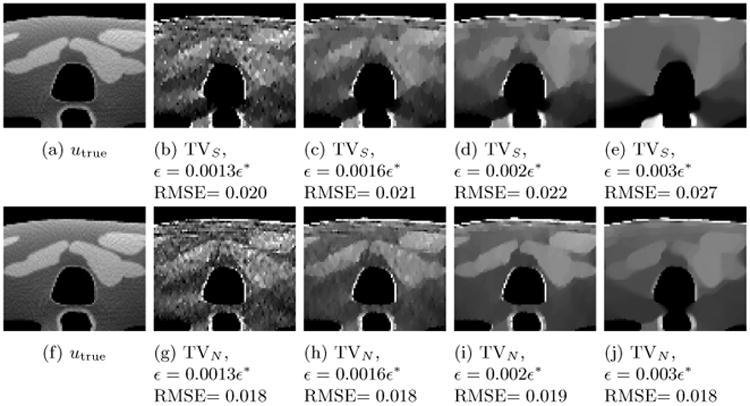
In this study we co-reconstruct the synthetic soft-tissue/bone image channels with the raw 80/140 kVp data. In general, the material decomposition greatly amplifies noise, so that the soft-tissue and bone images tend to have a much lower CNR than the raw 80 and 140 kVp images. This noise amplification is due to the ill-conditioning of the inversion step in the basis change, which is caused by the relatively poor spectral separation between basis materials. This poor spectral separation also explains the strong negative correlation between the synthesized material channels. We hypothesize that by coupling the high CNR raw image channels and the low CNR synthetic image channels, we may be able to improve noise suppression in the synthetic data. We call this technique of reconstructing the synthetic and raw data simultaneously "hybrid" reconstruction. We present ROI's from both the bone density image and the soft-tissue density image over a range of different ε values in Figures 8 and 9. We find that using the TV_N allows for a high degree of noise suppression (high values of ε) without significantly deteriorating bone or soft-tissue structures. However, when the naive channel-by-channel TV is used, these same e values eventually lead to significant blurring artifacts. We also point out that even though the soft-tissue, 80 kVp, and 140 kVp images have edges that are not present in the bone density image, the TV_N coupling does not falsely propagate these edges into the bone channel.

Figure 8.

Bone basis image, bone ROI comparison with channel-by-channel TV (top) and TV_N (bottom). Grayscale window in g/mL⁻¹ [0.00, 0.52]. The reference image u_true is an FBP reconstruction of the fully sampled (1200 views) noiseless data.

Figure 9.

soft-tissue basis image, soft-tissue ROI comparison with channel-by-channel TV (top) and TV_N (bottom). Grayscale window in g/mL⁻¹ [0.80, 1.07]. The reference image u_true is an FBP reconstruction of the fully sampled (1200 views) noiseless data.

5 Discussion

We have described a framework for jointly reconstructing multi-channel spectral CT images using a generalized vectorial regularizer. Specifically, we presented a multi-channel generalization of the total variation which couples the different image channels by encouraging their gradient vectors to point in a common direction. Preliminary results suggest that this coupling may allow for greater noise suppression with less blurring of image structures compared to the channel-by-channel TV. This regularization strategy can be used to reconstruct logged energy bin images, basis-material images, or even both simultaneously, such as in our hybrid reconstruction study. This hybrid approach may allow for better noise suppression in the synthetic material images, which typically suffer from elevated noise levels.

In this study, we only considered the case of multi-energy data with consistent rays to isolate the impact of the inter-channel coupling in the TNV. However, we suspect that by coupling the edge structure of the image channels, there may be additional benefits for data containing inconsistent rays. For example, in a fast kV switching system each energy channel contains slightly different geometric information about the object, due to the fact that the projection views are interleaved, and we hypothesize that the TNV penalty may allow some of this information to be shared between image channels during the reconstruction. In future work we will investigate the impact of the TNV penalty on configurations with inconsistent rays.

A final important note about this study is that the numerical XCAT phantom we used is piecewise constant. We expect our proposed TNV penalty to suffer from many of the same artifacts and limitations as the conventional TV penalty when applied to more realistic data, such as “staircasing” [41] and loss of contrast [42]. However, other works have demonstrated that TV can still perform somewhat well on data with low frequency structures and complex textures when balanced appropriately with the data-fidelity term [11, 43]. Any convex regularizer is likely to introduce unacceptable biases when over relied on. Some of these limitations of the TV have been addressed for scalar images by other authors, for example by considering higher-order spatial derivatives [44] or with non-convex generalizations of the TV [45, 46]. We expect that these improvements can also be extended to the multi-channel TNV but this is beyond the scope of this work.

Appendices

A Deriving the saddle-point problem

To derive the saddle-point formulation of our optimization problem, we used two fundamental results of convex analysis to “dualize” the data fidelity constraint as well as the VTV term. The transformation of the VTV term follows straightforwardly from the definition of the so-called “dual-norm,” which is defined by

$${\Vert x\Vert }^{\prime }=\underset{z}{\text{sup}}\langle x,z\rangle \mathrm{s}.\mathrm{t}.\Vert z\Vert \le 1.$$ (40)

Every norm ‖·‖ has an associated dual-norm ‖·‖′, that obeys this relationship. The ℓ₂ norm utilized in the scalar TV is self-dual, while the nuclear norm and spectral norm form a dual pair.

Dualizing the channel-by-channel TV

The channel-by-channel TV can be written as

$${\text{TV}}_S(\mathbf{u})=\sum _{\ell }\sum _{i,j}{\Vert {(J\mathbf{u})}_{\ell }(i,j)\Vert }_2.$$ (41)

The definition of the dual-norm allows us to rewrite this expression as

$${\text{TV}}_S(\mathbf{u})=\sum _{i,j}\sum _{\ell }\underset{Z}{\text{sup}}\langle {(J\mathbf{u})}_{\ell }(i,j),Z_{\ell }(i,j)\rangle \mathrm{s}.\mathrm{t}{\Vert Z_{\ell }(i,j)\Vert }_2\le 1=\underset{Z}{\text{sup}}{\langle J\mathbf{u},Z\rangle }_{\mathcal{G}}\mathrm{s}.\mathrm{t}{\Vert Z_{\ell }(i,j)\Vert }_2\le 1\forall i,j,m$$ (42)

which is equivalent to (33).

Dualizing the proposed TV_N

The proposed TV_N is

$${\text{TV}}_N(\mathbf{u})=\sum _{i,j}{\Vert (J\mathbf{u})(i,j)\Vert }_{\star }.$$ (43)

Substituting the definition of the dual-norm, we get

$${\text{TV}}_N(\mathbf{u})=\sum _{i,j}\underset{Z}{\text{sup}}\langle (J\mathbf{u})(i,j),Z(i,j)\rangle \mathrm{s}.\mathrm{t}{\sigma }_{max}(Z(i,j))\le 1=\underset{Z}{\text{sup}}{\langle J\mathbf{u},Z\rangle }_{\mathcal{G}}\mathrm{s}.\mathrm{t}{\sigma }_{max}(Z(i,j))\le 1\forall i,j,$$ (44)

which is equivalent to (35). We have used the fact that the spectral norm (maximum singular value) is dual to the nuclear norm.

Dualizing the data-fidelity term using the Fenchel conjugate

To dualize the data-fidelity term, we make use of the Fenchel conjugate. For a convex, lower semi-continuous function f, the conjugate f* is defined by

$$f^{\ast }(x)=\underset{x^{\prime }}{\text{sup}}\langle x,x^{\prime }\rangle -f(x^{\prime }),$$ (45)

where it is also true that (f*)* = f. Using this definition, it is easy to show that the following functions form a conjugate pair,

$${\delta }_{\epsilon }(x)\iff \epsilon {\Vert W^{-1/2}x\Vert }_2$$ (46)

where δ_ε(x) is the indicator function, defined by (31). This along with the definition of the Fenchel conjugate leads directly to Eqn. 32.

B The proximal map of εσ‖ W^−1/2q‖₂

The update equations for Algorithm 2 involve evaluating the proximal map of εσF_q = εσ‖ W^−1/2q‖₂, which does not admit a closed form. However, we will now show how it can still be efficiently evaluated using a simple root-finding procedure. First we explicitly write out the proximal mapping as

$${\mathbf{\text{prox}}}_{\epsilon \sigma F_q}({\mathbf{q}}^{\prime })=\underset{\mathbf{q}}{argmin}{\Vert W^{-1/2}\mathbf{q}\Vert }_2+\frac{1}{2\epsilon \sigma }{\Vert \mathbf{q}-{\mathbf{q}}^{\prime }\Vert }_2^2.$$ (47)

Next, we compare this optimization problem to a slightly easier problem,

$$\underset{\mathbf{q}}{argmin}\frac{1}{2}{\Vert W^{-1/2}\mathbf{q}\Vert }_2^2+\frac{1}{2\lambda \sigma }{\Vert \mathbf{q}-{\mathbf{q}}^{\prime }\Vert }_2^2,$$ (48)

and note that for some choice of ε and λ, these objectives both have the same set of level curves. We can find the solution to this problem by setting the gradient equal to zero, and for a symmetric weighting matrix W, it is given by

$${\mathbf{q}}^{\ast }={(I+\sigma \lambda W^{-1})}^{-1}{\mathbf{q}}^{\prime }.$$ (49)

If the gradient of this easier problem is equal to that of the original problem, then q* must be an optimizer of the original problem as well. Momentarily, we ignore the non-differentiable point q = 0, and set the gradients equal, which yields

$$\begin{array}{c}\epsilon =\lambda {\Vert W^{-1/2}{\mathbf{q}}^{\ast }\Vert }_2.\\ =\lambda {\Vert W^{-1/2}{(I+\sigma \lambda W^{-1})}^{-1}{\mathbf{q}}^{\prime }\Vert }_2.\end{array}$$ (50)

In this work, we will only consider the case where W is a diagonal matrix, which allows us to simplify this expression.

$${\epsilon }^2-{\lambda }^2\sum _{j=1}^J\frac{W_{jj}}{{(W_{jj}+\sigma \lambda )}^2}{[{\mathbf{q}}^{\prime }]}_j^2=0.$$ (51)

The index j is a linear index over every element of q. Now, we just need to perform a 1D search for a positive value of λ that satisfies this equation, which can be done very efficiently using Newton's method or a variety of other algorithms. Once this root, λ*, is found, we simply plug it back into (50):

$${\mathbf{\text{prox}}}_{\epsilon \sigma F_q}({\mathbf{q}}^{\prime })=\{\begin{array}{cc}{(I+\sigma {\lambda }^{\ast }{W}^{-1})}^{-1}{\mathbf{q}}^{\prime }& {\Vert W^{1/2}{\mathbf{q}}^{\prime }\Vert }_2>\sigma \epsilon \\ 0& {\Vert W^{1/2}{\mathbf{q}}^{\prime }\Vert }_2\le \sigma \epsilon \end{array}.$$ (52)

Note that because of the non-differentiability of ‖W^−1/2q‖₂ at q = 0, there will not always be a solution to equation 51. Specifically, if σε>‖W^1/2q′‖₂, then there is no viable root. In this case, we need not perform the root-finding procedure, because the optimum must occur at q = 0.

C Implementation of the projection operators Π_𝒮/𝒩

Π_𝒮 Now, we will describe the Euclidean projection onto the set 𝒮 defined in (34). Consider projecting Z ∈ 𝒢 onto 𝒮. We can define this operation element-wise on each vector Z_ℓ(i,j) ∈ ℝ² corresponding to the ℓ^th spectral channel and the pixel-location (i,j). The projection of this element is given by

$${\mathrm{\Pi }}_{\mathcal{S}}(Z_{\ell }(i,j))=\{\begin{array}{cc}{Z}_{\ell }(i,j)& {\Vert Z_{\ell }(i,j)\Vert }_2\le 1\\ \frac{Z_{\ell }(i,j)}{{\Vert Z_{\ell }(i,j)\Vert }_2}& \text{otherwise}\end{array}.$$ (53)

For every image channel ℓ and pixel location (i,j), we simply project the vector Z_ℓ(i,j) onto the unit ball.

Π_N The projection onto set 𝒩 defined by (36) is slightly more complicated. We define this operation element-wise on each ℳ × 2 matrix Z(i,j). This time we need to threshold the singular values of Z(i, j). This projection can be succinctly described by

$${\mathrm{\Pi }}_N(Z(i,j))=U{\sum }_p{V}^T,$$ (54)

where UΣV^T is the SVD of Z(i,j), and

$${\sum }_p=\text{sgn}(\sum )min(|1|,|\sum |)$$ (55)

is the thresholded version of Σ. To form Σ_p the singular values on the diagonal of Σ are simply thresholded so that their magnitude does not exceed 1. An equivalent projection formula that leads to a much more computationally efficient solution is given by

$${\mathrm{\Pi }}_N(Z(i,j))=Z(i,j)V{\sum }^{†}{\sum }_p{V}^T$$ (56)

The quantity Σ^† is the pseudo-inverse of Σ. Since we are only working with 2 spatial dimensions the matrix V will by a 2 × 2 square matrix. Therefore, to compute the projection according to (56) we only need to compute the eigenvalues and eigenvectors of a 2 × 2 matrix, for which a very simple closed form is available. This can also be done very efficiently for 3D images, where V will be 3 × 3. Because of this, the update equations that result from the proposed vectorial TV are only trivially more expensive than the channel-by-channel TV, and the projection/backprojection operations are likely to swamp this difference.