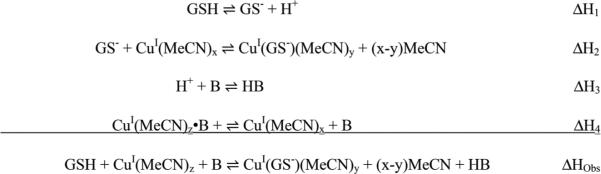Stabilization of Cu(I) for binding and calorimetric measurements in aqueous solution

Abstract

Conditions have been developed for the comproportionation reaction of Cu²⁺ and copper metal to prepare aqueous solutions of Cu⁺ that are stabilized from disproportionation by MeCN and other Cu⁺-stabilizing ligands. These solutions were then used in ITC measurements to quantify the thermodynamics of formation of a set of Cu⁺ complexes (Cu^I(MeCN)₃⁺, Cu^IMe₆Trien⁺, Cu^I(BCA)₂³⁻, Cu^I(BCS)₂³⁻), which have stabilities ranging over 15 orders of magnitude, for their use in binding and calorimetric measurements of Cu⁺ interaction with proteins and other biological macromolecules. These complexes were then used to determine the stability and thermodynamics of formation of a 1 : 1 complex of Cu⁺ with the biologically important tri-peptide glutathione, GSH. These results identify Me₆Trien as an attractive Cu⁺-stabilizing ligand for calorimetric experiments, and suggest that caution should be used with MeCN to stabilize Cu⁺ due to its potential for participating in unquantifiable ternary interactions.

Introduction

The physiologically relevant oxidation state of copper under reducing conditions, such as that found within cells, is Cu⁺.^1–3 However, the biochemistry of this ion is particularly challenging to study due to its oxidation under aerobic conditions (ΔG° = −414 kJ mol⁻¹), its complex chemistry in the presence of halides and oxides,⁴ and its tendency to undergo disproportionation (eqn (1))

$$2{{\mathrm{Cu}}^{+}}_{\left(\mathrm{aq}\right)}\rightleftharpoons {{\mathrm{Cu}}^{2+}}_{\left(\mathrm{aq}\right)}+{{\mathrm{Cu}}^0}_{\left(\mathrm{s}\right)}$$ (1)

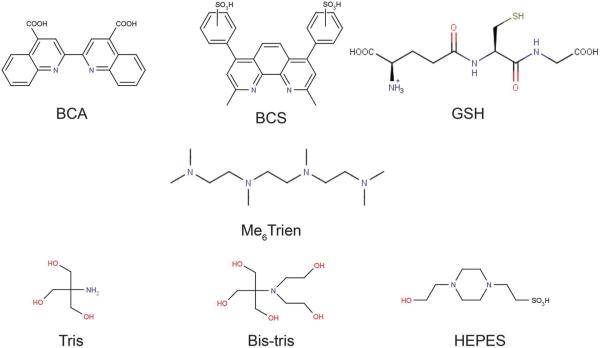
(K_disp = [Cu^II]/[Cu^I]² ≈ 10⁶) in aqueous solution. Further, due to its closed d shell, the cuprous ion lacks many of the spectral signatures of the open d shell cupric ion, limiting several traditional approaches for studying this metal ion. Not only is it diamagnetic and lacks ligand field transitions, but the charge transfer bands associated with Cu⁺ coordination are normally found in the near-UV and masked by intense protein or DNA absorbance.^5,6 Therefore, indirect methods are typically used to quantify Cu⁺ binding reactions. For example, competition with bicinchoninic acid (BCA) or bathocuproine disulfonic acid (BCS) is commonly used to determine the affinity of proteins for Cu⁺.^5–12 These molecules (Fig. 1) have a large preference for Cu⁺ over Cu²⁺ and gain intense spectral transitions in the visible region upon Cu^I(BCA)₂³⁻ or Cu^I(BCS)₂³⁻ formation. However, to determine the thermodynamics of Cu⁺ binding to proteins with these ligands would require an indirect van't Hoff analysis.

Fig. 1.

Ligands and buffers used in this study.

Isothermal titration calorimetry (ITC), which directly measures heat flow and is not dependent on photophysical properties to determine thermodynamic information, is an attractive technique for studying Cu⁺ binding reactions.¹³ This technique, however, has certain experimental constraints.¹⁴ Specifically, due to the inherent ability of ITC to detect all of the contributions to the heat that is evolved or consumed during a titration, it is necessary to eliminate or account for all chemical and physical processes that are coupled to the binding event of interest.¹⁵ This presents a unique challenge when working with Cu⁺ in aqueous solutions due to its inherent instability to oxidation and disproportionation. While oxidation is easily avoided by conducting the experiment under strictly anaerobic conditions, disproportionation occurs independent of O₂ and must be suppressed.

The aim of this study was to characterize the thermodynamic properties of Cu⁺ complexes for their use in binding measurements in aqueous solution, particularly those involving ITC. MeCN was considered initially due to its well-known Cu⁺ complex that has a modest stability. First, conditions for the preparation and stabilization of Cu⁺ by MeCN in aqueous buffered solutions by a comproportionation reaction (reverse of eqn (1)) were established. Then the thermodynamics of formation of increasingly stable Cu⁺ complexes with Me₆Trien, BCA and BCS were quantified. Finally, the thermodynamics of Cu⁺ interaction with the important cellular thiol glutathione (GSH) were determined. The results from this study indicate that the interaction between MeCN and Cu⁺ is under estimated in the literature, and enthalpically silent under the experimental conditions used here; further, MeCN has the potential to form ternary complexes that are difficult to accurately quantify, thereby masking the thermodynamic interactions of interest. We propose Me₆Trien as an alternate stabilizing ligand for Cu⁺ delivery due to its low potential for the formation of ternary complexes. These results provide a foundation for the accurate delivery of aqueous Cu⁺ in measurements of the binding thermodynamics of biological molecules that have a wide range of affinities for this metal ion.

Experimental

Materials and reagents

HEPES (4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid), MOPS (3-(N-morpholino)propanesulfonic acid), BisTris (2-(bis-(2-hydroxyethyl)amino)-2-(hydroxymethyl)propane-1,3-diol) and Tris (2-amino-2-hydroxymethyl-propane-1,3-diol) were obtained from VWR or Sigma, and buffer solutions were prepared using Milli-Q deionized water (>18 MΩ). Bathocuproine disulfonate disodium salt (BCS), bicinchoninic acid disodium salt hydrate (BCA), 1,1,4,7,10,10-hexamethyltriethylenetetramine (Me₆Trien), reduced glutathione (GSH), and 5,5′-dithiobis(2-nitrobenzoic acid) (DTNB, Ellman's Reagent) were procured in the highest purity available from Sigma-Aldrich. ACS grade acetonitrile (MeCN) from Sigma-Aldrich was used for all experiments. Copper(ii) chloride dehydrate (99.9%+) and trace metal grade nitric acid were obtained from Alfa Aesar.

Anaerobic sample preparation

All reactions were carried out either in a dual chamber CoyLab vinyl glove box with independent chambers for sample preparation and spectral characterization and ITC measurements, which was maintained with 97% N₂ and 3% H₂ by continuous circulation through the catalyst bed that maintains a consistent [O₂] < 0.1 ppm, or in a single chamber CoyLab rigid plexi-glass glove box maintained with 100% N₂. Prior to use, all buffer solutions and solvents were thoroughly degassed either by four iterations of a freeze–pump–thaw cycle in Airfree® glassware from Chemglass or by rigorous vacuum degasing followed by extensive purging with pure N₂ or Ar.

Spectrophotometry

Spectrophotometric measurements were carried out in triplicate in the glove box using a Thermo Scientific NanoDrop 2000c operating in cuvette mode. Literature molar extinction coefficients were used for Cu^I(BCA)₂³⁻ (ε₅₆₃ = 7900 M⁻ cm⁻¹) and Cu^I(BCS)₂³⁻ (ε₄₈₃ = 13 000 M⁻¹ cm⁻¹),^9–11 and for 2-nitro-5-thiobenzoic acid (ε₄₁₂ = 14 150 M⁻¹ cm⁻¹),¹⁶ which is the product of DTNB reacting with a free thiol.

Isothermal titration calorimetry (ITC)

All ITC measurements were carried out in triplicate using either a TA Instruments Nano ITC, housed in the CoyLab vinyl glove box, with a 170 μL sample cell, a 50 μL titration syringe, 1–2.5 μL injection volumes and 240–1200 second intervals between injections, as dictated by the experiment, or a Micro-Cal VP-ITC, housed in a custom anaerobic plexiglass glove box, with a 1.4 mL sample cell, a 300 μL titration syringe, 6–10 μL injection volumes and 600–1200 second intervals between injections. Note, the TA Instruments Nano ITC data are plotted with positive exothermic heat flow, while the MicroCal VP-ITC data are plotted with negative exothermic heat flow. In the figures of ITC measurements, the top panel shows the raw ITC data (power vs. time), where each spike represents the injection of titrant into the cell, and the bottom panel shows the integrated and normalized heat plotted vs. the molar ratio of titrant (syringe) to titrand (cell). The Residual Sum of Squares per Degree of Freedom (RSS/DoF) is reported as a measure of the goodness of fit. Prior to ITC titrations, the BCS and BCA concentrations were verified spectrophotometrically with excess Cu⁺, using the extinction coefficients listed above, and the concentration of reduced thiol in solutions of GSH was measured using the standard DTNB assay.¹⁶

Data were fit using the TA NanoAnalyze, Origin or SEDPHAT¹⁷ packages. The one-site model assumes n binding “sites”, each with identical binding properties, while the sequential model assumes that two or more complexes are formed in sequence (i.e., the ML complex must form prior to the ML₂ complex, where M = metal and L = ligand). Integer stoichiometry units are required for the sequential model. The overall equilibrium is defined by the standard β_n nomenclature, where ${\beta }_n=\frac{\left[{\mathrm{ML}}_n\right]}{\left[\mathrm{M}\right]{\left[\mathrm{L}\right]}^n}$.

In most cases, the error was calculated from the standard deviation of two or more titrations. When fitting GSH titration data in HEPES buffer to a sequential binding model, the standard deviation did not accurately reflect the error associated with the 2^nd binding event. In this case, the reported error was calculated by error propagation from three independent titrations.

Comproportionation reaction

The comproportionation reactions were carried out anaerobically using copper wire that had been incubated in ethylene-diaminetetraacetate (EDTA) for 2 hours to ensure the surface was free of metal ion contaminants. The wire was then washed 3–5 times in Milli-Q water to remove the EDTA and air dried prior to use. For the quantitative reactions, 1.00 ± 0.03 g pieces of the clean dry wire were cut and taken into the glove box; non-quantitative reactions used pieces that were ~5 cm in length. Reactions were set up in the glove box and incubated using a Thermo Scientific Labquake® Rotisserie rotator.

Metal analysis

The copper concentration was determined with two independent methods. The total soluble copper (Cu⁺ + Cu²⁺) was measured using a Perkin Elmer 560 Atomic Absorbance Spectrometer (AAS) with standards in the 0.5–5.0 ppm range (r² > 0.997). Average values were determined from a minimum of three measurements. The cuprous ion concentration was measured by adding a large excess of BCA in 25 mM MOPS, pH 6.0, and measuring the absorption at 563 nm (Cu^I(BCA)₂³⁻; ε₅₆₃ = 7900 M⁻¹ cm⁻¹). This pH was selected to minimize the hydroxide-mediated reduction of Cu²⁺ to Cu⁺ in the presence of BCA (unpublished results).

Coupled equilibrium calculations

The analysis to account for speciation (metal–ligand and proton) during ITC experiments is described elsewhere in detail.^15,18,19 Briefly, competition factors are calculated according to:

$$Q=\sum _{n=0}^x\left({\beta }_n{\left[\mathrm{X}\right]}^n\right)$$ (2)

where Q is the competition factor (typically called α what the competition comes from protons), β_n is the n^th overall affinity constant and X is the competing ligand (for metal competition) or proton (for pH corrections). The observed equilibrium constant is readily corrected by

$$K=K_{\mathrm{ITC}}Q$$ (3)

A combination of eqn (2) and (3) was used to determine the pH-independent formation constant for Cu^IMe₆Trien⁺ from Me₆Trien displacement by BCA or BCS. A sample calculation is reported in the ESI.†

$$K_{\mathrm{Cu}-\mathrm{BCA}}=K_{\mathrm{ITC}}\left(1+\frac{{\left[{\mathrm{Me}}_6\mathrm{Trien}\right]}_{\text{total}}}{\alpha }{K}_{{\mathrm{CuMe}}_6\mathrm{Trien}}\right)$$ (4)

Electron paramagnetic resonance (EPR)

The EPR spectra were recorded at 77 K on a Bruker EMX 300 X-band EPR spectrometer (Bruker Biosciences Corp.) using five signal-averaged scans with the following conditions: 9.68 GHz microwave frequency, 5.02 mW microwave power, 100 kHz modulation frequency, 5.00 G modulation amplitude and 81.92 ms time constant. Samples were prepared in gas tight quartz tubes by diluting a 50 mM Cu⁺ comproportionation reaction stock in MeCN. All samples were stored at −80 °C before the measurement.

Results and discussion

Acetonitrile

Preparation and characterization of Cu⁺_aq stabilized by MeCN

Acetonitrile is often used to stabilize Cu⁺ as the Cu^I(MeCN)₄⁺ complex;²⁰ indeed, anaerobic dissolution of Cu(MeCN)₄⁺ salts in neat MeCN is an established procedure for storing Cu⁺ and these solutions are used for biochemistry experiments involving this ion. In our hands, however, dilution of these MeCN solutions in some aqueous buffers resulted in visible precipitation of Cu⁺ species. As an alternate approach, we evaluated the comproportionation reaction of CuCl₂ with copper metal in the presence of excess MeCN to produce aqueous solutions of MeCN-stabilized Cu⁺. This approach inherently removes residual oxygen because any Cu²⁺ produced by oxidation will be readily converted back to Cu⁺; further, the cuprous ion is now in equilibrium with the aqueous conditions and other solutes (e.g., chloride). In addition, this approach is easily adapted for the preparation of solutions with Cu⁺ stabilized by other ligands, as demonstrated later with Me₆Trien.

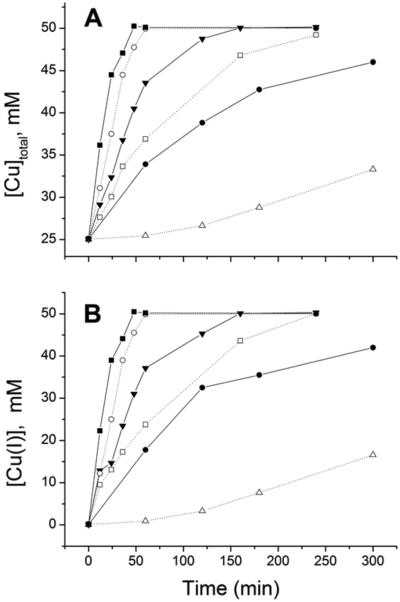
One mL solutions containing 25.00 mM CuCl₂ and 1.00 g clean copper wire (see Experimental for details) were incubated with increasing concentrations of MeCN under strictly anaerobic conditions. Reaction progress was monitored by the analysis of withdrawn aliquots with two methods: (a) atomic absorbance spectroscopy (Fig. 2A), and (b) addition of excess BCA and measurement of Abs₅₆₃, the characteristic wavelength of the Cu^I(BCA)₂³⁻ complex (Fig. 2B). These complementary methods provide a measure of the total soluble copper and [Cu⁺], respectively; the former should start at 25 mM (initial [Cu²⁺]) and progress to 50 mM, while the latter should begin at 0 mM and build to 50 mM because the BCA assay is specific for Cu⁺. The data from the two methods mirror each other, with only minor deviations. The extent of the reaction scales with [MeCN]; while the lower concentrations of MeCN (250 and 500 mM) stabilize some Cu⁺, they are not sufficient to drive the reaction to completion, even after many hours. The higher MeCN concentrations (1, 2, and 4 M) successfully convert all of the Cu²⁺ to Cu⁺. Based on these results, all comproportionation reactions were carried out with 1 M MeCN and 25 mM Cu²⁺ for at least 3 hours. The final solution was stored in the glove box in a sealed plastic test tube containing a small piece of copper wire. This solution remained colorless and periodic testing by AAS indicated negligible change in the total soluble copper over a 6-month period.

Fig. 2.

Progress of the comproportionation reaction of copper wire and 25.00 mM CuCl₂ in MeCN monitored by (A) total soluble copper by AAS and (B) [Cu⁺] by the BCA assay, described in the Experimental section. [MeCN] = 4 M (-■-), 2 M (-○-), 1 M (-▼-), 0.75 M (-□-), 0.5 (-●-) or 0.25 M (-△-).

Since oxidation or disproportionation of the cuprous ion will yield Cu²⁺, electron paramagnetic resonance (EPR) was used to quantify Cu²⁺ and thereby determine the MeCN concentration required to stabilize Cu⁺ in aqueous solutions used for titration experiments. The 50 mM stock Cu⁺ solution in 1 M MeCN was diluted to 125 μM Cu⁺ in 5 and 25 mM MeCN and transferred to gas tight EPR tubes for measurements at 77 K; the spectra of these solutions were then compared to those of 12.5 and 1.25 μM Cu²⁺ standards, which contain 10% and 1% of the copper in the experimental samples, respectively (Fig. 3). No Cu²⁺ EPR signal was detectable in the Cu⁺ sample with 25 mM MeCN, even when the gain was increased by 10. The Cu⁺ sample with 5 mM MeCN has a signal indicating the presence of ~4–5 μM Cu²⁺, based on peak intensity. Its origin from oxidation is unlikely since Cu²⁺ was not observed in the identically handled 25 mM MeCN sample. Therefore, the source of the oxidized copper is believed to be disproportionation; indeed, a BCA assay of a sample under these conditions indicates that [Cu⁺] is 85% of the expected value. Based on these results, the final [MeCN] was never less than 25 mM and the [MeCN]/[Cu⁺] ratio was maintained at >40, as established in the comproportionation reaction with 1 M MeCN.

Fig. 3.

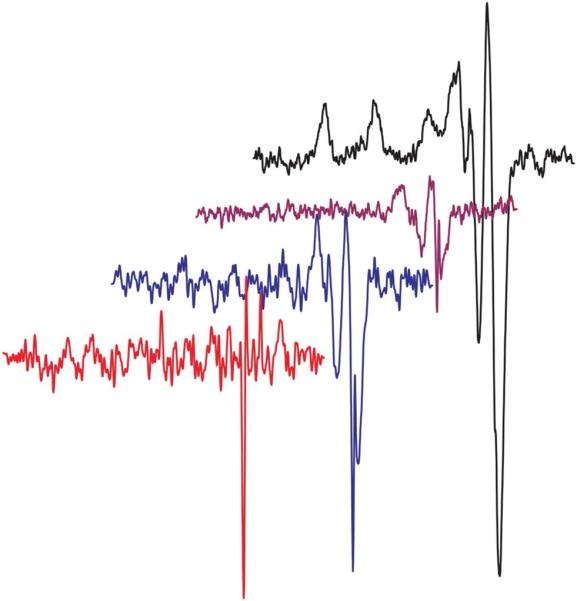
The 77 K EPR spectra (offset for clarity) of 12.5 μM (black line; g_∥ = 2.22, A_∥ = 196 G, g_⊥ = 2.01) and 1.25 μM (purple line) Cu²⁺ standards, and 125 μM Cu⁺ prepared by diluting the 50 mM Cu⁺ comproportionation stock solution in 5 mM (blue line) or 25 mM (red line, gain ×10) MeCN.

MeCN stabilization of Cu⁺_(aq)

Data in Fig. 2 confirm that acetonitrile at high concentration (>1 M) is able to rapidly and completely produce 50 mM Cu⁺ from 25 mM Cu²⁺ and Cu⁰ through a comproportionation reaction in aqueous solution. Oxidation of Cu⁺ is prevented by preparation and storage under strictly anaerobic conditions, and [Cu⁺] does not change over at least 6 months. EPR spectroscopy of experimental solutions indicates that 5 mM MeCN is not sufficient to stabilize 125 μM Cu⁺ but 25 mM MeCN maintains >99.5% Cu⁺.

The Cu⁺–MeCN equilibrium constants reported by Kamau and Jordan²⁰ predict a small amount of uncomplexed Cu⁺ under the solution conditions used in this study (ESI Table S1†), in which case the equilibrium would gradually shift away from Cu⁺ due to disproportionation. This is not consistent with our observation that 125 μM Cu⁺ is stable for days in 25 mM MeCN. Further, using their values in the analysis of our BCA titrations into MeCN-stabilized Cu⁺ (vide infra) gives a condition-independent log β₂ = 15.2 for Cu^I(BCA)₂⁺, which is two orders of magnitude smaller than the values reported by Wedd⁹ and Fahrni.²¹ While this may be due to different solution conditions, it is noteworthy that the most likely culprit, chloride, which may be interacting with Cu⁺ under the experimental conditions, has a negligible effect on the thermodynamics of Cu^I(BCA)₂³⁻ formation over a 1000-fold range of concentration (<0.1 mM–100 mM NaCl; ESI Table S2†). The ambiguity in the MeCN values is reinforced by noting that the NIST value²² for β₂ is 12% higher than the Kamau and Jordan value.²⁰ Thus, the published Cu⁺–MeCN affinity constants should be used with caution.

As an alternate approach, the well accepted β₂ value (3.16 × 10¹⁷)^9,21 for the formation of Cu^I(BCA)₂³⁻ can be used to quantify the MeCN competition for Cu⁺ (Q in eqn (2) and (3)), and thus its interaction with the metal ion, under the experimental conditions. Using this approach, we determined the average value of Q = 65 000 ± 5000 (K = β₂ = 3.16 × 10¹⁷ in eqn (3)). This value accounts for all the competition with BCA for the Cu⁺ under these conditions including, but not limited to, MeCN, buffer, and Cl⁻. To test this approach, the condition-independent β₂ value for the formation of Cu^I(BCS)₂³⁻ was calculated from the average best fit experimental value for BCS → Cu⁺ titrations in 25 mM MeCN (vide infra) using this value of Q; this leads to log β₂ = 20.6 ± 0.1, which is reassuringly bracketed by the values reported by Wedd (19.9)⁹ and Fahrni (20.8).²¹

Cu⁺–MeCN enthalpy

One of the main advantages of ITC is its ability to directly measure the enthalpy of binding reactions. For measurements of metal ions binding to proteins, the experimental enthalpy necessarily includes contributions from metal–ligand and metal–buffer interactions, which must be included in a post hoc analysis of the data to accurately quantify the metal–protein interactions. The aqueous solution chemistry of Cu⁺ prevents the direct measurement of Cu⁺–MeCN interactions by ITC; however, the enthalpy of this interaction can be estimated by systematically varying [MeCN] and observing the effect on the enthalpy of BCA → Cu⁺ titrations. ESI Table S1† reports the distribution of Cu⁺–MeCN species at 10, 25, 500, and 1000 mM MeCN, for which there is likely a modest error due to uncertainty in the stability constants, discussed above. These calculated values indicate that the average number of coordinated MeCN's ranges from 1.0 (68% Cu^I(MeCN) and 16% Cu^I(MeCN)₂) at 10 mM up to 2.6 (1% Cu^I(MeCN), 40% Cu^I(MeCN)₂ and 59% Cu^I(MeCN)₃) at 1000 mM. Strikingly, the reaction enthalpy for BCA → Cu⁺ titrations is not sensitive to [MeCN] over this range. This suggests that the enthalpy of Cu^I(MeCN)_n complex dissociation is within the error of this experiment (standard error = 0.23 kJ mol⁻¹). Based on these results, Cu–MeCN interactions under these conditions (25 mM Tris pH 8.0, 25 °C) are entropically driven and have an estimated enthalpy of only 0.00 ± 0.23 kJ mol⁻¹. Entropy-driven metal ligation is a well-documented phenomenon, whose origin is the displacement of the highly ordered solvent shell around the hydrated metal ion.²³

BCA and BCS

BCA–Cu⁺ interaction

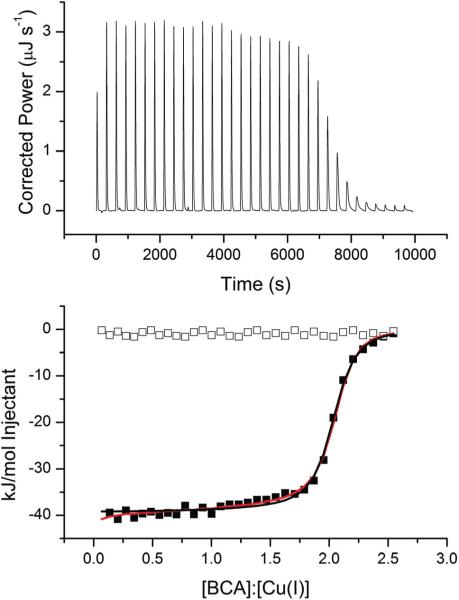
BCA forms a well-known 2 : 1 complex with Cu⁺ that is readily monitored by spectroscopic methods, making it easy to measure the concentration of this complex. Therefore, it was chosen to test MeCN stabilization of Cu⁺ for calorimetric measurements. The ITC data for BCA → Cu⁺ titrations in HEPES buffer at pH 7.0 show a sigmoidal titration curve with a major inflection at a 2 : 1 BCA : Cu⁺ ratio (Fig. 4). These data can be sufficiently fit using a one-site binding model with n = 2 (fit values summarized in Table 1), indicating that the two binding events have equivalent thermodynamic properties. Fitting the data to a sequential binding model provides a slightly better fit, according to a residual sum of squares analysis per degree of freedom (RSS/DoF_onesite = 7.71 vs. RSS/DoF_sequential = 4.04). The major difference between these two fits is the somewhat more exothermic ΔH₁ value in the sequential model than in the one-site model.

Fig. 4.

Representative ITC titration of 1.0 mM BCA into 125 μM Cu⁺ in 25 mM HEPES, 100 mM NaCl and 25 mM MeCN at pH 7.0 on a TA Instruments Nano ITC. The black line indicates the best fit using a one-site binding model (n = 2.01 ± 0.06, K = 1.7 ± 0.2 × 10⁶, ΔH = −37.3 ± 0.2 kJ mol⁻¹, RSS/DoF = 7.71) and the red line represents the best fit using a sequential binding model (K₁ = 8.9 ± 0.7 × 10⁵, ΔH₁ = −42.0 ± 0.2 kJ mol⁻¹, K₂ = 1.1 ± 0.1 × 10⁶, ΔH₂ = −36 ± 1 kJ mol⁻¹, RSS/DoF = 4.07). Open boxes indicate the heat of BCA dilution.

Table 1.

Average best fits of ITC experimental data for BCA/Cu⁺ titrations at 25 °C to a one-site binding model^a

Buffer	pH	[MeCN] (mM)	n	ΔH kJ mol–1 (kcal mol–1)	KITC (×106)
BCA → CuI
Tris	7.5	25	2.11 ± 0.05	–28 ± 1 (–6.7 ± 0.2)	2.2 ± 0.2
Tris	8.0	10b	1.96 ± 0.04	–27.3 ± 0.8 (–6.5 ± 0.2)	2.3 ± 0.3
Tris	8.0	25	2.02 ± 0.01	–27.0 ± 0.2 (–6.45 ± 0.05)	2.0 ± 0.3
Tris	8.0	500	1.9 ± 0.1	–28 ± 1 (–6.7 ± 0.2)	3.6 ± 0.3
Tris	8.0	1000	2.01 ± 0.09	–27.1 ± 0.7 (–6.5 ± 0.1)	1.1 ± 0.1
Tris	8.5	25	1.98 ± 0.03	–27.0 ± 0.5 (–6.5 ± 0.1)	0.8 ± 0.1
Bis-Tris	6.0	25	2.04 ± 0.01	–38.0 ± 0.2 (–9.09 ± 0.05)	2.4 ± 0.1
Bis-Tris	7.0	25	1.95 ± 0.01	–37.0 ± 0.4 (–8.84 ± 0.09)	2.3 ± 0.5
HEPES	7.0	25	2.08 ± 0.01	–37.0 ± 0.5 (–8.8 ± 0.1)	2.4 ± 0.4
CuI → BCA
Tris	8.0	500	0.51 ± 0.01	–53.2 ± 0.2 (–12.81 ± 0.05)	2±3
HEPES	7.0	500	0.48 ± 0.01	–72.4 ± 0.5 (–13.3 ± 0.1)	5±3

^aAll data collected in 25 mM buffer and 100 mM NaCl. Fit parameters represent the average of at least three independent titrations.

^b[Cu⁺] in reaction cell = 50 μM to ensure Cu⁺ stability. All other reactions are conducted with 125 μMCu⁺.

To test which model most accurately reflects the BCA/Cu⁺ binding chemistry, a reverse titration (Cu⁺ → BCA) was carried out under the same conditions. In this titration, BCA is in excess at the beginning of the titration, so the Cu^I(BCA)₂³⁻ complex forms in the first injections. Indeed, the best fit to these data gives an enthalpy that is twice that of the BCA → Cu⁺ titration (ΔH_obs = −72 kJ mol⁻¹), and no evidence of a second binding event is observed (ESI Fig. S1†). This result is consistent with the one-site model, which predicts two equivalent BCA binding events; as additional Cu⁺ is added to the Cu^I(BCA)₂³⁻ complex at stoichiometries of n > 0.5, the shift to two Cu^I(BCA)₁¹⁻ complexes would result in a net ΔH_obs = 0 (Scheme 1). Further, a global analysis of the forward and reverse titrations using SEDPHAT results in nearly identical parameters for each event.

Scheme 1.

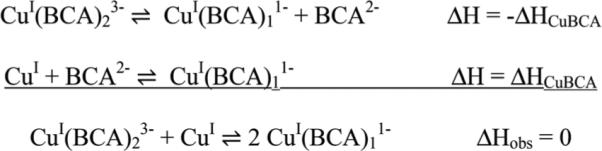
Equilibria for the second step of the reverse titration.

To verify these results, analogous measurements were made in Tris buffer at pH 8.0 and similar qualitative results were observed. However, the best fit of these BCA → Cu⁺ titrations with a one-site model yields ΔH = −27 kJ mol⁻¹, which is 10 kJ mol⁻¹ less exothermic than the same titration in HEPES buffer at pH 7.0 (Table 1). Since BCA lacks an ionizable proton in this pH range, it is unlikely that coupled proton flow is responsible for the difference, suggesting an alternate reason for the enthalpy difference. One difference between Tris and HEPES is the primary amine of the former and the tertiary amine of the latter (Fig. 1); this suggests that Tris may be able to compete with MeCN and coordinate the Cu⁺ while HEPES may not for steric reasons. To test this hypothesis, the same titration was carried out at pH 6.0 and 7.0 in BisTris buffer, which also has a tertiary amine. In both cases, the one-site fit values (Table 1) are essentially identical to those obtained in HEPES. Further, titrations in Tris at pH 7.5 and 8.5 give thermodynamic values that are similar to those observed at pH 8.0 (Table 1). However, a modest trend is observed in the stability, as a three-fold higher affinity is found at pH 7.5 relative to 8.5 (2.2 × 10⁶ and 0.8 × 10⁶, respectively). This observation is consistent with the basic form of the Tris primary amine competing for one of the metal coordination sites, although this trend does not show up in the binding enthalpy.

BCS–Cu⁺ interaction

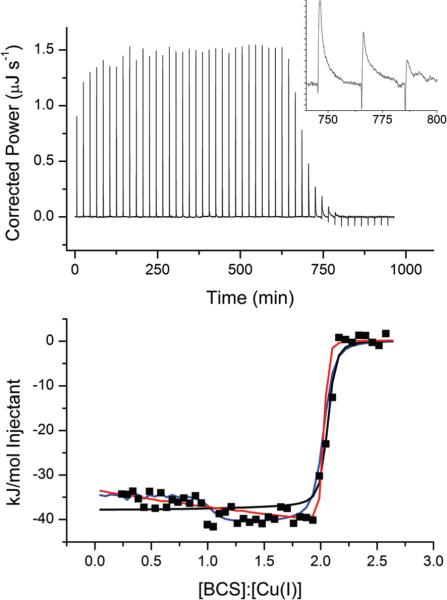
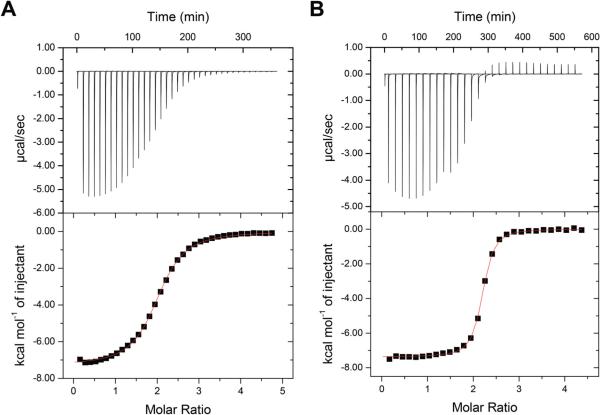
BCS has been an important tool in studies of the Cu⁺ affinity of cuproproteins,^5–12 and it is important to determine the thermodynamics of formation of the Cu^I(BCS)₂³⁻ complex. Fig. 5 shows a representative ITC titration of BCS into Cu⁺ stabilized by MeCN. The raw data (top panel) have a much slower return to baseline per injection than observed with other ligands; in fact, 20 minutes is required to completely finish the heat evolution of injections near the inflection point (see inset of Fig. 5). The data show a slow progression toward increasingly exothermic injections until a steep inflection is observed at 2 : 1, bringing the injection heat back to the baseline. While these data provide an accurate measure of the binding enthalpy, the binding constant determined from the steep inflection would have considerable uncertainty. Nevertheless, these data were fit to obtain K values for later comparison to stabilities that can be accurately determined.

Fig. 5.

Representative ITC titration of 1.0 mM BCS into 125 μM Cu⁺ in 25 mM Tris, 100 mM NaCl and 25 mM MeCN at pH 8.0 on a TA Instruments Nano ITC. The solid black line indicates the best fit using a one-site binding model (n = 2.03 ± 0.01, K = 1.8 ± 0.9 × 10⁷, ΔH = −37.9 ± 0.4 kJ mol⁻¹, RSS/DoF = 157) and the blue and red lines represent two independent fits using a sequential binding model (Blue: K₁ = 1.5 ± 0.1 × 10⁹, ΔH₁ = −34.7 ± 0.5 kJ mol⁻¹, K₂ = 4.75 ± 0.4 × 10⁶, ΔH₂ = −41.2 ± 0.6 kJ mol⁻¹, RSS/DoF = 50.5; Red: K₁ = 1.5 ± 0.6 × 10⁸, ΔH₁ = −33 ± 1 kJ mol⁻¹, K₂ = 4 ± 1 × 10⁷, ΔH₂ = −42 ± 1 kJ mol⁻¹, RSS/DoF = 67.75). The insert shows an expansion of the last three exothermic injections.

Table 2 summarizes the average fits using two different binding models. A one-site binding model provides a reasonably good fit of the data at the beginning of the titration, especially considering the scatter in these points, but fails to accurately capture the steepness of the inflection at 2 : 1, resulting in an underestimation of K. The other two fit lines in Fig. 5 (red and blue) represent two different fits (local minima) that consistently converge using a sequential binding model. The blue line more accurately captures the inflection observed at the 1 : 1 molar ratio but fails to reflect the steepness of the inflection at the 2 : 1 ratio. In contrast, the red line is biased toward the steep 2 : 1 inflection and does not recognize the ‘step’ at 1 : 1. The blue fit is somewhat better, according to a residual sum of squares analysis (RSS/DoF_blue = 50.5 and RSS/DoF_red = 67.75); however, this is largely due to the number of data points leading up to the major 2 : 1 inflection, and it fails to account for the poor fit of the major inflection. As such, the red model appears to be the more physically appropriate, and the data in Table 2 reflect this fit.

Table 2.

Average best fits of ITC experimental data for ligand → Cu⁺ titrations at 25 °C^a

Ligand	Model	n 1	ΔH1 kJ mol–1 (kcal mol–1)	K1 (×106)	ΔH2 kJ mol–1 (kcal mol–1)	K2 (×106)
25 mM Tris pH 8.0
BCS	One site	2.11 ± 0.05	–37 ± 1 (–8.84 ± 0.02)	22 ± 2
BCS	Sequential	—	–33 ± 1 (–7.9 ± 0.2)	150 ± 60	–42 ± 2 (–10.0 ± 0.5)	40 ± 1
GSH	One site	1.03 ± 0.3	–118.9 ± 0.7 (–28.4 ± 0.2)	1.3 ± 0.1
25 mM HEPES pH 7.5
GSH	One site	0.99 ± 0.01	–104 ± 4 (–24.9 ± 0.9)	0.32 ± 0.08
GSH	Sequential	—	–98 ± 2 (–23 ± 1)	0.3 ± 0.2	–6±20(–1 ± 5)	0.001 ± 0.001

^aAll data collected in 100 mM NaCl and 25 mM MeCN. Fit parameters represent the average of at least two independent titrations. Error is calculated by propagation of individual fits; see Experimental for explanation.

BCA and BCS stabilization of Cu⁺_(aq)

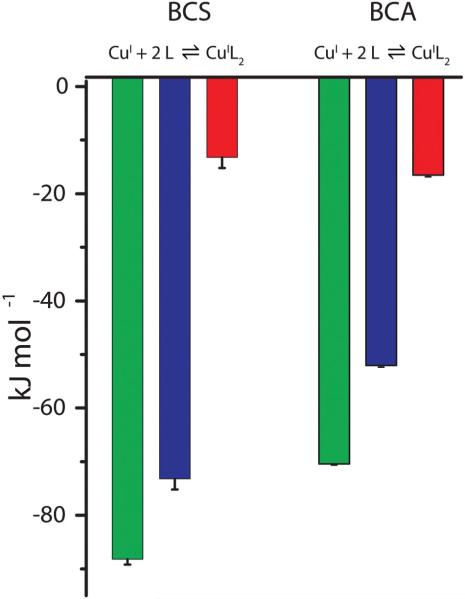
Both BCA and BCS are nitrogenous bidentate ligands that are selective for Cu⁺ over Cu²⁺ due to their firm requirement for a tetrahedral coordination geometry.^24,25 As summarized in Table 3, these two ligands form very stable 2 : 1 Cu⁺ complexes (β_2,BCA = 10^17.7 and β_2,BCS = 10^20.6) with the indicated enthalpies of formation. Their free energies of formation are ΔG_BCA = −101 kJ mol⁻¹ and ΔG_BCS = −118 kJ mol⁻¹, respectively, and Fig. 6 depicts the overall thermodynamic profiles for BCA and BCS binding to Cu⁺. The difference between their free energies of formation (ΔΔG = −16 kJ mol⁻¹) is predominantly due to the difference between their formation enthalpies (ΔΔH = −19 kJ mol⁻¹), indicating that the change in entropy for BCA and BCS binding to Cu⁺ is similar (−TΔS = −34 kJ mol⁻¹). This enthalpic difference is consistent with the fact that the BCS nitrogens are stronger Lewis bases than the BCA nitrogens, as indicated by the measurable pK_a (5.7) of BCS but not BCA.⁹ The thermo- dynamics of the two sequential binding events for BCA are identical but this is not so for BCS, as the first coordination has a favorable entropic contribution, while the second does not (ESI Table S3†). However, without information about the intermediate Cu^I(BCS)₁(MeCN)_x⁻¹ species, the source of this thermodynamic difference cannot be determined.

Table 3.

Condition-independent Cu⁺ stability constants and formation enthalpies at 25 °C

Ligand	n	β n	Log βn	Log βn (literature)	ΔHCU(I)L (kJ mol–1)
Me6Trien	1	3 ± 1 × 1012	12.4	11b	-17 ± 8
BCAa	2		17.6	17.5c	-75 ± 0.3
BCS	2	4±1 × 1020	20.6	20.4c	-95 ± 2

^aβ_n for BCA was used as a reference value.

^bLiterature value from Navon et al.²⁶

^cAverage literature value from Xiao et al.⁹ and Banci et al.²⁸

Fig. 6.

Thermodynamic profile for ligand binding to Cu⁺ at pH 8.0 in 25 mM MeCN and 100 mM NaCl. Green = ΔG, blue = ΔH, red = −TΔS. BCS: ΔG = −90 ± 1, ΔH = −75 ± 2, −TΔS = −15 ± 2; BCA: ΔG = −72 ± 1, ΔH = −54.0 ± 0.3, −TΔS = −18.0 ± 0.4.

The binding of BCS to Cu⁺ was uniquely slow among the ligands in this study. The long time required to return to baseline, especially near the 2 : 1 equivalence point where the concentration of MeCN-stabilized Cu⁺ is low (Fig. 5, inset), indicates slow ligand exchange kinetics for BCS. This contrasts with the observation that spectrophotometric titrations with BCS show no indication of slow kinetics (data not shown). It is possible that spectroscopically-observable binding events occur quickly and the slower heat evolution is due to a spectroscopically-unobservable rearrangement around the metal. Whatever the reason, this should be considered when designing experiments using this ligand for thermodynamic or kinetic studies.

Me₆Trien

Me₆Trien–Cu⁺ interaction

Since MeCN stabilizes Cu⁺ with a relatively low overall stability and the 2 : 1 Cu⁺ complexes with BCA and BCS are very stable, there is a need for a well-characterized Cu⁺ complex with intermediate stability. Such a complex is found with the tetradentate ligand hexamethyltriethylenetetramine, Me₆Trien, where the methyl groups enforce a Cu⁺-favoring tetrahedral coordination.^26,27 Initially we attempted to quantify the formation thermodynamics of Cu^I(Me₆Trien)⁺ by ITC titrations with MeCN-stabilized Cu⁺ solutions, as we did with BCA and BCS. However, the large excess of MeCN required to stabilize Cu⁺ and the proton competition with Cu⁺ for Me₆Trien (pK_a1 = 9.19, pK_a2 = 8.38, α = 651)²² at pH 7.4 led to immeasurable formation under these conditions. Therefore, we prepared the Cu^I(Me₆Trien)⁺ complex by comproportionation,²⁶ as described for MeCN, and measured Me₆Trien displacement by ligands with higher Cu⁺ affinity. Since this complex is more stable than the MeCN complex, only a 5–6 fold excess of Me₆Trien was necessary for the comproportionation, and a successful synthesis was indicated by complete loss of the initial deep blue color (ε₆₈₆ = 250 M⁻¹ cm⁻¹)^26,27 of Cu^IIMe₆Trien²⁺ (log K = 12.60, ε° = 60 mV at pH 7.0).²⁷ Since experimental titrations that deliver Cu⁺ as the Cu^IMe₆Trien⁺ complex necessarily involve the displacement of Me₆Trien by another ligand or a protein, a sufficient excess (>50 fold) of Me₆Trien in the titrant and titrand solutions ensures a relatively constant concentration over the course of the titration for a simplified binding analysis. This larger excess is recommended for the comproportionation preparation of Cu^IMe₆Trien⁺ as well.

Representative ITC data for a BCA titration of Cu^IMe₆Trien⁺ (Fig. 7a) show the expected 2 : 1 binding stoichiometry and the data can be reasonably fit to a one-site binding model, indicating either cooperative binding of both BCA ligands or similar enthalpies for each one binding to the Cu⁺. A reverse titration gives a single inflection at n = 0.5 and twice the enthalpy, indicating that the latter is the correct interpretation, as found for BCA titrations with MeCN-stabilized Cu⁺. Similar results (Fig. 7b), and a similar interpretation, are found for BCS titrations of Cu^IMe₆Trien⁺. Table 4 contains the average best-fit experimental values for the BCA and BCS titrations of Cu^IMe₆Trien⁺.

Fig. 7.

Representative ITC titrations of (A) 2.5 mM BCA and (B) 2.0 mM BCS into 100 μM Cu⁺ in 50 mM HEPES, 50 mM NaCl, 5 mM Me₆Trien, pH 7.4 on a MicroCal VP-ITC. Best fits to the data with a one-site binding model are: (A) n = 2.01 ± 0.01, K = 1.53 ± 0.04 × 10⁵, ΔH = −7.39 ± 0.02 kcal mol⁻¹ and (B) n = 2.14 ± 0.01, K = 1.55 ± 0.06 × 10⁶, ΔH = −7.36 ± 0.04 kcal mol⁻¹.

Table 4.

Average best fits of ITC experimental data for ligand → Cu^IMe₆Trien⁺ at 25 °C^a

Ligand	n 1	ΔH1 kJ mol–1 (kcal mol–1)	K1 (×106)	Log KCuMe6Trien+b
BCA	1.92 ± 0.04	–30 ±2 (–7.1 ± 0.4)	0.17 ± 0.04	12.1 ± 0.2
BCS	2.12 ± 0.03	–31 ±1 (–7.4 ± 0.3)	1.3 ± 0.8	12.8 ± 0.6

^aData collected in 50 mM HEPES at pH 7.4 with 100 mM NaCl and [Me₆Trien] = 50 × [Cu⁺]. Fit parameters represent the average of at least two independent titrations.

^bBuffer- and pH-independent values.

Me₆Trien stabilization of Cu⁺_(aq)

These results have shown that Me₆Trien can be used as a ligand for Cu⁺ delivery from a complex that is more stable than those with MeCN and avoids ternary intermediates. Comproportionation preparation of this species is shown by the complete conversion of Cu^IIMe₆Trien²⁺ to Cu^IMe₆Trien⁺. Analysis of the data in Table 4 that takes into account the stability and enthalpy of formation of Cu^I(BCA)₂³⁻, or analogous values for Cu^I(BCS)₂³⁻, as well as the pK_a's and protonation enthalpies of Me₆Trien and the buffer,²² leads to the buffer-independent stability constant and enthalpy of formation of Cu^IMeTrien⁺ (Table 3). In contrast to solutions of MeCN-stabilized Cu⁺, binding studies that use this complex to deliver Cu⁺ will depend on the pH and are somewhat more complicated to analyze due to the higher basicity of this ligand (representative calculations are found in the ESI†). A somewhat lower precision in the Cu^IMeTrien⁺ heat of formation is due to uncertainties in the heats of Me₆Trien protonation²² and a small discrepancy between the BCA and BCS titrations.

However, the Cu^IMeTrien⁺ stability (K = 10^12.4 at pH 7.4) bridges the gap between that of Cu^I(MeCN)₃⁺ (β₃ = 10^4.3) and Cu^I(BCA)₂³⁻ (β₂ = 10^17.5.

Buffers

Cu⁺–buffer interactions

Throughout this work, three experimental buffers have been used to assess the applicability of these Cu⁺-stabilizing complexes under a variety of experimental conditions. To test the effects of pH and the buffer, BCA titration data (Table 1) were used, since its interaction with Cu⁺ is independent of pH.⁹ No significant differences were observed when the pH was changed from 6.0 to 7.0 with BisTris or when the buffer was changed to HEPES at pH 7.0. However, a difference of 10 ± 1 kJ mol⁻¹ in the binding enthalpy was found when the buffer was changed to Tris at pH 7.5, 8.0, and 8.5, indicating that Tris is interacting with the Cu⁺–MeCN complex(es) and must be displaced. HEPES and BisTris both have an exchangeable proton on a tertiary amine, while the protonation site of Tris is a primary amine that is more accessible to coordinate to a metal (Fig. 1). The modest increase in the observed binding constant with decreasing pH (K_8.5 = 0.8 × 10⁶, K_8.0 = 2.0 × 10⁶, K_7.5 = 2.2 × 10⁶) in Tris is consistent with this hypothesis; as the solution becomes more acidic, the fraction of the basic form of Tris that is able to compete for the Cu⁺ decreases. However, any accompanying change in the binding enthalpy is within the error of the measurement, and this interaction with Tris does not shift the disproportionation equilibrium away from Cu⁺ under these experimental conditions. Further support for this interpretation of Tris effects on the Cu⁺ binding thermodynamics is found with preliminary BCA titrations of Cu^IMe₆Trien⁺ in the primary amine buffer ACES.

Glutathione

Glutathione–Cu⁺ interaction

Since GSH is the most abundant cytoplasmic thiol in most cells and is reported to have a high affinity for Cu⁺,²⁸ it is important to accurately determine the thermodynamics of GSH binding to Cu⁺. This was investigated with MeCN-stabilized Cu⁺ in Tris at pH 8.0 and HEPES at pH 7.5. Fig. 8 shows representative ITC data for the latter and the heat of GSH dilution. In this case, the GSH → Cu⁺ titration fails to reach the baseline established by the dilution titration. This is most likely due to a second binding event with low affinity and/or low heat that occurs subsequent to formation of the 1 : 1 complex. Fitting the data to a one-site binding model (black line) provides a reasonable fit with n = 1. However, this model cannot account for the small amount of heat that follows the inflection. All the data can be well fit to a sequential binding model (red line), although large errors are associated with the 2^nd binding event. Evidence of this 2^nd event is not observed in Tris buffer a pH 8, which may be due to Cu⁺–Tris interaction, as found with BCA and described above.

Fig. 8.

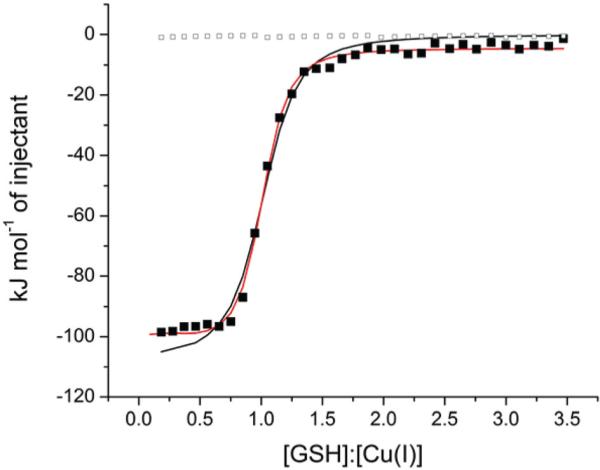
Integrated intensity of a representative ITC titration of 1.73 mM GSH into 168 μM Cu⁺ in 25 mM HEPES, 100 mM NaCl and 25 mM MeCN at pH 7.5 on a TA Instruments Nano ITC. The solid black line indicates the best fit using a one-site binding model (n = 0.98 ± 0.02, K = 2.9 ± 0.1 × 10⁵, ΔH = −108 ± 6 kJ mol⁻¹, RSS/DoF = 158.3) and the red line represents the best fit using a sequential binding model (K₁ = 6 ± 5 × 10⁵, ΔH₁ = −101 ± 3 kJ mol⁻¹, K₂ = 1 ± 8 × 10³, ΔH₂ = −10 ± 10 kJ mol⁻¹, RSS/DoF = 23.5). Open boxes indicate the heat of GSH dilution.

Using the best fits to the one-site model for comparison (Table 2), a significant difference in the binding enthalpy is found between the two buffers (ΔH_obs(Tris) = −118.9 ± 0.7 and ΔH_obs(HEPES) = −104 ± 4 kJ mol⁻¹). Unlike BCA, GSH binding to metal ions is necessarily coupled with a deprotonation at physiological pH due to coordination of the thiol (pK_a = 8.66).²² Therefore, a careful analysis of all equilibria that are coupled to the GSH–Cu⁺ interaction is needed to account for the difference in net enthalpy. Scheme 2, in which B represents the buffer and x, y, and z are unknown or mixed stoichiometric coefficients associated with Cu⁺–MeCN species, identifies the major events that occur during this reaction.

Scheme 2.

Equilibria associated with MeCN-stabilized Cu⁺ binding to GSH.

The proton that is displaced from the GSH thiol (ΔH₁ = −37 kJ mol⁻¹)²² will bind to the buffer, which generates heat from its protonation, ΔH₃;^15,18,29 because Tris and HEPES have different protonation enthalpies (−47.5 kJ mol⁻¹ and −21.4 kJ mol⁻¹, respectively), ΔH_obs is expected to differ by this difference (26.1 kJ mol⁻¹). However, subtracting ΔH₃ from ΔH_obs yields ΔH_(HEPES) = −82.6 kJ mol⁻¹ and ΔH_(Tris) = −71.4 kJ mol⁻¹. The difference between these two values (ΔΔH_(HEPES-Tris) = −11 ± 4 kJ mol⁻¹) is very similar to the observed difference in enthalpy between these two buffers in the BCA titrations of Cu⁺. Since all other equilibria are expected to be identical under the two conditions, this difference is likely associated with an additional Cu⁺–Tris interaction (ΔH₄).

The four-fold difference in K₁ between HEPES at pH 7.5 (K₁ = 3.2 × 10⁵) and Tris at pH 8.0 (K = 1.3 × 10⁶) in Table 2 can be explained by the experimental pH. The pK_a of the GSH thiol (8.66) leads to a proton competition factor (eqn (4)) of α = 6 at pH 8.0 and α = 15.5 at pH 7.5; accounting for this difference results in the very similar pH-independent binding constants of 7 × 10⁶ and 5 × 10⁶, respectively.

Glutathione binding to Cu⁺_(aq)

At pH 7.5 in HEPES buffer there is calorimetric evidence for two GSH binding events, although the second is weak and characterized by large fit errors (Table 2). This low affinity event is not observed in Tris buffer at pH 8.0, which may be due to Cu⁺–Tris interaction discussed above. Accounting for buffer ionization, the Cu⁺–GSH interaction is characterized by a striking entropic penalty that lowers the binding free energy (ESI Table S3†). Similar results are found with N-acetylcysteine binding to Cu⁺ (unpublished results). This affinity of GSH for Cu⁺ is consistent with the observation that it does not compete with copper-binding proteins for Cu⁺ in vitro.^11,30,31

Conclusions

The unique chemical properties of Cu⁺ provide experimental challenges to accurately quantify the thermodynamics of its binding to ligands, proteins and other biological molecules. This study has investigated and validated a method to prepare Cu⁺-stabilized complexes in aqueous solution for their use in binding measurements, specifically calorimetric measurements with ITC. The stability of these complexes varies over several orders of magnitude and their thermodynamics of formation have been determined (Table 3). This provides a set of well-characterized species for the delivery of Cu⁺ and the accurate determination of Cu⁺ binding thermodynamics with a wide range of biological ligands and protein sites. Two Cu⁺-stabilizing ligands are recommended from this work: MeCN and Me₆Trien. MeCN is attractive due to its low affinity and apparent “enthalpic silence”. However, as found with the GSH experiments, it has the potential to form ternary complexes that can unknowingly compromise measurements of the thermodynamics of Cu⁺ interactions. As such, it should be used with caution, and only when sequential binding events are not desired and the final complex accounts for all of the coordination sites. Me₆Trien, on the other hand, forms a well-characterized 1 : 1 complex with intermediate stability that avoids this problem, although its stabilization of Cu⁺ does depend on pH.