Detection of Locally Over-Represented GO Terms in Protein-Protein Interaction Networks

Abstract

High-throughput methods for identifying protein-protein interactions produce increasingly complex and intricate interaction networks. These networks are extremely rich in information, but extracting biologically meaningful hypotheses from them and representing them in a human-readable manner is challenging. We propose a method to identify Gene Ontology terms that are locally over-represented in a subnetwork of a given biological network. Specifically, we propose several methods to evaluate the degree of clustering of proteins associated to a particular GO term in both weighted and unweighted PPI networks, and describe efficient methods to estimate the statistical significance of the observed clustering. We show, using Monte Carlo simulations, that our best approximation methods accurately estimate the true p-value, for random scale-free graphs as well as for actual yeast and human networks. When applied to these two biological networks, our approach recovers many known complexes and pathways, but also suggests potential functions for many subnetworks. Online Supplementary Material is available at www.liebertonline.com.

1. INTRODUCTION

Gene ontologies provide a controlled, hierarchical vocabulary to describe various aspects of gene and protein function. The Gene Ontology (GO) Annotation project (Ashburner et al., 2000) is a literature-based annotation of a gene’s molecular function, cellular component, and biological processes. GO analyses have become a staple of a number of high-throughput biological studies that produce lists of genes behaving interestingly with respect to a particular experiment. For example, a microarray experiment may result in the identification of a set of genes that are differentially expressed between normal and disease conditions. A GO term (or category) τ is said to be over-represented in a given list if the number of genes labeled with τ contained in the list is unexpectedly large, given the size of the list and the overall abundance of genes labeled with τ in the species under consideration (see tools like GoMiner [Zeeberg et al., 2003], Fatigo [Al-Shahrour et al., 2004], or GoStat [Beissbarth and Speed, 2004]). Statistical over-representation is an indication that the GO category is directly or undirectly linked to the phenomenon under study. We say that this kind of set of differentially expressed genes is unstructured, in the sense that all genes within the list contribute equally to the analysis. A slightly more structured approach consists of considering an ordered list of genes, where genes are ranked by their “interest” with respect to a particular experiment (e.g., degree of differential expression). There, we seek GO terms what are surprisingly enriched near the top of the ranked list. This is the approach taken by the highly popular GSEA method (Subramanian et al., 2005), which generalizes this to include many kinds of gene annotations other than GO.

We propose taking this type of analysis one step further and applying GO term enrichment analysis to even more highly structured gene sets: biological networks. In such networks, genes (or their proteins) are vertices, and edges represent particular relationships (e.g., protein-protein interaction, regulatory interaction, genetic interaction). Given a fixed biological network G and a gene ontology annotation database, our goal is to identify every term τ such that the genes labeled with τ are unexpectedly clustered in the network (i.e., they mostly lie within the same “region” of the network). This local over-representation indicates that τ is likely to be linked to the function of that sub-network.¹ Indeed, and unsurprisingly, GO term clustering has been observed to occur in most types biological networks (Daraselia et al., 2007; Li et al., 2008), and has been used as a criterion to evaluate the accuracy of computational complex or module prediction (Mete et al., 2008). However, to our knowledge, the problem of identifying locally over-represented GO terms in a network has never been formulated or addressed before.

This problem has a number of applications. High-throughput technologies generate large networks (thousands of proteins and interactions) that are impossible to analyze manually. Graph layout approaches (reviewed in Suderman and Hallett, 2007), which are integrated in many network visualization packages such as VisANT (Hu et al., 2004) and Cytoscape (Shannon et al., 2003), can help humans extract biological meaning from the data, but revealing all aspects of a complex data set in a single layout is impossible, and often, key components of the network remain unstudied because the layout used did not reveal them visually. Various approaches have been proposed to ease the analysis of biological networks, including packages performing graph clustering and path analysis (e.g., NeAT [Brohe et al., 2008; Shannon et al., 2003]). Several methods have been proposed to identify pathways (Shlomi et al., 2006) within PPIs or combine expression data with PPI networks to infer signaling pathways (Scott et al., 2006). Expression data was also used to identify functional modules in PPI networks with a solution based on an integer-linear programming formulation (Dittrich et al., 2008). Another popular strategy starts by identifying dense subnetworks within the network (using, for example, MCL [Enright et al., 2002]), and then evaluates various biological properties of the subnetwork, including GO term enrichment (Sen et al., 2006).

Our proposed approach identifies subsets of genes that share the same GO annotation and are highly interconnected in the network, thus formulating the hypothesis that the function of the subnetwork is related to that GO annotation. This reduces the complexity of the data and allows easier grasp by human investigators. Our approach could be extended to help function prediction: genes with incomplete functional annotation that are found to be highly interconnected with a set of genes of known function can be expected to share that function (Chua et al., 2006; Sharan et al., 2007).

In this article, we define formally the problem of identification of locally enriched GO categories for unweighted and weighted undirected interaction networks. We start by defining two measures of clustering of a set of genes within a given weighted or unweighted network. We then discuss the critical question of assessing the statistical significance of the local clustering scores using analytical approaches of a given GO term within the network, under a null hypothesis where vertices are selected randomly (empirical approaches for shortest path distance significance have been proposed previously [Said et al., 2004]). We show that the exact computation of this probability is NP-hard, but we provide several efficient approximation methods. These p-value approximation methods are shown to be accurate on random scale-free graphs, as well as on large-scale yeast (Krogan et al., 2006) and human (Coulombe et al., 2008; Jeronimo et al., 2007) protein-protein interaction networks. We then refine each significant gene sets to core subsets that contribute the most to its statistical significance. Our analysis identifies regions of these two networks with known function. It also suggests interesting functions for regions of the network that are currently poorly understood.

2. METHODS

We are looking for GO terms whose distribution across a given network is non-random. In particular, we are interested in finding terms that are tightly clustered within the network. Let G = (V, E) be an undirected, unweighted graph, where V is a set of n proteins and E is a set of pairwise interactions between them. The Gene Ontology project assigns to each gene a set of functional annotations, using a controlled vocabulary. For a given GO term τ, let V (τ) ⊆ V be the subset of the proteins annotated with that term. Our goal is to investigate, for every possible term τ, whether V (τ) is particularly clustered in G, which would hint to the fact that τ is particularly relevant to the function of that subgraph. To this end, we introduce in Section 2.1 two measures of clustering, as well as their generalizations to weighted graph, and show in Section 2.2 how to measure their statistical significance.

2.1. Measures of clustering on a network

A number of approaches have been proposed to measure the clustering of a set of vertices within a given graph, and to identify dense clusters (e.g., MCL [Enright et al., 2002]; for see a review, Brohe and van Helden [2006]. We focus on two simple but effective clustering measures, for which the statistical significance can be accurately approximated analytically.

2.1.1. Total pairwise distance

Given two vertices u and v in V, let d_G (u, v) be the length of a shortest path from u to v in G. Since G is undirected, d_G is symmetric. The distance matrix d_G can be computed in time O(|V|³) using the Floyd-Warshall algorithm (Floyd, 1962; Warshall, 1962). Let W be a subset of V. Then, the total pairwise distance for W is defined as

$$\mathit{TPD}(W)=\sum _{u,v\in W,u<v}{d}_G(u,v).$$ (1)

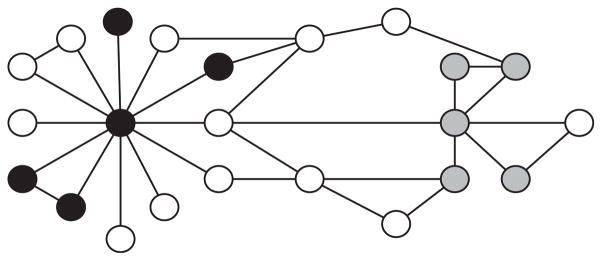
If most of the vertices in V (τ) are in the same region of the graph (e.g., the gray or black vertices in Fig. 1), then TPD(V (τ)) will be smaller than that of most random subsets of |V (τ)| vertices and τ will be reported as potentially interesting.

FIG. 1.

Example of a toy PPI network. The black and gray subsets of vertices obtain the same Total Pairwise Distance (13), but the gray subset obtains a higher Probability of Stopping within the Family (PSF).

2.1.2. Random-walk based similarity

One issue with the TPD clustering measure is that it does not take into consideration the degree of the nodes on the path between the two proteins, in such a way that, for example, the two sets of proteins shown in black and gray in Figure 1 will get the same total pairwise distance (and, eventually, the same p-value), although intuitively the gray cluster appears more interesting. In addition, if the vertices in W form more than one dense subgraphs, and these clusters are far away from each other, the TPD measure may not reveal anything unusual. We introduce an alternative to the total pairwise distance, which we call the Probability of Staying within the Family (PSF) clustering measure. This random-walk based similarity measure shares a relationship with diffusion kernels (Kondor and Lafferty, 2002). The PSF for a subset of vertices W is defined based on the following random process (similar to that modeled by MCL [Enright et al., 2002]), parameterized by a user-defined probability p: (i) Randomly select a vertex from W as a starting point; (ii) When at vertex u, stop with probability p, or, with probability 1 − p, continue to a vertex v uniformly chosen from the neighbors of u. Then, PSF_p(W) is defined as the probability that the vertex where the process stops is an element of W. We note first that this process does make a difference between the two subsets in Figure 1 and will also assign a high score to a subset W that would consist of several dense but widely separated clusters.

If A_G is the adjacency matrix of G and deg_G(u) is the degree of vertex u, then the transition probability matrix T_G for this random walk is defined as

$$T_G(u,v)=A_G(u,v)/\sum _{w\in V}{A}_G(u,w),$$ (2)

and the probability P_u,v of stopping at vertex v, starting from vertex u, is given by

$$P_{u,v}=\sum _{i=0}^{+\infty }p{(1-p)}^i({(T_G)}^i)(u,v).$$

Thus,

$${\mathit{PSF}}_p(W)=\sum _{u,v\in W}{P}_{u,v}/\mid W\mid =\sum _{u,v\in W}{s}_G(u,v),$$

and we obtain that, as for the total pairwise distance, the PSF measure is a sum of pairwise scores, with s_G(u,v) = P_u,v/|W|.

2.1.3. Generalization to weighted graphs

Edge weights are often used in protein-protein interaction networks to reflect the confidence that a given interaction is a true positive. Such scores can be provided by mass spectrometry analysis programs (e.g., Mascot [Perkins et al., 1999] or PeptideProphet [Choi and Nesvizhskii, 2007]). Both the TPD and PSF clustering measures can be adapted in the context of a weighted graph. The weighted TPD (WTPD) measure is obviously generalized using the weighted shortest path distances for d_G in Equation 1. In this case, edges are weighted as

$$w(e)=\{\begin{array}{ll}1+max(0,{log}_{10}(\mathit{maxMascot})-{log}_{10}(\mathit{mascot}(e)))\hfill & \text{if}e\in E\hfill \\ +\infty \hfill & \text{otherwise}\hfill \end{array}$$

where mascot(e) is the Mascot score associated with edge e and maxMascot = 500. The obtained weighted distance matrix will be referred as d_GW. This measure penalizes paths with low confidence scores, therefore when the vertices in V (τ) are located in the same region of the graph and edges connecting those vertices have high confidence, WTPD(V (τ)) will be small.

A generalization of PSF to WPSF is obtained by replacing the adjacency matrix A_G by the weighted adjacency matrix A_GW in Equation 2, where

$$A_{G_W}(e)=\{\begin{array}{ll}{log}_{10}(\mathit{mascot}(e))\hfill & \text{if}e\in E\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}$$

The resulting weighted similarity matrix will be referred to as s_GW.

The methods proposed in Section 2.2 to assess statistical significance apply to both TPD and PSF, and their respective weighted versions.

2.2. Measuring the statistical significance

Given a matrix M_|V|×|V| containing pairwise distances (d_G or d_GW), or similarities (s_G or s_GW), we consider the random variable obtained as follows. Let R = {r₁, r₂, …, r_k} ⊆ {1, …, n} be a randomly selected subset of proteins of cardinality k. We are interested in the distribution of the random variable S_k = Σ_{i, j∈R, i <j} M_{i, j}. When using the weighted or unweighted TPD clustering measure, the p-value for GO term τ will be obtained as p-value_TPD(τ) = Pr[S_{|V (τ)|} ≤ TPD(V (τ))], whereas when using the PSF clustering measure, the p-value will be obtained as pvalue_PSF(τ) = Pr[S_{|V (τ)|} ≥ PSF_p(V (τ))]. Note that there is no need to adjust the p-values for k since we are analyzing a different distribution for each S_k.

A note on complexity

We first observe that computing the exact distribution of S_k when M = d_G is NP-hard. Indeed, $Pr[S_k=\left(\begin{array}{c}k\\ 2\end{array}\right)]$ is non-zero if and only if G contains a k-clique. Therefore, we cannot expect an exact polynomial time algorithm. Although more difficult to prove, the same is likely true for PSF. We thus investigate three approaches that give approximations to the desired probability distributions.

2.3. Normal approximation

Being a sum of $\left(\begin{array}{c}k\\ 2\end{array}\right)$ random variables, the distribution of S_k should converge to a normal distribution as k and |V| become large (Central Limit Theorem), if these random variables were independent. Although these variables are clearly not independent (for example, in the case of TPD, they must satisfy the triangle inequality), it turns out that the normality assumption sometimes yields a useful approximation to the true distribution. The expectation of S_k can be calculated exactly in time O(|V|²). Let $E[S_2]=\frac{{\mathrm{\sum }}_{1\le a<b\le n}{M}_{a,b}}{\left(\begin{array}{c}n\\ 2\end{array}\right)}$ be the average pairwise score in M. Then

$$E[S_k]=\left(\begin{array}{c}k\\ 2\end{array}\right)·E[S_2]$$

The variance of S_k is more challenging to obtain. We have $\mathit{Var}[S_k]=E[S_k^2]-E{[S_k]}^2$, where

$$\begin{array}{l}E[S_k^2]=E\left[{\left(\sum _{a,b\in R,a<b}{M}_{a,b}\right)}^2\right]\\ =E[\left\{\sum _{a,b\in R,a<b}{(M_{a,b})}^2\right\}+\left\{2\sum _{a,b,c\in R,a<b<c}{M}_{a,b}{M}_{a,c}+M_{a,b}{M}_{b,c}+M_{a,c}{M}_{b,c}\right\}+2\left\{\sum _{a,b\in R,a<b}\sum _{c<d\in R,c\ne a,b,d\ne a,b}{M}_{a,b}{M}_{c,d}\right\}]\\ =\frac{\left(\begin{array}{c}c\\ k\end{array}\right)}{\left(\begin{array}{c}n\\ 2\end{array}\right)}\sum _{1\le a<b\le n}{(M_{a,b})}^2+2\frac{\left(\begin{array}{c}k\\ 3\end{array}\right)}{\left(\begin{array}{c}n\\ 3\end{array}\right)}\left\{\sum _{1\le a<b<c\le n}{M}_{a,b}{M}_{a,c}+M_{a,b}{M}_{b,c}+M_{a,c}{M}_{b,c}\right\}+2\left\{\sum _{a,b\in R,a<b}{M}_{a,b}\sum _{c<d\in R,c\ne a,b,d\ne a,b}{M}_{c,d}\right\}\end{array}$$

The running time of the variance computation is thus O(n⁴), which, in many cases, is prohibitive. However, when a ≠b ≠c ≠d, M_a,b is nearly independent from M_c,d, so

$$E[S_k^2]\approx \frac{\left(\begin{array}{c}k\\ 2\end{array}\right)}{\left(\begin{array}{c}n\\ 2\end{array}\right)}\sum _{1\le a<b\le n}{(M_{a,b})}^2+2\frac{\left(\begin{array}{c}k\\ 3\end{array}\right)}{\left(\begin{array}{c}n\\ 3\end{array}\right)}\left\{\sum _{1\le a<b<c\le n}{M}_{a,b}{M}_{a,c}+M_{a,b}{M}_{b,c}+M_{a,c}{M}_{b,c}\right\}+2\left(\begin{array}{c}k\\ 2\end{array}\right)\left\{\left(\begin{array}{c}k\\ 2\end{array}\right)-2k+3\right\}E{[S_2]}^2$$

We call this approach the normal approximation method.

2.4. Convolution-based approaches

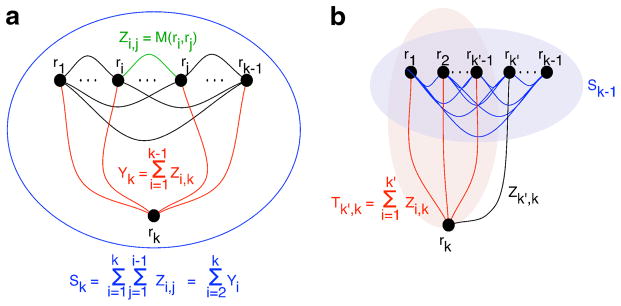
Considering again a random subset of vertices R = {r₁, r₂, …, r_k}, we define the random variables Z_i,j = M_ri,rj, for 1 ≤ i < j ≤ n and $Y_i={\sum }_{j=1}^{i-1}{M}_{r_j,r_i}$, for i = 2 …k (Fig. 2). In this section, we assume that the scores in M are integers. This will always be the case when M = d_G. When M = s_G, M = s_GW, or M = d_GW, we assume that elements of M has been appropriately discretized to integers. Observe that $S_k={\sum }_{i=1}^k{\sum }_{j=1}^{i-1}{Z}_{i,j}={\sum }_{i=2}^k{Y}_i$. The random variable S_k is a sum of $\left(\begin{array}{c}k\\ 2\end{array}\right)$ random but dependent variables. If we ignored the dependencies, the distribution of S_k could be obtained as the $\left(\begin{array}{c}k\\ 2\end{array}\right)$-fold self-convolution of the discrete distribution f_G, where $f_G(a)={\sum }_{1\le i<j\le \mid V\mid }{1}_{a=M_{i,j}}/\left(\begin{array}{c}\mid V\mid \\ 2\end{array}\right)$ is the fraction of entries in M with value a. This turns out to produce a very poor approximation of the distribution of S_k, severely underestimating the correct probability for small values of S_k. We can improve the situation by modeling some of the dependencies. Again, the family of Y random variables are dependent: in particular, if $S_{k-1}={\sum }_{i=2}^{k-1}{Y}_i$ is small, i.e., r₁, …, r_{k − 1} form a tight cluster, then the variance of Y_k is increased, because the variables Z_*,k are highly dependent on each other (e.g., if Z_i,k is small, then Z_{i′, k} is also likely to be small, because i and i′ belong to the same tight cluster). We consider two approaches to the problem: the first calculates nearly exactly the distribution of the Y_i’s but ignores their dependencies, while the second models the dependencies more accurately but is less accurate at the level of each distribution.

FIG. 2.

Definition of the variables used in the convolution approaches. (a) Y-convolution method. (b) Triangle decomposition method.

The Y-convolution method

Let $g_i(a)={\sum }_{j=1}^n{1}_{a=M_{i,j}}/(n-1)$ be the fraction of pairs of vertices (i,*) with score a and let $g_i^{(l)}$ be the l-fold self-convolution of g_i. Then, $y_l(a)=Pr[Y_l=a]\approx 1/n{\sum }_{i=1}^n(g_i^{(l-1)})(a)$ (this is an approximation because the convolution models a situation where the random subset R would be allowed to repeatedly pick the same pair of vertices). Assuming the independence of the Y_i’s, the distribution of S_k would be obtained by the convolution y₂ * y₃ * …* y_k. We will refer to this approximation as the Y-convolution method. Its running time is O(|V|²k²d²), where d is the diameter of G, although the use of Fast Fourier transforms to compute convolutions may yield significant improvements. In the context of WTPD, PSF, or WPSF the running time becomes O(|V|² k² (δ · κ)²), where δ is the discretization factor and κ is max_{u, v∈V, u<v} d_GW (u, v), max_{u, v∈V, u<v} s_G(u, v), or max_{u, v∈V, u<v} s_GW (u, v), respectively.

The triangle decomposition methods

An alternate approach is to use a dynamic programming algorithm to better model dependencies (Fig. 2b):

$$Pr[S_k=a]=Pr\left[\sum _{i=2}^k{Y}_i=a\right]=\{\begin{array}{ll}\sum _{a^{\prime }=1}^{a}Pr[S_{k-1}=a^{\prime }]·Pr[Y_k=a-a^{\prime }\mid S_{k-1}=a^{\prime }]\hfill & \text{if}k>1\hfill \\ 0\hfill & \text{if}k=1,a\ne 0\hfill \\ 1\hfill & \text{if}k=1,a=0\hfill \end{array}$$

Define $T_{k^{\prime },k}={\sum }_{j=1}^{k^{\prime }}{Z}_{j,k}$, for 1 ≤ k′ < k, so that Y_k = T_k−1,k. The term of the form Pr[Y_k = b|S_k−1 = c] = Pr[T_{k−1, k} = b|S_k−1 = c] is calculated using another convolution-based dynamic programming algorithm.

$$\begin{array}{l}Pr[T_{k^{\prime },k}=b\mid S_{k-1}=c]\\ =\{\begin{array}{ll}\sum _{d=1}^{b}Pr[T_{k^{\prime }-1,k}=d\mid S_{k-1}=c]·Pr[Z_{k^{\prime },k}=b-d\mid S_{k-1}=c,T_{k^{\prime }-1,k}=d]\hfill & \text{if}2\le k^{\prime }<k\hfill \\ Pr[Z_{1,k}=b\mid S_{k-1}=c]\hfill & \text{if}{k}^{\prime }=1\hfill \end{array}\end{array}$$

It is most likely impossible to calculate exactly and in polynomial time Pr [Z_{k′, k} = b − d|S_k−1 = c, T_{k′−1, k} = d], as otherwise the derivation above would give the exact probability distribution for S_k, which we have shown to be an NP-hard problem. Instead, we boil down the information in the condition (S_k−1 = c, T_{k′−1, k} = d)) to a simpler condition for which the conditional probability is easier to compute. Notice that if S_k−1 = c, the average pairwise distance among r₁, …, r_k−1 is $l_1=c/\left(\begin{array}{c}k-1\\ 2\end{array}\right)$. Also, if T_{k′−1, k} = d, then the average pairwise distance between r_k and r₁, …, r_{k′ − 1} is l₂ = d/(k′ − 1) is l₂ = d/(k′ −1).

Rounding approach

We assume that the desired condition can be represented as the condition Z_{1, k′} =Z_{2, k′} = …= Z_{k′ −1, k′}= [l₁], Z_{1, k} = Z_{2, k} = …= Z_{k′ −1, k} = [l₂], where [l₁] is the rounding of l₁, and similarly for l₂. The information on Z_{k′, k} thus comes in the form of k′ − 1 nearly independent pairs (Z_{i, k′} = [l₁], Z_{i, k} = [l₂]). Let t(a, b, c) be the number of triplets 1 ≤ i < j < k ≤ n such that M(i, j) = a, M(i, k) = b, M(j, k) = c. Assuming the independence of the k′ − 1 conditions, the desired posterior probability of Z_{k′, k} is obtained as:

$$\begin{array}{c}Pr[Z_{k^{\prime },k}=b-d\mid S_{k-1}=c,T_{k^{\prime }-1,k}=d]=Pr[S_{k-1}=c,T_{k^{\prime }-1,k}=d\mid Z_{k^{\prime },k}=b-d]·Pr[Z_{k^{\prime },k}=b-d]/\zeta \\ \approx {\left(\frac{t([l_1],[l_2],b-d)}{t(\ast ,\ast ,b-d)}\right)}^{k^{\prime }-1}·f_G(b-d)/\zeta ,\end{array}$$

where ζ is a normalizing constant that does not need to be computed (it is sufficient to normalize the distribution to make it sum to 1).

Interpolation approach

The rounding procedure yields a rather crude modeling of the actual posterior probability, especially when l₁ or l₂ are far from [l₁] or [l₂], respectively. A better modeling may be obtained as follows. Instead of assuming that all k′ − 1 condition pairs have the same values [l₁] and [l₂], we assume N₀₀ = frac(l₁) · frac(l₂) · (k′ − 1) pairs have values (⌊l₁⌋,⌊l₂⌋), N₀₁ = frac(l₁) · (1 − frac(l₂)) · (k′ − 1) pairs have values (⌊l₁⌋, ⌈l₂⌉), N₁₀ = (1 − frac(l₁)) · frac(l₂) · (k′ − 1) pairs have values (⌈l₁⌉, ⌊l₂⌋), and N₁₁ = (1 − frac(l₁)) · (1 − frac(l₂)) · (k′ − 1) pairs have values ⌈l₁⌉, ⌈l₂⌉). We thus approximate:

$$\begin{array}{l}Pr[Z_{k^{\prime },k}=b-d\mid S_{k-1}=c,T_{k^{\prime }-1,k}=d]\approx \\ {\left(\frac{t(\lfloor l_1\rfloor ,\lfloor l_2\rfloor ,b-d)}{t(\ast ,\ast ,b-d)}\right)}^{N_{00}}·{\left(\frac{t(\lceil l_1\rceil ,\lfloor l_2\rfloor ,b-d)}{t(\ast ,\ast ,b-d)}\right)}^{N_{10}}·{\left(\frac{t(\lfloor l_1\rfloor ,\lceil l_2\rceil ,b-d)}{t(\ast ,\ast ,b-d)}\right)}^{N_{01}}·{\left(\frac{t(\lceil l_1\rceil ,\lceil l_2\rceil ,b-d)}{t(\ast ,\ast ,b-d)}\right)}^{N_{11}}·f_G(b-d)/\zeta \end{array}$$

Both triangle convolution approaches run in time O(k⁶d³ + |V|³) in the case of TPD, where d is the diameter of G. For WTPD, PSF, or WPSF the running time is O(k⁶(δ · κ)³ + |V|³), where δ is the discretization factor and κ is max_{u, v∈V, u<v}d_GW (u, v), max_{u, v∈V, u<v} s_G (u, v), or max_{u, v∈V, u<v} s_GW (u, v), respectively.

2.5. Identification of core subgraphs

If a GO term τ obtains a small p-value from one of the methods described above, this means that the genes in V (τ) are unexpectedly clustered within G. This does not, however, mean that every gene in V (τ) belongs to that dense cluster, but only that a significant subset of V (τ) does. We call the core(τ) ⊆ V (τ) the set of mutually exclusive subsets of V (τ) that contributes the most to its statistical significance, i.e., the set of one or more subsets of genes in V (τ) that are the most significantly clustered. core(τ) may consist of a single dense cluster, or of several dense but distant clusters. In most situations, it is core(τ), rather than V (τ), that sheds the most light on the function of a portion of a network. We use a simple partitioning algorithm (Algorithm 1) to reduce V (τ) to core(τ), by first building a hierchical clustering tree of the proteins using average linkage algorithm and TPD, PSF, WTPD, or WPSF measures. Each node of the tree represents the set of proteins below it in the tree and p-values can be assigned to each node using one of the approaches proposed in Section 2.2. We then recursively traverse the tree starting from the root exploring, and deciding to keep the current cluster or to split it into two subclusters corresponding to the left and right subtrees, based on the p-values at the current node and the two children (see Algorithm 2). The construction of the tree with hierchical clustering runs in O(|V (τ)|² · log(|V (τ)|)) and identifying the cores runs in O(|V (τ)|). This heuristic algorithm does not guarantee optimality but generally succeeds at identifying the key components of V (τ). The results presented in Section 3.2 are the cores of the GO terms that obtained good p-values.

Algorithm 1.

Find core subgraph

Input: Graph G, Vertex subset V (τ), maximum p-value of interest maxPvalue

Output: Vertex subset core(τ)

root ←HierchicalClustering(V (τ))

return DivideCluster(root, maxPvalue)

Algorithm 2.

DivideCluster

Input: Root r, maximum p-value of interest maxPvalue

Output: A set of subsets of vertices of the subtree rooted at r that form significant clusters

if p-value(r)> maxPvalue then

return ϕ

else

if p-value(r) < p-value(leftChild(r)) and p-value(r) < p-value(leftChild(r)) then

return {V (r)} % where V(r) is the set of vertices in the subtree rooted at r.

else

return DivideCluster(leftChild(r), maxPvalue) ∪ DivideCluster(rightChild(r), maxPvalue)

end if

end if

2.6. Implementation considerations

The implementation of some of the four approximation schemes described in this section proves quite technically challenging, with issues of numerical precision arising for the two triangle convolution. Our crude approach to the problem is to make sure that, at every step, the intermediate probability distributions are properly normalized to sum to 1, although more subtle approaches would certainly improve our accuracy. Another issue is the time and memory required for the computation of the triangle convolution approaches, which require the storage of numerous large intermediate tables, currently limiting their utilization to the computation of p-values for values of k less than 25. Program optimizations were required to accelerate the running time for the triangle convolution approaches. They consist in stopping the computations of a distribution for a given S_k when the only probabilities left to compute are those at the right tail of the distribution that are smaller than the 64-bit double precision. The discretization level chosen to be applied for the PSF, WTPD, and WPSF methods was also an important aspect to consider in the implementation. A coarse discretization of the distributions can accelerate the running time for methods like the Y-convolution or both triangle convolutions, but provide a rather inaccurate estimation of the final distributions of S_k. On the other hand, a much finer discretization would require much more computational time but would yield a more accurate approximation. The challenge resides in determining the degree at which the distribution will be discretized in order to compute in reasonnable time an accurate distribution approximation.

3. RESULTS

3.1. Accuracy of p-value approximation methods

The accuracy of our four p-value approximation schemes can be assessed by Monte Carlo simulations: for a given graph G, repeatedly sample randomly a subset of k vertices and compute the sum of pairwise scores to eventually obtain an unbiased estimate of the true distribution. The limit of this approach is of course that the accuracy of the estimation depends on the number of samples, making small p-values difficult to estimate quickly.

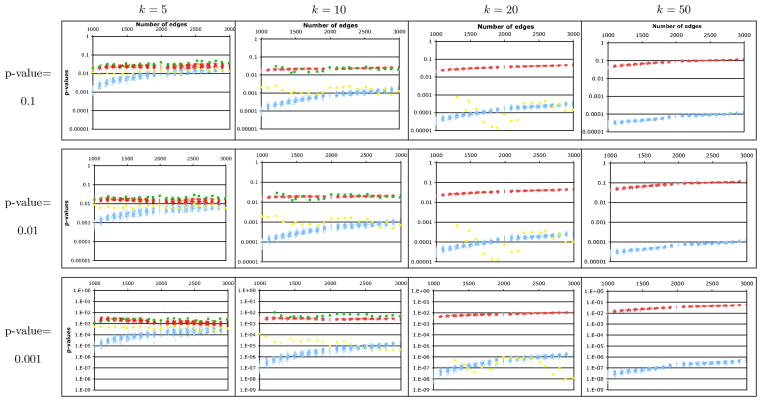
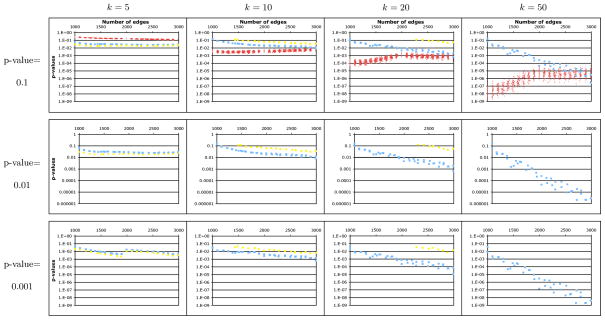
We have measured the accuracy of our approximation approaches on both simulated and actual biological networks. Protein-protein interaction networks have been reported to be accurately modeled by scale-free random graphs (Barabasi and Albert, 1999), although geometric random graphs have also been used (Przulj et al., 2004). We randomly generated scale-free graphs with 1000 vertices and a number of edges ranging from 1000 to 3000. In total, 2100 random graphs were generated. The distributions of the TPD and PSF score were estimated empirically, using 10⁶ samples, for each graph and each value of k = 5, 10, 20, 50. For each combination, critical values Z_0.1, Z_0.01, and Z_0.001 were estimated as being the value of TPD and PSF that obtains the empirical p-value 0.1, 0.01, and 0.001, respectively. Each of the four analytical approximation methods² were then used to estimate the p-values for Z_0.1, Z_0.01, and Z_0.001. Figures 3 and 4 report the accuracy of the p-values produced by each of our methods for the TPD and PSF clustering measures, for the target p-values 0.1, 0.01, and 0.001, and for k = 5, 10, 20, 50. We start by observing that although our p-value approximation methods apply in principle to both the TPD and PSF clustering measures, specificities of these data sets result in our methods behaving quite differently. This is due to the fact that the similarity scores that constitute the PSF clustering scores exhibit much stronger inter-dependencies than the pairwise distances that constitute the TPD clustering score, resulting in worse approximations when independence in assumed. Our observations are summarized below:

FIG. 3.

P-values predicted by our four approximation schemes (normal, red; Y-convolution, blue; triangle convolution with rounding, yellow; triangle convolution with interpolation, green) for the TPD clustering measure. Each data point records the approximated p-value (y-axis) for the TPD score that obtained the given empirical p-value (0.001, 0.01, 0.1), on a random scale-free graph with 1000 vertices and the given number of edges (x-axis). The triangle convolution with rounding method was too slow to be evaluated for k > 20, and that with interpolation could only be run for k = 5 and k = 10.

FIG. 4.

P-values predicted by three approximation schemes (normal, red; Y-convolution, blue; triangle convolution with rounding, yellow) for the PSF clustering measure. See caption of Figure 3. The triangle convolution with rounding method was too slow to be evaluated for k > 20 and some graphs for k = 20. The triangle convolution with interpolation was too slow for all k. The normal approximation method produced p-value estimates that were too poor to show on these graphs, usually erring by a factor of 10¹⁰ or more.

• Y-convolution: In the case of TPD, this method severely underestimates small p-values, by a factor ranging from 2 to 100 for k = 5 to more than 10⁴ for k = 50. This due to the fact that dependencies in the graph are greatly underestimated. However, the approximation improves with the edge density. On the contrary, the method works quite well on PSF clustering for graphs with low edge density, but it severely underestimates p-values of highly connected graphs.

• Normal approximation: This approximation obtains much better results than the Y-convolution approximation in the case of TPD clustering, producing p-values that generally slightly over-estimate the correct p-value (1- to 3-fold for small k, 10- to 50-fold for k = 50). Surprisingly, although, for small k, the quality of the approximation improves with the edge density, the opposite trend is observed for larger k. However, for PSF clustering, this yields an extremely poor approximation for all values of k, erring by a factor ranging from 10¹⁰ to 10⁶⁰ for a true p-value of 0.001.

• Triangle decomposition with rounding: We found that this method is an improvement to the Y-convolution approximation for TPD clustering since it does not underestimate as much p-values for small k (factor ranging from 2 to 10 for k = 5 and from 10 to 100 for k = 10). However, it behaves more irregularly for k = 20, underestimating the p-values by a factor greater than 100. This approach also yield good approximations for PSF clustering, overestimating small p-values for any k by a small margin. Interestingly, for both clustering measures, the accuracy of this approximation does not seem to be affected by the edge density of the network.

• Triangle decomposition with interpolation: The results obtained from this method on TPD clustering are comparable to the normal approximation estimation. For p-values 0.01 or less, computed p-values are slightly over-estimating the correct p-values (1- to 4-fold for small k). It sometimes even provides a tighter upper bound on the correct p-values. Again the accuracy of the p-value estimation for this method is not influenced by the edge density. We were unable to use this approximation for PSF because of high running time and memory requirements of the method.

Notably, all 4 methods behaved extremely similarly in terms of accuracy for both WTPD and WPSF compared to their respective unweighted version TPD and PSF. Overall, we conclude that given how quickly it can be computed, the normal approximation approach is the best tradeoff between running time and accuracy for TPD. However, the quality of that approximation degrades with the edge density, which is not the case for the two Triangle convolution approaches. This is an important point since we expect protein-protein interaction networks to gain in edge density as new high-throughput assays become available. The Triangle convolution approach is also the most accurate for PSF. It is the only method providing tight upper bounds on p-values even for large k in highly connected graphs. However, because of its intensive use of memory and slow running time, it is hard to obtain p-value approximations for very large k. Since it produces p-value approximations in a much more reasonable time, the Y-convolution method can be used in this situation.

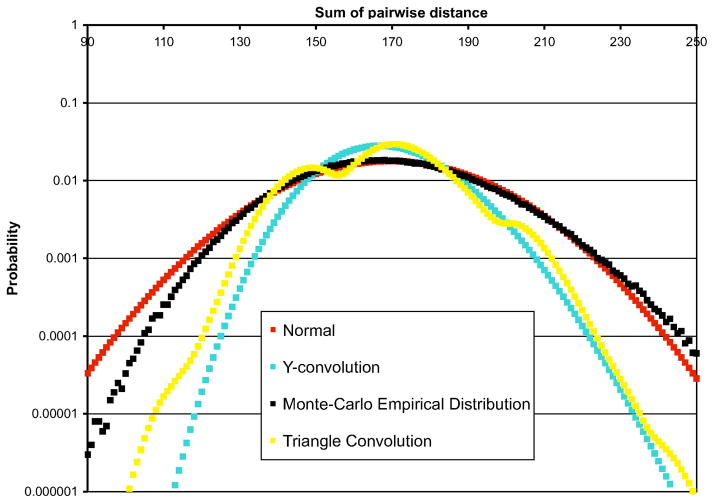
Our results on two larger actual PPI networks in yeast (Krogan et al., 2006) and human (Jeronimo et al., 2007) (see Section 3.2) largely confirm our observations on random graphs. Figure 5 shows the complete TPD distributions (for k = 10) obtained by Monte Carlo simulations, as well as each of our approximation methods, for the Krogan et al.’s yeast PPI network, which consists of more than 2500 proteins and 7000 interactions.

FIG. 5.

Empirical and approximated TPD distributions for the yeast PPI network, for k = 10.

Of the four approximation methods proposed, the fastest is the normal approximation (Table 1). The Y-convolution method is approximately 10-fold slower, while the two triangle-based convolution approaches are several orders of magnitude slower. Note that for PSF, Triangle convolution with interpolation runs several order of magnitude slower than the values presented.

Table 1.

Approximate Running Time, in Minutes, to Calculate One Clustering p-Value for a 1000-Vertex Scale-Free Graph with 2000 Edges, for the TPD Clustering Measure

	k = 10	k = 20	k = 50
Monte Carlo simulationa	2	5	20
Normal	0.3	0.7	1
Y-convolution	1	5	15
Triangle with rounding	2	300	>1000
Triangle with interpolation	5	600	>1000

^a10⁶ samplings were performed for the Monte Carlo simulations.

3.2. Biological analyses

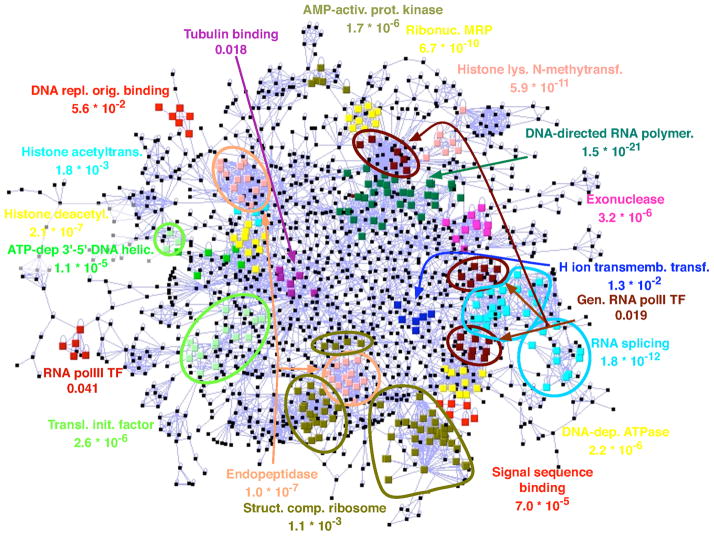
We first applied our analysis using TPD to the yeast protein-protein interaction data set produced by Krogan et al. (2006). We analyzed the largest connected component of their “core” network, which consists of 2559 proteins and 7037 interactions. Of the 299 GO terms present more than twice in the network, 91 obtained a normal approximation (conservative) p-value below 0.05 (corresponding to a $\text{FDR}=\frac{299\times 0.05}{91}\approx 16\%$), and 42 obtain a p-value below 0.001 ( $\text{FDR}=\frac{299\times 0.001}{42}\approx 0.7\%$). As seen in Figure 6, the GO terms with significant p-values allow the automated annotation of much of the network. For many of the GO terms reported, our results reflect known protein complexes (e.g., ribosome, ribo-nuclease MRP, general pol-II transcription factors). Other clusters, often the larger, more diffuse ones, do not correspond to complexes but rather contain proteins that interact with many of the same partners (e.g., the translation initiation factors or the signal sequence binding proteins). While most GO terms form a single, dense cluster, some (such as the structural components of the ribosome, the general RNA pol-II TFs, and the endopeptidases) are broken into two or three dense subgroups. Many of the fundamental functional interactions between groups of proteins of different function immediately stand out, for example the interplay between histone deacetylases (yellow), histone acetyltransferases (in cyan), and ATP-dependent 3′-5′ DNA helicases (in green). The annotated network is clearly more interpretable and readily allows the formulation of specific hypotheses about the function of various unannotated proteins and of the various interactions observed. For complete results, see online Supplementary Material at www.liebertonline.com.

FIG. 6.

Yeast PPI network from Krogan et al. (2006), annotated with the cores of some of the GO categories with significant clustering. The p-values given were obtained using the Normal approximation approach, which is almost always conservative. For readability, not all significant GO categories are shown. Subsets of core(τ) of size at least 3 are shown.

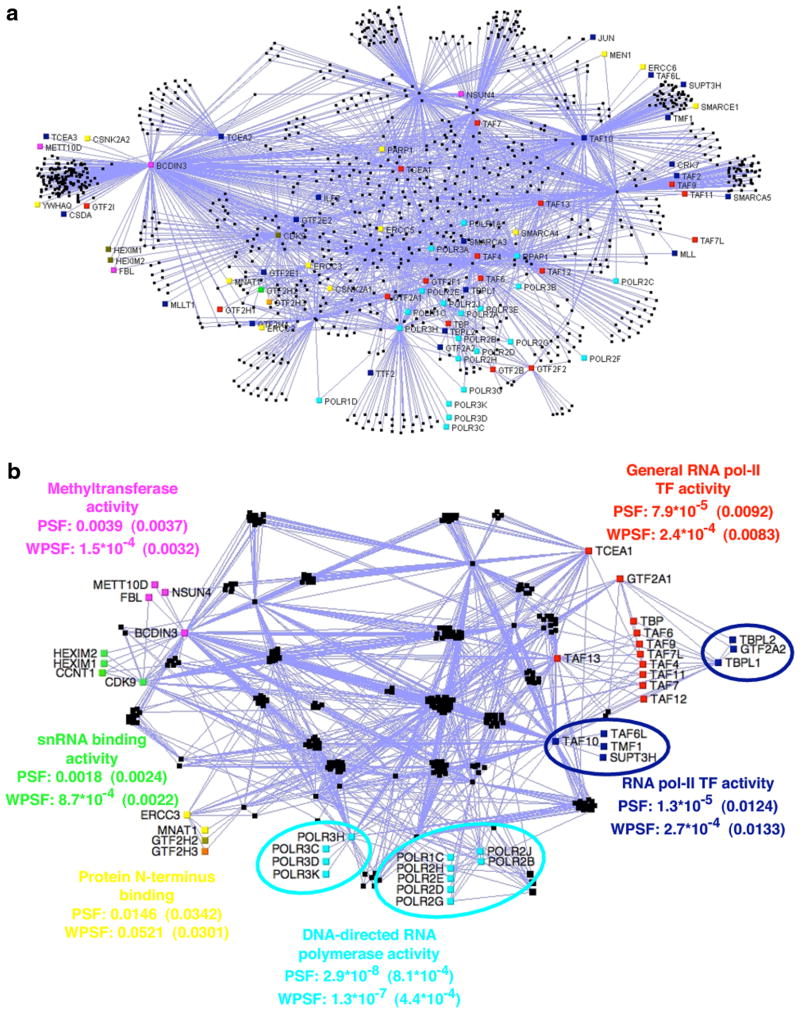
Finally, we analyzed a human protein-protein interaction network published by Jeronimo et al. [Coulombe et al., 2008] using PSF and WPSF. The network contains 1053 proteins and 2014 interactions, built from 32 tagged proteins and their interactors in the soluble fraction of HEK293 cells. The tagged proteins are predominantly proteins related to the (extended) transcription machinery. As can be seen from Figure 7a, the network is quite dense and existing automated layout systems fail to reveal much of the biological information contained in the graph. We ran our analyses on the network to identify which of the 135 GO categories present more than twice in the graph show unexpected clustering. Twenty-four GO categories obtained p-values below 0.05 ( $\text{FDR}=\frac{135\times 0.05}{24}\approx 28.1\%$ for PSF and 19 for WPSF ( $\text{FDR}=\frac{135\times 0.05}{19}\approx 35.5\%$; see online Supplementary Material at www.liebertonline.com). Genes belonging to some of these categories are colored coded in Figure 7b (several categories are somewhat redundant; only one representative per group is shown). When the graph is manually laid out to highlight the connectivity among the selected protein groups (Fig. 7b), the role of several subnetworks is clearly revealed. For example, we can easily identify subunits of the RNA polymerase I, II, and III, classified by GO as “DNA-directed RNA polymerase activity,” which are clustered together. We also notice that RPAP1 is tightly connected to the POLR2 subunits within that cluster. This corroborates the observation of Jeronimo et al. where RPAP1, XAB1, C1ORF82, and FLJ21908 (now referred to as RPAP2 and RPAP3, respectively) are forming an interface between the RNA polymerase II subunits and some molecular chaperone and prefoldins. We can also see that our method, by highlighting this GO term, facilitated the visualization of the interactions between the POLR2 subunits with the XAB1, RPAP2, and RPAP3 proteins. Hexamethylene bis-acetamide inducible (HEXIM) proteins were also found to be clustered with cyclin-dependent kinase 9 (CDK9) and cyclin T1 (CCNT1), both members of the P-TEFb complex (Peng et al., 1998). All of these are associated with the GO term “snRNA binding.” Interestingly, HEXIMs are known to be inhibitors of the cyclin-dependent kinase activity of P-TEFb (Barboric et al., 2005; Byers et al., 2005). In addition, BCDIN3 (also known as MEPCE) and SART3, which are part of the 7SK snRNP complex, itself containing P-TEFb, are closely associated with HEXIMs and CDK9 (Jeronimo et al., 2007; Coulombe et al., 2008). Finally, numerous TATA box binding protein (TBP)–associated factors (TAFs) and a general transcription factor II (GTF2A1), all sharing the “general RNA polymerase II transcription factor activity” GO function, were found to be significantly clustered. Many of these TAFs and GTF2A1 are interacting with TBPL1, another protein playing a key role in transcription (Ohbayashi et al., 1999).

FIG. 7.

(a) Human PPI network from Jeronimo et al. (2007), laid out using the “relaxed” automatic layout procedure of VisANT (Hu et al., 2004). (b) Groups of protein with a significant PSF and WPSF clustering p-value are highlighted in colors. The triangle convolution was used when the group size was small enough; otherwise, the Y-convolution was used. Monte Carlo estimated p-value are between parentheses. Network laid out manually to highlight the connectivity of the proteins within each GO category reported (to improve readablity, proteins that do not belong to any shortest path between pairs of proteins of the selected groups are not shown). GTF2H3 (in orange) is part of both red and yellow groups. GTF2H2 (in khaki green) is part of both the yellow and blue groups. Subsets of core(τ) of size at least 3 are shown. Clearly, without the information provided by our GO clustering approach, the PPI network showed at the top would be hard to interpret.

4. CONCLUSION

The idea described in this article, of seeking gene attributes that cluster within a given network, can be used to annotate PPI networks with any type of gene or protein features. Besides gene ontologies, we are currently expanding our tool to use protein domains from the PFAM database (Finn et al., 2008), pathways from the KEGG database (Kanehisa et al., 2008), and gene expression data. Indeed, any annotation coming in the form of gene sets can be used to annotate the network, including, for example, those collected through the laudable efforts of the GSEA (Subramanian et al., 2005) team.

In the future, we will try to improve the accuracy and efficiency of our approximation algorithm. We will also seek provable approximation bounds for the p-value estimation problem. Currently, one of the main computational issues is that some of our best approximation methods are quite slow and require a lot of memory. More efficient implementations would thus have a significant practical impact.

In this article, we only studied the simplest version of a family of interesting problems. A number of extensions will be considered. One important generalization is to consider directed graphs. In these graphs, the edge directions represent biological information about the tag experiment that was performed. For instance, an edge would connect two proteins from the tagged protein to the purified protein. We are also considering the problem where gene annotations are not in the binary form (i.e., they belong to a given gene set or now) but are more quantitative measures, such as gene expression.

As we discussed previously, our method could be used for protein function prediction. For a given set of proteins sharing the same GO term that are surprisingly clustered, uncharacterized proteins co-clustering with the GO term could be expected to share the same GO annotation. Another exciting prospect is to use this type of local over-representation to search for sequence motifs. One would seek motifs that are locally enriched in a subnetwork of the graph. Locally over-represented motifs found in protein sequences may correspond to new domains or localization signals. Those found in the 5′ or 3′ UTRs of genes may contain mRNA localization signals or post-transcriptional regulatory elements relevant to the subnetwork, while those found in the regulatory regions (promoters and enhancers) would allow the coordinated transcription of the proteins in the subnetwork.

The Java program used to identify GO terms enriched in subnetworks is available as online Supplementary Material at www.liebertonline.com.