Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2015 Dec 4;5:17815. doi: 10.1038/srep17815

Evolution of crystal and electronic structures of magnesium dicarbide at high pressure

Dashuai Wang 1, Yan Yan 2, Dan Zhou 3,a, Yanhui Liu 1,4,b
PMCID: PMC4669465  PMID: 26634906

Abstract

Carbon-based compounds exhibit unexpected structures and electronic behavior at high pressure arising from various bonding features of carbon (e.g., sp, sp2 and sp3 C-C bonds). Here we report evolution of crystal structures of MgC2 in a wide pressure range of 0–200 GPa as predicted through ab-initio calculations in combination with an unbiased swarm structure search. Three pressure-induced structural transformations are unraveled, following the phase sequence of ambient-pressure P42/mnm (α-phase) → Cmcm (β-phase) → C2m (γ-phase) → EuGe2-type P-3m1 (δ-phase), where significant C-C bonding modifications from C-C dimer to quasi 1-dimensionzigzag chain, to polymerized ribbon and then to winkled quasi 2- dimension graphite sheet are evident. The predicted β- and γ-phases with sp2 C-C hybridization are metals, while the δ- phase characterized by a sp3C-C hybridization is a narrow-gap semiconductor with a band gap of 0.667 eV. Strong electron-phonon couplings in the compressed β- and γ- phases arepredicted with β-phase showing a high superconducting critical temperature of 11.2 K. The current results indicate that pressure is effective in tuning the crystal and electronic structures of MgC2, which is expected to have impact on physical properties for potential applications.

Carbon has the ability to form various bonding states, e.g., graphite, diamond, nanotubes, fullerences, amorphous carbon and carbon-based compounds, etc., which exhibit its unique physical and chemical property1,2,3,4,5,6,7. Carbides have been focus of intense for more than half a century and remain a major center of scientific of technology attention in advanced functional materials8,9,10. Among them, alkali and alkaline earth metal carbides have reignited great interest that show exceptional structural and electronic properties, as well as high-temperature superconductivity11,12,13,14,15,16,17.

MgC2 was originally prepared in 1910 with a unique P42/mnm crystal symmetry, whereas the other dicarbides, namely, BeC2, CaC2, SrC2, and BaC2 adopt an I4/mmm crystal symmetry12,13. The crystal and electronic properties of the magnesium carbides have been systemically studied at ambient-pressure conditions12. Pressure induced reorientation of the dicarbide dumbbells similar to those in temperature-induced phase transitions has already been shown for LaC2 in its CaC2-type to ThC2-type phase change18,19,20. Recently, Li et al. reported that dumbbell carbon in CaC2 can be polymerized first into 1D chain and then into ribbon and further into 2D graphite sheet at higher pressure20. Especially, the high-pressure phase of CaC2 (Immm) with 2D graphite sheet has the high superconducting critical temperature Tc (7.9–9.8 K), which is comparable with the value of CaC6 (11.5 K)21. A pressing task is to understand the crystal and electronic structures of this special matter under the influence of external pressure conditions that may alter the underlying fundamental physics, which has motivated us to carry out the work.

Here, we unravel the convoluted structural evolution of MgC2 at high pressure using first-principles structural search method. We have identified three thermodynamically stable phases at high pressure. A systematic analysis of the electronic properties shows that the overlap between the conduction and the valence bands makes the β- and γ-phases metal, while the δ-phase is a narrow-gap semiconductor. Phonon-mediated superconducting behavior of two new metallic phases of MgC2 was revealed by exploring the electron–phonon coupling.

Results and Discussions

Crystal structures of MgC2

We performed variable-cell structure predictions with the simulation cell size of 1–4 formula at pressure of 0–200 GPa. At ambient pressure, our simulations revealed the experimental observed P42/mnm phase (denoted as α-structure/phase) has a lower enthalpy than all other candidates, indicating that it is the thermodynamic ground state12. This proved the reliability of our method for application to this dicarbide system. Interestingly, with in the whole pressure range studied, three new low-enthalpy structures with space group of orthorhombic Cmcm (β- phase), monoclinic C2/m (γ-phase) and EuGe2-type hexagonal P-3m1 (δ-phase) were explored.

The enthalpies of these new structures with respected to the experimental structure are shown as a function of pressure in Fig. 1. In order to investigate the phase transition pressure clearly, the enthalpy differences vs. pressure for the β- and γ-phases are given in insert of Fig. 1(a). As can be seen that, for compressed MgC2, the ambient-pressure α-phase is the most stable structure below 3.4 GPa, and the β-phase become more favorable at the pressure range from 3.4 to 9.4 GPa, and then the γ-phase is stable from 9.4 to 66.2 GPa, above which δ-phase is the energetically much superior to the γ-phase from 66.2 to 200 GPa. The current experimental techniques are readily accessible to these extreme conditions. The pressure evolution of the unite cell volume of MgC2 in the α-, β-, γ- and δ-structures are depicted in insert of Fig. 1(b). The abrupt volumecollapses of about 19.7%, 9.6% and 4.8% around 3.4, 9.4 and 66.2 GPa, respectively, indicating the first-order nature of these phase transitions in MgC2. No imaginary frequencies are observed throughout the whole Brillouin zone, declaring that the three novel phases are dynamically stable at studied pressure region.

Figure 1. Enthalpies per formula unit of various structures as a function of pressure with respect to ambient pressure of the α-phase.

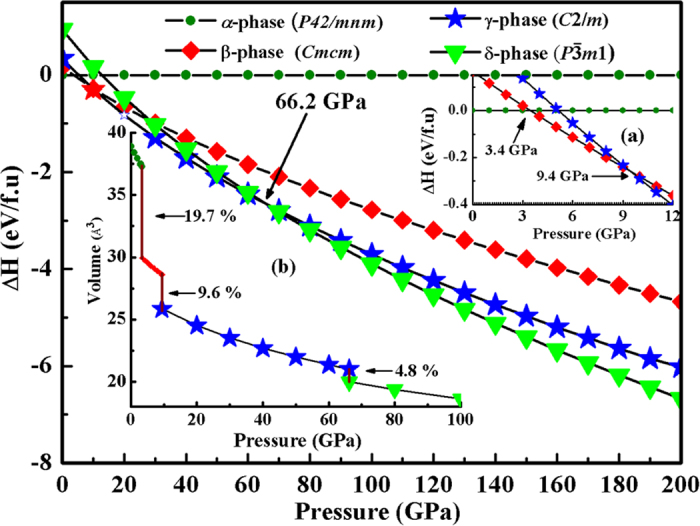
Figure 1

Open in a new tab

Insert: (a) The enthalpies of the β- and γ-phases with respect to the α-phase. (b) The calculated equations of states for the predicted structures.

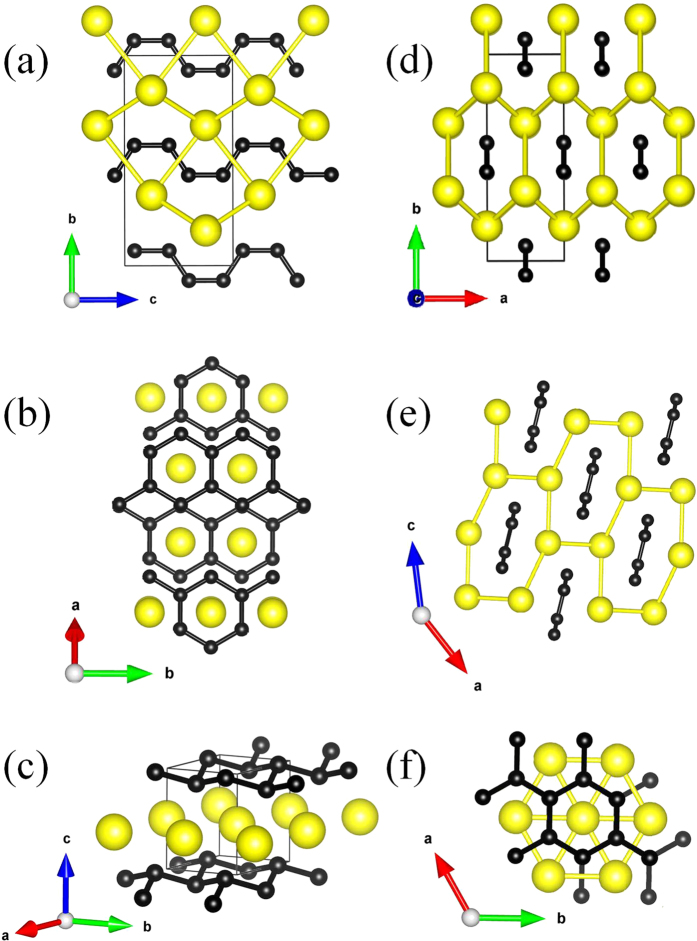
The optimized structure parameters at related pressures are listed in Table 1. The atomic arrangements of competing structures are shown in Fig. 2. The calculated lattice constants of the ambient-pressure have been widely demonstrated, consistent results with power X-ray and neutron powder diffraction measurements12. For the β-phase, the equilibrium lattices are a = 3.183 Å, b = 8.536 Å and c = 4.410 Å at 3.7 GPa. Four Mg atoms occupy the wyckoff 4c site and eight C atoms lie in 8f site in the unit cell. The β-structure is similar to the recently predicted of CaC2 for Cmcm phase20. Figure 3 shows the simulated X-ray diffraction data of these structures, indicating that their structures are differenr from each other.

Table 1. Lattices Parameters and atomic coordinates of α-, β-, γ-, and δ- phase at 0, 3.4, 9.4, and 66.2 GPa,respectively.

  Lattice Parameters (Å) Atoms x y z
α-phase a = 3.944 (3.934a) Mg(2b) 0.0 0.0 0.5
0 GPa b = 3.944 (3.934a) C(4f) 0.1123 0.1123 0.0
  c = 5.008 (5.021a)        
β-phase a = 3.183 Mg(4c) 0.0 0.1658 0.250
3.4 GPa b = 8.536 C(8f) 0.000 0.4286 0.0911
  c = 4.410        
γ-phase a = 8.321 Mg(4i) 0.0549 0.0 0.7096
9.4 GPa b = 2.609 C1(4i) 0.6145 0.0 0.2407
  c = 9.876 C2 (4i) 0.0626 0.0 0.1217
δ-phase a = 2.525 Mg(1b) 0.0 0.0 0.500
66.2 GPa b = 2.525 C(2d) 0.6667 0.3333 0.0718
  c  = 3.623        
Open in a new tab

Figure 2. Crystal structures of for MgC2.

Figure 2

Open in a new tab

The yellow and black balls represent Mg and C atoms, respectively. (a,d) The β-phase. (b,e) The γ-phase. (c,f) The δ-phase.

Figure 3. Simulated X-ray diffraction of MgC2.

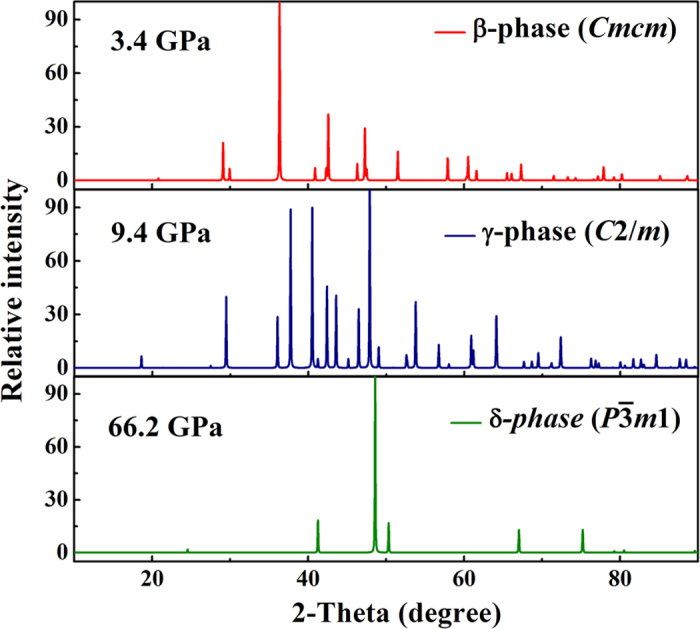
Figure 3

Open in a new tab

Thecalculated power X-ray diffraction (λ = 1.541 Å) for β-phase at 3.4 GPa (a), γ-phase at 9.4 GPa (b), and δ-phase at 66.2 GPa (c).

In this structure, one-dimension carbon chain along z direction lies in the center of the structure, in which the Mg atoms construct cylinder with hexagon cross-section. With increasing pressure, the γ-structure contains four molecules per unite cell. The optimized structural parameters are a = 8.321 Å, b = 2.609 Å and c = 9.304 Å. Four Mg atoms hold the wyckoff 4i site and the in-equivalent of two C atoms also lie in 4i site in the unit cell, respectively. The results show that carbon atoms are polymerized into ribbon with a six-membered ring. A carbon quasi 1-dimension ribbon lies in the center of cylinder constructed by Mg atoms. For the δ-phase with a EuGe2-type structure, including one molecule in unite cell, the equilibrium lattice are a = b = 2.525 Å and c = 3.623 Å at 66.2 GPa. One Mg atom occupies the wyckoff 1b site and two C atoms at 2d site. The plans of Mg atoms separate the hexagonal honeycombed layers of carbon atoms. It is obviously that the δ-phase consists of the bulking honeycomb-layered of carbon atoms separate by planes of Mg atoms.

We investigate the nature of carbon-carbon bonding in MgC2 with increasing pressure. The carbon-carbon bonding behavior reveals significant change with the external pressure and chemical precompression. At ambient pressure, the length of isolated dumbbell C-C bond in the α-phase (P42/mnm) is 1.253 Å, which is nearly identical to the experimental value of 1.215 Å12. With increasing pressure, the distance between the isolated dumbbell decreases, resulting in carbon atomic chain formed in the β-phase (Cmcm), consistent with the increase in the C-C distance (1.458 Å and 1.401 Å). Under further compressed, the carbon atomic chains polymerize to a well-organized arrangement, transforming to the monoclinic (C/2m) γ-phase. It is obviously that the carbon nanoribbons appear between neighboring Mg atomic layers. The two types of in-equivalent C-C bond lengths in the γ-structure referred as d1 and d2 as a function of the pressure is plotted as a function of pressure in Fig. 4. The difference (∆d) between d1 and d2 in ribbon with six-membered carbon ring is also explored. At higher pressure, the difference ∆d begins to decrease more smoothly and reaches 0.009 Å at 66.2 GPa. The C-C bond lengths are 1.445 Å and 1.454 Å close to that of graphite (1.420 Å). However, the C-C bond lengths in honeycomb layer is 1.544 Å in the δ-phase, larger than those of the γ- structure at 66.2 GPa. The increased bond length induced the well organized carbon six-ring collapse into the winkled quasi 2-dimension graphite sheet. Due to the occurrence of graphite sheet between neighboring Mg atomic layer, the γ-phase can be regarded as one of folded graphite intercalation compounds.

Figure 4. C-C bond lengths in the γ-structure as a function of the pressure.

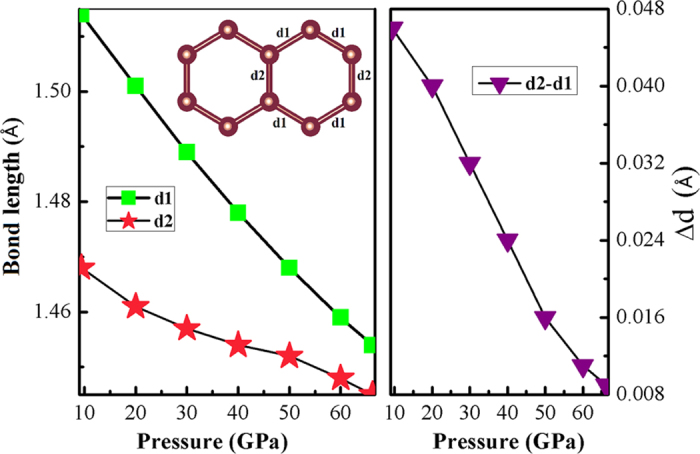
Figure 4

Open in a new tab

Left: the two kinds of C-C bonds length in the γ-phase as a function of the pressure. Right: the difference (∆d) between d1 and d2 as a function of pressure.

Electronic structuresof MgC2

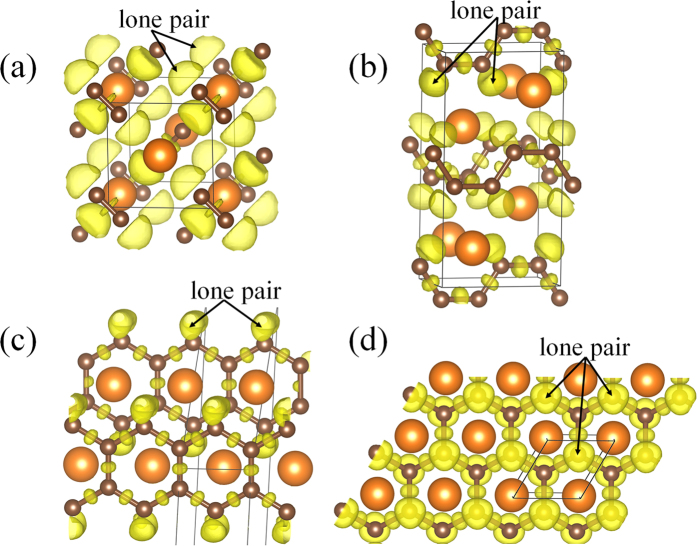
The calculated band structure and projected density of states are shown in Fig. 5. The ambient-pressure α-phase is an insulator with a larger indirect band gap of ~2.643 eV. The predicted overlap between the conduction and the valence bands shows the β- and γ-phases with sp2 hybridization are metallic with C-p orbital dominating the density of states at the Fermi level. However, there are few C-s electrons and Mg-s, p electrons near the Fermi level, showing a pressure-induced charge transfer from C-s and Mg-s, p to C-p electron. In the α-phase, the value of the band gap decreases with the increasing pressures as the molar volume decreases along with the van der Walls gap reduces, the orbital overlaps across the gap are enhanced and this would reduce the energy separation between bonding and anti-bonding interactions. The reduction of the band gap is a promising signal for reaching a metallic state. At 66.2 GPa, the δ-phase characterized by sp3 hybridization is most thermodynamically stable and is semiconductor with an indirect band gap of 0.667 eV. The significant evolution of electronic structures from sp2 to sp3 hybridization of carbon atoms between the γ- and δ- phases is similar to the fact of graphite transforms to diamond under sufficient compression. The pressure-induced insulator-metallization-semiconductor and related propertiesincent us to calculate the electron localization behavior of MgC2. Therefore, we have performed a chemical bonding analysis via calculation of the electron localization function (ELF)22. The calculated ELF isosurface (0.86) for the α-structure shows that two C atoms bond together to form a double bonded C2 dimer with a stable and localized lone-pair nonbonding state, as shown in Fig. 6. With increasing pressure, the distance between the isolated dumbbell decreases, constructing carbon atomic chain with armchair-type carbon chains in the β-phase. One can see that each C has one lone pair of electrons. In the γ-structure, the ribbon with a six-member carbon ring has the feature of sp2- like nature with each inner C atoms forming three C-C covalent bonds, while each outer C atoms has one electron lone pair and two C-C covalent bonds, while the remaining 2pz electrons of the C6 ring form a delocalized π system. In the δ-phase, the winkled honeycomb-layered structure lacks the system of delocalized π bonds with mobile electrons and has more localized electrons, as a result of which the obviously sp3 hybridization constructed. Each C atom has one electron lone pair and three covalent C-C bonds resembling diamond structure, accompanied with to appear insulator.

Figure 5. The electronic properties of MgC2.

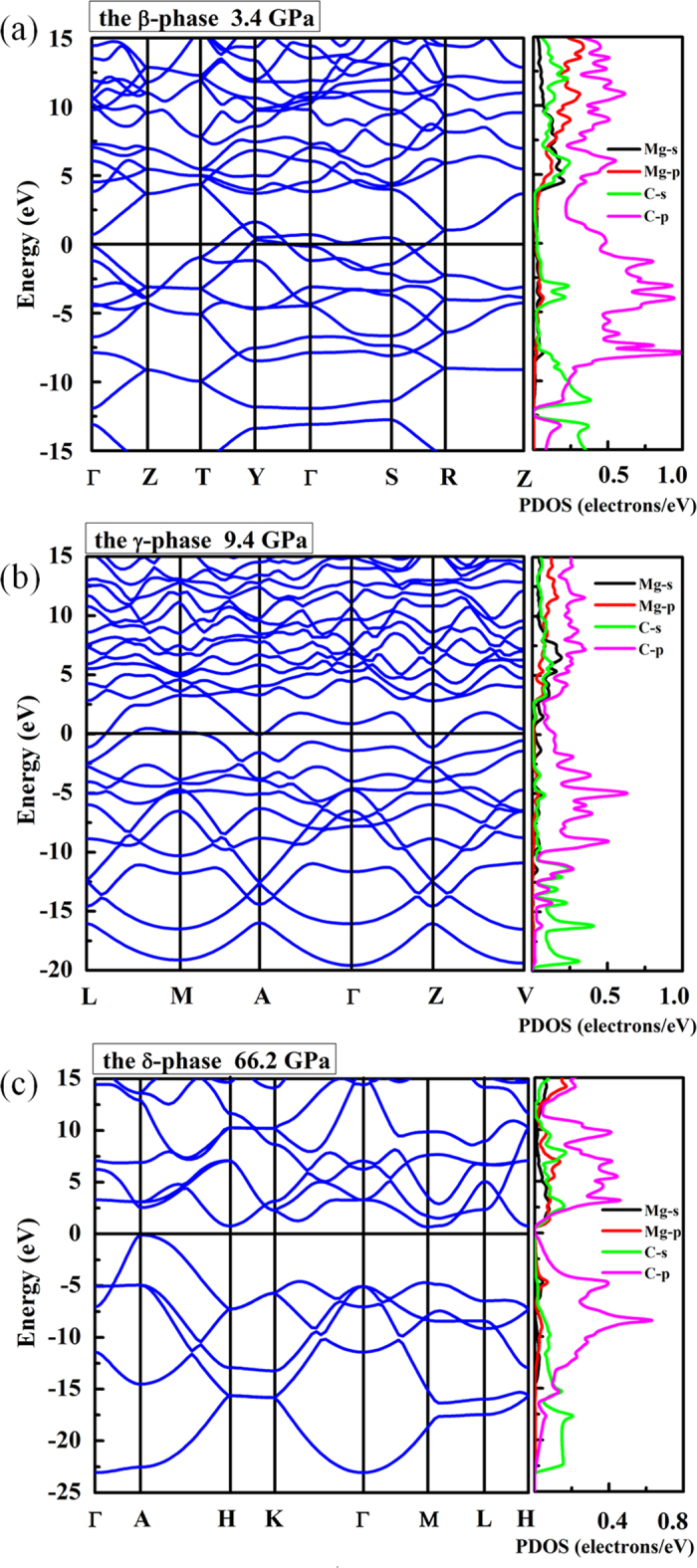
Figure 5

Open in a new tab

Band structure and electronic density of states of MgC2 for the (a) β-phase, (b) γ-phase, (c) and δ-phase. The zero of energy is at the Fermi level.

Figure 6. Calculated ELF of MgC2.

Figure 6

Open in a new tab

Contours of the ELF of MgC2 for the (a) α-phase, (b) β-phase, (c) γ-phase and (d) δ-phase with isosurface of 0.86.

Electron–phonon coupling of MgC2

The high-pressure β- and γ-phases of MgC2 exhibit charming features in the electronic band structure. As shown in Fig. 5, the electronic bands of the β-phase crossing the Fermi level along the Y-Γ-S-R are quite flat, and a narrow energy window located at the Fermi level results in large electronic density of states near the Fermi energy. The corresponding restricted conduction electrons near the band gap possess large effective mass with their group velocities approaching zero. However, the bands along the Γ-Z-T direction steeply cross the Fermi level, providing itinerant electrons with high conduction electron velocity. Above all, such flat bands with highly mobile and localized electrons should provide the strong electron-phonon coupling necessary for superconductivity. This encourages us to further investigate the superconductivity of MgC2 at high pressure. The calculated Tc values and logarithmicaverage frequency ωlog and the electron–phonon coupling parameter λ of MgC2 at different pressure were plotted in Fig. 7. For the β-phase, at 4 GPa, the coupling parameter λ is 0.558 with the logarithmicaverage of the phonon frequency ωlog of 648 K. Using the strong coupling Allen-Dynes equation and an extension of the McMillian theory23,24, with a nominal Coulomb pseudopotential parameter (μ*) of 0.1 the estimated superconducting critical Tc is 11.3 K. With the increase of pressure, the obtained Tc become slightly lower as 7.4 K at 9 GPa with the slightly smaller of λ 0.488 than that of values at 4 GPa. The calculated results show that ωlog has positive pressure dependence, and coupling parameter λ decreases with pressure. For the γ-phase, the estimated superconducting critical Tc is 7.1 K at 9.6 GPa, which is comparable with that of β-phase due to the similar of electron-phonon coupling integral (λ) 0.472.

Figure 7. Electron-phonon coupling of MgC2.

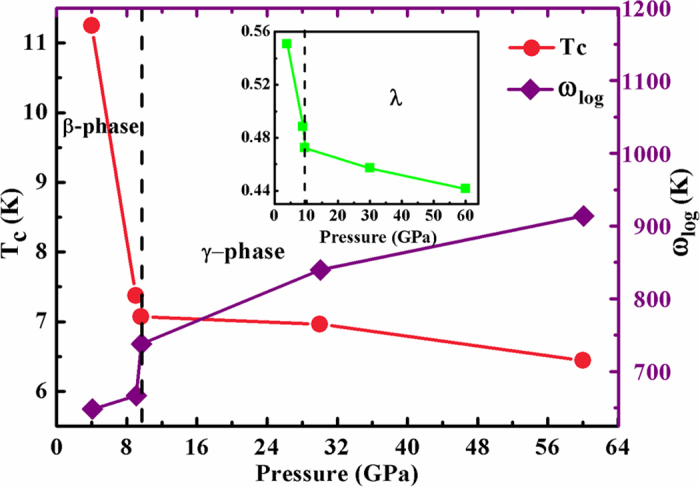
Figure 7

Open in a new tab

Calculated Tc values and the logarithmicaverage of the phonon frequency of ωlog as a function of pressure. Inset shows the electron-phonon coupling integration of λ(ω) as a function of pressure.

Conclusion

In summary, we have reported three high-pressure phases of MgC2, Cmcm (β-phase), C2m (γ-phase), P-3m1(δ-phase), which are stable in the pressure ranges of 3.4–9.4 GPa, 9.4–66.2 GPa and 66.2–200 GPa, respectively. The structural, dynamical, and electronic properties of high-pressure MgC2 were systemically investigated up to 200 GPa. The predicted α- to β-phase structural transition is accompanied with a metallization by band gap closure. The γ-phase transfers to the δ-phase with a narrow band gap characterized by C-C sp3 hybridized. Strong electron-phonon coupling in the compressed β- and γ-phases is found, in particular for the β-phase with carbon sp2-hybridization, which has the highest λ 0.558 value, leading to its high superconducting critical temperature Tc of 11.3 K, which is comparable with the 11.5 K value of CaC6. These results show that pressure has a strong influence on the fundamental crystal and electronic structure of MgC2, and as a result, the sensitive pressure tuning of the electronic properties offers an effective tool to modulate a wide range of physical properties for its potential applications.

Methods

The search for the stable structures is based on the CALYPSO (Crystal structure Analysis by Particle Swarm Optimization) methodology25,26,27 and the first-principles calculations using a global minimization of free energy surfaces. The remarkable feature of this methodology is the ability of predicting the stable structure with the knowledge of chemical composition under given external pressures28,29. Enthalpy calculations and geometry optimizations were performed within the framework of the Perdew-Burke-Ernzerhof parametrization for the exchange-correlation functional as implemented in the VASP (Vienna ab initio simulation package) code30. The projector augmented wave method31,32 has been adopted, with 2p6 3s2 and 2s2 2p2 treated as valence electrons for Mg and C atoms, respectively. For Brillouin zone integration, we used the Monkhorst−Pack scheme33 and checked convergence of ground state calculations with uniformly increasing k-point meshes for each structure. We used cutoff energy of 900 eV for the expansion of the wave function into the plane-wave basis-set. Monkhorst-Pack k-pointmeshes with a grid of 0.03 Å−1 for Brillouin zonesampling were chosen to achieve the total energy convergence of less than 1meV/atom. The phonon calculations were carried out by using a supercell approach as implemented in the PHONOPY code34. Electron–phonon coupling calculations were performed using the planewave pseudopotential method and density-functional perturbation theory as implemented in the QUANTUM ESPRESSO with a kinetic energy cutoff of 70 Ry35. 4 × 4 × 3 and 4 × 4 × 2 q-meshes in the first Brillouin zones were used in the EPC calculations for the β- and γ- structures, respectively.

Additional Information

How to cite this article: Wang, D.-S. et al. Evolution of crystal and electronic structures of magnesium dicarbide at high pressure. Sci. Rep. 5, 17815; doi: 10.1038/srep17815 (2015).

Acknowledgments

This work was supported by the China 973 Program (2011CB808200), the Natural Science Foundation of China under No. 11474125, 11274136, 51202084, 11104104, 11164031, 11404035 and the 2012 Changjiang Scholars Program of China, Changjiang Scholar and Innovative Research Team in University (IRT1132).

Footnotes

Author Contributions The idea was conceived by Y.-H.L. The simulation was performed by Y.-H.L. and D.-S.W., and the data analyses were performed by Y.-H.L., D.-S.W., Y.Y. and D.Z. This manuscript was written by Y.-H.L., D.-S.W. and D.Z. All authors discussed the results and contributed to the paper.

References

  1. Rice M. J., Bishop A. R. & Campbell D. K. Unusual soliton properties of the infinite polyyne chain. Phys. Rev. Lett. 51, 2136–2139 (1983). [Google Scholar]
  2. Hoffmann R., Janiak C. & Kollmar C. A chemical approach to the orbitals of organic polymers. Macromolecules 24, 3725–3746 (1991). [Google Scholar]
  3. Kou L. Z., Tang C., Chen C. F. & Guo W. L. Hybrid W-shaped graphene nanoribbons: distinct electronic and transport properties. J. Appl. Phys. 110, 124312–124316 (2011). [Google Scholar]
  4. Ye X. C. et al. Improved size-tunable synthesis of monodisperse gold nanorods through the use of aromatic additives. ACS nano 5(2), 1012–1017 (2012). [DOI] [PubMed] [Google Scholar]
  5. Zhong X. et al. Pressure stabilization of long-missing bare C6 hexagonal rings in binary sesquicarbides. Chem. Sci. 5, 3936–3940 (2014). [Google Scholar]
  6. Lu S. H., Wang Y. C., Liu H. Y., Miao M. S. & Ma Y. M. Self-assembled ultrathin nanotubes on diamond (100) surface. Nat. Commun. 5, 3666–3672 (2014). [DOI] [PubMed] [Google Scholar]
  7. Li Q. et al. Superhard and Superconducting Structures of BC5. J. Appl. Phys. 108, 023507–0235012 (2010). [Google Scholar]
  8. Li Q. et al. A novel low compressible and superhard carbon nitride: body-centered tetragonal CN2. Phys. Chem. Chem. Phys. 14, 13081–13087 (2012). [DOI] [PubMed] [Google Scholar]
  9. Zhang M. et al. Superhard BC3 in Cubic Diamond Structure. Phys. Rev. Lett. 114, 015502–015507 (2015). [DOI] [PubMed] [Google Scholar]
  10. Nylen J., Konar S., Lazor P. & Benson D. Structural behavior of acetylide carbides Li2C2 and CaC2 at high pressure. J. Chem. Phy. 137, 224507–224515 (2012). [DOI] [PubMed] [Google Scholar]
  11. Fjellvaag H. & Karen P. Crystal structure of magnesium sesquicarbide. Inor. Chem. 31, 3260–3263 (1992). [Google Scholar]
  12. Karen P., Kjekshus A., Huang Q. & Karen V. L. The crystal structure of magnesium dicarbide. J. Alloy. Comp. 282, 72–75 (1999). [Google Scholar]
  13. Xiao B., Feng J., Chen J. & Yu L. Crystal structures and electronic properties of MC2 (M = Mg, Ca, Sr, Ba) by comparative studies based on ab-initio calculations. Chem. Phys. Lett. 448, 35–40 (2007). [Google Scholar]
  14. Rahnejat K. C. et al. Charge density waves in the graphene sheets of the superconductor CaC6. Nat. Commun. 2, 558–564 (2011). [DOI] [PubMed] [Google Scholar]
  15. Weller T. E., Ellerby M., Saxena S. S., Smith R. P. & Skipper N. T. Superconductivity in the intercalated graphite compounds C6Yb and C6Ca. Nat. Phys. 1, 39–41 (2005). [Google Scholar]
  16. Emery N. et al. Superconductivity of Bulk CaC6. Phys. Rev. Lett. 95, 087003–087007 (2005). [DOI] [PubMed] [Google Scholar]
  17. Tütüncü H. M. & Srivastava G. P. A comparative ab initio study of superconductivity in the body centered tetragonal YC2 and LaC2. J. Appl. Phys. 117, 153902–1539010 (2015). [Google Scholar]
  18. Hannay N. B. et al. Superconductivity in Graphitic Compounds. Phys. Rev. Lett. 16, 225–226 (1965). [Google Scholar]
  19. Babizhetskyy V. et al. Structure and bonding of superconducting LaC2. J. Phys.: Condens. Matter 26, 025701–025711 (2014). [DOI] [PubMed] [Google Scholar]
  20. Li Y. L. et al. Pressure-induced Superconductivity in CaC2. Proc. Natl. Acad. Sci. USA. 110, 9289–9294 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Li Y. L. et al. Formation of nanofoam carbon andre-emergence of superconductivity incompressed CaC6. Sci. Rep. 3, 3331–3338 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Savin P. D. A., Nesper P. D. R., Wengert D. S. & F¨assler D. T. F. ELF: The Electron Localization Function. Angew. Chem., Int. Ed. Engl. 6, 1808–1832 (1997). [Google Scholar]
  23. McMillan W. L. Transition Temperature of Strong-Coupled Superconductors. Phys. Rev. 167, 331–344 (1968). [Google Scholar]
  24. Allen P. B. & Dynes R. C. Transition temperature ofstrong-coupledsuperconductors reanalyzed. Phys. Rev. B12, 905–922 (1975). [Google Scholar]
  25. Wang Y. C., Lv J., Zhu. L. & Ma Y. M. Crystal structure prediction viaparticle-swarm optimization. Phys. Rev. B 82, 094116–094124 (2010). [Google Scholar]
  26. Wang Y. C., Lv J., Zhu. L. & Ma Y. M. CALYPSO: A method for crystal structure prediction. Comput. Phys. Commun. 183, 2063–2070 (2012). [Google Scholar]
  27. Lv J., Wang Y. C., Zhu L. & Ma Y. M. Predicted novel high-pressure phases of lithium. Phys. Rev. Lett. 106, 015503–015507 (2011). [DOI] [PubMed] [Google Scholar]
  28. Zhu L. et al. Substitutional alloy of Bi and Te at high pressure. Phys. Rev. Lett. 106, 145501–145505 (2011). [DOI] [PubMed] [Google Scholar]
  29. Wang Y. C. et al. High pressure partially ionic phase of water ice. Nat. Commun. 2, 563–568 (2011). [DOI] [PubMed] [Google Scholar]
  30. Blöchl P. E. Projector augmented-wave method. Phy. Rev. B 50, 17953 (1994). [DOI] [PubMed] [Google Scholar]
  31. Kresse G. & Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775 (1999). [Google Scholar]
  32. Kresse G. & Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996). [DOI] [PubMed] [Google Scholar]
  33. Monkhorst H. J. & Pack J. D. Special points for Brillouin-zone integrations. Phys. Rev. B 13, 5188–5192 (1976). [Google Scholar]
  34. Baroni S., Giannozzi P. & Testa A. Green’s-function approach to linear response in solid. Phys. Rev. Lett. 58, 1861–1864 (1987). [DOI] [PubMed] [Google Scholar]
  35. Paolo G. et al. Quantum espresso: a modular and open-source software project for quantum simulations of materials. J. Phys: condens. Mat. 21, 395502 (2009). [DOI] [PubMed] [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES