In vivo mapping of cellular resolution neuropathology in brain ischemia with diffusion MRI

Abstract

Noninvasive mapping of cellular pathology can provide critical diagnostic and prognostic information. Recent advances in diffusion magnetic resonance imaging enabled in vivo examination of tissue microstructures well beyond the imaging resolution. Here, we proposed to use diffusion time–dependent diffusion kurtosis imaging (tDKI) to simultaneously assess cellular morphology and transmembrane permeability in hypoxic-ischemic (HI) brain injury. Through numerical simulations and organoid imaging, we demonstrated the feasibility of capturing effective size and permeability changes using tDKI. In vivo MRI of HI-injured mouse brains detected a shift of the tDKI peak to longer diffusion times, suggesting swelling of the cellular processes. Furthermore, we observed a faster decrease of the tDKI tail, reflecting increased transmembrane permeability associated with up-regulated water exchange or necrosis. Such information, unavailable from a single diffusion time, can predict salvageable tissues. Preliminary applications of tDKI in patients with ischemic stroke suggested increased transmembrane permeability in stroke regions, illustrating tDKI’s potential for detecting pathological changes in the clinics.

Time-dependent diffusion kurtosis imaging detects cellular morphology and transmembrane permeability changes in hypoxic ischemia.

INTRODUCTION

Disrupted cellular structure and membrane integrity are common indicators of acute tissue pathophysiology and injury in the brain. For instance, swelling of cell bodies and processes and disruptions of membrane structures are hallmarks of ischemic stroke (1). Now, the assessment of neuropathology at the cellular level mostly relies on histopathology, which is mostly postmortem and limited both spatially and temporally. In vivo, noninvasive mapping of brain pathology in real time, if available, would lead to accurate diagnosis and prognosis (e.g., tissue survival) to enable more effective and personalized treatments.

Magnetic resonance imaging (MRI) provides noninvasive tools to assess brain structure and physiology. Particularly, diffusion MRI (dMRI) uses diffusion of water molecules to probe tissue microstructure (2–5), and the acquired dMRI signals reflect ensemble-averaged micrometer-level tissue microstructural features well beyond the spatial resolution of MRI (millimeter level). A prime example is the use of dMRI to detect acute ischemic stroke (6), where the marked drop in water diffusivity within minutes after an ischemic insult (7) has been linked to tissue microstructural changes, although the exact pathology (e.g., neurons or astrocytes, cell bodies, or processes) that contributes to the drop remains unresolved. The diagnostic power of dMRI may be enhanced if it can be linked to specific cellular pathology.

A series of work on diffusion time (t)–dependent dMRI (8–11) offers an unprecedented opportunity to assess evolving cellular pathology. The measured t dependency is used to infer the spatial scale and statistical spatial distributions of tissue microstructure barriers to water diffusion (12–16). This technique has proven useful for interrogating ischemic brain injuries, as reported by us and others (17–21). The t dependency of dMRI signals also reflects transmembrane water exchange (11, 22–29), which is regulated by active and passive water channels located on cell membranes and, thus, can be linked to metabolism and membrane integrity. If the microstructural and exchange effects have distinct timescales, they can, in principle, be measured separately with t-dependent dMRI (28, 30). In the case of ischemic brain injury, this approach may provide critical insights into the dynamics of cellular swelling, beading, and membrane disruption. For instance, astrocytic activation after ischemic injury induces increased water fluxes via up-regulated aquaporin-4 (AQP4) channels (31) and also restructures the astrocytic processes to tune the volume (32), thus inflicting both microstructural size and membrane permeability.

In this study, we used t-dependent diffusional kurtosis imaging (tDKI) (33), which measures the t-dependent changes of the non-Gaussian diffusion component in dMRI signals (25, 26, 30, 33–35), to simultaneously infer microstructural size and membrane integrity via water exchange (Fig. 1). We hypothesize that these new markers are sensitive to cellular-level pathological changes after ischemic brain injury and can help identify subacutely salvageable tissue. We carried out numerical simulations, in vitro experiments, and in vivo experiments in a mouse model of neonatal hypoxia-ischemia (HI) to test the hypothesis, followed by a proof-of-concept study in patients with ischemic stroke.

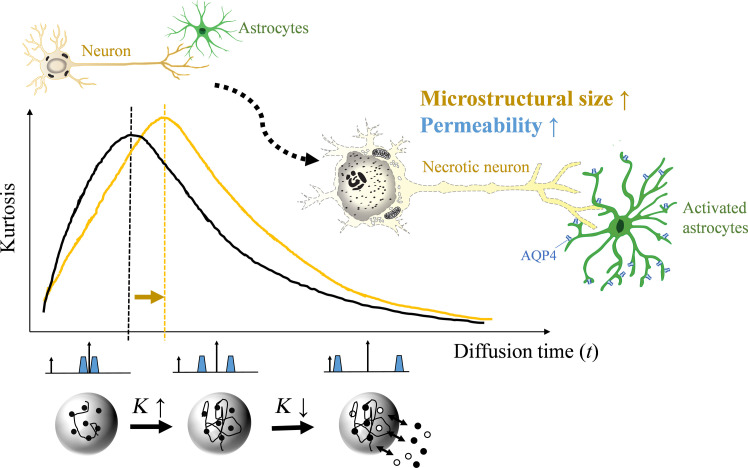
Fig. 1. Schematics of tDKI in measuring microstructural size and membrane integrity.

Normal neuron and astrocyte morphology is shown in the top left cartoon. Diffusion kurtosis (K) in biological tissues changes nonmonotonically as t increases, with an initial rise attributed to the water-restrictive effects of tissue barriers, followed by a descent as water molecules exchange between the intra- and extracellular spaces. We hypothesize that the peak t of the tDKI curve indicates the ensemble-averaged size of tissue barriers or effective structure size, while the postpeak descending curve reflects membrane permeability due to water redistribution, thereby enabling the assessment of key neuropathological features following hypoxic-ischemic stroke-like brain injuries, including neuronal swelling and membrane disruption, astrocytic activation and fragmentary degeneration, and changes of transmembrane water exchange.

RESULTS

Simulations illustrated the effects of microstructural size and permeability on tDKI for cell body and processes

Monte Carlo simulations (36, 37) were performed on phantoms of cylinders and spheres, representing a combination of cell processes (neurites/astrocytic processes, diameters of 1.0 to 1.4 μm) and cell bodies (diameters of 10 to 14 μm), respectively. The cylinders were dispersedly oriented at a degree of 40°, following observed dispersion in the brain (38), and combined with the spheres at different volume ratios and at the signal cumulant level (fig. S1). The results in Fig. 2 used a volume ratio of 0.84:0.12, based on a previous electron microscopy study of the mouse cortex (39), and demonstrated the behaviors of t-dependent diffusivity and kurtosis in response to changes in structural size and membrane permeability. The diffusivities rapidly dropped with increasing t, as a result of the coarse-graining process (10), i.e., the restrictive effects experienced by water molecules as they diffuse through structural barriers; and this process quickly completed above 10 ms for the hybrid phantom (Fig. 2, A and C).

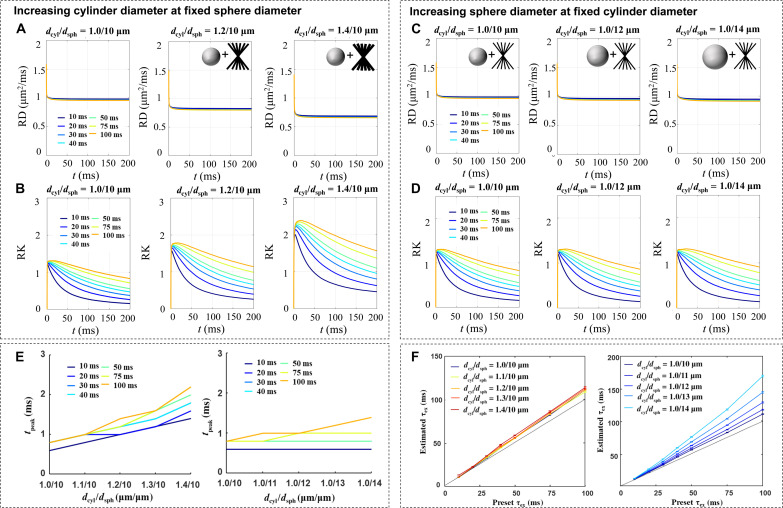
Fig. 2. Monte Carlo simulations of the t-dependent changes of the diffusivity and kurtosis at varying structure sizes and transmembrane exchange times (τ_ex).

The simulations were conducted in phantoms of cylinders and spheres at a volume ratio of 0.84:0.12, representing neurites and cell bodies, respectively. (A and B) Simulated diffusivity (A) and kurtosis (B) covered a t range of 0 to 200 ms, with the cylinder diameter changing from 1.0 to 1.4 μm and τ_ex from 10 to 100 ms, while fixing the sphere diameter at 10 μm. The intracellular volume fraction ranged from 0.4 to 0.6, which increased as the diameter increased. While diffusivity dropped rapidly and stabilized for t beyond 10 ms, the kurtosis first increased and subsequently decreased, with the t_peak shifting by almost twofold as the cylinder diameter increased from 1.0 to 1.4 μm. The kurtosis further decreased with t, and shorter τ_ex led to a fast decay of the kurtosis. (C and D) Simulated diffusivity (C) and kurtosis (D) with the sphere diameter changing from 10 to 14 μm while fixing the cylinder diameter at 1.0 μm. Similarly, shortening the τ_ex resulted in a faster decay of the kurtosis tail, but the t_peak position barely changed with the sphere diameter. (E) The change in t_peak with cylinder size from 1.0 to 1.4 μm at different τ_ex, while the sphere size was fixed 10 μm (left); and the change in t_peak with sphere size from 10 to 14 μm, while the cylinder size was fixed at 1.0 μm. (F) Estimated τ_ex based on the Kärger model compared with the present τ_ex, at different cylinder diameter (d_cyl) to sphere diameter (d_sph) pairs. SDs in the plots were based on the 95% confidence interval of nonlinear fitting. RD, radial diffusivity; RK, radial kurtosis.

Diffusion kurtosis, in contrast, demonstrated a nonmonotonical change that first increased and then decreased with t (Fig. 2, B and D). The rise time to peak (t_peak, the t at which kurtosis first rises to 90% of the maximum value) increased with both the structural sizes and exchange time (related with permeability) but by a different effect size. Particularly, t_peak shifted toward longer t as the cylinder size increased while keeping the sphere size the same (Fig. 2E). In comparison, an increase of the sphere size barely changed t_peak at fixed cylinder size, due to the relatively low volume of spheres under physiological condition (39). Although the increase of overall transmembrane water exchange time (τ_ex) also moved the t_peak, its effect was not strong within a physiological range of change (e.g., from 20 to 40 ms). τ_ex, on the other hand, had a large effect on the asymptotically decreasing tail of kurtosis with t, with a faster decrease associated with lower τ_ex. The estimated τ_ex based on the Kärger model (26, 40) largely agreed with the preset τ_ex, although overestimation was observed as the sphere size increased (Fig. 2F), possibly due to the longer t required to complete coarse graining. The estimation error can also occur when the assumption of two exchanging Gaussian compartments in the Kärger model was unmet. The effect of microstructural size on τ_ex estimation was illustrated in fig. S2. We also analyzed the error propagation by adding noise to the simulated signals and showed that the estimation errors of τ_ex were relatively low for signal-to-noise ratio (SNR) > 20, except for spheres with very fast exchanging (τ_ex = 10 ms) spheres (table S1).

Under pathological conditions, the morphology of cellular structure as well as membrane permeability may change simultaneously. The simulation results pointed out that decoupling the effects of size and permeability from tDKI is possible for cellular processes of small microstructural size, where coarse graining is relatively fast. In this case, the t_peak relates to the effective size of the restrictions, and the decreasing tail of the tDKI curve reflects the transmembrane water exchange, respectively.

In vitro tDKI in cultured brain organoids showed the feasibility of mapping structural size and membrane permeability

In real brain tissues with a mixture of neurons, glial cells, and their processes, can we extract information on effective structural size and membrane permeability from tDKI? To answer this question, we imaged three-dimensional (3D) forebrain-specific organoids differentiated from human-induced pluripotent stem cells (hiPSCs) (41), which resemble the cellular architecture of forebrain. In vitro scans of the fixed organoids were performed on an 11.7 Tesla nuclear magnetic resonance spectrometer using both pulsed gradient spin echo (PGSE) and stimulated echo acquisition mode (STEAM) dMRI sequences (fig. S3) to cover a wide range of t from 7 to 200 ms. The organoid core contained dead cells with membranes lacking integrity and digested, and the organoid rim contained more living cells with intact membranes before fixation, as illustrated in Fig. 3G. To simulate the effects of changing structure sizes, we acquired tDKI data with temperatures gradually increased from 300 to 320 K (300 K ≈ room temperature, 310 K ≈ body temperature). Because water diffusivity (D) increases with temperature, increasing temperature will increase the diffusion length scale L ($L=\sqrt{2\mathit{Dt}}$) or, equivalently, scale down the relative microstructure size experienced by the water molecules (Fig. 3A). As the temperature increased from 300 to 320 K, the diffusivity increased overall as expected, and the monotonic decrease with t was preserved (Fig. 3B).

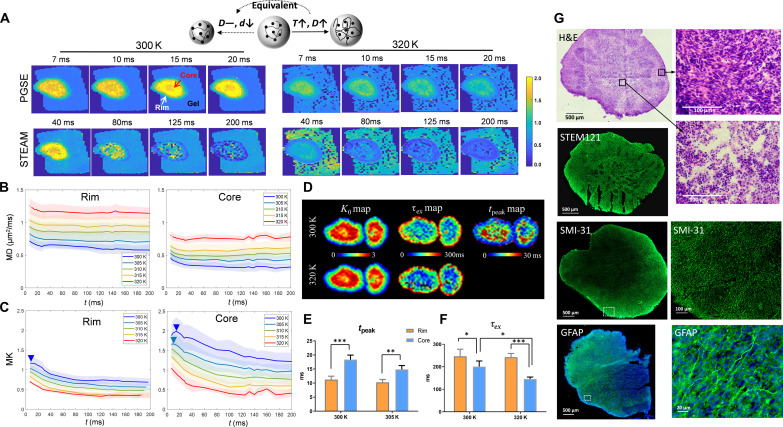
Fig. 3. tDKI of the in vitro organoids.

(A) Mean kurtosis maps of an organoid at varying ts from 7 to 200 ms at 300 and 320 K, using the PGSE (for 7 to 20 ms) and STEAM (for 40 to 200 ms) dMRI sequences. Here, increasing temperature has the equivalent effect of reducing microstructural size on dMRI signals, as illustrated in the cartoon. (B and C) t-dependent mean diffusivity (MD) and mean kurtosis (MK) curves at five different temperatures, obtained in the core and rim regions from eight organoid samples with the shadows showing the SDs. The MK curves in the core region showed a peak around 20 ms (blue arrowheads) at 300 K, which shifted to shorter t as the temperature increased. (D) Voxel-wise K₀ maps and τ_ex maps, as fitted from the Kärger model, and t_peak maps of the organoids scanned at temperatures of 300 and 320 K. (E) Statistical comparison of the t_peak detected in the core and rim regions at 300 and 305 K (n = 8). The peaks shifted below 7 ms above 305 K and became nondetectable. (F) Statistical comparison of the t_peak detected in the core and rim regions at 300 and 320 K. *P < 0.05, **P < 0.01, and ***P < 0.001 by paired t test. (G) Selected hematoxylin and eosin (H&E), STEM121, SMI-31, and glial fibrillary acidic protein (GFAP) staining from different organoids. The zoomed-in views of H&E indicated necrotic changes with pyknotic nuclei and eosinophilic cell bodies in the core region, and the increased SMI-31 and GFAP expression in the rim region indicated the presence of axons and astrocytes, greater than that seen in the core.

The tDKI curve measured at 300 K in the core area had a t_peak around 20 ms (Fig. 3C). As the temperature rose, the kurtosis peak gradually shifted to shorter ts (e.g., 15 ms at 305 K) and eventually below 7 ms (the shortest t used) at temperatures above 310 K (body temperature equivalent). Similar t-dependent changes were observed in the rim region. This temperature-dependent behavior of kurtosis agreed with the simulation results as the decreased effective structure size should shift the kurtosis peak toward shorter t. The short t_peak value (below 7 ms) at close to body temperature (Fig. 3E) also matched our simulations when the cell process component of small microstructural size (1 to 2 μm) was dominant. The maps of t_peak showed that the rim had shorter t_peak than those of the core (Fig. 3, D and E), which may be explained by more densely populated neurites and glial processes in the rim as shown in the SMI-31 and glial fibrillary acidic protein (GFAP) immunocytochemistry (Fig. 3G).

As the diffusivities remained largely unchanged for t > 20 ms, which suggested completed coarse graining, the observed tDKI tails mainly reflected water exchange. In addition, the descending tail of the kurtosis became steeper at higher temperatures. Fitting the Kärger model to the tDKI data, we observed a reduction in the estimated τ_ex as the temperature increased (n = 8 samples; Fig. 3F), likely due to increased water mobility and/or higher membrane permeability at higher temperature. In addition, significantly lower τ_ex (higher permeability) was observed in the core than the rim (Fig. 3, D and F), which was consistent with the necrotic cell pathology in the core as shown in the hematoxylin and eosin (H&E) and STEM121 staining (Fig. 3G), suggesting disrupted membrane integrity during necrosis. Note that only passive transport through water channels contributed to the transmembrane water exchange in the fixed organoids, since active transport was absent (29). The organoid data suggested that the effective structure size in brain tissue was closer to the size of cellular processes (e.g., glial processes and axons), and separation of structure size and exchange effects from tDKI signals was possible.

tDKI highlighted morphological changes in the cell processes upon HI injury

Taking into account the data from simulations and in vitro experiments of organoids supports the concept that tDKI can detect the size and membrane integrity of cellular processes. We next tested tDKI on a widely used mouse model of neonatal HI injury, which involved unilateral ligation of the carotid artery followed by hypoxia. This model exhibits a spectrum of ipsilateral stroke-like pathophysiology, including neuronal swelling, neurite beading, astrocytic activation, and both necrotic and apoptotic cell death. The contralateral hemisphere can serve as a nonstroke control comparator (1, 42). In about one-third of the mice (13 of 41; see table S2), severe edema in the ipsilateral cortex and hippocampus was observed as early as 3 hours after HI, as indicated by decreased diffusivity and increased kurtosis (by approximately 25 and 100% with respect to the contralateral side, respectively) and hyperintense T2 signals (Fig. 4, A and B).

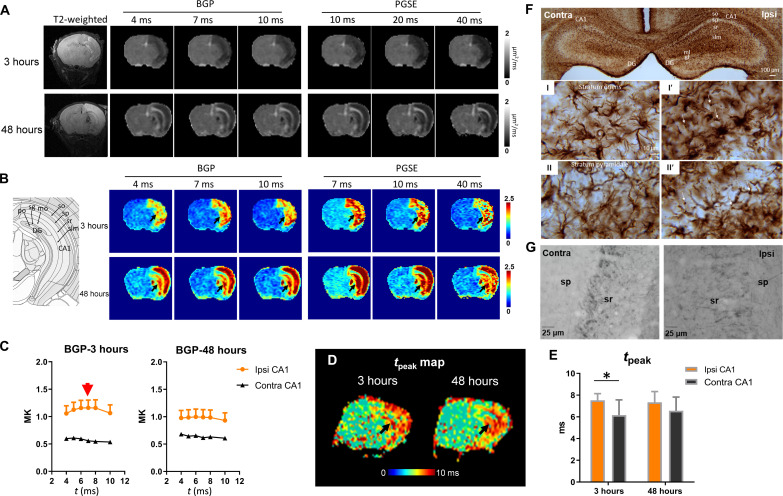
Fig. 4. tDKI-based t_peak and microstructural size alterations in a mouse model of neonatal HI injury.

(A and B) Diffusivity and kurtosis maps of a severely injured mouse brain scanned at 3 and 48 hours after the HI onset with t ranging from 4 to 40 ms using a bipolar pulsed gradient (BPG) and PGSE sequences. (C) t-dependent change in BGP-based mean kurtosis (MK) showed a peak around 7 ms (red arrow) in the ipsilateral CA1, while the contralateral CA1 did not show an apparent peak. (D) The t_peak map showed increased t_peak in the hippocampus (black arrows) of the HI-injured brain at 3 and 48 hours after HI. (E) Statistical comparison of peak positions in the ipsilateral and contralateral CA1 at 3 and 48 hours after HI (n = 6). *P < 0.05 by paired t test. (F) GFAP staining at 3 hours post-HI shows evident swelling of astrocytic body and processes, as well as beading in the astrocytic feet in stratum oriens (I′) and stratum pyramidale (II′) of the ipsilateral hippocampus (thin arrows). (G) Neurofilament staining showed axonal disruption and swelling in the stratum pyramidale and stratum radiatum of the ipsilateral hippocampus. contra, contralateral; ipsi, ipsilateral; sr, stratum radiatum; sp, stratum pyramidale; HP, hippocampus; DG, dentate gyrus.

In the edema region, diffusivity showed higher t dependency compared to the contralateral side (fig. S4, A to D), similar to our previous reports based on this model (18, 19). The tDKI curve measured using PGSE for t in the 7- to 40-ms range only showed the descending portion (fig. S4, E to H), suggesting that t_peak was shorter than 7 ms. To capture the tDKI peak, we used the bipolar pulsed gradient (BPG) diffusion encoding (fig. S3) to acquire dMRI signals with t of 4 to 10 ms. The tDKI peak appeared around 7 to 8 ms in the edema regions (e.g., the orange and black in Fig. 4C; see detailed data in table S3), which was less evident on the contralateral side, suggesting that normal tissue may have a t_peak below the measurement range. Voxel-wise mapping of the t_peak in severely injured mice further illustrated increased t_peak in the ipsilateral cortex and hippocampus at 3 hours after injury (Fig. 4D). The quantification of t_peak in Fig. 4E agreed with the simulation results and organoid experiments, and the shift of peak position to longer t in edema may reflect volume expansion, including swelling and beading of the astrocytic processes and neurites upon HI.

This interpretation is supported by the GFAP immunohistochemical staining at 3 hours after HI (Fig. 4F). The ipsilateral hippocampus showed enrichment of GFAP immunoreactivity overall compared to the contralateral hippocampus, which is particularly notable in the CA1 region. The enrichment appeared to be due to intensified GFAP immunoreactivity in ipsilateral swollen astrocytes and their processes in the neuropil of the stratum oriens and stratum pyramidale (Fig. 4F, I′ and II′), as well as beading in the astrocytic feet (indicated by thin arrows). Moreover, neurofilament staining indicates axonal swelling in the stratum pyramidale and stratum radiata of the hippocampus (Fig. 4G) at 3 hours. The tDKI peak was less evident at 48 hours (Fig. 4C), indicating that the swelling phenomenon may be transient.

In mice that had mild or no apparent edema (about two-thirds), slightly decreased diffusivity and increased kurtosis were found in limited regions (mostly in the hippocampus) with T2 hyperintensity (fig. S5, A and B). In the group-average kurtosis curves, the peak was not apparent in either the ipsilateral hippocampus or the control groups (fig. S5C), indicating no apparent morphological change associated with the cellular processes.

tDKI-based permeability indicated tissue survival after HI

We also examined transmembrane water exchange using tDKI in the mouse HI model. As shown in Fig. 5 (A and B), no abnormality was visible in the T2-weighted images of a severely injured mouse at 3 hours postinjury, but marked changes in diffusivity and kurtosis were already present. Kurtosis maps revealed considerable regional heterogeneity at 3 hours in the edema region (Fig. 5B). In particular, the cingulate cortex (indicated by pink arrows) had the highest kurtosis compared to neighboring regions, e.g., the sensory cortex (indicated by light blue arrows). On the basis of this, one might suspect that the cingulate cortex had more severe injury than the sensory cortex, but analyses of the tDKI curve indicated otherwise. Figure 5C shows that tDKI curve in the sensory cortex descended slightly faster than in the cingulate cortex (see exact data in tables S4 and S5), translating into lower τ_ex (higher permeability) in the sensory cortex (indicated by blue arrows in Fig. 5D). At 48 hours, kurtosis in the ipsilateral sensory cortex increased further, and the estimated τ_ex was significantly lower than the normal tissue; while the ipsilateral cingulate cortex showed reduced kurtosis compared to 3 hours, and τ_ex was almost back to normal (Fig. 5, C and E). Histology at 48 hours demonstrated severe infarct-like necrosis in the ipsilateral sensory cortex, which explained the drastically elevated transmembrane permeability, whereas the cingulate cortex had no apparent infarction and relatively preserved cytology (Fig. 5, F and G, and fig. S6). Therefore, the transmembrane permeability marker could be a predictor of tissue viability. The transiently increased permeability in the ipsilateral cingulate at 3 hours, on the other hand, may be explained by the substantial astrocyte activation (Fig. 5H and fig. S7), which gave rise to up-regulated water transport (43) and cytotoxic edema (32, 44).

Fig. 5. tDKI-based estimations of transmembrane water exchange in a mouse model of neonatal HI injury.

(A and B) Diffusivity and kurtosis maps of a severely injured mouse brain scanned at 3 and 48 hours after the HI onset, with t ranging from 4 to 40 ms using a combination of BPG and PGSE sequences. The pink and blue arrows point to the cingulate cortex and visual cortex, respectively. (C) t-dependent change in mean kurtosis (MK) between 7 and 40 ms illustrated a faster decay tail in the sensory cortex, compared to the nearby cingulate cortex and the contralateral side (n = 6). (D) τ_ex maps of a mouse brain at 3 and 48 hours after HI. (E) Group comparison of τ_ex between the ipsilateral and contralateral cortex (n = 6). At 3 hours after HI, both ipsilateral cingulate (pink) and sensory (blue) cortex had reduced τ_ex compared to the contralateral side (black); at 48 hours, τ_ex continued to decrease in the sensory cortex, while τ_ex gradually returned to normal in the cingulate cortex (*P < 0.05 and **P < 0.01 by paired t test). (F) Nissl staining of brain sections at 48 hours after HI reveals a stark difference between the infarcted sensory cortex and the almost intact cingulate cortex. Higher magnification shows the cellular pathologies in the contralateral (I) and ipsilateral cingulate cortex (II) and the border between ipsilateral cingulate and sensory cortex (III). (G) GFAP staining of the same sections as (F) at 48 hours after HI shows slight astrocytic activation in the ipsilateral cingulate cortex (II) but much higher astrocyte aggregation at the borders of the necrotic core in the sensory cortex (III). (H) GFAP staining of another mouse brain at 3 hours after HI revealed extensive astrocytic activation in the ipsilateral cingulate cortex. High-magnification images in fig. S6 further show swelling of the astrocytic processes.

The mild/moderate injury mice exhibited reduced diffusivity and increased kurtosis in the hippocampal CA1 region at 3 hours and typically developed apoptotic injury with slightly atrophic hippocampus. However, no abnormalities in the T2-weighted contrast, diffusivity, or kurtosis values were observed at 48 hours. Quantitative analysis of these mice showed no significant changes in τ_ex compared to the contralateral side or the shams (fig. S5D), indicating no apparent changes in membrane permeability.

tDKI detected reduced transmembrane exchange in patients with ischemic stroke

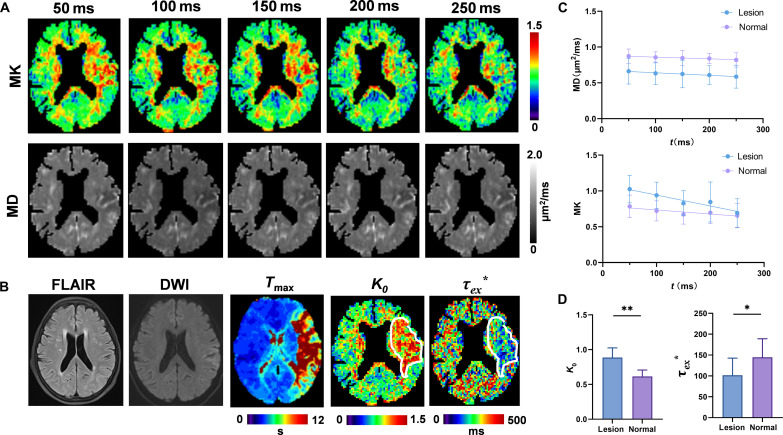
Encouraged by the findings from the mouse HI model, we went one step further to assess the clinical feasibility of tDKI in ischemic stroke. Five patients with stroke with acute ischemic brain injury (see clinical information in table S6) were scanned on a 3T clinical scanner using the STEAM diffusion encoding with t from 50 to 250 ms. Given the difference in cell size between mouse and human brains (45), especially for astrocytes, a much longer t range was required to approach the completion of coarse graining in the human brain (12). Figure 6 (A and B) demonstrated elevated kurtosis at short t and slightly reduced diffusivity in the lesion region in an acute stroke patient scanned at half an hour after onset, when no apparent injury was observed in the T2-weighted image. Figure 6C showed a very slow decrease in mean diffusivity, in contrast to a pronounced drop in mean kurtosis with increasing t. This finding is consistent with our previous report in the human cortical gray matter (28, 30), which suggested incomplete coarse graining. On the other hand, a recent study suggested that exchange effects dominate the effects of structural disorder in gray matters (27). Kärger model fitting revealed decreased exchange time τ_ex^* (* indicates that τ_ex fitting may not satisfy complete coarse-graining condition) and increased K₀ in the ischemic tissue (contoured region), which matched the observation from the HI-injured mouse brains. The differences in kurtosis between lesion and contralateral regions gradually decreased as t increased, and the lesion became indistinguishable at a t of 250 ms (Fig. 6, A and C), due to the faster descent of tDKI in the lesion area, while the K₀ map showed the largest area of lesion (Fig. 6B). Statistically, τ_ex^* were significantly lower, and K₀ were higher in the infarct lesions than in contralateral uninjured regions (P < 0.05; Fig. 6D and table S7), indicating increased transmembrane permeability and more restrictive diffusion in ischemic stroke regions.

Fig. 6. tDKI in patients with ischemia stroke.

(A) The mean kurtosis (MK) and mean diffusivity (MD) maps at each t from 50 to 250 ms. (B) The corresponding T2-weighted image, mean diffusion-weighted image (DWI) at b = 1 ms/μm², time to maximum of the residue function (T_max) map obtained from dynamic susceptibility contrast perfusion-weighted imaging, K₀ map, and τ_ex^* map (* indicates that τ_ex fitting may not satisfy complete coarse-graining condition). White contours label the infarct lesion. FLAIR, fluid attenuated inversion recovery. (C) t-dependent MK and MD curves from the infarct lesions in five patients and the normal-appearing tissues on the contralateral side (plotted as mean ± SD). (D) Statistical comparison of K₀ and τ_ex^* between the lesion and normal-appearing tissues. *P < 0.05 and **P < 0.01 by paired Wilcoxon test.

DISCUSSION

The tDKI provides a noninvasive, real-time approach to detect pathological events after ischemic injury at the cellular level, well beyond the resolution of conventional MRI. The pathophysiology of cerebral ischemia involves a chain of complex cellular and molecular processes, and in vivo mapping of such events is essential to identify the tissue damage and viability and design therapeutic strategies. During the process of HI, ionic and osmotic perturbations occur, resulting in water shifting to intracellular compartments as well as swelling of cell body and processes. The timing of neuropathology within different microdomains of neural cells is unclear and difficult to identify using conventional dMRI. Our results indicate that the morphological change detected by peak of the tDKI curve are likely associated with astrocytic processes and neurites. Simultaneously to the morphological changes, alterations in membrane permeability are measured using the tail of the tDKI curve, reflecting not only the transiently up-regulated astrocytic function but also disrupted membrane integrity that is vital to tissue outcome.

The observed t-dependent behaviors of diffusivity and kurtosis measurements hinted at the spatial scale of structural barriers. The relatively short t_peak of the tDKI curve (<10 ms) from in vitro and in vivo experiments agreed with the simulations, where the cylinder component (representing axons, dendrites, or glial processes with small diameters) was dominant. Therefore, the change of tDKI peak in acute edema regions might reflect the change of these structures, as supported by the observed swelling/beading of the astrocytic processes or neurites (axons and dendrites). Histopathology in this study showed more widespread swelling of the astrocyte compartments compared to sporadic axon beadings, suggesting that astrocytes may play a major role here. In addition, simulations of the beading effect indicated that the beading slightly elevated the tDKI tail but did not seem to change t_peak (fig. S8). Previous studies showed that the astrocytes play a critical regulatory role in ischemic stroke (46) and have become a potential treatment target (47). For instance, astrocytes rapidly sense the ischemic insult and rapidly tune their volumes and regulate their processes (32), partially by up-regulating the AQP4 channels on their endfeet to facilitate transmembrane water exchange (43, 48). The tDKI findings of microstructural size and permeability changes during the early evolving cytopathology of brain HI are consistent with predominance of protoplasmic astrocytes and their processes represented in the neuropil (49) and, therefore, provide the possibility for in vivo detection of astrocytic pathology.

Inspecting membrane integrity via water exchange using tDKI requires the completion of coarse graining. When the restrictive effect of microstructure is accounted for, the t-dependent change in kurtosis mainly reflects exchange effects, and faster decay of the tDKI tail corresponds to higher permeability. Previously, the t-dependent descent of kurtosis in the long-t range has been used to infer transmembrane water exchange in normal brain tissues (30, 35) and mammary tumors (33), and t-dependent kurtosis has been proposed for stroke prognosis (21). Our mouse model of HI suggests that in vivo mapping of transmembrane exchange or permeability may correlate with tissue integrity outcome. For example, at 3 hours after HI, the lower kurtosis in the ipsilateral sensory cortex compared to the cingulate cortex at a single t was misleading and contradictory to the final outcome. tDKI revealed higher permeability in the sensory cortex that matched its final progression into necrosis and severe tissue infarction. This is promising for the identification and prediction of salvageable tissues for which therapies can be useful. We further demonstrated that this technique was applicable to patients with ischemic stroke, who showed increased permeability in injured brain regions. Future clinical studies may design a longitudinal follow-up of patients with stroke to evaluate the clinical impact of the preclinical findings.

A variety of dMRI techniques have been proposed for neurite diameter mapping, including q-space approaches by acquiring dMRI signals in multiple diffusion directions and strengths (50–52), as well as t-dependent dMRI methods (14, 16). Most of these approaches involved complex multicompartmental modeling and lengthy sampling in the q-space or t-domain. On the other hand, methods for spatial mapping of transmembrane permeability are relatively few. The filter exchange imaging method (53) is designed to infer the apparent exchange rate (~1/τ_ex) by modulating the intracellular (low diffusivity) and extracellular (high diffusivity) signals with a variable exchange time, which has been tested in animal models (54) and the human brain (55); however, the SNR is a concern. The random permeable barrier model also allows for permeability estimation based on the power law of t-dependent diffusion (25, 56). The joint model by Jiang et al. (57) was built upon exchange between cells and extracellular space based on t-dependent diffusivity to estimate the intracellular water lifetime (τ_i). The Neurite Exchange Imaging model (28) and the Standard Model with Exchange (27) use the anisotropic Kärger model in a standard model composed of neurites and extraneurite compartments to infer τ_ex. Here, we demonstrated the use of the full spectrum of tDKI for simultaneously detecting changes in structural morphology and τ_ex without complex modeling. The clinical version of tDKI technique only takes 10 min and thus can be readily translated to clinical applications.

To take full advantage of tDKI, it is ideal to have a wide range of ts from ~1 to ~1000 ms, which is challenging using the same type of diffusion encoding. We used the BPG (58) encoding to access t < 10 ms, PGSE (59) diffusion encoding for the intermediate t range, and STEAM sequence (60) for t > 50 ms. During calibration, we found that PGSE and STEAM provided consistent kurtosis measurement, while BPG exhibited a bias (fig. S9). Therefore, in the current study, we combined PGSE and STEAM measurements in the in vitro organoid experiment; in the mouse brain study, we separately used BPG data to estimate the tDKI peak and PGSE data to fit the tail. When it comes to clinical applications, measurements at short t become difficult given the limited gradient strength (only ~¹/₁₀ of the animal scanners). Instead, we focused on the tDKI tail at long ts (50 to 250 ms) to map transmembrane permeability using the STEAM sequence. It should be noted that the unwanted diffusion weightings generated by the imaging gradients in the STEAM sequence should be properly corrected (61) before fitting kurtosis. Also, the reduced SNR that accompanies the increase of t in the STEAM sequence may introduce bias in the D(t) measurement, as the apparent diffusivity decreases with reduced SNR (62). In addition, the Kärger model based τ_ex estimation is sensitive to the t measurement window, as well as the choice of pulse sequence, e.g., τ_ex was estimated to be tens of milliseconds in the human cortex using the PGSE sequence with t of 20 to 100 ms (30), which was lower than our fitting results. A standardized protocol will be needed for clinical use in the future.

This study has several limitations. First, the Monte Carlo simulations were based on simplified phantoms, without incorporating the real-world geometry of neurons, astrocytes, or their processes, and the spheres and cylinders were combined at the signal cumulant level, assuming small impacts from geometrical differences in the extracellular space (63). Simulations with more realistic phantoms, e.g., those using electron microscopy data (38), will provide more precise information on the interplay between restrictive effects and exchange and is an active research area. Second, the tDKI tail reflects transmembrane exchange time τ_ex, which is itself a complex term that depends on both the intra/extracellular lifetime and intra/extracellular volume fraction, expressed as τ_ex = τ_i*v_e = τ_e*v_i. Thus, the change of microstructural morphology may change the volume fraction and, consequently, alter τ_ex. Decoupling the intra/extracellular lifetime and volume fraction is possible with advanced dMRI measurements and modeling (27) but may be hard to achieve for clinical use. Furthermore, we did not directly measure transmembrane permeability in this study but inferred the permeability change from histological observations of astrocyte physiopathology. Future studies on mice expressing fluorescent proteins exclusively in astrocytes to visualize their entire volumes and aquaporin or Na/K–adenosine triphosphatase distributions and activities could provide more direct evidence of transmembrane water exchange. In addition, the fitted τ_ex maps were relatively noisy given the complex Kärger model fitting and noise in the raw data. Bayesian fitting or machine learning approaches (64) may be attempted to improve the fitting results.

Nevertheless, the findings presented here using tDKI provided important information on structural morphology and transmembrane permeability in addition to existing MRI routines. The technique shows potential to detect astrocytic pathology and predict pathological outcomes related to reversible or irreversible damage in ischemic stroke. Further applications of tDKI in other diseases are also promising, such as in tumors where considerable changes in cellular microstructure and permeability take place.

MATERIALS AND METHODS

Monte Carlo simulation

We performed Monte Carlo simulation of diffusion (36) in cylinder and sphere phantoms to represent simplified geometry of axons and cells, respectively. For cylinder phantoms, we oriented the cylinders in 1000 directions that were sampled on the basis of a Watson distribution of concentration parameter = 2.57 or infinity, corresponding to a dispersion angle = 40° or 0° (38). The cylinder diameter ranged from 1 to 1.4 μm, and the intracylinder volume fraction was 0.4 for 1 μm and linearly increased with the cylinder diameter to 0.6 for 1.4 μm. The intrinsic diffusivity D₀ in the intra- and extra-axonal spaces were 1 and 2 μm²/ms, respectively. The spherical phantoms were configured similarly, with the diameters set at 10 to 14 μm, and the intrasphere volume fraction ranged from 0.4 (for 10 μm) to 0.6 (for 14 μm). The transmembrane exchange times varied from 10 to 100 ms.

Simulations were performed using the Realistic Microstructure Simulator (36) implemented in CUDA C++ and accelerated by using one core on an NVIDIA A40 GPU. For each simulation setting, 2 × 10⁶ walkers were randomly used in each phantom, diffusing over 1 × 10⁶ steps with a duration δt = 2 × 10⁻⁴ ms and a step size $\sqrt{6D_0\mathrm{\delta }t}$ = 0.035 and 0.049 μm inside and outside the cells, respectively. The second and the fourth order cumulants of diffusion displacements were calculated at 1000 time points t from 0.2 to 200 ms. Then, we calculated the radial diffusivity and radial kurtosis using the apparent diffusivity and apparent kurtosis perpendicular to the main direction of the Watson distribution. For sphere phantoms, we calculated the mean diffusivity and mean kurtosis by averaging the apparent diffusivity and apparent kurtosis in 100 random directions. To mix the cylinder and sphere phantoms at the signal level, we combined their diffusivity D_i(t) and kurtosis K_i(t) as follows (38)

$$D(t)=\sum _{\mathrm{i}}{f}_{\mathrm{i}}·D_i(t)$$ (1)

$$K(t)=\frac{1}{D^2(t)}\sum _{\mathrm{i}}\left\{3f_{\mathrm{i}}·{\left[D_{\mathrm{i}}(t)-D(t)\right]}^2+f_{\mathrm{i}}·D_{\mathrm{i}}^2(t)K_{\mathrm{i}}(t)\right\}$$ (2)

where f_i refers the volume fractions of cylinder and sphere phantoms.

To demonstrate the effect of neurite beadings on the time-dependent diffusivity and kurtosis, we generated two substrates composed of randomly positioned, randomly oriented fibers. The transmembrane exchange times were 25 or 100 ms for both substrates. The intrafiber volume fraction was 0.5. The first substrate consisted of straight cylinders in diameter = 1 μm without beadings, whereas the second substrate consisted of beaded fibers with beadings. The beaded fibers were generated on the basis of the following tissue parameters and bead profiles previously observed in a mouse brain electron microscopy data (38, 65): circular cross section, mean diameter = 1 μm, coefficient of variation of diameter = 0.2, randomly positioned beads with the bead distance = 5 ± 2.5 μm (mean ± SD), and Gaussian bead shape with a single bead width = 5 μm. The fiber microgeometry was sampled as a voxelized geometry in a 600 × 600 × 600 matrix, with a side length of 0.05 μm for each pixel. The intrinsic diffusivities (D₀) inside and outside the cells were 1 and 2 μm²/ms. In this part, 1 × 10⁷ walkers were randomly used in each phantom, diffusing over 1.2 × 10⁵ steps with a duration δt = 1.7 × 10⁻⁴ ms and a step size $\sqrt{6D_0\mathrm{\delta }t}$ = 0.032 and 0.045 μm inside and outside the cells, respectively. The second and the fourth order cumulants of diffusion displacements were calculated at 1000 time points t from 0.2 to 300 ms.

To evaluate the estimation error due to noise in the raw data, we first added Gaussian noise to the simulated signals and estimated the kurtosis based on the noisy signals at each t according to S = exp[−b · D + 1/6 · (b · D)² · K]. We then fitted the Kärger model to the kurtosis curve to estimate τ_ex. This process was repeated 50 times, and the root mean square error between the fitted τ_ex and the ground truth was calculated as an evaluation of the error.

dMRI pulse sequence

To access water diffusion experimentally over a wide range of t, three types of diffusion gradient waveforms were used. We used the BPG (58) to measure dMRI signals at short ts (4 to 10 ms), the PGSE (59) for intermediate ts (7 to 40 ms), and the STEAM (60, 66) for intermediate and long ts (15 to 200 ms for organoids and 50 to 250 ms for patient experiments). The sequence schematics and their effective ts were defined in fig. S3. These sequences were calibrated using a mineral oil phantom to ensure consistent diffusivity measurements. Note that the imaging gradients in the STEAM-dMRI sequence generate unwanted diffusion weighting, and this additional diffusion weighting increases with t. Therefore, the effective b-value was used for fitting DKI, which was calculated on the basis of the b-matrix considering both diffusion encoding and imaging gradients along three axes. The effective b-value in the b0 image (no diffusion encoding) at different diffusion times was listed in table S8 for the stroke patient study. A 3D STEAM sequence was used in the organoid experiment, which generated less unwanted b-value because the slab selection gradient was much weaker than the 2D multislice STEAM sequence used in the patient experiments. The change of t in STEAM-dMRI is also accompanied with a change of T1 relaxation weighting, although this effect was shown to be minor according to a previous investigation (67).

Note that kurtosis measurements in biological tissue may differ among the different diffusion encoding schemes, even at comparable t, as reported previously (68). In our experimental data (fig. S8), we found that BPG and PGSE resulted in similar diffusivity but different kurtosis at the same t, while PGSE and STEAM provided consistent results. Therefore, we analyzed the tDKI curves obtained by BPG and PGSE separately in the in vivo mouse brain study while using the PGSE and STEAM measurements jointly in the organoid experiment.

Forebrain organoid and in vitro MRI

The 3D brain organoids (3Dnamics Inc., Baltimore, MD, USA) were differentiated from hiPSCs to resemble the molecular and cellular features of the human forebrain. The hiPSCs derived from human adult somatic cells were cultured in forebrain differentiation medium, according to the protocol described in (69). The 3D organoids were placed in glass tubes surrounded by agarose gel for supporting and preventing hydration during scan. They were scanned on an 11.7T Bruker vertical spectrometer, with a 15-mm-volume transceiver coil, a Micro2.5 gradient system (maximum gradient strength = 1500 mT/m), and a temperature control system. dMRI data were acquired using PGSE sequence with diffusion gradient duration (δ) of 3 ms, diffusion separation (∆) of 7 to 30 ms (equivalent t = ∆ − δ/3), and two signal averages; and STEAM sequence with δ of 3 ms, ∆ of 15 to 200 ms, and eight signal averages to compensate for the SNR loss in STEAM. The other diffusion parameters were kept the same between PGSE and STEAM, including 30 diffusion directions, six b-values with b = 0.5, 1.0, 1.5, 2.0, 2.5, and 3.0 ms/μm², and five nondiffusion-weighted images. The effective b-values that considered the contributions of imaging gradients were calculated on the Bruker system and used in the following analyses. dMRI images were acquired using a single-shot 3D echo planar imaging (EPI) and the following parameters: echo time (TE)/repetition time (TR) = 38/3000 ms, in-plane resolution = 0.31 mm × 0.31 mm × 0.8 mm, and an imaging time of 18.5 min for PGSE and 1.23 hours for STEAM scans. The organoids were first imaged at room temperature (300 K), and then the scans were repeated at 305, 310, 315, and 320 K. We left at least 3-hour interval for the temperature transitions. Note that for the Kärger model fitting of the organoid data, we used t = 20 to 125 ms due to a few noisy data acquired at long t.

Mouse model of neonatal HI

All animal procedures were approved by the Animal Use and Care Committee of Johns Hopkins University School of Medicine (Animal Use and Care Committee no. M021M321). In this study, 28 C57BL/6 mouse pups (the Jackson Laboratory, Bar Harbor, ME, USA) underwent HI insult on postnatal day 10, using the Rice-Vannucci model adapted for the neonatal mouse (70). The injury was induced by unilateral ligation of the right carotid artery followed by 45 min of hypoxia (FiO₂ = 0.08), as described in (70). Fifteen pups (one to two from each litter) were subjected to sham injury, with right carotid artery exposed but no ligation or hypoxia. The first MRI was acquired at 3 to 6 hours after the hypoxia. Some of the mice were killed after imaging for pathology, and the rest of them survived up to 48 hours until they were scanned again and then killed for pathology. The use of the mice is specified in table S2.

In vivo MRI of the mouse brains

In vivo MRI was performed on a horizontal 11.7 Tesla scanner (Bruker Biospin, Billerica, MA, USA). MR images were acquired with a 15-mm receive-only planner surface coil, a 72-mm quadrature transmitter coil, and a B-GA 9S gradient system (maximum gradient strength = 740 mT/m). During imaging, mice were anesthetized with isoflurane (1%) together with air and oxygen mixed at 3:1 ratio via a vaporizer. PGSE sequence was acquired at δ = 4 ms and ∆ = 7, 10, 15, 20, and 40 ms, and BPG sequence was acquired at δ = 3 ms and ∆ = 4.1, 5, 6, 7, 8, and 10 ms. All dMRI protocols used 15 diffusion directions, three b-values with b = 1.0, 1.5, and 2.0 ms/μm², and four nondiffusion-weighted images. Both the PGSE and BPG scans were acquired using single-shot 2D multislice EPI with TE/TR = 55/5000 ms, one signal average, in-plane resolution =0.2 mm × 0.2 mm, 10 slices with slice thickness of 0.8 mm, and an imaging time of 4.1 min per scan. In addition, T2-weighted images were acquired using a fast spin echo sequence with TE/TR = 50/3000 ms, two signal averages, echo train length of 8, in-plane resolution of 0.1 mm × 0.1 mm, and 10 slices with thickness of 0.80 mm, coregistered to the dMRI data.

Histology and immunohistochemistry for neuropathology

Mice were perfused intracardially with phosphate-buffered saline followed by 4% paraformaldehyde. Dissected brains were cryoprotected in sucrose and sectioned at a thickness of 50 μm on a freezing sliding microtome. Every 10th section was stained with cresyl violet to visualize Nissl substance, and adjacent sections were stained with H&E. Near-adjacent sections were stained immunohistochemically using GFAP as an astrocyte marker, phosphorylated neurofilament antibody as a marker for axonal processes, and microtubule protein MAP2 as a marker for dendrites.

tDKI acquisition of patients with ischemic stroke

Five patients with ischemic stroke (five females, age = 70 ± 12 years old) were included in this study. The basic demographic and clinical information of these patients were listed in table S7. The study was approved by the Institutional Research Board at Shanghai Fourth People’s Hospital (Institutional Research Board no. 2023085-001), and written consents were collected from the patients. tDKI scan was performed on a 3T Siemens Prisma scanner (maximum gradient strength = 80 mT/m) using the STEAM dMRI sequence with the following protocol: TE/TR = 50/2500 ms, field of view = 220 ms by 220 ms, resolution = 2.3 ms × 2.3 ms, 14 slices with a slice thickness of 5 mm, 20 diffusion directions per b-value at two b-values of 1 and 2 ms/μm², and effective ts of 50, 100, 150, 200, and 250 ms. Total scan time was about 10 min. This effective b-value was calculated on the scanner system according to the b-matrix, and this information was recorded in the Dicom header.

Data processing

Mean diffusivity and mean kurtosis at each t were estimated using the MATLAB routine developed by Veraart et al. (71) (https://github.com/jelleveraart/RobustDKIFitting). On the basis of the tDKI curves, we fitted the peak positions using a Gaussian model, in which the center of the Gaussian corresponded to the peak position. For those curves that did not show a biphasic shape, the peak position was set to the shortest t in measurement. The transmembrane exchange time (τ_ex) was fitted on the basis of the Kärger model (40)

$$K(t_{\mathrm{d}})=2K_0\frac{{\mathrm{\tau }}_{\text{ex}}}{t_{\mathrm{d}}}\left\{1-\frac{{\mathrm{\tau }}_{\text{ex}}}{t_{\mathrm{d}}}\left[1-\text{exp}\left(-\frac{t_{\mathrm{d}}}{{\mathrm{\tau }}_{\text{ex}}}\right)\right]\right\}+K_{\text{inf}}$$ (3)

where K₀ is the kurtosis at infinitely short t, and τ_ex is the exchange time, which is inversely related to permeability. The additional K_inf term is the kurtosis at infinitely long t to account for the partial volume effect from cerebrospinal fluid or other nonexchanging compartments (30).

Regions of interest (ROIs) were manually defined, e.g., the rim and core of the organoids and the cingulate cortex, occipital cortex, dentate gyrus, and CA1/CA3 regions of the hippocampus in the mouse brains. The ROI-averaged diffusivity and kurtosis values were obtained for statistical analysis.

Statistical analysis

In the organoid experiment, the fitted kurtosis peak positions and τ_ex were compared between the rim and core and between different temperatures, using two-way analysis of variance (ANOVA), followed by post hoc t test with Sidak correction for multiple comparisons in GraphPad Prism (www.graphpad.com/scientific-software/prism/).

In the in vivo mouse brain experiment, the diffusivity and kurtosis were compared between different ROIs and between two time points at individual t, using multiway ANOVA, followed by post hoc pairwise t test with Sidak correction for multiple comparisons. The statistical differences were listed in tables S3 to S5. The fitted τ_ex or peak positions were compared between different ROIs and between 3 and 48 hours, using two-way ANOVA, followed by post hoc t test with Sidak correction. In the patient experiment, τ_ex and K₀ were compared between the stroke region and contralateral normal-appearing tissues using the paired Wilcoxon test.

Supplementary Materials

This PDF file includes:

Figs. S1 to S9

Tables S1 to S8