Estimation of Fano factor in inorganic scintillators

Abstract

The Fano factor of an integer-valued random variable is defined as the ratio of its variance to its mean. Correlation between the outputs of two photomultiplier tubes on opposite faces of a scintillation crystal was used to estimate the Fano factor of photoelectrons and scintillation photons.

Correlations between the integrals of the detector outputs were used to estimate the photoelectron and photon Fano factor for YAP:Ce, SrI₂:Eu and CsI:Na scintillator crystals. At 662 keV, SrI₂:Eu was found to be sub-Poisson, while CsI:Na and YAP:Ce were found to be super-Poisson.

An experiment setup inspired from the Hanbury Brown and Twiss experiment was used to measure the correlations as a function of time between the outputs of two photomultiplier tubes looking at the same scintillation event. A model of the scintillation and the detection processes was used to generate simulated detector outputs as a function of time for different values of Fano factor. The simulated outputs from the model for different Fano factors was compared to the experimentally measured detector outputs to estimate the Fano factor of the scintillation photons for YAP:Ce, LaBr₃:Ce scintillator crystals. At 662 keV, LaBr₃:Ce was found to be sub-Poisson, while YAP:Ce was found to be close to Poisson.

1. Introduction

Glenn Frederick Knoll had a huge influence on the world of engineering in general, and in particular on those who practice the art and science of radiation measurement – including the senior author of this paper. His seminal book, Radiation Detection and Measurement, has been a comprehensive, authoritative textbook and a Baedeker for new research in a wide range of applications of ionizing radiation. That a new edition came out approximately every ten years is a tribute to both the dynamism of our field and Glenn’s dedication to it.

As all good engineers do, Glenn recognized that the ultimate limitation in system performance was usually the availability and properties of the materials used in the design. One of the more intriguing material properties in radiation measurement is the Fano factor, a critical but as yet poorly understood factor in the performance of photon-counting x-ray and gamma-ray detectors.

To introduce the Fano factor, we can do no better than to quote from Radiation Detection and Measurement. After reviewing the Poisson limitations on energy resolution (denoted R), Knoll writes,

“Careful measurements of the energy resolution of some types of radiation detectors have shown that the achievable values for R can be lower by a factor as large as 3 or 4 than the minimum predicted by the statistical arguments given above. These results would indicate that the processes that give rise to the formation of each individual charge carrier are not independent, and therefore the number of charge carriers cannot be described by simple Poisson statistics. The Fano Factor has been introduced in an attempt to quantify the departure of the observed statistical fluctuations in the number of charge carriers from pure Poisson statistics and is defined by

$$R{|}_{\text{Statistical limit}}=\frac{\text{observed variance in}N}{\text{Poisson predicted variance}(=N)}$$

Although the Fano factor is substantially less than unity for semiconductor diode detectors and proportional counters, other types such as scintillation detectors appear to show a limiting resolution consistent with Poisson statistics, and the Fano factor would, in these cases, be unity.”

He goes on to discuss other processes that can increase R (degrade energy resolution) beyond these statistical limitations. Later he writes,

“The Fano factor reflects to some degree the fraction of all of the incident particle energy that is converted into information carriers within the detector, If the entire energy of the incident radiation were always converted to ion pairs, the number of pairs would always be the same and hence there would be no statistical fluctuations. Under these conditions, the Fano factor would be zero, If only a very small fraction of the incident radiation is converted, however, then the ion pairs would be formed far apart and with a relatively low probability, and there would be good reason to expect that the distribution in their number would follow a Poisson distribution.”

Inspired by these observations, we developed a new method for measuring the Fano factor in scintillators and published it in this journal [1]. The premise is that Poisson-distributed light (Fano factor F = 1) should produce statistically independent photoelectrons when two or more photodetectors receive light from the same scintillation event. The mathematics in that paper shows that sub-Poisson light (F < 1) will produce negative correlations in the photodetectors, and conversely the correlation coefficient can be used to infer the Fano factor of the light. In [1] we showed that F was very small in LaBr₃(Ce), in fact indistinguishable from zero within experimental error.

In the present paper, we present additional experimental results for other scintillators with the same methodology as in [1], and we present a completely new method for inferring the Fano factor from optical correlations. In essence, the new method is a version of the Hanbury Brown and Twiss experiment, which played a key role in differentiating between classical and quantum-mechanical light. The results confirm those in [1] and may provide new insights into the basic physics of scintillators.

It is fitting that these results be published in a journal for which Glenn Knoll was a long-time editor and where so many of the papers he accepted harked back to his own book.

2. Background

The Fano factor (F_N) has been defined to quantify the departure of the observed fluctuations in an integer-valued random variable N from Poisson statistics [2]. For a given energy deposited in a scintillator crystal by a gamma-ray photon, the Fano factor (F_N) for the number of scintillation photons is defined as

$$F_N=\frac{{\sigma }_N^2}{{\sigma }_{\mathit{\text{Poisson}}}^2}.$$ (1)

Here, ${\sigma }_N^2$ is the variance of the random variable N, and ${\sigma }_{\mathit{\text{Poisson}}}^2$ is the variance of a Poisson-distributed random variable with mean N̅. For a Poisson random variable, as ${\sigma }_{\mathit{\text{Poisson}}}^2=\overline{N}$, we rewrite Eq. 1 as

$$F_N=\frac{{\sigma }_N^2}{\overline{N}}.$$ (2)

A Poisson random variable has a Fano factor of one, a sub-Poisson random variable has a Fano factor less than one and a super-Poisson random variable has a Fano factor greater than one.

When a gamma-ray photon of energy E undergoes photoelectric interaction with an electron having binding energy B in a semiconductor or a scintillation detector, it produces a high-energy photoelectron with energy equal to the difference between the energy of the gamma-ray photon and the binding energy (E − B). The binding energy of the electron is released either as an x-ray photon (which can escape or be reabsorbed in the scintillator) or as an Auger electron. The high-energy photoelectron loses its energy in a complicated random cascade process, producing thousands of secondary electrons and holes [3; 4].

In semiconductor detectors like Si and Ge, the free electrons and holes produced by the gamma-ray interactions are separated using an applied electric field. Electron Fano factors in the range of 0.05–0.10 have been reported for semiconductors [5].

In a scintillator, the process of producing optical photons is more complicated; a free electron or a free hole can be captured at a dopant site followed by its oppositely charged particle to form an exciton at the dopant site. Another way to create an exciton at a dopant site is for an electron and a hole to form an exciton and then travel together to the dopant site. An exciton at the dopant site has a high probability of de-exciting radiatively. There are also many competing non-radiative decay modes.

Consider a photopeak event in which a gamma-ray photon of energy E undergoes a photoelectric interaction in the scintillation crystal and there is no escape of fluorescent x-rays or other excitations from the crystal. Then the gamma-ray photon deposits its entire energy E in the crystal and produces a random number N of optical photons.

Most scintillators have a nonlinear relationship between the deposited energy and the mean number optical photons emitted [6] given by the non-proportionality curves which are graphs of average light yield per unit energy vs. deposited energy. As the initial high-energy electron created from the gamma-ray interaction loses energy, it cascades down this non-proportionality curve. Thus the complete non-proportionality curve below the deposited energy affects the total number of emitted scintillation photons.

The Fano factor of scintillation photons is strongly affected by three competing effects – the statistics of the free electrons and holes created by the cascade of the high-energy electron, the efficiency of converting these free electrons and holes into optical photons, and scintillator non-proportionality.

The cascade of the high-energy electron which yields many free electrons and holes is essentially the same in semiconductors and scintillators. Therefore, as with a semiconductor, the Fano factor of the total number of secondary electrons and holes produced by the high-energy electron cascade in a scintillator should also be sub-Poisson [6].

If the efficiency of converting these free electrons and holes into optical photons is low, then by the law of rare events, the optical photons are emitted independently of each other yielding a Poisson distribution [7].

If the non-proportionality curve is flat, then the different cascade paths the high-energy electron takes along the non-proportionality curve will yield the same mean number of scintillation photons. However if the non-proportionality curve varies as a function of electron energy, different cascade paths along the non-proportionality curve yield different mean numbers of scintillation photons. This increases the variance in the number of scintillation photons, increasing the Fano factor.

If the statistics of the electrons and holes produced from the gamma-ray interaction dominate the scintillation photon statistics, the Fano factor of the scintillation photons will be less than one (sub-Poisson).

If the efficiency of conversion from electron and holes to scintillation photons is low, it will dominate the statistics of the scintillation photons and the Fano factor of the scintillation photons will approach one (Poisson).

If non-proportionality of the scintillator dominates the statistics of the scintillation photons then the Fano factor of the scintillator will be greater than one (super-Poisson).

If the same scintillation pulse is viewed with multiple optical detectors, the Poisson-distributed photons will result in uncorrelated detector outputs, while sub-Poisson distributed photons will result in negatively correlated and super-Poisson distributed photons in positively correlated detector outputs [8; 9]. We used the correlations between the integrals of the signals (integral correlations) from two photomultiplier tubes (PMT) using the method described in Bousselham et. al. [1] to estimate the Fano factor of scintillation photons in SrI₂:Eu, CsI:Na and YAP:Ce.

An experimental inspired from the Hanbury Brown and Twiss experiment was used to measure the correlations in time (temporal correlations) between signals from two photomultiplier tubes (PMT) to estimate the Fano factors of scintillation photons in LaBr₃:Ce and YAP:Ce [10].

3. Theory for integral correlations

3.1. Fano factor of optical photons and photoelectrons

Measurement of the Fano factor of scintillation photons is non-trivial because optical photons cannot be directly detected. An optical detector, on average, converts a fraction (η) of the optical photons to photoelectrons. If a random number of optical photons (N) are are produced, then a fraction of optical photons will produce a random number of photoelectrons in an optical detector (n). If we assume that the photoelectrons are produced independently, then the photon-to-photoelectron conversion process can be modeled as a binomial distribution with a probability of success η.

We can define two Fano factors in scintillation detectors – Fano factor of the optical photons F_N and Fano factor of photoelectrons F_n. Using straightforward mathematics, we derived the relationship between the photon Fano factor and the photoelectron Fano factor as [1; 11]

$$F_n=1+\eta (F_N-1).$$ (3)

From Eq. 3, we see that as η → 0, regardless of the value of F_N, F_n → 1. Therefore, if we have low quantum or geometrical efficiency then the photoelectrons Fano factor will tend to 1.

3.2. Modeling a two-detector experiment

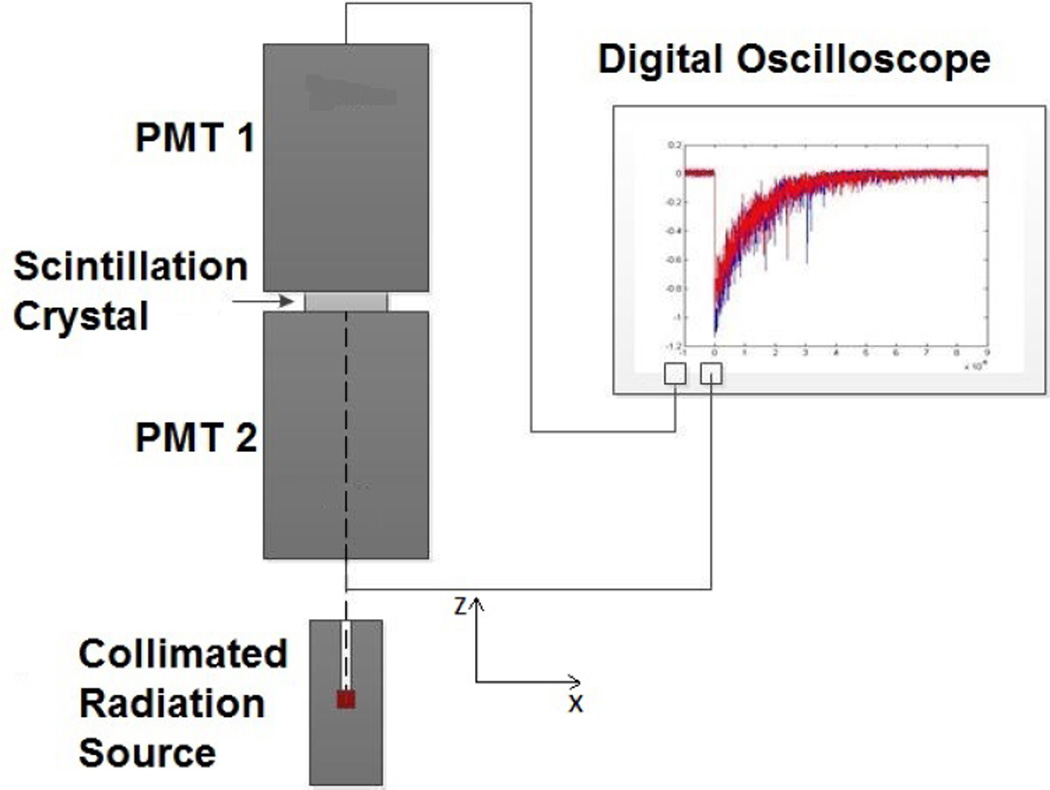
We use the experimental setup in Fig. 1 to estimate the correlation between the signals from two PMTs viewing the same scintillation event. The correlation between the two PMTs is used to estimate the Fano factor of the photoelectrons and the scintillation photons [1; 8; 11].

Figure 1.

Experimental setup to measure the Fano factor from the correlation of signals from two PMTs.

The experiment can be modeled as a trinomial distribution with η₁ the probability of producing a photoelectron in detector 1, η₂ the probability of producing a photoelectron in detector 2, and (1 − η₁ − η₂) the probability that the optical photon does not produce a photoelectron in either of the two detectors. The covariance in the number of photoelectrons at the two detectors is given by

$$K_{12}^{(n)}=\sum _{N=0}^{\infty }\sum _{n_1=0}^N\sum _{n_2=0}^N(n_1-{\overline{\overline{n}}}_1)(n_2-{\overline{\overline{n}}}_2)\mathit{\text{Pr}}(n_1,n_2|N)\mathit{\text{Pr}}(N|\overline{N}).$$ (4)

Here n̿₁, n̿₂ are the mean number of photoelectrons in detector 1 and detector 2, respectively, averaged over both the trinomial probability Pr(n₁, n₂|N) and the probability of N, Pr(N|N̅). The mean and variance of the i^th outcome of a trinomial distribution are η_iN̅ and η_i(1 − η_i)N̅ respectively. The covariance between the i^th and j^th outcomes of a trimonial distribution is −η_iη_jN̅. Using these results to simplify Eq. 4, we get

$$K_{12}^{(n)}={\eta }_1{\eta }_2\overline{N}(F_N-1).$$ (5)

The complete covariance matrix of the number of photoelectrons at the two detectors is given by

$$K^{(n)}=\overline{N}\left[\begin{array}{cc}\hfill {\eta }_1+{\eta }_1^2(F_N-1)\hfill & \hfill {\eta }_1{\eta }_2(F_N-1)\hfill \\ \hfill {\eta }_1{\eta }_2(F_N-1)\hfill & \hfill {\eta }_2+{\eta }_2^2(F_N-1)\hfill \end{array}\right].$$ (6)

To visualize the relationship between Fano factor and the correlation between the two detectors, consider the experimental setup in Fig. 1. The detectors are assumed to be identical and noiseless. The output of the experiment is represented as a scatter plot; each point on the plot corresponds to one scintillation event. For each point on the scatter plot, the x coordinate is the proportional to the number of photoelectrons detected by detector 1 and the y coordinate is proportional to the number of photoelectrons detected by detector 2 for the same scintillation event.

If the optical Fano factor is one (F_N = 1), then from Eq. 5, the two detector outputs have will have zero covariance. As shown in Fig. 2, the scatter plot of the photopeak in the Poisson case will be uncorrelated. If the optical Fano factor is less than one (F_N < 1), then from Eq. 5, the two detector outputs have will have negative covariance. As shown in Fig. 2, the scatter plot of the photopeak in the sub-Poisson case will be negatively correlated. If the optical Fano factor is more than one (F_N > 1), then from Eq. 5, the two detector outputs have will have positive covariance. As shown in Fig. 2, the scatter plot of the photopeak in the super-Poisson case will be positively correlated.

Figure 2.

Simulated scatter plots of photopeak events for super-Poisson (F_N > 1), Poisson light (F_N = 1) and sub-Poisson light (F_N < 1). The outputs of the two detectors are positively correlated for super-Poisson light, uncorrelated for Poisson light and negatively correlated for sub-Poisson light.

3.3. Signal processing and PMT gain variance

A photoelectron produced in the photocathode of a PMT is amplified through a number of dynodes before being collected at the anode. Due to this random gain process, a photoelectron at the photocathode produces a random number of electrons at the anode. A scintillation event produces many optical photons, some of which interact at the photocathode of a PMT to produce photoelectrons. The PMT output signal from a scintillation event is the sum of the individual single photoelectron responses.

In our experiment, the PMT output is directly read into a digital oscilloscope which has an input impedance R (usually 50 ohms). The electrons from the anode of the PMT flow through the input impedance of the oscilloscope which records the voltage waveform across it. The total charge on the anode of the PMT can be estimated by dividing this voltage waveform by the input impedance to get the current through the resistor, and then integrating the current. An estimate of the number of photoelectrons, denoted by n̂_j, produced on the j^th detector is given by dividing the total charge at the anode by the charge of an electron (e) and the mean gain (Ḡ):

$${\hat{n}}_j=\frac{1}{ḠeR}{\int }_0^T{v}_j(t)dt.$$ (7)

Here v_j is the voltage from the j^th PMT, and T is time duration for which we record a scintillation pulse. As the tail of the exponential decay of the scintillation pulse goes to zero at infinity, ideally T should be equal to infinity. In practice, we set T to a value greater than or equal to 4 times the decay time constant of the scintillation pulse (τ) to capture more than 98% of the pulse.

As Ḡ, R, e are constant during an experiment,

$${\hat{n}}_j\propto {\int }_0^T{v}_j(t)dt.$$ (8)

We define the signal from the j^th PMT as

$$s_j={\int }_0^T{v}_j(t)dt.$$ (9)

The gains G_j were converted into the same units of the signals (volts-seconds) by multiplying by the gain with the charge of an electron and the resistance of the oscilloscope M_j = G_jeT. Therefore, the mean signal is given by s̅_j = n̅_jM̅_j, here (M̅_j = G_jeR) and the variance of the signal is given by the Burgess variance theorem [12]

$$\mathit{\text{var}}(s_j)={\overline{n}}_j\mathit{\text{var}}(M_j)+{\overline{M}}_j^2\mathit{\text{var}}(n_j).$$ (10)

We define the gain variance coefficient as $\beta =\frac{\mathit{\text{var}}(M_j)}{{\overline{M}}_j^2}$, and use Eq. 3, to get

$$\mathit{\text{var}}(s_j)=\frac{{\overline{s}}_j^2}{{\eta }_j\overline{N}}[1+{\beta }_j+{\eta }_j(F_N-1)].$$ (11)

Since the amplification processes for the two detectors are independent, from Eq. 5, the covariance between the two detectors is given by

$$\mathit{\text{cov}}(s_1,s_2)=\frac{{\overline{s}}_1{\overline{s}}_2}{\overline{N}}(F_N-1).$$ (12)

The covariance matrix of the signals from the two detectors is given by

$$K^{(s)}=\left[\begin{array}{cc}\hfill {Ḡ}_1^2\overline{N}{\eta }_1(1+{\beta }_1+{\eta }_1(F_N-1))\hfill & \hfill {Ḡ}_1{Ḡ}_2\overline{N}{\eta }_1{\eta }_2(F_N-1)\hfill \\ \hfill {Ḡ}_1{Ḡ}_2\overline{N}{\eta }_1{\eta }_2(F_N-1)\hfill & \hfill {Ḡ}_2^2\overline{N}{\eta }_2(1+{\beta }_2+{\eta }_2(F_N-1))\hfill \end{array}\right].$$ (13)

If β₁ = β₂, and η₁ = η₂ the correlation coefficient is given by

$$r_{12}=\frac{k_{12}}{\sqrt{k_{11}{k}_{22}}}=\frac{\eta (F_N-1)}{1+\beta +\eta (F_N-1)}.$$ (14)

4. Experimental setup for integral correlations

A thin crystal about 10 mm × 10 mm × 1 mm was sandwiched between two Hamamatsu R3998-100-02 PMTs as shown in Fig. 1.

The scintillator crystal was coupled to the PMTs by optical grease and mineral oil, or just mineral oil. Hygroscopic crystals were polished with 1500 grit emery paper and, to prevent moisture damage, completely immersed in mineral oil for the duration of the experiment. The assembly was wrapped tightly with black electrical tape to keep out ambient light and placed in a rigid sleeve to prevent the PMTs and the scintillator from shifting during the measurement.

Scintillator crystal and PMT non-uniformities as well as variation in geometrical efficiency for different interaction points make the measurement sensitive to the position of interaction. As shown in Fig. 1, by using a collimated Cs-137 (662 keV) source of 1.3 mm diameter incident at the center of the scintillator we localized the position of interaction in the x−y plane (plane parallel to the detector faces). A thin scintillation crystal was used to minimize variation along the z-axis.

Detecting a high fraction of optical photons is important for the experiment. Equation 3 tells us that as η decreases, the photoelectron Fano factor tends to a value of one and becomes less dependent on the photon Fano factor. We define η as the product of geometrical efficiency and quantum efficiency. For a gamma-ray interaction at a given location in the scintillator, the geometrical efficiency of a detector is defined as the fraction of emitted optical photons that are incident on the detector. The quantum efficiency of a detector is the fraction of incident photons that create a photoelectron.

The geometrical efficiency is maximized by using a thin crystal centered and sandwiched between PMT windows bigger than the crystal faces. The centered and collimated source localizes the point of interaction in the scintillation crystal to a small area at the center of the crystal in the x−y plane. At these points of interactions, the two PMTs subtend a solid angle of nearly 2π steradians each. If we assume that the scintillation photons are emitted isotropically, the geometrical efficiencies of the PMTs are close to 50%. We chose high-quantum-efficiency super bialkali PMTs which have a maximum quantum efficiency of 35%.

The quantum-efficiency measurements by the manufacturer are usually made with the incident light normal to the PMT. Optical photons at higher angles of incidence have a larger effective photocathode thickness, increasing their detection probability [8; 13]. However, optical photons at higher angles of incidence also suffer higher reflection losses. These two opposing effects dictate changes in quantum efficiency at different angles of incidence. In our geometry, a photon reflected off one PMT has a high probability of absorption in the other PMT. Hence, in our experiment, the light collection efficiency of the PMTs denoted by η is expected to be higher than the product of the published quantum efficiency and the geometrical efficiency. We assume the value of η to be 0.28. The impact of an error in the estimate of η is discussed later in Appendix B.

The gain variance was accounted for in Eq. 13 by the gain variance coefficient (β). This parameter was measured by using a pulsed light-emitting diode operating at a low voltage so that the PMT had a high probability of detecting only one photoelectron during each pulse. Signal processing techniques were used to identify the pulses with only one photoelectron, and a histogram of the area under these pulses was plotted to give us the single-photoelectron response. The gain variance coefficient for the PMT was estimated using the width and the mean value of the single-photoelectron response. To simplify calculations, the two PMTs were assumed to be identical with the same quantum efficiency and gain variance coefficient.

4.1. Data analysis

Twenty to fifty thousand scintillation pulses were recorded and processed as per Sec. 3.3 to get signals s₁ and s₂ for each scintillation event. A scatter plot with coordinates (s₁, s₂) was plotted. As shown in Eq. 8 and 9, s₁ and s₂ are proportional to the estimate for the number of photoelectrons n₁ and n₂ detected on the PMTs respectively. The photopeak events were separated from the Compton events by thresholding just above the Compton edge. The photopeak scatter plot was windowed along and perpendicular to the s₁ = s₂ axis. We used a least-squares approach to fit a similarly windowed 2D Gaussian to the scatter plot (See Fig. 3). The Gaussian fit was used to estimate the covariance matrix of the signals.

Figure 3.

The windowed photopeak data from a dataset is on the top left. The windowed Gaussian fit to the data is on the top right. The bottom graphs are sums of sections perpendicular (major axis) and parallel (minor axis) to the s₁ = s₂ line.

The experimental measurement is very sensitive to the contact between the scintillator and the detectors and to imperfections in the crystal. To reject experimental artifacts and avoid bias, only measurements with a narrow and symmetric scatter plot of the Compton region (see Fig. 12, 13 and 14) and an energy resolution within a percentage point of the published values were used.

Figure 12.

Scatter plot for SrI₂:Eu. In the photopeak region, the two PMTs are negatively correlated.

4.2. Estimation of Fano factor

We used Eq. 3 and 14 to get the expression for the estimate of the Fano factor of the photoelectrons as

$${\hat{F}}_n=\left(\frac{1+\beta {\hat{r}}_{12}}{1-{\hat{r}}_{12}}\right).$$ (15)

Equation 14 can be rewritten to get an expression for the estimate of the Fano factor of the scintillation photons (F̂_N) in terms of the estimate of the correlation coefficient (r̂₁₂):

$${\hat{F}}_N=1+\left(\frac{{\hat{r}}_{12}}{1-{\hat{r}}_{12}}\right)\left(\frac{1+\beta }{\eta }\right).$$ (16)

5. Theory for temporal correlations

The classical or wave theory of light treats light as a complex signal V(r⃗, t), whose squared absolute value I(r⃗, t) = |V(r⃗, t)|² is the irradiance [14]. The classical theory restricts the Fano factor to values greater than one. The quantum theory of light recognizes the wave-particle duality of light and allows for Fano factors less than one. Therefore, light with Fano factor less than one is often referred to as ”non-classical” light.

In the next sub-sections we will define point processes, renewal processes, gamma distributions, and make a statistical model using all these concepts. We will also relate the covariance, correlation and coherence to these models.

5.1. Point process

A point process is defined as a random process for which a realization consists of a set of isolated points in some space. Thus, a realization of a point process can be described as a set of delta functions in the dimensions of that space. A point process in time has one-dimensional delta functions and is called a temporal point process. A point process in space and time has delta functions in four dimensions (x, y, z, t) and is called a spatiotemporal point process [9].

The scintillation process is a stochastic point process in time, producing a random number (N) of scintillation photons at random times t₁, t₂ … t_N. In this section, we study, model and measure the temporal correlations in the scintillation light from different scintillator materials.

5.2. Renewal process

A renewal process is a continuous-time Markov process on positive integers in which the inter-event times are independent and identically distributed at each event. Therefore, a renewal process is by definition, a stationary process [15].

5.3. Classification of point processes

Based on the time spacing between successive points, a temporal point process can be classified as bunched, Poisson, or anti-bunched [16].

In a Poisson Point Process (PPP), the occurrence of an event does not increase or decrease the probability of the occurrence of next event. All the events are independent of each other and completely random. In a bunched point process, the events are less uniformly spaced as compared to the PPP, while in an anti-bunched point process, the events are more uniformly spaced than a PPP (See Fig. 4).

Figure 4.

The realization of a Poisson point process in (b) has randomly spaced points. The realization of an anti-bunched point process in (a) is more evenly spaced as compared to the Poisson point process. The realization of the bunched point process (c) is less evenly spaced as compared to the Poisson point process.

5.4. Modeling the inter-event time as a gamma distribution

The inter-event time of a generic point process is often modeled as a gamma distribution [15]. The gamma distribution is a two-parameter continuous distribution and can be used to model bunched, Poisson and anti-bunched events. The gamma distribution given by

$$\mathit{\text{pr}}(\mathrm{\Delta }t|k,\theta )=\{\begin{array}{cc}\frac{1}{\mathrm{\Gamma }(k){\theta }^k}{(\mathrm{\Delta }t)}^{k-1}{e}^{(-\mathrm{\Delta }t/\theta )},\hfill & \mathrm{\Delta }t\ge 0\hfill \\ 0,\hfill & \mathrm{\Delta }t<0.\hfill \end{array}$$ (17)

Here, k is the shape factor, θ is the scale factor and Γ(k) is the gamma function evaluated at k. The mean and variance of the gamma distribution are given by $\overline{\mathrm{\Delta }t}=k\theta$ and ${\sigma }_{\mathrm{\Delta }t}^2=k{\theta }^2$ respectively. The exponential distribution used to model the inter-event time in the PPP is a special case of the gamma distribution with k = 1, and $\overline{\mathrm{\Delta }t}=\theta$ [16]

$$\mathit{\text{pr}}(\mathrm{\Delta }t|\theta )=\{\begin{array}{cc}\frac{1}{\theta }{e}^{(-\mathrm{\Delta }t/\theta )},\hfill & \mathrm{\Delta }t\ge 0\hfill \\ 0,\hfill & \mathrm{\Delta }t<0.\hfill \end{array}$$ (18)

The coefficient of variation denoted by c is a quantity analogous the Fano factor. It is defined as the ratio of the standard deviation of the inter-event time to the mean inter-event time.

$$c=\frac{{\sigma }_{\mathrm{\Delta }t}}{\overline{\mathrm{\Delta }t}}=\frac{1}{\sqrt{k}}.$$ (19)

For a Poisson point process with exponentially distributed inter-event times, the standard deviation of the inter-event times is equal to the mean inter-event time $({\sigma }_{\mathrm{\Delta }t}=\overline{\mathrm{\Delta }t})$, giving us k = c = 1. When c > 1, then k < 1 and the standard deviation of the inter-event times is greater than the standard deviation of a PPP with the same mean. This implies that the events are more ”bunched” than in the PPP. For c < 1, k > 1, the standard deviation of the inter-event time is less than the standard deviation of a PPP with the same mean. This implies that the events are more uniformly spaced than the PPP. Such events are also called anti-bunched events [16; 17].

The PDF of gamma distributions for the same mean but different values of shape factor are given in Fig. 5. An inset figure shows the zoomed-in tail section of Fig. 5 to show that the PDF of the bunched and anti-bunched events again cross the PDF of the exponential curve for large values of inter-event time.

Figure 5.

The PDF for bunched events is greater than the Poisson distribution PDF for small and large inter-event times, so the events are more likely to bunch together. Anti-bunched events follow the opposite trend to bunched events and are more regularly spaced than Poisson events. The tail portion of the gamma PDF for bunched, Poisson and anti-bunched events is magnified in the inset image. The PDF of the bunched, and anti-bunched events cross the Poisson PDF in the tail region of the gamma pdf from opposite sides.

The anti-bunched inter-event PDF rises from zero, and crosses the exponential PDF for the PPP, and then in the tail region drops again to a value below the exponential PDF for the PPP. This indicates that compared to Poisson events, anti-bunched events are more likely to occur in the middle range of the inter-event times and less likely to occur at the smaller and the larger inter-event times. Therefore, anti-bunched events are more uniformly spaced than Poisson events. The bunched events have the opposite behavior, they have a higher probability than the PPP events at small inter-event times and at large inter-event times, but have a lower probability of occurring in the middle ranges of the inter-event times. Therefore, bunched events are less uniformly spaced than the Poisson events.

5.5. Relationship between shape factor and Fano factor for a stationary point process

The shape factor of the gamma distribution is defined on the statistics of the inter-event time, while the Fano factor is defined on the statistics of the number of events in a given time. The properties of the renewal process were used to derive the relationship between the shape factor and the Fano factor [15; 18]

$$F=\frac{1}{k}.$$ (20)

We modeled the inter-event times (Δt₁, Δt₂, ⋯ Δt_N) between successive points of our point process as a gamma distribution. As the mean emission rate of photons is not constant in a scintillation pulse, the scintillation process is by definition, nonstationary. In Sec. 5.6, we investigate whether the relationship between the Fano factor and the shape factor for a renewal process (by definition a stationary process) given by Eq. 20 is also valid for scintillation light.

5.6. Relationship between shape factor and Fano factor for a non-stationary point process

The inter-event arrival time in a scintillation process was modeled as a gamma distribution with a constant shape factor k, and a scale factor θ that varies as the pulse decays. We performed a Monte-Carlo simulation to find the relationship between the Fano factor and the shape factor for a non-stationary process.

We simulated 5000 scintillation pulses with gamma-distributed inter-event times with a constant shape factor and varying scale factor. The total number of events (N_sim) recorded during the acquisition time were used to estimate the Fano factor of the events generated with a given shape factor:

$${\hat{F}}_{\mathit{\text{sim}}}=\frac{\mathit{\text{var}}(N_{\mathit{\text{sim}}})}{{\overline{N}}_{\mathit{\text{sim}}}}.$$ (21)

The estimates of the Fano factor from the simulation of scintillation light and the Fano factor calculated from the shape factor using the renewal theory equation in Eq. 20 was found to be consistent with each other (see Fig. 6). Therefore, the shape factor can be used to estimate the Fano factor of the scintillation light.

Figure 6.

Estimate of the Fano factor from Monte-Carlo simulations of a point process with gamma-distributed inter-event times with a constant shape factor, and changing scale factor. The Fano factor estimated using renewal theory (see Eq. 20) and the Fano factor estimated from the Monte-Carlo simulation are in agreement with each other.

5.7. Correlation, Covariance and Coherence

The correlation function of the optical fields for two space-time points (r⃗₁, t₁) and (r⃗₂, t₂) is given as [19; 16; 10]

$$G^{(1)}({\overrightarrow{r}}_1,t_1,{\overrightarrow{r}}_2,t_2)=\langle V^{*}({\overrightarrow{r}}_1,t_1)V({\overrightarrow{r}}_2.t_2)\rangle .$$ (22)

Here, V(r⃗₁, t₁) is the complex field at position r⃗₁ and time t₁. The angle brackets indicate an ensemble average. Detectors cannot directly measure the field V, but respond to the irradiance which is the square modulus of the field, often referred to as intensity (I = |V|²). The second-order correlation function, also known as the intensity correlation is given by

$$G^{(2)}({\overrightarrow{r}}_1,t_1,{\overrightarrow{r}}_2,t_2)=\langle I({\overrightarrow{r}}_1,t_1)I({\overrightarrow{r}}_2.t_2)\rangle .$$ (23)

Cross covariance compares the detector signals to their means. The intensity cross-covariance cov(r⃗₁, t₁, r⃗₂.t₂)) is calculated by subtracting by the average intensity and then averaging over the ensemble as given below

$$\mathit{\text{cov}}({\overrightarrow{r}}_1,t_1,{\overrightarrow{r}}_2,t_2)=\langle [I({\overrightarrow{r}}_1,t_1)-Ī({\overrightarrow{r}}_1,t_1)][I({\overrightarrow{r}}_2.t_2)-Ī({\overrightarrow{r}}_2.t_2)]\rangle .$$ (24)

The relationship between bunching or anti-bunching of events and their cross-covariance can be visualized with the following example. We measure the intensity of the field using two detectors at positions, $\overrightarrow{r_1}$ and $\overrightarrow{r_2}$ at time, t₁ = t₂ = t. At a given time t, if both the two detector signals are more likely to be either above or below their mean values, then their cross-covariance curve is positive. Similarly, if the two detector signals are more likely to be on opposite sides of their mean values, then the cross-covariance will be negative. If the two signals are independent of each other, then the cross-covariance curve will be zero.

The uncertainty or randomness in the emission and detection of scintillation photons is averaged out in the mean signal. Therefore, the mean signal is a smooth function in time and independent of the coefficient of variation defined in Eq. 19. Consider a bunched point process; when a bunch of events is emitted, both detectors record signals that are likely to be larger than their mean. Similarly, in the time between two bunches, when a few or no events arrive, both the detectors record a signal that is likely to be smaller than their means. Therefore, a bunched process will yield a positive cross covariance. Conversely, an anti-bunched point process will yield a negative cross-covariance curve and a Poisson point process will yield zero cross covariance. Therefore, the cross-covariance curve is expected to be negative for Fano factors less than one, positive for Fano factors greater than one and zero for a Fano factor of one.

The normalized correlation function, also known as second order coherence, is given by normalizing the correlation function with the mean intensities as given below

$$g^{(2)}({\overrightarrow{r}}_1,t_1,{\overrightarrow{r}}_2,t_2)=\frac{G^{(2)}({\overrightarrow{r}}_1,t_1,{\overrightarrow{r}}_2,t_2)}{\langle I({\overrightarrow{r}}_1,t_1)\rangle \langle I({\overrightarrow{r}}_2.t_2)\rangle }=\frac{\langle I({\overrightarrow{r}}_1,t_1)I({\overrightarrow{r}}_2.t_2)\rangle }{\langle I({\overrightarrow{r}}_1,t_1)\rangle \langle I({\overrightarrow{r}}_2.t_2)\rangle }.$$ (25)

The normalized cross-covariance function, is given by

$$\sigma ({\overrightarrow{r}}_1,t_1,{\overrightarrow{r}}_2,t_2)=\frac{\mathit{\text{cov}}({\overrightarrow{r}}_1,t_1,{\overrightarrow{r}}_2,t_2)}{\langle I({\overrightarrow{r}}_1,t_1)\rangle \langle I({\overrightarrow{r}}_2.t_2)\rangle }=\frac{\langle [I({\overrightarrow{r}}_1,t_1)-Ī({\overrightarrow{r}}_1,t_1)][I({\overrightarrow{r}}_2.t_2)-Ī({\overrightarrow{r}}_2.t_2)]\rangle }{\langle I({\overrightarrow{r}}_1,t_1)\rangle \langle I({\overrightarrow{r}}_2.t_2)\rangle }.$$ (26)

Straightforward mathematics gives us the relationship between normalized cross-covariance σ(r⃗₁, t₁, r⃗₂, t₂) and second-order coherence g⁽²⁾(r⃗₁, t₁, r⃗₂, t₂) as

$$\sigma ({\overrightarrow{r}}_1,t_1,{\overrightarrow{r}}_2,t_2)=g^{(2)}({\overrightarrow{r}}_1,t_1,{\overrightarrow{r}}_2,t_2)-1.$$ (27)

The second-order coherence function defined in Eq. 25 was historically used with stationary light statistics. As scintillation light is not stationary (the mean intensity varies as a function of time), we cannot directly use the second-order coherence function for scintillation light. In addition, as the scintillation pulse decays with time, the mean signals become very small making the denominator of the normalized cross-covariance function close to zero. To avoid dividing by small numbers, we integrate the numerator and the denominators of Eq. 26 for the duration of pulse and calculate the Normalized Area Under the Cross- Covariance Curve (AUCCC). In the equation below, we have substituted t₁ = t, t₂ = t + τ. Unless explicitly specified, in the next sections we have used the normalized AUCCC with τ = 0.

$$\text{Norm}\mathrm{A}\mathrm{U}\mathrm{C}\mathrm{C}\mathrm{C}==\frac{\underset{t=0}{\overset{T}{\int }}\langle [I({\overrightarrow{r}}_1,t)-Ī({\overrightarrow{r}}_1,t)][I({\overrightarrow{r}}_2,t+\tau )-Ī({\overrightarrow{r}}_2,t+\tau )]\rangle dt}{\underset{t=0}{\overset{T}{\int }}\langle I({\overrightarrow{r}}_1,t)\rangle \langle I({\overrightarrow{r}}_2,t+\tau )\rangle dt}.$$ (28)

6. Implementation for temporal correlations

6.1. Simulation

We performed Monte-Carlo simulations with the model described below to find an empirical relationship between the Fano factor of the scintillation photons and the normalized AUCCC of the PMT signals..

6.1.1. Model

We modeled the emission and detection of scintillation photons and the process of generation of the detector signals.

The mean emission rate of the scintillation photons is calculated from the mean number of emitted photons, the time constant of the scintillation pulse and the sampling time. The shape factor is assumed to be constant for the duration of the scintillation pulse, depending only on the scintillator material and the deposited gamma-ray energy. The scale factor θ(t) is calculated from the emission rate of the scintillation photons and the shape factor.

The emitted photon can have three possible outcomes – it can be detected by detector 1, or by detector 2 or not be detected. The collection efficiency of a detector is the fraction of total emitted light collected. It is a product of the quantum efficiency and the geometrical efficiency. In the Monte-Carlo simulation, we assume that the collection efficiencies of the detectors are independent of the position and angle of incidence of the scintillation photons. We use a uniform random variable to simulate the probability of detection of a scintillation photon.

The time it takes the scintillation photon to travel from the point of emission to the detector is much smaller (in the low picosecond range) than the detector response time (in the nanosecond range). Therefore, we neglect the propagation time of the scintillation photons from the point of emission to the detector. A scintillation photon emitted at time t_i is assumed to be instantaneously detected at the detectors [20; 21].

The Normalized Detector Response Function (NDRF) is the normalized detector response in volts as a function of time. The normalization ensures that the area under the NDRF is equal to the product of the charge of an electron (q) and the input resistance of the oscilloscope (R).

$$\underset{0}{\overset{\infty }{\int }}\mathrm{N}\mathrm{D}\mathrm{R}\mathrm{F}(t)dt=qR$$ (29)

The response of the detector in volts to a scintillation photon is given by multiplying the NDRF with the gain. We assume that the gain variances are normally distributed with mean gains of Ḡ₁, Ḡ₂, and variances of ${\sigma }_{G_1}^2={\beta }_1{Ḡ}_1^2,{\sigma }_{G_2}^2={\beta }_2{Ḡ}_2^2$ respectively. Here, β₁ and β₂ are the gain-noise factors for detector 1 and detector 2, respectively, defined as the ratio of the variance of their gain and the square of their mean gain. The NDRF was modeled as a Gaussian function of time with an experimentally observed Full-Width at Half Maximum (FWHM) of 1 ns.

The flowchart in Fig. 7 indicates the steps involved in creating the simulated detector outputs (s_s1, s_s2) from a scintillation pulse with known shape factor. The inputs to the algorithm are the scintillation photon properties like the shape factor (k), the mean number of scintillation photons emitted (N̅) and the decay constant of the scintillator (τ); the characteristics of the two detectors such as their collection efficiencies (η₁, η₂), mean gains (Ḡ₁, Ḡ₂), and gain variance factors are defined as $({\beta }_1=\frac{{\sigma }_{G_1}^2}{{Ḡ}_1^2},{\beta }_2=\frac{{\sigma }_{G_2}^2}{{Ḡ}_2^2})$ respectively.

Figure 7.

Flowchart to simulate detector pulses produced from scintillation light with known shape factor.

6.1.2. Assumptions made in the simulations

We have made the following assumptions in this simulation:

• The shape factor (k) of the scintillation pulse does not change for the duration of the pulse. This assumption might not be true for scintillators with afterglow or multiple decay-time constants indicating the dominance of different underlying physical processes at different times of the scintillation pulse.

• The mean number of photons emitted by the scintillator per photoelectric gamma-ray interaction is known.

• The detector is operating in its linear region, and each photoelectron is amplified independently.

• Different PMT gains change the amplitude and the area under the NDRF waveform, but not the shape of the NDRF.

• The quantum efficiency of the detectors is assumed to be independent of the position of interaction.

The results for the simulations with these assumptions are highly dependent on one more crucial factor – the ratio of the decay time of the scintillator to the width of the single photoelectron response. If the detector response is orders of magnitude faster than the time constant of the scintillator, then the events captured are likely to be a set of separated photoelectrons. Because of the rarity condition of the Poisson postulates, the measured statistics of this point process will be close to Poisson [9]. Therefore, we have limited this study to fast scintillators YAP:Ce with a decay time of 30 ns and LaBr₃:Ce with a decay time of 15.4 ns.

6.1.3. Free Input parameters on the estimation of Fano factor

The free parameters in the simulation are the collection efficiencies (η₁, η₂), the mean gains and gain variances of the PMTs (Ḡ₁, Ḡ₂, β₁, β₂), and the mean number of photons emitted (N̅). Equation 30 is used to introduce a constraint and reduce the number of free parameters that we need to choose.

$$\underset{0}{\overset{T}{\int }}{s}_j(t)dt={\eta }_j{Ḡ}_j\overline{N},j=1,2.$$ (30)

If we assume values of N̅ and η_j. (j = 1, 2), then the values of G_j are constrained. Therefore, we only treat N̅, $\overline{{\eta }_1},\overline{{\eta }_2}$, β₁, β₂ as free parameters. We performed Monte-Carlo simulations to test impact of each of these parameters. The simulations were performed for shape factors of 0.1 and 10 and therefore, Fano factors of 10 and 0.1, respectively.

In the first simulation, we varied the value of N̅ from 20,000 to 60,000 scintillation photons with η₁ = η₂ = 0.28, β₁ = β₂ = 0.25. To satisfy Eq. 30, for different values of N̅, we varied the mean gains Ḡ₁ and Ḡ₂ to keep the mean signal constant. We see in Fig. 8, that the normalized AUCCC asymptotically tends towards zero with higher values of N̅ for Fano factor = 0.1 and Fano factor = 10. Therefore, an uncertainty in the estimate of N̅ will be result in uncertainty in the estimate of the Fano factor.

Figure 8.

The normalized AUCCCs for different values of N̅. As the values of normalized AUCCC increased, the value of mean gains had to be lowered to ensure that the equation of the mean signals is satisfied. Simulated datasets with Fano factors of 0.1 and 10 are plotted above; the normalized AUCCC tends towards zero with increasing value of N̅. The solid line drawn at zero normalized AUCCC serves as a visual reference.

In other simulations, we varied the values of the collection efficiency η₁, η₂ and the gain variance factors of the two detectors β₁, β₂ while keeping all other parameters constant. To satisfy Eq. 30 for different values of η₁, η₂, we varied the mean gain Ḡ₁, Ḡ₁ to keep the mean signal constant. We found that the normalized AUCCC is independent of the values of the collection efficiencies as well as gain variances of the detectors for Fano factor = 0.1 and Fano factor = 10.

6.1.4. Invariance of the area under the covariance curve for thin energy windows of data

Our model assumes that the gamma-ray energy deposited in the scintillator is a constant. This is achieved in an experiment by windowing the photopeak region (which corresponds to photoelectric gamma-ray interactions) of the energy spectrum to separate it from the Compton region. In this section we investigate the impact of the size and location of the photopeak window on the normalized AUCCC.

To test the impact of the location and size of the energy window on the cross-covariance curves, we conducted a simulation study and generated a simulated data set with the following parameters : N̅ = 43692, η₁ = η₂ = 0.28, β1 = β₂ = 0.25, Ḡ₁ = 6133, Ḡ₂ = 5771. We calculated the cross-covariance curve using Eq. 31 and used four different energy windows to generate the results shown in Fig. 9.

$$\text{cov}({\mathrm{s}}_1(\mathrm{t}),{\mathrm{s}}_2(\mathrm{t})=(s_1(t)-{\overline{s}}_1(t))(s_2(t)-{\overline{s}}_2(t)).$$ (31)

Figure 9.

The cross-covariance curve for different energy windows of the same simulated dataset. The simulated dataset was generated with a shape factor of 10, and therefore, a Fano factor of 0.1. The plots in the left half of the figure show the parts of the photopeak histogram that were used to calculate the cross-covariance in the right half of the figure. The normalized AUCCC for the simulated data does not appear to be sensitive to the energy window of the histogram used to calculate it.

The sub-figure (a) is the histogram of all 2000 photopeak events. The cross-covariance curve of the complete photopeak is plotted in (b). Only the left half (c), the right half (e) and the central region (g) of the energy spectrum were used to calculate the cross-covariance curve shown in (d), (f) and (h) respectively. Although the mean signals of the partial datasets in (a), (c), (e) and (g) are different, the cross-covariance curves, and therefore, the normalized AUCCC of the two detector signals are similar and independent of the energy window selected.

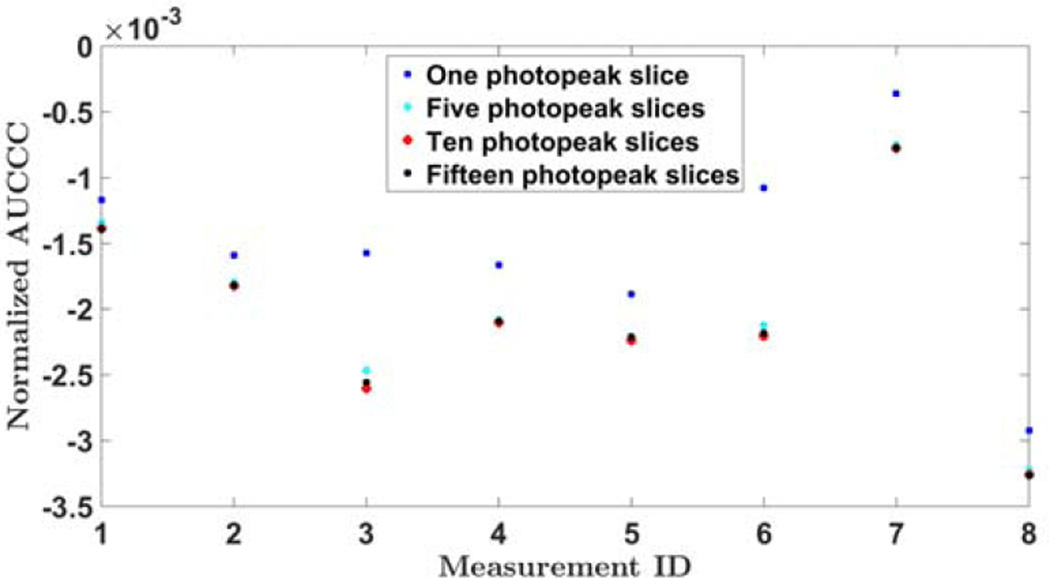
We divided the photopeak into a different number of energy windows and averaged the normalized AUCCCs from all the energy windows. Figure 10 shows that the average normalized AUCCC does not depend on the size or the number of the energy windows.

Figure 10.

Average normalized AUCCC for simulated dataset as a function of number of energy windows the photopeak was divided into.

In summary, we have numerically studied the impact of the different free parameters on our model. By fixing our mean detector outputs $(\underset{0}{\overset{T}{\int }}{s}_j(t)dt,(j=1,2))$ to the experimentally measured value, the normalized AUCCC is independent of the collection efficiency, gain variance and size of the energy window used for analysis. The estimate of the mean number of scintillation photons per photoelectric gamma-ray interaction N̅ does impact the normalized AUCCC and an error in the value of N̅ will be propagated to the final estimates of the Fano factor. We now have the tools and the model to compare against experimental data.

6.2. Experiment

The experiment to measure the temporal correlations in scintillation light uses the same geometry as the experiment to measure the integral correlations in (See Fig. 1). The temporal correlation experimental setups used two modified Hamamatsu R9880U-210 PMTs for detecting the scintillation light. The R9880U-210 PMTs have a cover which prevented us from directly coupling two PMTs to a thin scintillator. On our request, custom R9880U-210 PMTs were manufactured without the outer covers as shown in Fig. 11. This modification does not affect the PMT’s optical or electrical properties.

Figure 11.

Modified R9880U-210 PMT.

To record data from the faster PMT’s we used a Tektronix DPO72004B oscilloscope at 20 GHz bandwidth at a sampling period of 20 ps for our measurements. A negative-edge AND trigger was used to trigger the oscilloscope. The recorded pulses corresponding to the photopeak were selected and corrected for uncertainty in triggering. The oscilloscope also adds quantization and electronic noise to the detector signals. The noise in the two oscilloscope outputs was characterized by studying them without any signal. For a scintillation event, the noise between the two oscilloscope outputs was found to be uncorrelated; therefore, it does not affect the area under the cross-covariance curves. The drifts in the baseline signals were measured by averaging the oscilloscope outputs from the initial part of the scintillation pulses before the start of the scintillation event. The drifts in the oscilloscope outputs were subtracted from the respective detector signals to remove the offsets.

Loss mechanisms like x-ray escape or low-angle Compton scattering can result in energy depositions that are lower than for the original gamma-ray interaction. These lossy gamma-ray events can be hard to distinguish from events in which all the original gamma-ray energy was deposited into the crystal. Inconsistent optical contact between scintillator and the crystal, can also result in broadening of the photopeak. Thus, the normalized AUCCC from the experimentally measured photopeak events will be biased towards positive cross-covariance.

If we choose a large energy window consisting of multiple gamma-ray energies deposited, then the mean pulses will correspond to the average of all the gamma-ray energy deposited. Events with higher-than-average gamma-ray energy deposited are more likely to produce pulses with amplitudes larger than the mean pulse, and events with lower than average gamma-ray energy deposited are more likely to produce pulses with amplitudes smaller than the mean pulse. Therefore, a large window corresponding to multiple gamma-ray energies will always result in a positive cross-correlation curve.

The simulations in Sec. 6.1.4 indicate that if we choose a small energy window, which has only part of the spectrum of a single gamma-ray energy, then we should get more accurate and less biased values for normalized AUCCC.

7. Results from integral correlations

7.0.1. SrI₂:Eu

SrI₂:Eu has high light output (≈100,000 photons / MeV) and excellent published energy resolution of 3% [22] at 662 keV. The energy resolutions in our measurements varied from 3.3%–3.5%.

We made twelve measurements on two samples of SrI₂:Eu that met the acceptance criteria described in Sec. 4.1 and were used for estimating Fano factors. We found the integral of the detector outputs to be negatively correlated, and therefore, concluded that SrI₂:Eu has sub-Poisson scintillation light at 662 keV gamma-ray interactions.

7.0.2. YAP:Ce

The chemical formula for YAP is YAlO₃. YAP:Ce has a low light output (18,000 photons/MeV), but has good published energy resolution of 4.4% [23] at 662 keV. Our measured energy resolutions varied from 3.47% to 4.42%.

We had only one sample of YAP:Ce, and we made eight measurements that met the acceptance criteria described in Sec. 4.1 for estimating Fano factor. We found the integral of the detector outputs to be slightly positively correlated, and therefore, concluded that YAP:Ce’s scintillation light at 662 keV gamma-ray interactions is either super-Poisson or close to Poisson.

7.0.3. CsI:Na

CsI:Na has good light output (43,000 photons/MeV) but relatively poor published energy resolution of 7.07% at 662 keV [24]. Another study has reported an energy resolution of 5.8% with longer than usual shaping time of 12 µs [25]. We had two samples of CsI:Na and we made ten measurements that met the acceptance criteria described in Sec. 4.1 for estimating Fano factor. Eight of our measurements captured pulses for 4 µs while two measurements integrated for 10 µs. The energy resolutions in our measurements varied between 4.6%–6.7%.

We found positive correlation between the integrals of the signals from the two PMTs and found the scintillation light from CsI:Na at 662 keV gamma-ray energy to be super-Poisson. The high positive correlation in CsI:Na could be a result of varying energy distribution between the primary radiatively decay processes and the millisecond afterglow process. Integrating the CsI:Na signals for longer durations to capture all the afterglow could result in smaller estimates of Fano factor.

7.0.4. Fano Factor Estimates

Using the experiment and the estimation process described above, we estimated the correlation coefficient between the two detector outputs. We then used estimates of the correlation coefficient, and equations 15 and 16 to estimate the Fano factor of the photoelectrons and the scintillation photons.

Table 1 shows the estimates of the photoelectron and scintillation photons Fano factor for β = 0.07 and η = 0.28. The uncertainty in estimation of correlation coefficient was propagated to estimate the uncertainty in the estimates of F_n and F_N. The estimates of correlation coefficient of LaBr₃:Ce are reproduced here from [1].

Table 1.

Photoelectron and Photon Fano factor Estimates β = 0.07 and η = 0.28. The results for LaBr₃:Ce are reproduced from [1].

	Correlation Coefficient (r12)	Photoelectron Fano factor (Fn)	Photon Fano factor (FN)
SrI2:Eu	−0.3134 ±0.04	0.7526 ±0.02	0.1165 ±0.11
YAP:Ce	0.1036 ±0.02	1.13 ±0.033	1.464 ±0.13
CsI:Na	0.4192 ±0.07	1.949 ±0.18	4.391 ±0.68
LaBr3:Ce	−0.32 ± 0.17	0.7333 ± 0.11	0.01235±0.40

8. Results from temporal correlations

8.1. Simulation results

8.1.1. Relationship between Fano factor, shape factor and normalized AUCCC

We used the method described in Sec. 6.1.1 to simulate 2000 scintillation events with photoelectric interaction for the parameters of LaBr₃:Ce and YAP:Ce for different values of Fano factor. The normalized AUCCC between the two sets simulated pulses s₁ and s₂ was calculated using equation Eq. 28. We used the proportional model below to model the relationship between the normalized AUCCC and the Fano factor.

$${\hat{F}}_N=c+\frac{\mathrm{A}}{m}.$$ (32)

Here F̂_N is the estimated Fano factor of the scintillation photons, A is the measured normalized AUCCC, c is the x-intercept, and m is the slope of the model. As expected, if the Fano factor of the scintillation photons is one, then the two signals are expected to be uncorrelated and the normalized AUCCC is zero. As the Fano factor increases beyond one, the photons are bunched and the normalized AUCCC is positive. For Fano factors less than one, the photons are anti-bunched and the normalized AUCCC is negative. If the Fano factor is one, the normalized AUCCC must be zero (A= 0), and c = 1. Therefore, we need only to estimate the inverse of the slope for our model, and our model reduces to

$${\hat{F}}_N=1+\frac{\mathrm{A}}{m}.$$ (33)

8.1.2. Model for LaBr₃:Ce

The simulation was set up to match the experiment. The LaBr₃:Ce scintillator was assumed to produce 0.662 MeV × 66,000 (photons per MeV) = 43692 scintillation photons. The collection efficiencies of both PMT’s were assumed to be 0.28, and experimentally observed mean values of photopeaks of the two PMTs were set as ${\langle \underset{0}{\overset{T}{\int }}{s}_1(t)dt\rangle }_{PP}=3.22\times {10}^{-10}$ volt-seconds, and ${\langle \underset{0}{\overset{T}{\int }}{s}_2(t)dt\rangle }_{PP}=3.03\times {10}^{-10}$ volt-seconds. The rise time of the scintillation pulse was assumed to be zero, and the decay time was estimated from the measurements as 15.4 ns. The mean gains were calculated from Eq. 30, and the mean gain variance factors were set to β₁ = β₂ = 0.25. The model for the relationship between the normalized AUCCC (Normalized AUCCC_LaBr3:Ce) and the Fano factor for LaBr₃:Ce is

$$F_{N_{\mathrm{L}\mathrm{a}\mathrm{B}{\mathrm{r}}_3:\mathrm{C}\mathrm{e}}}=1+473.9847\times {(\text{Normalized}\mathrm{A}\mathrm{U}\mathrm{C}\mathrm{C}\mathrm{C})}_{\mathrm{L}\mathrm{a}\mathrm{B}{\mathrm{r}}_3:\mathrm{C}\mathrm{e}}.$$ (34)

8.1.3. Model for YAP:Ce

The YAP:Ce scintillator was assumed to produce 0.662 MeV × 15,000 photons per MeV = 9930 scintillation photons. The collection efficiencies of each of the PMT’s was assumed to be 0.28, and the experimentally observed mean values of the photopeaks of the two PMTs were set as ${\langle \underset{0}{\overset{T}{\int }}{s}_1(t)dt\rangle }_{PP}=4.52\times {10}^{-9}$ volt-seconds, ${\langle \underset{0}{\overset{T}{\int }}{s}_2(t)dt\rangle }_{PP}=4.68\times {10}^{-9}$ volt-seconds were used as the detector means. The rise time of the scintillation pulse was assumed to be zero, and the decay time was estimated from the measurements as 30 ns. The mean gains were calculated from Eq. 30 and the mean gain variance factors were set to β₁ = β₂ = 0.25.

The model for the relationship between the normalized AUCCC (Normalized AUCCC_YAP:Ce) and the Fano factor for YAP:Ce is The model of our experiment for YAP:Ce is

$$F_{N_{\mathrm{Y}\mathrm{A}\mathrm{P}:\mathrm{C}\mathrm{e}}}=1+55.1314\times {(\text{Normalized}\mathrm{A}\mathrm{U}\mathrm{C}\mathrm{C}\mathrm{C})}_{\mathrm{Y}\mathrm{A}\mathrm{P}:\mathrm{C}\mathrm{e}}.$$ (35)

8.2. Experimental results

The experimental setup described in Sec. 6.2 was used to make measurements on YAP:Ce and LaBr₃:Ce scintillators. Waveforms from two PMTs collecting light from the same event were recorded with a fast detector and a fast oscilloscope and their cross-covariance curve computed. The normalized AUCCC was then computed and stored.

The measurements for LaBr₃:Ce were conducted with PMT voltages of 500 V, while the measurements for YAP:Ce were conducted with PMT voltages of 700 V. Lower LaBr₃:Ce PMT voltages were used to ensure that the higher rate of photon emission in LaBr₃:Ce does not saturate the PMTs. The cross-covariance for the complete photopeak from a LaBr₃:Ce scintillation crystal is shown in the top row in Fig. 17.

Figure 17.

The cross-covariance curve for different energy windows of the photopeak of an experimental measurement on LaBr₃:Ce. The plots in the left half of the figure show the parts of the photopeak histogram that were used to calculate the cross-covariance in the right half of the figure. The cross-covariance curve of the measured data does not appear to be sensitive to the energy window of the photopeak used to calculate it.

We have to threshold the experimental data to isolate photopeak events from Compton events. Unlike the simulated data, the experimental data cannot be assumed to originate from one gamma-ray energy. In Fig. 17 we see that the cross-covariance curves do not change substantially for different energy windows of the photopeak histogram.

We can also see from Fig. 18 and Fig. 19 that the average normalized AUCCC became more negative when we divided the photopeak into five or more equal energy windows as compared to using the complete photopeak (One energy window). Dividing the photopeak into five, ten or fifteen energy windows does not significantly change the normalized AUCCC. This behavior could be because a smaller energy window contains interactions from fewer gamma-ray energies. The measurements with the worst energy resolutions (measurement 3 and 6 in Fig. 17) also recorded the biggest drops between the normalized AUCCCs for one photopeak energy window and the five photopeak energy windows.

Figure 18.

The average normalized AUCCC for different number of energy windows of the photopeak of an experimental measurement on LaBr₃:Ce. The normalized AUCCCs for the measured data does not appear to be sensitive to the size of the energy window of the photopeak used to calculate it.

Figure 19.

The average normalized AUCCC for different number of energy windows of the photopeak of an experimental measurement on YAP:Ce. The normalized AUCCCs for the measured data does not appear to be sensitive to the width energy windows of the energy spectrum used to calculate it.

As we have shown in Sec. 6.1.4, if we only have data from only one gamma-ray energy, the normalized AUCCC is independent of the size of the energy window, so we must choose a smaller energy window to minimize the presence of other gamma-ray energies. Although, we expect the photopeak region to yield better results, windowing the energy into small windows also gives us an option to use the Compton region of the energy spectrum.

8.3. Estimates of the Fano factor

The normalized AUCCC’s for YAP:Ce and LaBr₃:Ce were estimated by using the experimental data with 10 energy windows. The Fano factors for YAP:Ce and LaBr₃:Ce were estimated using Eq. 35 and Eq. 34, respectively.

9. Comparison of Fano factor estimates from temporal and integral correlations

The estimates of Fano factor from the temporal correlations for both the scintillators were smaller than the estimates from the integral correlations in the previous chapter. This could be a result of a bias towards lower Fano factor values in the time-correlation estimates, or a bias towards higher Fano factor values in the integral-correlation estimates or both.

The different loss mechanisms like x-ray escape and low angle Compton scattering will bias the Fano factor estimates from integral correlations biased towards higher Fano factors. The photon Fano factor estimates of LaBr₃:Ce from both the methods are within each others error bars. We are not aware of a bias in our measurements from the temporal correlations.

The estimate of the correlation coefficient of YAP:Ce is close to zero (r̂_12YAP:Ce = 0.10), and as a result the estimate of the photoelectron Fano factor was close to one (F̂_nYAP:Ce = 1.13). The estimates of the photon Fano factor are sensitive to the value of η. The value of η amplifies the deviation of the correlation coefficient from zero. As a result the small deviation from zero in the estimate of the correlation coefficient is amplified and the estimate of the photon Fano factor for YAP is F_NYAP:Ce = 1.46. For example, a value of r̂₁₂ = −0.1 will yield a photon Fano factor of (F_N = 0.6526). The value of the correlation coefficient of r̂₁₂ = −0.0165 will yields the Fano factor estimate from the temporal correlation.

10. Conclusion

The Fano factors of scintillation photons and photoelectrons were estimated using the correlation of signals from two optical detectors viewing the same scintillation event. The scintillation light from different scintillators has Fano factors ranging from sub-Poisson to approximately Poisson to super-Poisson. The Fano estimates from the temporal and the integral correlations were close to each other for the two materials for which both were performed: LaBr₃:Ce and YAP:Ce.

Figure 13.

Scatter plot for YAP:Ce. The photopeak of the scatter plot has little or no correlation.

Figure 14.

Scatter plot for CsI:Na, the photopeak is positively correlated.

Figure 15.

Model for the relationship between the normalized AUCCC and the Fano factor for LaBr₃:Ce. The normalized AUCCC has a proportional relationship with the Fano factor.

Figure 16.

Model for the relationship between the normalized AUCCC and the Fano factor for YAP:Ce. The normalized AUCCC has a proportional relationship with the Fano factor.

Table 2.

Fano factor estimates from Normalized AUCCC

	Normalized AUCCC	Photon Fano factor (FN)
YAP:Ce	−1.1×10−3±5.2×10−5	0.9385 ± 0.0107
LaBr3:Ce	−2.0×10−3±9.3×10−5	0.0292 ± 0.1565

Appendix A

Cross-covariance for different values of relative time shift

The Hanbury Brown and Twiss experiment measured the cross-covariance of the two detector outputs as a function of relative time shift. We used Eq. A.1 to calculate the cross-covariance for different values of the relative time shift τ.

$$\mathit{\text{cov}}(t,\tau )=\langle [s_1(t)-\langle s_1(t)\rangle ][s_2(t+\tau )-\langle s_2(t+\tau )\rangle ]\rangle .$$ (A.1)

The resulting matrix is shown in Fig. A.20 with time t varying along the x-axis and the time shift τ along the y axis. The region above the diagonal (t = τ line) is zero because there is no overlap between the non-zero regions of the two pulses. A small time region before the start of the scintillation signal was also recorded, this causes an offset in the most negative region of the image, and results in the shift of that region from the diagonal.

Figure A.20.

Cross-covariance as a function of the detector signal as a funtion of time t and shift τ.

While most of the Fig. A.20 is either zero or negative, there is a small region at τ = 0, t ≈ 7.5 ns that is positive. This is an experimental artifact caused by the uncertainty in the triggering mechanism of our system. The mean detector signals are calculated from an ensemble from all the photopeak detector signals, they start rising from zero at t ≈ 7 ns. If a scintillation pulse arrives a little before the time when mean detector signals start to rise, for a small amount of time after the scintillation pulse arrives, the detector signals are positive, but the mean signals are still zero. Therefore, both differences between the amplitudes of the signals and their respective mean signals will be positive, giving us a positive cross-covariance. Similarly, if the detector pulses arrive a little earlier, the cross-covariance will again be positive.

As the scintillation pulse decays, due to the rarity, the statistics tend towards Poisson statistics. Therefore, for larger values of t the cross-covariance tends toward zero. As τ increases beyond 30 ns, the cross-correlations decrease and tend towards zero [9].

Appendix B

Impact of choice of gain variance coefficient and quantum efficiency on Fano estimates from integral correlations

The value of the photoelectron Fano factor is independent of the estimate of η (See Eq. 15). To test the impact of an error in our estimate of η on the photon Fano factor estimates, the photon Fano factor for different values of η at β = 0.07 are shown in Table B.3. An error in the estimate of η has a significant impact on the estimates of the photon Fano factors. A small value of η pushes the Fano factor estimates away from one – the estimates of the Fano factor of sub-Poisson scintillators become more sub-Poisson and the estimates of the Fano factor of super-Poisson scintillators become more super-Poisson. A smaller value of η also increases the uncertainty in the measurement for all the scintillators. The values of η below 0.24 result in unphysical negative estimates of photon Fano factor for SrI₂:Eu.

Table B.3.

Photon Fano factor estimates for different values of η with β = 0.07

	Photon Fano factor (FN)
(η)	SrI2:Eu	YAP	CsI:Na
0.2	−0.2369 ±0.18	1.65 ±0.18	5.747 ±1
0.22	−0.1244 ±0.16	1.591 ±0.16	5.316 ±0.9
0.24	−0.03073 ±0.14	1.542 ±0.15	4.956 ±0.81
0.26	0.04855 ±0.12	1.5 ±0.14	4.652 ±0.74
0.28	0.1165 ±0.11	1.464 ±0.13	4.391 ±0.68
0.3	0.1754 ±0.1	1.433 ±0.12	4.165 ±0.63
0.32	0.227 ±0.093	1.406 ±0.11	3.967 ±0.59
0.34	0.2724 ±0.086	1.382 ±0.1	3.792 ±0.55
0.36	0.3128 ±0.08	1.361 ±0.096	3.637 ±0.52

To illustrate the impact of an error in our estimate of β on the Fano factor estimates, we calculated the mean and standard deviation of the estimates of photoelectron and photon Fano factor for different values of β at η = 0.28. From Table B.4, we conclude that the gain variance coefficient (β) does not have a large impact on the estimates of the photoelectron or the photon Fano factor.

Table B.4.

Photoelectron and photon Fano factor estimates for different values of β with η = 0.28

	Photoelectron Fano factor (Fn)			Photon Fano factor (FN)
Gain Noise Factor (β)	SrI2:Eu	YAP	CsI:Na	SrI2:Eu	YAP	CsI:Na
0.05	0.7572 ±0.024	1.128 ±0.033	1.932 ±0.18	0.133 ±0.11	1.456 ±0.12	4.327 ±0.67
0.06	0.7549 ±0.024	1.129 ±0.033	1.941 ±0.18	0.1248 ±0.11	1.46 ±0.12	4.359 ±0.68
0.07	0.7526 ±0.024	1.13 ±0.033	1.949 ±0.18	0.1165 ±0.11	1.464 ±0.13	4.391 ±0.68
0.08	0.7503 ±0.025	1.131 ±0.034	1.958 ±0.18	0.1083 ±0.11	1.469 ±0.13	4.422 ±0.69
0.09	0.748 ±0.025	1.132 ±0.034	1.967 ±0.18	0.1 ±0.11	1.473 ±0.13	4.454 ±0.7