Axial-Stereo 3-D Optical Metrology for Inner Profile of Pipes Using a Scanning Laser Endoscope

Abstract

As the rapid progress in the development of optoelectronic components and computational power, 3D optical metrology becomes more and more popular in manufacturing and quality control due to its flexibility and high speed. However, most of the optical metrology methods are limited to external surfaces. This paper proposed a new approach to measure tiny internal 3D surfaces with a scanning fiber endoscope and axial-stereo vision algorithm. A dense, accurate point cloud of internally machined threads was generated to compare with its corresponding X-ray 3D data as ground truth, and the quantification was analyzed by Iterative Closest Points algorithm.

I. Introduction

Three-dimensional (3D) metrology is a process that utilizes physical measurement equipment to quantify the actual size or distance from a given object. The generated point cloud can be directly utilized in virtual design, simulation, reverse engineering, and quality control [1]. Modern 3D metrology can be mainly achieved actively by interfere with the object either mechanically (contact) or radiometrically (non-contact). An example of contact active 3D reconstruction method is using depth gauge to measure the distance of each surface point of the object, and collect these 3D data into a point cloud, such as Coordinate Measurement Machine (CMM) [2]. Non-contact active methods are mainly using optical techniques. Time of flight (ToF) [3, 4] is one non-contact method that can retrieve the depth between light source and object by measuring the time that light flies. X-ray computed tomography (CT) can produce the 3D surface and interior structure of an object by using x-ray to generate tomographic images [5]. Another common active non-contact approach is based on structured-light [6, 7, 8]. By projecting structured-light of known pattern onto a 3D surface, such as grid, fringe, or speckle patterns, a distorted pattern image is captured from other perspective than where the projection light source is. The dense 3D information can be recovered by analyzing how the pattern distorted. Nowadays, 3D optical metrology becomes more and more popular due to its flexibility and high speed, as the rapid progress in the development of optoelectronic components and availability of increased computational power [9, 10]. But most of current 3D optical metrology systems are only feasible to external machined surface, but internal one. The relative large size of detectors of current metrology systems restricts their application for the tiny internally machined parts, such as internal threads in automotive industry.

The threaded hole in an engine is very crucial to the performance of a car. The main function of threaded hole is to joint two mechanical parts, such as engine block and engine head. The quality of thread joints in the car engine is critical to safety, efficiency and longevity. Nowadays, the automobile manufacturers spend lots of labor, energy and time to control the threads quality by using manual Go/No-Go gauges [11]. This tactile inspection is fast but comes with several disadvantages, 1) it couldn’t provide variable data; 2) it depends on the operators’ skills; 3) it causes undesirable mechanical wear; and 4) its labor cost is high.

To solve these issues of internal threads measurement with manual contact gauge, one possible solution is X-ray CT [12]. It can provide high quality 3D metrology data, but it is too slow to be used as an in-line manufacturing process. Wakayama et al. proposed another possible 3D optical metrology approach for the inner profile of pipes by using a ring beam device [13]. It can generate accurate 3D measurement data, but the size of the device limited its application for small internal threaded hole. Hence a new 3D optical metrology approach for the internal surface of tiny pipes was proposed in this paper by utilizing a miniature Scanning Fiber Endoscope (SFE) [14] and axial-stereo vision technique [15].

The SFE is a tiny flexible endoscope of only 1.2 mm in outer diameter (OD). It can achieve high resolution (608 × 608 pixels) and wide field of view (70–120 degree FOV) with imaging rate at 30 Hz. The SFE generates a full color 2D image from scanning a single beam of RGB (red, green and blue) laser light, simultaneously capturing the reflected light by a ring of multimodal returning fibers, and amplifying return signals with photomultiplier tubes (PMTs). Current endoscopic lenses can generate 20–50 micron spatial resolution in luminal spaces from 3–30 mm in diameter. By utilizing this miniature endoscope, the imaging of most of the standard internal threads can be achieved with high-resolution in real-time.

An accurate 3D reconstruction algorithm with a SFE video of internal surface has been developed in our previous study in medical field based on SIFT features (scale-invariant feature transform) [16,17,18]. It does not meet the requirement of high-quality dense reconstruction for industry application since there are much fewer features in the internally machined metal parts and it is a sparse 3D reconstruction. In this study, a stereo vision technique was applied to generate the dense 3D model. Instead of using lateral-stereo (conventional stereopsis), axial-stereo vision [15] was established with two SFE images by moving SFE along with the axis of threaded hole.

This paper is a proof-of-concept study, demonstrating the feasibility of our proposed axial-stereo vision system for 3D optical metrology on tiny internally machined surface. The basic theory is shown in section II method; one experiment with moving SFE in a threaded hole is shown in section III experiment; 3D dense reconstruction results, error analysis and discussion are presented in section IV; conclusion was drawn in section V.

II. Method

A. Axial-stereo Vision

Stereo vision is a common approach to extract 3D information of scene from two digital images that captured by two cameras with known spatial positions and orientations. Conventional stereo vision system contains two side-by-side cameras, in a manner similar to human binocular vision [19]. To satisfy the goals of reducing space, cost, and complexity of examining small restricted spaces such as a threaded hole, a single SFE (monocular vision) was utilized to establish an axial-stereo vision by moving SFE along the axis of hole to generate the 3D model, which had been barely studied [15, 20].

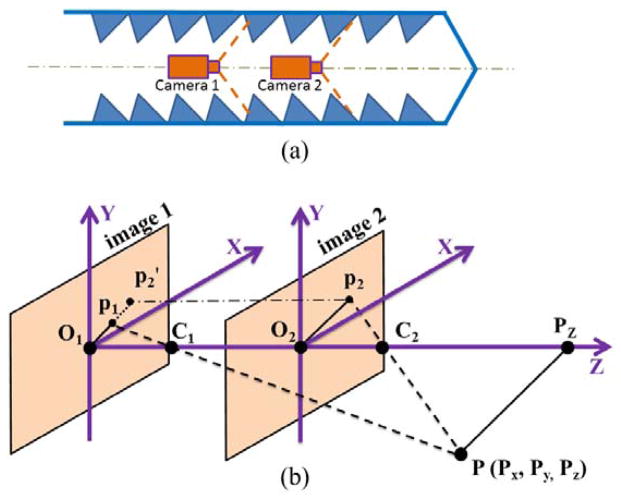
Figure 1 shows the schematics of axial-stereo vision. Two cameras are set up as their optical axis coincided, shown as Z direction in the schematics. The FOV of cameras are large enough to capture the valley of the threads. The X and Y axis of these two image plane should be kept paralleled. For a point P(P_x, P_y, P_z) in 3D space, its projections in two images 1 and 2 locate at P₁ and P₂, respectively. P₂′ is the orthogonal projection of P₂ on the image 1. O and C represent center of image planes and the pinhole of cameras, respectively. The $\overline{O_1-C_1}$ and $\overline{O_2-C_2}$ are the focal length of SFE f_SFE, which was known from calibration. By knowing the distance of $\overline{O_1-O_2}$, the depth information of P can be calculated in the form of disparity ( $\overline{{P_2}^{\prime }-P_1}$), which was obtained by image processing.

Fig. 1.

Geometrical model of axial stereo vision system. (a) Two images of the internal surface are captured as the camera move along the optical axis. (b) The same 3D point has two different projections on the two SFE images.

From the triangular relationship shown in Fig. 1, two equations were satisfied as:

$$\frac{\overline{P_2-O_2}}{\overline{P-Pz}}=\frac{\overline{C_2-O_2}}{\overline{C_2-Pz}};$$ (1)

$$\frac{\overline{P_1-O_1}}{\overline{P-Pz}}=\frac{\overline{C_1-O_1}}{\overline{C_1-Pz}}=\frac{\overline{C_1-O_1}}{\overline{C_2-Pz}+\overline{C_1-C_2}};$$ (2)

From Eq. (1) and Eq. (2), the depth of P was obtained from Eq. (3), which is defined as $P(z)=\overline{C_2-Pz}$.

$$P(z)=\overline{C_2-Pz}=\frac{\overline{P_1-O_1}}{\overline{{P_2}^{\prime }-P_1}}\times \overline{O_1-O_2}$$ (3)

The only unknown variable in Eq. (3) is the disparity between P₂ ′ and P₁, which can be considered as the projection difference of the same 3D point P in two images. Once the depth of P is obtained, the X and Y coordinate of P, represented as P(x) and P(y), can be calculated with known focal length f_SFE:

$$P(x,y)=\frac{P_2(x,y)}{C_2-O_2}\times P(z)=\frac{P_2(x,y)}{f_{\mathit{SFE}}}\times P(z)$$ (4)

B. Disparity Computation

To compute the disparity of the projection of each point in the 3D scene, we have to find out the corresponding points in the two axial images. In previous studies [16, 17, 18], SIFT algorithm was used to detect and match the corresponding features. But in the metrology of internally machined metal hole, there are very limited features available for dense matching. In this study, we employed block matching algorithm to find the corresponding [21]. For every pixel in image 2 (see Fig. 1), we extracted an n-by-n-pixel block round it and search around the same location in image 1 over both X and Y directions. The sum of absolute difference (SAD) was calculated in each block comparison. The block with the minimum SAD value is the matching one. Once we have the corresponding points, the 3D information of the scene can be reconstructed by the Eq. (3) and Eq. (4).

III. Experiment

To demonstrate the feasibility of our proposed axial-stereo vision system, the 1.2mm OD SFE was attached to a micro-positioning stage, representing a manufacture robot that can provide accurate position and orientation of SFE, shown in Fig. 2a. The micro-positioning stage we used in this study was ULTRAlign^™ precision integrated crossed-roller bearing linear stage, model 462-xyz-m. The position and orientation of SFE was adjusted so that the optical axis of SFE is perpendicular downwards and coincides with the axis of threaded hole of 8mm major diameter and 7mm minor diameter.

Fig. 2.

The experiment setup of axial-stereo vision system for internal 3D metrology of thread block. (a) The SFE was attachment to a mirco-positioning stage, aligning with the axis of threaded hole. (b) the photographs of SFE (up) and thread block (bottom).

The SFE was moving downwards with 0.25 mm interval, two images were captured with size of 608 × 608 pixels, shown in Fig. 3. Only the front flank of the threads was captured, with almost identical thread pattern and limited features in the images. The SFE position of the right image (Fig. 3b) was 0.25mm deeper than the one of the left image (Fig. 3a).

Fig. 3.

The two SFE video frames were captured with different axial depth (0.25mm) along the axis of a threaded hole of 8mm as major diameter and 7mm as minor diameter.

IV. Results

In this study, a block size of 7×7 pixels was chosen to search the corresponding points from Fig. 3b to Fig. 3a. The returned disparities of the corresponding points were all integer-valued and noisy, shown in Fig. 4a. A sub-pixel correction was incorporated to eliminate the integer-valued discontinuity issue [22]; dynamic programming [23] was applied to eliminate the noise and imaging pyramid [24] was utilized to guide the block matching. The final result was smooth, shown in Fig. 4b. By knowing the disparity of each pixel in the SFE images, the 3D scene would be reconstructed by Eq. (3) and Eq. (4). In our study, a total of 164,579 3D points were generated (Fig. 4c), and a zoom-in view showed that the 3D reconstruction is dense (Fig. 4d). The triangular mesh could be generated by finding the neighbor points along the X and Y directions.

Fig. 4.

The 3D reconstruciton of two SFE images that captured along the axis of a threaded hole. (a) The disparity map of basic block matching. (b) The disparity map of block matching with imaging pyramid, sub-pixel correction and dynamic programming. (c) The 3D dense reconstruction of internal threads. (d) the zoom-in view of the 3D reconstruction showing four clear threads.

All the codes are MATLAB implemented, and running on a workstation Dell Precision M4700 with 2.7 GHz Intel i7-3740QM CPUs, 20.0 GB memory. It took 250 sec to generate the dense 3D model.

To quantify the reconstruction result, Iterative Closest Point (ICP) [25] was employed to align and compare the reconstructed dense point cloud to the X-ray point cloud (ground truth model) of the same thread block. The obtained ICP error value was 0.4333mm, which was relatively large. This error may come from the inaccurate experiment setup and SFE calibration, distortion of SFE images and also the round error of disparity computation.

To test the feasibility of our algorithm for more general application with different imaging devices, we duplicated the same experiment on the same test piece, but using a commercial rigid scope instead of our custom designed and flexible SFE. A Stryker^™ forward-view borescope (model # 502-503-010) with 5 mm OD was used to collect axial images (1280 × 1024 pixels) in this additional experiment. The 3D reconstruction process was repeated and also the same data analysis. The obtained ICP error was 0.4632mm, which was almost the same (6.90% higher) as the result using the SFE. Although the images that were captured by the commercial scope were at higher resolution and less image distortion comparing with SFE images, the noise was much larger in the images, which decreased the accuracy since the reconstruction algorithm was based on pixel values.

V. Conclusion and discussion

The 3D reconstruction result of this proof-of-concept study shows very clear threads with texture information since it is image-based measurement. This is a unique advantage comparing with X-ray 3D metrology, which only generates geometry information. And also the obtained point cloud can provide more quantitative quality control and monitoring of tool wear comparing with current common method of Go/No-Go contact gauges, which causes heavier workload, lower efficiency and higher levels of uncertainty depending on the operator’s skill [11]. Moreover, this proposed approach can be also utilized for the 3D metrology of the internal surfaces of curved tubes by accurately moving the tiny, flexible SFE along the centerline of the pipe.

The ICP distance between the reconstructed 3D point cloud and the X-ray is large. One reason is the inaccurate experiment setup, which can be solved by utilizing three linear motion stages and two tilt adjustment stages [11]. Another reason is image distortion, it can be dramatically reduced by non-parametric distortion correction algorithm [26]. The 3D optical metrology result also contains a very noisy rim (Fig. 4c). The reason is that the outer scans of original SFE image were dark, which introduced much noise. Moreover, only the front flank of threads were captured and reconstructed in this study. A small round mirror could be held in front of the SFE distal end to image the backside of threads in the future study.

By utilizing the axial-stereo vision algorithm, the SFE motion along the axis of a tiny internal threaded hole (7 mm as minor diameter) can generate a high-resolution 3D model in this proof-of-concept study, which demonstrated the feasibility of our proposed axial-stereo metrology method. Future work is to improve the accuracy of this algorithm by taking advantage of multiple axial images that are captured in the threaded hole. The accuracy also can be analyzed by other methods, such as Gauss-Newton method [27]. Instead of using two images, each 3D point would have several projections in the multiple axial images, from which the estimation of the 3D points is more robust and accurate. Moreover, considering the inaccuracy of linear motion of the camera in practical applications, a bound constrained optimization algorithm can be implemented by utilizing the motion error as a priori knowledge [28].