Abstract
Bayesian theories of neural coding propose that sensory uncertainty is represented by a probability distribution encoded in neural population activity, but direct neural evidence supporting this hypothesis is currently lacking. Using fMRI in combination with a generative model-based analysis, we found that probability distributions reflecting sensory uncertainty could reliably be estimated from human visual cortex and, moreover, that observers appeared to use knowledge of this uncertainty in their perceptual decisions.
The information that the brain receives from the senses is typically consistent with a range of possible stimulus values; consequently, all of our perceptual decisions have to be made under uncertainty. It is well known that this sensory uncertainty can affect behavior1,2, but how the fidelity of sensory knowledge is represented in cortex remains unclear. Bayesian theories of neural coding postulate that a probability distribution over sensory stimuli is encoded in the activity of a whole population of neurons, with the width of this distribution reflecting the degree of uncertainty about the stimulus3–6. Although indirect neurophysiological evidence is consistent with this notion7,8, this hypothesis has yet to be tested directly in sensory cortex. We used functional magnetic resonance imaging (fMRI) in combination with a model-based analysis to address two fundamental questions. First, can a probability distribution that reflects sensory uncertainty be extracted from population activity in human visual cortex? Second, do observers use knowledge of this uncertainty in their perceptual decisions? Notably, unlike previous behavioral studies on probabilistically optimal inference, no external noise was added to the visual stimuli to manipulate uncertainty, as changes in physical stimulus properties could then act as external cues to reliability9. We hypothesized that varying degrees of internal neural noise might nonetheless affect sensory processing on a trial-by-trial basis; if uncertainty is part of the neural sensory code, then these fluctuations in uncertainty should alter human perceptual decision-making.
Participants viewed annular gratings of random orientations while we measured activity in visual cortex using fMRI. Shortly after the presentation of each grating, observers reported its orientation by rotating a bar presented at fixation. Observers generally performed well on this task. The mean angular difference between reported and actual orientations was 4.5°, ranging between 0.003° and 37.68° on individual trials. These fluctuations in behavioral accuracy are often thought to arise, in part, from internal neural noise affecting the fidelity of cortical orientation representations. We asked whether this trial-by-trial variability in the fidelity of internal knowledge was reflected in fMRI activation patterns. We addressed this question using a model-based decoding approach to analyzing fMRI data (Online Methods). Specifically, using a generative model incorporating the orientation preferences of voxels as well as their (correlated) noise, we approximated on each trial the posterior probability distribution over orientation, given the pattern of blood oxygen level–dependent (BOLD) activity. This approach differs from conventional fMRI decoding studies10–12 in that it explicitly recovers a full probability distribution over stimulus values, rather than a single stimulus estimate. The (circular) mean of the posterior distribution serves as an estimate of the presented orientation, and its width (circular s.d.) as a measure of the degree of stimulus uncertainty in the cortical representation. Regions of interest were those portions of visual areas V1–V3 that corresponded to the retinotopic representation of the stimuli.
To benchmark our approach, we first tested its ability to identify the presented orientation from activity patterns in areas V1–V3 (Supplementary Fig. 1a,b). The decoded and presented orientations were significantly correlated (r = 0.69, P ≈ 0), consistent with previous findings13,14. We then turned to the degree of trial-by-trial uncertainty about orientation. The decoder’s estimates of uncertainty varied from trial to trial as a result of noise in the fMRI measurements (Fig. 1a). To the extent that our decoding approach appropriately models the fMRI data, uncertainty on a single trial should be related to variability across trials. Accordingly, to verify the decoder’s assumptions and test whether the decoded uncertainty followed the actual degree of noise in the fMRI data, we binned the data according to posterior width, and calculated the trial-by-trial variability in decoded orientation estimates for each of the bins (Supplementary Fig. 1c). We found that the decoded uncertainty was indeed significantly correlated with the across-trial variability in decoded orientations (r = 0.91, P ≈ 0). A comparison between different noise models revealed that the one used here best captured the fMRI data (Supplementary Fig. 2). Altogether, these findings corroborate the validity of our assumptions and suggest that posterior width captures the overall degree of uncertainty in the data on a trial-by-trial basis.
Figure 1.
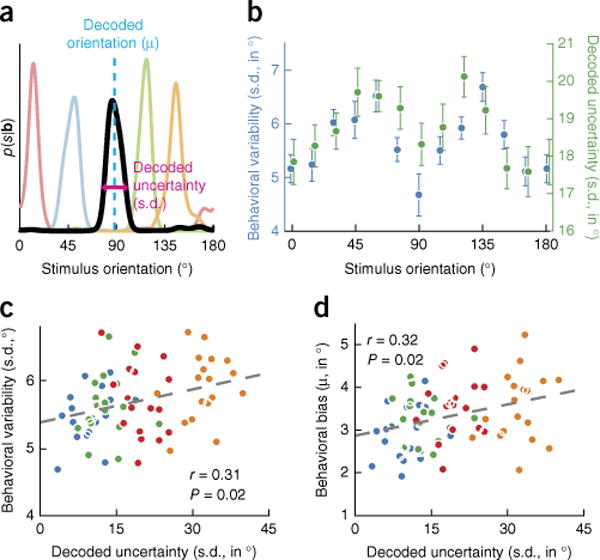
Stimulus uncertainty decoded from human visual cortex correlates with behavior. (a) Examples of probability distributions over stimulus orientation, decoded from fMRI activation patterns obtained from areas V1–V3, and five different trials (trials indicated by different colors; s, stimulus orientation; b, BOLD activity). (b) Both behavioral variability and decoded uncertainty increased for more oblique stimulus orientations in areas V1–V3 (behavioral variability, t(53) = 4.71, P = 1.8 × 10−5; decoded uncertainty, t(53) = 2.75, P = 0.008). For illustrative purposes, trials were sorted into 12 equally spaced orientation bins. (c) Behavioral variability was significantly correlated with posterior width in areas V1–V3 (t(52) = 2.39, P = 0.021). (d) Behavioral biases increased with increasing width of the posterior distribution in areas V1–V3 (t(52) = 2.46, P = 0.017). In c and d, colors indicate four within-observer bins of increasing decoded uncertainty (for each of 18 observers). In all plots, error bars represent ±1 s.e.m., dashed lines represent best linear fits and reported r values are partial correlation coefficients obtained from a linear regression analysis (Online Methods). Similar results were found for visual areas V1–V3 (Supplementary Fig. 1).
Having established that the decoded uncertainty reflects the aggregate of all fMRI noise sources, we next asked whether it captures variability in cortical stimulus representations in particular. We addressed this question in two sets of analyses, focusing first on gratings of different orientations. Consistent with previous work15,16, behavioral orientation judgments were more accurate for cardinal than for oblique orientation stimuli (correlation between behavioral variability and the angle of the presented stimulus with the nearest cardinal axis: r = 0.54, P = 1.8 × 10−5; Fig. 1b). Because behavioral accuracy is directly related to uncertainty, we tested whether this oblique effect in behavior was paralleled in visual cortical responses. Indeed, the width of the decoded posterior probability distribution was narrower for stimulus orientations closer to the cardinal axes (r = 0.35, P = 0.008; Fig. 1b). Thus, similar to behavior, horizontal and vertical orientations are represented with greater precision in visual cortex.
For the second set of analyses, we focused on repeated presentations of physically identical orientation stimuli. We reasoned that, if the posterior distribution also captures random, trial-by-trial fluctuations in cortical activity, then more certain decoder estimates should be linked to reduced variability in the observer’s behavior, even for physically identical orientation stimuli6. To test this relationship, we divided each participant’s data into bins of increasing decoded uncertainty, calculated the across-trial variability in participant behavior for each of the bins and computed the partial correlation coefficient between the two (while controlling for stimulus orientation and between-subject variability, Online Methods). This revealed that observers clearly made more accurate decisions when the information decoded from their visual activity was more precise (r = 0.31, P = 0.021; Fig. 1c). By contrast, neither the error in decoded orientation (Supplementary Fig. 3) nor the amplitude or width of the estimated neural population response (Supplementary Fig. 4) reliably predicted behavioral variability, demonstrating the power of the posterior distribution in capturing trial-by-trial fluctuations in cortical processing. Control analyses established that these results could not be accounted for by differences in eye movements, gross BOLD amplitude or subject head motion (Supplementary Fig. 5), and were specific to voxels tuned to the retinotopic location of the stimulus (that is, we found no reliable correlation between decoded uncertainty and behavioral variability when selecting V1–V3 voxels preferring other retinotopic locations, P = 0.17). Taken together, these results demonstrate that the fidelity of a sensory representation can reliably be extracted from fMRI activation patterns.
Armed with the ability to estimate uncertainty in sensory representations, the critical question is whether observers take this uncertainty into account when making perceptual decisions. If so, then this would provide strong empirical support for probabilistic models of perception6. To address this question, we relied on a well-established behavioral finding17,18 that we replicated here: orientation judgments were biased away from the cardinal axes (Supplementary Fig. 6). Although the precise neural mechanisms underlying such repulsive biases have yet to be determined, all theoretical models18–20 of these biases generate the same prediction: if the observer takes into account the uncertainty in perceptual representations, the amount of behavioral bias should depend on the degree of sensory uncertainty. Indeed, we found that behavioral biases increased when the decoded fidelity of cortical information about the visual stimulus was low (r = 0.32, P = 0.017; Fig. 1d), consistent with a recent theoretical prediction that the repulsive bias should increase with increasing levels of internal uncertainty20. Given that the physical stimulus was held constant, this suggests that human observers use knowledge of internal uncertainty in their perceptual decision-making and, moreover, that they monitor fluctuations therein on a trial-by-trial basis.
A major limitation of previous work on probabilistically optimal inference has been the use of external sources of noise, leaving open the possibility that observers simply monitor certain image properties, such as blurriness or contrast, as external cues to uncertainty. For this reason, we held physical stimulus properties constant and relied on fluctuations in internal noise to make perceptual information more or less reliable to the observer. We found that the uncertainty in perceptual representations could reliably be extracted as a probability distribution from human visual cortex with fMRI, and, moreover, that human observers appeared to rely on the uncertainty in this internal evidence when making perceptual decisions. These results suggest that neural activity encodes probability distributions over stimulus values, rather than merely point estimates, and that the brain uses this probabilistic information in its computations.
METHODS
Methods and any associated references are available in the online version of the paper.
ONLINE METHODS
Participants
18 healthy adult volunteers (aged 22–31, seven female), with normal or corrected-to-normal vision, participated in this study. All participants provided informed written consent. The study was approved by the Radboud University Institutional Review Board. Assuming effect sizes similar to those reported here, a power analysis indicated that 18 subjects would produce a power level of 0.76–0.86. Indeed, this sample size is consistent with previous decoding studies21,22.
Data acquisition
MRI data were acquired using a Siemens 3T Magnetom Trio scanner with an eight-channel occipital coil located at the Donders Center for Cognitive Neuroimaging. For each participant, a high-resolution T1-weighted magnetization-prepared rapid gradient echo anatomical scan (MPRAGE, FOV 256 × 256, 1-mm isotropic voxels) was collected at the start of the session. Functional imaging data were acquired using T2*-weighted gradient-echo echoplanar imaging, in 30 slices oriented perpendicular to the calcarine sulcus, covering all of the occipital and part of posterior parietal and temporal cortex (TR 2,000 ms, TE 30 ms, flip angle 90°, FOV 64 × 64, slice thickness 2.2 mm, in-plane resolution 2.2 × 2.2 mm).
Experimental design and stimuli
Stimuli were generated by a Macbook Pro computer running Matlab and the Psychophysics Toolbox23,24, and displayed on a rear-projection screen using a luminance-calibrated EIKI projector (resolution 1,024 × 768 pixels, refresh rate 60 Hz). Observers viewed the visual display through a mirror mounted on the head coil.
Participants were required to maintain fixation on a central bull’s eye target (radius: 0.25°) throughout each experimental run. Each run consisted of an initial fixation period (4 s), followed by 18 stimulus trials (12 s) and a final fixation period (4 s). Trials were separated by a 4-s inter-trial interval. Each trial started with the presentation of an orientation stimulus (1.5 s). Orientation stimuli were counterphasing sinusoidal gratings (contrast: 10%, spatial frequency: 1 cycle per °, randomized spatial phase, 2-Hz sinusoidal contrast modulation) presented in an annulus surrounding fixation (inner radius: 1.5°, outer radius: 7.5°, grating contrast decreased linearly to 0 over the outer and inner 0.5° radius of the annulus). The orientation of the stimulus was determined pseudo-randomly (from 0–179°) to ensure an approximately even sampling of orientations in each run. The grating was followed by a fixation interval (6.5 s), and then a response period (4 s) in which a black line (length: 2.8°, width: 0.1°) appeared at the center of the screen at an initially random orientation. The line disappeared gradually over the last 1 s of the response period to indicate the approaching end of this window. Subjects reported the orientation of the grating by rotating the line using separate buttons for clockwise or counterclockwise rotation on an MRI-compatible button box.
Participants completed 10–18 stimulus runs. Each scan session also included two visual localizer runs, in which flickering checkerboard patterns were presented within the same aperture as the gratings (check size: 0.5°, display rate: 10 Hz, contrast: 100%). Checkerboards were presented in 12-s blocks, interleaved with fixation blocks of equal duration.
Retinotopic maps of visual cortex were acquired in a separate scan session using conventional retinotopic mapping procedures25–27.
fMRI data preprocessing and regions of interest
Functional images were motion corrected using FSL’s MCFLIRT28 and passed through a high-pass temporal filter with a cut-off period of 40 s to remove slow drifts in the BOLD signal. Residual motion-induced fluctuations in the BOLD signal were removed through linear regression, based on the alignment parameters generated by MCFLIRT. Functional volumes were aligned to a previously collected anatomical reference scan using FreeSurfer29.
Regions of interest (ROIs; V1, V2 and V3) were defined on the reconstructed cortical surface using standard procedures25–27. In each area, we selected all voxels that responded to the localizer stimulus at a lenient threshold (P < 0.05 uncorrected) for subsequent analysis, in the native space for each participant. Control analyses verified that our results were not strongly affected by the number of voxels selected for analysis (Supplementary Fig. 7). In one of our control analyses, we tested the degree to which the decoded uncertainty was specific to the retinotopic location of the stimulus. For this analysis, we selected those voxels in areas V1–V3 combined that were not significantly activated by the localizer stimulus (at a statistical threshold of P > 0.2), obtaining on average 1,257 voxels per subject (by comparison, the average number of voxels in individual ROIs was 660; Supplementary Fig. 1).
The time series of each voxel was z-normalized using the corresponding time points of all trials in a given run. Activation patterns for each trial were defined by averaging together the first 4 s of each trial, after adding a 4-s temporal shift to account for hemodynamic delay. This relatively short time window (4 s) was chosen in order to ensure that activity from the response window was excluded from analysis. Control analyses verified that this time window was close to the peak of the hemodynamic response function (time series for this analysis were normalized to percentage signal change units, defined relative to the average activation level across each run; Supplementary Fig. 8). In addition, temporally expanding the time window to include an earlier time point did not greatly affect any of our results. For the control analyses of Supplementary Figure 5, mean BOLD intensity values were obtained by averaging across all voxels in a given ROI. Subject head motion was calculated as the Euclidian norm of the temporal derivatives of the realignment parameters generated by the motion correction algorithm – a quantity that reflects the total amount of head motion per time step. We averaged across TRs 3 and 4 of each trial, similar to our decoding analyses.
Decoding analysis
The generative model
Our decoding approach started with the assumption that voxels in early visual cortex are selective to orientation10,11,13,14,30,31, and that voxel activity varies across trials due to (correlated) noise32,33. More specifically, we assumed that the BOLD response of voxel i to orientation s can be characterized as a linearly weighted combination of the idealized tuning functions f(s) of K neural populations13,14 (K = 8), each tuned to a different orientation, combined with Gaussian noise
| (1) |
Here, fk(s) is the mean response (or tuning curve) of the kth population as a function of stimulus orientation s, Wik is the contribution of population k to the response of voxel i, and both ηk and νi model sources of noise. The latent (unobserved) variable η is normally distributed as , and specifies noise that is shared among neural populations of similar orientation preference (which is why it is weighted by W). It models global changes in the population response due to, for example, shifts in response gain. The variable ν was included to capture various remaining sources of noise, such as variability in the fMRI signal due to thermal, electrical or physiological noise, as well as residual sources of neural noise. The distribution of ν is given by
| (2) |
| (3) |
Thus, ν describes noise specific to individual voxels (with variance τi2 for voxel i), as well as noise shared globally among voxels irrespective of their tuning properties (scaled by ρ). Population tuning curves (or basis functions) f(s) are half wave-rectified cosine functions, raised to the fifth power13
| (4) |
where φk is the preferred orientation of the kth population. Preferred orientations are equally spaced between 0–180°, with one basis function maximally tuned toward horizontal.
The conditional probability of a voxel activation pattern given a noisy population response (f(s) + η) is then defined as
| (5) |
Marginalizing over η results in
| (6) |
| (7) |
When developing the model, we considered four different, increasingly complex models. The current model was found to best capture the data on two relevant benchmark tests (Supplementary Fig. 2). Supplementary Table 1 provides an overview of all parameters.
Training and testing
Model parameters were estimated using the fMRI activation patterns for the orientation stimuli in a leave-one-run-out cross-validation procedure. Data were divided into a training data set (consisting of data from all but one fMRI run) and a testing data set (consisting of data from the remaining run). The average training data set consisted of 249 trials and 1,981 voxels. When training the model, we maximized the likelihood of the model parameters given the orientation stimuli. Model parameters were estimated in a two-step training procedure to constrain the number of free parameters and prevent overfitting of the covariance matrix. In the first step of this estimation procedure, we imposed a regularizing prior on the covariance matrix, assuming that σ = 0. This reduces the number of free parameters in the covariance matrix considerably (from ((K+1)M + 2) to (M + 2)), but results in a predictable underestimation of σ in the second step of the estimation procedure (see below), when we relaxed the prior on σ. However, simulations indicated that this did not seriously affect our ability to reconstruct the uncertainty present in the activation patterns (see Supplementary Fig. 9). Under the assumption that σ = 0, the maximum likelihood estimation of W is simplified to an ordinary least-squares (OLS) regression.
| (8) |
In the second step of the estimation procedure, we relaxed the regularizing assumption on σ, and maximized the likelihood of the remaining parameters (ρ, τ and σ), conditioned on Ŵ. This maximization step was performed numerically, using a Matlab implementation of the conjugate gradient method. The resulting parameter estimates are summarized in Supplementary Figure 10.
After fitting the model to the training data set, we tested the model on the held-out (independent) testing data set. By applying Bayes rule and using a flat stimulus prior (see below), we obtained for each test trial the posterior probability distribution over stimulus orientation given the fitted model parameters
| (9) |
where , and the normalization constant was computed numerically. The circular mean of the posterior served as an estimate of the presented stimulus orientation, and its circular s.d. as a measure of the degree of uncertainty in the orientation estimate. Both of these summary statistics were computed using numerical integration. The cross-validation procedure was repeated until each run served as a test run once, resulting in a single posterior probability distribution for each trial of BOLD activity.
The prior
Unlike our decoding algorithm, human observers appear to employ in their behavior a more naturalistic prior favoring cardinal orientations16. Would it have been more appropriate to apply such a non-uniform prior in our analyses? The answer to this question is negative. From a decoding perspective, a uniform prior correctly represents the a priori knowledge that all orientations were presented equally often in the current experiment. Had we instead used a prior favoring cardinal orientations, this would have (wrongfully) biased the decoder’s estimates toward horizontal and vertical orientations, and automatically changed the width of the posterior distribution for cardinal and oblique orientations, even when there was no evidence for an oblique effect in brain activity.
Behavioral data
The observer’s behavioral error on a given trial was computed as the acute-angle difference between the reported orientation and the presented orientation. Behavioral variability was calculated after correcting for an orientation-dependent shift in mean (Supplementary Fig. 6), by fitting a 4-degree polynomial to each observer’s behavioral errors as a function of stimulus orientation. We then used the residuals from this fit, i.e. the bias-corrected behavioral errors, in our calculation of behavioral variability.
In general, participants finished adjusting the probe’s orientation well before the end of the response window, taking on average 2,254 ± 47 ms (mean ± s.e.m.) to respond. On 0–6 trials (out of 180–324), the behavioral error exceeded the mean error (for that observer) by more than 3 s.d., suggesting that the participant randomly guessed the orientation of the grating. These trials were excluded from further analysis.
Eye tracking
Eye-tracking data were acquired for 12 of 18 subjects, using an SR Research Eyelink 1000 eye-tracking system. Gaze position was sampled at 1 kHz. After removing blinks, we applied a band-pass temporal filter with a low-frequency cut-off period of 100 s, and a high-frequency cut-off period of 0.1 s. Similar to all fMRI analyses, the mean and s.d. of eye position were computed for the time window corresponding to stimulus presentation. Specifically, with respect to mean eye position, we first calculated the average x- and y-coordinates of the gaze data during the first 4 s of each trial, and then took the absolute distance from this average (x, y) position to the central fixation target. Eye movement (that is, variability in eye position) was quantified by first calculating, for each sample of (x, y) gaze coordinates, the absolute distance to the mean (x, y) eye position. This distance was then averaged across the first 4 s of each trial.
Statistical procedures
Decoding accuracy was computed by taking, for each individual observer, the circular correlation coefficient between the presented and decoded orientations. This correlation coefficient was subsequently Fisher transformed and standardized to a Z-score across observers. Its (two-sided) P value was derived from the inverse cumulative normal distribution, and the average of the Fisher transformed values was converted back to the correlation scale for reporting.
Many of our analyses focused on the relationship between decoded uncertainty and across-trial error distributions. For these analyses, data were binned and summary statistics were computed for each bin. When testing for an oblique effect in BOLD activity, trials were sorted into four equally spaced bins of increasing angle between the stimulus orientation and the nearest cardinal axis (for illustrative reasons, Fig. 1b shows the data sorted into 12 equally spaced orientation bins). Behavioral variability was computed as the circular s.d. of all (bias-corrected) behavioral errors in each of the bins. When testing for the link between decoded uncertainty and behavioral variability or bias, trials were sorted into four bins of increasing decoded uncertainty. Behavioral variability was computed as the circular s.d. of all (bias-corrected) behavioral errors in each of the bins, while behavioral bias was calculated as the mean of all (biased) behavioral errors in the bins. We used the same number of bins for each participant (four), with a constant number of samples across bins within each participant. To test whether decoded uncertainty was correlated with the variable of interest, we calculated partial correlation coefficients via a multiple linear regression analysis. Independent variables were distance to cardinal axis (Fig. 1b–d and Supplementary Fig. 1d–f) and decoded uncertainty (Fig. 1c,d and Supplementary Fig. 1c,e–f). All regression analyses furthermore included subject-specific intercepts to remove between-subject variability. Dependent variables were decoded uncertainty (Fig. 1b and Supplementary Fig. 1d), behavioral variability (Fig. 1b,c and Supplementary Fig. 1e), and behavioral bias (Fig. 1d and Supplementary Fig. 1f). The significance of individual regression coefficients was assessed with a (two-sided) t test. We verified that the residuals of all regression analyses were independent (Durbin-Watson test) and normally distributed (Anderson-Darling test), and that our results were not affected by violations of homoscedasticity. For ease of exposition, regression coefficients were standardized to partial correlation coefficients, and in Figure 1c,d, data are displayed in the form of partial residual plots, showing the partial relationships of interest and residuals obtained from the regressions (but omitting any effects of the variables-of-no-interest, as well as between-subject differences in intercept).
Code availability
Custom code written in Matlab is available on request.
Supplementary Material
Acknowledgments
We thank S. Ling for valuable comments and discussion, K. Ambroziak for help with data collection, C. Beckmann for advice on statistical analyses, and P. Gaalman for MRI support.
Footnotes
Note: Any Supplementary Information and Source Data files are available in the online version of the paper.
AUTHOR CONTRIBUTIONS
R.S.v.B., W.J.M. and J.F.M.J. conceived and designed the experiments. R.S.v.B. collected data. R.S.v.B. analyzed data, with help from W.J.M., M.S.P. and J.F.M.J. R.S.v.B., W.J.M., M.S.P. and J.F.M.J. wrote the paper.
COMPETING FINANCIAL INTERESTS
The authors declare no competing financial interests.
A Supplementary Methods Checklist is available.
References
- 1.Ernst MO, Banks MS. Nature. 2002;415:429–433. doi: 10.1038/415429a. [DOI] [PubMed] [Google Scholar]
- 2.Körding KP, Wolpert DM. Nature. 2004;427:244–247. doi: 10.1038/nature02169. [DOI] [PubMed] [Google Scholar]
- 3.Ma WJ, Beck JM, Latham PE, Pouget A. Nat Neurosci. 2006;9:1432–1438. doi: 10.1038/nn1790. [DOI] [PubMed] [Google Scholar]
- 4.Jazayeri M, Movshon JA. Nat Neurosci. 2006;9:690–696. doi: 10.1038/nn1691. [DOI] [PubMed] [Google Scholar]
- 5.Vilares I, Kording K. Ann N Y Acad Sci. 2011;1224:22–39. doi: 10.1111/j.1749-6632.2011.05965.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Pouget A. Nat Neurosci. 2013;16:1170–1178. doi: 10.1038/nn.3495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Fetsch CR, Pouget A, DeAngelis GC, Angelaki DE. Nat Neurosci. 2012;15:146–154. doi: 10.1038/nn.2983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Beck JM, et al. Neuron. 2008;60:1142–1152. doi: 10.1016/j.neuron.2008.09.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Barthelmé S, Mamassian P. Proc Natl Acad Sci USA. 2010;107:20834–20839. doi: 10.1073/pnas.1007704107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Kamitani Y, Tong F. Nat Neurosci. 2005;8:679–685. doi: 10.1038/nn1444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Haynes JD, Rees G. Nat Neurosci. 2005;8:686–691. doi: 10.1038/nn1445. [DOI] [PubMed] [Google Scholar]
- 12.Jehee JFM, Brady DK, Tong F. J Neurosci. 2011;31:8210–8219. doi: 10.1523/JNEUROSCI.6153-09.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Brouwer GJ, Heeger DJ. J Neurophysiol. 2011;106:2108–2119. doi: 10.1152/jn.00540.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Serences JT, Saproo S, Scolari M, Ho T, Muftuler LT. Neuroimage. 2009;44:223–231. doi: 10.1016/j.neuroimage.2008.07.043. [DOI] [PubMed] [Google Scholar]
- 15.Appelle S. Psychol Bull. 1972;78:266–278. doi: 10.1037/h0033117. [DOI] [PubMed] [Google Scholar]
- 16.Girshick AR, Landy MS, Simoncelli EP. Nat Neurosci. 2011;14:926–932. doi: 10.1038/nn.2831. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Huttenlocher J, Hedges LV, Duncan S. Psychol Rev. 1991;98:352–376. doi: 10.1037/0033-295x.98.3.352. [DOI] [PubMed] [Google Scholar]
- 18.Jazayeri M, Movshon JA. Nature. 2007;446:912–915. doi: 10.1038/nature05739. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Stocker AA, Simoncelli EP. Adv Neural Inf Process Syst. 2008;20:1409–1416. [PMC free article] [PubMed] [Google Scholar]
- 20.Wei XX, Stocker AA. Nat Neurosci. 2015;18:1509–1517. doi: 10.1038/nn.4105. [DOI] [PubMed] [Google Scholar]
- 21.Kok P, Jehee JFM, De Lange FP. Neuron. 2012;75:265–270. doi: 10.1016/j.neuron.2012.04.034. [DOI] [PubMed] [Google Scholar]
- 22.Ester EF, Anderson DE, Serences JT, Awh E. J Cogn Neurosci. 2013;25:754–761. doi: 10.1162/jocn_a_00357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Brainard DH. Spat Vis. 1997;10:433–436. [PubMed] [Google Scholar]
- 24.Pelli DG. Spat Vis. 1997;10:437–442. [PubMed] [Google Scholar]
- 25.Sereno MI, et al. Science. 1995;268:889–893. doi: 10.1126/science.7754376. [DOI] [PubMed] [Google Scholar]
- 26.DeYoe EA, et al. Proc. Natl Acad Sci USA. 1996;93:2382–2386. doi: 10.1073/pnas.93.6.2382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Engel SA, Glover GH, Wandell BA. Cereb Cortex. 1997;7:181–192. doi: 10.1093/cercor/7.2.181. [DOI] [PubMed] [Google Scholar]
- 28.Jenkinson M, Bannister P, Brady M, Smith S. Neuroimage. 2002;17:825–841. doi: 10.1016/s1053-8119(02)91132-8. [DOI] [PubMed] [Google Scholar]
- 29.Fischl B, Sereno MI, Dale AM. Neuroimage. 1999;9:195–207. doi: 10.1006/nimg.1998.0396. [DOI] [PubMed] [Google Scholar]
- 30.Kay KN, Naselaris T, Prenger RJ, Gallant JL. Nature. 2008;452:352–355. doi: 10.1038/nature06713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Jehee JFM, Ling S, Swisher JD, van Bergen RS, Tong F. J Neurosci. 2012;32:16747–16753. doi: 10.1523/JNEUROSCI.6112-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Smith MA, Kohn A. J Neurosci. 2008;28:12591–12603. doi: 10.1523/JNEUROSCI.2929-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Goris RLT, Movshon JA, Simoncelli EP. Nat Neurosci. 2014;17:858–865. doi: 10.1038/nn.3711. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


