All-Systolic Non-ECG-gated Myocardial Perfusion MRI: Feasibility of Multi-Slice Continuous First-Pass Imaging

Abstract

Purpose

To develop and test the feasibility of a new method for non-ECG-gated first-pass perfusion (FPP) cardiac MR capable of imaging multiple short-axis slices at the same systolic cardiac phase.

Methods

A magnetization-driven pulse sequence was developed for non-ECG-gated FPP imaging without saturation-recovery preparation using continuous slice-interleaved radial sampling. The image reconstruction method, dubbed TRACE, employed self-gating based on reconstruction of a real-time image-based navigator combined with reference-constrained compressed sensing. Data from ischemic animal studies (n=5) was used in a simulation framework to evaluate temporal fidelity. Healthy subjects (n=5) were studied using both the proposed and conventional method to compare the myocardial contrast-to-noise ratio (CNR). Patients (n=2) underwent adenosine stress studies using the proposed method.

Results

Temporal fidelity of the developed method was shown to be sufficient at high heart-rates. The healthy volunteers studies demonstrated normal perfusion and no artifacts. Compared to the conventional scheme, myocardial CNR for the proposed method was slightly higher (8.6±0.6 vs. 8.0±0.7). Patient studies showed stress-induced perfusion defects consistent with invasive angiography.

Conclusions

The presented methods and results demonstrate feasibility of the proposed approach for high-resolution non-ECG-gated FPP imaging and indicate its potential for achieving desirable image quality (high CNR, no dark-rim artifacts) with a 3-slice spatial coverage, all imaged at the same systolic phase.

Introduction

First-pass perfusion (FPP) cardiac MRI (1–4) is an emerging alternative to nuclear myocardial perfusion imaging as an accurate method for diagnosis of coronary artery disease (CAD); yet, it is plagued by technical challenges that have contributed to its limited role in clinical management of patients with suspected ischemic heart disease (5–7). In fact, FPP cardiac MRI is one of the most challenging dynamic MRI applications and the optimal FPP technique is not yet fully known (8–10). Although major technical improvements have been made over the past two decades (5,10), most notably parallel-imaging acceleration, current commercially available FPP methods still suffer from technical challenges including presence of common image artifacts, particularly the so-called subendocardial dark-rim artifact (DRA) (11–15) in addition to inadequate or unreliable image quality for vasodilator stress scans.

A major contributing factor for inadequate image quality in stress scans is that data acquisition in state-of-the-art FPP methods is typically synchronized with the electrocardiogram (ECG) signal, and thereby relies on nearly periodic and accurate ECG triggers. However, variations in heart rate are common during stress scans—even in relatively healthy subjects—and are particularly challenging in the growing population of CAD patients with chronic arrhythmia (16). Moreover, ECG tracing is often contaminated in the MRI environment, especially at 3T, due to magnetohydrodynamic effects (17). Non-ECG-gated cardiac MRI methods (18–22) simplify the data acquisition workflow and offer the potential for improved robustness to such factors.

In this work, we build upon our recent development of a single-slice, non-ECG-gated, “magnetization-driven” FPP technique (23,24) to develop and test a new FPP method that can image multiple 2-dimensional (2D) slices, all at the same systolic phase. FPP pulse sequences without magnetization preparation and instead using magnetization-driven (approximate steady state) generation of T1 contrast were first described twenty years ago (25) and have recently received significant interest (22–24,26). In particular, the work by DiBella et al. (22) was the first to show the feasibility of 3D steady-state gradient recalled echo (GRE) FPP imaging without ECG gating or saturation recovery (SR) magnetization preparation using a stack-of-stars radial sampling trajectory. More recently, we demonstrated the feasibility of accurately detecting ischemic myocardial regions with adequate myocardial contrast at high heart-rates using a single-slice 2D magnetization-driven approach (23,24).

In this study, phantom experiments and simulations based on ischemic animal studies are conducted for optimizing the pulse sequence and testing the temporal fidelity of the proposed accelerated FPP imaging scheme. In-vivo results comprising healthy volunteer scans and limited patient studies are presented to demonstrate the feasibility of the proposed all-systolic approach for non-ECG-gated FPP imaging. Our motivation for all-systolic FPP imaging is to improve visualization of perfusion gradients across myocardial layers, which may in turn enable more accurate detection of subendocardial hypoperfusion (16,27–29).

Methods

Pulse Sequence: Multi-slice magnetization-driven acquisition for FPP imaging

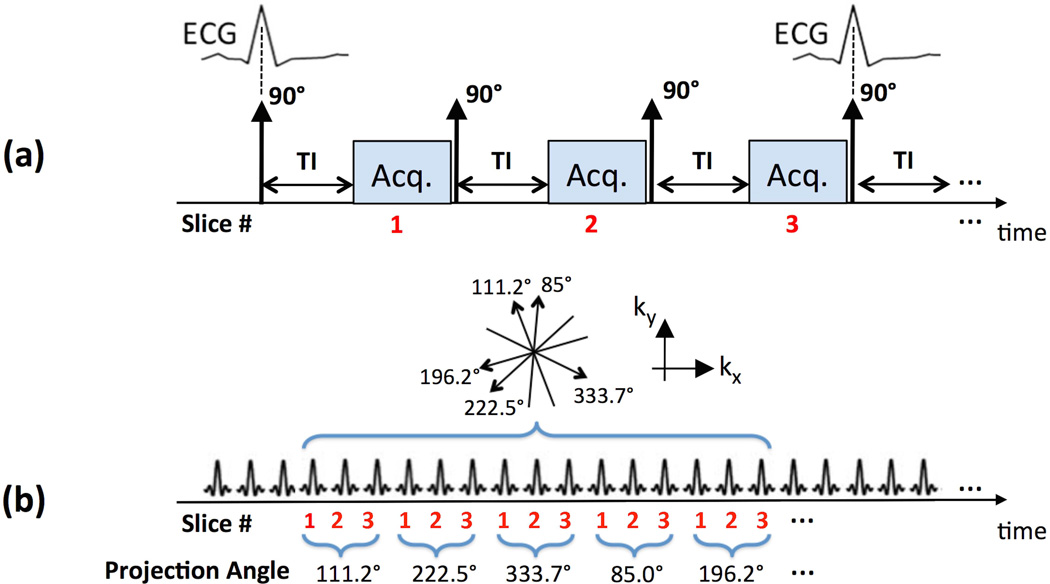
Our data acquisition approach in this work belongs to the class of “magnetization driven” FPP pulse sequences (22–25,30–32), which unlike conventional FPP approaches do not use a magnetization-preparation pulse (saturation/inversion recovery) and instead rely on the T1 contrast generated by the approximate steady-state following/during an RF pulse train. Based on our previously developed single-slice continuous FPP approach (23,24), a multi-slice RF-spoiled non-ECG-gated GRE pulse sequence was developed (30,32), capable of acquiring multiple short-axis slices in a continuous slice-interleaved fashion along a golden-ratio radial k-space trajectory (111.246° angular spacing between consecutive radial readouts). The sequence is demonstrated in Fig. 1, which also highlights the main differences of the proposed acquisition scheme compared with the SR-prepared “conventional FPP” pulse sequence. In the conventional scheme shown in Fig. 1(a), 3 short-axis slices are acquired using a GRE readout, synchronized with the ECG gating signal at a pre-defined TI time (≈100 ms), along an undersampled Cartesian trajectory and reconstructed using parallel imaging. As shown in Fig. 1(b), our proposed acquisition scheme, referred to as “continuous FPP,” acquires the FPP data for 3 short-axis slices without needing or recording the ECG signal or other forms of cardiac synchronization. Throughout this work, an image matrix of size 160×160 pixels is prescribed for the in-vivo continuous FPP scans with an isotropic in-plane resolution of 1.4 × 1.4 mm and slice thickness of 10 mm.

Figure 1.

Data acquisition schemes for (a) conventional FPP imaging, and (b) the proposed non-ECG-gated continuous multi-slice FPP imaging scheme. (a): Schematic for a conventional SR-prepared ECG-gated GRE acquisition; typically, 3 slices are acquired, synchronized with the ECG gating signal, at a pre-defined TI time along an undersampled Cartesian k-space trajectory and reconstructed using parallel imaging. (b): Schematic for the proposed “magnetization driven” multi-slice continuous FPP scheme using a non-ECG-gated RF-spoiled GRE pulse sequence with golden-angle continuous radial sampling (111.246° angular spacing between consecutive projections). Three short-axis slices are acquired without ECG gating and continuously with the projections acquired in a slice-interleaved order. No external ECG signal or other forms of cardiac synchronization is needed/recorded for the proposed method.

Pulse Sequence: Choice of flip angle for optimal CNR performance

In the proposed pulse sequence, the same flip angle (FA) and repetition time (TR) is used for all readouts. In designing the pulse sequence, we seek to optimize the FA while using a short TR to enable fast imaging. The goal of the optimization is to maximize the myocardial contrast-to-noise (CNR) in line with the diagnostic task in FPP imaging, which is to delineate normal and hypoperfused tissue. We have recently shown, based on simulations and in-vivo experiments, that α = 14° is a near-optimal FA choice for achieving desirable CNR in single-slice 2D imaging at 3T with TR = 2.5 ms (24). For the 3-slice continuous FPP sequence (Fig. 1b), however, the effective TR experienced by each slice is 3 times longer than that of the single-slice sequence — implying that the optimal FA should be different. In fact, because of the higher TR, a higher optimal FA and a higher CNR value is expected for 3-slice imaging compared with single-slice acquisition (33).

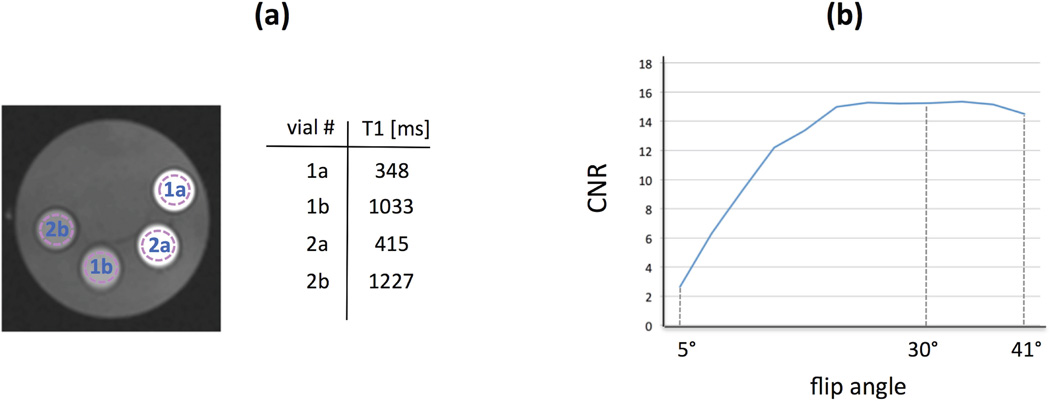
To find the optimal FA, we conducted a phantom study using the developed 3-slice continuous FPP sequence. Based on typical contrast concentrations in normal myocardium during the myocardial enhancement phase of the FPP scan (34), and given a longitudinal relaxivity constant of 4.5 mM⁻¹s⁻¹ for the gadolinium-based contrast agent, we assumed pre-contrast and peak-enhancement myocardial T1s at 3T to be: T1_pre ≈ 1050 ms and T1_peak ≈ 350 ms, respectively. We then constructed a phantom consisting of two pairs of vials as shown in Fig. 2(a), containing Gadolinium-doped saline with different contrast concentrations resulting in a pair of T1s close to the above-mentioned numbers (vials 1 and 3), and a second pair with slightly higher T1s (vials 2 and 4). These T1 values in each of the 4 vials were measured using a spin-echo T1 mapping sequence.

Figure 2.

Phantom studies for determination of the optimal flip angle (FA) in the 3-slice continuous acquisition scheme. (a): a view of the mechanical phantom (middle slice) consisting of 2 pairs of vials containing Gadolinium-doped saline with different contrast concentrations resulting in the listed T1 values (measured using a spin-echo T1 mapping sequence). The dotted circles show the selected ROIs in each vial. The phantom image shown here was acquired using the proposed pulse sequence (3-slice RF-spoiled FLASH sequence with TR = 8.0 ms) with FA=30°. (b): The CNR between the vials for the middle slice (averaged between pair 1 and pair 2) measured at different FAs using the proposed pulse sequence. Since the results in (b) show that higher FAs do not result in a noticeable loss in CNR and, in turn, are expected (assuming perfect RF spoiling) to minimize the loss of T1-weighting in case of steady-state perturbations, the relatively high FA = 30° was used in the subsequent in-vivo experiments.

Next, phantom scan data was acquired using the developed 3-slice continuous FPP pulse sequence (mid slice position is shown in Fig. 2a) for a wide range of FAs (from 5° to 41° in 3° increments) on a 3T clinical scanner (Magnetom Verio, Siemens Healthcare, Erlangen, Germany) using the following parameters: RF-spoiled FLASH sequence, echo spacing = 2.67 ms resulting in TR (for each slice) = 8.0 ms, TE = 1.38 ms; 160 × 160 matrix size with 160 projections per slice and regridding reconstruction, 1.6 × 1.6 mm² in-plane resolution, 10 mm slice thickness. A total of 1,160 projections were acquired continuously with the first 1,000 projections disregarded to ensure that steady-state was reached for all of the FA choices (including the low FAs). Also, the default RF pulse duration (400 µs for “Fast RF” mode) was increased to 600 µs in order to reduce the specific absorption rate (SAR) level for the continuous pulse sequence, thereby enabling prescription of high FAs (up to 41°). The CNR between a pair of vials was computed as the mean signal intensity (SI) difference in pre-selected regions of interest (ROIs; shown in Fig. 2a) divided by the standard deviation in the ROI of the vial with shorter T1. The measurements at different FAs (CNR for the middle slice averaged between the two pairs of vials) are plotted in Fig. 2(b) and showed that using a higher FA (up to 37°) would not lead to a noticeable CNR loss in this setting.

The above treatment assumed an exact steady-state condition for the longitudinal magnetization. In practice, cardiac MRI of a 2D short-axis slice involves through-plane motion and in-flow, which continually disrupt the steady state. Since the condition TE≪T2* generally holds in FPP imaging, the tissue SI following a train of n excitation pulses with FA = α can be expressed as:

$$\mathrm{S}{\mathrm{I}}_{\alpha }(T1)=M_0\text{sin}\alpha (f_z+(1-f_z){\left(e^{-\frac{TR}{T1}}\text{cos}\alpha \right)}^{n-1})$$ [1]

where M₀ is the equilibrium magnetization and f_z is the steady-state longitudinal magnetization in an RF-spoiled GRE sequence (assuming perfect RF spoiling). This derivation assumes that all readouts have equal contribution to the signal contrast, which is a reasonable approximation for radial sampling (since the central k-space region is sampled in each readout). According to Eq. [1], transition to steady-state is faster for the higher FAs. Specifically, it is easy to show that based on Eq. [1] with α=30° and starting from the initial condition of M₀, it only takes n=24 pulses (duration: 192 ms with TR = 8 ms) to reach ≈90% of steady-state CNR between two tissue regions with T1_pre ≈ 1050 ms and T1_peak ≈ 350 ms (assuming the same noise level for the two regions).

Therefore, since higher FAs are theoretically expected to have the desirable property of reduced T1-weighting loss in case of steady-state perturbations, we selected a relatively high FA of 30° in the subsequent in-vivo experiments. This choice was based on the following two empirical observations: (a) the phantom experiments (described above) indicate that FA = 30° yields a near-optimum CNR; (b) in our hardware setting (3T Verio Scanner), FA = 30° did not raise SAR-limit issues in the in-vivo studies (with TR = 8.0 ms). In the final step of the phantom studies, we compared the CNR (mid slice) for the proposed method with FA=30° and the conventional SR-prepared sequence (TI = 100 ms, Cartesian sampling without parallel imaging and otherwise similar parameters as above). The measured CNR (pair 1) was 13.2 for the conventional method and 14.9 for the proposed 3-slice continuously sampled sequence.

Image Reconstruction: Automatic image-based systolic self-gating

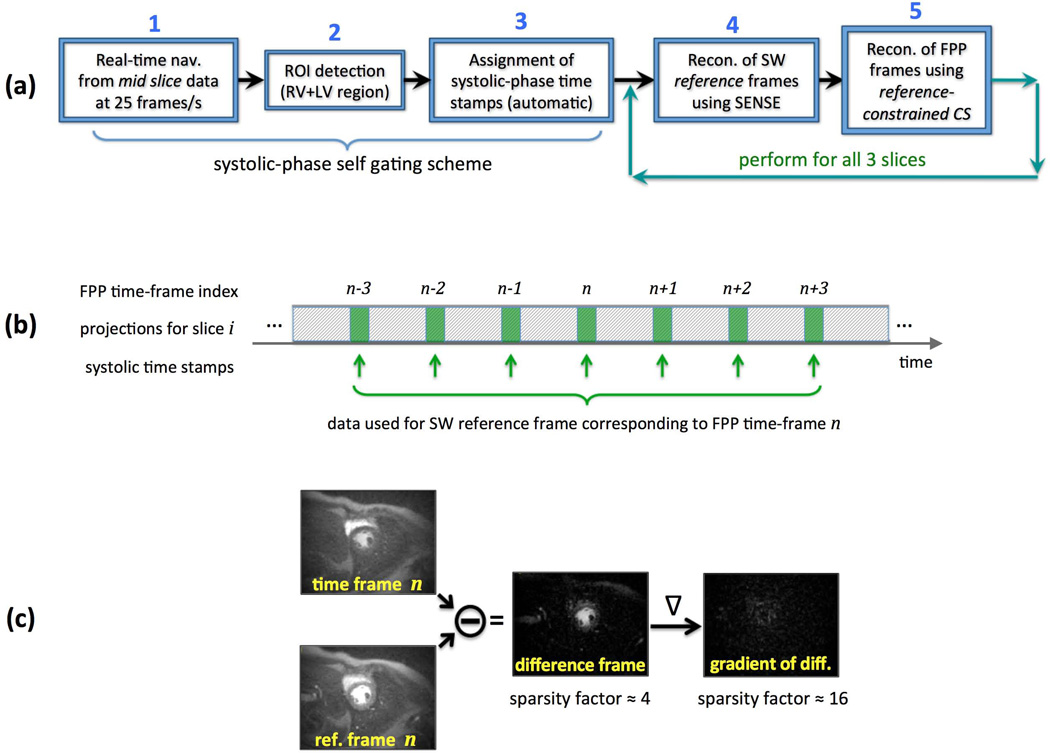
An overview of the image reconstruction procedure is presented in Fig. 3(a). The reconstruction goal in Step 1 is to retrospectively generate an image-based navigator with high temporal resolution from the acquired continuously-sampled FPP data that captures the cardiac motion in real time, referred to as the “real-time nav.” The cardiac phase information is then extracted from this real-time nav and is used to enable systolic self-gating. To this end, following eigen-based coil profile estimation from the time-averaged data (35), a low-resolution reconstruction is performed for the mid-ventricular slice at a rate of 25 frames/second without temporal acceleration (i.e., no data is shared between consecutive frames). Specifically, each frame of the real-time nav is reconstructed from only 8 projections using non-Cartesian SENSE implemented as a conjugate gradient (CG) algorithm (36). The reconstruction is performed with a 5-projection sliding window (duration: 40 ms, given that TR is 8 ms) yielding the 25 reconstructed frames per second. To reduce the streaking artifacts resulting from the extreme undersampling rate, very few CG-SENSE iterations were performed for each frame (at the cost of image blurring) by using the following CG stopping criterion: <4% change in 2-norm of the solution between consecutive CG iterations. Furthermore, the generated image series for the real-time nav (1000 frames for a 40-second scan) was filtered using a nonlinear edge-preserving filter in a post-processing step to further reduce streaking (37). Although the resulting image series has poor image quality (low effective resolution due to blurring and residual streaking), it contains sufficient cardiac phase information (systole vs. diastole) needed for the next step of the reconstruction procedure (example images are shown in Results).

Figure 3.

(a): Overview of the proposed image reconstruction scheme; In Step 1, a low-resolution 2D image-based navigator is generated from the acquired projection data of the mid-ventricular slice capturing the cardiac motion in real time at a frame rate of 25 frames/s, hence the short-hand “real-time nav”; ROI detection in Step 2 and systolic-phase time stamps in Step 3 are automatically generated without the need for ECG signal; Following systolic-phase self gating, in Step 4 a set of sliding window (SW) “reference frames” are reconstructed using CG-SENSE for each of the 3 slices; Finally, in Step 5, a reference-constrained CS reconstruction scheme, dubbed TRACE, is employed to reconstruct one systolic frame per heartbeat per slice. (b): Description of the scheme used for forming the SW reference frames. For FPP time-frame n, systolic-phase projection data (21 projections around the time stamps generated in Step 3) from 7 heartbeats (frame n−3 to frame n+3) is used for reconstruction of the corresponding SW reference frame. (c): An example for the improvement in sparsity factor after application of the difference operator followed by the gradient operator (image-domain finite differences). Sparsity of the difference frame (FPP time frame subtracted from the reference frame) and its gradient are exploited in the TRACE reconstruction technique (Step 5).

In Step 2, an automatic ROI detection algorithm is applied to isolate the heart region (including both ventricles) based on the following algorithm. First, a pixel-wise map of the standard deviation of SI changes over time is calculated from the first 20 seconds of the real-time nav images (generated in Step 1) after skipping the first 2 seconds (i.e., only using frames number 51 to 550). The heart region is expected to have the highest pixel value in the generated temporal standard-deviation map. Finally, a circular region with a 75 mm radius (54 pixels assuming a 1.4 mm pixel size) is found that has the maximum average intensity by exhaustive search of the (x, y) pixel coordinates of its center.

In Step 3, systolic-phase “time stamps” (one per each heartbeat; similar to R-wave tags in ECG-gated imaging) are automatically determined for the k-space data as follows. First, a 1D plot is generated by calculating the 2-norm of each real-time nav frame (Step 1) cropped to the detected ROI in Step 2. Then, a 3-piece cubic B-spline is fitted to the 1D plot using nonlinear least-squares fitting. Finally, the local minima in each of the detected intervals (intersection points with the spline curve) are identified as a systolic-phase time stamp. The same time stamps are applied to the k-space data for the other 2 slices, enabling selection of the same cardiac phase for all slices in the subsequent reconstruction steps (based on the slice-interleaved pulse sequence design in Fig. 1(b), time stamps for the 1^st and 3^rd slices differ by 2 × TR/3 ≈ 5 ms, which is negligible).

Image Reconstruction: Compressed sensing with data-adaptive sparsity transform

In Step 4 of the image reconstruction scheme (Fig. 3a), first the systolic-phase time stamps are used to extract radial k-space data that correspond to the systolic phase (at or close to end systole) for all 3 slices of the acquired non-ECG-gated continuous FPP dataset. Specifically, 21 projections are selected centered at the systolic-phase time stamp for each of the 3 slices (168 ms temporal footprint for each slice). The rest of the raw data is not used in the subsequent steps of image reconstruction. Next, a 7-heartbeat sliding window (SW) is used to reconstruct a set of “reference frames” using CG-SENSE for all 3 slices (CG stopping criterion: <1% change in 2-norm between consecutive iterations). Finally, in Step 5, a reference-constrained compressed sensing (CS) reconstruction algorithm is employed combined with non-Cartesian SENSE to reconstruct one systolic frame per heartbeat for each of the 3 slices (further explained in the next subsection). As described in Fig. 3(b), the SW reference frame used to constrain the CS reconstruction of the n-th dynamic FPP time-frame (n ≥ 4) uses a SW containing the following 7 heartbeat indices: {n−3, n−2, …, n, n+1, …, n+3}. The reference frames for the first/last 3 heartbeats use a SW that is shifted to the left/right as needed.

The proposed dynamic image reconstruction method is dubbed Time-varying Reference-constrained Adaptive Compressed-sensing with sensitivity-Encoding (TRACE) reconstruction. After forming the SW reference frames in Step 4, sparsity of the difference between the n-th dynamic time frame and the reference frame (called the “difference frame”) and its gradient (first-order finite differences) are exploited in the CS technique (Step 5). The schematic in Fig. 3(c) shows an example for the difference frame and the improvement in sparsity factor after application of a gradient operator to it. The optimization problem for the TRACE reconstruction scheme is formulated as follows:

$$\widehat{x_t}=\underset{x_t}{\text{argmin}}\{\frac{1}{2}\sum _{c=1}^{N_c}{\Vert y_{c;t}-A_t(S_c{x}_t)\Vert }_2^2+\lambda \mathrm{T}\mathrm{V}(x_t-r_t)+\eta {\Vert x_t-r_t\Vert }_1\}$$ [2]

where x_t is the unknown image for the time-frame that is being reconstructed, r_t is its corresponding SW reference frame (reconstructed in Step 4), A_t is the radial sampling operator based on the golden-ratio trajectory for the current time-frame, y_c;t and S_c are the k-space data and the coil sensitivity for c-th channel (c ranging from 1 to the total number of channels N_c), and (λ, η) are the reconstruction parameters (enabling trade-off of data fidelity vs. sparsity constraints). The operators ‖·‖₂, ‖·‖₁ denote the 2-norm and 1-norm of “vectorized” images, respectively. The term TV(x_t − r_t) denotes the total variation (TV) of the difference frame, further described in Appendix A.

Each of the sparsity constraints incorporated through the penalty terms in Eq. [2] is equivalent to a data-adaptive and time-varying sparsity transform. The TV term (weighted by λ) incorporates the prior knowledge that the difference between the unknown time-frame x_t and the time-varying SW reference frame r_t is piece-wise smooth; and the 1-norm term (weighted by η) incorporates the prior knowledge that, compared to r_t, the dynamic changes within the unknown time-frame x_t involve sparsely localized pixels. Of course, both of these constraints are weighted against the multi-channel data-fidelity term as noted in Eq. [2]. Optimization of the cost functional in Eq. [2] is implemented using an iteratively reweighted least-squares algorithm (38,39), with more details provided in Appendix A. The total acceleration factor (combined SENSE and CS) achieved in this step is 11.97 fold (if non-Cartesian sampling is ignored, the acceleration factor is 160/21 = 7.62 fold; considering the π/2 factor in the Nyquist criterion for radial sampling, the acceleration factor becomes 7.62 × π/2 = 11.97 fold).

Automatic optimization of reconstruction parameters remains an open problem in the general context of nonlinearly regularized imaging and in particular CS-based approaches – although several heuristics have been proposed (40,41). In this work, the two reconstruction parameters in Eq. [2] were selected based on visual inspection of the image quality and considering the temporal fidelity trade-offs (discussed in the next subsection). For our all of the in-vivo datasets, the acquired raw data was scaled prior to image reconstruction so that k-space samples had a maximum magnitude of 1 (same scaling factor for all slices and all readouts); the following reconstruction parameters were then used: λ = 5η = 0.001. It should be noted that: (i) while these parameter choices were fixed for all of the in-vivo studies, the sparsity transform itself is adapted to each scan and each frame (since the method employs a “data-adaptive transform” as noted above) and consequently the proposed CS scheme should be less sensitive to the specific choice of these parameters compared to CS schemes that use fixed/generic sparsity transforms; (ii) while these parameter choices performed desirably for our imaging platform at 3T (specifics described in the “Imaging Experiments” subsection), they may be suboptimal in case of 1.5T imaging. Regarding the latter issue, although our studies were limited to 3T imaging, we still expect the same parameter choices to perform well in case of 1.5T imaging (thanks to the data-adaptive scheme). However, if the hardware platform has a significantly lower capability for parallel-imaging (e.g., in case of an obsolete coil-array which may result in poor SENSE performance (36)), we expect that the optimal parameter choices will be larger (because of the need for higher temporal acceleration to compensate for the reduced parallel-imaging capability).

To eliminate ringing-induced dark-rim artifacts, the iterative radial SENSE reconstructions in Step 5 are apodized similarly to the method described in (15) for conventional FPP imaging with radial sampling. The resolution reduction factor (15) was 1.16 (widening of the full-width at half-maximum of the main lobe of the point spread function). This implies a reconstructed in-plane resolution of 1.6×1.6 mm given the acquired resolution of 1.4×1.4 mm (exact resolution analysis for nonlinear CS schemes is generally difficult and beyond the scope of this work).

Image reconstruction for the continuous FPP datasets was performed offline on a workstation (Processor: Intel Xeon-E5 2.7 GHz with 12 computational cores) in MATLAB (Mathworks, Natick, MA, USA). The total computation time using 12-fold parallel computation was approximately 78–94 minutes for a complete 3-slice Stress and Rest FPP study (the variability is due to the difference in the number of selected coil-array channels). All reconstructed images were converted to DICOM format using tags generated by the scanner software. Following each FPP scan, a simple scheme was developed to instantaneously generate a single “place-holder” image, which contained no diagnostic information but was sufficient to rapidly verify successful injection of the contrast bolus.

Simulation Studies: Testing of temporal fidelity using 1-slice ischemic animal studies

Given the high acceleration factor of the proposed FPP imaging scheme, it is desirable to test the temporal fidelity of the developed reconstruction scheme. One approach for evaluation of temporal fidelity is to reconstruct a similarly-acquired dataset, for which the “ground truth” is known, and compare the accelerated reconstruction to the ground truth. In our previous work on 2D continuous FPP imaging (24), we conducted single-slice continuous FPP ischemic dog studies using a simple frame-by-frame reconstruction method without any temporal acceleration (i.e., without any “sharing of data” between consecutive time frames). Here, we use those datasets to: (i) generate the frame-by-frame reconstruction, considered to be the ground truth; (ii) retrospectively subsample the single-slice projection data by 3 fold to “simulate” the 3-slice continuous FPP acquisition scheme; (iii) reconstruct the 3-fold subsampled data using the proposed accelerated scheme and compare it to the ground truth.

Specifically, n=5 canines were studied in a 3T clinical scanner (1-slice imaging, TR = 2.54 ms, FA = 14°). One dog was studied as a control and the other 4 had reversible ischemia (induced within the MR scanner) in the left anterior descending (LAD) artery territory during the FPP scan (24), using a contrast dose of 0.05 mmol/kg. The average heart rate for ischemic dogs was 92±21 beats per minute. Images were reconstructed according to the 5-step procedure summarized in Fig. 3(a) using 21 projections from each heartbeat to reconstruct systolic frames for the 5 FPP studies (TR = 7.62 ms). The “ground truth” reconstruction from the fully sampled data (TR = 2.54 ms) was performed on a frame-by-frame basis using CG-SENSE from 3×21=63 projections (same exact acquisition time window as the 3-fold undersampled reconstruction) without any temporal acceleration. For comparison, a simple 7-heartbeat SW reconstruction (resembling the reference frames used in the TRACE scheme) was also performed.

For evaluation of temporal fidelity, ROIs were placed in the left-ventricular (LV) bloodpool and “normal” myocardium (excluding the ischemic region) of each reconstructed image series and the resulting SI curves were extracted. Compared to the normal myocardium, the LV bloodpool SI has a significantly faster dynamics (steeper slope) and therefore was chosen as the primary marker for evaluation of temporal fidelity. In contrast, the ischemic myocardial SI has slow dynamics and was therefore not used (since even a method with poor temporal fidelity will likely capture the slow dynamics). For quantitative comparison of the SI time curves, only the upslope portion of the 1D curve (first 13–15 frames) was considered. In addition to the SI slope comparison (measured using a least-squares line fit), the root-mean-squared error for the subsampled reconstruction was measured relative to the ground-truth SI time-curve and was normalized by the difference between peak SI and baseline SI of the ground-truth curve.

Imaging Experiments: Healthy volunteers studies with comparison to conventional FPP

A total of 10 FPP studies were conducted in 5 healthy volunteers (mean age: 27±4 years; 3 females) using the same 3T scanner (standard vendor-provided 12-channel cardiac-torso coil array) to test the feasibility of the proposed all-systolic 3-slice FPP scheme and compare its CNR performance to the conventional FPP method. To avoid the confounding effects of residual contrast on the CNR comparisons when multiple FPP scans are performed in a single study, a 2-day study protocol was used with only one FPP scan performed on each day. For the first 4 volunteers, resting FPP data was acquired on the first day using the proposed continuous FPP sequence in 3 short-axis slices (apical, mid ventricular, and basal positions) using the following parameters: FA = 30° using the same RF pulse duration as in the phantom studies and an integrated 3-second post-scan “delay” to circumvent the SAR limit warnings, TR (for each slice) = 3 × 2.67 ms = 8.0 ms, TE = 1.38 ms; 160×160 matrix size, 1.4×1.4 mm² acquired in-plane resolution, 10 mm slice thickness. For comparison, a conventional FPP scan was also acquired on another day (7–12 days later) using the following parameters: 3-slice SR-prepared ECG-gated FLASH, FA = 12°, TI = 100–110 ms, Cartesian sampling with parallel imaging rate 2 [TGRAPPA (42)], resolution: 2.8×2.0 mm², slice thickness: 10 mm, TR/TE = 2.6/1.4 ms. For the 5^th volunteer, the study was performed with the same protocol during adenosine stress [standard infusion of 140 µg/kg/min of Adenoscan (Astellas Pharma, Northbrook, IL, USA) for ≈160 seconds]. The acquisition start time for the stress scan was 2 minutes after start of adenosine infusion. In all FPP studies, the contrast injection dose (gadoversetamide, Mallinckrodt, Hazelwood, MO, USA) was 0.05 mmol/kg, and a 40-second breathhold scan was conducted by continuously acquiring 15,000 projections (i.e. 5000 per slice). For testing purposes, the ECG signal was logged (independent of the pulse sequence) during the continuous FPP scan. In 3 of the 4 resting volunteer studies, the heart-rate information from a pulse oximeter (MR-compatible infra-red sensor) was also recorded during the continuous scan.

For the CNR measurement scheme, using a DICOM viewer (Osirix, Pixmeo, Switzerland), a fixed ROI was placed in the septal myocardium for all time frames (mid ventricular slice). Next, the image with peak myocardial SI (measured from the ROI) was selected as the “peak enhancement” frame, and the first image showing LV bloodpool enhancement was selected as the “pre contrast” frame. The apparent CNR (in short referred to as CNR) was calculated as the difference between the mean myocardial SI for the pre-contrast and peak-enhancement frames divided by the estimated noise standard deviation (computed as the standard deviation of the myocardial SI in the ROI). In addition to CNR quantification, the images were qualitatively reviewed by 2 readers in consensus for presence of perfusion defects or image artifacts in the myocardium, including DRA and streaking.

Imaging Experiments: Stress/Rest studies in CAD patients

Adenosine stress myocardial perfusion MRI was performed in 2 patients with no history of prior myocardial infarction using the same protocol (same hardware and acquisition specifications) as described in the previous subsection. The first patient had CAD based on prior invasive coronary angiography (performed before the MRI study with no intervening intervention). The stress scan in this patient was followed by a rest FPP scan (15-minute gap) and a delayed enhancement study (after an additional 0.1 mmol/kg contrast injection). The second patient underwent a stress-only FPP study (no delayed enhancement study), which was followed up 3 weeks later by invasive angiography that demonstrated the presence of significant CAD.

Results

Image-based systolic self gating

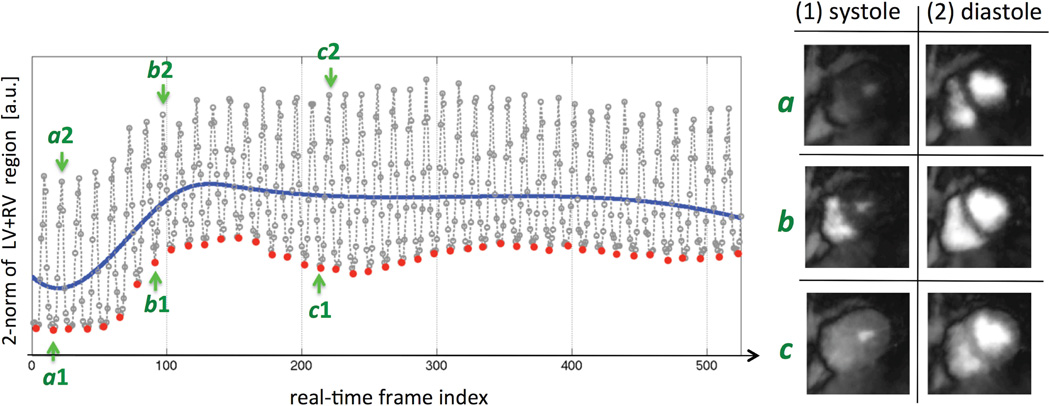
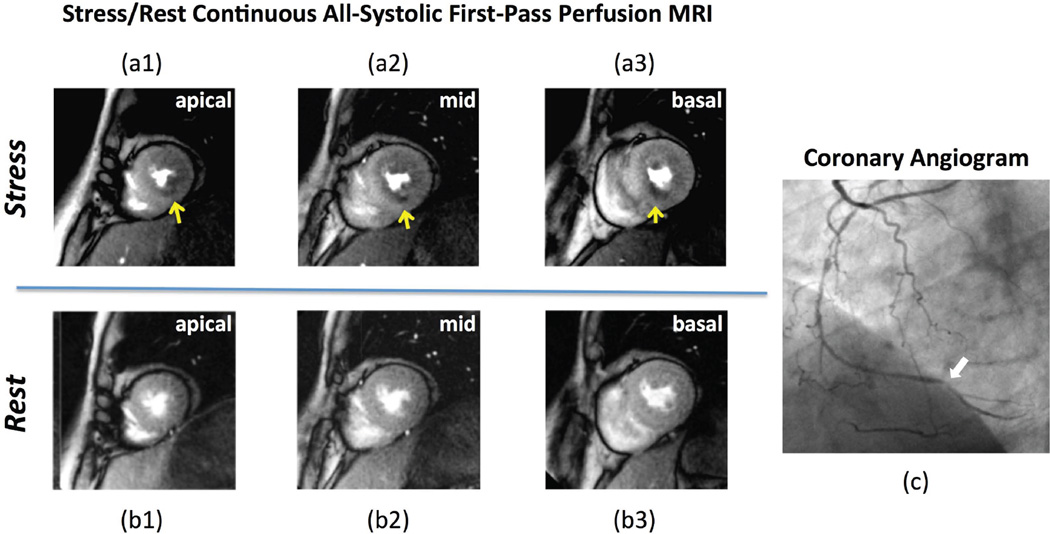
Figure 4 shows an example result for the automatic systolic-phase detection algorithm in Step 3 of the image reconstruction scheme (Fig. 3a), corresponding to a stress FPP scan in the first patient (the same case as the one presented in Fig. 8). The left panel demonstrates the 2-norm time curve generated from the 25 frame/s real-time nav image series (Step 1) measured within the automatically-detected ROI (Step 2). The fitted 3-piece cubic B-spline is the blue curve superimposed on the plot, and the systolic time stamps are highlighted as red dots. The right panel shows the corresponding real-time nav images (generated in Step 1 of the reconstruction procedure) at 3 different points of the time curve shown on the left. The logged ECG signal was corrupted with severe noise (due to interference/artifacts caused by a combination of rapid RF excitation with a relatively high FA combined with fast switching gradients needed for continuous golden-angle encoding) leading to poor R-wave detection and was therefore not useful for testing the accuracy of beat-by-beat cycle period measured based on the self-gating scheme. However, the mean cardiac-cycle period recorded by the pulse oximeter (averaged during the 40-second continuous FPP scan) was compared to the measurement based on the systolic self-gating result and showed a close match (difference range for the 3 scans: −27 ms to +34 ms).

Figure 4.

(Left): Example result for the automatic systolic-phase detection algorithm in Step 3 of the image reconstruction scheme, corresponding to a stress FPP scan in a CAD patient (the case presented in Fig. 8). The 1D plot is generated by calculating the 2-norm of the real-time nav reconstructed in Step 1 (frame rate: 25 frames/s) cropped to the automatically-detected ROI in Step 2 of the reconstruction scheme (consisting of both the left and right ventricles). Then, a 3-piece cubic B-spline curve (blue curve) is fitted to this 1D plot using nonlinear least-squares fitting, and the local minima in each of the detected intervals (intersection points with the blue spline curve) are identified as systolic-phase “time stamps” (red dots). The result is one systolic-phase time stamp per heartbeat, similar to R-wave tags in ECG-gated imaging but corresponding to the systolic phase. (Right): The corresponding real-time nav images generated in Step 1 of the reconstruction procedure at 3 different points in the 1D time curve shown on the left.

Figure 8.

(a,b): Stress/rest myocardial perfusion MR images, and (c) coronary angiogram in a patient with a history of CAD with multiple coronary artery stents. First-pass perfusion MRI was performed using the proposed non-ECG-gated all-systolic continuous FPP scheme. The stress-induced perfusion defects (yellow arrows) are consistent with the angiogram, which shows a subtotal chronic occlusion of the distal right coronary artery (RCA) highlighted by the white arrow in (c). The angiogram showed that the RCA after the subtotal occlusion was filled by collaterals through the left circumflex artery. Transmural gradients for the hypoperfused subendocardium in the stress scan are clearly visualized along the inferior wall for all 3 slices (yellow arrows). No subendocardial dark-rim artifact is observed. The rest perfusion is normal. Delayed enhancement images (not shown) demonstrated no evidence of myocardial infarction.

Evaluation of temporal fidelity

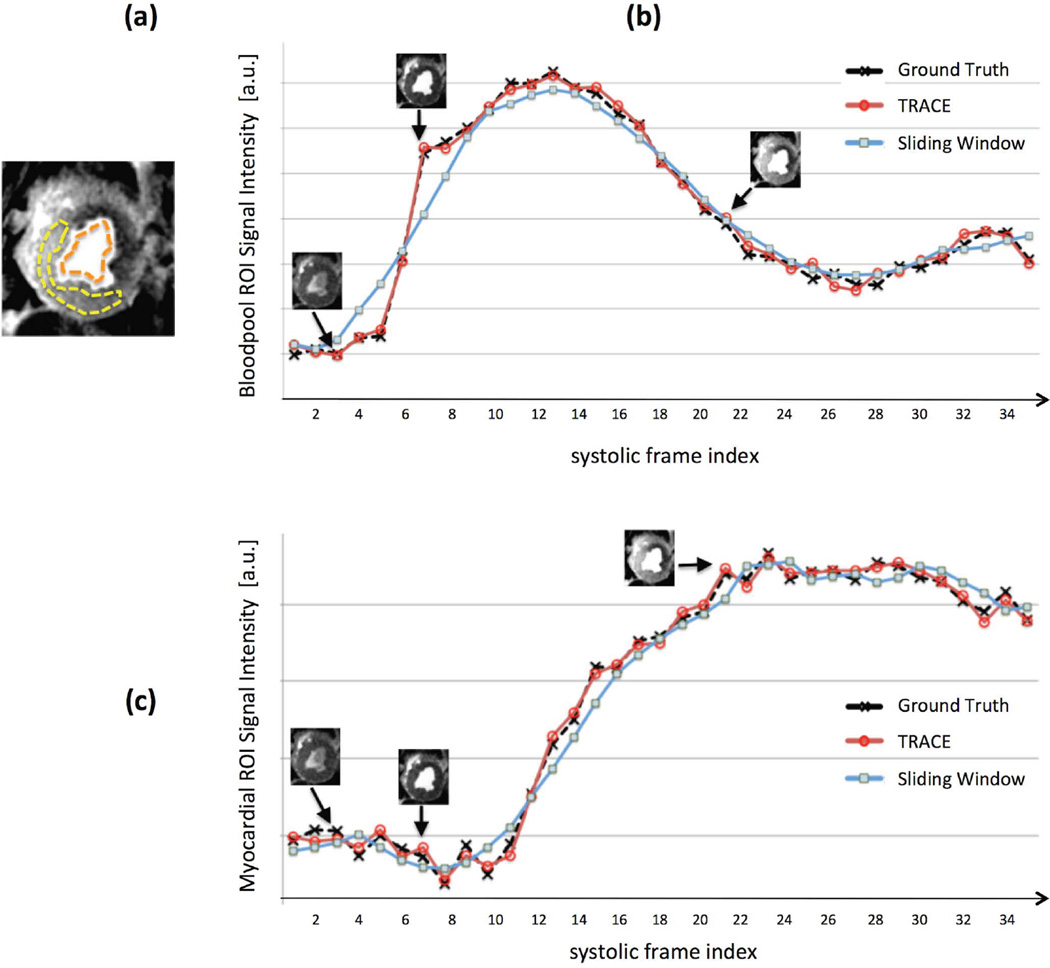
Figure 5 describes the results of the temporal fidelity testing scheme using retrospective projection undersampling to simulate 3-slice imaging. Panel (a) shows an example case for the single-slice ischemic dog studies (LAD stenosis) with the selected LV bloodpool and myocardial ROIs. For the same study, Figs. 5(b,c) demonstrate the bloodpool and myocardial SI time-curves corresponding to the ground-truth reconstruction from fully-sampled data, and two reconstructions from 3-fold undersampled data using: (i) the proposed TRACE reconstruction method; (ii) the 7-heartbeat SW reconstruction. The SI time curves corresponding to the proposed TRACE reconstruction scheme closely matched the ground-truth curves in all of the n=5 studied dogs (normalized error: 1.7% ± 0.4% for bloodpool ROI and 2.6% ± 0.5% for myocardial ROI). However, the SW reconstruction performed poorly as expected (normalized error: 10.2% ± 3.0% for bloodpool ROI and 8.4% ± 1.8% for myocardial ROI). The SI upslopes in the myocardial ROI behaved similarly (normalized error: 1.5% ± 0.4% for TRACE vs. 10.8% ± 3.2% for the SW reconstruction).

Figure 5.

Description of the temporal fidelity testing scheme using retrospective projection undersampling to simulate 3-slice imaging. (a): Peak-enhancement FPP image corresponding to an example case of the single-slice ischemic dog studies (LAD stenosis); the selected ROIs in the LV bloodpool and myocardium are shown. (b): Signal intensity time-curves for the bloodpool (mean intensity in the ROI) corresponding to the same ischemic dog, where the “ground truth” curve corresponds to the frame-by-frame reconstruction from the fully-sampled data using CG-SENSE; the other two curves correspond to reconstructions from 3-fold undersampled data (same temporal foot-print as the ground-truth reconstruction) using the proposed TRACE reconstruction method and also a simple sliding-window (SW) reconstruction (CG-SENSE using data from a 7-heartbeat SW). (c): Corresponding time-curves for myocardial signal intensity (mean intensity in the ROI). In all studied animals (n=5), the up-slope portion of the time-curves closely matched the ground-truth for the proposed scheme but showed significant disagreement for the SW reconstruction in both ROIs.

Healthy volunteers studies with comparison to conventional FPP imaging

Results for a representative rest FPP study in a healthy volunteer is shown in Fig. 6. The top row (Panel a) shows the pre-contrast and peak myocardial enhancement phase for the 3 short-axis slices imaged using the proposed all-systolic non-ECG-gated continuous FPP scheme (first FPP study on this subject). The bottom row (Panel b) corresponds to the conventional ECG-gated FPP rest scan for the same subject (studied a week later). The measured CNR for the continuous FPP and conventional FPP image series were 8.1 and 7.3, respectively. Furthermore, comparing (a1-3) to (b1-3), it is seen that the apical and basal slices for the conventional scheme are in the diastolic phase — making it difficult to visualize the subendocardium. Also, the mid and basal slices exhibit mild-to-moderate DRAs. In comparison, no DRA is seen in the continuous FPP images in panel (a) and all slices are reconstructed in the same systolic phase, together enabling improved visualization of the subendocardial layer. The corresponding movies for this study are included as supporting videos in the online Supplementary Material (see the caption for Fig. 6).

Figure 6.

Results for a representative healthy volunteer rest study using the proposed 3-slice all-systolic continuous FPP acquisition and reconstruction scheme in comparison to the conventional ECG-gated SR-papered method (performed 7 days later). The first-pass perfusion movies corresponding to panels (a) and (b) are included as Supporting Videos S1a and S1b in the online Supplementary Materials, respectively. (a): Rest first-pass perfusion frames for the pre-contrast phase (initial LV bloodpool enhancement) and peak myocardial enhancement phase. (b): Corresponding conventional rest scan images for the same subject (studied a week later). The measured CNR for the continuous vs. conventional FPP results were 8.1 and 7.3, respectively. Comparing (a1-3) to (b1-3), it is seen that the apical and basal slices for the conventional scheme (b1,b3) are in the diastolic phase hence making it difficult to visualize the subendocardium (compared to a1,a3). In addition, the mid and basal slices for the conventional scheme (b2,b3) show mild/moderate DRA in the inferior and lateral segments (more severe DRAs are seen in the earlier frames), while no DRA is seen in the continuous FPP images.

Figure 7 demonstrates the results for adenosine stress study in the 5^th healthy volunteer. Similarly to Fig. 6, the pre-contrast and peak-enhancement images corresponding to the proposed method are shown in the top row (Panel a) and those corresponding to the conventional FPP method (separate study) are shown in the bottom row (Panel b). The measured CNR for the continuous vs. conventional FPP results were 9.6 and 8.9, respectively. Overall, among the 10 FPP studies (5 volunteers), the CNR for the continuous all-systolic FPP method on average was slightly higher than the conventional FPP scheme (8.6±0.6 vs. 8.0±0.7) — although no statistical analysis was possible due to the small sample size. All continuous FPP images from the 5 healthy volunteer subjects were of high quality (no DRA or streaking artifacts were observed in the myocardium) and all studies demonstrated normal myocardial perfusion. In contrast, among the conventional FPP results 5 out of 15 imaged slices contained mild to moderate DRA in the myocardial enhancement phase (details provided in captions of Figs. 6–7).

Figure 7.

Stress myocardial perfusion images in a healthy volunteer using both the continuous and conventional FPP schemes, studied on two separate days (8 days apart). (a): Adenosine stress FPP images at pre-contrast and peak myocardial enhancement phases for the 3 imaged short axis slices; (b): Corresponding stress FPP images using the conventional ECG-gated scheme for the same subject. The measured CNR in these two stress studies using the continuous vs. conventional FPP methods were 9.6 and 8.9, respectively.

Stress/Rest studies in patients with CAD

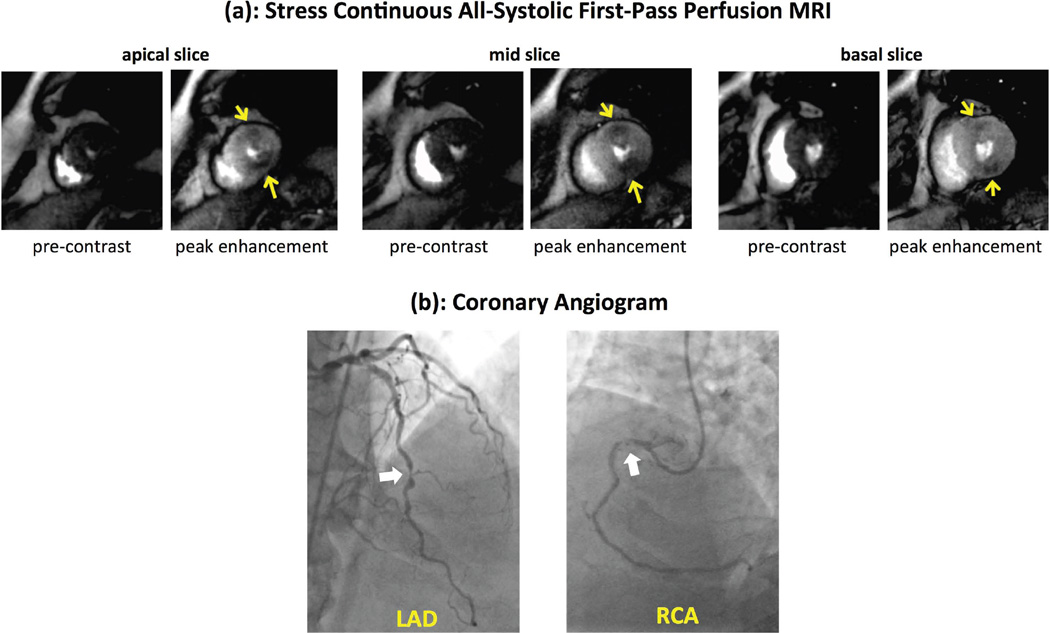
Figure 8 shows stress/rest myocardial perfusion MR images for the first patient with CAD obtained using the proposed all-systolic 3-slice continuous FPP scheme. Stress-induced perfusion defects are seen in the inferior wall, consistent with the subtotal chronic occlusion of distal right coronary artery (RCA) shown on the coronary angiogram (further details are included in the figure caption). The hypoperfused subendocardium is clearly visualized (arrows) for the stress images in the inferior wall for all 3 slices — owing to the two main features of the proposed non-ECG-gated method: all-systolic imaging and elimination of ringing-induced DRAs. The rest scan was normal, consistent with patient’s clinical history and normal delayed enhancement images obtained in the same MRI study. Figure 9 demonstrates the all-systolic stress myocardial perfusion images in the second patient. The observed stress-induced perfusion defects (arrows) are consistent with the coronary angiogram, which indicated significant stenoses in mid LAD coronary artery and a high-grade stenosis in the proximal RCA (further details are included in the figure caption). All images are DRA-free and excellent image contrast is observed between hypoperfused and normal myocardial territories. The average heart rate during stress FPP scans for the patient studies corresponding to Figs. 8 and 9 were 95 and 89 beats per minute, respectively.

Figure 9.

(a): Adenosine stress myocardial perfusion MR images at the apical, mid, and basal ventricular levels, and (b) coronary angiogram performed 3 weeks after the MRI study in a second CAD patient. MRI was performed using the proposed all-systolic non-ECG-gated approach. For each slice in (a), the left panel shows pre-contrast phase for the stress scan and the right panel shows the peak myocardial enhancement phase (no rest study was performed). The observed stress perfusion defects, highlighted by yellow arrows, are consistent with the angiographic images in (b), which show significant stenoses (≈70%) in mid LAD and a high-grade stenosis (≈90%) in proximal RCA (dominant vessel). All images are of high quality, specifically in terms of the myocardial contrast between hypoperfused vs. normal territories, and no subendocardial dark-rim artifact is seen.

Discussion

Stress first-pass perfusion (FPP) MRI has been shown to be an accurate method for assessment of the presence and extent of coronary artery disease (CAD). Its widespread acceptance in clinical practice, however, has been hindered by the technical complexity of the examination and artifactual or unreliable image quality, especially in the subendocardial layer. In this work, we demonstrate the feasibility of an innovative non-ECG-gated FPP imaging technique with continuous radial sampling enabling multi-slice all-systolic myocardial perfusion MRI. Initial results in healthy volunteers and two CAD patients indicate the potential of this approach for reducing the complexity of FPP imaging (non-ECG-gated acquisition with fixed sequence parameters) and improving its accuracy for assessment of subendocardial perfusion (high-resolution all-systolic imaging with minimized dark-rim artifacts). The latter also implies the potential for accurate visualization of perfusion gradients across myocardial layers, which is of particular importance in cases of multi-vessel CAD (29,43) and microvascular coronary dysfunction (44,45).

Benefits of systolic myocardial perfusion imaging have been recently recognized in the context of 3D ECG-gated FPP imaging (16,29,46). However, the need for cardiac gating in such approaches imposes practical difficulties and potentially reduces the diagnostic performance in patients undergoing stress MRI studies for assessment of CAD. Following our initial reports (30,32), the in-vivo results presented in this work are the first demonstration of a magnetization-driven FPP method capable of imaging multiple 2D slices at the same systolic phase without needing to acquire an ECG signal or other forms of cardiac synchronization. Our results show that the proposed continuously-sampled method can yield high-resolution images for 3 short-axis slices (Figs. 6–7), and stress-induced perfusion defects for the studied CAD patients can be clearly visualized with desirable CNR (Figs. 8–9). The absence of dark-rim artifacts can be attributed to apodization of k-space data, which eliminates ringing-induced (Gibbs effect) artifacts for radial imaging (15,24).

Our results demonstrate that the developed TRACE (data-adaptive compressed sensing) image reconstruction scheme achieves sufficient temporal fidelity (in ischemic animal studies with average heart rate of 92 beats per minute), and can produce dark-rim-free images for all 3 imaged slices, all while achieving similar or slightly better CNR compared to the conventional FPP approach. Another potential advantage of the method compared to other ECG-gated (whether conventional or accelerated 2D/3D methods) and alternative SR-prepared non-ECG-gated FPP methods is that it can guarantee one systolic frame per heartbeat for all slices regardless of how the heart-rate will change during the stress/rest scans and whether arrhythmia is present or not. It should, however, be noted that significant arrhythmia, e.g., an ectopic beat, may reduce the image quality of the corresponding reconstructed frame (because of increased cardiac motion during the 168 ms temporal footprint for each slice). Despite the multiple advantages of non-ECG-gated perfusion imaging (laid out in Introduction), acquisition of ECG signal is needed for conventional comprehensive cardiac MRI protocols, specifically for imaging of myocardial function and viability. The proposed method, however, can be considered as a stepping stone towards a fully non-ECG-gated comprehensive exam.

Compared to our proposed technique, the non-ECG-gated radial FPP method by DiBella et al. in (22) employed a 3D steady-state GRE pulse sequence based on an undersampled stack-of-stars trajectory (with lower flip angle) and a different image reconstruction approach. It remains to be seen how such 3D steady-state imaging approach compares to multi-slice 2D magnetization-driven imaging presented in this work. However, as the authors in (22) point out, the temporal footprint for their 3D method (≈310 ms) is likely too slow for high heart-rates observed in stress imaging. At the expense of reduced spatial coverage, the developed method in this work is capable of achieving desirable image quality (no artifacts) and high in-plane spatial resolution in stress FPP studies. Unlike our approach or the work in (22), the non-ECG-gated multi-slice 2D method by Harrison et al. in (53) uses a SR pulse for magnetization preparation, yet can generate systolic images for all slices. Ungated images are first reconstructed for each slice at arbitrary cardiac phases and then deformable registration is used to post-process the frames to a systolic (or diastolic) phase (53). Such post processing is not needed in our all-systolic imaging approach. The SR time delay (≈50 ms needed for signal recovery) and the sequential acquisition scheme for each slice (unlike the slice-interleaved readout scheme in our work) may potentially reduce the accuracy of “all systolic” reconstruction using SR-prepared methods compared to our SR-free continuous acquisition scheme. Nevertheless, further studies are needed to provide a systematic comparison in terms of image quality and diagnostic capabilities between magnetization-driven ungated FPP imaging approaches such as the one presented in this work and magnetization-prepared ungated approaches such as the work in (53).

The idea of constraining the dynamic reconstruction to reference images (time-varying set of references) is similar to HYPR-based approaches (47–49) or other reference-regularized schemes (50–52). However, the proposed reconstruction method enables us to potentially achieve higher effective acceleration factors and thereby improved temporal fidelity by: (a) incorporating a flexible compressed-sensing-based framework that can include improved data-adaptive sparsifying transforms, e.g., the image-domain gradient operator; (b) incorporating non-Cartesian SENSE as a complementary source of acceleration (itself capable of providing up to ≈4 fold acceleration in our experience at 3T). The acceleration factor relative to projection-imaging Nyquist criteria is quite high (12 fold). However, 21 projections per frame contains enough temporal information to encode the dynamics of bloodpool and myocardial enhancement as shown in the retrospective ischemic dog studies (Fig. 5). This is in line with previous work on accelerated radial FPP imaging whether ECG-gated (48,49,54) or without ECG gating (53).

Study limitations and future work

The presented in-vivo results are to demonstrate the feasibility of the proposed multi-slice continuous FPP methodology as a new approach for non-ECG-gated myocardial perfusion MRI. Although promising, the presented in-vivo results are limited and more studies are needed to further evaluate the clinical effectiveness of the proposed method and its benefits compared to conventional ECG-gated or non-ECG-gated SR-prepared techniques. The healthy volunteer studies are also limited by the small number of cases and should be followed-up to include a larger sample size. Furthermore, a direct head-to-head comparison of the proposed approach versus conventional FPP imaging in patients with suspected CAD would be of importance. This comparison should include both image quality aspects (e.g., myocardial CNR and subendocardial dark-rim artifact) and also testing of the ability of the proposed approach to detect all defects observed in a conventional FPP study. We expect that such future studies will help determine the benefits of all-systolic artifact-minimized FPP imaging.

One factor that perturbs the magnetization steady-state and therefore may reduce the CNR of the presented method is cardiac and/or breathing motion (causing through-plane motion during each heartbeat), which may result in small but noticeable myocardial signal intensity modulations due to changes in T1 weighting. Although it remains to be seen how the method will perform under free-breathing conditions, we expect the relatively high FA used in the proposed method to help with rapid return of near-steady-state T1 weighting and provide high myocardial CNR as demonstrated in the stress perfusion studies of the two CAD patients in this work (both of which included relatively mild respiratory motion during the stress exam). In addition, significant through-plane motion in presence of deep breathing poses a challenge for the reference-based image reconstruction scheme since it may result in blurred reference frames and thereby reduced image quality in the reconstructed FPP time frames. A related issue is changing of myocardial T1 during the first-pass acquisition caused by wash in/out of gadolinium contrast, which perturbs the signal steady-state. However, such effects are expected to be relatively slow compared to the speed with which the continuous GRE sequence transitions from such perturbed state back to near steady-state. As pointed out in our prior work on single-slice 2D magnetization-driven imaging (24), quantification of myocardial blood flow is complicated by the above effects and also due to saturation of the arterial input function (LV bloodpool signal).

Conclusions

The presented methods and results demonstrate, for the first time, the feasibility of all-systolic multi-slice 2D non-ECG-gated first-pass perfusion MRI. The developed continuous acquisition and highly accelerated reconstruction method was tested in myocardial perfusion studies of both healthy volunteer and patients with CAD, demonstrating that the method can potentially achieve desirable image quality (sufficient myocardial CNR, high spatial resolution, and no subendocardial dark-rim artifact) while providing 3-slice spatial coverage. The promising results provide a foundation for future studies aimed at evaluating the potential benefits of this new approach for FPP imaging in clinical applications.

Supplementary Material

Supp VideoS1. Supporting Video S1a.

First-pass perfusion images series corresponding to the continuous FPP scan (proposed method) presented in Fig. 6(a).

Supp VideoS2. Supporting Video S1b.

First-pass perfusion images series corresponding to the conventional FPP scan presented in Fig. 6(b).

Appendix A

Computational approach for Step 5 of the image reconstruction procedure

The proposed TRACE reconstruction scheme (reference-constrained compressed sensing) aims to a minimize a nonlinear functional (Eq. [2]) that has a mixture of 2-norm (data fidelity term) and 1-norms (regularization terms). The TV term (isotropic TV definition) is a 1-norm measure of the image-domain gradients of the difference frame μ_t = x_t − r_t:

$$\mathrm{T}\mathrm{V}(u_t)={\Vert \sqrt{{({\nabla }_x{u}_t)}^2+{({\nabla }_y{u}_t)}^2}\Vert }_1=\sum _i\sqrt{{({\nabla }_x{u}_t)}_i^2+{({\nabla }_y{u}_t)}_i^2}$$ [3]

where ∇_x, ∇_y denote the image-domain gradient operators along x and y dimensions, respectively. This TV term in the reconstruction cost functional in Eq. [2] enforces the constraint that the difference frame x_t − r_t is expected to be piece-wise smooth [example shown in Fig. 3(c)]. As stated in Methods, the computational algorithm for the optimization task in Eq. [2] is implemented using an iteratively reweighted least-squares algorithm (38,39). However, such algorithms are designed to deal with 1-norm terms whose arguments are only stated in terms of the unknown vector x_t, i.e., simple 1-norm terms that are free of the reference-frame argument r_t, unlike the formulation in Eq. [2]. To convert the cost functional in Eq. [2] to such a simplified form, we apply a change-of-variable as follows:

$$\widehat{u_t}=\underset{u_t}{\text{argmin}}\{\frac{1}{2}\sum _{c=1}^{N_c}{\Vert {ỹ}_{c;t}-A_t(S_c{u}_t)\Vert }_2^2+\lambda \mathrm{T}\mathrm{V}(u_t)+\eta {\Vert u_t\Vert }_1\}$$ [4]

where μ_t, defined above, is the new optimization variable and: ỹ_c;t = y_c;t − A_t(S_cr_t) for c = 1, …, N_c. Once the minimizer of the cost function in Eq. [4] is found, the reconstructed time-frame is computed as: $\widehat{x_t}=\widehat{u_t}+r_t$. It is worth mentioning that, in Step 4 of the reconstruction scheme (Fig. 3a), the reference frame r_t should be reconstructed using CG-SENSE rather than standard regridding to ensure correct recovery of the image intensity amplitudes for the reference frame. This is because correct scaling of the image intensities for the reference frame is needed for validity of the sparsity constraints (complex-valued subtraction) in Eqs. [2] and [4]. In our implementation, we did not use any pre-conditioning schemes (e.g., density compensation as described in [36]) to speed up the CG-SENSE iterations.