Spatially Regularized Machine Learning for Task and Resting-state fMRI

Abstract

Background

Reliable mapping of brain function across sessions and/or subjects in task- and resting-state has been a critical challenge for quantitative fMRI studies although it has been intensively addressed in the past decades.

New Method

A spatially regularized support vector machine (SVM) technique was developed for the reliable brain mapping in task- and resting-state. Unlike most existing SVM-based brain mapping techniques, which implement supervised classifications of specific brain functional states or disorders, the proposed method performs a semi-supervised classification for the general brain function mapping where spatial correlation of fMRI is integrated into the SVM learning. The method can adapt to intra- and inter-subject variations induced by fMRI nonstationarity, and identify a true boundary between active and inactive voxels, or between functionally connected and unconnected voxels in a feature space.

Results

The method was evaluated using synthetic and experimental data at the individual and group level. Multiple features were evaluated in terms of their contributions to the spatially regularized SVM learning. Reliable mapping results in both task- and resting-state were obtained from individual subjects and at the group level.

Comparison with Existing Methods

A comparison study was performed with independent component analysis, general linear model, and correlation analysis methods. Experimental results indicate that the proposed method can provide a better or comparable mapping performance at the individual and group level.

Conclusions

The proposed method can provide accurate and reliable mapping of brain function in task- and resting-state, and is applicable to a variety of quantitative fMRI studies.

1. Introduction

Blood oxygen level dependent (BOLD) functional magnetic resonance imaging (fMRI) is an efficient tool for the mapping of brain functional activity in task- and resting-state. Due to fMRI nonstationarity, which is typically caused by physiological fluctuation, brain plasticity, subject attention, fatigue, mood, head movement, machine instability, etc., fMRI data exhibit significant intra- and inter-subject variations. As a result, the reliable mapping of brain function across sessions and/or subjects in task- and resting-state remains a great challenge for various quantitative fMRI studies.

Statistical model-driven techniques have been widely used for brain function mapping. Typical methods include general linear model (GLM) based methods and correlation analysis (Friston et al., 1995; Woolrich et al., 2009). In these methods, fMRI data/features are characterized by a statistical model, and test statistics are computed based on the model and data/features. If a voxel's test statistic is great than a threshold, the voxel is identified as “active” or functionally “connected”. The statistical model and threshold are usually experientially determined and fixed in each study. If a quantitative fMRI study requires multiple scan sessions over certain period of time and/or across multiple subjects, a fixed statistical model and threshold won't be sufficient to adapt to the intra- and inter-subject variations (Genovese et al., 2002, Voyvodic et al., 2009, Wang et al., 2011).

Data-driven techniques can overcome some limitations of model-driven methods because they do not superimpose parametric models to fMRI data/features. Semi-supervised and unsupervised data-driven approaches can adapt to changes of data characteristics with or without training data with known class labels. A widely used data-driven method is independent component analysis (ICA) (McKeown et al., 1998; Calhoun et al., 2001; Van de Ven et al., 2004; Beckmann et al., 2005), which assumes that fMRI data is a linear combination of independent signal and noise sources in the spatial or temporal domain. ICA can characterize high order statistics among multiple voxels. Due to its unsupervised learning mechanism, ICA can adapt to the intra- and inter-subject variations of fMRI data. In addition, ICA results may be transferred into probability measures to enable a “soft” decision (Beckmann et al., 2004). Since the real number of signal and noise sources in fMRI data is unknown, a major issue of ICA is that each spatial or temporal component could be a combination of multiple sources, and a visual inspection or template matching of ICA results has to be performed to identify expected task activation or resting-state networks (Greicius et al., 2003; Van de Ven et al., 2004; Schöpf et al., 2010).

Another data-driven technique, support vector machine (SVM), is becoming a popular tool for fMRI data analysis. SVM and its extensions can provide a unique solution with a good out-of-sample generalization and an implicit implementation of nonlinear classification using the kernel technique (Vapnik, 1998). SVM has been used to perform supervised classifications of specific brain functional states/disorders in a variety of task conditions (Cox et al., 2003; Mitchell et al., 2004; LaConte et al., 2005). More recently, SVM has been applied to the supervised classifications of resting-state fMRI data for different purposes (Craddock et al., 2009; Supekar et al., 2009; Deshpande et al., 2010, Dosenbach et al., 2010; Shen et al., 2010; Shah et al., 2011; Zhang et al., 2011; Meier et al., 2012). Because of the intra- and inter-subject variability, an SVM classifier trained using a subject's data acquired from one scan session may not perform well on data collected from different sessions and/or different subjects. Therefore, the SVM-based methods are not suitable for the general mapping of brain function in task- and resting-state. In our previous work (Song et al., 2009), an SVM-based technique was proposed to detect active voxels in task stimuli, and it was recently extended to the mapping of resting-state network (Song et al., 2014). The basic idea of the method is to formulate the mapping of active/functionally connected voxels as an outlier detection process. Since active voxels in a task condition or functionally connected voxels in a resting-state network are spatially grouped together at multiple anatomic locations, in order to improve the mapping performance, it is necessary to introduce spatial regularization into the SVM learning. In this work, we propose a spatially regularized semi-supervised SVM method that unifies the analysis of task- and resting-state fMRI data into the same process. The proposed technique can perform functional mapping for an entire brain or a single slice at the individual and group level.

2. Materials and Methods

In this work, the mapping of active/functionally connected voxels is formulated as an outlier detection procedure. This is based upon an assumption that active voxels under a task condition, or functionally connected voxels in a resting-state network are less than 50% of all voxels. Our observation from the results of a study of 8000+ subjects indicates that active brain voxels associated with a task stimulation are less than a half of all brain voxels (Laird et al., 2011). Due to a close correspondence between active functional networks and resting-state connectivity (Smith et al., 2009), this observation is applicable to both task-related and resting-state fMRI studies, and forms the basic assumption of the proposed method. In this context, “outliers” indicate active voxels in a task-related study, or functionally connected voxels in a resting-state network. As the opposite class of “outliers”, “majority” corresponds to inactive voxels in a task condition or functionally unconnected voxels in resting-state.

In the proposed method, the outlier detection is implemented using the one-class SVM (OCSVM). OCSVM is a special type of the traditional two-class SVM (TCSVM) that estimates a classification hyperplane in a feature space to isolate a pre-specified part of data from the origin with the maximum distance (Schőlkopf et al., 2001b). The formulations of TCSVM and OCSVM are based upon the assumption that each data sample is independently drawn from an unknown probability distribution (Burges 1998). It is well known that there exists strong spatial correlations between neighboring voxels in fMRI data, and ignoring such correlations may deteriorate the functional mapping performance. There are different ways to integrate this spatial constraint into the mapping process. One approach is to use spatial smoothing in the preprocessing, which has been a routine step in most fMRI studies (Lindquist 2008). Another approach is to use features containing spatial correlation information in the mapping process (Goutte et al., 1999; Song X et al., 2010, 2014). In our previous work, a spatial constraint based prototype selection approach was used to identify spatially grouped voxels in task-related and resting-state studies for SVM learning (Song X et al., 2010, 2014). Efforts were also made to integrate spatial constraints into the data classifier training (Liang et al., 2006; Baldassano et al., 2012, Cuingnet et al., 2013). In this work, a spatially regularized SVM method was developed where all of the aforementioned ways of integrating spatial constraints are considered.

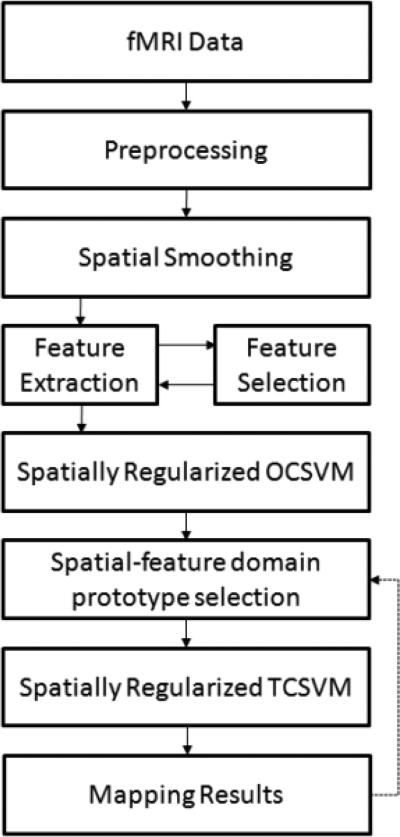
Figure 1 shows the block diagram of the proposed method. An input fMRI time series acquired from a task-related or resting-state study is first preprocessed to remove subject movement artifacts and low frequency scanner drift. Spatial smoothing is performed using a wavelet domain Bayesian shrinkage method (Song et al., 2006). After the spatial smoothing, multiple features are extracted from each voxel. An offline feature selection is performed to select a subset of salient features to represent each voxel. The feature selection is aimed to improve the computational efficiency and to reduce potential effects from irrelevant features. After this, a spatially regularized OCSVM (SR-OCSVM) learning is performed to generate an initial mapping of brain function. Next, a spatial-feature domain prototype selection is used to identify voxels that are correctly classified by the SR-OCSVM. Then, the identified voxels are used to train a spatially regularized TCSVM (SR-TCSVM) to reclassify all input voxels and finally to obtain a refined functional map. Although it is not necessary, the prototype selection and SR-TCSVM reclassification could be repeated several times till the change in the final mapping results is zero or below a predefined threshold. The details of the method are described in the following subsections.

Figure 1.

Block diagram of the proposed method

2.1 Preprocessing

Subject head movement artifacts are first attenuated using a six degree-of-freedom rigid body registration tool in FSL (Jenkinson et al., 2002; Woolrich et al., 2009). Then an in-house Matlab program is used to remove the linear trend in fMRI data. Resting-state data are low-pass filtered at a cut-off frequency of 0.1 Hz to extract low frequency fluctuations-of-interest. For any task-related study, the expected haemodynamic response (HDR) is estimated by convolving the experimental paradigm with the canonical haemodynamic response function (Friston et al., 1995). For the resting-state study, a seed is selected from a brain region that is part of a network-of-interest based on previously reported seed locations. For group level study, the motion corrected fMRI data are spatially normalized to the 2 mm Montreal Neurological Institute (MNI) template using a twelve degree-of-freedom registration (Jenkinson et al., 2002).

2.2 Spatial Smoothing

The fMRI data are spatially smoothed using a multiscale wavelet domain Bayesian noise removal method (Song et al., 2006). In this method, each voxel is transformed into the multiscale wavelet domain using the stationary wavelet transform (Nason et al., 1995). The wavelet coefficients are characterized by a 2-component Gaussian mixture model (GMM). The student's t-test is performed on each voxel's time course in the wavelet domain to provide a prior information about the significance of the wavelet coefficients. The expectation maximization (EM) algorithm is used to estimate the GMM parameters and obtain a posterior estimation of the wavelet coefficients (Dempster et al., 1977). After the wavelet domain analysis, the spatially smoothed fMRI data are obtained by performing an inverse wavelet transform. This method can effectively attenuate spatial noise while preserving signal details without over-smoothing the data.

2.3 Feature Extraction

Given the expected HDR or predefined seed region, multiple candidate features are calculated from each voxel's time course (TC) and its neighboring voxels. For a task-related study, the following candidate features are computed: maximum intensity of the voxel's TC, Pearson's correlation coefficient (cc) value between the TC and expected HDR, signed extreme value of the cross-correlation function (ccf) between the TC and HDR, average between-trial cc value of each voxel, minimum, average, and maximum cc values between the HDR and voxels within its 3×3 neighborhood for the single-slice analysis (3×3×3 neighborhood for the multi-slice or whole brain analysis), minimum, average, and maximum signed extreme value of ccfs between the voxel and its neighboring voxels. For resting-state data, a similar set of features are considered: maximum intensity of the voxel's TC, cc value between the seed and voxel, signed extreme value of the ccf between the seed and voxel, minimum, average, and maximum cc values between the voxel and its neighboring voxels, minimum, average, and maximum cc values between the seed and the voxel's neighboring voxels, average signed extreme value of the ccf between the seed and the voxel's neighboring voxels. Each candidate feature is scaled between 0 and 1.

2.4 Feature Selection

Feature selection aims to identify most representative candidate features in terms of the classification performance or other criteria. Feature selection is not always considered in fMRI studies. A reduced feature set may exclude part of remaining noise and artifacts in the original feature set and improve the mapping performance and computational efficiency. Feature selection is typically implemented offline, and the selected feature categories will be fixed for future studies. In this work, an SVM-based feature selection technique was used to quantify how each candidate feature affects the learning of SVM classification hyperplane (Evgeniou et al., 2003). During the SVM learning, the contribution index from the m^th candidate feature I^m is quantified as:

$$I^m={\sum }_{i=1}^{N_{SV}}\mid {\sum }_{j=1}^{N_{SV}}{\alpha }_j{y}_j{\mathit{K}}^m({\mathit{x}}_j,{\mathit{x}}_i)\mid ,$$ (1)

where N_SV is the total number of support vectors, x_i and x_j are the i^th and j^th support vectors, y_j is the class label of x_j, α_j is the Lagrange multiplier in the SVM formulation (Vapnik 1998), and K^m(x_j, x_i) is the first derivative of a kernel matrix K(x_j, x_i) regarding the m^th dimension evaluated at x_i. After evaluating all candidate features, those resulting in the largest I^m values are selected. In our recent study (Song et al., 2014), this feature selection method was used to evaluate candidate feature extracted from resting-state fMRI data under the conventional formulation of TCSVM. In this work, this method was used to evaluate candidates features for both task and resting-state fMRI data under the spatially regularized SVM formulation.

2.5 Spatially Regularized Support Vector Machines

SVM, which is also termed two-class SVM (TCSVM), is a supervised classification technique (Vapnik, 1998). In this work, the two classes are “active” and “inactive” in task-related studies, and functionally “connected” and “unconnected” in resting-state fMRI. The TCSVM learning constructs a linear classification hyperplane in a feature space to maximally separate two classes in training data. Given a set of independent identically distributed training data samples x_i ∈ R^m, i = 1, ... n, and their class labels y_i, the TCSVM learning aims to maximize the following objective function:

$${\min }_{\mathit{w},b,\xi }\frac{1}{2}{\Vert \mathit{w}\Vert }^2+C{\sum }_{i=1}^n{\xi }_i,$$ (2)

subject to $y_i(\langle \mathit{w}.{\mathit{x}}_i\rangle +b)\ge 1-{\xi }_i$, where w is a normal vector defining the hyperplane with the offset parameter $b,{\xi }_i\ge 0$ is the slack variable corresponding to training errors, and parameter C controls a tradeoff between the hyperplane complexity and training error. One-class SVM (OCSVM) is an extension of TCSVM. It constructs a classification hyperplane in a feature space to maximally separate a majority of the learning data from the origin, and the two classes in TCSVM become the “majority” and “outliers” classes (Schőlkopf et al., 2001b). The OCSVM learning minimizes the following objective function:

$${\min }_{\mathit{w},\rho ,\xi }\frac{1}{2}{\Vert \mathit{w}\Vert }^2+\frac{1}{vl}{\sum }_i{\xi }_i-\rho ,$$ (3)

subject to $\langle w,\varphi \left(x_i\right)\rangle \ge \rho -{\xi }_i$, where ρ is the offset parameter, ${\xi }_i\ge 0$ is the slack variable corresponding to outliers, and ν ∈ (0,1] controls an upper bound of outliers.

The OCSVM and TCSVM learning can be unified into a more general regularization framework (Belkin et al., 2006):

$$J\left(f\right)=arg{\min }_{\mathit{w}\in \mathcal{H}}\frac{1}{n}{\sum }_{i=1}^{n}V(\mathit{w},{\mathit{x}}_i,y_i)+{\lambda }_r{\Vert \mathit{w}\Vert }_{\mathcal{H}}^2,$$ (4)

where V is a loss function, $\mathcal{H}$ represents a reproducing kernel Hilbert space (RKHS), ${\Vert \mathit{w}\Vert }_{\mathcal{H}}^2$ is the norm of the classification function in $\mathcal{H}$, and ${\lambda }_r$ is a regularization parameter. According to the Representer theorem (Schőlkopf et al., 2001a), the solution of (4) is in the form of :

$$f\left(x\right)={\sum }_{i=1}^n{a}_{i}K(\mathit{x},{\mathit{x}}_i).$$ (5)

Based upon an assumption that fMRI data/features lie in a manifold of a high dimensional space (Shen et al., 2008), the mapping of active or functionally connected voxels is a classification problem regularized by the geometry of the underlying manifold. In our work, the manifold is estimated by characterizing the spatial correlation of neighboring voxels in fMRI data using a graph representation, where each voxel is considered as a vertex and connected to its neighboring voxels through edges. The connection strength of each edge is quantified by a weight. Based upon the graph representation of this spatial constraint, an adjacency matrix $ϴ$ can be formed with each entry θ_i,j showing the connectivity strength of the edge between the i^th voxel and its j^th neighbor, and a penalty term can be formed as follows:

$$\mathcal{L}\left(\mathit{w}\right)=\frac{1}{nk}{\sum }_{i=1}^n{\sum }_{j=1}^k{\theta }_{i,j}{\Vert f\left({\mathit{x}}_i\right)-f\left({\mathit{x}}_j\right)\Vert }^2,$$ (6)

where k is the number of neighboring voxels of the i^th voxel. If this spatial constraint is integrated into the SVM learning, then the modified formulation of (4) becomes:

$$f^{\ast }=arg{\min }_{\mathit{w}\in \mathcal{H}}\frac{1}{n}{\sum }_{i=1}^{n}V(\mathit{w},{\mathit{x}}_i,y_i)+{\lambda }_r{\Vert \mathit{w}\Vert }_{\mathcal{H}}^2+{\lambda }_s\mathcal{L}\left(\mathit{w}\right),$$ (7)

where λ_s is the weight of the penalty term. The optimization of SVMs is typically performed on their dual forms (Burges 1998, Schőlkopf et al., 2001b). It was shown that the inclusion of the penalty form in (6) to the SVM formulation in (7) is equivalent to replacing the original kernel matrix K with a modified kernel matrix $\tilde{\mathit{K}}$ in the dual forms of OCSVM and TCSVM (Sindhwani et al., 2005):

$$\tilde{\mathit{K}}=\mathit{K}-{\mathit{K}}^T{(I+\mathit{MK})}^{-1}\mathit{MK}$$ (8)

where M = λ_sL, and L is the graph Laplacian defined as $\mathit{L}=\mathit{D}-ϴ$, and D is a diagonal matrix with each element computed as: $D_{i,i}={\sum }_{j=1}^n{\theta }_{i,j}$. The corresponding spatial regularized OCSVM and TCSVM are denoted as SR-OCSVM and SR-TCSVM in this work.

Different approaches was considered to determine $ϴ$. A typical way is to assign an equal weight to all edges (Stoeckel et al., 2005; Dundar et al., 2006; Liang et al., 2006; Baldassano et al., 2012; Flamary et al., 2013). Another way is to use the RBF kernel defined as: $e^{-\frac{{\Vert {\mathit{x}}_i-{\mathit{x}}_j\Vert }^2}{2{\sigma }^2}}$, and in this case, the algorithm becomes the Laplacian SVM (Belkin et al., 2006). The equal weight does not reflect the true similarity between neighboring voxels, and could bring ambiguity in mapping results around the boundaries of active or functionally connected brain regions. The use of RBF kernel needs a proper selection of kernel width σ, which is usually experimentally or experientially determined, and could be affected by spatial resolution, feature characteristics, and other unknown factors. In this work, a different method was proposed to calculate the adjacency matrix $ϴ$:

$${\theta }_{i,j}=cc({\mathit{x}}_i,{\mathit{x}}_j)∕{\sum }_{l=1}^{k}cc({\mathit{x}}_i,x_l),$$ (9)

where cc(x_i, x_j) is the Pearson's cc value (normalized by the Fisher r-to-z transformation) between the i^th and j^th voxels. This correlation-based edge weight may reflect the true similarity between neighboring voxels and is expected to provide an improved boundary specificity in the mapping results.

Before performing the SR-OCSVM learning, the parameter ν needs to be set to provide an upper bound of the number of voxels identified as active or functionally connected. This parameter is task-, network-, session-, and subject-dependent, and cannot be accurately estimated. A more realistic solution is to make the algorithm insensitive to the variation of ν when ν is set within a predefined range. This issue was addressed previously using the standard OCSVM and TCSVM learning techniques (Song et al., 2009, 2014). In this work, instead of using experiential ν values in a predefined range, the correlation analysis with Bonferroni correction was performed to obtain an initial estimation of ν. This estimation is conservative and the final ν was obtained by multiplying the estimated ν value by a number ranging from 1.0 to 3.5. The sensitivity of the proposed method to ν was investigated under the spatially regularized SVM formulations.

The SR-TCSVM results can be transferred into probability estimates (Wu et al., 2004). The final decision is made via a “soft” decision by comparing each voxel's probabilities of “active” and “inactive” in a task condition, or probabilities of functionally “connected” and “unconnected” in resting-state. For group level mapping in a task condition, each voxel's probabilities of active and inactive are averaged over all sessions and subjects. A final decision is made by comparing the averaged probabilities. The same procedure is used for the group level resting-state network mapping.

2.6 Spatial-feature Domain Prototype Selection

A prototype consists of the feature vector of a voxel and its class label. SR-OCSVM results may contain a significant number of mis-classifications due to the deviation of ν from its true value and/or indistinguishable voxels in the feature space. As a result, before using the SR-OCSVM results to train a SR-TCSVM to reclassify the initial input, a prototype selection procedure is necessary to identify voxels that are most possible to be correctly classified by SR-OCSVM. Using the graph representation of each voxel, if the class assigned to a voxel is the dominant class in its predefined neighborhood, then this voxel is selected as a training sample for SR-TCSVM. To improve the representativeness of training data, 5% voxels in the majority and outlier classes that are closest to the SR-OCSVM classification hyperplane in the feature space are excluded from the training data in light of a higher chance of them to be mis-classified.

2.7 Evaluation Methods

The proposed method was evaluated using both synthetic and experimental fMRI data. The effects of the three different edge weighting methods were evaluated using the SR-OCSVM results of the synthetic data based upon three numerical criteria, including accuracy, precision, and recall. Accuracy is the overall classification accuracy. Precision is defined as a ratio of the number of truly active/connected voxels to the number of identified active/connected voxels. Recall is defined as a ratio of the number of identified truly active/connected voxels to the number of all truly active/connected voxels. The weighting method that provided the best numerical performance was used in the study of experimental data. The effects of the SR-OCSVM parameter ν on the final mapping results were also investigated using the synthetic data. When the experimental data were used, the mapping performance was examined for individual subjects and at the group level in both task- and resting-state.

The proposed method was compared to several widely used brain mapping techniques in the experimental study. In the study of individual subjects, the probabilistic ICA (PICA) was used for the comparison (Beckmann et al., 2004). In the PICA method, the intensity values of each independent component (IC) are transferred into spatial Z-scores and a GMM is used to characterize the Z-scores. The final decision can be made with a probability threshold of 0.5, which is equivalent to the soft decision of the proposed method by comparing the probabilities of active/connected and inactive/unconnected. In the group level analysis of task data, the group ICA (GICA) and a GLM-based Bayesian methods were performed (Calhoun et al., 2009, Woolrich et al., 2009). The group level activation maps obtained from the task data were evaluated in terms of the distributions of average contrast-to-noise ratio (CNR). The CNR measure of each voxel was computed using the method proposed by Menon et al. (Menon et al., 1997). In the individual level analyses of resting-state data, the proposed and PICA methods were assessed in terms of their performances on the mapping of the default mode network (DMN) and sensori-motor network (SMN). In the group level analysis, mapping results of DMN and SMN obtained from GICA and the correlation analysis with false discovery rate (FDR) control were compared to those obtained from the proposed method. The seeds used in the correlation analysis are the same as those used in the feature extraction stage of the proposed method.

Kendall's coefficient of concordance (KCC) was also calculated to measure the regional homogeneity of active or functionally connected regions identified by the methods used in the experimental study (Zang et al., 2004). KCC was used with mapping results together to evaluate the mapping performance. If active or functionally connected regions are sufficiently identified, a higher KCC value indicates that the measured mapping results better match the true functional regions as compared to others.

2.8 fMRI Data

2.8.1 Synthetic Data

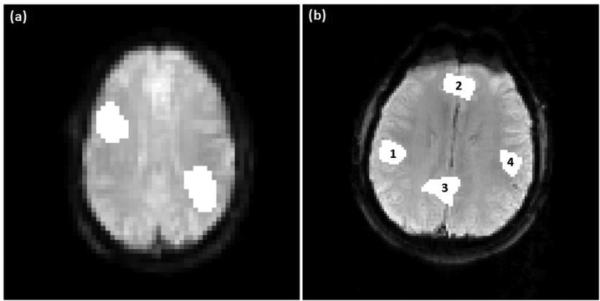
The synthetic task data was generated from a single slice echo planar imaging (EPI) image of size 64 × 64. A 60-image time series was formed using this image with a simulated block design paradigm: 20 images off, 20 images on, and 20 images off. Figure 2 (a) shows the image overlaid by two artificially added active regions of irregular shapes. The active region on the top left represents 3.93% of the brain area, and the bold increase during the task period is 2% of the baseline average. The active region on the bottom right covers 4.52% of the brain area with a BOLD increase of 3% to the baseline. The synthetic resting-state time series was generated from another single slice EPI image of size 120 × 120. The time series consists of 100 images with four artificially added functionally connected regions of irregular shapes, as shown in Figure 2 (b). Regions 1~4 represents 2.03%, 2.45%, 2.79% and 1.64% of the brain area, respectively. Sinusoid signals were added to regions 1 and 4 at a frequency of 0.08 Hz. The signal amplitude in region 1 is 107% of the baseline average, and that in region 4 is 104% of the baseline average. The signal in region 4 has a phase shift of −0.52 radians compared to that in region 1. Regions 1 and 4 form network A. Sinusoidal signals were added to regions 2 and 3 at a frequency of 0.03 Hz. The signal amplitudes are 102% of the baseline average in region 2, and 103% of the baseline average in region 3. The signal phase in region 2 lags that in region 3 by 0.78 radians. The corresponding network is denoted as network B. Rician noise was added to the synthetic task and resting-state data using a method proposed by Wink et al. (Wink et al., 2004). After mean-centering the data, the SNR is 6.5 × 10⁻⁵dB for the task data, and −23.92dB for the resting-state data.

Figure 2.

(a) Synthetic task fMRI data with two artificially added active regions. (b) Synthetic resting-state fMRI data with two artificially generated functional networks each of which consists of two functionally connected regions: regions 1 and 4 are connected to form network A, and regions 2 and 3 are connected to form network B.

2.8.2 Experimental Data

Multiple task-related experimental datasets collected from three fMRI experiments were used in the study. In the first experiment, one dataset was obtained using a 3 Tesla (T) GE system with an 8-channel coil at Duke University Medical Center. The dataset was collected from a healthy subject using a T2*-weighted EPI sequence with SENSE acceleration factor of 2. The subject was instructed to perform a right-hand finger-tapping motor task with a blocked-design paradigm, which consisted of four 25-second task blocks and five 25-second off blocks. Repetition time (TR) was 2 seconds, echo time (TE) was 30 milliseconds, and the flip angle was 90^°. Thirty axial-slices were collected in each volume with 4 mm slice thickness and 1mm gap. Field of view (FOV) was 24 cm × 24 cm, and image matrix size was 120 × 120. A 15-second dummy scan was performed at the beginning and excluded from the analysis.

In the second experiment, three datasets were acquired from a single subject using a 3 T Siemens Allegra scanner at New York University Center for Brain Imaging (cbi.nyu.edu). The first two datasets were collected using a single channel head coil, and the third dataset was acquired using a surface coil. Imaging parameters include: TR=1.5 seconds, TE= 30 milliseconds, and flip angle=70°. A visual stimulation was used by alternatively showing a left and right circular hemifield stimulus of alternating checks at full contrast. There are 150 volumes in each dataset with twenty five axial-slices in each volume. The image matrix size was 64 × 80, and spatial resolution of each isotropic voxel was 3 × 3 × 3 mm³.

The datasets in the third experiment were acquired from eight right-handed healthy subjects using a 1.5 T GE MR scanner at Brigham and Women's Hospital (Yoo et al., 2005). Nine scan sessions were implemented for each subject with an inter-session gap between 21 and 140 days. The overall experiment period for each subject ranged from 378 to 536 days, with an average of 454.9 ± 47.2 days. During each scan session, the subject was performing a right hand finger tapping task, and the block design paradigm consisted of four 30-second task blocks and five 30-second off blocks. The EPI parameters were: TR=2.5 seconds, TE=50 milliseconds, and flip angle=90°. Twenty four axial-slices were acquired for each volume with a slice thickness of 6 mm. The matrix size was 64 × 64. A total of 114 volumes were collected in each scan, and the first 6 volumes were removed as the dummy scan. Thus, there are 108 volumes in each scan that were used in the analysis.

Multiple resting-state fMRI datasets collected from three experiments were used to evaluate the proposed method. The first experiment was performed using a 3 T GE system with an eight-channel coil at Duke University Medical Center. A dataset was acquired from a healthy adult subject using a T2*-weighted parallel EPI with an acceleration factor of 2, while the subject was looking at a crosshair. The scan lasted 5 minutes. EPI parameters included a TR of 2 seconds, a TE of 25 milliseconds, and a flip angle of 90°. Thirty five axial-slices were acquired in each volume with a slice thickness of 3 mm. FOV was 24 cm × 24 cm, and the image matrix size was 64 × 64.

The second experiment was performed using the same scanner as the first experiment. A dataset was acquired from another healthy adult who was instructed to look at a crosshair during the scan. The imaging parameters included a TR of 4 second, a TE of 35 milliseconds, and a flip angle of 90°. The FOV was 24 cm × 24 cm, and the matrix size was 140 × 140. 56 axial-slices were collected to cove the brain volume with a 3-mm slice thickness, and a total of 74 volumes were collected in this dataset.

The resting-state fMRI data in the third experiment were acquired from eight healthy subjects using a 1.5 T GE MR scanner at Brigham and Women's Hospital (Chou et al., 2012). Nine scan sessions were performed for each subject, with an inter-session gap ranged from 21 to 133 days. The entire experiment period for each subject ranged from 384 to 554 days, with an average of 463±58.4 days. In each scan, twenty four EPI axial-slices were acquired to cover the entire brain volume with 6 mm slice thickness and no gap. The imaging parameters comprised a TR of 2.5 seconds, a TE of 50 milliseconds, and a flip angle of 90°. The matrix size was 64 × 64, and the FOV was 24cm × 24cm. 114 volumes were collected in each scan, and the first 6 volumes were removed as dummy scans, resulting a total of 108 volumes in each scan. Due to a computer storage failure, not all task and resting-state data acquired at Brigham and Women's Hospital were retrievable. In the task data, there are five subjects with all nine sessions of data available, two subjects with eight sessions, and one subject with five sessions. In the resting-state data, there were six subjects with nine sessions of data available, one subject with eight sessions, and one subject with sessions.

3. Results

3.1 Feature Selection

Feature selection was performed using all experimental fMRI data included in this work. Table 1 shows the average feature contribution in the task-related experiments. Each value was averaged over all feature selection results of individual datasets, and normalized against the largest value. It was found that the feature contribution varies across subjects and sessions, but three features always rank higher than the others, including the cc value between each voxel's TC and the expected HDR, the average and minimum cc value of each voxels’ neighboring voxels and the HDR. The top five features were finally used to represent each voxel in the analysis. For the resting-state datasets, the top three features are: cc value between each voxel's TC and a seed, the average and maximum cc between each voxel's neighboring voxels and a seed, as shown in Table 2. The top five features were finally used in the study.

Table 1.

Feature selection results of task-related fMRI experimental data.

Candidate feature	Im value	Rank
AVG_CC_HDR	1	1
MIN_CC_HDR	0.86	2
CC_HDR	0.75	3
MAX_CC_HDR	0.72	4
AVG_XC_NB_HDR	0.57	5
MAX_XC_NB_HDR	0.56	6
MAX_XC_HDR	0.43	7
MIN_XC_NB_HDR	0.39	8
MAX_TC	0.31	9
SELF_CC	0.30	10

All I^m values were normalized against the largest one. (AVG/MAX/MIN_CC_HDR: average/maximum/minimum cc value between neighboring voxels of a voxel and the expected HDR; AVG/MAX/MIN_XC_NB_HDR: average/maximum/minimum signed extreme value of the ccfs between a voxel's neighboring voxels and the expected HDR; CC_HDR: cc value between a voxel and the expected HDR; MAX_TC: maximum intensity of a voxel's time course; MAX_XC_HDR: the signed extreme value of the ccf between a voxel and the HDR; SELF_CC: the average between-trial cc value of each voxel.)

Table 2.

Feature selection results of resting-state fMRI experimental data.

Candidate feature	Im value	Rank
MAX_CC_SEED	1	1
AVG_CC_SEED	0.98	2
CC_SEED	0.83	3
AVG_CC_NB	0.48	4
MIN_CC_SEED	0.39	5
AVG_XC_NB_SEED	0.40	6
MAX_CC_NB	0.38	7
MAX_XC_SEED	0.26	8
MAX_TC	0.14	9
MIN_CC_NB	0.01	10

All I^m values were normalized against the largest one. (AVG/MAX/MIN_CC_SEED: average/maximum/minimum cc value between neighboring voxels of a voxel and a seed; AVG/MAX/MIN_CC_NB: average/maximum/minimum cc value between a voxel and its neighboring voxels; AVG_XC_NB_SEED: the average signed extreme value of the ccfs between neighboring voxels of a voxel and a seed; CC_SEED: cc value between a voxel and a seed; MAX_TC: maximum intensity of a voxel's time course; MAX_XC_SEED: the signed extreme value of the ccf between a voxel and a seed.)

3.2 Synthetic Data

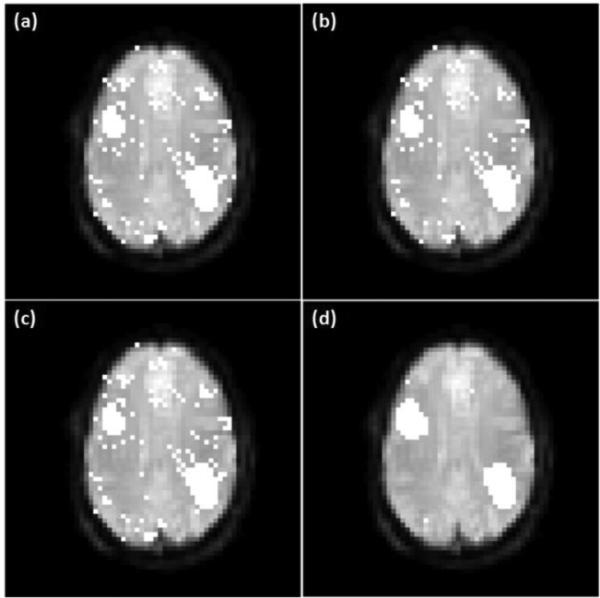
When the proposed SR-OCSVM was evaluated on the synthetic data, the following parameter settings were used: λ_r = 0.01, λ_s = 0.001, ν = 0.15 for the mapping of the synthetic task data, and ν = 0.1 for the mapping of the synthetic resting-state data. The RBF kernel was used to implement nonlinear support vector learning with a kernel width σ = 1.58 determined by the cross validation. When the RBF kernel was used to compute the edge weight in the adjacency matrix $ϴ$, the same kernel width was used. Figure 3 (a) shows the activation map of the synthetic task data obtained using the conventional OCSVM, and (b)-(d) are the mapping results obtained from SR-OCSVM with the three edge weighting methods. It was observed that SR-OCSVM with the correlation-based edge weighting provides a better performance compared to the others, and the SR-OCSVM results with the equal and RBF-based edge weighting are similar to each other.

Figure 3.

A comparison of the mapping result of the synthetic task data obtained using: (a) OCSVM, (b) SR-OCSVM with the equal edge weighting, (c) SR-OCSVM with the RBF-based edge weighting, and (d) SR-OCSVM with the correlation-based edge weighting.

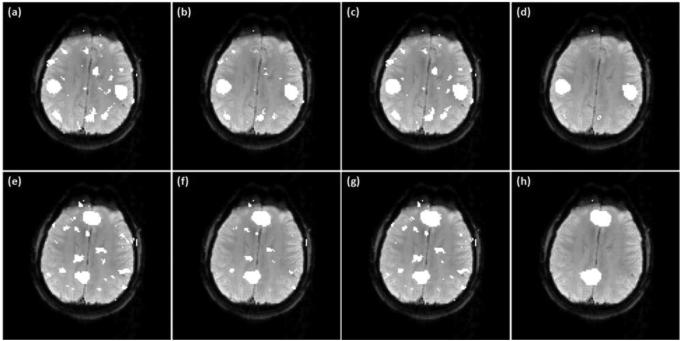
Figure 4 shows another comparison using the synthetic resting-state data, where (a) is the mapping result of network A obtained usingx OCSVM, and (b)-(d) show the connectivity maps obtained using SROCSVM with the three different edge weighting methods. Figures 4 (e)-(h) show a similar set of mapping results for network B. Tables 3 and 4 list the accuracy, precision and recall rates computed from the mapping results shown in Figures 3 and 4. It can be seen that SR-OCSVM outperforms the original OCSVM, and the correlation-based edge weighting outperforms the other two weighting methods when SR-OCSVM is used.

Figure 4.

A comparison of OCSVM and SR-OCSVM using the synthetic resting-state data. (a)-(d) are network A identified using (a) OCSVM, (b) SR-OCSVM with the equal edge weighting, (c) SR-OCSVM with the RBF-based edge weighting, and (d) SR-OCSVM with the correlation-based edge weighting. (e)-(h) Network B identified by the same order of algorithm settings as (a)-(d).

Table 3.

Numerical performances of OCSVM and SR-OCSVM computed from the mapping results of the synthetic task fMRI data shown in Figure 3.

	Accuracy (%)	Precision (%)	Recall (%)
OCSVM	89.96	44.75	80.2
SR-OCSVM (equal weight)	91.46	49.69	80.2
SR-OCSVM (RBF kernel)	90.21	45.51	80.2
SR-OCSVM (correlation)	99.75	97.12	100

Table 4.

Numerical performances of OCSVM and SR-OCSVM calculated from the mapping results of the synthetic resting-state fMRI data shown in Figure 4.

	Accuracy (%)		Precision (%)		Recall (%)
	Network A	Network B	Network A	Network B	Network A	Network B
OCSVM	93.51	93.25	35.94	42.4	98.0	80.84
SR-OCSVM (equal weight)	97.04	96.65	55.39	62.96	99.33	87.38
SR-OCSVM (RBF kernel)	93.61	94.03	36.43	46.32	99.33	88.32
SR-OCSVM (correlation)	98.7	97.94	74.13	72.73	99.33	97.2

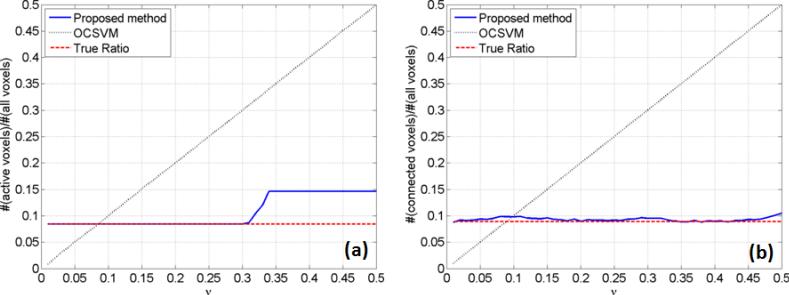
Figure 5 (a) shows the dependence of final mapping results on the OCSVM/SR-OCSVM parameter ν obtained from the synthetic task fMRI data, where the solid line indicates the ratio of active voxels identified by the proposed method to all voxels in the brain area. The dashed line is the true ratio value, which is 0.0845, and the dotted line is the ratio obtained from the OCSVM results. When ν is between 0.01 and 0.3, the ratio obtained from the proposed method is the same as the true ratio, and when ν is greater than 0.3, the ratio increases but is still much less than those from OCSVM. This implies that if we do not know the true ratio of active voxels, but set ν between 0.01 and 0.3, then the ratio obtained from the proposed method is quite close or the same to its true value. Figure 5 (b) shows the same dependence patterns obtained from the synthetic resting-state data. The true ratio calculated from networks A and B is 0.0891. The ratio obtained from the proposed method slightly varies around the true ratio when ν is between 0.01 and 0.5. The dependence on ν is much less than that of OCSVM.

Figure 5.

Dependence of the final mapping results on the OCSVM/SR-OCSVM parameter ν obtained using (a) synthetic task fMRI data, and (b) synthetic resting-state fMRI data.

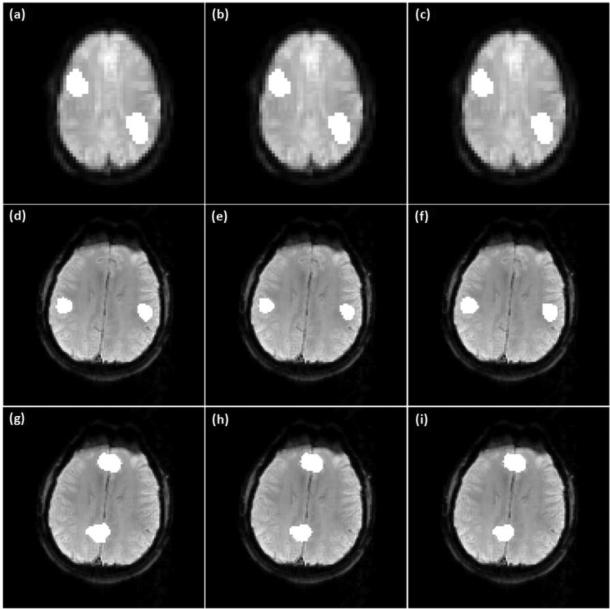
Figures 6 (a)-(c) show the final mapping results of the synthetic task fMRI data obtained from the proposed method using three different ν values: (a) 0.1, (b) 0.2, and (c) 0.3. The identified active regions match the ground truth very well. Figures 6 (d)-(i) show networks A and B identified by the proposed method using the same set of ν values as (a)-(c). There are slight variations in the numbers of functionally connected voxels identified around the boundaries of functionally connected regions, but no false positives were observed in other brain regions.

Figure 6.

(a)-(c) Mapping results of the synthetic task data obtained by the proposed method with three different ν values: (a) 0.1, (b) 0.2, (c) 0.3. (d)-(f) Network A identified by the proposed method with the same set ν values as (a)-(c). (g)-(i) Network B obtained by the proposed method using the same set of ν values as (a)-(c).

3.3 Experimental Data

3.3.1 Task-related Experimental Data

The performance of the proposed method on the task-related fMRI experimental data was first investigated on the motor and visual task data acquired from the individual subjects in the first and second task-related experiments. The values of λ_r and λ_s were the same as those for the synthetic data. The SR-OCSVM parameter ν was estimated using the correlation analysis.

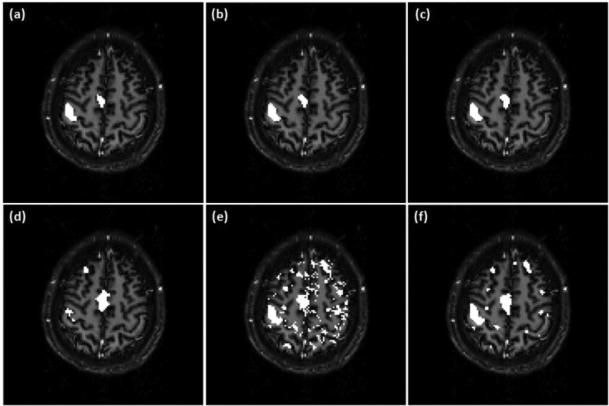
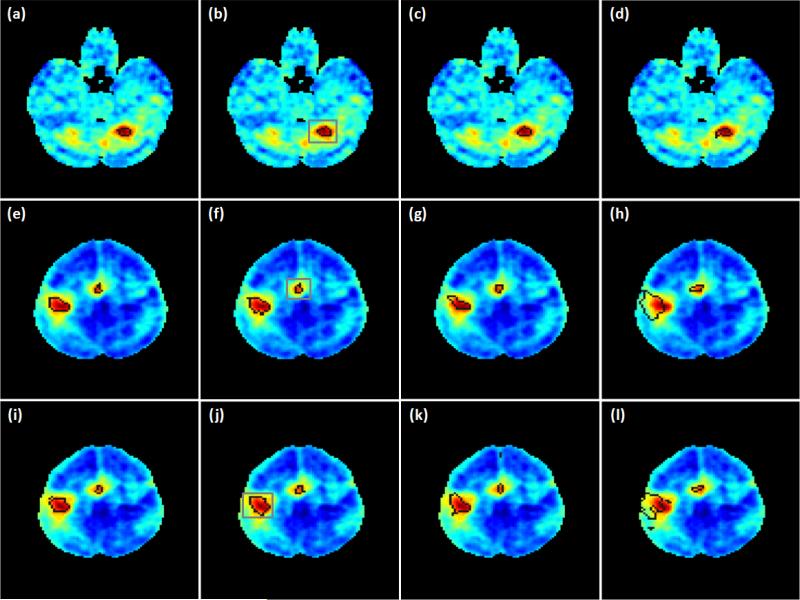
Figures 7 (a)-(c) show the activation maps overlaid on an individual slice covering part of motor cortex identified by the proposed method using three ν values: ν=0.14, 0.18, and 0.21, which are 2, 2.5, and 3 times the originally estimated ν value. Figure 7 (d) is the mapping result of PICA. All ICs obtained from PICA were visually inspected and those relevant to the motor task were combined together to form the activation map. The final decision of PICA is made in the same way as the proposed method by comparing each voxel's probabilities of active and inactive. When PICA is used, more voxels are identified to be active in the supplementary motor cortex area, but fewer active voxels are detected in the primary/pre-motor cortex region compared to those obtained by the proposed method. The KCC values of active regions shown in Figures 7 (a)-(d) are 0.178, 0.171, 0.171 and 0.142, respectively. The mapping results of this dataset obtained from the proposed method exhibit a higher regional homogeneity than those from PICA.

Figure 7.

(a)-(c) Mapping results of the motor task fMRI data from an individual subject obtained using the proposed method with three different ν values: (a) 0.14, (b) 0.18, (c) 0.21. (d) PICA result. (e) SR-OCSVM result (ν=0.21). (f) Mapping result of the proposed method without using the prototype selection procedure (ν=0.21).

Figure 7 (e) shows the initial mapping result obtained from SR-OCSVM when ν=0.21 and the prototype selection and SR-TCSVM reclassification steps were not performed. Figure 7 (f) shows the mapping result of the proposed method when ν=0.21 and the prototype selection procedure was not used. False positives can be visually identified from these two figures in brain regions that are not relevant to the motor task. This indicates that the prototype selection and SR-TCSVM reclassification are two necessary procedures to obtain reliable mapping results.

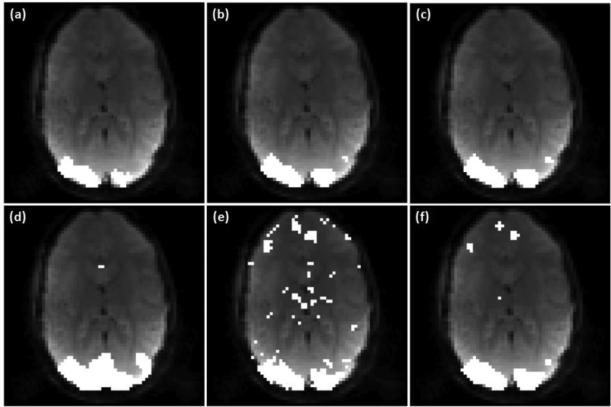
Figure 8 shows the activation maps from the subject in the visual task experiment, where (a)-(c) were obtained using the proposed method with three ν values: 0.11, 0.14, and 0.17, which are 2, 2.5, and 3 times the estimated ν value. Figure 8 (d) shows the PICA result, and (e), (f) are the mapping results obtained by using SR-OCSVM (ν=0.17) and the proposed method (ν=0.17) without the prototype selection step. Again, the observed false positives in (e) and (f) indicate the necessity of the prototype selection and SR-TCSVM reclassification procedures. Since the left and right eyes were alternatively stimulated, the temporal variation in the left and right visual cortex are significantly different. Therefore, the regional homogeneity was evaluated using the identified active voxels in the left visual cortex region, and the computed KCC values of Figures 8 (a)-(d) are 0.215, 0.206, 0.206 and 0.157, respectively. Higher KCC values were obtained from the mapping results of the proposed method.

Figure 8.

(a)-(c) Mapping results of the visual task fMRI data from an individual subject using the proposed method with three different ν values: (a) 0.11, (b) 0.14, (c) 0.17. (d) PICA result. (e) SR-OCSVM result (ν=0.17). (f) Mapping result of the proposed method without using the prototype selection step (ν=0.17).

For the group analysis of the motor task data in the third task experiment, both λ_r and λ_s were set to be 0.1 after trying different combinations of them. The group level activation maps obtained from the proposed method, GICA, and the GLM-based method are illustrated in Figure 9 over the average CNR map computed from all data in the third task experiment. Regions encircled by the dark lines in (a)-(d) are the group level active regions in the ipsilateral cerebellar area, where (a) and (b) were obtained using the proposed method with ν values 2.0 and 3.0 times the originally estimated values. Figures 9 (c) and (d) are the mapping results of the GICA and GLM methods. These two approaches do not provide a probability-based decision and a threshold is required to make the final mapping. In order to make the comparison meaningful, a rectangular region encircled by the grey line was defined in Figure 9 (b) to include the ipsilateral cerebellar area. The thresholds of the GICA and GLM methods were adjusted to identify the same number of active voxels as that in (b) in this region. Then the comparison was based on the same level of mapping sensitivity in this brain area. The boundaries of active regions were evaluated in terms of the CNR distribution. It can be seen that the active regions identified by the proposed technique and GICA better match the high CNR region compared to that identified by the GLM method.

Figure 9.

Group level mapping results of the motor task fMRI data using the proposed method, GICA, and GLM-based method. (a)-(b), (e)-(f), (i)-(j) Active regions in the ipsilateral cerebellar, primary/pre-motor and supplementary motor cortex areas identified by the proposed method with ν values 2.0 (a, e, i) and 3.0 (b, f, j) times the originally estimated values. (c),(g),(k) GICA mapping results. (d),(h),(l) Mapping results of the GLM method. Dark lines indicate the boundaries of the identified active regions. The thresholds of GICA and GLM methods were selected to identify the same numbers of active voxels in the regions encircled by the grey lines as shown in (b), (f), and (j).

Figures 9 (e)-(h) show the mapping results from a slice partially covering the primary/pre-motor and supplementary motor cortex areas, where (e) and (f) were obtained using the proposed method with ν values 2.0 and 3.0 times the estimated ones. The supplementary motor cortex region is encircled by the grey rectangular in Figure 9 (f), and the thresholds of the GICA and GLM methods were selected to identify the same number of active voxels in this region, as shown in (g) and (h). The boundary of the identified active region in the primary/pre-motor area is also encircled by the dark lines as shown in Figures 9 (e)-(h). It was observed that the variation of ν value does not result in apparent changes in the activation maps when the proposed method was used. Under the same mapping sensitivity, the active regions in the supplementary motor cortex identified by the proposed technique and GICA match the high CNR region well. However, the active region in the primary/pre-motor areas identified by the proposed method from the same slice better matches the high CNR region in this area compared to the GICA result, as shown in Figures 9 (f) and (g). The active regions identified by the GLM method do not match the high CNR regions so well as the proposed and GICA methods in this slice.

Figures 9 (i)-(l) illustrate the mapping results from another slice, where those shown in (i) and (j) were obtained using the proposed method with ν values 2.0 and 3.0 times the estimated ones. The activation maps shown in (k) and (l) were obtained from the GICA and GLM methods. The primary/pre-motor areas in this slice is encircled by the grey line as shown in Figure 9 (j), and the thresholds of the GICA and GLM methods were set to identify the same number of active voxels as that in the rectangular region shown in (j). The active region in the supplementary motor cortex is also illustrated in each of the mapping results. It can be seen that the activation maps shown in Figures 9 (i) and (j) better match the high CNR regions in the primary/pre-motor and supplementary motor cortex areas compared to those shown in Figures 9 (k) and (l). In addition, the activation maps obtained using GICA better match the CNR distribution than those identified by the GLM method. The regional homogeneity of the identified active voxels in each encircled region shown in Figure 9 was computed and is listed in Table 5. The average and standard deviation of KCC values computed from the active regions in the ipsilateral cerebellar and primary/pre-motor cortex areas identified by the three methods are slightly different with several permillage or percentage points. But the average KCC values of the active regions in the supplementary motor cortex identified by the proposed and GICA methods are apparently greater than that obtained from the GLM method.

Table 5.

Regional homogeneity (KCC) of the group level mapping results in the three brain areas obtained by the proposed, GICA, and GLM methods. The mean and standard deviation (std) of KCC values were computed across all subjects and sessions.

	Proposed Method		GICA		GLM
	Mean	Std	Mean	Std	Mean	Std
Ipsilateral cerebellar	0.573	0.131	0.579	0.132	0.566	0.132
Supplementary motor cortex	0.63	0.074	0.638	0.078	0.507	0.083
Primary/pre-motor cortex	0.417	0.07	0.403	0.067	0.406	0.081

3.3.2 Resting-state Experimental Data

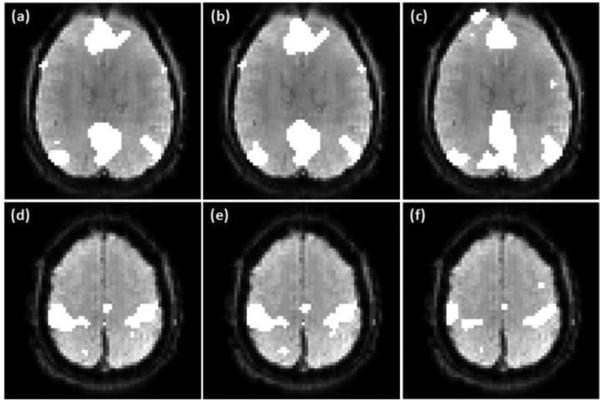
For the analysis of the individual subjects’ data from the first two resting-state experiments, the following parameter settings were used: λ_r = 0.01, λ_s = 0.005. Initial ν values were estimated using the correlation analysis based on predefined seeds. Figures 10 (a) and (b) show part of DMN overlaid on an individual slice from the subject in the first resting-state experiment identified using the proposed method with ν = (a) 0.27 and (b) 0.41, which are 2.0 and 3.0 times the originally estimated value. Figure 10 (c) shows the mapping result of PICA. The KCC values of the identified functionally connected regions in (a)-(c) are 0.115, 0.118 and 0.098, respectively. Figures 10 (d)-(f) show part of SMN overlaid on another slice from the same subject, where (d) and (e) were obtained using the proposed method with ν = (d) 0.25 and (e) 0.34, corresponding to 1.5 and 2.0 times the estimated one. Figure 10 (f) shows the PICA mapping result. The KCC values of the identified regions in (d)-(f) are 0.117, 0.121 and 0.123, respectively. The regions identified by the proposed method show a higher regional homogeneity for DMN and a slightly lower homogeneity for SMN as compared to those obtained from PICA.

Figure 10.

(a)-(b) Part of DMN identified from an individual subject using the proposed method with two ν values: (a) 0.27, (b) 0.41. (d)-(e) Part of SMN obtained using the proposed method with ν equal to (d) 0.25 and (e) 0.34. (c), (f) PICA mapping results.

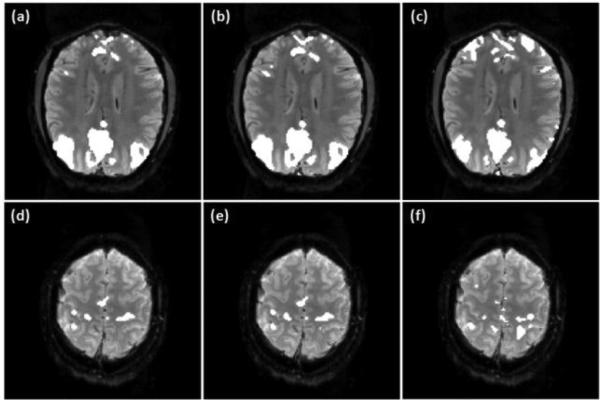
Figure 11 shows part of DMN and SMN from the subject in the second resting-state experiment. The network maps in (a) and (b) were obtained using the proposed method with ν = (a) 0.17 and (b) 0.25, corresponding to 2.0 and 3.0 times the estimated value. Figure 11 (c) was obtained from PICA. A total of 6915 voxels in this slice were used in the analysis. When ν value increases from 0.17 to 0.25, there are only 103 more voxels identified as part of DMN by the proposed method, indicating 5.37 times less dependence on the change of ν than OCSVM. The network maps shown in Figures 11 (d) and (e) were obtained using the proposed method with ν = (d) 0.34 and (e) 0.43, corresponding to 2.0 and 2.5 times the estimated one. Figure 11 (f) is the network map identified by PICA. There are 3116 voxels in this slice involved to the analysis, and only 12 more voxels are identified as part of SMN by the proposed method when ν increases from 0.34 to 0.43, showing 23.37 times less dependence on the change of ν than OCSVM. The regional homogeneity of the identified regions in Figures 11 (a)-(f) are 0.621, 0.63, 0.539, 0.224, 0.226 and 0.226, respectively. The regions identified by the proposed method show a higher or similar regional homogeneity compared to the PICA results.

Figure 11.

(a)-(b) Part of DMN obtained from another individual subject using the proposed method with two ν values: (a) 0.17, (b) 0.28. (d)-(e) Part of SMN mapped using the proposed method with ν equal to (d) 0.34 and (e) 0.43. (c), (f) PICA mapping results.

In the group analysis of the resting-state data from the third experiment, the settings of λ_r and λ_s were the same as the group analysis for the motor task data. Figure 12 shows the mapping results of DMN and SMN, where the connectivity maps shown in (a),(b) and (e),(f) were obtained using the proposed method with ν equal to 2.0 and 3 times the originated estimated values, those shown in (c) and (g) were obtained using GICA, and those shown in (d) and (h) were generated using the correlation analysis with FDR control. The thresholds of the GICA and correlation analysis methods were chosen to generate the same numbers of functionally connected voxels in the encircled regions shown in Figures 12 (b) and (f). The regional homogeneity of functionally connected regions identified by the three methods was computed for each network, and is listed in Table 6. The SMN regions identified by the three methods show quite similar regional homogeneity in terms of the average and standard deviation of KCC values. For DMN, the average KCC value of the regions identified by the correlation analysis is slightly higher than that obtained by the proposed method, and the regions identified by GICA have the lowest average KCC value. It was observed that at the same level of mapping sensitivity in the posterior cingulate cortex area, the functionally connected voxels in media prefrontal cortex are not sufficiently identified by GICA, and those in left and right inferior parietal cortex are not sufficiently detected by the correlation analysis.

Figure 12.

(a), (b) Part of DMN identified in the group study using the proposed method with ν equal to (a) 1.0 and (b) 3.0 times the estimated ones. (e), (f) Part of SMN identified at the group level using the proposed method with ν equal to (e) 1.0, and (f) 3.0 times the originally estimated values. (c), (g) GICA mapping results. (d), (h) Mapping results from the correlation analysis with FDR control. The thresholds of the GICA and correlation analysis methods were selected to identify the same numbers of functionally connected voxels in the encircled regions as shown in (b) and (f).

Table 6.

Regional homogeneity (KCC) of mapping results obtained by the proposed, GICA, and correlation methods in the group level resting-state study. The mean and standard deviation (std) of KCC values were computed across all subjects and sessions.

	Proposed Method		GICA		Correlation Analysis
	Mean	Std	Mean	Std	Mean	Std
DMN	0.205	0.055	0.18	0.054	0.238	0.056
SMN	0.275	0.074	0.272	0.072	0.273	0.078

4. Discussion

The feature selection method used in this study is heuristic and can only provide an approximate estimation of the features’ contributions to the spatially regularized SVM learning. It was found that the computed feature contribution index values vary across sessions and subjects. There are multiple possible factors that could affect the estimation, including but not limited to: remaining head movement artifacts, physiological noise, imaging artifacts, and data preprocessing. In order to provide a reliable estimation, all experimental data were used and the estimated feature contribution index values were averaged over all experimental data. Although it might not be absolutely accurate, the averaged feature contribution index values may provide guidance about what category of features can contribute more to the spatially regularized SVM learning. For instance, it was observed that four of the top five features selected from the task-related experimental data are computed using each voxel's neighboring voxels. Similarly, four of the top five features selected from the resting-state experimental data also involve each voxel's neighboring voxels. These features, which are denoted by “spatiotemporal features” in our study, not only capture the temporal correlation between each voxel and an expected HDR or a predefined seed region, but also contain spatial correlation information within the voxel's neighborhood. This observation is consistent to our previous studies where no spatial regularization was considered for the SVM learning (Song et al., 2009, 2014). The between-trial cc value of each voxel, which is also called temporal self-correlation of the voxel, is usually considered as a useful feature in task fMRI studies where multiple trials are acquired in each scan session (Ngan et al., 2001, Lu et al., 2003). However, this feature shows less contribution compared to the others in the experimental study. There are two possible reasons for this observation. First, temporal self-correlation does not contain any spatial information, and for the spatial regularized SVM learning, it is not helpful in forming spatially grouped active regions. Second, the cardiac- and respiration-induced physiological noise in fMRI data may introduce global temporal correlation in grey matters, ventricle and other regions close to large blood vessels. As a result, most of the voxels in these regions may exhibit a relatively high temporal correlation, and the contributions from the between-trial cc values of truly active voxels could be overwhelmed. The peak delay of the ccf could be another useful feature if the TR is sufficiently short, but it was not considered in this study because relatively large TRs of the experimental data. The feature study in this work did not cover all possible features that can be extracted from fMRI data. Any features that could contribute to the SVM learning can be added to the candidate feature set and assessed.

From the comparison study of the three edge weighting methods, it was found from Figures 3, 4 and Table 3 that the proposed correlation-based edge weighting is a better choice as compared to the equal edge weighting and the RBF kernel-based edge weighting. Using an equal weight for all edges with neighboring voxels may bring ambiguities around boundaries of active or functionally connected regions, and is not appropriate to be applied to different experimental data with different spatial resolutions because the spatial correlation between neighboring voxels is affected by voxel size. The RBF-based edge weighting needs a proper setting of the RBF kernel width, which is unknown but should be adjusted according to spatial resolution as well. Correlation-based weighting can automatically reflect the true spatial correlation between neighboring voxels and adapt to the spatial resolution. Consequently, it can potentially better characterize the boundaries of active or functionally connected regions. The neighborhood size is another factor that may affect the final mapping performance. In our study, it was found that a 3×3 neighbor (the single-slice case) is sufficient for all datasets used in the experiments. With an increased image resolution, a greater neighborhood might be needed.

In the proposed method, the SR-OCSVM parameter ν is usually set greater than the initially estimated value in order to obtain a sufficient mapping sensitivity. This leads to false positives in the initial mapping results. The effects from the false positives can be maximally removed by using the prototype selection and SR-TCSVM reclassification. The reason to use SR-TCSVM instead of SR-OCSVM for the reclassification is that SR-TCSVM provides a better mechanism to control the generalization performance of SVM learning. It was found that the dependence of the proposed method to ν is further decreased in the group study compared to those shown in the individual subject studies. For instance, two more ν values were tested for the proposed method in the group level motor task study: ν=1.5 and 3.5, and the corresponding mapping results are almost the same as those shown in Figure 9. This indicates that the proposed method is a reliable tool for group level fMRI data analysis.

In the group level analyses of task and resting state data, the thresholds of the GICA, GLM, and correlation methods were adjusted for each individual slice to achieve the same mapping sensitivity as the proposed method in a pre-specified region. This resulted in multiple thresholds in each analysis. For instance, three different thresholds were used in the GLM method in order to obtain the activition maps shown in Figures 9 (d), (h), and (j). If only one threshold is used, which is typical when the GICA, GLM, and correlation methods are used, these methods cannot achieve the same mapping performance as the proposed method. For example, it was found that if the threshold used to obtain the map shown in Figure 9 (d) is used for all slices, then the activation in the supplementary motor cortex cannot be identified by the GLM method.

Since the fMRI spatial correlation is considered not only in the SR-OCSVM and SR-TCSVM learning, but also in the preprocessing (spatial smoothing), feature representation of each voxel, and prototype selection, it would not be necessary to assign large values to the regularization parameters λ_r and λ_s, and our experimental study verified this. There is no theoretical guidance about how to set these two parameters, and they were experimentally determined in this work. It was also found that slight changes of these two parameters won't bring considerable variations in the final mapping results.

“Soft” decision (or a probability threshold of 0.5) is used in the proposed method and PICA by comparing each voxel's probabilities of active and inactive, or functionally connected and unconnected. This is equivalent to assigning equal loss to false positives and false negatives (Hartvig et al., 2000; Beckmann et al., 2004). If a lower level of false positive rate or a higher mapping sensitivity is required in a study, we may switch to a “hard” decision by choosing a probability threshold above or below 0.5. But in such situations, the equivalent SVM classification hyperplane might not well match the true boundary between active/connected and inactive/unconnected voxels in the feature space.

KCC was used to estimate the regional homogeneity of identified active or functionally connected regions to provide supportive information for the evaluation of the mapping performance. Typically, false positives may lead to a decreased regional homogeneity. For instance, active regions shown in Figure 7 (d) comprise mis-identified voxels, and the computed KCC value is lower than that calculated from active regions shown in Figure 7 (c). It is noted that KCC cannot be used alone for the performance evaluation because insufficiently identified functional regions may result in greater KCC values than sufficiently identified ones. Therefore, KCC should be used together with mapping results to evaluate the mapping performance.

Unlike most SVM-based brain mapping methods, which perform supervised learning and classifications on specific brain cognitive states or disorders, the proposed technique is aimed to provide a general mapping of brain function in various task conditions or resting-state. For this purpose, supervised learning was not considered because there exist significant variations in brain functions in different task conditions or resting-state, and it is costly and inconvenient to obtain training data for each brain mapping task. Therefore, semi-supervised or unsupervised learning techniques are more appropriate in such circumstances. The proposed method is a semi-supervised technique that can adapt to the intra- and inter-subject variations of fMRI data. Users need to provide prior information from an expected HDR in a specific task condition, or a seed region related to a specific network-of-interest in resting-state to perform brain functional mapping. ICA is an unsupervised approach that does not require the expected HDR or seed information, and can simultaneously generate all possible signal and noise patterns indicated by ICs. However, all ICs have to be visually inspected or compared to predefined templates to identify functional patterns-of-interest. The experimental results in this work indicate that the proposed method can provide similar or better mapping performance compared to ICA at the individual and group level.

The proposed method has several advantages. First, it is data-driven and SR-OCSVM and SR-TCSVM do not superimpose any parametric models to fMRI data/computed features. Second, the semi-supervised learning procedure enables it to adapt to the intra- and inter-subject variations of fMRI data, and no fixed thresholds are required for the final decision. Third, by formulating the brain functional mapping as an outlier detection process, the proposed method can identify a small number of active or functionally connected voxels that might not be revealed by conventional techniques (Miller et al., 2008). Finally, it can identify brain function in individual slices and whole brain for individual subjects and at the group level, and can be used as a general tool for brain functional mapping in various task-related and resting-state studies. It is worth noting that the application of the proposed technique is not limited by the basic assumption that the number of active voxels in a task condition or functionally connected voxels in a specific network is less than 50% of that of all voxels in brain. Under certain circumstances, for instance, a sufficiently low noise level and/or a complete characterization of BOLD effects in different brain areas, observable brain functional activations induced by a task stimulation could expand to a majority of brain (Gonzalez-Castillo et al., 2012). In such cases, the mapping of brain function can be implemented by using the proposed technique in two different ways. One is to perform the mapping multiple times with each time associated with a specific temporal pattern of BOLD response, and to combine the mapping results together. The other is to perform the proposed analysis in an opposite way by treating the majority class identified by SR-OCSVM as active or functionally connected voxels.

The limitations of the proposed method primarily lie in two aspects. First, a change of seed location in the resting-state studies may affect the mapping results. In this work, all seed regions were chosen based on previously reported works. It was found that a shift of the seed position by one or two voxels usually leads to a negligible change of mapping results in the group level study, but may result in more changes in mapping results of individual subjects. Second, the proposed method is sensitive to remaining imaging artifacts and noise in fMRI data, such as the subject head movement artifacts and cardiac- and respiration-induced physiological noise. Thus some preprocessing steps are necessary to attenuate these effects.

5. Conclusion

In summary, a spatially regularized SVM method was developed for the general mapping of brain function in task- and resting-state. The method implements a semi-supervised learning to adapt to the intra- and inter-subject variations of fMRI data, and can approximate a true boundary between active/connected and inactive/unconnected voxels in a feature space. The primary innovation of the method is to integrate the spatial regularization into the OCSVM and TCSVM learning with a correlation-based edge weighting for the initial and final mapping. The method was compared to PICA in the experimental study of individual subjects’ data acquired from the task- and resting-state. Group level studies were also performed based on the comparison with the GICA, GLM, and correlation analysis methods using the multi-subject motor task and resting-state fMRI data. Experimental results indicate that the proposed method can provide a similar to better mapping performance compared to the others, and be used as a brain functional mapping tool in various quantitative fMRI studies.

Highlights.

• A quantitative method is developed for task- and resting-state fMRI data analysis.

• The brain functional mapping is formulated as an outlier detection process.

• Support vector machines are used to implement a semi-supervised learning.

• Spatial constraints are integrated into the support vector learning.

• Salient features are identified for the brain mapping in task- and resting-state.