Comparative assessment of parametric neuroreceptor mapping approaches based on the simplified reference tissue model using [¹¹C]ABP688 PET

Abstract

In recent years, several linearized model approaches for fast and reliable parametric neuroreceptor mapping based on dynamic nuclear imaging have been developed from the simplified reference tissue model (SRTM) equation. All the methods share the basic SRTM assumptions, but use different schemes to alleviate the effect of noise in dynamic-image voxels. Thus, this study aimed to compare those approaches in terms of their performance in parametric image generation. We used the basis function method and MRTM2 (multilinear reference tissue model with two parameters), which require a division process to obtain the distribution volume ratio (DVR). In addition, a linear model with the DVR as a model parameter (multilinear SRTM) was used in two forms: one based on linear least squares and the other based on extension of total least squares (TLS). Assessment using simulated and actual dynamic [¹¹C]ABP688 positron emission tomography data revealed their equivalence with the SRTM, except for different noise susceptibilities. In the DVR image production, the two multilinear SRTM approaches achieved better image quality and regional compatibility with the SRTM than the others, with slightly better performance in the TLS-based method.

Introduction

The simplified reference tissue model (SRTM)¹ has been used extensively in quantitative studies of a reversibly binding radiotracer using dynamic positron emission tomography (PET) and single photon emission computed tomography, owing to its noninvasiveness and robustness in the estimation of kinetic parameters.^{2, 3, 4, 5} The model parameters have been estimated mainly using nonlinear least squares (NLS), which can provide unbiased solutions for parameter estimation from time-activity curves (TACs) with low- or moderate-level noise. In the use of NLS, however, highly noisy data may bring several limitations such as dependency on initial values, long computation time, and a high level of uncertainty.^{2, 4, 6, 7, 8} Therefore, the NLS-based standard SRTM (NLS-SRTM) is undesirable for parametric image generation (voxel-by-voxel analysis) characterized by large amounts of voxel data with high-level noise. Consequently, the application of NLS-SRTM is limited to the analysis of regional average TACs that are much less noisy than voxel TACs.^{2, 4}

Several linearized model approaches, capable of implementing the SRTM, have been developed to achieve fast and reliable voxel-wise parameter estimation for the generation of parametric images of neuroreceptor binding.^{2, 4, 5, 9} One of them is the basis function method (BFM)² that uses a set of basis functions to convert the SRTM equation into a multiple linear regression model. Another method is a multilinear reference tissue model with two parameters (MRTM2),⁹ whose underlying linear regression model with three parameters (MRTM) was originally derived independently of any specific model structures but is able to represent the standard SRTM if one-tissue compartment is assumed.^{4, 5} In these two methods, only two parameters need to be calculated through linear least squares (LLS) estimation. However, the unknown model parameters in these methods are not major kinetic parameters of interest (nondisplaceable binding potential or the distribution volume ratio (DVR))¹⁰ but their combinations with other parameters. Therefore, we need further division of the estimated parameters to obtain the parameters of interest, increasing the variability of the final result and yielding noisy parametric images.^{11, 12}

Conversely, Zhou et al⁴ suggested the following linearized SRTM (called multilinear SRTM throughout this paper) that has the DVR as one of its parameters,

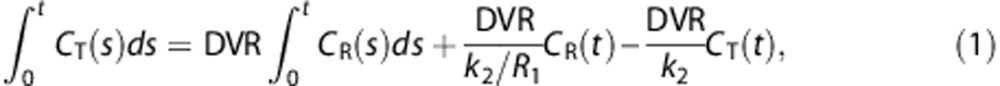where C_T(t) and C_R(t) are the tissue and reference TACs (kBq/mL), respectively. The last independent variable C_T(t) in the above model normally has high noise levels at each voxel, though LLS basically assumes that all independent variables are noiseless and only a dependent variable (here, 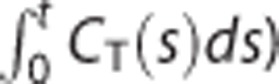) is contaminated with noise.^{13, 14} Since this violation of the model assumption because of noisy C_T(t) can introduce severe underestimations in the model parameters estimated by the LLS method,^{15, 16, 17} Zhou et al⁴ proposed to use the denoised C_T(t) through spatial smoothing.

In the presence of noisy independent variables, total least squares (TLS) estimation¹⁴ may be a plausible alternative to the LLS method; TLS provides consistent and unbiased estimates without suffering from the underestimation issue of the LLS method by taking into account the noise in both dependent and independent variables. Though the TLS problem is based on the fact that all variables in a linear model are measured with noise, the first independent variable and sometimes even the second one in equation (1) are often assumed to be effectively noise free. Thus, we can also consider an approach based on an extension of TLS, called mixed LS-TLS (MTLS),¹⁴ that allows noise in dependent and only some independent variables.

Because the aforementioned linear approaches can be derived from the standard SRTM, they are fundamentally equivalent to NLS-SRTM except for different susceptibilities to noise, leading to distinguishable performances in parametric imaging. Although BFM and MRTM2 have been evaluated and frequently used in the literature,^{3, 5, 11} a comparative analysis of them with the methods based on the multilinear SRTM has been rarely performed. In Zhou et al,⁴ the regularization-based MRTM (a method of indirect DVR estimation) showed worse variance property than the multilinear SRTM with spatial smoothing (a method of direct DVR estimation) because of the former's unavoidable error propagation caused by the division of parameters. In light of this, in the present study, we compare all those linear approaches in terms of their compatibility with NLS-SRTM and the quality of DVR parametric images. We hypothesized that the methods for multilinear SRTM would perform better in parametric imaging than the others based on a parameter division.

For their comparison and evaluation, we applied these methods to both simulated and real dynamic [¹¹C]ABP688 (3-(6-methyl-pyridin-2-ylethynyl)-cyclohex-2-enone-O-¹¹C-methyl-oxime)¹⁸ human brain PET data. [¹¹C]ABP688 is a highly selective and promising radioligand recently developed for the in vivo imaging of metabotropic glutamate receptor 5 (mGluR5), a potential therapeutic target in various brain diseases.^{18, 19, 20, 21} [¹¹C]ABP688 shows fast kinetics and its binding can be reliably quantified using the NLS-SRTM as shown in previous PET studies in both animals^{22, 23, 24} and humans,²⁵ where the results of NLS-SRTM showed a high correlation (r⩾0.97) with those of a two-tissue compartment model despite small bias (see section Reference Region for [¹¹C]ABP688). Although its uptake pattern is consistent with mGluR5 distribution in the human brain,^{19, 26} a relatively moderate uptake in the brain due to lower affinity of [¹¹C]ABP688 to mGluR5 compared with others,^{20, 27, 28} and the short half-life of [¹¹C] usually yield noisy dynamic PET data. Such noise properties of [¹¹C]ABP688, in addition to the wide distribution of the binding sites in the brain, should well allow differences to be seen at high noise levels among the parametric imaging approaches.

Materials and methods

Data Acquisition and Processing

The Institutional Review Board of Seoul National University Hospital approved this study and signed, informed consents were obtained from all participants. Thirty participants, including 9 healthy volunteers and 21 Parkinson's disease patients, underwent 60-minute dynamic [¹¹C]ABP688 PET scan using a Siemens Biograph mMR PET/MRI scanner (PET spatial resolution: 4.4-mm at 1 cm and 5.2-mm FWHM at 10 cm offset from the center of transverse field-of-view). For each participant, about 370 MBq (10.0 mCi) [¹¹C]ABP688 (mean specific activity: 139.6 GBq/μmol) was administrated with an intravenous bolus injection, and then the PET data were acquired in a 3D list mode without arterial blood sampling. A total of 44 dynamic PET frames (8 × 15, 16 × 30, 10 × 60, 10 frames × 240 seconds) were reconstructed using filtered back projection followed by 4-mm Gaussian postfiltering, with routine corrections for physical effects such as radioactive decay and attention (using UTE MR-based attenuation map). The reconstructed individual frames consisted of 127 transaxial slices with a matrix size of 256 × 256, a pixel size of 1.40 × 1.40 mm², and a slice thickness of 2.03 mm.

Simultaneously with the PET data, sagittal T1-weighted MR images (256 × 256 matrix and 208 sagittal slices with 0.98 × 0.98 × 1.00 mm³ voxel size) were acquired using a 3D Turbo FLASH sequence with a repetition time of 1,670 ms, a echo time of 1.89 ms, and a flip angle of 9°. Then, region-of-interest (ROI) masks for various brain regions at each hemisphere were automatically delineated from the individual T1 MR image using the FMRIB Integrated Registration and Segmentation Tool (FIRST, FSL v4.0, Oxford University, Oxford UK, http://www.fmrib.ox.ac.uk/fsl); the ROIs include the caudate nucleus, hippocampus, and putamen, which are receptor-rich brain regions, the thalamus with moderate-mGluR5 density, and the cerebellum (reference region) known to have almost no expression of the mGluR5.^{19, 28} By directly placing those ROIs on the reconstructed PET images without any coregistration between both modalities, we obtained regional TACs.

Kinetic Analysis

In this study, DVR was the parameter of interest to be compared among the methods. In all DVR estimations, cerebellar TAC was used as a reference input function, and a weighted sum of squared residuals was minimized to account for noise-level differences among the 44 data points. For the weights, we used the frame durations.^{4, 8}

Simulation data

We first performed a simulation to evaluate bias and variability of DVR estimates by all method. We obtained simulation parameters ((β₁, β₂, β₃)=(0.915, 0.072, 0.063) resulting in DVR=2.051) by fitting the NLS-SRTM to a real hippocampal ROI TAC. For the input function, we used the average of cerebellar TACs over all participants that we assumed to be noiseless. We generated 60-minute noiseless tissue TAC using the SRTM equation. Then, Poisson-like noise at each of 11 noise levels (5% to 100%), modeled as in previous studies,^{9, 12, 29, 30} was added to the noiseless tissue TAC, yielding 100,000 noisy TACs for each level. The noise level was defined as averaged coefficient of variation (CV) of the later portion of TAC (5 to 60 minutes); 5% and 50% correspond to the noise levels of real ROI and voxel data, respectively (see Supplementary Figure E3 for example TACs). In addition, we simulated noisy input functions at 5% and 10% levels to examine the effect of noise in the input function.

From each set of tissue and reference TACs, DVR was estimated by applying LLS to the multilinear SRTM (LLS-SRTM), by applying MTLS while assuming that only C_T(t) is noisy (MTLS1), and also assuming that both C_T(t) and C_R(t) are noisy (MTLS2). We also applied LLS-SRTM after smoothing the independent variable C_T(t) (LLS-SRTM-SC), MTLS1-based and MTLS2-based regularization with a spatial constraint (MTLS1-SC and MTLS2-SC, respectively). Then, we compared their results with those from BFM and MRTM2, by measuring their bias and CV¹² based on the true DVR after removing outliers; we defined outliers as extreme values that are more than 1.5 interquartile ranges below the first quartile or above the third quartile in a given set of 100,000 estimates. Descriptions of all the approaches used will be presented in next subsections.

Human Positron Emission Tomography data

Before analyzing dynamic PET data at each voxel to produce DVR parametric images, regional DVR values were calculated from ROI TACs to illuminate the noise effect on parametric imaging relative to the regional analysis and to provide a gold standard (NLS-SRTM) for the comparisons at both ROI and voxel levels. From ROI TACs, DVRs were estimated by LLS-SRTM, MTLS1, and MTLS2. In addition, BFM and MRTM2 were also applied to confirm the adequacies of the parameter bounds for BFM and of the k̄_2R value for MRTM2. For each method, the resulting ROI DVR estimates were compared with the gold standard in terms of correlation coefficients and linear regression. Then, the resulting coefficients and fitted regression lines of all the methods were compared with each other.

Meanwhile, DVR parametric images were generated by applying LLS-SRTM-SC, MTLS1-SC, MTLS2-SC, BFM, and MRTM2 as well as LLS-SRTM, MTLS1, and MTLS2 methods to whole-voxel data. Regional mean values of the DVR images were extracted by applying the ROI masks to the images, and then their linear relationships with the NLS-SRTM ROI results (the gold standard) were also analyzed and compared among the methods. Moreover, the qualities of the parametric images were assessed by comparing the spatial variation of DVR values in image space among the methods. Because we evaluated all the results against the NLS-SRTM results, the term bias in the real data analysis will mean a deviation from the NLS-SRTM results throughout the paper.

Multilinear Simplified Reference Tissue Model Based on Linear Least Squares

With dynamic PET measurements of n frames, equation (1) gives rise to an over-determined system of n linear equations in P=3 unknowns (DVR, ), represented in a matrix form by

where X is an n × p matrix and its ith row is given as 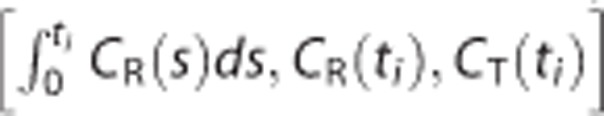, y is an n × 1 vector whose ith element is 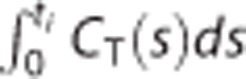for ith mid-frame time t_i (1⩽i⩽n) and .

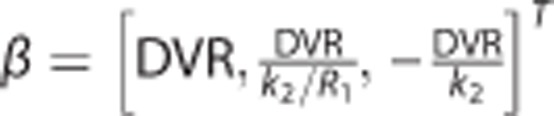Given n measurements of one dependent variable (y) and p independent variables (X), the LLS estimation finds a solution (β̂_LLS) minimizing the sum of squared distances from the n measured points to the fitted p-dimensional hyperplane as follows:

The meaning of the minimized cost function in equation (3) is the minimal perturbation of noisy data such that the modified set ŷ =Xβ has a solution. Such perturbation is based on the assumptions that X is exactly measured, and that y is a perturbed measurement of ŷ (due to noise) satisfying an exact linear relationship ŷ =Xβ. The LLS estimate is given as .

In equation (1), 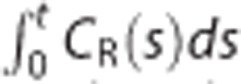and sometimes C_R(t) could be considered as effectively noise-free data, because the integration reduces fluctuations in TAC and C_R(t) is obtained by averaging voxel TACs over a reference ROI. Hence, in general, the noise level of C_T(t) determines whether the LLS assumption about X is valid or not. For data with low-level noise such as ROI TACs, LLS can produce a good estimate for the unknown parameters β. However, at voxel levels with large contamination, LLS can introduce a negative bias to β estimates because of the violation of the LLS assumption.

Multilinear Simplified Reference Tissue Model Based on Linear Least Squares with Spatial Constraints

An intuitive and direct approach to address the aforementioned bias issue in parametric imaging via LLS-SRTM would be to reduce the noise level of C_T(t). For this purpose, Zhou et al⁴ suggested replacing the original noisy C_T(t) with its spatially smoothed values. The denoised C_T(t) serves as a spatial constraint, forcing the regional mean values of parametric images to be close to the corresponding regional analysis results.⁴ The resolution loss associated with spatial smoothing is not directly propagated into the final parametric images because the smoothed data are only used as an independent variable, in the estimation process. In this study, we used a 2D mean filter with a window size of 10 × 10 pixels.

Multilinear Simplified Reference Tissue Model Based on Mixed LS-Total Least Squares

The MTLS¹⁴ considers noisy and noise-free independent variables together. Whereas the LLS method confines the directions of fitting to be along only the coordinate axis of y, MTLS searches all possible perturbations of n measured points along not only y but also the coordinate axes corresponding to noisy independent variables.

In this study, the MTLS solution, denoted by β₀, was computed using the closed form solution (equation B.4) of the original MTLS problem described in Supplementary Appendix B. Meanwhile, we also derived the following minimization problem that is equivalent to the original MTLS problem,

where P is a diagonal matrix whose diagonal entries have values of 1 and 0 corresponding to noisy and effectively noise-free columns of X, respectively. Notice that the new formulation of equation (4) is very convenient for setting a regularization problem in the context of the MTLS problem as shown in the next subsection and, to our knowledge, has not yet been reported elsewhere.

Although MTLS assumes that some of the independent variables are exactly known, all data in tracer kinetic models are contaminated with noise to some extent. Therefore, care has to be taken to identify which independent variables in equation (1), particularly C_R(t), can be considered to be almost noise free. Therefore, we tested two different assumptions that only C_T(t) (for MTLS1) and both C_T(t) and C_R(t) (for MTLS2) are noisy. For the two assumptions, 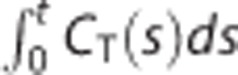is assumed to be noise free. We used P=diag(0, 0, 1) for MTLS1 and diag(0, 1, 1) for MTLS2.

Mixed LS-Total Least Squares With Spatial Constraints

In theory, MTLS provides an estimate with better accuracy but larger variance than LLS.¹⁴ Furthermore, highly noise contaminated voxel data and strong correlation between independent variables in kinetic models can exacerbate the variability in the MTLS results (β₀), giving rise to large spatial noise in parametric image space. Since a regularization technique can drastically reduce variance at the expense of acceptable bias, we adapted one strategy introduced in Zhou et al⁴ for MTLS so that the resulting solution is regularized in the context of the MTLS problem; by adding a penalty term to equation (4), we formulated the following regularization problem,

where β_s is a spatial constraint that restricts the range of bias allowed in the final solution, λ is a regularization parameter to control the balance between the cost function and the penalty (or the balance between bias and variance), and L is a diagonal matrix that assigns different weights to each component of β. As the penalty term increases (or decreases), the solution converges to β_s (or β₀). Hence, the penalty in equation (5) spatially constrains the resulting parameters to be around the values of neighboring voxels.

The implementation of solving the above regularized MTLS with a spatial constraint (MTLS-SC) includes two steps. In the first step, the spatial constraint β_s is prepared by computing β₀ images using the MTLS method and subsequently by applying a spatial smoothing filter to the β₀ images. In the final step, the β̂_MTLS−SC parametric images, the solution to the MTLS-SC problem (equation (5)) is computed by

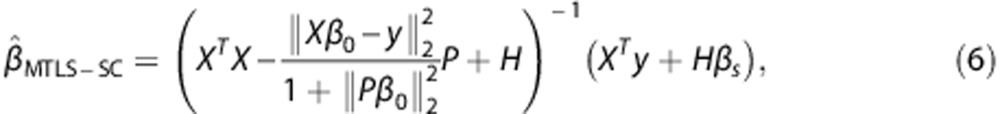where H is a diagonal matrix and its diagonal elements h_j (j=1, 2, 3 in multilinear SRTM) are calculated as follows:

Here, β_0j and β_Sj are the jth elements of vector β₀ and β_s, respectively, and σ̂² is the noise level of the data estimated as 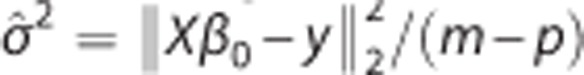. For both simulated and real data, we used a 2D median filter (window size: 5 × 5 pixels) followed by a 2D mean filter (window size: 5 × 5 pixels) to obtain β_s.

Basis Function Method

The BFM is based on the analytical solution of the original SRTM rewritten as

where (β₁, β₂, β₃)^T=(R₁, k₂–R₁k′₂, k′₂)^T, R₁(unitless) is the tissue-to-reference ratio of the rate constants for the influx from plasma, k₂ (1/min) is the efflux rate constant from tissue to plasma, and k′₂ (1/min) denotes the apparent efflux rate constant from tissue when the tissue region can be approximately described with one compartment given as 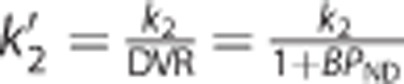. Unlike the original SRTM that uses NLS to fit equation (8), the BFM applies LLS for a set of linear models that are derived from equation (8) as follows

where each 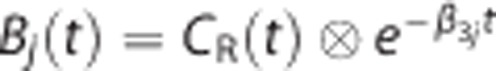is called a basis function, β_3j is the jth value in a predefined discrete pool of β₃ values, and m is the number of the predefined β₃ values or the corresponding basis functions. As the result, LLS estimates of [β̂_1j, β̂_2j] are obtained for each β_3j (or B_j(t)). Then, over all the m sets of [β̂_1j, β̂_2j, β̂_3j], the BFM solution [β̂₁, β̂₂, β̂₃] is determined as the one with the smallest sum of squared errors. Finally, DVR is computed by (β̂_2j/β̂_3j+β̂_1j. In clinical data analysis, we assumed that β₃ is bounded between 0.03 and 0.60 (1/min) by considering the parameter estimates from the other methods used in this study, and 100 discrete values spaced logarithmically between the bounds were used as the lookup table. For simulation studies, we added a true value of β₃ to that lookup table.

Multilinear Reference Tissue Model with Two Parameters

The MRTM2 is based on the following model with two parameters [β_1,β₂]^T=[k₂,−k′₂]^T,

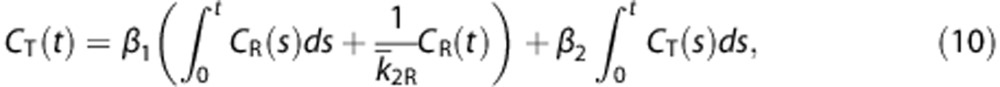where k̄_2R is the preliminarily estimate of the values for the efflux rate constant in the reference region (k_2R), and is usually estimated by averaging the k₂ estimates obtained from several ROI TACs.⁹ For real data analysis, in this study, we obtained k̄_2R for each participant by applying the original model with three parameters (MRTM)⁹ to ROI TACs, in advance; its mean over all participants was 0.240±0.046. Subsequently, the parameter estimates β̂₁ and β̂₂ were computed using LLS and DVR is determined as 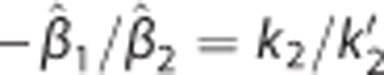. In simulation studies, we used a true value for k̄_2R.

It is noteworthy that the MRTM and MRTM2 were derived from graphical analysis without specifying a specific compartmental configuration for tissue region and without assuming the same K₁/k₂ for both tissue and reference regions. Thus, they are mainly fitted to only the later parts of the dynamic frames after a certain time point t*(⩾0). Besides, when one-tissue model assumed, the MRTM with t*=0 was proved able to implement the SRTM.^{4, 5} In this study, we confined the application of the MRTM and MRTM2 to the one-tissue compartment case for the compatibility with the SRTM, and therefore fitted the MRTM (only for pre-estimation of k̄_2R) and MRTM2 to the whole frames.

Results

Simulation Studies

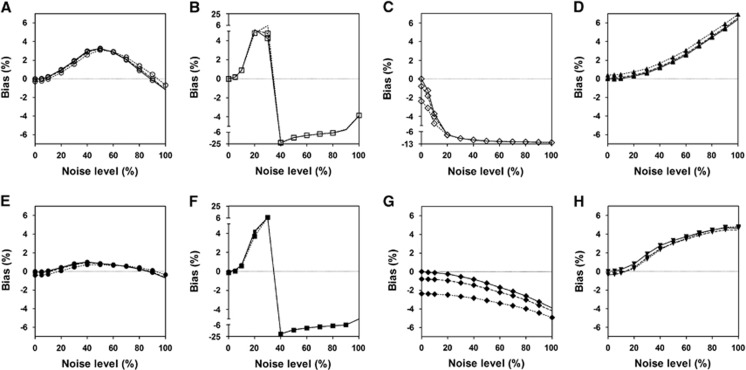
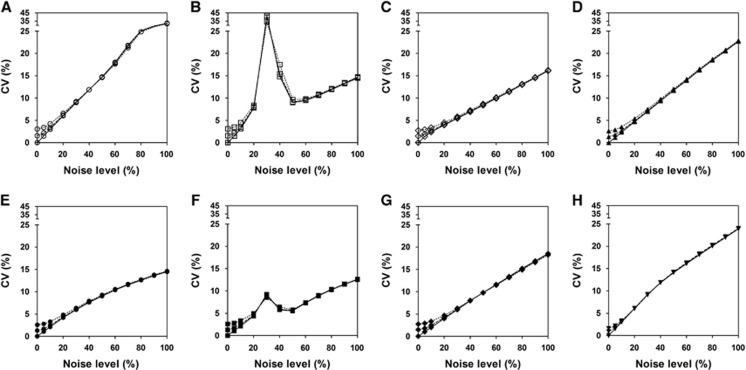
Figures 1 and 2 show the bias and CV of DVRs estimated by each method for different levels of input function noise. For noiseless input data (solid lines), all the methods showed almost no bias at low tissue-noise levels (⩽10%) but very different bias properties with increasing tissue-noise levels. The biases of results from LLS-SRTM, MTLS2 and MTLS2-SC have larger extents than the others at almost all tissue-noise levels. The negative bias of LLS-SRTM rapidly increased and then converged to a certain value while those of MTLS2 and MTLS2-SC showed fast and more complicated change. The other five approaches showed much slower changes in bias, while maintaining small values; among them, MTLS1-SC provided the most stable and the smallest bias. However, the CV also increased with higher tissue-noise levels for all the methods except for MTLS2 and MTLS2-SC; the two methods showed very complicated behavior in CV like in bias, possibly due to violation of assumption for noise level of independent variables. MTLS1 yielded the largest CVs at the expense of achieving small bias whereas LLS-SRTM showed the smallest CVs. The DVRs directly estimated by MTLS1-SC and LLS-SRTM-SC showed better precision than those computed by division of parameter estimates in BFM and MRTM2.

Figure 1.

Comparison of bias of distribution volume ratio (DVR) values estimated by various methods from simulated tissue time-activity curves (TACs) of [¹¹C]ABP688 at different noise levels ranging from 0% to 100% and reference region input functions at noise levels of 0% (solid line), 5% (dashed line), and 10% (dotted line). We used eight different linear estimation methods based on the standard simplified reference tissue model (SRTM) including (A) MTLS1; (B) MTLS2; (C) LLS-SRTM; (D) MRTM2; (E) MTLS1-SC; (F) MTLS2-SC; (G) LLS-SRTM-SC; and (H) BFM. The bias and CV were computed after removing outliers. BFM, basis function method; LLS, linear least squares; LLS-SRTM, multilinear SRTM based on LLS; LLS-SRTM-SC, LLS-SRTM with denoised C_T(t); MRTM2, multilinear reference tissue model with two parameters; MTLS, mixed LS-TLS; MTLS1, multilinear SRTM based on MTLS considering only tissue concentration C_T(t) as noisy data; MTLS2, multilinear SRTM based on MTLS considering both C_T(t) and reference region concentration C_R(t) as noisy data; MTLS1-SC, MTLS1-based regularization with spatial constraint; MTLS2-SC, MTLS2-based regularization with spatial constraint; SRTM, simple reference tissue model; TLS, total least squares.

Figure 2.

Comparison of coefficient of variance (CV) of distribution volume ratio (DVR) values, presented as in Figure 1. (A) MTLS1; (B) MTLS2; (C) LLS-SRTM; (D) MRTM2; (E) MTLS1-SC; (F) MTLS2-SC; (G) LLS-SRTM-SC; and (H) BFM. BFM, basis function method; LLS-SRTM-SC, LLS-SRTM with denoised C_T(t); MRTM2, multilinear reference tissue model with two parameters; MTLS, mixed LS-TLS; MTLS1, multilinear SRTM based on MTLS considering only tissue concentration C_T(t) as noisy data; MTLS2, multilinear SRTM based on MTLS considering both C_T(t) and reference region concentration C_R(t) as noisy data; MTLS1-SC, MTLS1-based regularization with spatial constraint; SRTM, simplified reference tissue model; TLS, total least squares.

As shown in Figures 1 and 2, similar overall trend of the bias and CV for each method was observed when using noisier reference input function. Only LLS-SRTM and LLS-SRTM-SC showed noticeable changes in bias (Figure 1); there was additional noise-induced negative bias that decreases as the noise of tissue TAC increases and becomes dominant compared with the noise of input function. The effect of noisy input function on the bias by the other methods was marginal and very consistent over all tissue-noise levels. However, the noisy input function affected the CV similarly for all the methods, only at low tissue-noise levels that are not very different from the noise levels of input function (Figure 2). As the tissue-noise becomes dominant, the effect of noisy input function on CV diminished.

Human Positron Emission Tomography Studies

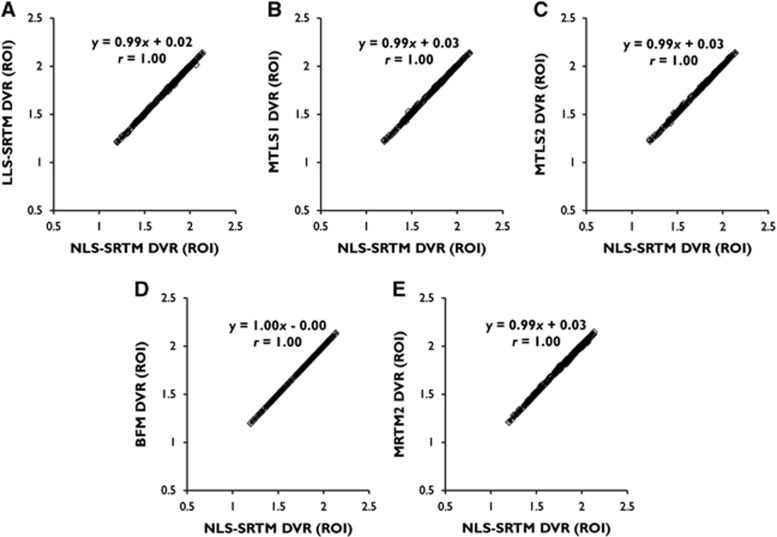
For ROI TACs with low noise level in general, the DVRs from LLS-SRTM, MTLS1, and MTLS2 (for a multilinear SRTM) were almost identical to those from NLS-SRTM (y=0.99x+0.02, r=1.00 for LLS-SRTM; and y=0.99x+0.03, r=1.00 for MTLS1 and MTLS2) as shown in Figure 3. In addition, BFM and MRTM2 (requiring division of model parameters for DVR estimation) also showed very similar results (y=1.00x−0.00, r=1.00 for BFM; and y=0.99x+0.03, r=1.00 for MRTM2), confirming reasonable parameter constraints for each method.

Figure 3.

Linear relationship between distribution volume ratios (DVRs) from several linear estimation methods based on the simplified reference tissue model (SRTM) and those from the SRTM using nonlinear least squares (NLS-SRTM) for region-of-interest (ROI) TACs from dynamic [¹¹C]ABP688 positron emission tomography (PET) data. (A) LLS-SRTM; (B) MTLS1; (C) MTLS2; (D) BFM; (E) MRTM2. Individual points in each scatter plot correspond to the DVR pairs from individual ROI TACs in the left and right sides of the caudate nucleus, hippocampus, putamen, and thalamus of total 30 participants. BFM, basis function method; LLS, linear least squares; MRTM2, multilinear reference tissue model with two parameters; MTLS, mixed LS-TLS; MTLS1, multilinear SRTM based on MTLS considering only tissue concentration C_T(t) as noisy data; MTLS2, multilinear SRTM based on MTLS considering both C_T(t) and reference region concentration C_R(t) as noisy data; TAC, time-activity curve; TLS, total least squares.

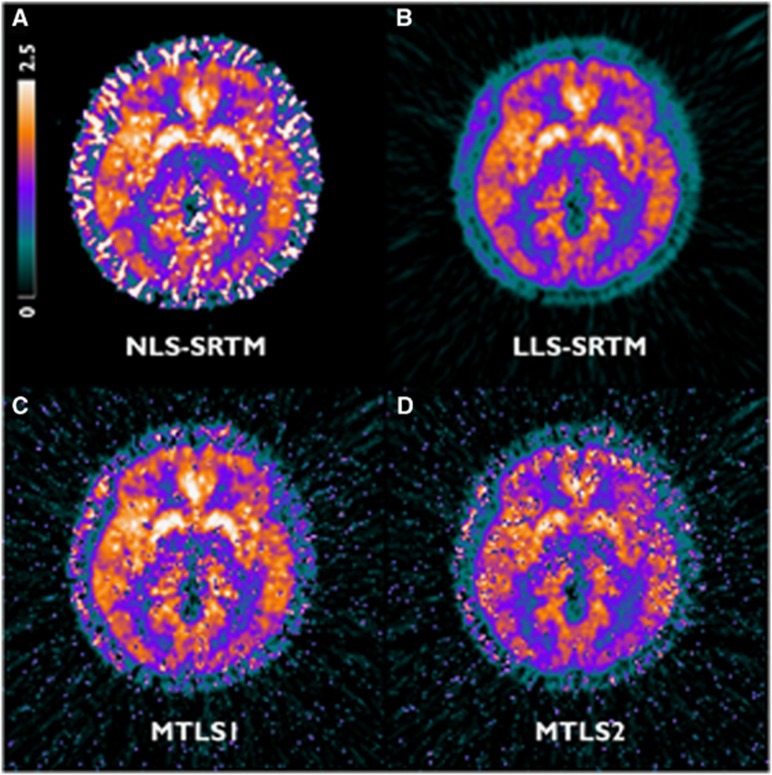
The different effects of noise become apparent in parametric images (Figures 4 and 6). Figure 4 shows the representative [¹¹C]ABP688 DVR parametric images generated using LLS-SRTM (A), MTLS1 (B), and MTLS2 (C) in which no spatial constraints were applied. Regional mean values in the LLS-SRTM DVR images revealed a bias relative to the gold standard obtained from ROI TACs using NLS-SRTM (y=0.85x+0.24, r=0.98; Figure 5A). Thus, despite better image quality, their image intensities were remarkably lower than those obtained by other methods shown in Figures 4 and 6. MTLS1 DVR images that considered only C_T(t) as a noisy independent variable exhibited remarkable spatial variability (Figure 4C). However, their regional mean values showed good agreement with the gold standard (y=1.01x+0.01, r=1.00; Figure 5B) when we removed outliers that are more than 1.5 interquartile ranges below the first quartile or above the third quartile of voxel DVRs in ROI; the outliers cause salt-and-pepper noise in the MTLS1 DVR images. MTLS2 introduced more severe noise into the resulting DVR images (Figure 4D) and also a relative bias in their regional mean values (y=0.81x+0.31, r=0.90; Figure 5C), even after removing outliers, implying the violation of assumption that both C_T(t) and C_R(t) are noisy data. Collectively, LLS-SRTM, MTLS1, or MTLS2 was not good for generating DVR images.

Figure 4.

Transverse planes of representative [¹¹C]ABP688 distribution volume ratio (DVR) parametric images generated using (A) NLS-SRTM and several methods based on multilinear SRTM without using spatial constraints: (B) LLS-SRTM, (C) MTLS1, and (D) MTLS2. For (A), initial parameter values for nonlinear fitting were obtained by fitting NLS-SRTM to spatially smoothed dynamic images in advance. MTLS, mixed LS-TLS; MTLS1, multilinear SRTM based on MTLS considering only tissue concentration C_T(t) as noisy data; MTLS2, multilinear SRTM based on MTLS considering both C_T(t) and reference region concentration C_R(t) as noisy data; NLS, nonlinear least squares; SRTM, simplified reference tissue model; TLS, total least squares.

Figure 5.

Linear relationship between regional mean values of distribution volume ratio (DVR) images generated using (A) LLS-SRTM-SC, (B) MTLS1-SC, and (C) MTLS2-SC and the same gold standard used for ROI-level comparison in Figure 3 (the ROI DVRs from NLS-SRTM). All the data points were obtained after removing outliers. MTLS, mixed LS-TLS; MTLS1, multilinear SRTM based on MTLS considering only tissue concentration C_T(t) as noisy data; MTLS2, multilinear SRTM based on MTLS considering both C_T(t) and reference region concentration C_R(t) as noisy data; NLS, nonlinear least squares; ROI, region of interst; SRTM, simplified reference tissue model; TLS, total least squares.

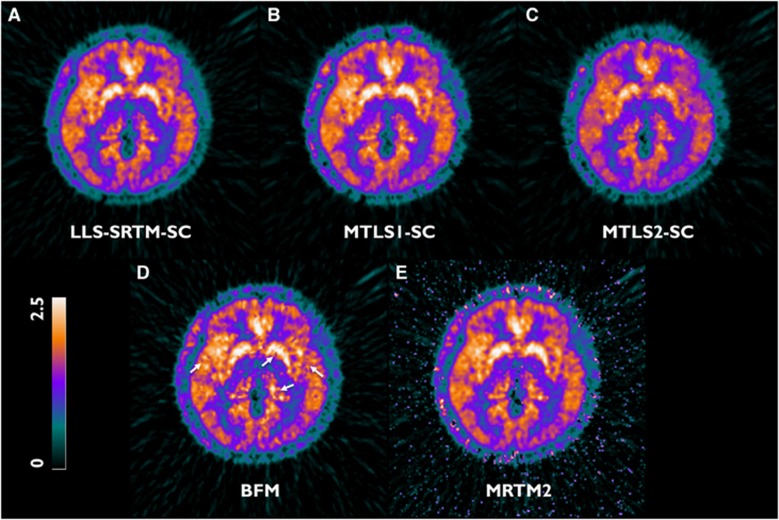
Figure 6.

Transverse planes of representative parametric images of distribution volume ratio (DVR) acquired using various methods from data of the same subject as Figure 4. (A) LLS-SRTM-SC, (B) MTLS1-SC, (C) MTLS2-SC, (D) BFM (white arrows point to blob-like artifacts that are possibly due to the spatial correlation of noise), and (E) MRTM2. BFM, basis function method; MRTM2, multilinear reference tissue model with two parameters; MTLS, mixed LS-TLS; MTLS1, multilinear SRTM based on MTLS considering only tissue concentration C_T(t) as noisy data; MTLS2, multilinear SRTM based on MTLS considering both C_T(t) and reference region concentration C_R(t) as noisy data; NLS, nonlinear least squares; SRTM, simplified reference tissue model; TLS, total least squares.

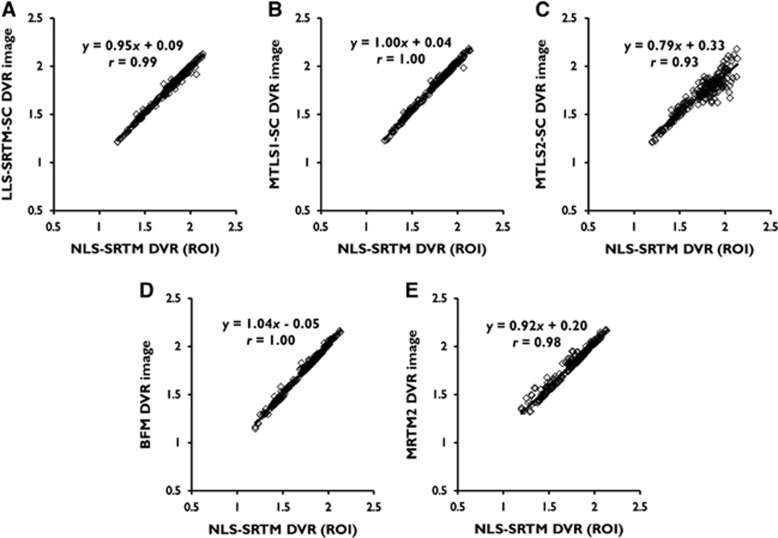
However, the use of a spatial constraint improved the results of LLS-SRTM and MTLS1 as shown in Figures 6 and 7. By use of the denoised C_T(t) (the spatial constraint constructed by spatial smoothing), LLS-SRTM-SC reduced the bias in the resulting DVR images while maintaining image quality and resolution (Figures 6A and 7A). MTLS1-SC achieved remarkable improvement in the quality of the DVR images without increasing bias (Figures 6B and 7B); this was achieved by successfully removing salt-and-pepper noise in the MTLS1 DVR images through regularization with a spatial constraint. The quality of MTLS1-SC images was comparable to the LLS-SRTM-SC images. Conversely, as illustrated in Figures 6C and 7C, MTLS2-SC still yielded severe bias in the DVR images.

Figure 7.

Linear relationship between regional mean values of distribution volume ratio (DVR) images generated using various methods and the same gold standard used for ROI level comparison in Figure 3 (the ROI DVRs from NLS-SRTM). All the data points were obtained after removing outliers. Each panel corresponds to a DVR image in Figure 6. (A) LLS-SRTM-SC, (B) MTLS1-SC, (C) MTLS2-SC, (D) BFM, and (E) MRTM2. BFM, basis function method; MRTM2, multilinear reference tissue model with two parameters; MTLS, mixed LS-TLS; MTLS1, multilinear SRTM based on MTLS considering only tissue concentration C_T(t) as noisy data; MTLS2, multilinear SRTM based on MTLS considering both C_T(t) and reference region concentration C_R(t) as noisy data; NLS, nonlinear least squares; ROI, region of interst; SRTM, simplified reference tissue model; TLS, total least squares.

Basis function method and MRTM2 produced DVR images of similar intensity levels. However, their parametric images were slightly noisier, as shown in Figures 6D and 6E. Although DVR images from BFM had ROI-mean values similar to those of gold standard (Figure 7D), they introduced some blob-like artifacts, possibly due to the spatial correlation of noise, indicated by the white arrows. MRTM2 have a larger number of outliers that deteriorate correlation with gold standard (Figure 7E) and produced noisy parametric image voxels in low binding regions (usually found in some subjects with relatively lower inject dose) and the background region outside the brain.

Discussion

In the present study, we have compared several different parametric neuroreceptor mapping approaches whose underlying models can be derived by the linearization of the standard SRTM equation. These methods share the basic assumptions of the SRTM except for how to handle the major noise source, C_T(t), which primarily leads to different properties among the resulting parametric images. Thus, the main objective of this study was to compare the SRTM-based approaches in terms of the effects of noise on parametric images. We first assessed their statistical properties using simulated [¹¹C]ABP688 data at various noise levels. Then, we applied these methods to dynamic [¹¹C]ABP688 PET images, whose image voxels have a small size and high-level noise. Besides the parametric imaging, we also performed ROI analysis to validate each method's compatibility with NLS-SRTM at low noise levels, to highlight the dissimilar effects of high-level noise by contrasting with the low-noise effect, and to assess the validity of a priori information required for BFM or MRTM2.

Comparison Between Direct and Indirect Approaches for Distribution Volume Ratio Estimation

Our simulation studies verified that the methods considered are radically equivalent to NLS-SRTM but have different susceptibilities to image noise. This is consistent with our human PET studies; in the ROI analysis, all the methods showed equivalently good results (Figure 3) whereas those of the corresponding parametric imaging approaches were distinguishable from each other (Figures 4–7). The major distinction in parametric imaging appeared between two categories of methods: ones that provide direct estimation of DVR using multilinear SRTM (LLS-SRTM or LLS- SRTM-SC and MTLS or MTLS-SC) and the others that produce DVR indirectly through division of other parameter estimates (BFM and MRTM2). In addition, the former direct methods estimate three parameters (including DVR) in weighted least squares manner by using C_T(t) as an independent variable and 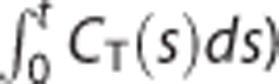as a dependent variable in their basis model (equation (1)) whereas the indirect ones estimate only two parameters (different from DVR) by using C_T(t) and 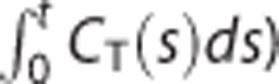as dependent and independent variables, respectively (equations (9) and (10)).

Those differences caused the direct approaches except for MTLS to achieve better image quality than the indirect ones (Figure 6). In general, the variability of the estimated model parameters depends on the noise level of the dependent variable. Because of the lower noise level of 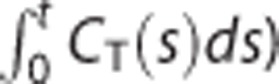in multilinear SRTM, even without use of any variance reduction technique, the results from LLS-SRTM or LLS-SRTM-SC generally have lower variability than those from the indirect methods; instead, LLS-SRTM may have negative bias caused by the higher-level noise in C_T(t). Although the use of MTLS for multilinear SRTM may increase the variability at the expense of reducing the bias, the regularization step in MTLS-SC can remove the additional variability of MTLS. Conversely, in the indirect methods, the higher-level noise in C_T(t) increases predominantly the variability of the estimated model parameters rather than the bias. To alleviate the inherently high variability, the indirect methods estimate only two parameters through variance reduction approaches such as the preestimation of one parameter or the incorporation of parameter bounds (see section Variance Reduction Techniques). However, despite estimating a smaller number of parameters, the indirect approaches showed larger CV values at high noise levels (Figure 2) and generated noisier DVR images (Figure 6) because the division process can amplify even small errors.

Noise-Level Assumptions for Independent Variables

The different noise susceptibilities among the direct methods stem from the different assumptions regarding noise levels of independent variables in multilinear SRTM, C_T(t), and C_R(t). Nevertheless, in the ROI analysis, LLS-SRTM, MTLS1, and MTLS2 showed very similar results that are in good agreements with NLS-SRTM (Figure 3). Conversely, the effects of their different assumptions were more evident in the analysis of voxel data; only MTLS1 generated nearly unbiased DVR images, suggesting that C_R(t) can be considered as almost noise free or to have negligible noise effect. A similar trend was observed in simulation studies as noise increased (Figures 1 and 2).

The similar ROI results are based on the low noise levels of the ROI TAC data for both C_T(t) and C_R(t) that were reduced by averaging highly noisy voxel TACs over the corresponding ROI regions. Hence, C_T(t) and C_R(t) would have negligible effects (negligible biases) on the LLS estimates like Figure 3A because they satisfied the LLS assumption.

The effects of noisy C_T(t) and almost noise-free C_R(t) on the parametric images were expressed as negative bias in the results from LLS-SRTM, additional variability in MTLS1 at the expense of avoiding such negative bias, and more variability in MTLS2 (Figure 4). The limitations in LLS-SRTM or MTLS1 were overcome in LLS-SRTM-SC or MTLS1-SC, respectively, by performing additional processes based on spatial constraints; consequently, good quality DVR images were generated (Figures 6A and 6B) with regional mean values equivalent to the gold standard (Figures 7A and 7B). However, the improvement of the image quality of MTLS2 after applying a spatial constraint was not sufficient. The spatial constraint could not effectively compensate for the increased variability in DVR estimates because of the unnecessary assumption of noise in C_R(t).

Bias Reduction Strategies

The LLS method has been widely used to estimate kinetic parameters from various linear models as well as multilinear SRTM, BFM, and MRTM2 assessed in this paper.^{2, 4, 7, 8, 9, 12, 29, 31, 32, 33} However, the noise-induced negative bias in LLS estimates is a well-known phenomenon in tracer kinetic modeling,^{15, 16, 17}

To address the bias issue, various strategies have been suggested including graphical analysis methods^{11, 30, 34, 35} (see Seo et al⁷ for a recent review of them) and others relied on more complicated models such as MRTM.^{4, 9, 29} Among them, applying smoothing techniques to the dynamic data may be the most simple and straightforward strategy to reduce the bias in the LLS estimates without modifying the associated linear models. However, spatially smoothing 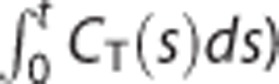as well as C_T(t) can yield a loss of spatial resolution and additional partial volume effects;^{7, 33} therefore, the smoothing-based approaches were usually based on temporal smoothing^{30, 34} or wavelet-based denoising techniques.¹¹ Conversely, LLS-SRTM-SC uses spatial smoothing not for 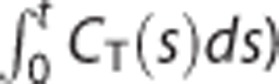but only for C_T(t); as a result, it was robust to the resolution loss as shown in Figure 6.

The theory of TLS was introduced for the first time to improve a result from the Logan graphical analysis with plasma input³² by Varga and Szabo.³⁵ However, successful bias reduction in the original work was not reproduced well in other studies where the TLS only partially removed bias.^{7, 11, 29, 34} The remaining bias is possibly because of the high noise correlation between the dependent and independent variables of the Logan model equations,^{14, 29} which comes from sharing C_T(t) in the denominators of those variables. On the contrary, MTLS-based methods yielded nearly unbiased results for both ROI and voxel data (except for outliers because of high variability). This would be because the dependent and independent variables of multilinear SRTM show much lower noise correlation than those in the Logan equations.²⁹

Variance Reduction Techniques

In parametric image generation using MTLS, bias reduction was accompanied by a variability increase (Figure 4C). To alleviate the increased variability, the nearly unbiased MTLS estimates were incorporated after smoothing as a spatial constraint into a subsequent regularized MTLS problem (MTLS-SC). The DVR images from MTLS1-SC showed a similar level of spatial variability compared with the level of LLS images (Figure 6D versus Figure 4B). For the regularization step, we used the ridge regression-based regularization strategy⁴ but with a modification to regularize the solution in terms of the MTLS cost function. In the field of numerical analysis, regularization in the context of the TLS problem has been solidly studied to address stability issues arising from the ill-conditioning of problems and high-level noise in the data.^{36, 37} However, the regularization of MTLS has not been treated explicitly. Hence, in the present study, we derived for the first time a new formulation of the MTLS problem (equation (4), Supplementary Appendix C) to use it as the main cost function in a regularized MTLS problem (equation (5), Supplementary Appendix D).

As mentioned in section Comparison Between Direct and Indirect Approaches for Distribution Volume Ratio Estimation, to enhance the stability of important parameters, MRTM2 (equation (10)) was proposed as a reduced model of MRTM given by

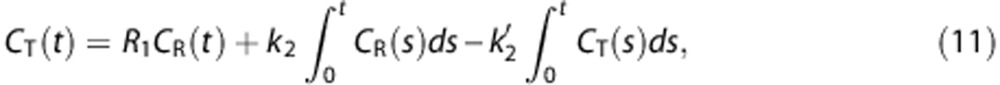by fixing one parameter in MRTM using 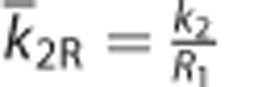.⁹ Despite decreasing the number of parameters, MRTM2 still showed relatively poor precision compared with the other methods we used, yielding lower correlation with gold standard (Figure 7). The remaining outliers should be partly attributable to high-level noise in the dependent variable. Similarly, to reduce the variability because of noise in C_T(t) in equation (11), Zhou et al⁴ suggested a ridge regression with spatial constraint, but the improvement of image quality was limited. The poorest results of MRTM2 would be also attributed to the inaccuracy in predetermined k̄_2R, which can be amplified by a division process.

Similarly, BFM avoids the variability arising from highly noisy C_T(t) by estimating only two parameters with the benefit of incorporating parameter bounds to one parameter (k′₂) among three. Although the resulting estimates of the other two parameters are optimal in terms of LLS for a fixed k′₂, the whole set of estimates is still suboptimal because of the discretely chosen estimate for k′₂, possibly introducing small biases. Furthermore, the performance of BFM depends on the selection of the parameter bounds and also the range of DVR values.¹¹ Any small biases or errors in the set of parameters can be increased by a division process.

Reference Region for [¹¹C]ABP688

In previous human studies using [¹¹C]ABP688 PET,^{19, 26, 38} the ROI TACs for various brain regions including the cerebellum or its gray matter were best fitted by a two-tissue compartment model. The violation of the single-tissue compartment assumption for the reference region (and also tissue) would introduce biases to the gold standard.³ Probably because of such violation, the assessment of the reference region approaches for [¹¹C]ABP688 PET in humans has been very limited.^{3, 25} Although the possibility of low specific binding in the cerebellum was raised as a reason for the violation based on the results from several studies,^{19, 26, 28} mGluR5 protein expression in that region was not detected in a postmortem study.³⁹ Meanwhile, Milella et al²⁵ reported a high correlation (r=0.97) between results from NLS-SRTM and two-tissue compartment model without mentioning the amount of bias. Furthermore, in several studies, the cerebellum was used as a reference region for the ratio analysis in [¹¹C]ABP688 PET human brain studies using a bolus-infusion protocol.^{39, 40}

Noise in Reference Region Data

In this study, we assumed the cerebellar TAC (Supplementary Figure E3) as almost noiseless reference region input function because of its large size. However, in general, the noise level of the reference TAC may change depending on several factors such as size of the region and injection dose.⁵ With simulation, therefore, we explored the effect of noise in reference region by increasing the noise levels up to 10% to cover small-sized reference region or noisier reference region data. In our simulation, only the results from LLS-SRTM and LLS-SRTM-SC were notably influenced by the noise in reference region data (Figures 1 and 2). Although the noisy input function violates the MTLS1 assumption about noise-level of independent variables, its impact on the results from MTLS1 and MTLS1-SC was insignificant. Conversely, MTLS2 yielded poor results at high levels of tissue noise even if noisy input function used, because predominance of the tissue noise over the input noise would give rise to a violation of the MTLS2 assumption. Therefore, we may claim that noise in reference region can be considered as noiseless in the application of MTLS-based method, making MTLS1-based methods be optimal choice.

Conclusions

In the present study, we have compared several SRTM-based parametric neuroreceptor mapping approaches. Very consistent results under ROI-level noise proved that the methods considered are fundamentally equivalent to NLS-SRTM. Meanwhile, discrepancies between the generated parametric images or the results under high-level noise indicated different noise susceptibilities among those methods. Basically, by incorporating different prior information or spatial constraints, all the methods sacrificed a reasonable or negligible bias to improve the quality of the parametric image. However, in general, the methods for multilinear SRTM achieved better image quality and regional compatibility with the SRTM than the others; this is because the former methods directly estimate DVR whereas the latter methods have increasing variability due to division and directly apply the prior information to the model parameters. Two different approaches for reducing the bias in multilinear SRTM (LLS-SRTM-SC and MTLS1-SC) were similarly effective, with slightly better performance in MTLS1-SC, especially given noisy reference region data. Unlike MTLS2 and MTLS2-SC, MTLS1 and MTLS1-SC are less dependent on noise-level assumption for reference region data, indicating that MTLS1-SC is the optimal choice for parametric imaging.

The authors declare no conflict of interest.