Molecular Dynamics Evaluation of Dielectric-Constant Mixing Rules for H₂O-CO₂ at Geologic Conditions

Abstract

Modeling of mineral reaction equilibria and aqueous-phase speciation of C-O-H fluids requires the dielectric constant of the fluid mixture, which is not known from experiment and is typically estimated by some rule for mixing pure-component values. In order to evaluate different proposed mixing rules, we use molecular dynamics simulation to calculate the dielectric constant of a model H₂O–CO₂ mixture at temperatures of 700 K and 1000 K at pressures up to 3 GPa.

We find that theoretically based mixing rules that depend on combining the molar polarizations of the pure fluids systematically overestimate the dielectric constant of the mixture, as would be expected for mixtures of nonpolar and strongly polar components. The commonly used semiempirical mixing rule due to Looyenga works well for this system at the lower pressures studied, but somewhat underestimates the dielectric constant at higher pressures and densities, especially at the water-rich end of the composition range.

1 Introduction

The static dielectric constant (relative permittivity) is a key quantity in continuum descriptions of the thermodynamics of ions in solution. In geochemistry, the dielectric constant of water appears in the Born contribution to Gibbs energies of ionic species in the widely used Helgeson-Kirkham-Flowers (HKF) approach to aqueous thermodynamics [1-7]. The uses and limitations of such models have recently been reviewed by Dolejš [8]. This approach has proven useful in estimating equilibrium constants and other thermodynamic properties that are essential in modeling the distribution and transport of components between minerals and fluids. However, its range of application has been limited in pressure (to 0.5 GPa) and to conditions where the solvent can be assumed to be H₂O with the amount of dissolved gas or other solutes too small to significantly affect the dielectric constant.

Recently, there has been interest in extending these methods to conditions of the deep crust and upper mantle [8-12]. Aqueous fluids at these conditions would typically have a large fraction of H₂O, but would also have significant fractions of other species such as CO₂ and CH₄ [13-16]. Some modeling studies have examined the effect of the temperature, pressure, and composition dependence of the dielectric constant of these high-pressure mixed fluids on mineral reaction equilibria and speciation in the aqueous phase [9,17-19]. The paper of Galvez et al. [19] was to our knowledge the first to examine in detail the effects of dielectric mixing rules on calculated equilibria at these conditions, but they had no way to evaluate the accuracy of the mixing rules used.

There are no experimental measurements of mixture dielectric constants at these extreme conditions, so it is necessary to make estimates based on theory and/or on mixing extrapolated pure-component values. For pure H₂O, reasonable estimates at geologic conditions can be made; the standard formulation of the International Association for the Properties of Water and Steam (IAPWS) [20,21] extends to 873 K and 1 GPa and extrapolates reasonably to higher temperatures and pressures. Estimates have also been developed based on semiempirical extrapolation [11]. A recent study [22] used ab initio molecular dynamics to calculate the dielectric constant up to approximately 2000 K and 10 GPa. For nonpolar fluids such as CO₂ and CH₄, the Clausius-Mosotti relationship can be used to extrapolate correlations based on reliable measurements [23] to more extreme conditions, provided that a reliable equation of state (EOS) exists to calculate the density as a function of temperature and pressure.

For mixtures, however, the situation is much less clear. It is logical to obtain the mixture dielectric constant εmix at temperature T and pressure p from some weighted combination of the pure-component values, but there is no consensus on the best approach. It has been common in geochemistry to use a mixing rule attributed to Looyenga [24,25]:

$${\epsilon }_{\text{mix}}={\left(\sum _i{\Phi }_i{\epsilon }_1^{1∕3}\right)}^3,$$ (1)

where ${\Phi }_i=x_i{v}_i/{\sum }_j{x}_j{v}_j$ is the volume fraction of component i (based on pure-component molar volumes v_i at T and p) and ε_i is its dielectric constant at T and p. However, Looyenga’s equation is derived for heterogeneous dispersions with small differences among ε_i. Neither of these assumptions is correct for the aqueous mixtures of interest in geologic settings, making the use of Eq. 1 for such systems questionable.

In the theory of electric polarization (see for example Böttcher [26]), the physically significant variable is not the dielectric constant itself, but rather the dielectric polarization. A convenient quantity to work with is the dielectric polarization per unit volume, which is the molar polarization ([P] in Böttcher’s notation) divided by the molar volume; we will write this quantity as P and refer to it as the “polarization” for short. There is no rigorous general relationship between ε and P. However, for polar fluids (or mixtures containing polar components), a relationship due to Kirkwood [27] is widely and successfully used:

$$P_{\mathrm{K}}=\frac{(\epsilon -1)(2\epsilon +1)}{9\epsilon }.$$ (2)

A well-established way to estimate the polarization of a mixture when pure-component values are available is due to Oster [28]:

$${(P∕\rho )}_{\text{mix}}=\sum _i{x}_i{\left(\frac{P(T,p)}{\rho (T,p)}\right)}_i,$$ (3)

where x_i is the mole fraction of component i and ρ is the molar density. Equation 3 becomes a linear volume-fraction mixing rule if the excess volume of mixing V^E at (T, p) is zero;

$$P_{\text{mix}}=\sum _i{\Phi }_i{P}_i(T,p)[V^{\mathrm{E}}=0].$$ (4)

Equation 4, with Kirkwood’s expression (Eq. 2) used to relate P to ε, was used by Wang and Anderko [29] to calculate the dielectric constants of mixtures of liquid solvents. Oster’s Eq. 3 (attributed to Orlov and Smirnov [30]) was used by Akinfiev and Zotov [18] in their modeling of equilibria in hydrothermal solutions.

Harvey and Prausnitz [31] proposed a mixing rule similar to Eq. 3, but with the mixing performed not at constant pressure but rather at constant reduced density:

$$P_{\text{mix}}=\sum _i{\Phi }_i^{\ast }{P}_i\left(T,\frac{{\rho }_{\mathrm{r},\text{mix}}}{v_i^{\ast }}\right),$$ (5)

where $v_i^{\ast }$ is a characteristic molar volume (usually taken as the critical volume) for component i, ${\Phi }_i^{\ast }=x_i{v}_i^{\ast }/{\sum }_j{x}_j{v}_j^{\ast }$ is a volume fraction defined with these characteristic volumes, and ρ_r,mix is the dimensionless reduced molar density of the mixture, ${\rho }_{\text{r},\text{mix}}={\rho }_{\text{mix}}{\sum }_i{x}_i{v}_i^{\ast }$.

Harvey and Lemmon [23] applied Eq. 5 to model the dielectric constant of mixtures of natural gas components, finding that it gave a modest improvement over Oster’s rule (Eq. 3) for systems where the pure-component densities at (T, p) were widely different (for example, if one pure component was a gas and the other a liquid at those conditions). They also found that inclusion of the excess volume of mixing was essential for accurate results.

However, the assumption behind both the mixing rules of Oster and of Harvey and Prausnitz is that the contribution of each component to the polarization is unchanged upon mixing. This seems less likely to be true for mixtures such as the geologic fluids of interest here, where soluble nonpolar components will modify the hydrogen-bond structure of the water. Harvey and Prausnitz [31] reported some cases where their mixing rule was inaccurate for polar/nonpolar liquid mixtures.

The purpose of the present work is to evaluate these mixing rules, at geologic temperatures and pressures, by molecular simulation of a model that qualitatively represents the H₂O-CO₂ mixture (ignoring complicating factors like ionization that might be present in the real system). Quantitative representation of the dielectric constant by the molecular model is not necessary for this purpose; in a “real” situation, values for the pure-component dielectric constants would be available, so the aspect to be tested is how the pure-component values combine to yield a mixture value. In this work, we test the mixing rules by simulating the static dielectric constant of molecular models for H₂O, CO₂, and their mixtures at temperatures of 700 K and 1000 K and pressures from 0.1 GPa to 3 GPa.

2 Molecular Simulation

2.1 Intermolecular Potentials

The simulations reported here make use of rigid, three-site models for H₂O and CO₂. The SPC/E model for water [32] has been shown to generate reasonable values for the dielectric constant at the elevated temperatures and pressures of interest here [22].

There have been several examinations of how well various interaction potential models for CO₂ predict thermodynamic properties at elevated temperatures and pressures [33-35]. The rigid, three-site model developed by Zhang and Duan (ZD) [33] performs well and slightly better than the TraPPE model [36] at these conditions. Further, there are, for the ZD model interacting with SPC/E water, ab initio based interaction parameters [37] that are more accurate than those based on the commonly used Lorentz-Berthelot [38] or Kong [39] combining rules.

Both the SPC/E and ZD potentials that are used here have the form of Lennard-Jones (12-6) plus Coulomb interactions between sites on molecule pairs. The Lennard-Jones sites are characterized by an interaction energy ε_LJ and a distance parameter σ, while the Coulomb interactions are characterized by partial charges q. The potential parameters are listed in Table 1. Note that while the special combining rule is used for H₂O-CO₂ interactions, the Lorentz-Berthelot rule is used for carbon-oxygen interactions between pairs of CO₂ molecules.

Table 1.

Lennard-Jones parameters and partial charges for H₂O [32], CO₂ [33], and the H₂O–CO₂ interaction [37]

Site	εLJ, kJ·mol−1	σ, Å	q, e
	H2O
O	0.65	3.1657	−0.8476
H	0.0		0.4238
	CO2
C	0.2404	2.7918	0.5888
O	0.6888	3.00	−0.2944
	H2O–CO2
C–OW	0.2937	3.1156
OC–OW	0.5500	3.0297
C–H	0.3004	2.8142
OC–H	0.3932	2.1942

The Lennard-Jones interactions are truncated at separations equal to 1/2 the edge of the cubic simulation cell and a long-range correction for the pressure is included. The long-range part of the Coulomb interactions is determined by the Ewald summation method with conducting boundary conditions [40].

2.2 Molecular Dynamics Details

The equations of motion used in the simulations generate trajectories in the isothermal-isobaric (NPT) ensemble [41]. The equations of motion for the molecules and for the thermostats and barostat are integrated using a velocity-Verlet algorithm [42] adapted to include quaternions [43] to describe the orientational degrees of freedom of the rigid molecules. The coupling time for the thermostats controlling the translational and rotational degrees of freedom is 0.1 ps, the time for the barostat is 1.1 ps, and the time for the thermostat controlling the barostat is 0.11 ps. The time step for the integration of the equations is 1 fs. These values provide stable regulation of the pressure and temperature at the specified values as determined using 1 ps duration block averages to determine the standard uncertainty [44] in the estimates for the average values of the temperature, pressure, and volume. The standard uncertainties of these quantities are found to be less than 0.1% of the average values for all states examined.

The simulation times needed for good convergence of the dielectric constant were obtained by determining the sampling time needed for the long-time average of the square of the dipole-moment function <M²> (see Eq. 7 below) to achieve a stable value. The simulation time for production runs for CO₂ and mixtures is 1 ns. Longer times are needed for convergence of the results for the fluctuations in the total dipole moment of water, so production runs of 3 ns are used for H₂O. Simulations are divided into blocks of 1 ps duration; the standard deviation of this set of results is used to obtain the standard uncertainty of calculated values.

The systems examined contain a total of 500 molecules. The explicit compositions of the various cases examined are listed in Sec. 3.

2.3 Calculating the Dielectric Constant

As noted above, the more physically significant variable is the dielectric polarization P rather than the dielectric constant ε. There are two contributions to P that are to be obtained for H₂O, CO₂, and their mixtures.

The nonpolar part of P is obtained from the molar density, ρ_i, and the molecular polarizability, α_i, of the components by

$$P_{\text{non}}=\frac{4\pi }{3}{N}_A\sum _i{\alpha }_i{\rho }_i,$$ (6)

where N_A is the Avogadro constant. We use values of the polarizability of 2.912×10⁻²⁴ cm³ for CO₂ [23] and 1.457×10⁻²⁴ cm³ for H₂O [45].

The polar contribution (which is zero for pure CO₂ since it has no permanent dipole moment) comes from the fluctuations in the total dipole moment of the ensemble of molecules. The quantity εpol is obtained from the simulations using the fluctuation expression appropriate for conducting boundary conditions for the electrostatics [46]:

$${\epsilon }_{\text{pol}}=1+\frac{4\pi \langle {\mathbf{M}}^2\rangle }{3V{k}_{\mathrm{B}}T}.$$ (7)

Here <M²> is the long-time average value of the square of the total dipole moment of the fluid in a volume V at temperature T and kB is Boltzmann’s constant. <M²> is determined in the simulation by evaluating at each time step ${\mathbf{M}}^2={\left({\sum }_i{\mu }_i\right)}^2$ where μ_i is the dipole moment vector of molecule i.

Next, one determines Ppol from Eq. 2:

$$P_{\text{pol}}=\frac{({\epsilon }_{\text{pol}}-1)(2{\epsilon }_{\text{pol}}+1)}{9{\epsilon }_{\text{pol}}}$$ (8)

The total polarization is then P = Pnon + Ppol. The dielectric constant is obtained by solving the Kirkwood relation, Eq. 2, for ε:

$$\epsilon =\frac{1}{4}\{(1+9P)+{[{(1+9P)}^2+8]}^{1∕2}\}.$$ (9)

3 Results

Simulations were performed for H₂O, CO₂, and their mixtures at temperatures of 700 K and 1000 K for pressures of 0.1 GPa, 0.3 GPa, 1 GPa, and 3 GPa. For these temperatures and pressures, mixtures were simulated with water mole fractions, xw, of 0.9, 0.75, 0.5, and 0.25.

3.1 Pure H₂O

The results from the H₂O simulations are reported in Table 2. The standard uncertainty for the molar density ρ is on the order of 0.1 % of the average value, while the standard uncertainty for the dielectric constant ε is on the order of 1 %.

Table 2.

Simulation results for H₂O

T, K	p, GPa	ρ, mol·cm −3	ε	ρiapws, mol·cm−3	ε iapws
700	0.1	0.03431	13.51	0.03618	13.75
	0.3	0.04515	18.70	0.04612	19.93
	1.0	0.05785	26.45	0.05794	28.60
	3.0	0.07192	35.49	0.07164	43.94
1000	0.1	0.01509	3.525	0.01473	2.956
	0.3	0.03233	7.956	0.03312	8.250
	1.0	0.04998	13.56	0.05061	15.72
	3.0	0.06656	19.79	0.06684	26.09

Table 2 also shows the values calculated from the IAPWS correlations for ε [20,21] and for ρ [47,48]. While a close match is not necessary for our purpose of testing mixing rules, the qualitative agreement indicates that the SPC/E model is physically reasonable for the dielectric behavior of water at these conditions.

3.2 Pure CO₂

The results from the CO₂ simulations are reported in Table 3. The standard uncertainty for the molar density ρ is on the order of 0.1 % of the average value. Since the value of ε for CO₂ is calculated directly from the simulated density, its uncertainty is similar.

Table 3.

Simulation results for CO₂

T, K	p, GPa	ρ, mol·cm −3	ε
700	0.1	0.01251	1.299
	0.3	0.02079	1.517
	1.0	0.02954	1.761
	3.0	0.03788	2.002
1000	0.1	0.009007	1.211
	0.3	0.01704	1.416
	1.0	0.02659	1.677
	3.0	0.03565	1.937

3.3 Mixtures

The results from the simulations of mixtures at water mole fractions, xw, of 0.9, 0.75, 0.5, and 0.25, are reported in Table 4. The standard uncertainty for the tabulated results is approximately the same as the uncertainty for pure H₂O as discussed in Sec. 3.1.

Table 4.

Simulation results for H₂O–CO₂ mixtures

T, K	p, GPa	ρ, mol·cm −3	ε
xw = 0.9
700	0.1	0.02889	9.285
	0.3	0.04060	14.60
	1.0	0.05312	20.46
	3.0	0.06642	26.72
1000	0.1	0.01364	2.992
	0.3	0.02918	6.279
	1.0	0.04582	10.70
	3.0	0.06132	15.23
xw = 0.75
700	0.1	0.02287	5.842
	0.3	0.03486	9.526
	1.0	0.04696	14.01
	3.0	0.05922	18.50
1000	0.1	0.01211	2.441
	0.3	0.02556	4.600
	1.0	0.04062	7.724
	3.0	0.05466	10.93
xw = 0.5
700	0.1	0.01704	3.036
	0.3	0.02804	4.766
	1.0	0.03909	6.782
	3.0	0.04981	8.864
1000	0.1	0.01051	1.800
	0.3	0.02142	2.797
	1.0	0.03424	4.189
	3.0	0.04623	5.580
xw = 0.25
700	0.1	0.01401	1.942
	0.3	0.02361	2.704
	1.0	0.03351	3.545
	3.0	0.04295	4.374
1000	0.1	0.009533	1.478
	0.3	0.01876	2.009
	1.0	0.02975	2.700
	3.0	0.04013	3.386

Because mixtures of water and CO₂ can undergo phase separation (which would distort the dielectric results) at some high-temperature, high-pressure conditions [49-51], we checked for signs of phase separation by examining the unlike pair distribution functions. No unusual compositional order was observed at any of the simulated conditions, indicating that the simulations were within the one-phase region.

4 Analysis of Mixing Rules

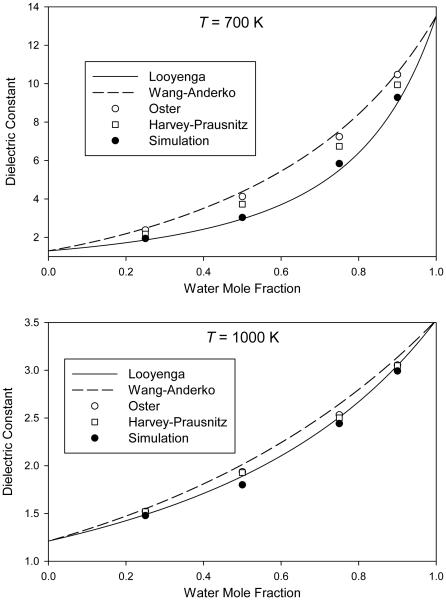
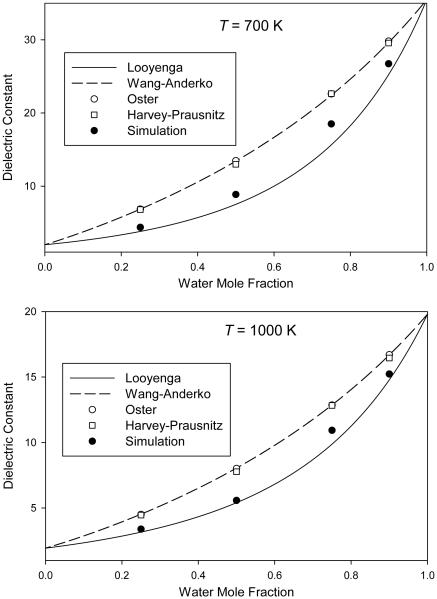
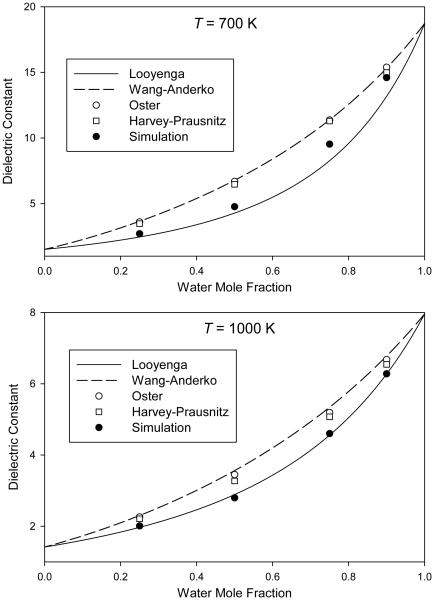
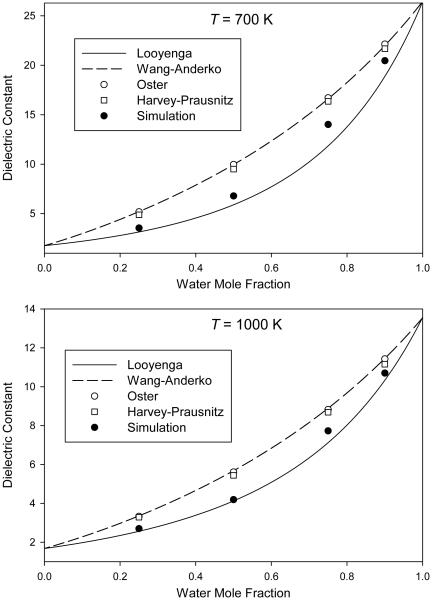
In Figs. 1-4, we plot the simulated dielectric constants from Table 4 for mixtures at pressures of 0.1 GPa, 0.3 GPa, 1 GPa, and 3 GPa, respectively. We also plot the values predicted by the different mixing rules discussed in Sec. 1.

Fig. 1.

Mixture dielectric constant from molecular simulation at a pressure of 0.1 GPa compared to predictions of various mixing rules

Fig. 4.

Mixture dielectric constant from molecular simulation at a pressure of 3.0 GPa compared to predictions of various mixing rules

For the mixing rules of Looyenga [24,25] (Eq. 1) and of Wang and Anderko [29] (Eq. 4), the mixture dielectric constant is obtained at any composition from knowledge of the pure-component values at the same temperature and pressure. Results from these two mixing rules can therefore be plotted as continuous curves on Figs. 1-4.

For the mixing rule of Oster [28] (Eq. 3), the mixture density is required; these mixture densities are taken from Table 4 and therefore only individual points are plotted. We note that, in order to provide a self-consistent test of the mixing rules, we must use the simulated densities of the molecular model, which may or may not accurately represent the densities of real H₂O–CO₂ mixtures.

The mixing rule of Harvey and Prausnitz [31] (Eq. 5) requires not only mixture densities but also pure-component dielectric constants computed at the temperature of interest and a density corresponding to the reduced density of the mixture. This required additional simulations on pure H₂O for each point, which were performed as described in Sec. 2. It also requires the critical volumes, which were taken from reference equations of state for H₂O [47] and CO₂ [52].

It is worth noting that, while the Oster and Harvey-Prausnitz mixing rules both required additional computations for the testing procedure in this paper (simulation of density, and also extra pure-H₂O simulations for the Harvey-Prausnitz rule), this would not be a problem in actual use. In practical application, one would have correlations for the pure-component dielectric constants as functions of temperature and density (such as that of IAPWS [20,21] or Sverjensky et al. [11] for water), and that would provide sufficient information for any of the mixing rules.

5 Discussion

The purpose of this work is to test mixing rules, not to provide quantitatively accurate dielectric constants for real H₂O–CO₂ mixtures. The important feature in Figs. 1-4 is therefore the way in which the simulation data and the various mixing rules interpolate between the pure-component endpoints.

Some patterns can be seen in the results. In all cases, the Looyenga mixing rule predicts a lower dielectric constant than the other approaches; this difference is more pronounced at 700 K than at 1000 K and also becomes more pronounced at higher pressures. The Wang-Anderko and Oster approaches give similar results (except at 1000 K and 0.1 GPa, which is the lowest-density state simulated), indicating that the excess volume of mixing is small for this molecular model at the conditions simulated.

None of the mixing rules quantitatively reproduces the simulated mixture behavior at all conditions. The Looyenga approach is fairly accurate at lower pressures, and does well at all pressures for low water mole fractions. However, it underestimates the mixture dielectric constant at higher pressures for xw = 0.90 and xw = 0.75. The three mixing rules that use a theory-based combination of the pure-component polarizations generally overpredict the dielectric constant, in most cases producing greater errors than the Looyenga rule. The Harvey-Prausnitz mixing rule is closer to the data than are the mixing rules of Wang and Anderko or of Oster, but the improvement is relatively small.

It is not surprising that mixing rules based on combining pure-component polarizations overestimate the dielectric constant for these mixtures. The dielectric constant of polar fluids is dominated by correlations among dipoles [27]. For water, this correlation is largely due to hydrogen bonding. It is plausible that nonpolar solutes such as CO₂ disrupt the hydrogen-bonding network, reducing the dielectric polarization of the remaining water from that in pure water. This disruption of hydrogen-bonding networks by CO₂ in high-temperature water has been observed in neutron-diffraction experiments at 673 K and 0.13 GPa [53]. More generally, both Oster [28] and Harvey and Prausnitz [31] observed that Eqs. (3) and (5), respectively, did not accurately predict the dielectric constant for polar/nonpolar mixtures.

As for the question of which mixing rule should be used in geochemical studies such as those in Ref. [19], unfortunately there is no clear best choice. Looyenga’s mixing rule tends to be the least inaccurate, but it should be recognized that it will probably underestimate the mixture dielectric constant at high pressures at the water-rich end of the composition range, which is the region of most geochemical interest. It might be wise to perform geochemical computations that are sensitive to the mixture dielectric constant with both the Looyenga rule and the Harvey-Prausnitz rule, which seem to provide lower and upper bounds. Such calculations would give an indication of the uncertainty introduced by the uncertainty of the mixture dielectric constant.

Similar tests of dielectric-constant mixing rules could in principle be performed with ab initio models for H₂O–CO₂ mixtures, as has been done for pure H₂O [22]. This would be a difficult calculation, but might be feasible with modern supercomputers. It would be interesting to see whether such a different model for the system showed similar mixing behavior for the dielectric constant.

Fig. 2.

Mixture dielectric constant from molecular simulation at a pressure of 0.3 GPa compared to predictions of various mixing rules

Fig. 3.

Mixture dielectric constant from molecular simulation at a pressure of 1.0 GPa compared to predictions of various mixing rules