Preferred conformations of N-glycan core pentasaccharide in solution and in glycoproteins

Abstract

N-linked glycans are on protein surfaces and have direct and water/ion-mediated interactions with surrounding amino acids. Such contacts could restrict their conformational freedom compared to the same glycans free in solution. In this work, we have examined the conformational freedom of the N-glycan core pentasaccharide moiety in solution using standard molecular dynamics (MD) simulations as well as temperature replica-exchange MD simulations. Both simulations yield the comparable conformational variability of the pentasaccharide in solution, indicating the convergence of both simulations. The glycoprotein crystal structures are analyzed to compare the conformational freedom of the N-glycan on the protein surface with the simulation result. Surprisingly, the pentasaccharide free in solution shows more restricted conformational variability than the N-glycan on the protein surface. The interactions between the carbohydrate and the protein side chain appear to be responsible for the increased conformational diversity of the N-glycan on the protein surface. Finally, the transfer entropy analysis of the simulation trajectory also reveals an unexpected causality relationship between intramolecular hydrogen bonds and the conformational states in that the hydrogen bonds play a role in maintaining the conformational states rather than driving the change in glycosidic torsional states.

Introduction

A carbohydrate moiety in a glycoprotein, referred to as a glycan, comes in a variety of sequences and structures and plays critical roles in a vast array of biological processes, such as protein quality control in the endoplasmic reticulum (ER) (Helenius and Aebi 2004; Ito et al. 2005; Lederkremer 2009), protein trafficking (Guo et al. 2004; Shi and Elliott 2004; Martinez-Fleites et al. 2008), and protein stability increase (Solá et al. 2007; Hanson et al. 2009; Chen et al. 2010; Culyba et al. 2011; Ellis et al. 2012). These carbohydrate moieties can be covalently attached to asparagine (Asn) side chains of a nascent polypeptide in the ER through the process known as N-glycosylation (Schwarz and Aebi 2011). N-linked oligosaccharide moieties (N-glycans) initially have the same primary sequences, but they are processed later by the enzymes in the ER and the Golgi to become diverse glycoforms (Lederkremer 2009; Aebi et al. 2010). In addition to being a simple appendage to a protein, many N-glycans are involved in molecular recognition in a sequence-dependent manner (Wooten et al. 1990; Wormald et al. 1997; Skehel and Wiley 2000; Shinya et al. 2006; Shah et al. 2008; Zhong et al. 2008; Ferrara et al. 2011). These recognition events require specific carbohydrate structures and are sensitive to small differences in carbohydrate sequence or conformation (Siebert et al. 2003; McLellan et al. 2011; Rose 2012). Thus, understanding the conformational preference of N-glycans can provide valuable insight into mechanisms and specificities of carbohydrate recognition events.

In general, N-glycans are in close contact with protein surface residues, and thus it has been of great interest whether the protein structure affects the N-glycan conformation, or vice versa (Wormald et al. 1991, 2002; Chen et al. 2010; Culyba et al. 2011; Ellis et al. 2012; Lee et al. 2015). An earlier nuclear magnetic resonance (NMR) study on the conformational freedom of free oligosaccharides in solution and N-linked oligosaccharides concluded that the covalent attachment to the protein does not significantly affect the conformational freedom of the oligosaccharides (Wormald et al. 1991). However, it is well known that the carbohydrates in the vicinity of the protein can engage in specific interactions with protein side chains, which can affect the conformational freedom of oligosaccharides (Culyba et al. 2011; Ellis et al. 2012). Structural changes of a protein due to different glycoform sequences are also observed through a systematic crystallization study (Krapp et al. 2003), although the impacts of N-glycans on protein structure are generally very minor in the available Protein Data Bank (PDB) protein structures (Lee et al. 2015). Interestingly, a recent survey of glycoprotein crystal structures in the PDB revealed that the protein structure affects the conformations of N-glycans (Jo et al. 2013).

To gain a better understanding of the conformational preference of oligosaccharides, it is essential to obtain their atomic resolution structures in various environments. However, experimental determination of oligosaccharide conformations using either X-ray crystallography or NMR is still challenging due to the flexible nature of glycosidic linkages and the crowding of NMR spectra (Wormald et al. 2002; Almond et al. 2004; Lütteke 2009; Slynko et al. 2009). Alternatively, computational simulation studies of oligosaccharides can provide valuable insight into the conformational preference of oligosaccharides at the atomic level (Nishima et al. 2012; Wehle et al. 2012). Recent advances in the carbohydrate force fields have enabled researchers to study diverse glycan sequences ranging from monosaccharides to polysaccharides, and the results thus far appear to match experimental properties well (Kirschner et al. 2008; Guvench et al. 2009; Fadda and Woods 2010; Wu et al. 2013).

In this work, we have performed computational simulations of the N-glycan core pentasaccharide (Man₃GlcNAc₂; Figure 1) in explicit water using standard molecular dynamics (MD) simulations (a total of 5 µs) and temperature replica-exchange molecular dynamics (T-REXMD) simulations (Sugita and Okamoto 2000) (a total of 4.8 µs). Earlier computational studies of carbohydrates are often restricted to mono- or disaccharides due to computational resources (Kirschner and Woods 2001; Almond 2005; Salisburg et al. 2009; Perić-Hassler et al. 2010), but it is not clear whether the observations made in such studies can be expanded to larger oligosaccharides because of non-neighboring interactions. In rare occasions, simulations of larger oligosaccharides were performed (Woods et al. 1998; Martin-Pastor and Bush 2000; Almond et al. 2004), but the simulation time (<50 ns) was typically not long enough to produce well-converged conformational states for those oligosaccharides. The pentasaccharide sequence used in this study is small enough to exhaustively sample its conformational states, but still big enough to investigate the presence of non-neighboring interactions.

Fig. 1.

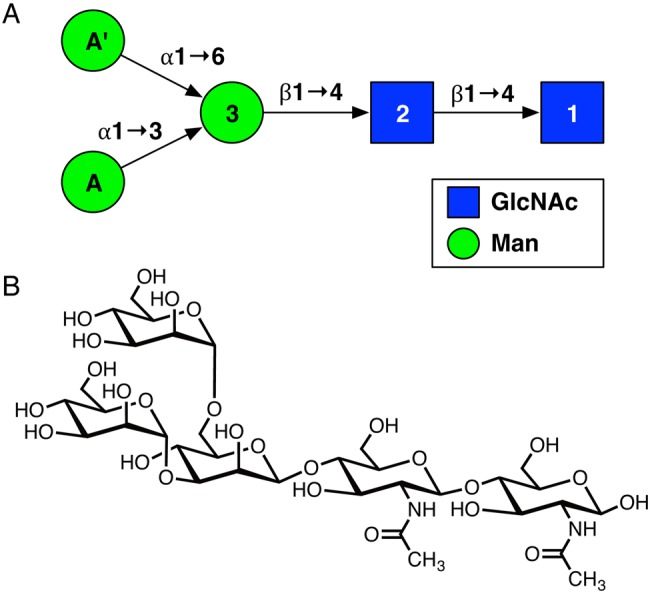
Pentasaccharide sequence used in this study: (A) symbolic notation and (B) chemical structure. This figure is available in black and white in print and color at Glycobiology online.

Our aim is to utilize the simulation trajectory to characterize the conformational preference of the pentasaccharide in solution and compare the results with the N-glycan conformations found in the glycoprotein crystal structures in the PDB database (Berman et al. 2000). We first examine the conformational preference and variability of the pentasaccharide in solution. The simulation results are then compared with those of the covalently N-linked pentasaccharide in the PDB glycoproteins. Finally, the correlation between hydrogen bond formation/deformation and changes of conformational states in solution is examined by the information theory transfer entropy analysis (Schreiber 2000; Kamberaj and van der Vaart 2009; Qi and Im 2013). As the N-glycan core pentasaccharide sequence is found virtually in all N-linked oligosaccharide chains (Lederkremer 2009; Aebi et al. 2010), this study is expected to provide valuable insight into the conformational preference and dynamics of larger N-linked oligosaccharides in glycoproteins.

Methods

Simulations detail

The initial glycan conformations for the MD simulations were selected by using the Glycan Fragment Database (GFDB; http://www.glycanstructure.org/fragment-db) (Jo and Im 2013). PDB entries whose resolution is less than 3 Å were searched. The filtering options provided by the GFDB were used to remove distorted residues and redundant entries. From the searched glycan entries, five representative structures were selected using the clustering facility in the GFDB and used as the initial conformations for the MD simulations (Table I).

Table I.

Initial conformations of the pentasaccharide and the information of the MD simulation systems

	T1	T2	T3	T4	System size (Å)	# Water
#1	(−85, 105)	(−91, 94)	(78, −112)	(75, 105, 60)	44 × 44 × 44	2611
#2	(−77, 113)	(−80, 127)	(76, −107)	(65, 14, −64)	45 × 45 × 45	2872
#3	(−80, 130)	(−77, 118)	(71, −133)	(64, 92, 73)	44 × 44 × 44	2611
#4	(−82, 127)	(−39, 112)	(75, −142)	(97, 85, −71)	45 × 45 × 45	2870
#5	(−73, 126)	(−91, 88)	(81, −98)	(138, 146, 37)	45 × 45 × 45	2872

T1, T2, and T3 represent the glycosidic torsion angles (ϕ, ψ) between residue pairs (1 and 2), (2 and 3), and (3 and A), respectively, in degree. T4 represents the glycosidic torsion angles (ϕ, ψ, ω) in the residue pair (3 and A′) in degree. The glycosidic torsion angle definitions are: ${\text{O}}_5-{\text{C}}_1-{\text{O}}_1-{\text{C}{\hspace{0.17em}}^{\mathrm{\prime }}}_x(\varphi ),$ ${\text{C}}_1-{\text{O}}_1-{{\text{C}}^{\mathrm{\prime }}}_x-{{{\text{C}}^{\mathrm{\prime }}}_x}_{x-1}(\psi )$, and ${\text{O}}_1-{{\text{C}}^{\mathrm{\prime }}}_6-{{\text{C}}^{\mathrm{\prime }}}_5-{{\text{O}}^{\mathrm{\prime }}}_5(\omega )$. The residue names are given in Figure 1.

The selected initial structures were briefly minimized without water prior to the system building. Glycan Reader and Quick MD Setup in CHARMM-GUI (Jo et al. 2008, 2011) were used to build each initial MD simulation system. The system size was determined so that the resulting systems have at least a 12.5 Å water layer in every direction. The solvated simulation systems were minimized while the positional harmonic restraint was applied to the non-hydrogen atoms of the pentasaccharide using CHARMM simulation software (Brooks et al. 2009). Each of the minimized simulation systems was subjected to 1-µs MD simulation at 300 K using the NPT (constant particle number, pressure, and temperature) ensemble and NAMD simulation software (Phillips et al. 2005), which gave a total simulation time of 5 µs.

All simulations were performed using the recently updated CHARMM36 carbohydrate force field (Guvench et al. 2009; Patel et al. 2014) and TIP3P water model (Jorgensen et al. 1983). The van der Waals (vdW) interactions were smoothly switched off between 10 and 12 Å by a forced-based switching function (Steinbach and Brooks 1994). Long-range electrostatic interactions were calculated using the particle-mesh Ewald (PME) method (Darden et al. 1993). An interpolation order of 6 and a direct space tolerance of 10⁻⁶ were used for the PME method. A time-step of 2 fs was used with the SHAKE algorithm (Ryckaert et al. 1977). For the NAMD simulations, Langevin dynamics was used to maintain constant temperatures for each system, while the Nose-Hoover Langevin-piston algorithm (Martyna et al. 1994; Feller et al. 1995) was used to maintain constant pressure at 1 bar.

In addition, 100-ns T-REXMD simulation with explicit water was performed using the NVT (constant particle number, volume, and temperature) ensemble and NAMD simulation software (Phillips et al. 2005). A total of 48 replicas were used to cover the temperature range from 300 to 450 K (i.e., a total simulation time of 4.8 µs). The initial configuration of the first MD simulation system was equilibrated at 1 bar using the NPT ensemble to determine the appropriate system size, which resulted in the system dimension of 42.9 × 42.9 × 42.9 ų. The resulting snapshot was then duplicated and used as the initial configuration for each replica.

Measurement of conformational variability

The conformational variability was measured by calculating the pair-wise root-mean-square deviation (RMSD) distribution using the RMSDYN module in CHARMM (Brooks et al. 2009). To calculate the pair-wise RMSD distribution, a set of conformations was selected from the trajectory and the RMSDs were calculated for each pair of these conformations using all non-hydrogen atoms for structural alignment. For the MD simulation trajectories, the conformations were selected from the aggregated trajectories in every 2.5 ns interval, which resulted in 4000 conformers. For T-REXMD simulation, the conformations in the lowest temperature (300 K) replica were selected every 50 ps, which resulted in 2000 conformers. To estimate the upper limit of the conformational variability of the pentasaccharide, a random conformation pool was built based on the protocol used in Jo et al. (2013). Briefly, a conformation pool of 1,000,000 conformers was built in an iterative fashion. For each iteration, a new torsion angle value was assigned to a randomly selected glycosidic linkage, and the new conformation was accepted if there was no bad contact (i.e., the vdW energy less than 100 kcal/mol). The torsion angle values were selected among the precalculated accessible torsion angles based on the adiabatic map of the corresponding glycosidic linkage. To calculate the pair-wise RMSD distribution of the random glycan conformation pool, the conformations generated every 1000th iteration were extracted, which resulted in 1000 conformers, and the RMSDs were calculated for all possible pairs.

Selection of PDB entries for comparison of conformational preference

The N-glycan pentasaccharide crystal structures in the PDB glycoproteins were selected from the GFDB. Various filtering options available in the GFDB were used to refine the selection and to remove potentially erroneous entries. For example, X-ray structures whose resolution is larger than 3 Å were removed, and the glycan chains that contain at least one distorted carbohydrate structures or inaccurate residue name annotation were also excluded. In addition, redundant PDB entries were removed to prevent over-representation of certain conformations. The two parent glycoproteins having sequence similarity more than 70% were considered as redundant and thus removed. The precalculated sequence similarity information provided by the PDB was used. Any N-glycan entry that contains the pentasaccharide sequence (Figure 1) was searched, which resulted in 132 entries as of August, 2015.

Lastly, B-factors of glycan residues were considered. A B-factor provides a measure of localization of electron density in a data set and represents how disordered the atom is within the crystal environment. Atoms found in the mobile region of the protein tend to have higher B-factors. The average B-factors of residues 1, 2, 3, A and A′ are 43, 48, 58, 64 and 69 Ų in the 132 entries, respectively. Glycans are commonly found in a loop region, which has high mobility, thus it is expected to have higher B-factor and the B-factor alone cannot be used to judge the quality of the crystal structure. However, very high B-factor might not be suitable for structural analysis that we performed here. Thus, for the further analysis, we have removed glycan structures that have average B-factors greater than 100 Ų, which resulted in 117 entries.

Coarse-graining of conformational states using glycosidic torsion angles

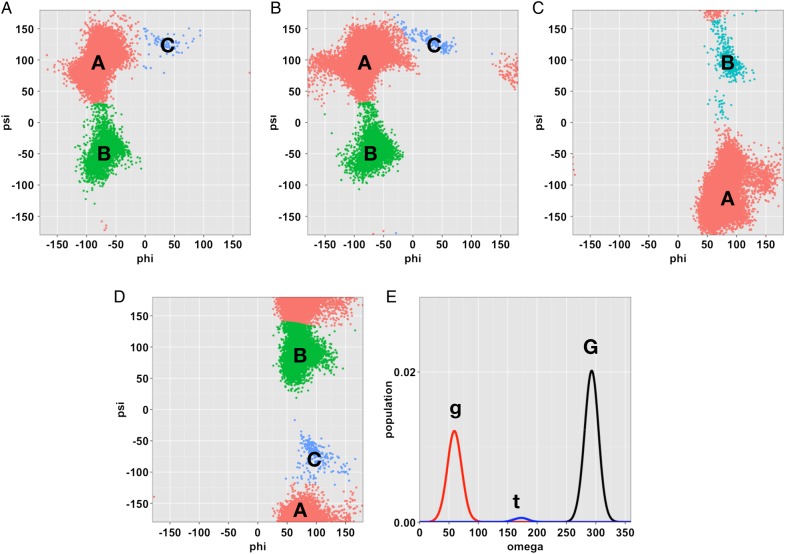
The torsion angle distribution from the highest temperature replica in the T-REXMD simulation was used to identify a set of conformational basins as shown in Figure 2. The following glycosidic torsion angle definitions adopted from the crystallographic definition were used; ${\text{O}}_5-{\text{C}}_1-{\text{O}}_1-{{\text{C}}^{\mathrm{\prime }}}_x(\varphi ),$ ${\text{C}}_1-{\text{O}}_1-{{\text{C}}^{\mathrm{\prime }}}_x-{{{\text{C}}^{\mathrm{\prime }}}_x}_{x-1}(\psi )$, and ${\text{O}}_1-{{\text{C}}^{\mathrm{\prime }}}_6-{{\text{C}}^{\mathrm{\prime }}}_5-{{\text{O}}^{\mathrm{\prime }}}_5(\omega )$. The atom names are based on the CHARMM topology. For each glycosidic linkage, several well-defined basins were readily identifiable by examining the torsion angle distributions. Once the basins were roughly identified, the basins were refined by assigning the torsion angles observed during the simulations to the nearest basin using the k-medoid algorithm (Park and Jun 2009). The angular distance metric (Gaile and Burt 1980) was used to preserve the periodicity between the two torsion angle values during the clustering procedure.

Fig. 2.

Glycosidic torsion angle distributions from the T-REXMD simulation at 450 K and the assignment of the torsion angle states of each glycosidic linkage. (A) GlcNAc β(1 → 4) GlcNAc, (B) Man β(1 → 4) GlcNAc, (C) Man α(1 → 3) Man, (D) Man α(1 → 6) Man, and (E) ω torsion angle of the Man α(1 → 6) Man linkage. This figure is available in black and white in print and color at Glycobiology online.

We denoted the torsional states of each glycosidic linkage (except the omega torsion angle) based on the size of the basin, i.e., “A” refers to the largest basin, “B” refers to the second largest basin and so on. For the omega torsion angle, the basins are named after the well-known staggered rotameric states of the omega torsion angle along the ${{\text{C}}^{\mathrm{\prime }}}_6-{{\text{C}}^{\mathrm{\prime }}}_5$ bond: G (gauche-gauche), g (gauche-trans), and t (trans-gauche). Note that the k-medoid algorithm sometimes does not preserve the initial basin assignment when the basin is too small, so such basins were manually assigned, e.g., the basin C for the first glycosidic linkage (Figure 2A). By combining the torsion angle states, the pentasaccharide conformation can be described with a five-letter notation, starting from the residue 1 in Figure 1. For example, “AAAAG” indicates the each glycosidic (ϕ, ψ) torsion angles adopts their largest basin, and the omega torsion angle adopts the gauche-gauche orientation.

Transfer entropy between conformational states and hydrogen bonds

Transfer entropy (TE) is a measure that quantifies the information flow from the past of one time series y(t) to the future of another time series x(t), i.e., the causality between x(t) and y(t) (Schreiber 2000). In the present work, the following form is used

$$\begin{array}{ll}\text{T}{\text{E}}_{y\to x}& =H(x_{t+1}|x_t^{(k)})-H(x_{t+1}|x_t^{(k)},y_t^{(l)})\\ & =H(x_{t+1}|x_t^{(k)})+H(x_t,y_t^{(l)})-H(x_{t+1},x_t^{(k)},y_t^{(l)})-H(x_t^{(k)}),\end{array}$$

where k and l are the embedding dimensions that are the number of steps to be included from the past of x(t) and y(t), which were set to 1. $H(x)=-\sum p(x_i)logp(x_i)$ is Shannon entropy, where p(x_i) is the probability of one state and the summation is over all possible combinations of states. H(|) is conditional Shannon entropy. Due to finite sample size of the time series, even two irrelevant series can have non-zero (statistically insignificant) TE. To remove this bias, the shuffling method has been used to calculate the effective transfer entropy TE_eff, which is defined as (Kamberaj and van der Vaart 2009; Marschinski and Kantz 2002)

$${\text{TE}}_{y\to x}^{\mathrm{eff}}=\mathrm{T}{\text{E}}_{y\to x}-\frac{1}{N}\sum _{n=1}^N\text{T}{\text{E}}_{y^{\mathrm{shuffled}}\to x},$$

where N, the number of shuffling, was set to 500 for all calculations in this study. Using the effective TE, a normalized directional index can be derived as

$$D_{y\to x}=\frac{{\text{TE}}_{y\to x}^{\mathrm{eff}}}{H(x_{t+1}|x_t^{(k)})}-\frac{{\text{TE}}_{x\to y}^{\mathrm{eff}}}{H(y_{t+1}|y_t^{(l)})}\in [-1,1],$$

where $H(x_{t+1}|x_t^{(k)})$ and $H(y_{t+1}|y_t^{(l)})$ are the maximal TE. A positive D_y→x value indicates an information flow from y to x (i.e., y drives x), and vice versa for a negative value. For two completely uncorrelated time series, D_y→x and TE^eff are 0. Only the |D_y→x| values larger than 0.1 and having p-value smaller than 0.05 were taken into further analysis.

For the TE analysis, two time series of instantaneous conformational states (a combination of torsional states of each glycosidic linkage and the omega torsion angle, e.g., AAAAG) and hydrogen bonds between atom pairs were generated from the standard MD simulation trajectories. For the instantaneous conformational state, the torsional angle state definition for each glycosidic linkage was used (Figure 2). A hydrogen bond was defined as the distance between the donor and the acceptor below 2.8 Å and the angle below 120°.

Results and discussion

Convergence of glycosidic torsion angle distributions

The average acceptance ratio of replica exchange in the T-REXMD simulation was 50.7%, and the random walk of the replicas in the temperature space was very efficient as multiple travels between the lowest and highest temperatures were observed (Supplementary data, Figure S1). Although an efficient replica travel does not guarantee a converged simulation, it is necessary for a reliable sampling during a T-REXMD simulation. The glycosidic torsion angle distributions from the standard MD and T-REXMD simulations are first compared to assess the level of convergence.

Figures S2 and S3 (Supplementary data) show the individual glycosidic torsion angle distributions from the five independent MD simulations started with different initial conformations and from the lowest temperature (300 K) replica in the T-REXMD simulation. The individual glycosidic linkage distribution qualitatively matches with the distribution obtained from several other NMR and modeling studies (Homans et al. 1987; Weller et al. 1996; Petrescu et al. 1997; Woods et al. 1998; Sayers and Prestegard 2000). To the best of our knowledge, a set of comprehensive NMR observables for the Man₃GlcNAc₂ pentasaccharide is not available, so we have calculated and compared inter-proton distances with the available NMR data (Supplementary data, Table S1). Given that the NMR experiments are performed in different sequences, the two results agree well.

The exo-anomeric effect favors the glycosidic ϕ conformation in gauche conformations (Rao 1998). For example, the exo-anomeric effect favors ϕ = −60° for the first two glycosidic linkages. But, small populations were observed around ϕ = 60° for these glycosidic linkages (Supplementary data, Figure S2). Structural examination reveals that these non exo-anomeric populations are stabilized by the formation of additional hydrogen bonds. A hydrogen bond between the amine group in the second GlcNAc and the hydroxyl group at C3 of the first residue can be formed when the first glycosidic linkage adopts ϕ = 60° (Supplementary data, Figure S4A), and a hydrogen bond between the C3 hydroxyl group in the second GlcNAc and the C2 hydroxyl group in the third residue can be formed when the second glycosidic linkage adopts ϕ = 60° (Supplementary data, Figure S4B).

The individual glycosidic torsion angles appear to be converged among the independent MD simulations, however, the sampling in terms of global conformation appears to be slow and is not yet converged within 1-µs simulation time. Supplementary data, Figure S5 shows 100-ns block average population of the top five conformational states (see “Methods” for the definition of the conformational state) from the standard MD simulations. The bias from the initial configuration is resolved within 100–200 ns, but even after 1-µs simulation time, these five independent simulations have not yet reached similar population distributions. This suggests that conformational transitions between some conformational states are very slow even for the relatively small size of the pentasaccharide molecule. When all five MD simulation trajectories are aggregated, the conformational distribution becomes more converged and matches well with the ones from the T-REXMD simulation (Supplementary data, Figure S6). These observations emphasize difficulties in reaching a convergence from a single long-trajectory simulation for a carbohydrate system and encourage use of either enhanced sampling techniques or an ensemble of independent simulations (Re et al. 2011; Nishima et al. 2012). In our analysis below, all MD simulation results are based on the aggregated trajectories, unless explicitly stated otherwise.

Conformational variation of the pentasaccharide in solution

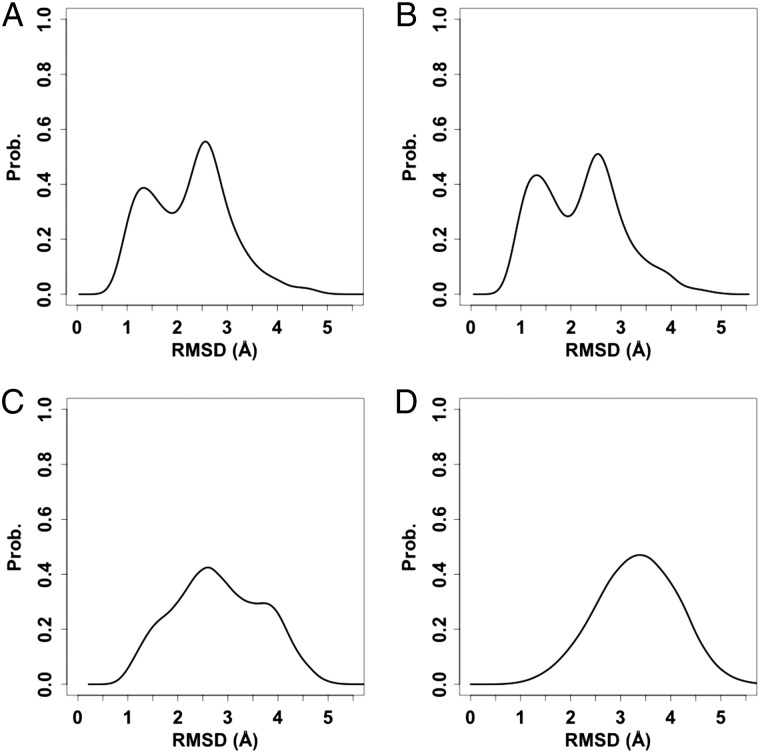
It is generally assumed that oligosaccharides in solution are flexible, but how flexible are they? Figure 3 shows the pair-wise RMSD distributions that can be used to characterize general conformational variability of the pentasaccharide. The conformational variability of the pentasaccharide in solution at 300 K appears to be around 1–3 Å in terms of RMSD. Although the frequencies of sampled conformations in building the pair-wise RMSD distribution were different in the MD simulations and the T-REXMD simulation (i.e., more frequent in T-REXMD; see ‘Methods’ section), the resulting distributions at 300 K agree well with each other. In addition, there are two prominent peaks in the pair-wise RMSD distribution, indicating that there are a few well-defined conformational states in solution. The conformational variability of the pentasaccharide in solution at 300 K is smaller compared with the variability at a higher temperature (450 K) or when compared with the random glycan conformation pool, where the variability is around 2–4.5 Å.

Fig. 3.

Conformational variability of the pentasaccharide in solution. The pair-wise RMSD distribution is calculated from (A) standard MD simulations, (B) T-REXMD simulation at 300 K, (C) T-REXMD simulation at 450 K, and (D) random conformation pool.

Conformational preference of the pentasaccharide in solution

To gain further insight into the conformational preference of the pentasaccharide in solution, as shown in Figure 2, the conformational states are defined using glycosidic torsion angle distributions from the highest temperature ensemble in the T-REXMD simulation (see ‘Methods’ for the details). Such a description of the conformational states using dihedral angles is common in protein/peptide conformational analysis (Buchete and Hummer 2008). The basins from each glycosidic linkage result in a total of 3 × 3 × 2 × 3 × 3 = 162 possible conformation states, but not every state is visited in the simulation. In fact, only 57 states were visited in the T-REXMD simulation at 450 K, while 21 and 42 states were visited in the T-REXMD simulation at 300 K and the standard MD simulations, respectively. Nonetheless, surprisingly, the statistically significant conformational states are limited to only a few states (Table II). For example, the “AAAAG” state accounts for more than 50% of the total simulation trajectories, and the top five conformational states account for more than 95% of the conformations visited in the MD simulations. In addition, the dominant conformational states observed from the standard MD simulations are consistent to those in the T-REXMD simulation at 300 K, indicating robust, converged conformational sampling from both simulations.

Table II.

Conformational states of the N-glycan core pentasaccharide in solution and in glycoprotein

	MD		REXMD	(300 K)	REXMD	(450 K)	PDB
#1	AAAAG	51.9%	AAAAG	57.4%	AAAAG	35.9%	AAABG	26% (31)
#2	AAAAg	32.4%	AAAAg	25.1%	AAAAg	22.5%	AAAAG	26% (30)
#3	AAABG	3.8%	AAABG	5.1%	AAABG	8.3%	AAAAG	25% (29)
#4	AAABg	3.7%	AAABg	3.7%	AAABg	5.9%	AAACg	4% (5)
#5	BAAAG	2.5%	BAAAG	2.9%	BAAAG	5.5%	AAABt	3% (4)
#6	ABAAG	1.9%	ABAAG	1.8%	ABAAG	4.7%	AABBG	3% (4)
#7	ABAAg	1.4%	ABAAg	1.2%	ABAAg	3.9%	AAABg	3% (3)
#8	ABABG	0.9%	BAAAg	1.1%	ABABG	2.5%	AAACG	2% (2)
#9	BAABG	0.4%	AAACg	0.7%	BAAAg	2.1%	AABAG	2% (2)
#10	BAABg	0.2%	ABABG	0.3%	BAABG	1.5%	AABBt	2% (2)
Sum		99.1%		99.3%		92.8%		96% (112)

The numbers in the parenthesis refer to the number of PDB entries.

To validate the assignment of the conformational states using the glycosidic torsion angle distribution, the conformational variability within each state was compared. From each conformational state, 1000 conformers were arbitrarily chosen and the pair-wise RMSD distribution within each state was calculated (Supplementary data, Figure S7). The overall RMSD of the conformations that belong to the same conformational state is about 1–2 Å. Only a single peak is present in the distribution, indicating that the conformations in the same state are similar to each other.

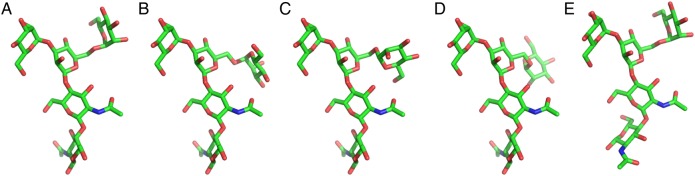
The free energy difference between the most populated state (AAAAG) and the second most populated state (AAAAg) is about ΔG = −k_BT ln P₂/P₁≈ 0.3 kcal/mol. When the representative structures of the top conformational states are compared (Figure 4), the state AAAAG has more extended conformations, whereas the state AAAAg has a conformation in which the terminal residue (A′ in Figure 1A) is folded back to itself. Therefore, the latter has more intramolecular interactions. In fact, on average, the AAAAg has 2.4 ± 1.0 (direct) and 2.8 ± 1.9 (water-mediated) hydrogen bonds, while AAAAG has 1.5 ± 0.8 (direct) and 2.4 ± 1.7 (water-mediated) hydrogen bonds.

Fig. 4.

Representative pentasaccharide conformations in solution from the five major conformational states in Table II. Each conformation corresponds to the average structure from the state: (A) AAAAG, (B) AAAAg, (C) AAABG, (D) AAABg, and (E) BAAAG. This figure is available in black and white in print and color at Glycobiology online.

To investigate the dynamics of conformational transition, we have constructed a Markov state model using MSMBuilder software (Beauchamp et al. 2011), which utilizes a maximum likelihood estimation method to estimate the transition matrix (Pande et al. 2010; Prinz et al. 2011). With a lag time of 200 ps, the slowest conformational transition corresponds to the conversion between the state AAAAG and AAAAg, and the timescale of this transition is about 94 ns. This extremely slow transition matches our observation from the simulation and suggests a lower bound of simulation length for sufficient sampling. A single simulation of 1-µs simulation appears to be too short as shown in this study, and either use of accelerated simulation technique or a set of long simulations started from a distinctive conformation would be helpful for an effective sampling.

It is interesting to note that NMR experiments (Homans et al. 1986) and a recent MD simulation study (Nishima et al. 2012) show significantly increased fold-back conformation in larger N-glycans. Overall, these observations suggest that there could be a competition between the entropic and enthalpic contributions, as shown in polymer models (Rubinstein and Colby 2003). For example, in a smaller N-glycan, the number of interactions is not enough to favor a fold-back conformation and the entropic contribution dominates. However, as the number of sugars increases, there are more interactions that can compensate for the entropy loss for the fold-back conformation.

Conformational variation of the pentasaccharide on the protein surface

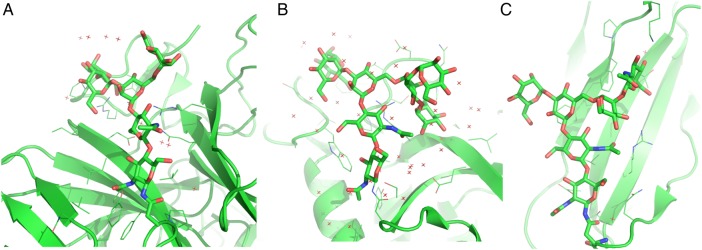
The protein–glycan interactions appear to play a significant role in stabilizing the conformational state that would be otherwise less favorable in solution. For example, the “AAABG” state is only populated 3−5% in solution, but it is observed in more than 20% of glycoproteins. Figure 5 shows the glycoprotein crystal structures having three major conformational states. In these examples, numerous contacts between proteins and the pentasaccharide are observed. These observations suggest that the protein–glycan interactions can stabilize glycan conformations that are not favorable in solution. In addition, crystal contacts also appear to be important in stabilizing the unfavorable conformations. Although the number of observations is limited, there are several examples of favorable protein–glycan interactions through crystal packing (Figure 6).

Fig. 5.

Examples of glycan structures in glycoproteins with the conformational states: (A) AAAAG (PDB:3PPS), (B) AAABG (PDB:3GLY), and (C) AAAAg (PDB:2DTS). The protein structure is drawn in cartoon representation and the protein side chains within 5 Å from the N-glycan chain are drawn as lines. The crystal water molecules are drawn as red points. This figure is available in black and white in print and color at Glycobiology online.

Fig. 6.

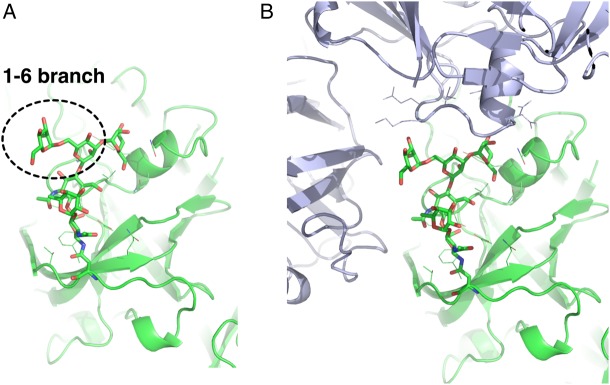
Example of a glycoprotein structure (PDB:1B5F) having an N-glycan conformational state that is less populated in solution (AAACy). (A) The N-glycan 1–6 branch is extended away from the protein, yet adopted an unfavorable conformation. (B) The N-glycan 1–6 branch is involved in close contact with the neighboring crystal units (drawn in purple). The protein structure is drawn in cartoon representation and the protein side chains within 5 Å from the N-glycan chain are drawn as lines. This figure is available in black and white in print and color at Glycobiology online.

Typically, the first two GlcNAc residues of N-glycans (Figure 1) have extensive interactions with surrounding protein residues (Petrescu et al. 2004). Interestingly, the first two sugar residues in glycoprotein crystals are generally in the well-defined conformational states that are also favorable in solution, but the residues at the termini are more variable. This suggests that the residues closer to the protein have limited degrees of conformational freedom. Similar observations were made in the recent survey of N-glycan structures in the PDB (Jo and Im 2013). Here, crystal structures were used to compare the conformational preference, but the crystal structure itself may reduce the apparent dynamics of glycans. Such sampling bias could be removed by having a large number of crystal structures, but the number of crystal structures available is limited, so care must be taken to interpret crystal structure observations.

To examine stabilization of glycan conformations provided by the protein–glycan interactions, we have extended the MD simulations performed by Im and coworkers (Lee et al. 2015). The detailed simulation protocol can be found in Lee et al. 2015. Briefly, four glycoprotein systems (PDB:1E04, PDB:1CXP, PDB:1L6X, and PDB:1RRB), which had 200-ns simulation trajectories in each of three independent replicates, are extended to 1-µs simulation time using Anton hardware (Shaw et al. 2008), yielding a total simulation time of 12 µs. Table S2 (Supplementary data) shows the conformational states that the glycans visited during the simulation. Overall, the glycans adopt conformational states similar to those from the glycan-only solution simulations. This could because the glycans are rather exposed to the bulk solvent in our simulation systems. The glycans in the Fc fragment (PDB:1L6X) is tightly bound to the protein surface in the crystal structure and show most deviations from the solution conformational distribution. In addition, increased population of less favorable conformational states such as AAAAt is observed more in glycoprotein simulations, suggesting that the protein–glycan interactions could increase the propensity of adopting glycan conformations that are less favorable in solution.

It should be noted that there is a greater uncertainty in glycan conformations near the protein in our study. First of all, the number of well-resolved glycoprotein crystal structures is small, so the glycan structures that contain the pentasaccharide sequence were used in our study. Also, it is difficult to know the exact glycan in the crystal structure, as the glycan structures used in our study could be a part of much large glycan structure that is not completely resolved.

Causality relationship between hydrogen bonding and conformation exchange

The hydrogen bonds are known to play an important role in determining the conformation of oligosaccharides (Woods et al. 1998; Almond 2005; Almond et al. 2004; Ellis et al. 2012; Nishima et al. 2012). Here, we examine the role of hydrogen bonds in solution conformations of the N-glycan core pentasaccharide. Figure 7 shows the hydrogen bond pattern between the pentasaccharide residues. Strong direct and water-mediated hydrogen bonds are observed between neighboring residues. Hydrogen bonds between non-neighboring residues are not common, but somewhat strong hydrogen bonds between residues 2 and A′ are observed.

Fig. 7.

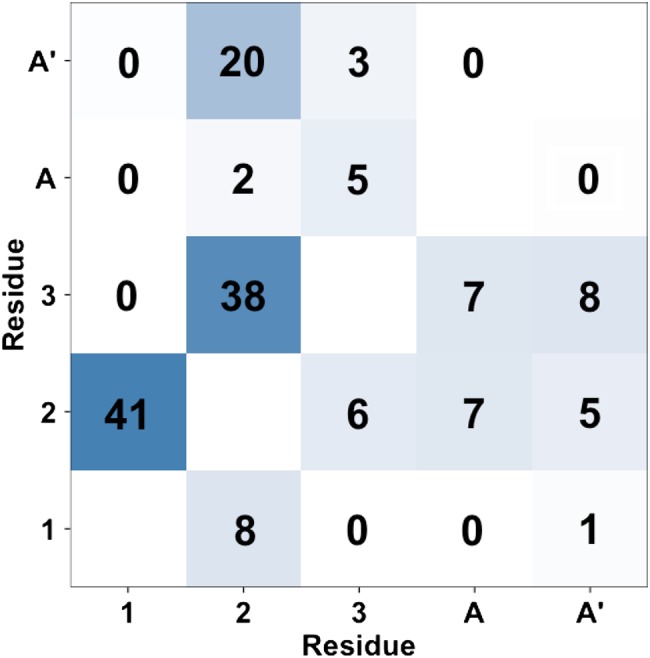
Hydrogen bonding pattern of the N-glycan pentasaccharide in solution. The upper and lower triangle shows the direct hydrogen bonds between two carbohydrate residues and water-mediated hydrogen bonds, respectively. The number and the color in each square represent the occupancy of the hydrogen bonds as a percent of the total trajectory. This figure is available in black and white in print and color at Glycobiology online.

Some hydrogen bonds appear to be tightly associated with different conformational states. There is consensus that hydrogen bonds between the oligosaccharide residues are important in maintaining certain conformations, but it is not clear whether these hydrogen bonds are responsible for the formation of specific conformational states. In other words, does hydrogen bond formation/deformation drive the conformational change? TE in information theory was employed to quantify the causality relationship between the time series of a conformational state change (i.e., glycosidic torsion angles) and the hydrogen bonding formation.

Table III shows the TE values between the conformational state and the hydrogen bond formation/deformation of specific atom pairs. The TE values are bound between −1 and 1, with the positive value meaning the former time series drives the latter one and the negative value meaning the opposite. A TE value of zero indicates no causality relationship between the two time series. The negative TE values from the simulation trajectories indicate that the hydrogen-bond formation/deformation is driven by the change of glycosidic torsional states. Therefore, our TE analysis shows that the hydrogen bonds are not responsible for the conformational change of the pentasaccharide used in this study. This, in turn, suggests that the hydrogen bonds in small glycans are more important for maintaining the conformational states. It would be interesting to see how this relationship changes in a larger oligosaccharide, since the cooperative hydrogen bond formation (and thus driving a conformation change) may still exist in larger oligosaccharides. Hydrogen bond formation is expected to depend on the solvent model used in a simulation, and the current result is based on TIP3P water model (Jorgensen et al. 1983).

Table III.

TE (D_y→x) values between time series of hydrogen bonds (y) and the conformational states (x)

H-bond	#1	#2	#3	#4	#5
2:O5-A′:HO4	−0.25	−0.11	−0.15	−0.20	−0.23
2:O3-W-A′:HO6	−0.16	−0.17	−0.12	−0.16	−0.28

The magnitude of each number represents how strongly one time series is “driving” the other time series. Each column is from the different, independent MD simulation trajectories. A hydrogen bond between two atoms is designated as (residue):(atom)-W (water bridge, if exists)-(residue):(atom).

Conclusions

Despite their biological importance, understanding glycan conformation and its implication on protein structure, dynamics, and function is generally lacking. In this study, we have used standard MD simulations (total of 5 µs) and T-REXMD simulation (total of 4.8 µs) to exhaustively sample conformational preferences of the N-glycan core pentasaccharide in solution and compare them with the N-glycans in the PDB glycoproteins.

The conformational variability of the pentasaccharide in solution at 300 K appears to be limited compared with the ones from the high temperature or random glycan conformation models. Moreover, there are only a few dominant conformational states in solution. To systematically examine the conformational preference of the pentasaccharide, the conformational states are defined using the glycosidic torsion angle distributions, which allow us to quantify conformational preferences. A detailed analysis on the conformational preference of the pentasaccharide shows two major dominant conformations (84%) and several minor conformations (with about 1–3% each). The 1–6 linkage brings the most conformational diversity in the pentasaccharide since it can completely extend or fold-back to itself. The timescale of this transition is on the order of 100 ns. These observations match with the previous NMR experiments (Woods et al. 1998; Wormald et al. 2002), which were inconsistent with a single conformation.

The conformational distribution appears to be determined by the competition between the entropic and enthalpic contributions. In the major conformational state, the 1–6 linkage extends into the solvent (state AAAAG of about 50%), which is entropically favorable, whereas the 1–6 linkage folds back onto itself in the minor states (state AAAAg of ∼30%). The fold-back conformation has slightly more intramolecular interactions, but the added favorable interactions appear to be insufficient to overcome the entropic penalty. From other NMR experiments and computational studies, the preference of the extended conformation over the fold-back conformation changes in a sequence-dependent manner, suggesting that the entropy–enthalpy compensation plays an important role in the conformational preference of oligosaccharides in solution.

We have used crystal structures of glycoproteins to examine the conformational preference of the N-glycan core pentasaccharide when they are attached to proteins. The N-glycosylated pentasaccharide structures in the PDB database show considerable deviation from their conformational preference observed in solution and several conformational states are equally probable (∼20% each for AAAAG, AAABG, and AAAAg). The increased conformational preferences for the states that are less populated in solution are typically accompanied by favorable interactions with proteins (sometimes through crystal packing). Although care must be taken to interpret the data as the number of crystal structures is limited, the results indicate that the N-glycans in the vicinity of protein may have significantly different conformational preference due to the interactions with protein. This suggests that modeling of oligosaccharides in solution and glycosylated forms must take the environment into account.

Finally, the transfer entropy analysis was employed to examine whether the hydrogen bond formation/deformation drives the conformational change or vice versa. There are a few hydrogen bonds that are tightly associated with changes in conformational states. The analysis indicates that hydrogen bonds do not appear to cause conformational change of the pentasaccharide. Instead, the conformational changes through thermal fluctuations along glycosidic torsion angles drive formation of certain hydrogen bonds. The pentasaccharide used in this study is relatively small, and the hydrogen bond between residues far apart is hard to be observed. It would be interesting to examine larger oligosaccharides since they may have more hydrogen bonds involved and thus cooperatively induce conformational changes.

Supplementary data

Supplementary data for this article is available online at http://glycob.oxfordjournals.org/.

Conflict of interest statement

None declared.

Funding

This work was supported by the University of Kansas General Research Fund allocation #2301552, NSF IIA-1359530, NIH U54GM087519 and XSEDE MCB070009. Anton computer time was provided by the National Center for Multiscale Modeling of Biological Systems (MMBioS) through Grant P41GM103712-S1 from the National Institutes of Health and the Pittsburgh Supercomputing Center (PSC). The Anton machine at PSC was generously made available by D.E. Shaw Research.

Abbreviations

Asn, asparagine; GFDB, Glycan Fragment Database; MD, molecular dynamics; PDB, Protein Data Bank; PME, particle-mesh Ewald; TE, transfer entropy; T-REXMD, temperature replica-exchange molecular dynamics.