Controlling Selectivity by Controlling the Path of Trajectories

Abstract

Consideration of the role of dynamic trajectories in [1,2]- and [2,3]-sigmatropic rearrangements suggests a counterintuitive approach to controlling the selectivity. In our hypothesis, [2,3] selectivity can be promoted by reaction conditions that thermodynamically disfavor the [2,3] rearrangement step and thereby make the transition state later. The application of this idea has led to a successful prescription for dictating the selectivity in Stevens/Sommelet-Hauser rearrangements of ammonium ylides. A combination of kinetic isotope effects, crossover experiments, and computational dynamic trajectories support the idea that the selectivity is controlled through control of the path of trajectories.

The advent of new physical ideas in reaction mechanisms is interesting in itself, but it can also provide new approaches to the rational control of reactions. We describe here how recognition of the role of dynamics in sigmatropic rearrangements leads to a counterintuitive but successful strategy for dictating the product of these reactions.

In conventional chemistry, it is implicitly assumed that the selectivity of reactions is decided by the relative energy of the transition states leading to the products. Selectivity can then be enhanced by lowering the energy of the transition state leading to the desired product or raising the energy of alternative transition states. Synthetic chemists routinely apply this idea in a qualitative fashion, for example, when adjusting a steric environment to favor one stereoisomer over another.

We recently suggested that the pervasive co-occurrence of formally allowed [2,3]-sigmatropic rearrangements and formally forbidden [1,2]-sigmatropic rearrangements is the result of a partitioning of dynamic trajectories passing through a single [2,3]-rearrangement transition state.¹ This idea poses a thorny problem from a synthetic standpoint: how can one direct the selectivity for a reaction with only one transition state? There has been a long history of attempts to control the [2,3] versus [1,2] selectivity of these reactions.²⁻⁵ Reactant structural effects can certainly direct which product is formed. Control of the product for a given reactant of interest is much more difficult. Attempts at control through changes in reaction conditions have most often met with little success, peppered with occasional results that are spectacular but enigmatic.^4,6−8

In previous work, we examined the factors impacting selectivity as trajectories passing through a single transition state are partitioned into separate products.⁹ A critical factor determining the selectivity is a form of “dynamic matching,”¹⁰ in which the favored product is the result of a linear continuation of the motions passing through the initial transition state. We reasoned that in desired [2,3]-sigmatropic rearrangements, dynamic matching engenders a particular problem. That is, transition states for [2,3]-sigmatropic rearrangements tend to be both “early” (reactant-like) and “loose,” so that motion through the transition state (the transition vector) is largely dissociative in character (Figure 1).¹ The continuation of this motion leads to fragment radical or pairs that ultimately lead to [1,2]-rearrangement products.

Figure 1.

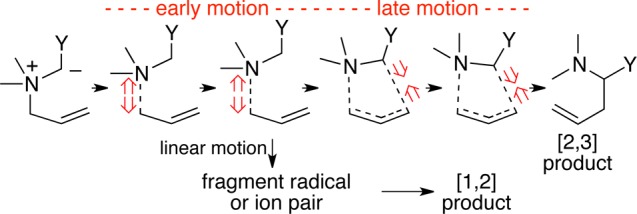
Qualitative depiction of atomic motions along the reaction coordinate for a [2,3]-sigmatropic rearrangement of an ammonium ylide. With a loose transition state, the early motion is dominated by bond breaking.

From this analysis, the fragmentation leading to [1,2] products can be minimized if the transition state is made either “tighter” or “later.” There is no obvious way to engineer tighter transition states without changing the reactant structure. By Hammond’s postulate, however, the transition state should shift later when the reaction is made more endergonic. In reactions of ylides, this may be achieved using reaction conditions that stabilize the polar starting material relative to the neutral product. Overall, our hypothesis is that selectivity may be shifted from [1,2] to [2,3] by conditions that thermodynamically disfavor the [2,3] rearrangement.

To explore this idea, we chose the base-mediated rearrangement of 1a.¹¹ With the ylide 2a derived from 1a, the [1,2] (Stevens) rearrangement product 4a predominates under ordinary reaction conditions. For example, treatment of 1 with KH, KOMe, or NaOMe in DMSO affords exclusively 4a (Table 1). These conditions were hypothesized to involve an uncoordinated “naked” ylide. Neither solvent polarity nor the presence of small amounts of methanol (from the NaOMe) affected the selectivity (Table 1, entries 2–4). Switching to methanol as the solvent, however, led to a reversal of the selectivity, giving the [2,3] (Sommelet-Hauser) rearrangement product 5a in a 75:25 ratio versus 4a. In methanol, the enolate oxygen of ylide 2a should be tightly hydrogen bonded, increasing the barrier for the reaction. In line with this, the reaction in methanol is impractically slow, several orders of magnitude slower than the reaction in DMSO (see the Supporting Information (SI)).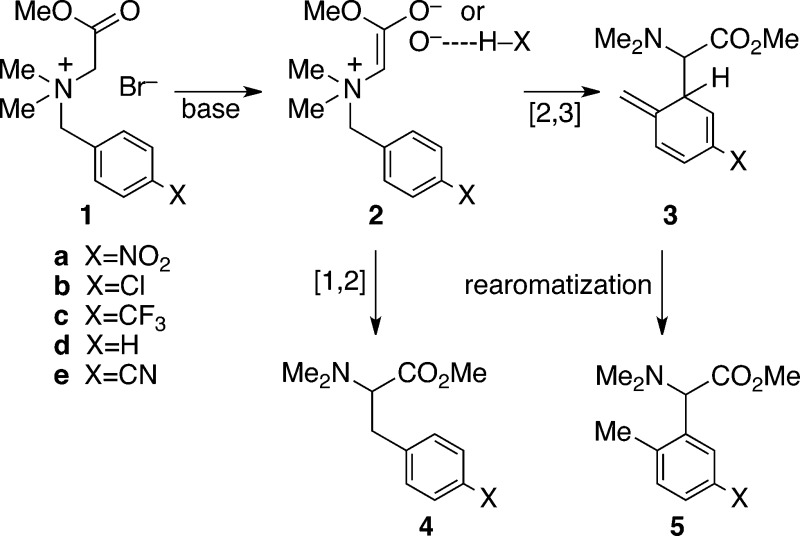

Table 1. Effect of Reaction Conditions on [1,2]- versus [2,3]-Sigmatropic Rearrangements^a.

entry	reactant	solvent	base	5/4 ([2,3]/[1,2])
1	1a	DMSO	KH	0:100 (70%)b
2	1a	DMSO	NaOMe	0:100
3	1a	CH2Cl2	NaOMe	0:100
4	1a	CCl4	NaOMe	0:100
5	1a	MeOH	NaOMe	75:25
6	1a	MeOH	DBU	75:25
7	1a	DMSO	DBU	33:67
8	1a	MeCN	DBU	45:55
9	1a	acetone	DBU	80:20
10	1a	2-butanone	DBU	89:11
11	1a	CH2Cl2	DBU	94:6
12	1a	CCl4	DBU	99:1 (91%)b,c
13	1b	CH2Cl2	KH	0:100 (70%)
14	1c	CH2Cl2	KH	8:92 (56%)b,d
15	1d	CH2Cl2	KH	0:100 (65%)b
16	1e	CH2Cl2	KH	5:95 (57%)
17	1b	CH2Cl2	DBU	87:13 (76%)b,d
18	1c	CH2Cl2	DBU	98:2 (86%)b
19	1d	CH2Cl2	DBU	55:45
20	1e	CH2Cl2	DBU	98:2 (90%)b

^aUnless otherwise noted, the reactions were carried out at 25 °C. The reaction times were 5 min or 1 h for product ratios and ranged from 15 min to 3 h for isolated yields.

^bIsolated yield of purified major product.

^cIsolated yield obtained using a mixture of CCl₄ and CH₂Cl₂ as solvent.

^dIsolated yield obtained at 43 °C.

To maximize the expected influence of ylide hydrogen bonding, we explored the use of amine bases. No reaction occurred with simple amines, but rapid reactions occurred with the stronger base DBU. Most strikingly, the DBU-mediated reactions result in substantial formation of the [2,3]-product 5. The impact of the DBU increased as the solvent polarity was decreased (Table 1, entries 7 to 12), culminating in a 99:1 ratio of [2,3] to [1,2] products when DBU was used with CCl₄ as solvent.

This provides a prescription for controlling the outcome of these reactions in the related examples in Table 1. The naked ylides obtained using alkali metal bases lead to predominant or exclusive [1,2] rearrangement (entries 1–4, 13–16). Maximally hydrogen-bonded ylides obtained using DBU in a nonpolar solvent afford major or predominant [2,3] rearrangement (entries 12, 17–20). The contrasting conditions allow a choice of products in high yields.

In principle, the DBU could simply be catalyzing the rearomatization of 3 to 5, preventing its reversal to 2 or cleavage leading to 4. This has been previously proposed in other systems.⁷ However, varying the amount of DBU from 0.5 to 2 equiv had no effect on the product ratio in CH₂Cl₂ or DMSO. The use of excess NaOMe also had no effect on the selectivity in DMSO or methanol. The selectivity was not affected by ultraviolet irradiation. These results weigh against the importance of rearomatization in the selectivity.

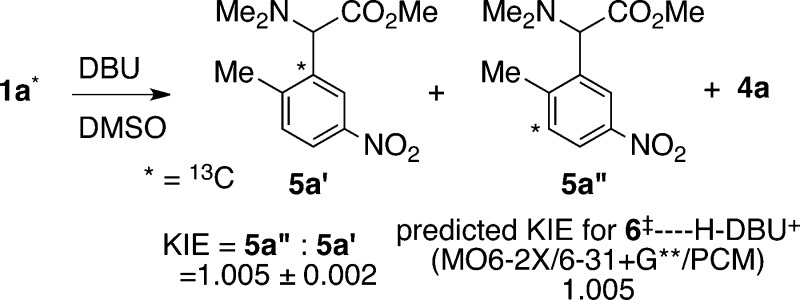
To more directly probe the nature of the transition state leading to the [2,3] product, the intramolecular kinetic isotope effect (KIE) for the formation of 5a was determined. When 1a contains a ¹³C ortho to the ammonium group, the ¹³C may end up in either the substituted position (5a′) or in the spectator position (5a″) (Figure 2). The ratio of these products is the intramolecular KIE, and this was readily determined at natural abundance by NMR methodology.¹² A total of 12 KIE measurements were made on samples of 5a obtained from two independent reactions of 1a mediated by DBU in DMSO. The observed KIE of 1.005 ± 0.002 is significant but quite small. Qualitatively, the KIE does not fit well with any transition state involving substantial bonding changes at the ortho carbon, such as product-determining deprotonation of 3. The KIE would fit with a sufficiently loose and early [2,3]-sigmatropic transition state. Quantitatively, the KIE matches that predicted below based on the relevant calculated transition structure.

Figure 2.

Experimental and predicted intramolecular KIE for the formation of 5a (25 °C).

Crossover observations were used to gauge the intramolecular versus intermolecular nature of the rearrangements. Crossover was negligible (∼1%) in the [2,3]-product 5d obtained from a DBU-mediated reaction of a mixture of 1d and 1d-D₁₃ (labeled in both the benzylic and dimethylamino groups) in acetonitrile. This shows that the [2,3] product is predominantly formed by an intramolecular process. Crossover in the [1,2]-product 4d was significant (∼14%), showing that the [1,2] product results from a mixture of intermolecular and intramolecular processes. This is consistent with partial recombination/partial diffusional separation of a geminate pair, as seen previously with allylic rearrangements.¹ It is uncertain whether the geminate pair is diradical or ionic in nature, but it seems notable that electron-rich aromatics are unreactive under these conditions.^11b

The lowest-energy transition structure for the reaction of 2a in diverse calculations (see the SI) is 6^‡.¹¹ In the gas phase using M06-2X/6-31+G** calculations,¹³6^‡ is formally a [2,3]-rearrangement transition structure. That is, the minimum-energy path (MEP) through 6^‡ leads to the [2,3] initial product 3a. The geometry of 6^‡ changes negligibly (only 0.01 Å in key distances a and b) in calculations employing a PCM solvent model for CH₂Cl₂ or DMSO, but the MEP through 6^‡ no longer affords 3a. Instead, the MEP leads to a complex of iminium ion 7 and nitrobenzyl anion 8. The 7–8 complex is a potential energy minimum, but it will be seen below that trajectories rarely linger in this area.

Although solvent polarity has no effect on 6^‡, hydrogen bonding to the enolate oxygen of the ylide by methanol or the conjugate acid of DBU (H-DBU⁺) has substantial effects (Table 2). The stabilization of the ylide in either case lowers the ylide free energy versus 3a by over 5 kcal/mol, and this predictably leads to a later transition state. The C–N distance a in 6^‡ is increased by about 0.2 Å, while the C–C distance b is decreased. The predicted intramolecular KIE for 6^‡–H-DBU⁺ is 1.005, matching the experimental KIE.

Table 2. Polarity and Hydrogen-Bonding Effects on ΔG°, Transition State Distances, and Trajectory Results for the Rearrangement of 2a.

conditions	ΔG°a	a	b	trajectory results [2,3]/dissociation
DMSO, no coord.	4.0	2.19	2.74	0:108 (exptl: 0:100)
CH2Cl2, no coord.	2.8	2.19	2.74	0:54 (exptl: 0:100)
hydrogen bonded to H-OMe in MeOH	9.1	2.36	2.68	17:29 (exptl: 75:25)
hydrogen bonded to H-DBU+ in CCl4	9.6	2.36	2.67	58:2 (exptl: 99:1)

^aCalculated from M06-2X/6-31+G**/PCM free energies of 3a versus 2a (kcal/mol), hydrogen-bonded when appropriate.

The outcome of trajectories passing through 6^‡ in its various forms was studied by direct-dynamics calculations.¹⁴ For reactions in DMSO, CH₂Cl₂, and CCl₄, quasiclassical trajectories were initiated at 25 °C from the transition structures (see the SI for details) and integrated forward and backward in time on an M06-2X/6-31+G**/PCM surface until the [2,3]-adduct 3a was formed, 2a was reformed, or the fragments fully separated (defined by a and b > 3.2 Å; this process will be referred to here as “dissociation” though the fragments are initially still associated within a solvent cage). No trajectories were observed to form 4a, and it was assumed that 4a ensues from the dissociation process. For the reaction in methanol, fully classical trajectories were performed in a sphere of 101 methanol molecules on an ONIOM surface, using M06-2X/6-31G* for the solute and PM3 for the solvent molecules. Equilibrated trajectories constrained to the area of 6^‡ in methanol were deconstrained then integrated forward and backward in time.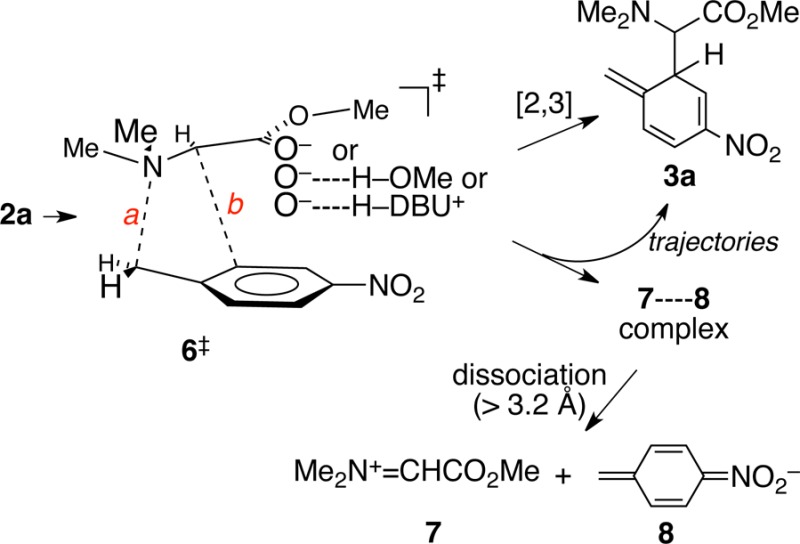

The trajectory results (Table 2) reflect the trends seen in the experimental observations. The trajectories of naked ylides in both DMSO and CH₂Cl₂ rapidly pass through the area of the 7–8 complex and dissociate with median times after 6^‡ of 118 and 134 fs, respectively. This dissociation is in line with the exclusive formation of 4 in each solvent using alkali-metal bases. Methanol as solvent leads to a 75:25 ratio of [2,3] and [1,2] products experimentally, while the trajectories in explicit methanol modestly favor dissociation leading to the [1,2] product. Considering the limitations of the calculations, the agreement of the ratios is satisfactory. Most importantly, the trajectories involving hydrogen bonding to 6^‡ by H-DBU⁺ lead predominantly to the [2,3]-adduct 3 in CCl₄, matching the experimental observation.

There is no intrinsic reason to expect high accuracy in the M06-2X surface for this reaction, and our previous exploration of a [2,3]-sigmatropic rearrangement found that DFT methods provided an exceptional diversity of predictions.¹ Rather, the calculations here should be viewed as providing a mechanistic model that accounts for both the selectivity observations and the experimental KIE. We can then query this model for further insight into the selectivity.

Examination of the trajectories suggests that our initial hypothesis for selectivity control was only partially accurate. Approximately 50% of the 6^‡–H-DBU⁺ trajectories afford 3a within 80–160 fs. Such trajectories are indistinguishable from ordinary concerted trajectories in asynchronous pericyclic reactions. It is notable that the MEP through 6^‡–H-DBU⁺ leads to the 7–8 complex, but the “quick” half of the trajectories bypass the complex to give 3a directly. (See the SI for plots of the course of the trajectories.) The remaining “slow” trajectories complete C–N bond breakage without progressing in the C–C bond formation that would consummate the [2,3] rearrangement. Instead, these trajectories pass into the area of the 7–8 complex. Yet these trajectories rarely dissociate, unlike the inevitable fragment separation seen in reactions of naked ylides. Instead, they return to the [2,3] product, mostly within a 160–350 fs. A plausible explanation is that the nascent 7 is held to 8 by the combination of hydrogen bonding between 7 and H-DBU⁺ and the electrostatic attraction of 8 and H-DBU⁺. Overall then, the H-DBU⁺ controls the paths of the trajectories on two levels, the first arising from its effect on the transition state geometry, promoting simple concerted trajectories, and the second being its inhibition of dissociative trajectories. Our initial hypothesis anticipated the first control element but not the second.

The trajectory results in methanol allow an interesting comparison of rearrangement trajectories with those undergoing dissociation. The [2,3]-rearrangement trajectories giving 3a in discrete methanol are fast, occurring with a median time of 210 fs and with 80% finishing within 300 fs. The dissociative trajectories are slow, taking a median time of 560 fs. As was seen with 6^‡–H-DBU⁺, the trajectories rapidly forming 3a have bypassed the formation of the MEP-favored 7–8 complex. Unlike with 6^‡–H-DBU⁺, the trajectories that proceed into the area of the 7–8 complex mainly dissociate. In this way, the methanol reaction lacks the second level of trajectory control present in the DBU reaction, and the selectivity for the [2,3] product is lower.

Mechanistic understanding is the key to the rational design and control of reactions, but it is fair to ask how much detail is really needed in mechanisms. Simple “electron-pushing” mechanisms certainly provide substantial insight by themselves. Rate laws, rate-limiting steps, and the understanding of transition state geometries and energies provide much more insight, and this knowledge is integral to modern reaction development. The results here show that the consideration of dynamics in reactions can also be important and can provide unexpected strategies for the direction of reactions. We are continuing to pursue the application of dynamics-based ideas to the control of reactions.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/jacs.5b08635.

• Complete descriptions of experimental and computational procedures, calculated structures and energies, and trajectory plots (PDF)

The authors declare no competing financial interest.