Significance
Noise is not only a source of disturbance, but it also can be beneficial for neuronal information processing. The release of neurotransmitter vesicles in synapses is an unreliable process, especially in the central nervous system. Here we show that the probabilistic nature of neurotransmitter release directly influences the functional role of a synapse, and that a small probability of release per docked vesicle helps reduce the error in the reconstruction of desired signals from the time series of vesicle release events.
Keywords: synaptic transmission, stochastic vesicle release, release probability, optimal filter
Abstract
The probabilistic nature of neurotransmitter release in synapses is believed to be one of the most significant sources of noise in the central nervous system. We show how p0, the probability of release per docked vesicle when an action potential arrives, affects the dynamics of the rate of vesicle release in response to changes in the rate of arrival of action potentials. Furthermore, we examine the theoretical capability of a synapse in the estimation of desired signals using information from the stochastic vesicle release events under the framework of optimal linear filter theory. We find that a small p0, such as 0.1, reduces the error in the reconstruction of the input, or in the reconstruction of the time derivative of the input, from the time series of vesicle release events. Our results imply that the probabilistic nature of synaptic vesicle release plays a direct functional role in synaptic transmission.
Randomness is present in almost all levels of all nervous systems, such as in ionic channels of individual neurons, in synapses between neurons, and in environmental stimuli. The probabilistic nature of the synaptic vesicle release process is believed to be one of the most significant sources of randomness. Stochastic vesicle release affects information transfer from a presynaptic neuron to a postsynaptic neuron, and hence may play not only an important role in synaptic plasticity (1, 2) but also a significant role in determining the functionality of certain synapses, a point we will argue in this article. The functional role of stochastic vesicle release in synaptic transmission is likely to be more significant in those synapses in the central nervous system, where the size of the readily releasable vesicle pool is usually smaller than those in the periphery.
Synaptic vesicle release has only recently been studied in a probabilistic or information–theoretic manner (3–5). A systematic perspective on how stochastic vesicle release affects neural code processing at synapses is still lacking. On the experimental front, a comprehensive, quantitative knowledge about the nature of vesicle docking, priming, fusing, undocking, replenishing, and recycling is far from complete, and hence a biophysically detailed model of the entire vesicle release process is not yet possible.
Despite current limited understanding of the synaptic vesicle release process, a probabilistic model that captures the essential elements of that process can still be built to study the effect of various sources of randomness on synaptic transmission. Rosenbaum et al. (3) recently constructed such a model to study how variability in vesicle dynamics affects information transfer from one neuron to another. They found that the depletion of docked vesicles at higher rates of arrival of action potentials makes the synapse act as a high-pass filter from a signal processing point of view. Motivated by Rosenbaum et al.’s (3) model of the presynaptic vesicle release process, we here build a probabilistic model that includes four stochastic subprocesses involved in synaptic vesicle release: the stochastic process that generates the presynaptic spike density , the randomness of the interspike intervals in the presynaptic spike train, the randomness in vesicle docking, and the probabilistic nature of vesicle release. Based on this presynaptic model, we use optimal linear filter theory to determine the best possible linear response of the postsynaptic neuron to each vesicle release event with the aim of reconstructing desired signals derived from . This optimization approach contrasts with that of Manwani and Koch (4), in which biophysical details are used to formulate a model of the postsynaptic response. Instead, we ask what the best response is given the goal to reconstruct some aspect of the input signal . For example, if the function of this synapse is to simply relay and preserve the original presynaptic signal , then our model answers the question of how various sources of randomness in the vesicle release process affect the theoretical capability of the synapse in the reconstruction of . As another example, if this synapse serves as an edge detector, then our model can be used to study how various sources of randomness in the vesicle release process affect the reconstruction of the derivative of . In both cases we find that a smaller probability of release per docked vesicle, such as 0.1, is preferable to a larger probability of release, such as 0.5 or 1.
More generally, we provide a systematic framework, based on a cascade of stochastic models of the presynaptic vesicle docking and release processes coupled with optimal linear filter theory, to address how various sources of randomness in synaptic vesicle release affect synaptic transmission between two neurons. We believe that our model framework can be further extended or modified to incorporate biophysical details of the synaptic vesicle release process, or by changing the objective function used in the optimal filter theory, to study various issues in synaptic transmission.
The Presynaptic Model of Synaptic Vesicle Release
We first build a model of stochastic vesicle release in the presynaptic neuron.
A key assumption of our model is that we allow for an unlimited number of docking sites. Let vesicle docking occur by a homogeneous Poisson process with mean rate , so that is the probability per unit time that the number of docked vesicles increases by one. Note that is the rate at which the total number of docked vesicles in the entire synapse increases in the absence of vesicle release. In fact, if a given neuron makes multiple synapses onto a given postsynaptic neuron, then, under the assumption of our model, these synapses may be regarded as one large model synapse with a parameter that is the sum of the individual ’s.
Let presynaptic action potentials occur by a stochastic process with mean rate , so that is the probability per unit time of the occurrence of action potentials in the presynaptic neuron [i.e., is the presynaptic spike density]. Of course, the rate does not fully characterize the statistics of the spike train. We consider some particular cases later. Denote the time of the kth presynaptic action potential by , Later, we shall regard as a sample of a stochastic process , but when we write lowercase , we are conditioning on , for all t. The vesicle docking process and the process that generates action potentials are independent of each other, regardless of whether we condition on S; this is a consequence of the assumption of an unlimited number of docking sites. Otherwise, vesicle release by action potentials would increase the rate of docking by making more sites available.
When an action potential occurs in the presynaptic neuron, each vesicle that is docked has a probability of being released, this choice being made independently for all of the vesicles that happen to be docked at that moment. Note that is not the same as , which is commonly used to refer to the probability of vesicle release for the entire synapse (6). In fact, is the probability that at least one vesicle is released when an action potential occurs, whereas is the probability of release per docked vesicle when an action potential occurs. Hence, , where n is the number of docked vesicles when the action potential occurs.
The Expected Rate of Synaptic Vesicle Release
Using the above model of the presynaptic vesicle docking and release processes, we first study how , the probability of release per docked vesicle when an action potential occurs, affects the expected rate of synaptic vesicle release. In this section only, we assume that the presynaptic action potentials occur by an inhomogeneous Poisson process with a given mean rate .
Let be the expected number of vesicles that dock during , and let be the expected number of vesicles that are released during . Then is the expected number of vesicles that are docked at time t, and the expected rate of vesicle release () satisfies the differential equation
| [1] |
On the right-hand side of Eq. 1, the product of and gives the expected number of vesicles released when a single action potential arrives in the presynaptic neuron at time t. Further multiplying this product by the spike density gives us the expected rate of vesicle release, , at time t.
If we differentiate Eq. 1 with respect to time on both sides and make use of , we get
| [2] |
Let , then Eq. 2 becomes
| [3] |
Dividing both sides by [recall that ] and rearranging the terms, we see that Eq. 3 can be written simply as
| [4] |
Although the above derivation is informal, Eq. 4 is rigorously correct given our assumptions, including the assumption of a Poisson spike train; it can be derived, for example, from the master equation for the process by taking first moments to get expected values.
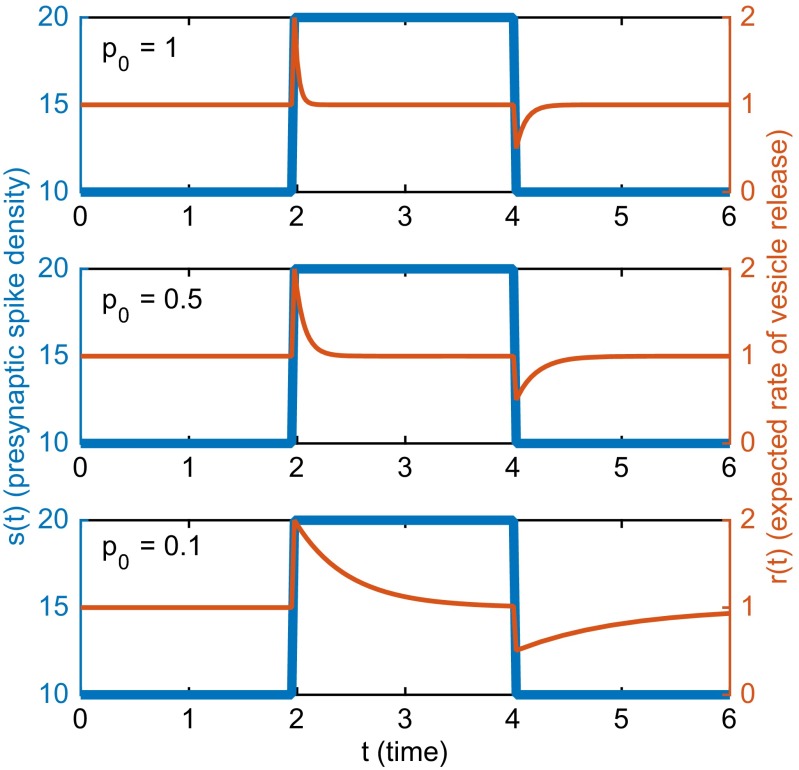
To our knowledge, Eq. 4 is new. In its linearized form, however, it is closely related to the theory of Rosenbaum et al. (3). Eq. 4 shows that during any time interval in which the spike density is constant, the expected rate of vesicle release approaches the mean rate of vesicle docking . However, if jumps, Eq. 4 shows that the variable must be continuous, so also jumps proportionally, which shows that the stochastic vesicle release process provides a synaptic mechanism through which the Weber–Fechner principle (7) in the sensory system can be realized.
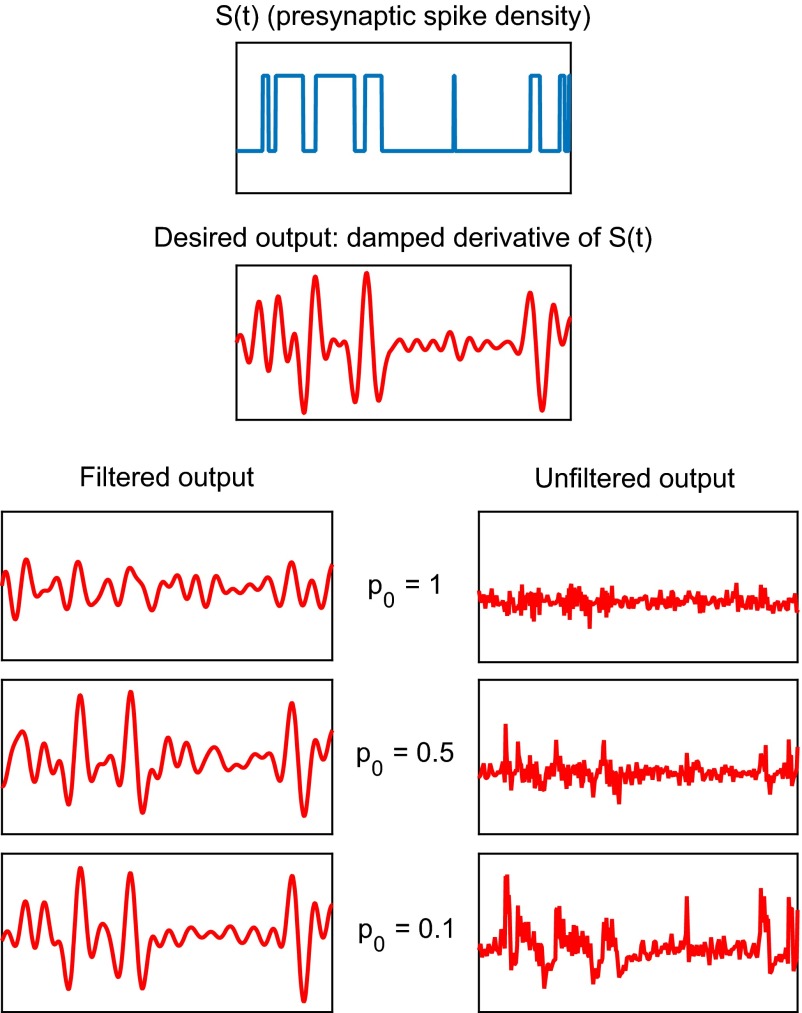
Plotted in Fig. 1 are the probability per unit time of an action potential in the presynaptic neuron [blue curve, also referred to as the presynaptic spike density ] and the corresponding expected rate of vesicle release [red curve, ] under three values of : 1, 0.5, and 0.1. For all three cases, the expected rate of vesicle release exponentially approaches the vesicle docking rate when the presynaptic spike density remains constant. The rate constant for the approach to the steady level is . In particular, the rate constant is larger during the transient following the upward jump in and smaller during the transient following the downward jump. When is large, the rate of vesicle release converges rapidly back to whenever there is a jump in . In the extreme case, when , the time constant of the exponential approach is equal to the mean interspike interval after the jump in rate, and this means in practice that the transient is too fast to be detected by the postsynaptic neuron in the presence of noise. In contrast, when is small, it takes longer for the rate of vesicle release to get close to , and this makes it easier for the transient to be detected. An example of this phenomenon can be seen in Fig. 2. Note in particular that the unfiltered output in the case of shows essentially no semblance of the original signal, and that hints of the original signal begin to appear in the unfiltered output as is reduced.
Fig. 1.
Effect of probability of release per docked vesicle () on the expected rate of vesicle release (r) for a spike train generated by an inhomogeneous Poisson process with mean rate . Results for = 1, 0.5, and 0.1 are plotted in Top, Middle, and Bottom, respectively. is plotted in blue, and is plotted in red. Parameters used: for and , for ; .
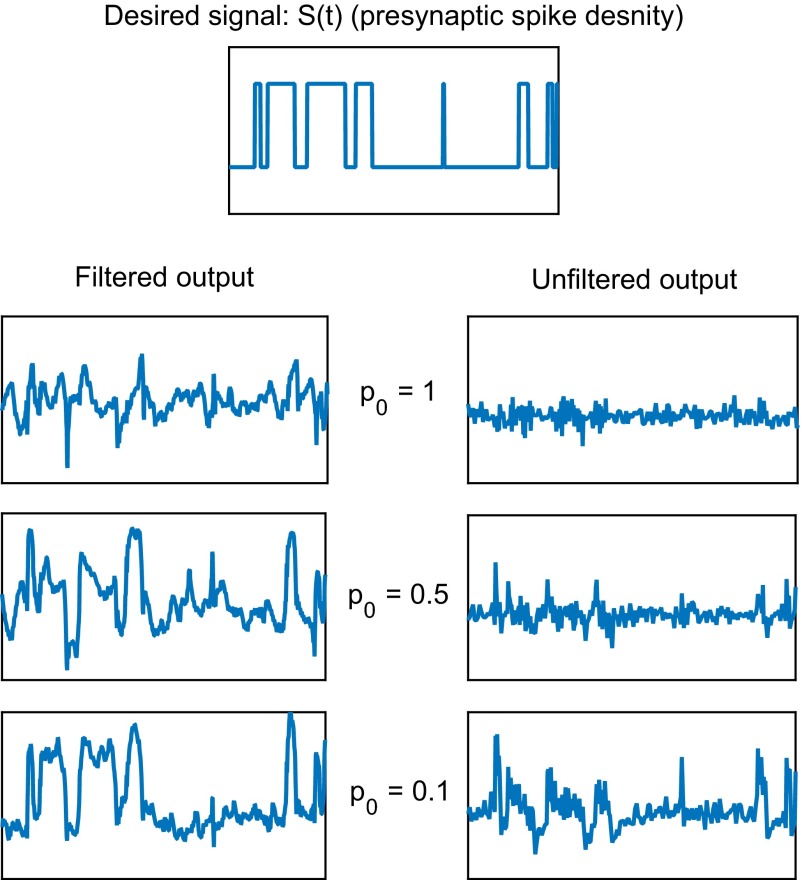
Fig. 2.
Effect of probability of release per docked vesicle () on the synapse’s ability to estimate the presynaptic spike density . In this numerical experiment, the goal of the synapse is to simply relay and preserve the presynaptic spike density , plotted in the topmost frame. We repeat this experiment for = 1, 0.5, and 0.1; results are shown in two columns: (Left) estimation of from Eq. 5 (filtered output), obtained by applying the optimal filter to the rate of vesicle release ; (Right) instantaneous rate of vesicle release (unfiltered output), defined (13) by , where is the number of vesicles released at the kth action potential, and is the time of the occurrence that action potential. Note that the optimal filter is different for each (see SI Materials and Methods for the shape of the optimal filter). The design of the optimal filter is based upon the statistical properties of the ensemble of the presynaptic spike density, the spike generation, and the vesicle docking and release processes, but not upon the particular presynaptic spike density used in the experiment. Data shown are for a time duration of 20 s, with . All panels in this figure cover the time interval (65 s, 85 s).
Note that in our model, any steady level constant leads eventually to the same vesicle release rate ; this is because, in any steady state, the rate of vesicle release must equal the rate of vesicle docking. This result is a general feature of our model, and is not dependent on the Poisson assumption used in this section; it is a consequence, however, of our assumption that there is an unlimited number of docking sites available. The functional significance of this feature of our model is that the model synapse is completely insensitive to the steady level of stimulation and communicates only transient changes in the level of stimulation to the postsynaptic neuron. A similar but less extreme insensitivity to low-frequency signals would occur if we assumed a limited number of docking sites (SI Materials and Methods) (3).
SI Materials and Methods
Synaptic Vesicle Release with Finite Docking Sites.
Suppose there are m docking sites, and let be the probability per unit time that an empty docking site becomes filled.
Recall from the main text that is the probability per unit time of release of any docked vesicle when an action potential arrives, is the rate of arrival of action potentials that are generated by an inhomogeneous Poisson process, is the expected number of vesicles released during , and is the expected number of vesicles that dock during . Hence, is the expected number of vesicles that are docked at time t.
Then Eq. 1 in the main text implies that the expected rate of vesicle release satisfies
| [S1] |
But
| [S2] |
and hence
| [S3] |
or
| [S4] |
Now consider a small-amplitude perturbation to around and the resulting perturbation to :
| [S5] |
| [S6] |
in which ε is a small number, is the relative perturbation to around , is the resulting first-order relative perturbation to around , collects all higher-order terms of ε, and and satisfy the steady-state equation
| [S7] |
Then
| [S8] |
and the first-order equation is
| [S9] |
or
| [S10] |
After taking Fourier transforms, this becomes
| [S11] |
or
| [S12] |
where and are the Fourier transforms of and , respectively, in which ω is the frequency variable and t is the time variable.
Let
| [S13] |
so that
| [S14] |
we have
| [S15] |
| [S16] |
Thus, the system is always high-pass, but to make this a strong effect, we require . If we let vary with other parameters fixed, we find that the high-pass effect is strongest when = 1, but even then it is only a strong effect if .
To obtain the case of an unlimited number of docking sites, let
| [S17] |
| [S18] |
in such a way that
| [S19] |
Then and , regardless of the value of .
Optimal Filter.
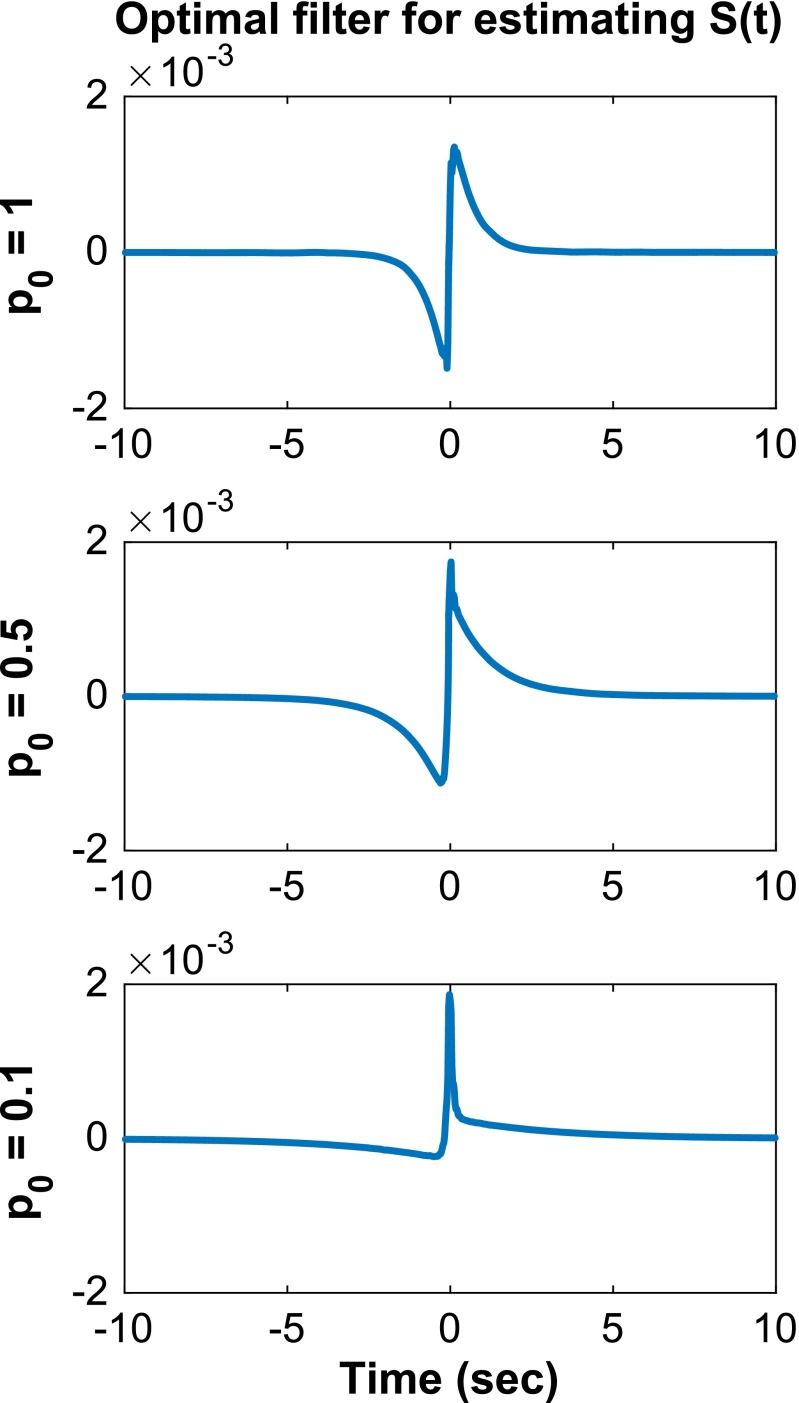
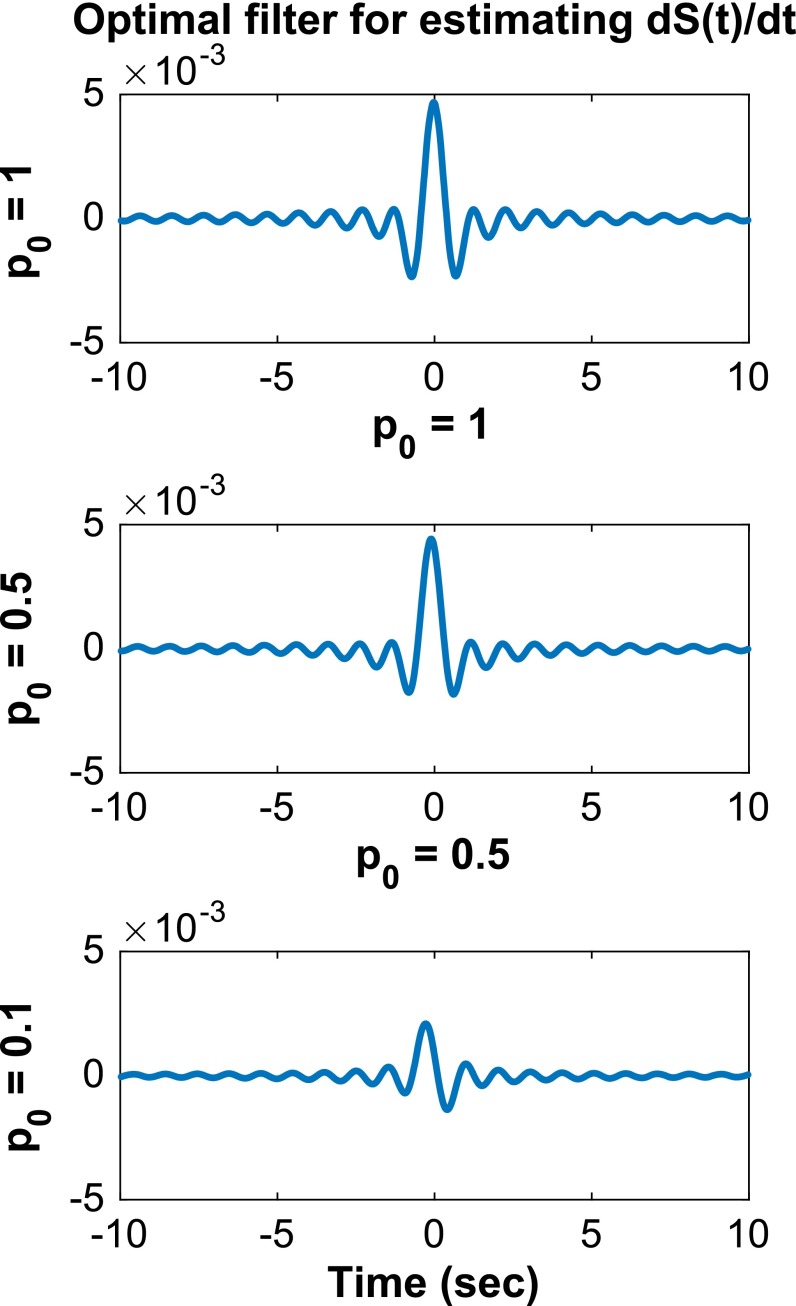
Plotted in Figs. S1 and S2 are the optimal filters used in Figs. 2 and 3, respectively, for different values of .
Fig. S1.
The optimal filters in the estimation of for = 1, 0.5, 0.1. Parameters are described in Fig. 2.
Fig. S2.
The optimal filters in the estimation of for = 1, 0.5, 0.1. Parameters are described in Fig. 3.
Fig. 3.
Effect of probability of release per docked vesicle () on the synapse’s ability to estimate the damped derivative of the presynaptic spike density, plotted in the second frame. Layout of panels and parameter values are as in Fig. 2.
Synapse as an Optimal Filter
So far we have only discussed the effect of randomness on the expected rate of vesicle release. In this section, we address the theoretical capability of a postsynaptic neuron in using the time series of vesicle release events to estimate the instantaneous rate of action potentials in the presynaptic spike train , or the time derivative of ; the ability of the synapse to do so involves not only the expected rate of vesicle release but also the noise in the vesicle docking and release processes and the noise in the stochastic processes for generating the presynaptic spike density and the spike train.
We consider the optimal filtering of the rate of synaptic vesicle release , where is the number of vesicles that have been released during . From here on, we regard the presynaptic spike density as a realization of a stochastic process . Note that is a continuous-time, nondecreasing, integer-valued time series determined by the entire stochastic vesicle release process that includes four sequential subprocesses: the randomness in the presynaptic spike density , the randomness of interspike intervals in the presynaptic spike train, the randomness in vesicle docking, and the probabilistic release of docked vesicles when an action potential arrives in the presynaptic neuron.
Let and describe filters that are applied to and , respectively. The outputs of these filters are
| [5] |
and
| [6] |
The filtered output is the actual output signal produced by the postsynaptic neuron, whereas is the desired output signal that we prescribe. can be thought of as the postsynaptic membrane potential. Note that f is actually a sum, because is a sum of Dirac delta functions at the action potential times weighted by the numbers of vesicles released at those times. gives different desired output signals for different choices of . For example, if is the Dirac delta function , then gives the presynaptic spike density itself, and if is the derivative of , then gives the derivative of .
Note also that we do not impose any causality constraint on the optimal filter ; i.e., can take nonzero values for all t because we are idealizing the postsynaptic neuron as an observer who can record the vesicle release events and process them at leisure to reconstruct the desired signal. It is well known in optimal filter theory that such an ideal observer can be approximated by a real observer whose task is to produce the desired signal after some specified delay. The approximation improves as the delay increases (8).
The actual postsynaptic neuron, of course, does not have this luxury. In future work we shall consider the causal case in which for .
The point of view here is that we are given , and we seek to make and as close as possible. In defining the error, however, we ignore the mean values. Thus, we let
| [7] |
where and , in which means the expectation of the corresponding random variable.
Two remarks are of importance here. First, the optimization problem is not fully specified until we define the stochastic processes that generate the presynaptic spike density and interspike intervals. The second remark is that we seem to have a separate optimization problem for each time t at which we choose to minimize the error. This difficulty will disappear, however, if we take the limit and also assume that is generated by a stationary stochastic process.
The mean square error is minimized when satisfies the following equation (Materials and Methods):
| [8] |
in which
| [9] |
| [10] |
Taking Fourier transforms on both sides of Eq. 8, we get
| [11] |
in which are the Fourier transforms of their respective original variables, is known as the auto power spectral density of , and is known as the cross-power spectral density of and .
Therefore, to find the optimal filter , we need to evaluate the expressions on the right-hand sides of Eqs. 9 and 10; this can be done semianalytically for some specific choices of the stochastic processes for vesicle docking and release by first finding the right-hand sides of Eqs. 9 and 10 conditioned on and then taking a numerical average over a sufficiently large number of samples of . The optimal filter can also be obtained entirely numerically by simulating the stochastic vesicle release process for a sufficiently large number of samples of .
Once we obtain the optimal filter for the synapse, we can evaluate the mean square error over the ensemble of the presynaptic spike density . measures the accuracy of the estimation of a desired signal from the rate of vesicle release events and is a property of the stochastic processes for generating , interspike intervals, vesicle docking, and vesicle release. The filtering property of an actual synapse is determined by various factors, such as the shape of postsynaptic potentials and the molecular mechanisms of exocytosis of synaptic vesicles (9).
The perspective we adopt here is to provide a theoretical upper bound on how well the synapse can possibly perform in the estimation of a desired signal in the mean square sense under optimal linear filter theory. Using this method, we can address how various sources of randomness in synaptic vesicle release affect the fidelity of synaptic transmission.
A Small Enhances Synaptic Transmission
In this section, we show that a small value of , the probability of release per docked vesicle when a presynaptic action potential occurs, enhances the fidelity of synaptic transmission. Recall that the determination of the optimal filter is not possible until we specify the stochastic processes that generate the presynaptic spike density and interspike intervals.
We assume that the presynaptic spike density is generated by a dichotomous jump process, i.e., a process with two discrete levels: and with . Let , and we define to be the probability per unit time that jumps up from to , and to be the probability per unit time that jumps down from to .
We assume that the presynaptic spike train , where is the time of the kth action potential, is generated using the following two steps: first, generate a provisional spike train such that the interspike interval is chosen from a prescribed distribution and has a mean of one unit of time, i.e., let , where and the are independent, identically distributed random variables with mean . Second, rescale the time variable by , where is the old time variable in the provisional spike train and t is the new (physical) time variable. Then our desired spike train with a time-dependent spike density , under the new time variable t, is given by
| [12] |
This rescale of time variable accelerates time when the spike density is high and decelerates time when the spike density is low so that under the new time variable the neuron has an instantaneous spike density . This way of generating synaptic spike times from the spike density is also known as the “faithful copy” property introduced by Knight (10) and analyzed by Sirovich (11) (see also ref. 12). Experimental evidence of neurons that follow the faithful copy property is also presented in ref. 11. A faithful copy neuron allows the user to generate a spike train with expected spike rate equal to , independent of the user’s choice of the shape of the interspike interval distribution. In the examples used in this section, we assume that the interspike intervals in the provisional spike train are normally distributed, i.e., we choose , where is the normal distribution with mean and SD , such that the intervals always happen to be positive numbers. A spike train generated by an inhomogeneous Poisson process with mean rate is another special case of the output of a faithful copy neuron, but such a spike train is too irregular for the performance of the optimal filter to be satisfactory, especially if the goal is to estimate the derivative of .
We simulate numerically the stochastic synaptic vesicle release process defined above at different values of . A direct simulation of the vesicle docking and release processes can be computationally prohibitive because one needs to keep track of the status of each individual vesicle. Instead, we simulate the vesicle docking and release events using an efficient method relying on our theory that the number of vesicles released at each action potential conditioned on the spike times is independent and Poisson distributed (Materials and Methods). For each , we calculate the optimal estimations of two different desired signals: the presynaptic spike density and the damped derivative (defined below) of . Results are shown in Figs. 2 and 3, respectively.
The filtered outputs in Fig. 2 clearly show the gradual improvement of the estimation of the presynaptic spike density as is lowered. Note that the square bumps are already present at ; such bumps are not easy to discern at . In Fig. 3, a good estimation of the damped derivative of the presynaptic spike density also emerges at . Note that because is discontinuous at the jump times, we have defined the damped derivative of by removing frequency components higher than the mean frequency of jump events in , which is 1 Hz in these examples, so that the damped derivative of is bounded and continuous.
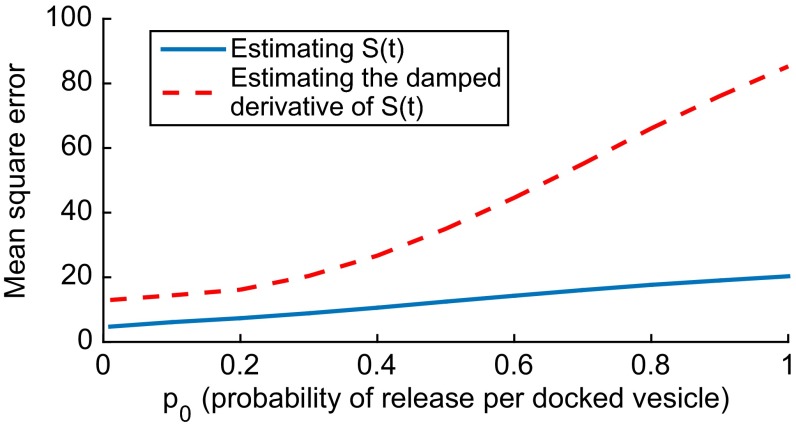
Fig. 4 plots the mean square error as a function of in the estimation of (blue solid curve) and in the estimation of the damped derivative of (red dashed curve). As approaches 0 (but not reaching 0), monotonically decreases for both cases. A smaller value of indicates a more accurate estimation of the desired signal.
Fig. 4.
Effect of probability of release per docked vesicle () on the mean square error [] in the estimation of the presynaptic spike density and its damped derivative. The units of are s−2 in the case of estimation of and s−4 in the case of estimation of the damped derivative of . is obtained numerically by simulating the stochastic vesicle release process for 2,500 independent sample paths, each of which lasts 100 s. Parameter values are as in Fig. 2.
The perspective adopted in this paper is that we do not presume the biophysical details of a synapse’s postsynaptic response to the presynaptic vesicle release events, but instead we use optimal linear filter theory to address the ability of our idealized postsynaptic neuron to estimate a desired signal derived from the presynaptic rate of arrival of action potentials as a function of time, given that we know the statistical properties of the ensemble from which the presynaptic rate of arrival of action potentials as a function of time has been drawn. We have shown in this paper how the optimal filter is calculated, and that a lower probability of release per docked vesicle upon arrival of a presynaptic spike leads to a more accurate estimation of two kinds of desired signals; we believe that this result goes a long way to explain why synaptic vesicle release is a random process.
Materials and Methods
Derivation of the Optimal Linear Filter.
Our goal is to find an optimal linear filter that minimizes the mean square error
| [13] |
If minimizes , then for arbitrary we have, to first order in ,
| [14] |
Because is arbitrary, we must have
| [15] |
Note that here is a perturbation to , not to be confused with the Dirac delta function used previously.
Now take the limit , and make the assumption that there exists functions and , each of one variable, such that
| [16] |
| [17] |
Then Eq. 15 becomes
| [18] |
It is easy to check that Eq. 18 holds for all if and only if it holds for . Thus, is minimized when satisfies Eq. 8.
Simulation of the Vesicle Docking and Release Processes.
Under the assumption that vesicle docking occurs by a homogeneous Poisson process, we show that , the number of vesicles that are released at the kth action potential, are independent and Poisson distributed, conditioned on the presynaptic spike times . This fact allows us to simulate the vesicle release events in an efficient manner without the need to directly simulate the docking and release process by tracking the status of each individual vesicle.
To see this fact, let us first define () to be the number of vesicles released at the kth action potential that docked during the time interval . Recall that is the time of the jth action potential, presumed to be given. Then .
The process that generates the numbers for a fixed j can be described as follows: first, choose D from Poisson distribution with mean . Second, let each of the D vesicles independently undergo a branching process such that each unreleased vesicle has a probability of to be released whenever an action potential occurs. For each individual vesicle, suppose there are K possible outcomes; there are action potentials under consideration and the K possible outcomes are release on any one of those, and nonrelease.
Let be the probability of the kth outcome, and be the number of individual vesicles that are released on the kth action potential (), or not released (outcome K). Then, and
For any integers , , , let , then
| [19] |
Noting that
| [20] |
| [21] |
we have
| [22] |
where ; this shows that is Poisson distributed with mean , and that are independent random variables. Therefore, for each j, are independent and Poisson distributed with
| [23] |
Note that the random variables are also independent for different j, because different j refers to different cohort of vesicles, and both docking and release are independent for different vesicles. Because the sum of independent, Poisson-distributed random variables is a Poisson-distributed random variable with its mean equal to the sum of the means of the original Poisson-distributed random variables, we conclude that are independent and Poisson distributed. Also,
| [24] |
Hence, given the presynaptic spike times , the number of vesicles released at the kth action potential can be simulated in an efficient manner by drawing a number from Poisson distribution with its mean defined by the above Eq. 24.
Acknowledgments
C.Z. is a Courant Instructor. C.S.P. is partially supported by the Systems Biology Center New York under NIH Grant P50-GM071558.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1513160112/-/DCSupplemental.
References
- 1.Han EB, Stevens CF. Development regulates a switch between post- and presynaptic strengthening in response to activity deprivation. Proc Natl Acad Sci USA. 2009;106(26):10817–10822. doi: 10.1073/pnas.0903603106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Pan B, Zucker RS. A general model of synaptic transmission and short-term plasticity. Neuron. 2009;62(4):539–554. doi: 10.1016/j.neuron.2009.03.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Rosenbaum R, Rubin J, Doiron B. Short term synaptic depression imposes a frequency dependent filter on synaptic information transfer. PLOS Comput Biol. 2012;8(6):e1002557. doi: 10.1371/journal.pcbi.1002557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Manwani A, Koch C. Detecting and estimating signals over noisy and unreliable synapses: Information-theoretic analysis. Neural Comput. 2001;13(1):1–33. doi: 10.1162/089976601300014619. [DOI] [PubMed] [Google Scholar]
- 5.Arleo A, et al. How synaptic release probability shapes neuronal transmission: Information-theoretic analysis in a cerebellar granule cell. Neural Comput. 2010;22(8):2031–2058. doi: 10.1162/NECO_a_00006-Arleo. [DOI] [PubMed] [Google Scholar]
- 6.Branco T, Staras K. The probability of neurotransmitter release: Variability and feedback control at single synapses. Nat Rev Neurosci. 2009;10(5):373–383. doi: 10.1038/nrn2634. [DOI] [PubMed] [Google Scholar]
- 7.Hall JE. Textbook of Medical Physiology. Saunders; Philadelphia: 2011. [Google Scholar]
- 8.Lee YW. Statistical Theory of Communication. Wiley; New York: 1960. [Google Scholar]
- 9.Jahn R, Fasshauer D. Molecular machines governing exocytosis of synaptic vesicles. Nature. 2012;490(7419):201–207. doi: 10.1038/nature11320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Knight BW. 2008. Some hidden physiology in naturalistic spike rasters. The faithful copy neuron. Knight Laboratory Paper 4. Available at hdl.handle.net/10209/251.
- 11.Sirovich L. The faithful copy neuron. J Comput Neurosci. 2012;32(3):377–385. doi: 10.1007/s10827-011-0356-6. [DOI] [PubMed] [Google Scholar]
- 12.Gestri G. Pulse frequency modulation in neural systems. A random model. Biophys J. 1971;11(1):98–109. doi: 10.1016/S0006-3495(71)86198-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Knight BW. The relationship between the firing rate of a single neuron and the level of activity in a population of neurons. Experimental evidence for resonant enhancement in the population response. J Gen Physiol. 1972;59(6):767–778. doi: 10.1085/jgp.59.6.767. [DOI] [PMC free article] [PubMed] [Google Scholar]