Effects of confinement on models of intracellular macromolecular dynamics

Significance

We use Brownian and Stokesian dynamics simulations to explore diffusion processes within an idealized biological cell. Although most studies assume processes occurring in an infinite medium, we focus on the effect that confinement within a cellular membrane may have on intracellular dynamics. One finding is that model proteins near the membrane tend to diffuse along the membrane; this may give additional time for signal transduction across the membrane to occur. We also observe more strongly correlated motions near the membrane than in the cell’s interior, potentially facilitating interactions between proteins there. Finally, we find that deep in the interior of the model cell, the confining effects of the finite size of a cell on the dynamics can be neglected.

Abstract

The motions of particles in a viscous fluid confined within a spherical cell have been simulated using Brownian and Stokesian dynamics simulations. High volume fractions mimicking the crowded interior of biological cells were used. Importantly, although confinement yields an overall slowdown in motion, the qualitative effects of motion in the interior of the cell can be effectively modeled as if the system were an infinite periodic system. However, we observe layering of particles at the cell wall due to steric interactions in the confined space. Motions of nearby particles are also strongly correlated at the cell wall, and these correlations increase when hydrodynamic interactions are modeled. Further, particles near the cell wall have a tendency to remain near the cell wall. A consequence of these effects is that the mean contact time between particles is longer at the cell wall than in the interior of the cell. These findings identify a specific way that confinement affects the interactions between particles and points to a previously unidentified mechanism that may play a role in signal transduction and other processes near the membrane of biological cells.

Brownian dynamics (BD) simulations have been used to help qualitatively understand the motions and interactions of proteins and other macromolecules inside biological cells (1–5). Quantitative accuracy for diffusion rates of different sized particles has also been obtained with Stokesian dynamics (SD) simulations (6). In all these studies, a small portion of the interior of the cell is simulated, generally using a periodic simulation box that effectively mimics the motion in an unconfined, infinite system. However, in actual cells, macromolecules diffuse in a confined space and also interact with the cell wall, even at long range. These features may play an important role in the motion of macromolecules within the cell.

As a first step toward developing and understanding coarse grained models of entire biological cells, we performed BD simulations, with and without hydrodynamic interactions (HIs), of monodisperse particle suspensions in a confined space, mimicking a biological cell. We also performed SD simulations, which include short-range HIs, called lubrication forces. SD is considered to be more accurate for high volume fraction systems such as the crowded interiors of biological cells. Our goal is to understand the effect of confinement on macromolecular diffusion inside biological cells. Near the cell wall, we hypothesize increased correlated particle motions (1, 6). Away from the wall, we are interested in the extent to which models and simulation methods can neglect the cell wall and effects of confinement.

Previous theoretical and experimental studies have shown that diffusion slows down near planar membranes and that this is due to HI (7). Most studies of diffusion in confined spaces have addressed simple geometries such as parallel walls, in part for their simplicity and in part for their application to microfluidic devices (8–10). Other methods such as the fluctuating immersed boundary method (11) have recently been developed for simulating Stokes flow in confined geometries. Our use of BD and SD easily allows us to determine the importance of short- and long-range HI in our models of intracellular macromolecular dynamics.

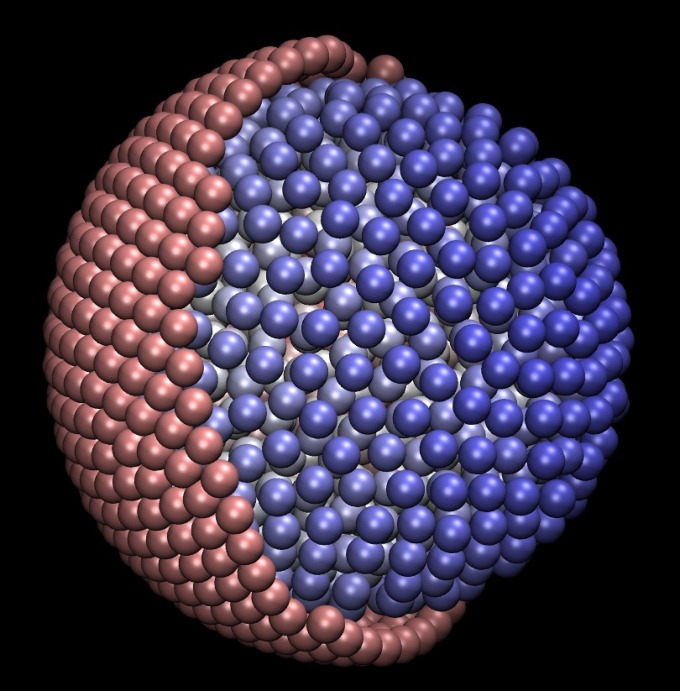
To study the effects of confinement on macromolecular diffusion, we simulated a suspension of monodisperse particles in a viscous fluid confined within a spherical shell. The shell itself is composed of closely spaced particles. To differentiate between these two types of particles, in analogy to the cytoplasm and wall of a biological cell, we refer to the particles in the interior of the confined region as “cytoplasm particles” and refer to the particles comprising the spherical shell as “wall particles.” For BD, confinement is affected primarily by steric interactions between the cytoplasm particles and the wall particles. For SD, confinement is affected primarily by lubrication forces that prevent particles from overlapping. An example configuration is shown in Fig. 1. In this idealized model, the radii of all particles, whether cytoplasm or wall, are identical, and this feature does not appear to alter our results, as shown below. The radius of the spherical shell wall is chosen such that the volume fraction of cytoplasm particles is $\varphi =0.3$, mimicking the crowded interiors of biological cells. Simulations were performed with 1,000 cytoplasm particles in a spherical shell with a radius of ∼14.4, where the radius of an individual particle is 1. Selected simulations were also performed with 20,000 cytoplasm particles in a spherical shell with a radius of ∼40.0. For purposes of comparison, BD and SD simulations were also performed under periodic conditions to approximate an infinite, unconfined system. Some BD simulations were also performed without HI, to test the effect of HI on the results.

Fig. 1.

Configuration for a simulation with 1,000 cytoplasm particles (in blue) and 841 wall particles (in pink). A hemisphere of the wall particles is removed to show the interior of the model.

Simulations were performed and results are reported in dimensionless units. Length is in units of the particle radius a; i.e., in dimensionless units, the radius of a particle is 1. Time is in units of $a^2/D_0$ where $D_0=k_{B}T/\left(6\pi \eta a\right)$ is the diffusion coefficient of a single particle in infinitely dilute conditions. In the above, $k_B$ is the Boltzmann constant, T is the absolute temperature, and η is the viscosity.

Results

Slowdown of Diffusion due to Confinement.

In confined systems, the displacement of a Brownian particle is limited, and thus measurements of the mean square displacement (MSD) over time appear reduced compared with the unconfined case. Over long time intervals, the MSD is meaningless and is simply the square of the average distance between any two particle positions (12). Over short time intervals, a particle that encounters the boundary of the confined region will appear to diffuse more slowly than a particle that does not encounter the boundary. Thus, MSD must be interpreted carefully, especially when measured over long time intervals, where the reduction in the apparent diffusion rate compared with the unconfined case will partially be artificial, which is an artifact of the measurement.

Fig. 2A shows the MSD of 1,000 particles in BD simulations with HI for a periodic system and for a system confined in a spherical cell whose radius is ∼14.4. Both systems have a volume fraction of 0.3. The MSD in the confined case is smaller than in the periodic case, even when the MSD is measured only for particles originating in the interior of the cell and unlikely to directly encounter the cell wall over the short time interval considered. We say that a particle is in the interior of the cell if its center is within a distance 3 of the center of the cell. Is this reduction in MSD completely an artifact of the measurement due to the fact that the system is confined, or does there exist a real reduction in diffusion due to intermolecular interactions in the confined case?

Fig. 2.

MSD for 1,000 particles under periodic and confined conditions, the latter in a spherical cell of radius 14.4. (A) For BD with HI, there is a slowdown of particles in the confined case compared with the periodic case. This slowdown is also observed, but is very small, for particles in the interior of the cell that never encounter the boundary. (B) For independent but confined Brownian particles, the artificial slowdown of diffusion compared with diffusion in periodic simulations is very small over a time interval of 0.3.

To answer this question, Fig. 2B shows the MSD of independent Brownian particles confined to the same spherical space as above and using the same time step size. Here, there are no interactions between particles, and only Brownian displacements that keep particles within the confined region are allowed. The figure shows a very small reduction in MSD due to encounters with the wall for the short time interval considered. This small reduction implies that the reduction in MSD shown in Fig. 2A represents a real reduction in average diffusion rates in the confined case for the system with intermolecular repulsions compared with the periodic case. The diffusion rates differ near the wall and far from the wall, and this will be examined later in this paper.

Packing of Particles at the Cell Wall.

Fig. 3 shows the particle count profile as a function of radial position for BD and SD simulations. The profile shows a higher than average count of particles packed in a layer inside and along the wall, at radial position $r\approx 13.5$. Packing of a second layer at $r\approx 11.5$ is also evident. These results suggest that there may also exist a packing of proteins along the cell membrane in actual biological cells.

Fig. 3.

Particle count profile for confined BD and SD simulations (with HI) for 1,000 particles, with the wall on the right. The profile shows the particle packing along the wall. The dotted line is proportional to $4\pi r^2$ where r is the radial position. Bin widths of 0.2 were used to discretize the radial position. The y axis is the particle count normalized by the total number of particles over all time points considered.

The packing structure is independent of HI, as the density profile without HI shows the same behavior. This independence is what is expected, as particle density is an equilibrium property that is independent of the particle dynamics. However, SD simulations do not use a steric interaction potential and thus show a slightly different density profile, with more pronounced structure. Here, the peaks in the profile are slightly larger than the BD case, and a third packing layer at $r\approx 9.5$ can also be seen. We also note that particles cannot overlap the cell wall in SD simulations, which explains the small offset of the peaks to the left in SD compared with BD.

We remark that cytoplasm and wall particles have identical radii in our idealized model. To check that this feature is not responsible for the packing of the particles (and other features later in this paper), we performed a BD simulation without HI with closely spaced wall particles of radius $a/2$ while cytoplasm particles have radius a. The resulting particle count profile was nearly identical to that when the cytoplasm and wall particles have the same radii.

Decrease in Diffusion Toward the Cell Wall due to Hydrodynamic Interactions.

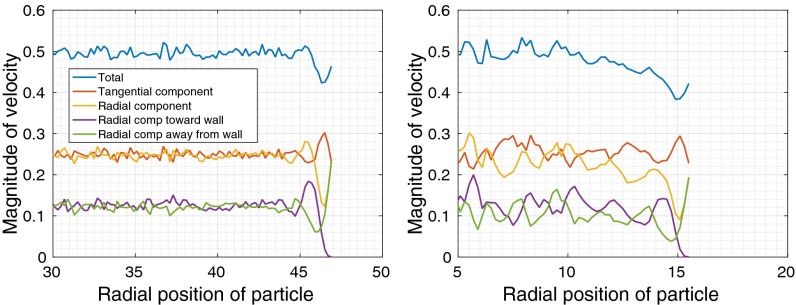
A velocity profile shows the average magnitude of the velocity of a particle as a function of the particle’s initial radial position. We define τ to be the length of time over which the velocity is measured. Fig. 4 plots the velocity profiles for BD simulations with and without HI for 20,000 confined cytoplasm particles, for $\tau =2$. We observe two regimes, the regime near the wall, with radial position $r>35$, and the regime in the interior with $r<35$. In particular, we observe different behavior with and without HI in the interior regime.

Fig. 4.

Velocity profiles for BD simulations of a 20,000 particle system confined in a cell of radius 40.0. Only the profiles a distance of 20–40 from the center of the cell are shown. (A) For BD without HI, there is no slowdown of velocity across the model cell except close to the cell wall. (B) For BD with HI, there is a slowdown of velocity in the interior of the cell as the wall is approached.

A first observation is that the average velocity in the interior regime is higher with HI than without HI. Further, without HI, the total velocity profile (blue) in the interior regime is constant. With HI, the total velocity profile in the interior decreases toward the wall. This slowdown in diffusion due to HI is expected from both theoretical and experimental studies (7). By separately measuring the tangential (red) and radial (orange) components of velocity, we also observe that the slowdown toward the wall is entirely in the radial component.

In the regime near the wall, we observe strong effects of the wall, which are qualitatively similar with and without HI, i.e., due to steric interactions alone. The average velocity is a minimum for particles along the wall but far enough from the wall to not be repelled by the wall. For particles even closer to the wall, the increased radial component of the velocity is entirely due to repulsion from the wall (green).

For particles at the wall, the tangential component of the velocity is approximately twice the size of the radial component (0.7 vs. 0.35 at $r\approx 39$), indicating a preference for motion along the tangential direction and along the wall. This tendency of particles at the wall to stay near the wall will be visualized geometrically below.

Near the wall, particles also have a strong tendency to move toward or away from the wall depending on their radial position, leading to highly correlated radial motions. This tendency can be observed by separately measuring the component toward the wall (purple) and away from the wall (green). This correlation in radial motion near the wall will be measured directly later in this paper. We also found that the tangential motions are not correlated near the wall.

We now examine velocity profiles for SD simulations, to see how particle dynamics differ when lubrication forces are modeled. Due to the high computational cost of SD simulations, simulations used 1,000 cytoplasm particles in a cell with radius 14.4. Fig. 5 compares the velocity profiles for BD and SD simulations, again measured over a time interval $\tau =2$. Lubrication forces significantly slow down the particle velocities in SD compared with BD. We also observe that in the interior regime ($r<10$ in this case), velocity does not decrease as rapidly toward the wall in SD simulations as it does in BD simulations. This effect in SD is likely due to the strong lubrication forces affecting the motion.

Fig. 5.

Velocity profiles for 1,000 confined cytoplasm particles: (A) BD with HI and (B) SD. Besides a slowdown in diffusion, SD simulations show a more structured velocity profile penetrating deeper into the interior of the cell.

SD simulations also show a more structured velocity profile than BD simulations. At $r\approx 13.5$, preferred motion is in the tangential direction. At $r\approx 12.5$, preferred motion is slightly greater in the radial direction. This waviness in the velocity profiles persists deeper into the interior of the cell than in BD simulations.

Note that for periodic BD simulations with HI, the average velocity magnitude is 1.27 (measured over $\tau =2$), which is slightly higher than the maximum 1.20 observed in Fig. 5A. Thus, there is an overall slowdown in diffusion due to confinement, as also suggested earlier in Fig. 2A.

Particles at the Cell Wall Tend to Stay at the Cell Wall.

To further understand the difference in the motion of particles at the wall and away from the wall, Fig. 6A plots the distribution of positions after a time interval of 10 for a particle initially at the wall. Due to symmetry, results are plotted on a semicircular disk. The figure shows that the particle has a tendency to stay near the wall. Fig. 6B plots the distribution for a particle slightly interior from the wall. In this case it appears that the particle has a tendency to diffuse relatively uniformly.

Fig. 6.

Particle distribution after a time interval of 10 for the case of 20,000 cytoplasm particles in BD simulations with HI. Results are plotted on a portion of a semicircular disk of radius 40 and centered on the plane at (40,0). (A) When the particle is initially at the wall, the particle has a tendency to stay near the wall. (B) For a particle initially away from the wall, at (10,0), the particle has a tendency to diffuse relatively uniformly.

Correlated Motions Near and Away from the Cell Wall.

The correlation of the motion between a pair of particles i and j may be measured by the pair correlation

$$C_{ij}\left(d,\tau \right)=\frac{{\displaystyle \sum \left[\mathrm{\Delta }{\mathbf{r}}_i\left(\tau \right)\cdot \mathrm{\Delta }{\mathbf{r}}_j\left(\tau \right)\right]\delta \left(d-d_{ij}\right)}}{\sqrt{{\displaystyle \sum {\left|\text{Δ}{\mathbf{r}}_i\left(\tau \right)\delta \left(d-d_{ij}\right)\right|}^2}}\sqrt{{\displaystyle \sum {\left|\text{Δ}{\mathbf{r}}_j\left(\tau \right)\delta \left(d-d_{ij}\right)\right|}^2}}},$$

which is a function of the distance d and the time interval τ over which the correlation is measured (6). The quantity $d_{ij}$ is the center-to-center separation of the pair. We use δ to denote the Dirac delta function. The summation is over all time points. The correlation $C_{ij}$ ranges from −1 to 1.

Fig. 7 plots the pair correlation for pairs of nearby particles at different radial positions. Pairs are nearby if their centers are within a distance 3 of each other and the radial position of the pair is the midpoint between the two particles. We observe that at the cell wall, the pair correlation is large. This correlation is due to steric interactions, because it is also observed in cases without HI. This effect is also in agreement with the structured velocity profiles near the cell wall. HI has the effect of increasing the correlation by up to 0.2 across the cell.

Fig. 7.

Pair correlation for nearby particles (within distance 3) at different radial positions, for confined simulations with 1,000 cytoplasm particles. Correlation was measured for $\tau =2$. High correlation can be observed near the cell wall, due to steric interactions. HIs increase the correlations.

In the interior, without HI, there are no significant correlations. Also, particles are less correlated in SD simulations than in BD simulations. It is likely that large lubrication forces decorrelate some of the motions in the SD case.

Contact Time Is Lengthened for Particle Pairs Near the Cell Wall.

In our model cell, we observed several effects near the cell wall: reduction in diffusion, tendency of the motion to be along the wall rather than toward the interior, and high correlated motion. These effects suggest that the average length of time that particles remain in contact with each other is also lengthened at the cell wall compared with in the interior of the cell. We illustrate this fact now.

We define two particles as being in contact if their centers are within a distance 3 of each other (surface separation of 1). Contact time is the length of time that two particles remain in contact, where the persistence of a contact is checked at intervals of 0.1. We computed the contact time for pairs of particles located at the wall (at least one particle initially at the wall) and for pairs of particles located in the interior (at least one particle initially within distance 3 of the center of the cell). For a baseline, we also computed the contact time in periodic simulations. Results are shown in Table 1.

Table 1.

Mean contact times

Simulation type	1,000 particles			20,000 particles
	No HI	BD	SD	No HI	BD
Confined/wall	0.83	1.36	2.36	0.77	0.96
Confined/interior	0.63	0.84	1.73	0.56	0.71
Periodic	0.55	0.78	1.26	(0.55)	(0.78)

Numbers in parentheses are from periodic simulations with 1,000 particles.

Mean contact times are significantly larger for BD simulations with HI than without HI. This result is likely due to increased correlated motions with HI. SD simulations show even longer contact times, but this effect is most likely due to overall slower diffusion in the presence of lubrication forces (Fig. 5), especially because correlations are generally smaller in SD than in BD (Fig. 7). More importantly, mean contact time is longer at the wall than in the interior of the cell. This result may be due to a combination of effects at the wall, as mentioned above. On average, contact times are greater in confined simulations than in periodic simulations.

Fig. 8 shows the distribution of contact times. Most contact times are very short, but the distribution has a long tail. Results are compared for pairs at the wall and in the interior of the cell. The distribution of contact times near the wall show a different distribution than in the interior, leading to a larger mean. The contact time distribution in the interior somewhat matches the distributions found in periodic simulations. In particular, in the BD case, the distribution of contact times for pairs in the interior follows closely the distribution of contact times for periodic simulations.

Fig. 8.

Distributions of particle pair contact times for (A) BD without HI, (B) BD with HI, and (C) SD. Results are compared for pairs at the wall and in the interior of the cell. The contact time distributions in the interior of the cell somewhat match the distributions found in periodic simulations.

The Interior of the Cell Can Be Approximated as an Infinite, Unconfined System.

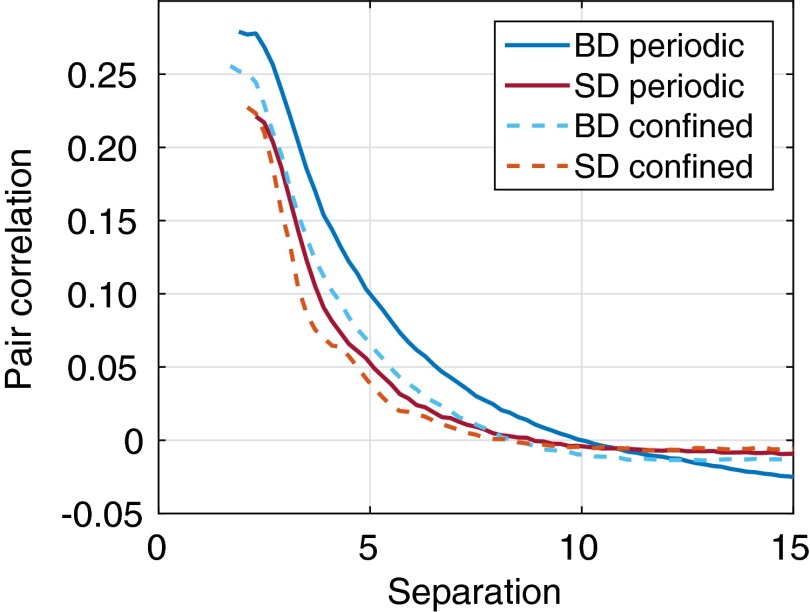
Can the interior of the cell, far from the cell wall, be meaningfully modeled without the cell wall and simulated within a periodic box? Fig. 9 plots the correlation between a particle near the center of the cell and other particles. We consider a particle to be near the center of the cell if its center is a distance less than 3 from the center of the cell. For comparison, the pair correlation is also shown for periodic simulations.

Fig. 9.

Pair correlation as a function of separation in confined simulations for a particle near the center of the cell and other particles. For comparison, the pair correlation is also shown for periodic simulations. Results are for simulations with 1,000 particles and time interval 2. The results show a similar shape in the pair correlation curves. We note that for simulations without HI, the correlations are negligible.

The results show a similar shape in the pair correlation curves, suggesting that the interior in some sense is similar in conditions to those of periodic simulations. However, there are some differences. Correlations in confined simulations appear smaller in magnitude than those of periodic simulations. Particularly in the periodic BD case, very distant particles display negative correlations, which represents backflow, i.e., by these particles “moving out of the way” of other particles. In other cases, including the periodic SD case, although there must be backflow, the negative correlations are very weak.

In general, however, these differences are small. We showed earlier that there is a reduction in diffusion due to confinement in the interior of the cell, but this reduction is small and is expected to be smaller for larger cells (Fig. 2). Also, we showed that the contact time distribution for pairs of particles in the interior of the cell is similar to that for periodic simulations (Fig. 8).

Discussion

The simulation results show significant differences in the motion of particles at the wall and in the interior of a model biological cell. Particles have a tendency to line themselves up against the cell wall. This packed structure is associated with the highly correlated motions along the cell wall and is due to steric interactions. These correlated motions lead to the longer mean contact time between particles near the cell wall, which in turn may be a mechanism by which protein binding is facilitated.

Particles in the interior of our idealized cell have motions qualitatively similar to particles in a periodic box with no cell wall. In particular, far enough from the wall, there are no long range correlations due to the wall itself. However, we do observe an overall slowdown in diffusion due to confinement, which is likely dependent on cell radius. Nevertheless, at this juncture it appears that the qualitative effects of motion in the interior of the cell can be effectively modeled as if the system were an infinite periodic system.

What are appropriate hydrodynamic models for systems such as an entire biological cell? The major effects of confinement appear to be related primarily to steric effects. However, the qualitative behavior of systems with and without HI are different. HI tends to result in greater correlated behavior both far from as well as near the cell wall. SD simulations further show some qualitatively different features than BD simulations with HI, such as a slowdown in diffusion, a reduction in correlated motions of nearby particles, and structure in the velocity profiles that persists farther into the interior of the cell. SD simulations more accurately model the crowded interiors of cells than BD simulations, because they account for lubrication forces that cannot be neglected at short range. Thus, we suspect that the structure of the velocity profiles in actual cells more closely match what we observe in SD than in BD. However, whether or not these differences lead to functional consequences cannot be concluded at this point.

The results of our simulations could be related to some biological functions. For example, the fact that the model proteins near the model cell wall tend to diffuse along the wall is consistent with the conjecture (13) that there is an increase in concentration near the wall. Here, we show that the cause is primarily steric and does not require any specific interaction. Moreover, the tendency of the model protein molecules to diffuse along the membrane and remain localized might give additional time for signal transduction across a membrane to occur.

As shown in SI Text, our findings on the behavior of particles near the cell wall due to steric interactions do not change for a larger system comprised of 500,000 particles, which has a ratio of cell radius to particle radius of 118.6. Furthermore, our results are qualitatively unchanged if we consider a bidisperse system comprised of a relatively small number of particles of radius 4 surrounded by a sea of particles of radius 1, constructed such that the overall volume fraction remains at 0.3.

We note that as seen previously in the examination of diffusion in confined fluids and the air–water interface, particles tend to move faster parallel to the boundary than perpendicular to it (14). Further, there is a speed up in hydrogen bond dynamics as one moves toward the air–water interface from the bulk region (15). Similarly, there is a slowdown in dynamics as one moves toward water–solid interfaces (16). In addition, the layered structure of colloidal particles near hard surfaces has been observed by microscopy (17), as well as in theoretical studies using simulations of classical hard spheres in a channel (18). Thus, both enhanced diffusion parallel to the cell wall and the increased density near the wall are quite likely general effects that are dominated by steric interactions and as such are independent of the particular system studied.

In future work, we will examine more realistic models of biological cells where the cytoplasm particles have different radii in physiologically accurate concentrations and that contain models of both DNA and proteins.

Materials and Methods

BD simulations were performed using the algorithm of Ermak and McCammon (19). The diffusion matrix in this algorithm was modeled by the Rotne–Prager–Yamakawa (RPY) tensor (20, 21). For overlapping particles in the bidisperse case, we used the RPY tensor derived in ref. 22.

To model steric interactions, overlapping particles experience a repulsive potential

$$V_s=\{\begin{array}{ll}\frac{1}{2}{k}_s{\left(x-2a\right)}^2\hfill & \text{if\hspace{0.17em}}x<2a\hfill \\ 0\hfill & \text{if\hspace{0.17em}}x\ge 2a\hfill \end{array},$$

where x is the center-to-center distance between two particles, and the force constant $k_s=125$ $k_{B}T/a^2$, the value used in earlier studies (23). This potential is applied between all pairs of particles, including pairs of wall particles.

In simulations with confined geometries, the positions of the wall particles are not fixed, but are restrained by the potential

$$V_i=\frac{1}{2}{k}_w{\left|{\mathbf{r}}_i-{\overline{\mathbf{r}}}_i\right|}^2,$$

where ${\mathbf{r}}_i$ is the position of the particle, and ${\overline{\mathbf{r}}}_i$ is the rest position of the particle. The force constant $k_w=100$ $k_{B}T/a^2$ was used.

The “rest” position of the wall particles is one that minimizes the potential energy

$${\displaystyle \sum _{i\ne j}\frac{1}{\left|{\overline{\mathbf{r}}}_i-{\overline{\mathbf{r}}}_j\right|}},$$

where ${\overline{\mathbf{r}}}_i$ is the position of the ith wall particle. Such configurations for different numbers of particles on the sphere have been precomputed and are available from ref. 24 (see also, ref. 25).

SD simulations were performed using the method of Durlofsky et al. (26). The lubrication resistance matrix is from Jeffrey and Onishi (27). A model for steric interactions is not necessary because lubrication forces prevent particles from overlapping. Fixman’s midpoint method was used for numerical integration (28, 29), which handles the nondivergence free nature of the SD resistance matrix.

All BD and SD simulations were performed with a time step of size $\mathrm{\Delta }t={10}^{-4}$. At this time step size, cytoplasm particles did not escape the enclosure formed by the wall particles. We note that one unit of time corresponds to the transition between short-time diffusion to long-time diffusion.

Table 2 summarizes the simulations that were performed for our study. For simulations with 1,000 particles, the diffusion and resistance matrices were formed explicitly, and Cholesky decomposition was used for computing Brownian displacements and forces. For BD simulations with 20,000 particles, this approach is not feasible. Instead, we compute the action of the diffusion matrix on a vector and use the Lanczos algorithm to compute Brownian displacements. Five iterations of the Lanczos algorithm were used, which produces Brownian displacement vectors of sufficient accuracy (23).

Table 2.

Simulations performed

Simulation	Number of particles	Total length (time)
Confined, no HI	1,000	1,000.0
Confined, BD	1,000	1,000.0
Confined, SD*	1,000	1,203.0
Confined, no HI	20,000	210.1
Confined, BD*	20,000	257.5
Confined, no HI	1,000	1,000.0
Periodic, BD	1,000	1,000.0
Periodic, SD	1,000	470.0

For confined simulations of 1,000 cytoplasm particles, 841 wall particles were used; for confined simulations of 20,000 cytoplasm particles, 6,084 wall particles were used. Additional simulations are described in SI Text, including for the case of 500,000 cytoplasm particles.

^*Total length is the combined length of seven independent simulations.

Starting particle configurations were generated by placing n particles randomly within the spherical shell of wall particles and then applying a force algorithm to produce a configuration with no particle overlaps. This starting configuration equilibrates rapidly: the total number of overlapping pairs of particles and the potential energy stabilizes within 1 unit of time (10,000 time steps). This first unit of time of each simulation was discarded in our analyses.

For purposes of comparison, BD and SD simulations were also performed under periodic conditions, using a system of 1,000 particles in a periodic box of width $L=24.08$ (volume fraction, 0.3). For simulations under periodic conditions, Ewald summation of the RPY tensor (30) was used to compute the diffusion matrix. The initial configuration used in these simulations was also a nonoverlapping set of particles. Again the first 1 unit of time was discarded.

In our idealized model of the biological cell, cytoplasm particles and wall particles have the same radii. To check that this feature is not responsible for the packing of the particles and the structured velocity profiles at the cell wall, we performed BD simulations with closely spaced wall particles of radius $a/2$, whereas cytoplasm particles have radius a. Only steric interactions were modeled, as HI are not responsible for the particle density and velocity distributions, as explained above. The steric interactions between possibly different sized particles are defined by the potential

$$V_s=\{\begin{array}{ll}\frac{1}{2}{k}_s{\left(x\prime -2\right)}^2\hfill & \text{if\hspace{0.17em}}x\prime <2\hfill \\ 0\hfill & \text{if\hspace{0.17em}}x\prime \ge 2\hfill \end{array},$$

where $x\prime =2x/\left(a_i+a_j\right)$ is a normalized distance between two particles, where x is the actual distance, and $a_i$ and $a_j$ are the radii of the two particles.

This model is comprised of 1,000 cytoplasm particles and 3,136 wall particles. The resulting particle distribution and velocity profiles were nearly identical to those of simulations of the same number of cytoplasm particles where cytoplasm and wall particles have the same radii. Thus, the structure that arises near the cell wall is not an artifact of our idealized model with equal particle radii.

SI Text

Large Simulations.

To verify our findings for a model of a size approaching that of a biological cell, we performed simulations with 500,000 cytoplasm particles and a ratio of cell radius to particle radius of 118.6. This configuration gives a particle volume fraction of 0.3. These simulations were carried out using BD simulations without HI to a length of 127.0 units of time. Figs. S1–S3 show the results for velocity profiles, pair correlations, and pair contact times, respectively. The results are comparable to those of smaller systems shown earlier, showing no significant qualitative differences for the system sizes tested.

Fig. S1.

Velocity profiles for large confined BD simulations without HI with 500,000 cytoplasm particles. The cell wall is at radial position 118.6. The profiles are qualitatively similar to those for smaller simulations, e.g., Fig. 4A.

Fig. S3.

Distribution of pair contact times for large confined BD simulations without HI. Contact time is longer at the wall than in the interior of the cell. For these simulations, the persistence of a contact was checked every 1 unit of time (rather than 0.1 used earlier).

Fig. S2.

Pair correlation for nearby particles (within distance 3) at different radial positions, for large confined BD simulations without HI. Correlation was measured for τ = 2. High correlation is observed near the cell wall (at radial position 118.6). The result is qualitatively similar to that from smaller simulations, e.g., Fig. 7.

Bidisperse Systems.

Simulations of confined bidisperse systems were also performed to determine the effect that polydisperity in actual cells might have on our findings for monodisperse systems. Bidisperse systems were generated with large particles of radius 4 and small particles of radius 1. The ratio of the number of large to small particles was chosen to be 1:64 so that the volume fraction of each size of particle is the same. In particular, two simulations were performed: (i) 300 large cytoplasm particles and 19,200 small cytoplasm particles (cell radius, 50.4) using BD simulations without HI to a length of 293.0 units of time, and (ii) 16 large cytoplasm particles and 1,024 small cytoplasm particles (cell radius, 19.0) using BD simulations with HI to a length of 753.0 units of time. The cell radii were chosen to produce systems with volume fraction of 0.3. Fig. S4 shows an example of the larger of these two configurations.

Fig. S4.

Configuration for a confined system of bidisperse cytoplasm particles (300 large particles and 19,200 small particles). A hemisphere of the wall particles is removed to show the cytoplasm particles.

Perhaps surprisingly, the results from simulations of confined bidisperse systems show the same qualitative features as those of monodisperse systems. Fig. S5 shows the velocity profiles for the small particles, revealing the characteristic decrease in radial velocity and increase in tangential velocity of particles at the cell wall. When HI is modeled, degradation in total velocity occurs farther into the interior of the cell, as was also observed in the monodisperse case. Fig. S6 shows the velocity profiles for the large particles. Due to the relatively small number of large particles, and given the duration of the simulations we performed, these profiles are not smooth. However, the same characteristics in the velocity profiles can be observed.

Fig. S5.

Velocity profiles of small particles (radius 1) in BD simulations of confined bidisperse systems (A) without HI with the cell wall at radial position 50.4 and (B) with HI with the cell wall at radial position 19.0.

Fig. S6.

Velocity profiles of large particles (radius 4) in BD simulations of confined bidisperse systems (A) without HI with the cell wall at radial position 50.4 and (B) with HI with the cell wall at radial position 19.0.

Fig. S7 shows the correlation between pairs of nearby particles as a function of the radial position of the pair in the cell. As was observed for confined monodisperse systems, correlation is higher near the cell wall, and correlations are increased in the presence of HI. Finally, Fig. S8 shows the distribution of pair contact times. Again as observed for confined monodisperse systems, contact times for pairs near the cell wall and in the interior of the cell follow different distributions and are lengthened near the wall.

Fig. S7.

Pair correlation for nearby small particles (within distance 3) at different radial positions for BD simulations of confined bidisperse systems. Large particles are ignored in the calculation and contribute little to the average correlation due to their small relative number. Figures show simulations (A) without HI with the cell wall at radial position 50.4 and (B) with HI with the cell wall at radial position 19.0. The figures show similar results to those of Fig. 7 for confined monodisperse systems.

Fig. S8.

Distributions of particle pair contact times for BD simulations of confined bidisperse systems. Large particles are ignored in the calculation and contribute little due to their small relative number. Figures show simulations (A) without HI in a cell of radius 50.4 and (B) with HI in a cell of radius 19.0. In A, persistence of a contact was checked every 1 unit of time; in B, persistence was checked every 0.1 units of time. The figures show similar results to those of Fig. 8 for confined monodisperse systems.