Anatomy of funded research in science

Significance

The study of scientific collaborations has been predominately focused on characterizing publication coauthorships. Here, we study instead collaboration networks by looking at project partnerships funded over the years and show clearly the substantial impact of funding shifts on the pattern of interactions. We find that the leading universities form a cohesive clique among themselves and occupy brokerage positions between otherwise disconnected entities, and as the inequality in the distribution of funding grows over time, so does the degree of brokerage. Specifically, the elites overattract resources but they also reward in variety of research and quality. We are the first to our knowledge to systematically quantify the far-reaching effects of external forces on the complex interactions in team research that underpin the production and evolution of science.

Abstract

Seeking research funding is an essential part of academic life. Funded projects are primarily collaborative in nature through internal and external partnerships, but what role does funding play in the formulation of these partnerships? Here, by examining over 43,000 scientific projects funded over the past three decades by one of the major government research agencies in the world, we characterize how the funding landscape has changed and its impacts on the underlying collaboration networks across different scales. We observed rising inequality in the distribution of funding and that its effect was most noticeable at the institutional level—the leading universities diversified their collaborations and increasingly became the knowledge brokers in the collaboration network. Furthermore, it emerged that these leading universities formed a rich club (i.e., a cohesive core through their close ties) and this reliance among them seemed to be a determining factor for their research success, with the elites in the core overattracting resources but also rewarding in terms of both research breadth and depth. Our results reveal how collaboration networks organize in response to external driving forces, which can have major ramifications on future research strategy and government policy.

Higher education institutions are nationally assessed in a periodic manner across the globe [examples include the Research Excellence Framework (www.ref.ac.uk) in the United Kingdom, Excellenzinitiative (mediathek.dfg.de/thema/die-exzellenzinitiative/) in Germany, and Star Metrics (https://www.starmetrics.nih.gov/) in the United States], and tremendous effort has been put in place in maximizing research output, because assessment outcomes often have a direct financial impact on an institution’s revenue (1). Bibliometrics are commonly used for this kind of performance evaluations (2–7), and the volume of grant income is also generally seen as a good indicator of performance. Although many studies have examined the collaboration patterns originating from publication information (8–14), little is known about the characteristics of project collaborations supported by research funding, which is undoubtedly a type of research output in its own right, but also the origin of other research outputs.

The volume of funding is often subject to direct and indirect constraints arising from internal research strategies and different levels of policy set out by the funding bodies and ultimately by the national government. This manifests into different emphases on both the research area and mode of collaboration, and potentially influences the way we form a project team. We have already seen examples of adaptive changes in our collaboration practices. For instance, research in the science and engineering sector is said to be increasingly interorganizational (15). In addition, there are different theories on the factors that may affect the establishment of a collaboration and how well a research team operates (13, 16). Elite universities were recognized as catalysts for facilitating large-scale multipartner research collaborations (15), and multidisciplinary collaborations were found to have higher potential to foster research outcomes (17). As a result, the setup of a project consortium for a grant application might require considerable strategic planning, because who and how we collaborate with can potentially affect the outcome of a bid, and we are yet to fully understand the underlying mechanics and dynamics.

To shed light into the relations between funding landscapes and scientific collaborations, we here examine over 43,000 projects funded between 1985 and 2013 by the Engineering and Physical Sciences Research Council (EPSRC), the government body in the United Kingdom that provides funding to universities to undertake research in engineering and physical sciences, including mathematics, chemistry, materials science, energy, information and communications technology, and innovative manufacturing. For each year, we constructed two different types of collaboration networks in which the nodes are investigators and their affiliations, respectively, and an edge represents a funded project partnership between two nodes. We applied a network-based approach to analyze the local and global interlinkage in these networks; the former was performed by calculating the degree of brokerage (18–21) of individual nodes, which gauges the connectivity in the neighborhood of a node. As for the global level, we calculated the rich-club coefficient (22, 23) of the network and characterized the members of such core structure using a recently introduced profiling technique (24). In addition, we explored how these patterns evolved over time with the total funding in each year and how they correlated with research performance. Our results allow us to gain an insight into how changes in the funding landscape shaped the way we form research partnerships, providing a case study that is highly reflective of other countries in the European Union and possibly other developed countries worldwide.

Results

Changes in the Funding Landscape.

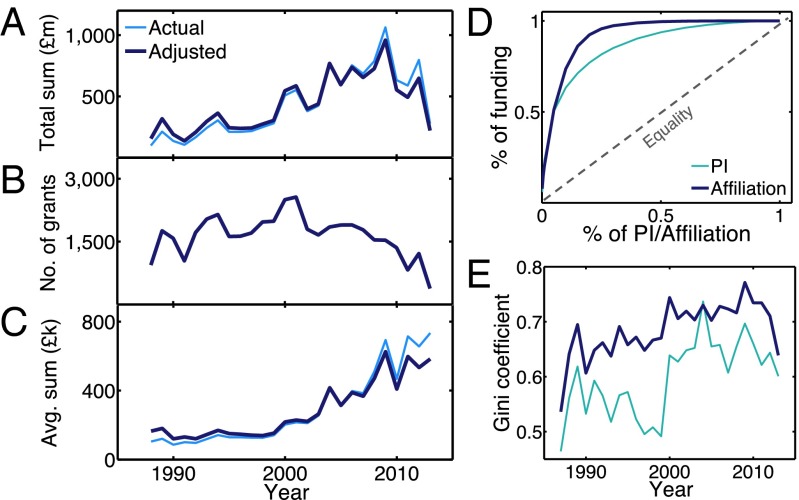
During the period of study we found that the total funding in each year increased steadily over time, until it peaked in 2009 (Fig. 1A). The number of grants fluctuated over time with a general decline after 2001 (Fig. 1B) and, in essence, there was an obvious trend of fewer grants but of much larger monetary values (Fig. 1C). This coincided with the emergence of larger research teams (Fig. S1) and the timing of this tied in with the EPSRC’s initiative on developing larger specialist units in the United Kingdom [EPSRC Delivery Plan Scorecard 2008-11 (https://www.epsrc.ac.uk/)], such as establishing doctoral training centres in selected universities. Investigators associated with a grant were classified into principal investigators (PIs), coinvestigators (CIs), and other investigators (OIs). There were a total of 13,275 PIs from 201 different affiliations (out of a total of 1,834), and the average number of grants per PI was 3.25. About half of the grants were associated with one or more CIs and/or OIs, and there was a noticeable rise in the average number of investigators per grant since 2000, which is in line with the observed increase in the typical number of collaborators in scientific publications (9, 25). We did not observe the same degree of widening participation in affiliations; the average number of affiliations associated with a grant only marginally increased (Fig. S1).

Fig. 1.

The funding landscape over the last three decades. (A) The total amount of funding awarded by EPSRC showed a general increase, with a peak in 2009, and then a decrease. “Actual” refers to the actual value on record and “adjusted” refers to the value after the adjustment made with reference to the Consumer Prices Index (Materials and Methods). (B) The total number of grants awarded by EPSRC peaked in 2001. (C) The average amount of funding per grant continued to rise over time. (D) Overall distribution of funding among PIs and affiliations. Individual awardees (PIs or affiliations) were sorted in descending order of their total awarded funding, and the percentage of funding was plotted against the corresponding percentage of awardees. The dotted line denotes where true equality lies and both cases showed strong inequality. (E) Distribution of funding consistently showed a high degree of inequality over time, in both cases of PIs and affiliations.

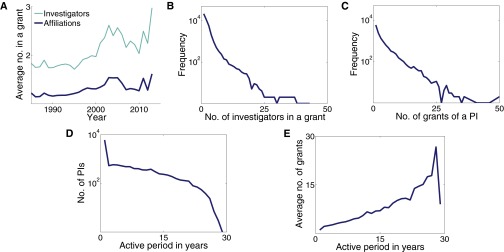
Fig. S1.

Patterns between grants and principle investigators. (A) The average number of investigators and associated affiliations generally increased over time. (B) The number of investigators in a grant (include all PIs, CIs, and OIs) and its frequency. (C) Most PIs had only one successful grant and the number of grants a PI received declined sharply; for example, there were fewer than 10 PIs who have managed to obtain more than 20 grants. (D) The number of PIs against the number of active years, which is defined as the sojourn time between the first and last recorded grants of a given PI. (E) The average number of grants obtained by a PI generally increased with his/her career length.

The way in which funding has been awarded was highly skewed; we found that in both cases of PIs and affiliations about half of the overall funding was awarded to the top 8% (Fig. 1D), although the distribution of funding among the remaining PIs showed a much greater homogeneity. On the contrary, we observed over 90% of all of the funding was awarded just to the top 20% of the affiliations, suggesting a high level of focused funding in selected places. Furthermore, we referred to the Gini coefficient (26) to measure how the distribution of funding over a population deviates from a perfectly uniform distribution, with values $G=0$ and $G=1$ denoting maximum equality and inequality, respectively. Overall, we observed substantial inequality in both cases of PIs and affiliations of PIs. By examining how the Gini coefficient changes over time, we found that the level of inequality intensified as the coefficient became closer to 1 (Fig. 1E), and this was particularly the case among the affiliations.

Network Brokerage.

We examined the two constructed collaboration networks in which nodes are investigators and affiliations, respectively, and an edge represents a funded partnership between two nodes and found that network properties evolved over time depending on the total funding in a given year (Figs. S2 and S3). The investigator network seemed to be sparsely connected and consisted of a large number of disjointed parts, which means that collaborations were largely localized to small groups of investigators; this is in stark contrast with previous findings on coauthorships (9, 10). Conversely, the affiliation network was found to be well-connected with the (largest) giant component (GC) being almost the size of the network.

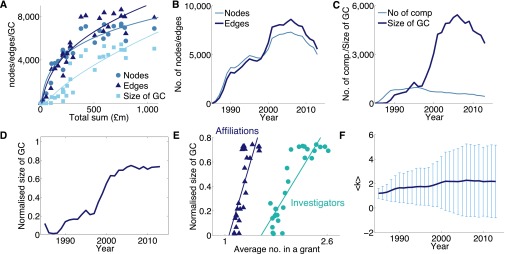
Fig. S2.

Network properties of the investigator network. (A) The number of nodes and edges and the size of the GC covaried with the total funding made available by the EPSRC of a given year. (B) The number of nodes and edges in the investigator network over time. (C) The number of components in the network and the size of the GC. (D) The GC grew over time; the normalized size of the GC is obtained by dividing the size of the GC by the total number of nodes. (E) The size of the GC increased with the average number of (i) investigators and (ii) affiliations per grant. Each point corresponds to one year. (F) The average degree remained very low throughout the period of study.

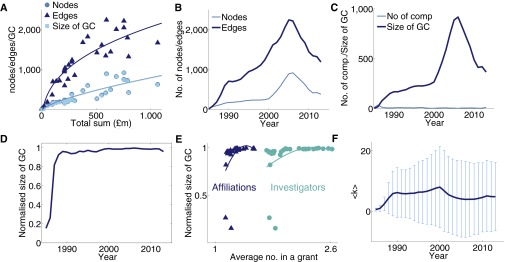
Fig. S3.

Network properties of the affiliation network. (A) The number of nodes and edges and the size of the GC covaried with the total funding. (B) The number of nodes and edges in the affiliation network over time. (C) The number of components in the network and the size of the GC. (D) The network has remained well connected as the size of the GC remained equal to or very close to the size of the network. (E) The relationship between the size of the GC and the average number of (i) investigators and (ii) affiliations per grant. Each point corresponds to 1 yr. (F) The average degree was variable.

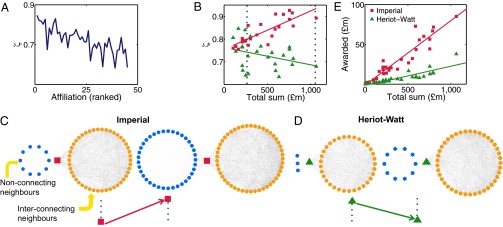
To further examine this noticeable level of interconnectedness in the affiliation network, we examined the extent of local cohesion between affiliations and their partners in the form of brokerage (18–21): A node is said to be a broker if it occupies an advantageous location in the network for detecting and developing opportunities through its connections to nonoverlapping clusters. This was performed by computing the normalized effective size, ${\zeta }_i=1-\left(k_i-1/k_i\right)C_i$, where $k_i$ is the degree of the node and $C_i$ is its clustering coefficient, of the neighborhood of each affiliation i in the network (21). Such a quantity ranges from 0 to 1. It takes its smallest value when i is part of a clique (i.e., a fully cohesive structure), and it is equal to 1 when i is the center of a star and there is no link between any of its partners. Generally, the larger the value of ${\zeta }_i$, the less connected the neighborhood of i is, and consequently, the higher the brokerage opportunities of affiliation i. Overall, we found that the effective size of an affiliation increases with its awarded funds (Fig. 2A), with the top-funded universities occupying brokerage positions between otherwise disconnected affiliations, potentially playing a key role in developing new access to information and opportunities (19, 27, 28).

Fig. 2.

The brokers of the affiliation network. (A) The level of brokerage, as measured by the yearly average effective size ζ, is reported for the top quartile affiliations ranked in descending order of their total awarded research funding. (B) The level of brokerage of Imperial College and Heriot-Watt University exhibited opposite trends with the rise of the total funding. (C) Connectivity between Imperial College and its partners when the total funding from the EPSRC was £250 million and over £1 billion as indicated by the dotted lines in B. Both nonconnecting and interconnecting neighbors of Imperial College are shown. (D) Same as C but for Heriot-Watt University and its partners. (E) Research funds obtained by Imperial and Heriot-Watt continued to rise linearly with the total funding. In B and E, each marker corresponds to a data point of 1 yr.

To gain a better insight into the factors that may contribute toward success in terms of awarded grants, we examined how the brokerage behavior of the leading affiliations has changed with the total funding over the last three decades. We found that the rise in the volume of the total funding, which coincided with the emergence of investment on focused research, has resulted in further centralization of the local networks of the top 10 funded affiliations, as reflected by the increase of ζ with the total funding. This is clearly shown in the case of Imperial College (Fig. 2B), which increasingly acted as an information broker between otherwise unconnected neighbors (Fig. 2C); this is most likely due to its ability as a large institution to facilitate new research partnerships (29). On the contrary, the lesser-funded affiliations were found to exhibit the opposite trend, as shown in the case of Heriot-Watt University (Fig. 2B). Notwithstanding the fact the number of noninterconnecting first neighbors of Heriot-Watt University increased, the value of ζ decreased with the total funding, mainly due to the rise of (about 24%) interconnecting neighbors, and to the higher level of interconnectedness among them (Fig. 2D). The two different collaboration strategies we observed in response to changes in funding policy seemed both to be effective ways to secure research grants, because all of the well-funded affiliations we examined, both the top 10 and those less-funded, have directly benefited from their respective strategies and their awarded research funds continued to rise with the total funding (Fig. 2E and Fig. S4).

Fig. S4.

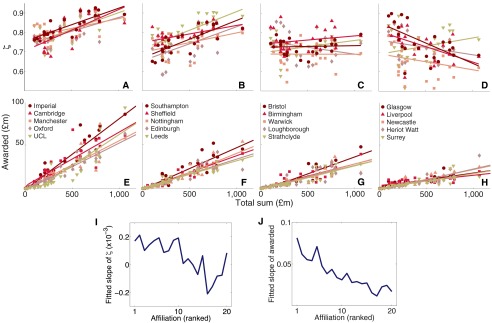
Collaboration patterns of the top 20 funded affiliations covaried with the total funding. (A–H) The effective size and awarded funding of the top 20 funded affiliations, which provides an extension of Fig. 2 B and E in the main text, whereby only results of Imperial and Heriot-Watt are shown. (A and B) Brokerage among the top 10 affiliations clearly increased with the total funding. Other less-well-funded affiliations showed a less distinct trend (C) whereas most affiliations in the last quantile decreased in brokerage as the funding increased (D). (E–H) Funding obtained by the top 20 affiliations continued to increase with the total funding. (I) Overall effective size, with reference to the fitted slopes, systematically declined with an affiliation’s ranking. (J) Similarly, the fitted slope based on the amount of awarded funding also declined with ranking.

The Rich Core of Leading Universities.

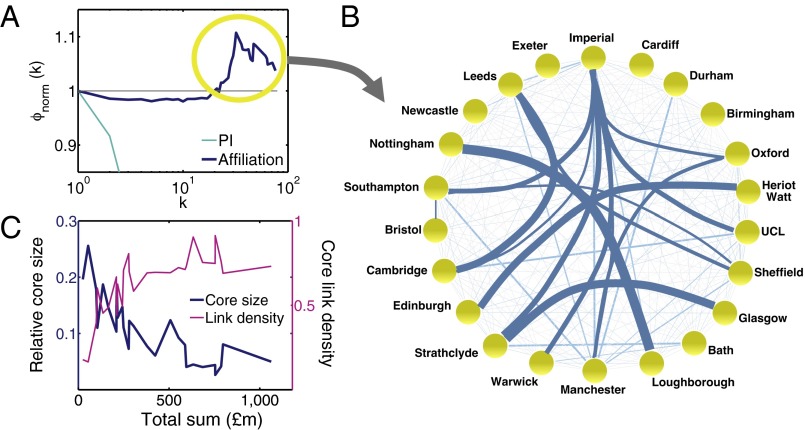
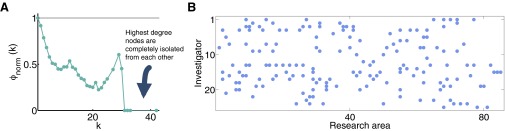
We examined the level of global interconnectedness among the leading PIs and affiliations, which correspond to the nodes with the largest degree, the so-called hubs, by detecting the rich-club phenomenon in the networks (22, 23). To do so, we evaluated the number of edges $E\left(k\right)$ among the $N\left(k\right)$ nodes of degree larger than a given value k, and we computed the rich-club coefficient, ${\varphi }_{norm}\left(k\right)$, normalized with respect to the case of 1,000 random graphs with the same node degrees as in the empirical networks (30). A value ${\varphi }_{norm}\left(k\right)>1$ for large k is an indication that the hubs of a network have organized into a rich club. Indeed, we observed this phenomenon in the affiliation network, but not in the case of investigators (Fig. 3A). This suggests that the affiliations with a high number of grants tended preferentially to collaborate among each other, forming tightly interconnected communities, more than we would expect in a random case. Conversely, the investigator network shows an anti-rich-club behavior. This is not surprising given the sparseness of the network and also due to the isolation among high-degree investigators who were found to be working in largely nonoverlapping research areas (Fig. S5).

Fig. 3.

Elitism in scientific collaborations. (A) The affiliation network exhibited the rich-club phenomenon, with ${\varphi }_{norm}\left(k\right)>1$ for high degree nodes, whereas such a behavior was not present in the PI network (the year 2010 is shown; other years give the same results). (B) The rich core for year 2010 showing the cohesive community formed by the high-degree nodes. Each edge is weighted by the frequency of the partnerships found in that year. (C) The relative size of the rich core of the affiliation network, in general, shrank with the total funding, whereas the density of partnerships among the affiliations in the rich core continued to rise with the total funding.

Fig. S5.

Anti-rich-club behavior in the investigator network. (A) The normalized rich-club coefficient ${\varphi }_{norm}\left(k\right)$ for the investigator network in 2010 was smaller than 1 and decreased with k. High-degree nodes were totally disconnected from each other or had very little linkage among them. (B) High-degree investigators largely research in nonoverlapping topics, which helps explain the lack of connectivity among them. Here, investigators were ranked by their degree; the person with the highest degree is first and appears on the top. Projects associated with these investigators stretched over 80 different areas (out of a total of 375 defined by the EPSRC), and only active areas of these investigators are shown.

We applied a core profiling method (24) that is based on the escape time of a random walker to extract members of the rich club for each of the 28 y and obtained a total of 45 affiliations (Table S1). Imperial College and University of Oxford were among those in the so-called rich core during the entire period of study, closely followed by other frequently found members that were only absent during the early years and have remained in the rich core ever since. For example, the rich core in 2010 was composed predominantly of the leading affiliations (Fig. 3B), and in particular the top-funded affiliations were not only well-connected with the rest of the core but also showed strong interlinkages among themselves whereby they formed the center of the core.

Table S1.

Members of the rich core

Affiliation	Abbreviation	Grants	Total £	${\zeta }_{avg}$	$N_{core}$	$N_{core}^w$
Imperial College	Imperial	2,658	880,042,691	0.847	28	27
University of Cambridge	Cambridge	2,182	785,600,273	0.806	27	28
University of Manchester	Manchester	2,351	612,256,769	0.830	27	28
University of Oxford	Oxford	1,966	557,758,967	0.818	28	28
University College London	UCL	1,417	543,449,634	0.828	27	27
University of Southampton	Southampton	1,373	508,545,865	0.763	27	26
University of Sheffield	Sheffield	1,367	408,240,769	0.803	28	27
University of Nottingham	Nottingham	1,411	393,624,426	0.755	27	26
University of Edinburgh	Edinburgh	1,191	376,515,957	0.747	25	27
University of Leeds	Leeds	1,452	369,915,734	0.822	28	27
University of Bristol	Bristol	1,259	357,784,563	0.751	27	15
University of Birmingham	Birmingham	1,059	320,365,372	0.784	27	18
University of Warwick	Warwick	1,111	299,106,838	0.712	27	10
Loughborough University	Loughborough	971	292,614,129	0.747	25	17
University of Strathclyde	Strathclyde	1,004	267,072,205	0.746	24	19
University of Glasgow	Glasgow	857	247,098,481	0.777	24	15
University of Liverpool	Liverpool	966	240,086,056	0.760	26	15
University of Bath	Bath	992	238,851,816	0.675	27	19
Newcastle University	Newcastle	813	222,668,660	0.748	26	20
Heriot-Watt University	Heriot-Watt	857	202,088,932	0.754	24	21
University of Surrey	Surrey	783	200,322,051	0.726	24	11
Durham University	Durham	776	172,691,133	0.684	25	11
University of St Andrews	St Andrews	515	166,131,172	0.687	8	0
Cranfield University	Cranfield	578	164,867,131	0.714	18	0
Queen’s University Belfast	Queen’s	660	142,904,945	0.712	14	2
Queen Mary, UoL	QMUL	618	139,471,209	0.685	12	5
Cardiff University	Cardiff	648	133,551,032	0.740	23	6
University of York	York	611	128,477,800	0.703	16	2
Swansea University	Swansea	488	110,663,780	0.735	7	2
Lancaster University	Lancaster	516	107,044,160	0.682	14	4
Brunel University	Brunel	415	91,665,418	0.714	18	0
King’s College London	King’s	530	88,242,899	0.708	9	4
University of Exeter	Exeter	454	86,135,975	0.618	17	2
University of Reading	Reading	467	78,721,875	0.682	17	0
University of Salford	Salford	470	75,592,400	0.770	18	4
STFC - Laboratories	STFC	215	69,769,793	0.589	12	0
University of Leicester	Leicester	382	48,127,442	0.585	1	0
University of Kent	Kent	335	45,236,232	0.678	1	0
University of East Anglia	E. Anglia	308	42,871,012	0.652	2	0
University of Hull	Hull	320	41,882,084	0.655	1	0
University of Dundee	Dundee	236	40,908,598	0.690	5	0
University of Bradford	Bradford	287	36,219,345	0.737	1	0
Royal Holloway, UoL	R. Holloway	191	34,035,831	0.675	1	0
Keele University	Keele	213	22,234,981	0.670	1	0
Bangor University	Bangor	193	18,407,971	0.582	1	0

Affiliations were sorted in descending order of their total funding. For each affiliation, their total number of grants (Grants) and total amount funding awarded (Total £), yearly average effective size (${\zeta }_{avg}$), and frequency found in the unweighted ($N_{core}$) and in the weighted rich core ($N_{core}^{\text{w}}$) are shown. Data for 1985 have been omitted because the network only had eight affiliations.

We also found that the relative size of the rich core decreased gradually with the total funding (Fig. 3C). The rich core initially contained over 25% of the affiliations and the rise in focused funding since the start of the millennium (which coincided with rising total funding) has caused the rich core to shrink further and to be maintained to a relatively small size since (4–8%), and this agrees with existing theory that stress in a system (rising Gini coefficient and falling number of grants in this case) is often manifested in a reduction in core size (31, 32). The emergence in focused funding, however, has fostered higher interlinkage among the affiliations in the rich core; the density of links was initially found to be low and gradually increased during the same period. The density was found to be the highest when the rich core was the smallest. The presence of a rich core of leading affiliations is a reflection of close collaborations among their researchers, and the increased level of interlinkage among these affiliations demonstrates a tendency for their researchers to collaborate with their peers in comparably reputable places, suggesting that homophily (33, 34) with respect to affiliation excellence accounts for one of the driving forces of scientific collaborations.

Research Performance.

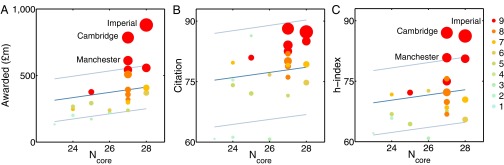
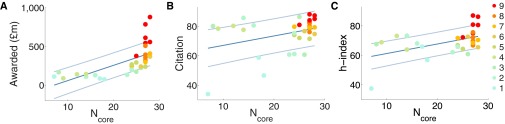
Could participating in the rich core be a contributing factor toward success in research? To answer such a question, we investigated the significance of the rich core in terms of inputs versus outputs by examining the amount of funds its member affiliations received and their overall research performance (5, 15). First, we found that the received research funds of an affiliation over the 28 y linearly correlated with the number of times, $N_{core}$, the affiliation was present in the rich core (Fig. 4A and Fig. S6), with the exception of Imperial College, University of Cambridge, and University of Manchester, which have accumulated research funds beyond what is expected from a linear behavior. In addition, we referred to the number of research areas of an affiliation as a measure of the breadth of its research, and we observed this quantity generally declines as $N_{core}$ decreases. We also considered the relative citation score and the h-index (35, 36) of each affiliation to capture the quantity and the depth of research, respectively; the former gauges the volume of citations among researchers in an affiliation, and the latter additionally captures quality. We found that the citation score increased linearly with $N_{core}$ (Fig. 4B). The absence of an obvious deviation from the average trend here suggests that the capital requirement on developing a full breadth of research areas is nontrivial; whereas the top three affiliations seemed to have successfully done so by scoring in all areas, they did not receive citations exceedingly. As for the h-index, again we observed that Imperial College, University of Cambridge, and University of Manchester outperformed the rest of the universities in this metric, showing a marked deviation from the linear behavior (Fig. 4C) in all similar to that observed in the awarded research funds. Their outstanding funding profiles seemed to have enabled them to develop the depth of research that has led to the generation of high-quality papers; University of Cambridge was particularly the case with the highest average h-index.

Fig. 4.

Fundings and research performance of the rich core. (A) The total research fund received by each university over the entire 28 y is plotted as a function of the number of times an affiliation was found in the rich core, $N_{core}$. Node size is proportional to the total research fund, and the color denotes the number of active research areas that have received a score. Dark and light blue lines denote the mean and one SD from the mean, respectively. (B) The citation scores of the most frequently found affiliations increased with their appearance in the rich core. (C) Similarly, the appearance in the core is indicative of an affiliation’s h-index.

Fig. S6.

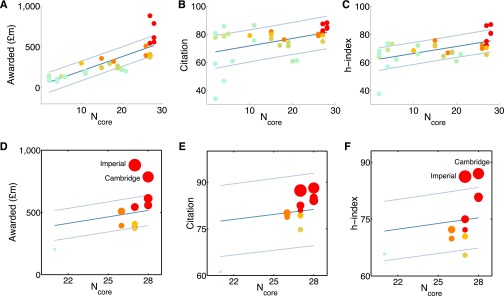
Funding and research performance of the rich core. This figure is the full version of Fig. 4 in the main text, which only shows affiliations with $N_{core}>20$. (A) The more an affiliation appeared in the core, the more funding it was likely to receive. Color denotes the number of active research areas that have received a score. Dark and light blue lines denote the mean and one SD from the mean, respectively. (B) Most frequently found affiliations in the rich core; their citation score increased with their appearance in the rich core. (C) Similarly, the appearance in the core is indicative of an affiliation’s h-index.

We repeated our analysis on a weighted version of the network where the edge weights were defined by the number of project partnerships between institutions and obtained similar results. In particular, the leading affiliations were found to be more profound in the core, because the core appearance of other affiliations that had fewer active research areas plunged sharply when the weights of partnerships were taken into account (Table S1 and Fig. S7).

Fig. S7.

Funding and research performance of the weighted rich core. Edges were weighted by the total number of project partnerships shared between institutions, and a weighted rich core was extracted for each year. (A–C) Same as Fig. S6 but for the weighted version of the network. We observed a cluster of affiliations that have appeared much more frequently in the core than the rest of the affiliations. (D–F) Focal views of A–C that contain affiliations with $N_{core}>20$ only. Here, a separation of the leading group of affiliations is clearly shown and these affiliations were active in noticeably higher numbers of research areas.

Discussion

There is today an open question on the kind of collaboration mechanics that underpin success in science and, up to now, such an issue has been mainly explored by characterizing the structural patterns of collaborations based on how scientists publish together (8–10). Our approach complements those studies based on coauthorship networks, addressing the question by looking at how scientists collaborate to obtain funds for their research.

Our results demonstrate that there has been a marked change in the funding landscape in the United Kingdom in the last three decades, with the largest engineering and physical sciences funding agency providing focused research investment to selected places. This has also shaped the anatomy of collaborations among investigators and among universities in terms of both the local cohesiveness and global interlinkage among them. In particular, the network analysis of successful project partnerships among affiliations has shown that the leading universities have been able to capitalize on this competitive and rapidly changing environment; they have extensively become the knowledge brokers of the network, orchestrating partnerships through a diverse source. This is likely to have arisen due to their ability to develop a broad range of expertise and extend partnerships with specialist entities (29). In addition to that, these universities formed the very center of a rich core through their strong reliance.

Indeed, our findings show the presence of an elite group of affiliations overattracting resources, and many in the research community would find such inequality in funding distribution highly controversial (37). However, the effect seemed not to be entirely adverse, because arguably those elite affiliations that have successfully become very rich seemed to have produced in both the variety of research and unmistakably in quality. The prominent role of elite universities is often said to have a wider impact in driving science forward (15, 38). Here, this is demonstrated by the fact that other well-funded places, which might have less capacity to expand, have consistently benefited from their association with the elites through the rich core. This agrees with previous claims on the importance of elite universities in facilitating multipartner collaborations (15).

We revealed how collaboration networks constantly undergo adaptive organization in response to funding, resulting in an evident shift in network configuration across different scales. These shifts in collaboration patterns may potentially mean a change in the nature of these partnerships, altering their strengths (e.g., frequency and financial value). This line of research remains to be explored more thoroughly and, hence, a comprehensive study on the weighted version of these networks will provide a leap in understanding the magnitude of these variations in patterns. Furthermore, study into other attributes that may also covary with funding, such as the degree of interdisciplinary research, will allow us to gain an insight into how mechanisms (39, 40) for formulating partnerships have evolved, because the impact of funding is highly likely to be multidimensional.

Funding is an essential part of research because it provides the sought-after resources to support related activities. Applying for funding is highly competitive (41), as suggested by the low average success rate, and in many countries the economic recession observed in recent years has led to considerable pressure on the research budget. A better understanding of successful project formations, therefore, provides an insight into how to thrive in such a challenging landscape, and can potentially have far-reaching implications for government policy on research investment worldwide.

Materials and Methods

Dataset: EPSRC Grants on the Web.

The EPSRC, formerly the Science and Engineering Research Council (SERC), was created in 1981 to reflect the increased emphasis on engineering research. The dataset was collected from the EPSRC Grants on the Web (GoW) system (gow.epsrc.ac.uk/ ), which, at the time of data collection, contained a total of 43,193 projects awarded between 1985 and 2013 (only grants starting before October 1, 2013 were available). For each project, we recorded the title and the total value, the PI, any CIs and/or OIs, the start and end dates, affiliation(s) of the investigators(s), and the associated research area(s). Funding was considered to be awarded to the PI and the affiliation of the PI. Information on how the overall funding of a given grant was divided among the rest of the investigators (and their affiliations) was not made available.

Adjustment to Monetary Values.

Because the period of study spans three decades, the Consumer Prices Index (CPI) with respect to 2005, provided by the Office for National Statistics (www.ons.gov.uk/ons/index.html), has been applied to adjust the figures so that the monetary values of grants were made comparable across the whole period of study. This index was chosen because the costing associated with a grant is often originated from salaries, travel, and equipment (including consumables), and their changes in value over time are well captured by the CPI.

Network Construction.

Two types of networks were constructed based on the EPSRC GoW. First, we referred to a project partnership between a PI and a collaborator (a CI or an OI) as an edge and the resultant network was referred to as the investigator network. Grants consisting of only one investigator (i.e., only the PI) have been excluded from the network construction. Similarly, we referred to a project partnership between the affiliations of a PI and a collaborator (a CI or an OI) as an edge and obtained the affiliation network. In both cases, we constructed a network for each year by referring to all of the active projects, and in this case an edge would be present for the duration of a project. For example, if a project started in 1990 and ended in 1993, the associated edges would be present between 1990 and 1993 inclusively. All networks were studied as undirected graphs.

The Rich-Club Phenomenon and the Rich Core.

To detect the presence of the rich-club phenomenon we first ranked the network nodes according to their degree, k. We then calculated for each value of k the quantity $\varphi \left(k\right)=2E\left(k\right)/k\left(k-1\right)$, where $E\left(k\right)$ is the number of edges among nodes with a degree $\ge k$ (22). To determine ${\varphi }_{norm}\left(k\right)$, we compared $\varphi \left(k\right)$ of the empirical network to that obtained from an ensemble of random graphs. Specifically, for a given empirical network, we constructed 1,000 random graphs with the same degree sequence as the empirical network (30) and obtained ${\varphi }_{rand}\left(k\right)$ by averaging over the ensemble of networks. Finally, ${\varphi }_{norm}\left(k\right)=\varphi \left(k\right)/{\varphi }_{rand}\left(k\right)$ (23).

Once we have established that high-degree affiliations exhibited the rich-club phenomenon, we characterized the membership of the club in each year by applying a core profiling method that is based on the escape time of a random walker (24). We ranked the nodes in descending order of their degree, such that the node with the highest degree is ranked first, and so on. For a given node, its links are divided into two groups: those with nodes of a higher rank and those with nodes of a lower rank. Therefore, a node with a rank r has degree $k_r$; the number of links it shares with nodes of a higher rank is $k_r^{+}$ and the number of links with nodes of a lower rank is $k_r-k_r^{+}$. Starting from the highest-rank node, as r increases the number of links $k_r^{+}$ that node r shares with nodes of a higher rank fluctuates. We denote the node $r^{\ast }$ whereby $k_r^{+}$ reaches the maximum and $k_r^{+}$ is always less than $k_{r^{*}}^{+}$ thereafter. This reflects a change in the connectivity among the highly ranked nodes reflected by the escape time of a random walker, which also defines the boundary of the rich core: The nodes with a rank less than or equal to $r^{\ast }$ form the core and the rest are in the periphery. The rich-club coefficient can be expressed in terms of r as

$$\varphi \left(r\right)=\frac{2E\left(r\right)}{r\left(r-1\right)}=\frac{2{\displaystyle {\sum }_{i=1}^r{k}_i^{+}}}{r\left(r-1\right)},$$ [1]

where $E\left(r\right)$ is the number of links between the r nodes. The relationship between the escape time and the rich-club coefficient has been shown as (24)

$${\alpha }_r=\frac{r\left(r-1\right)\varphi \left(r\right)}{{\displaystyle {\sum }_{i=1}^r{k}_i}}.$$ [2]

Research Performance.

We evaluated the research performance of an affiliation by its relative citation score (The methodology for calculating the citation score is available at www.iu.qs.com/university-rankings/subject-tables/) and the h-index (35, 36) in 2013. The former accounts for the total number of citations per faculty member in an affiliation and is considered a measure of the volume of research (i.e., quantity). The latter takes into consideration the citations of the best papers per faculty member in an affiliation and is considered as a measure of the depth of research (i.e., quality). The scores for individual affiliations were obtained from the QS World University Rankings (www.topuniversities.com) and they were calculated based on bibliometric data on Scopus (www.scopus.com). Both quantities were normalized to take values in the range of 0–100. Scores were available in a range of disciplines and only subject areas related to the engineering and physical sciences domains were selected, including chemistry, computer science and information systems, engineering (chemical, civil, and structural; electrical and electronic; and mechanical), materials sciences, mathematics, and physics. Individual subject citation scores and h-indexes of a given affiliation were averaged, providing the mean ratings over all individual members of a given affiliation, and used as a measure of performance. It is worth noting that the h-index is strongly influenced by the longevity of one’s research career, which needs to be taken into consideration when interpreting the findings. Only Imperial, Cambridge, Manchester, Oxford, University College London, and Edinburgh have scored in all areas.

Changes in the Funding Landscape

About half of the grants (21,954, to be precise) were associated with one or more CIs and/or OIs. Both the average number of investigators and affiliations increased over time (Fig. S1A). Although a grant could have over 40 investigators, by and large the majority of grants consisted of a small number of investigators (Fig. S1B). The number of grants awarded to a PI decreased exponentially (Fig. S1C). We defined an active period of a PI as the number of years between his/her first and last recorded grants. Fig. S1D shows a gentle decline on the number of PIs as the number of active years increased. We observed a direct correlation between the length of active research period and the number of grants one obtained (Fig. S1E).

Networks of Investigators and Affiliations

In the network of investigators, the network size in terms of both the number of investigators and collaborations correlated with the total funding (Fig. S2A). We observed a threshold at about £500 million in which network growth slowed down with further increase in the total funding. The total funding reached over this threshold in 2000 (Fig. S2B); in fact, the network reduced in size when there was a noticeable rise in funding in 2009. Similarly, an increased funding also resulted in a larger GC in the network, implying better interconnectivity among different local groups of investigators (Fig. S2 C and D). We found that the rising level of larger-scale collaboration between investigators from across higher numbers of affiliations was found to be a contributing factor (Fig. S2E) to the sharp rise in the size of the GC. In particular, the effect of cross-institutional collaboration was found to be most profound because a small rise in the average number of affiliations in a grant caused the size of the GC to soar. The emergence of larger research teams is a reflection of a higher level of collectivity among researchers within the same discipline or complementary subject areas, and the invisible colleges (42–44) formed by the interpersonal contact among scientists were likely to be a fertile ground for facilitating the expansion in collaboration, potentially making parts of the invisible colleges visible as previously informal liaisons have been formalized by the establishment of project partnerships (45). The overall connectivity of the investigator network remained sparse; the average degree was low and variable (Fig. S2F).

We observed similar covariance between the total funding and network size (Fig. S3A) in the network of affiliations. Again, the network shrank in size as a result of the sharp increase in the total funding in 2009 (Fig. S3B); this provides other evidence on heterogeneous distribution of funding. In contrast to the investigator network, the affiliation network was well-connected with very few disjointed components (Fig. S3 C and D). Given that the GC contained most of the nodes in the network during the period of study in this case, we did not observe any significant increase in size as the average number of investigators and affiliations rose (Fig. S3E). The average degree was significantly higher than that of the investigator network, and of much higher level of variability (Fig. S3F).