Persistent states in vision break universality and time invariance

Significance

Studies of perception usually measure overt variables—how sensory stimulation governs what is perceived. Here we show that perception is also governed by hidden variables that we call perceptual states. These hidden variables—two of which we study in this paper—can be inferred as systematic biases governing the perception of two families of ambiguous 3D stimuli. They vary widely across individuals, causing observers to often perceive the same stimulus in opposite ways. The variables change cumulatively over time and thus constitute a previously unknown type of perceptual memory. We document dynamics on time scales from minutes to months (the latter scale virtually unknown in perception), showing that aspects of the variables’ behavior can be modeled by random walks.

Abstract

Studies of perception usually emphasize processes that are largely universal across observers and—except for short-term fluctuations—stationary over time. Here we test the universality and stationarity assumptions with two families of ambiguous visual stimuli. Each stimulus can be perceived in two different ways, parameterized by two opposite directions from a continuous circular variable. A large-sample study showed that almost all observers have preferred directions or biases, with directions lying within 90 degrees of the bias direction nearly always perceived and opposite directions almost never perceived. The biases differ dramatically from one observer to the next, and although nearly every bias direction occurs in the population, the population distributions of the biases are nonuniform, featuring asymmetric peaks in the cardinal directions. The biases for the two families of stimuli are independent and have distinct population distributions. Following external perturbations and spontaneous fluctuations, the biases decay over tens of seconds toward their initial values. Persistent changes in the biases are found on time scales of several minutes to 1 hour. On scales of days to months, the biases undergo a variety of dynamical processes such as drifts, jumps, and oscillations. The global statistics of a majority of these long-term time series are well modeled as random walk processes. The measurable fluctuations of these hitherto unknown degrees of freedom show that the assumptions of universality and stationarity in perception may be unwarranted and that models of perception must include both directly observable variables as well as covert, persistent states.

The neural networks underlying visual perception are complex systems and, as such, undoubtedly have internal states. The formal notion of “state” can be defined as the minimal set of variables that, together with the input to a system and the fixed processing mechanisms, allows one to predict the system’s output (1). If perception is a function of both the sensory input and internal states, then—because states can vary both across individual observers and over time—the presence of an internal state would manifest itself as potentially large individual differences in the perception of the same stimulus and in coherent temporal variations of perception of the same stimulus over time in a single observer. It is known that visual functions can be modulated (2) on brief time scales by priming (3–6), aftereffects (7–9), and sequence effects (10–13) [and sometimes on larger time scales as well (14)]; can undergo visible short-term fluctuations in the presence of multistable stimuli (15–20); and can undergo long-term or permanent changes in their structure through learning (21–24). Despite these examples, little is known about internal states of the visual system. In terms of underlying mechanisms, the internal state is represented naturally in recurrent but not in feed-forward neural networks (25, 26).

Here we measure patterns of biases in two families of visual stimuli and show that, contrary to most known cases, these patterns can vary radically from one observer to the next, leading to stimuli that are often perceived in opposite ways by different observers. We show that these bias patterns can be predicted to a large extent by simple variables. We therefore call these parameters “state variables.” They constitute a form of long-term but dynamic memory in perception and are related to but distinct from the phenomenon of short-term coherence in the perception of multistable stimuli known as sensory memory (15–20), as we discuss below.

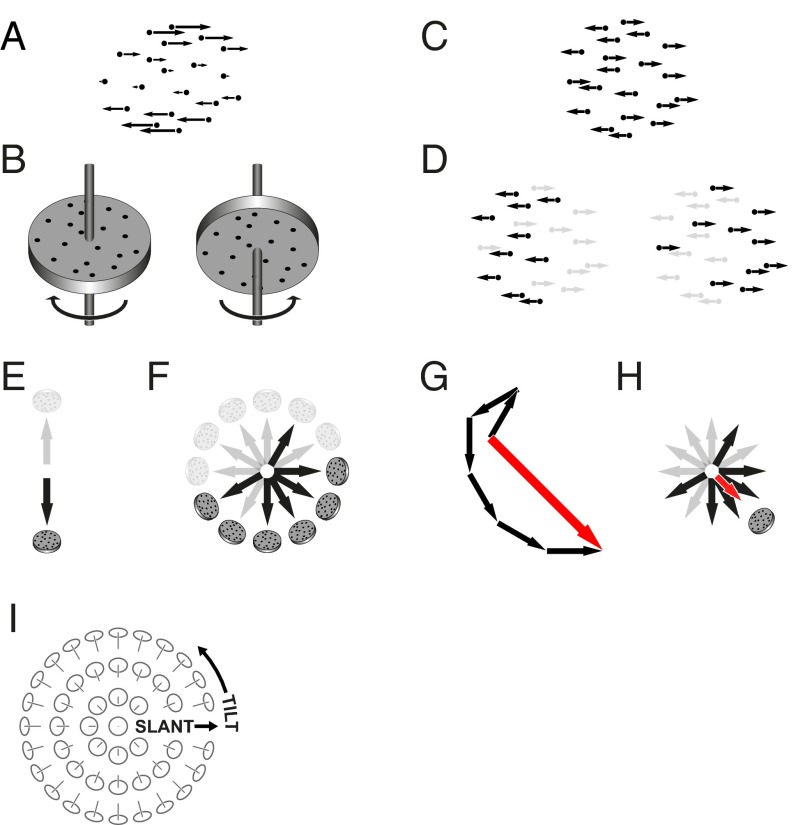
The stimuli in the first family, which we call structure–from–motion (SFM), consist of moving dots simulating planes rotating in depth (Fig. 1A). [Examples of stimuli and response procedures for the two families of stimuli may be seen at lab-perception.org/demo/p/sfm and lab-perception.org/demo/p/tfm. Following the 16-trial session, the web page displays the participant’s bias.] Each stimulus can be perceived as having one of two tilts (27–29), separated by 180 degrees (Fig. 1 B and I). The stimuli in the second family, transparency–from–motion (TFM), consist of two sets of dots moving in opposite directions (Fig. 1C). The two sets of dots are usually perceived as transparent layers, one of which is seen as being closer or more salient (30–32), also giving rise to a 180 degree ambiguity (Fig. 1D). Observers reported which of the two tilts they perceived for SFM stimuli and which of the two motion directions they perceived closer for TFM stimuli. Successive stimuli had different orientations (tilts or motion directions), sampled in random order from the entire 360 degree range—in contrast to procedures used to study spontaneous fluctuations (15–20), in which only one stimulus is presented. To reduce spontaneous fluctuations, stimuli were brief (0.5 s).

Fig. 1.

The two families of ambiguous stimuli and summary of data analysis. (A and B) SFM stimuli. Optic flow such as in A is ambiguous because it can be generated by the two configurations shown in B, corresponding to surfaces with tilts that differ by 180 degrees (see I for definition) and opposite directions of rotation. (Stimuli used in the study had 45 degrees between tilts and rotation axes, rather than 0 degrees, as shown here.) (C and D) TFM stimuli. Two sets of dots moving in opposite directions (C), with no explicit depth cues, are usually perceived as segregated by motion direction into two transparent layers, with one of the layers seen as closer or more salient than the other; (D) the motion direction of the front or salient layer is ambiguous by 180 degrees. (E) We represent one stimulus by two opposite-facing arrows, corresponding to the two possible tilts (SFM, shown here) or front-layer motion directions (TFM) that can be perceived. We will represent the tilt or motion direction that was reported by the darker arrow. (F) A typical pattern of responses obtained when we present a series of tilts or motion directions. Actual experiments had more values of tilts or directions. (G) To calculate the bias vector, we take the sum of the unit vectors corresponding to the perceived tilts or motion directions. (H) The direction of the bias vector yields the preferred tilt or motion direction, whereas its length (normalized by its maximum value) is a measure of bias strength. (I) Illustration of slant and tilt, the variables we use to parametrize surface orientations in SFM stimuli. Tilt is the orientation in the image plane of the projection of the surface normal vector.

Each twofold ambiguity at a different stimulus orientation could have been resolved as an independent stochastic decision, which would have yielded an isotropic pattern of perceptual decisions across stimulus orientations. As we shall show, however, perceptions at different orientations are far from isotropic, following a pattern that is both highly stereotypical and idiosyncratic. The individual differences are governed by state variables—bias parameters that exhibit coherence over time, while also undergoing cumulative changes—whose dynamics we explore below.

Results

Experiment 1: Population Distribution and Stability of State Variables.

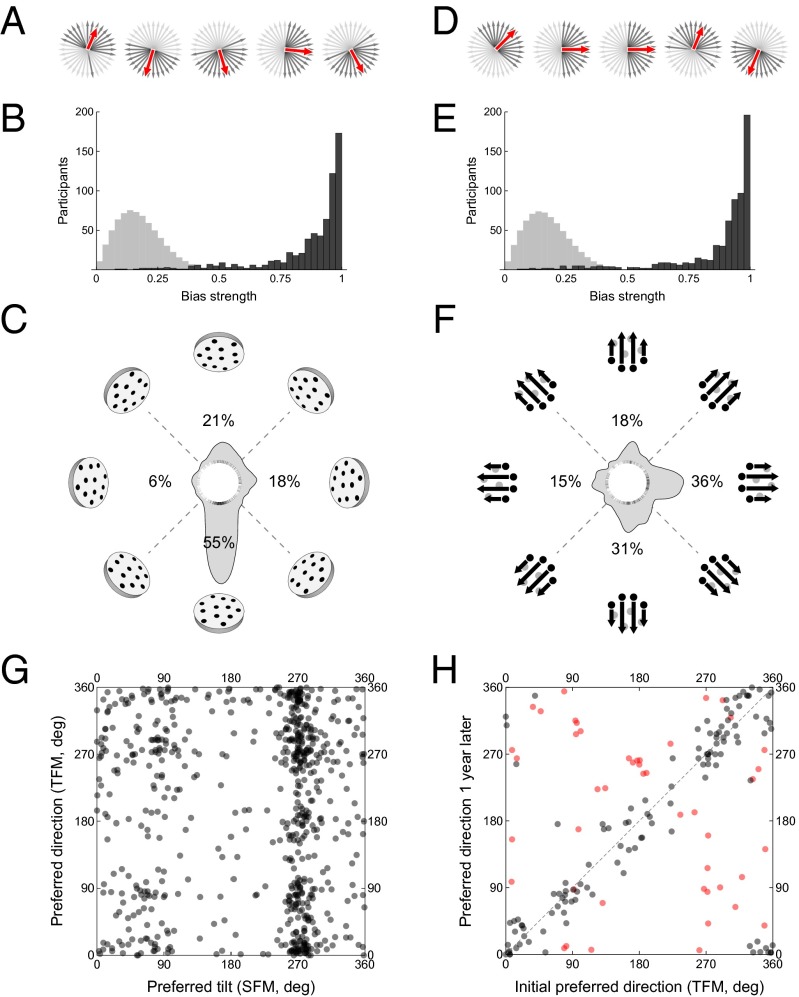
In a large-scale internet-sourced study, we were able to gather reliable psychophysical data on 704 participants (see SI Appendix for details). Individual responses will be presented using the conventions described in Fig. 1 E and F. The responses of several representative participants (Fig. 2 A and D) show that perceived tilts and motion directions generally lay in 180 degree fans. Inspection of the responses of all participants (SI Appendix, Fig. S1) reveals that fan-shaped patterns are extremely common—but with different fan orientations in different participants. This pattern may be described as a bias in favor of tilts or motion directions with a positive projection on a “bias vector” (shown as red arrows in Fig. 2 A and D and SI Appendix, Fig. S1). Individual bias vectors can be estimated as a sum of unit vectors corresponding to reported tilts or motion directions; the normalized length of the bias vector yields the bias strength and its direction, the preferred tilt, or motion direction (Fig. 1 G and H). The population distributions of bias strengths (Fig. 2 B and E) were very different from those expected for the null hypothesis of random responses (Kolmogorov–Smirnov tests, P < 0.0001).

Fig. 2.

Results of the population distribution experiment (experiment 1). (A) Data of five representative participants (out of 691—the rest are shown in SI Appendix, Fig. S1) in the SFM condition. Data are represented using the conventions in Fig. 1 E and F. The red arrows are the bias vectors (Fig. 1 G and H). For visual clarity, only one out of four of the trials is shown. (B) Population distribution of bias strength (dark bars) compared with the null hypothesis arising from isotropically random tilt choice (light bars). Of the participants, 97.4% had significantly fan-shaped distributions (Rayleigh test, Benjamini–Hochberg correction for multiple tests with false discovery rate, 0.05). (C) Circular histogram of the population distribution of bias directions (smoothed using a 15 degree-wide kernel). Individual bias directions are shown as strokes on the rim of the white circle. Some corresponding plane orientations are shown for reference. The distribution is highly anisotropic (Kuiper’s test, P < 0.0001). Percentages indicate fractions of the population with peaks within ±45 degrees of the cardinal directions. (D–F) Corresponding results for the TFM condition, where 95.9% of observers had significantly fan-shaped distributions. The population distribution (E) resembles the distribution in a previous study (31), obtained with a much smaller sample in laboratory conditions. (G) Relationship between SFM and TFM bias directions, with each dot representing one participant. The two state variables are uncorrelated and independent. (H) Significant correlation between preferred TFM preferred directions as measured initially (x axis) and 1 y later (y axis), with each dot representing one participant. Participants whose preferred directions underwent significant change are shown in red. Similar results were obtained for the SFM preferred tilts.

Although a large majority of observers had strong fan-shaped biases, individual observers had very diverse bias directions. Two randomly chosen subjects disagreed with one another on the average of 45.3% of the stimuli (almost the maximum possible incoherence of 50%, given the binary responses) but were coherent in their own response patterns, giving the same response in 85.5% of the repetitions of the same stimulus. The empirical population distributions of the bias directions (Fig. 2 C and F) show that nearly every bias direction occurs in the population in the two stimulus families. However, the distributions of bias directions were notably anisotropic. Both SFM and TFM distributions had peaks in the cardinal directions (72.9% and 68.5% of participants had biases within 22.5 degrees of the cardinal directions). The cardinal peaks could not arise from decision bias, as observers typically reported nearly all directions within 90 degrees of their preferred direction; thus, all observers perceived tilts and motions in both cardinal and noncardinal directions. Moreover, as can be seen in Fig. 2 C and F, the cardinal peaks in the population distributions were asymmetric, with different patterns for SFM and TFM. In SFM (Fig. 2C), the largest peak corresponded to surfaces oriented near the ground plane (55%), reflecting the known and probabilistically justifiable bias in favor of surfaces seen from above (33); however, significant minorities preferred the ceiling and the right wall orientations. Of the participants, 18% had a preferred tilt within 45 degrees of the right wall orientation but only 6% within 45 degrees of the left wall—with the difference statistically significant. In fact, the differences between the left and right, and between the up and down peaks, were significant in both distributions (bootstrap test, P < 0.0001).

The SFM and TFM bias directions are independent variables: Their population distributions were significantly different from one another (Watson’s U² test, P < 0.0001) and had no within-participant correlation [Fig. 2G; Fisher–Lee circular correlation (34), ∏ = 0.001, 95% bootstrap confidence interval (–0.008, 0.011)]. We found few effects of age, gender, or hand preference on the distributions of preferred directions (SI Appendix, Fig. S3). Whereas the right–left asymmetry disappeared in left-handed participants in the SFM population distribution, it became more pronounced in the TFM distribution.

Are the biases, which are so different in different observers, stable or changing? We will come back to this question repeatedly, but it can be tested in the data of experiment 1, where blocks lasted only 3 min on the average. We calculated the mean absolute angular differences between responses on all pairs of trials separated by a given lag. If the biases are stable, the mean difference should be flat as a function of lag. Averaging over the many hundreds of participants revealed a signal emerging from the noise due to the random order of stimuli: Responses on trials closer together in time tend to be closer than responses farther apart (SI Appendix, Fig. S4). A simple explanation for this temporal proximity effect is that, at any given point in time, each observer has a definite bias but that this bias undergoes cumulative change (such as drifts or random walks) even over brief durations.

To test the long-term stability of the biases, we invited the participants to repeat the measurements about 2 wk later (235 did so) and 1 y later (175 did so). Fig. 2H shows the original TFM bias directions versus their values 1 y later, with significant changes highlighted (see SI Appendix, Fig. S5 for other comparisons). The SFM bias direction changed by a median value of only 11.0 degrees over 2 wk and 22.5 degrees over 1 y; the TFM changes were 14.1 degrees over 2 wk and 26.3 degrees over 1 y. Although some of the long-term stability was due to the nonuniformity of the population distributions, especially for SFM, the biases showed strong coherence on the individual level (SI Appendix). The 1-y changes were significantly larger (Mann–Whitney test, P < 0.0001) than the 2-wk ones (SI Appendix, Fig. S5). We found no significant within-participant correlations between changes in the two biases or between 2-wk and 1-y steps. Thus, although most biases are stable even over periods as long as 1 y, significant (and sometimes large) changes do occur.

Experiment 2: Effect of Biases on Unambiguous Stimuli.

Although the patterns of biases we have found are striking, they are “cost-free,” because each stimulus is completely twofold ambiguous. We wondered to what extent the biases can overcome perceptual cues to one or the other solution and therefore performed an experiment in which we applied binocular disparities to disambiguate SFM stimuli. We found that the individual biases persisted and significantly affected reported surface orientations at disparities above threshold in most participants, although there were large individual variations in response to the disparity cue (SI Appendix, Fig. S6). Thus, the biases are operative even in the face of significant perceptual counterevidence, at least in many observers.

Experiment 3: Long-Term Temporal Dynamics.

Because we found that biases do change over time, we wished to study their temporal evolution. A fundamental property of a time series is whether its value at a given time is predictive of later values. A nonpredictive series consists of independently drawn samples from a fixed distribution, also known as “white noise.” Values in the series may vary, but successive values are uncorrelated, the power spectrum is flat, and the mean distance between values is independent of the time lag between them. A predictive time series, on the other hand, consists of values that retain information about the past. In this sense, we may say that a process that generates such a time series has its own state—the information retained from past values. Predictive series have correlated values, power spectra that vary with frequency, and mean distance between samples that depends on lag. Moreover, predictive series can be either stationary—with properties such as mean and variance independent of time—or nonstationary. Stationary series fluctuate in an autocorrelated fashion about fixed values, whereas nonstationary series, such as random walks, can wander away. The finding in experiment 1 that the biases change more over 1 y than over 2 wk is a first indication that the bias time series retain state information.

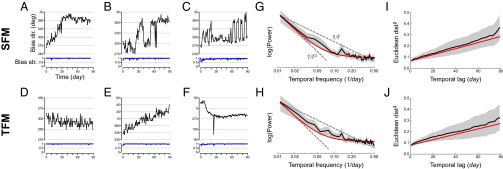
To study bias time series in greater detail, we performed a second large-scale internet-based study in which we measured the SFM and TFM biases once a day for about 3 mo in a group of 97 participants, yielding an average of 87.8 nearly daily measurements for each. The daily measurements were performed similarly to experiment 1, each involving a block of randomly ordered, equally spaced 48 trials. Representative examples of the time series are shown in Fig. 3 and for all participants in SI Appendix, Table T2. There was an almost bewildering variety of individual behaviors: stability (Fig. 3D), slow drifts with constant speed (Fig. 3E) or variable speed (Fig. 3 A and F), temporary excursions (Fig. 3F), abrupt transitions (Fig. 3B), oscillations between discrete values (Fig. 3 B and C), and oscillations at multiple frequencies (Fig. 3C). Although we cannot exclude that perhaps some of the abrupt transitions were due to changing experimental conditions that were not under our complete control, the slow and regular drifts are very likely to represent authentic evolution in the state variables, all the more so when the drift occurred in one of the variables but not the other (as was often the case; SI Appendix, Table T2).

Fig. 3.

Results of the 3-mo time-series study (experiment 3). (A–F) Examples of daily time series of the SFM (A–C) and TFM (D–F) variables in six participants. For each series, the bias direction is shown in black as a function of time in days and the bias strength in blue. (G–J) Macroscopic analysis of time series data. Black curves show the means, the gray regions the 95% confidence intervals (between-participant bootstrap), and the red curves the predictions of the fitted noisy random walk or IMA(1, 1) model. Power spectra of the (G) SFM and (H) TFM series, on a log–log scale. The dashed lines show 1/f and 1/f² spectra for comparison. MSED between (I) SFM and (J) TFM bias vectors measured on different days, as a function of time between measurements (lag) in days. Because bias vectors lie inside the unit circle, variables range from –1 to +1, and maximum square distance is 4.

To quantitatively characterize the time series, we calculated several types of macroscopic statistics. First, we calculated the temporal power spectra of the bias vectors (Fig. 3 G and H). Spectra for both SFM and TFM had peaks at low temporal frequencies that fell off and then flattened out at higher frequencies. Linearly regressing the individual participant’s spectra on a log–log scale, we found that 95% of the SFM spectra and 98% of the TFM showed decreasing power with higher frequencies. Second, we calculated the mean squared Euclidean distance (MSED) between the measurements as a function of lag—days between measurements. We found that MSED increased with increasing lag (Fig. 3 I and J); performing a linear regression of MSED versus lag, we found that 79% of the participants had biases that systematically drifted farther apart with increasing lag. (Many of the others had biases that wandered off only to loop back near their initial values.) Stationary series should have a mean distance that flattens out for large lag; the functions in Fig. 3 I and J show no evidence for such flattening, at least for averaged data. Third, we calculated autocorrelations of the differenced time series and found a nonzero autocorrelation at lag 1 (see SI Appendix, Fig. S7 for details). These observations strongly imply that biases are predictive, stateful time series and suggest that they are nonstationary.

To characterize the microscopic behavior of the time series, we modeled them within the Box–Jenkins autoregressive integrated moving-average (ARIMA) framework (35). Briefly (for details, see SI Appendix), we first searched a space of model families, including white noise, to find one that best approximated each series (the Cartesian components of each participant’s SFM or TFM series were modeled separately). We found that only 18% of the SFM series and 24% of the TFM series were best fit by stateless, white-noise processes. One model family, integrated moving average or IMA(1, 1), was much more common than the rest. The autocorrelation functions of the differenced series (SI Appendix, Fig. S7) also strongly imply that the series were IMA(1, 1). In a second step, we fitted all of the individual series with models from this family and found that 93% of the SFM and 88% of the TFM series were well fitted, as revealed by a randomness test on the residuals.

The IMA(1, 1) family are series $v_t$ with the following dynamical behavior: $v_t=v_{t-1}+{\epsilon }_t-b{\epsilon }_{t-1}$, where ${\epsilon }_t$ is an independent identically distributed (i.i.d.) variable. It can be shown (35) (also see SI Appendix) that such time series are equivalent to “random walks” or “Brownian motion” subject to measurement noise. In other words, an underlying state variable, $u_t$, was given by the random walk $u_t=u_{t-1}+{\alpha }_t$, where ${\alpha }_t$, the random step, is an i.i.d. variable with variance ${\sigma }_{\alpha }^2$. This variable constitutes the system’s memory, its cumulative value being carried over from one measurement to the next: Although successive steps are independent, their effects are cumulative. However, the state variable was not observed directly but filtered through independent measurement noise: $v_t=u_t+{\beta }_t$, where ${\beta }_t$, the measurement noise, is i.d.d. with variance ${\sigma }_{\beta }^2$. We found that the median random step ${\sigma }_{\alpha }$ in our population was 0.022 [0.009, 0.041] (25/75 percentiles in brackets) for SFM and 0.020 [0.008, 0.036] for TFM, with our variables ranging from –1 to +1. The measurement noise ${\sigma }_{\beta }$ was 0.103 [0.068, 0.144] for SFM and 0.122 [0.078, 0.157]. In terms of bias angles, the maximum median steps were 1.3 and 1.2 degrees for SFM and TFM and measurement noise 6.3 and 7.4 degrees. The power spectrum of a noisy random walk asymptotically approaches 1/f² at low frequencies (the random walk component) and flattens out at high frequencies (the white noise), precisely what we found in the mean power spectra (Fig. 3 G and H). The model predictions, shown in red in Fig. 3 G–I, are at least good qualitative approximations to the macroscopic statistics of the time series.

Similar to the population distribution experiment, we found no trace of correlation between the daily values of the SFM and TFM biases. However, we did find moderate but robust correlations between the magnitudes of the daily steps in the SFM and TFM biases, both within and between participants (SI Appendix).

A histogram of all of the daily bias directions is shown in SI Appendix, Fig. S8. These distributions strongly resemble those obtained in experiment 1 (Fig. 2 C and F), namely having peaks near the cardinal directions, with the same left–right and top–bottom asymmetries, on an almost completely different sample (10 out of 97 participants had participated in experiment 1). A simple random walk model obviously cannot account for all features of the data, such as the nonuniform bias distributions or the structured macroscopic features of the individual time series (Fig. 3). Even so, the random walk model gives a surprisingly good fit to intraindividual statistical properties of the time series (see Fig. 3, for instance).

Experiment 4: Short-Term Temporal Dynamics.

To check if the biases had stateful behavior on time scales shorter than 90 days, we performed a laboratory experiment in which SFM bias was repeatedly measured over 90 min in 15 participants. We presented a sequence of stimuli lasting 30 min, resulting in a mean of 13 independent measures of the bias. To compare the roles of external stimulation and internal dynamics in driving bias change, we also measured the bias once 30 min before and once 30 min after this sequence, with the participants remaining in complete darkness in the intervening periods.

The individual bias time series are shown in SI Appendix, Fig. S9. Spectral power that decreases with frequency, increasing distance between biases with lag, and autocorrelations all point to stateful series that can be modeled as noisy random walks (SI Appendix). In three cases, the bias changed significantly after 30 min in complete darkness (marked by asterisks in SI Appendix, Fig. S9), suggesting that internal CNS dynamics can drive change in the bias variable. We found that biases changed faster during the 30-min sequences of continuous measures than over the 30 min of darkness (see SI Appendix for details). Thus, repeatedly showing SFM stimuli over many hundreds of trials seems to “excite” change in the bias variable. [Another finding of experiment 4, performed in complete darkness with nothing but the stimulus visible, is that the cardinal peaks in the bias direction distributions (Fig. 2C)—also found here—do not seem to be caused by visual edges with cardinally oriented orientations (monitor edges, etc.; see SI Appendix for details).]

Experiment 5: Deliberate Perturbation of State Variables.

We wondered whether it is possible to modify the values of the state variables using visual stimuli. We measured observers’ SFM and TFM biases and then perturbed them for about 30 s using stimuli whose depth was unambiguously specified by the addition of binocular disparity and whose tilts or motion directions differed from the biases by 90–135 degrees, alternating the direction of the perturbation on successive blocks. Following this sequence of perturbing stimuli, we remeasured biases over a 100-s period, using a multiblock design to increase the temporal resolution of the measurement down to 1–2 s (SI Appendix, Fig. S10).

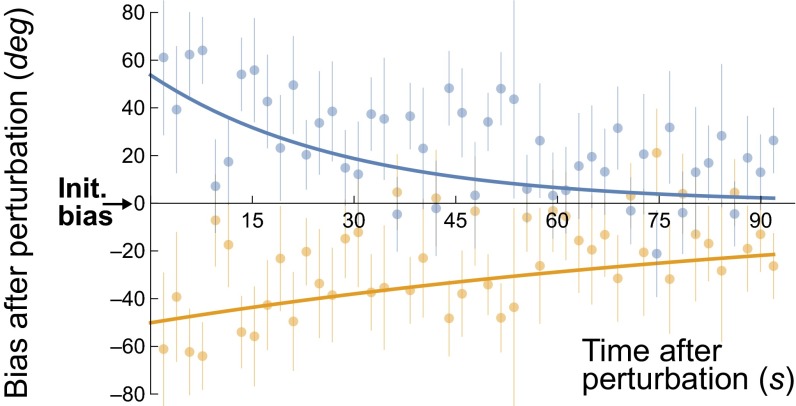
Results for individual participants (see Fig. 4 for a representative participant and SI Appendix, Fig. S11 for all participants) show that the aftereffect of the perturbation on the bias variable was attractive, “pulling” the bias variable toward the perturbation, but with decay toward the preperturbation value over several tens of seconds. Fitting exponential decay functions to the time evolution curves, we found that the amplitude of the effect immediately following the perturbation had a median value of 37.2 degrees in SFM and 41.7 degrees in TFM, with effects significantly attractive in all participants and conditions. The half-life of the perturbation—the time it takes for the effect to decay to half its initial value—had median values of 21.1 s for SFM and 42.4 s for TFM.

Fig. 4.

The effect of deliberate perturbation on the biases using nonambiguous stimuli (experiment 5). Data are shown for one representative participant for TFM stimuli (data for all participants are shown in SI Appendix, Fig. S11). The x axis shows the time immediately following the perturbation in seconds. The y axis shows the effect of the perturbation: the difference in degrees between the measured direction bias and the initial, preperturbation bias. On every other block, the perturbation stimuli were chosen between +90 and +135 degrees away from the initial bias direction (blue dots, bars, and curves), whereas on the other blocks the perturbation was in the opposite direction, between –90 and –135 (orange). Error bars denote SEs over multiple blocks. The curves are exponential fits.

Experiment 6: Effect of Bistable Fluctuations on Biases.

Any one of our ambiguous stimuli, when repeatedly presented at the same orientation, is bistable: Its perception spontaneously fluctuates between the possible interpretations (15–20). We wondered whether such fluctuations modify the state variables, temporarily or durably. We first measured SFM bias direction in six participants. Then, we repeatedly exposed each participant to the surface oriented at his or her own bias tilt, until obtaining a spontaneous tilt reversal that persisted for 10–20 stimulus presentations (several tens of seconds), so that the participant perceived the tilt opposite to his or her own initial bias. We then remeasured the bias in the usual way over the next several minutes. We found (SI Appendix, Fig. S12) that the bias returned to near its original value in all participants in at most a few minutes. Thus, fluctuations in bistable stimuli seem to have, at most, short-term effects on the state variables.

Experiment 7: Existence of the Bias Before the First Stimulus.

Studies of bistable perception have brought to light a phenomenon known as sensory or perceptual memory, where a single interpretation of an intermittently presented stimulus can last for a large number of trials (17, 19, 20). Are state variables sensory memories formed at or near the first stimulus, or do they exist in the visual system before exposure to our stimuli? To answer this question, we performed an experiment using SFM stimuli on 30 participants, with responses recorded from the very first stimulus (i.e., no practice trials). We predicted that if the biases were sensory memories, then the response on the first trial would be completely random and unbiased but then become “frozen in” as a sensory memory, in effect becoming the bias. A more complex version of the hypothesis would have the vector average of the responses on the first n trials becoming the sensory memory. For each i, we calculated the absolute angular difference between the bias direction calculated using trials $1,\dots ,i$ and the bias direction from all trials. The sensory memory hypotheses predicted local minima in this curve. We found no evidence for such local minima, and the data were in perfect agreement with a simple model of preexisting bias (see SI Appendix, Fig. S13 for details). Thus, experiments 6 and 7 both show that the state variables are independent of bistability phenomena, namely of spontaneous reversals and sensory memory.

Discussion

Although most studies of perception emphasize processes that are largely universal across measurements on different observers and different points in time, we have demonstrated large-scale differences among observers that undergo stateful, cumulative fluctuations over time scales from tens of seconds to months. There have been several recent reports of stable idiosyncratic biases arising in different contexts in human vision (36–40). Here, we have shown for the first time, to our knowledge, that two of these biases are state variables, in two different ways. First, we found that the appearance of suprathreshold stimuli depends not only on the stimulus but also strongly on the bias variables’ values. Second, the variables retain information about their past values when undergoing fluctuations in time, with their temporal dynamics at least partly described by a random walk model. Although the successive steps in the random walk are independent, its value accumulates the steps and constitutes a new kind of perceptual memory. Although random walk or diffusion models have been used to account for neurophysiological and behavioral data on perceptual decision making and other processes on brief time scales (41, 42), perceptual parameters have not previously been shown directly to undergo random walks, and on time scales as long as several months.

An open question is what drives change in the state variables: visual stimuli (if so, which ones) or internal dynamics. Our results suggest that both factors can drive change: On one hand, state change can be primarily stimulus-driven (cf. the perturbation experiment); on the other hand, state change seems to sometimes occur in total absence of external visual stimulation (the short-term temporal dynamics experiment). Results showing the importance of endogenous (43) and initial (44) perceptual decisions to subsequent cue learning may be germane to these issues.

The continuous presentation of an unchanging ambiguous stimulus (e.g., an SFM or TFM stimulus at a fixed orientation) leads to spontaneous fluctuations between the two interpretations usually every several seconds (15, 16, 18), whereas intermittent presentation leads to a lengthening of the duration of each interpretation up to several minutes, a phenomenon known as sensory memory (17, 19, 20). The main methodological difference between studies of these bistability phenomena and our studies is that we present successive stimuli at different orientations rather than repeating the exact same stimulus. The spontaneous fluctuations found in the bistability studies also exhibit a kind of perceptual state or memory, because successive interpretations are correlated. In experiments 6 and 7, however, we have shown that spontaneous fluctuations do not lead to long-terms changes of the state variables and that the state variables are unlikely to be sensory memories newly formed by exposure to our stimuli. However, state variables may be closely related to the independent and idiosyncratic initial phase of bistable fluctuations, known as onset rivalry (36, 45).

We have demonstrated the existence of two state variables that have the same formal structure and whose instantaneous values are independent (the amplitudes of their changes are weakly but robustly correlated). This raises the question of the universality of this perceptual structure. Recently, the perception of a third family of stimuli—ambiguous one-dimensional apparent motion—has been shown to admit the same kind of biases as studied here (40). Semicircular-shaped biases with individual differences are not limited to vision: An identical structure is found in hearing (46). It is not known whether these other biases show stateful behavior, what their temporal dynamics may be like, and whether they have any correlations with the two variables studied here. It would be interesting to know how many other state variables might there be and if some variables control more than one type of stimulus.

The presence of state in perceptual processes pleads in favor of recurrent neural architectures, which represent state in a natural way (25, 26). Brain imaging studies of the related phenomenon of bistable perception have identified activity in ventro-occipital and intraparietal as well as frontoparietal regions (47–49) correlated to transitions between states. Interestingly, some of the interindividual variability in perceptual dynamics of bistable perception is correlated with local gray-matter density in the parietal cortex (50). It would be interesting to check whether these functional activations or anatomical features are correlated parametrically to the values of the state variables or to their transitions. Another line of research for future studies will be to determine the genetic contributions to individual variations in our state variables, similarly to what has been done for bistable perception (51). If the state variables capture at least some functional aspects of the underlying neural networks, the identification and measurement of these variables may open the door to a psychophysics of neural state.

Methods

Trials typically consisted of twofold ambiguous SFM or TFM stimuli presented at different orientations in random order for 500 ms, after which the participant chose one of the two shape (SFM) or motion (TFM) percepts compatible with the stimulus. Experiments 1 and 3 were performed by participants on their own computers and ran inside internet browsers and were implemented in Javascript and HTML5. Experiments 2 and 4–7 were performed in the laboratory using more traditional methods. For further details, see SI Appendix. Informed consent was obtained prior to all experiments in accordance with the Declaration of Helsinki. In France, the legal ethics committees do not examine non-invasive behavioral studies.