Patient-specific meta-analysis for risk assessment using multivariate proportional hazards regression

Abstract

We propose a method for assessing an individual patient’s risk of a future clinical event using clinical trial or cohort data and Cox proportional hazards regression, combining the information from several studies using meta-analysis techniques. The method combines patient-specific estimates of the log cumulative hazard across studies, weighting by the relative precision of the estimates, using either fixed- or random-effects meta-analysis calculations. Risk assessment can be done for any future patient using a few key summary statistics determined once and for all from each study. Generalizations of the method to logistic regression and linear models are immediate. We evaluate the methods using simulation studies and illustrate their application using real data.

1. Introduction

The concept of meta-analysis dates back to when Fisher [9] proposed a method to combine p-values from several studies to obtain an overall significance test. In addition to hypothesis testing, meta-analyses techniques are used to combine estimates from several studies to get an overall estimate. Examples using clinical trials include the meta-analyses to assess therapeutic benefit performed by the Early Breast Cancer Trialists’ Collaborative Group [8] and the Colorectal Cancer Collaborative Group [4]. Meta-analysis methods have also been applied to risk assessment studies [3,19].

In clinical settings, the inference of standard meta-analysis is to a patient population. However, in the era of personalized medicine, we are often interested in assessing an individual patient’s risk of a particular clinical event or outcome. This objective calls for another approach. The information relevant to the individual patient is likely to vary among studies, depending on the joint distribution of the covariates in each study. Suppose, for example, that we are trying to assess the risk of post-surgical cancer recurrence based on a patient’s tumor grade and tumor size. If the individual patient being assessed has a large tumor, a study having a substantial number of patients with large tumors will be more informative than a study that has primarily smaller tumors.

Hence, when using multiple studies to assess the risk of a clinical event for an individual patient, it is sensible to account for the amount of information that each study provides for the individual. We refer to this method as ‘patient-specific meta-analysis’. We develop the method in Sections 2.1–2.5 for multivariate Cox proportional hazards regression applied to time-to-event data that may be right-censored, with the usual assumption that, conditional on the covariates, censoring is independent of the event time. Generalizations to logistic regression analysis of a binary endpoint and linear models for a continuous numerical outcome are given in Section 2.6. Simulation studies examining the performance of both fixed-effect and random-effect estimators and confidence intervals (CIs) are described in Section 3. The motivation for this work was the development of a multivariate risk assessment tool for the recurrence of breast cancer based on two large studies. The studies and the results of the analysis using methods described here are described in Section 4 and in more detail by Tang et al. [16].

2. Methods

Suppose we wish to estimate the risk that a specific outcome or event occurs by a specified time t₀ for an individual patient with vector of covariates z based on Cox proportional hazards regression [5]. Suppose further that we have a set of K studies of the relevant patient population with time to this event, possibly right-censored, as an endpoint. Denote the study sample sizes by n₁, n₂, …, n_K and the observed covariate vector for patient i = l, 2, …, n_k in study k by ${\mathbf{z}}_i^{(k)}={(z_{i1}^{(k)},z_{i2}^{(k)},\dots ,z_{ip}^{(k)})}^{\mathrm{T}}$. Let β̂_k = (β̂_k1, β̂_k2, …, β̂_kp)^T represent the vector of proportional hazards regression maximum partial likelihood parameter estimates in study k, and let V̂_k be its estimated covariance matrix.

Given a patient with covariate vector z, our approach will be to estimate the patient-specific log cumulative hazard at time t₀ for each study combine the estimates across studies using the meta-analysis principle of weighting each estimate by the inverse of its variance, then transform the result to obtain a risk estimate.

2.1 Estimating the patient-specific log cumulative hazard for each study

Let $Y_i^{(k)}(t)=1$ if patient i in study k is in the risk set at time t and 0 if not, and let N̄^(k)(t) denote the number of events in study k in the interval [0, t]. The Breslow [2] estimator of the baseline cumulative hazard function at time t₀ for study k is 

$${\widehat{\mathrm{\Lambda }}}_0^{(k)}(t_0)={\int }_0^{t_0}\frac{\mathrm{d}{\overline{N}}^{(k)}(t)}{{\sum }_{i=1}^{n_k}{Y}_i^{(k)}(t)exp({\widehat{\mathbf{\beta }}}_k^{\mathrm{T}}{\mathbf{z}}_i^{(k)})},$$

and a consistent estimator of its variance is

$$\widehat{\text{Var}}\{{\widehat{\mathrm{\Lambda }}}_0^{(k)}(t_0)\}={\int }_0^{t_0}\frac{\mathrm{d}{\overline{N}}^{(k)}(t)}{{\left\{{\sum }_{i=1}^{n_k}{Y}_i^{(k)}(t)exp({\widehat{\mathbf{\beta }}}_k^{\mathrm{T}}{\mathbf{z}}_i^{(k)})\right\}}^2}$$

(see [17]). Tsiatis [18] showed that the Breslow estimator and the estimator of its variance are consistent under the mild regularity condition that E_z{z exp(β^Tz)} is uniformly bounded in a neighborhood of β. Now consider an individual patient with covariate vector z. The proportional hazards regression estimator of the cumulative hazard at time t₀ is ${\widehat{\mathrm{\Lambda }}}^{(k)}(t_0;\mathbf{z})=exp({\widehat{\mathbf{\beta }}}_k^{\mathrm{T}}\mathbf{z}){\widehat{\mathrm{\Lambda }}}_0^{(k)}(t_0)$. Tsiatis [18] derived a consistent estimator for the variance of Λ̂^(k)(t₀;z), which can be written as 

$$\widehat{\text{Var}}\{{\widehat{\mathrm{\Lambda }}}^{(k)}(t_0;\mathbf{z})\}=exp(2{\widehat{\mathbf{\beta }}}_k^{\mathrm{T}}\mathbf{z})\{\widehat{\text{Var}}\{{\widehat{\mathrm{\Lambda }}}_0^{(k)}(t_0)\}+{({\widehat{\mathrm{\Lambda }}}_0^{(k)}(t_0)\mathbf{z}-{\mathit{\gamma }}_k)}^{\mathrm{T}}{\widehat{\mathbf{V}}}_k({\widehat{\mathrm{\Lambda }}}_0^{(k)}(t_0)\mathbf{z}-{\mathit{\gamma }}_k)\},$$ (1)

where

$${\mathit{\gamma }}_k={\int }_0^{t_0}\frac{{\sum }_{i=1}^{n_k}{\mathbf{z}}_i^{(k)}{Y}_i^{(k)}(t)exp({\widehat{\mathbf{\beta }}}_k^{\mathrm{T}}{\mathbf{z}}_i^{(k)})\mathrm{d}{\overline{N}}^{(k)}(t)}{{\left\{{\sum }_{i=1}^{n_k}{Y}_i^{(k)}(t)exp({\widehat{\mathbf{\beta }}}_k^{\mathrm{T}}{\mathbf{z}}_i^{(k)})\right\}}^2}$$ (2)

(see Appendix A.1). The log cumulative hazard at time t₀ is estimated consistently by ${\widehat{\rho }}_k(\mathbf{z})=ln{\widehat{\mathrm{\Lambda }}}^{(k)}(t_0;\mathbf{z})=ln{\widehat{\mathrm{\Lambda }}}_0^{(k)}(t_0)+{\widehat{\mathbf{\beta }}}_k^{\mathrm{T}}\mathbf{z}$ and, using the delta method, the variance of the estimate is consistently estimated by

$${\widehat{\sigma }}_k^2(\mathbf{z})=\frac{\widehat{\text{Var}}\{{\widehat{\mathrm{\Lambda }}}^{(k)}(t_0;\mathbf{z})\}}{{\{{\widehat{\mathrm{\Lambda }}}^{(k)}(t_0;\mathbf{z})\}}^2}.$$ (3)

2.2 Meta-analysis combination of the patient-specific estimates

If the available studies can be reasonably assumed to be equal in the background level of risk after having accounted for differences between study populations in the distributions of the covariates (that is, if a study patient with specified covariate values would have the same risk regardless of the study in which the patient participated), we can use the fixed-effects meta-analysis linear combination that weights each study by the inverse-variance of its patient-specific estimate of log cumulative hazard, that is 

$$\widehat{\rho }(\mathbf{z})=\frac{{\sum }_{k=1}^K{\widehat{\rho }}_k(\mathbf{z})/{\widehat{\sigma }}_k^2(\mathbf{z})}{{\sum }_{k=1}^{K}1/{\widehat{\sigma }}_k^2(\mathbf{z})},$$ (4)

which has variance consistently estimated by

$${\widehat{\sigma }}^2(\mathbf{z})=\frac{1}{{\sum }_{k=1}^{K}1/{\widehat{\sigma }}_k^2(\mathbf{z})}.$$ (5)

As shown in, for example, Hedges and Vevea [10], the linear combination (4) minimizes the estimated variance (5). It weights more precise estimates more heavily than less precise ones. Since the survival function is always equal to the exponential of the negative cumulative hazard function, the risk of occurrence of an event by time t₀ is estimated consistently by 

$$\widehat{r}(\mathbf{z})=1-exp[-exp\{\widehat{\rho }(\mathbf{z})\}],$$ (6)

with an asymptotic 100(1 − α)% CI given by 

$$\left(1-exp\left[-exp\left\{\widehat{\rho }(\mathbf{z})-{\mathrm{\Phi }}^{-1}\left(1-\frac{\alpha }{2}\right)\widehat{\sigma }(\mathbf{z})\right\}\right],1-exp\left[-exp\left\{\widehat{\rho }(\mathbf{z})+{\mathrm{\Phi }}^{-1}\left(1-\frac{\alpha }{2}\right)\widehat{\sigma }(\mathbf{z})\right\}\right]\right),$$ (7)

where Φ⁻¹ is the inverse cumulative distribution function of the standard normal distribution.

If we believe that there is a variation among the studies in the level of risk after accounting for the covariates, and if we have a sufficient number of studies to reasonably estimate this inter-study variation, a random-effects meta-analysis estimate of the log cumulative hazard at time t₀ can be derived from the estimates for the individual studies, using the method of Paule and Mandel [12] as adapted by DerSimonian and Kacker [6]. The combined estimate is 

$$\widehat{\rho }(\mathbf{z})=\frac{{\sum }_{k=1}^K{W}_k({\widehat{\tau }}^2(\mathbf{z})){\widehat{\rho }}_k(\mathbf{z})}{{\sum }_{k=1}^K{W}_k({\widehat{\tau }}^2(\mathbf{z}))},$$ (8)

where $W_k({\widehat{\tau }}^2(\mathbf{z}))=1/\{{\widehat{\sigma }}_k^2(\mathbf{z})+{\widehat{\tau }}^2(\mathbf{z})\}$ and τ̂² (z), an estimate of inter-study variability in the log cumulative hazard, is the unique solution to the estimating equation 

$$F({\tau }^2)=\sum _{k=1}^K{W}_k({\tau }^2){\{{\widehat{\rho }}_k(\mathbf{z})-{\rho }_W({\tau }^2)\}}^2-(K-1)=0,$$ (9)

where ${\rho }_W({\tau }^2)={\sum }_{k=1}^K{W}_k({\tau }^2){\widehat{\rho }}_k(\mathbf{z})/{\sum }_{k=1}^K{W}_k({\tau }^2)$. This is essentially the method of moments, the solution τ² = τ̂²(z) being the inter-study variance estimate for which the sum in Equation (9) is equal to the expected value of a chi-square random variable with K − 1 degrees of freedom, which this sum should approximately follow if the weights W_k(τ²) are the true variances of the ρ̂_k(z). The solution to Equation (9) can be found using Newton–Raphson iteration [6]; if the solution is negative, we set τ̂²(z) = 0. Rukhin et al. [15] showed that τ̂²(z) is an approximate restricted maximum likelihood estimator (over the parameter space τ² ≥ 0). We can rewrite Equation (8) as $\widehat{\rho }(\mathbf{z})={\sum }_{k=1}^K{w}_k({\widehat{\tau }}^2(\mathbf{z})){\widehat{\rho }}_k(\mathbf{z})$, where $w_k({\widehat{\tau }}^2(\mathbf{z}))=W_k({\widehat{\tau }}^2(\mathbf{z}))/{\sum }_{j=1}^K{W}_j({\widehat{\tau }}^2(\mathbf{z}))$ are weights that sum to one. The estimator ρ̂(z) is asymptotically normal with variance approximately equal to ${\widehat{\sigma }}_c^2(\mathbf{z})=1/{\sum }_{k=1}^K{W}_k({\widehat{\tau }}^2(\mathbf{z}))$.

However, the variance estimator ${\widehat{\sigma }}_c^2(\mathbf{z})$ does not account for variability in the estimate of inter-study variation τ̂²(z) and thus underestimates the variance of ρ̂(z). Using the second-order delta method, a consistent variance estimator of ρ̂(z) that accounts for the variation in the estimator τ̂²(z) is 

$${\widehat{\sigma }}^2(\mathbf{z})=\frac{1}{{\sum }_{k=1}^K{W}_k({\widehat{\tau }}^2(\mathbf{z}))}+\widehat{\text{Var}}({\widehat{\tau }}^2(\mathbf{z}))D_1^2(\mathbf{z})+\frac{1}{2}{D}_2^2(\mathbf{z}){\{\widehat{\text{Var}}({\widehat{\tau }}^2(\mathbf{z}))\}}^2,$$ (10)

where D₁(z) and D₂(z) are the first and second derivatives of ρ̂(z) with respect to τ̂²(z). Closed form expressions for $\widehat{\text{Var}}({\widehat{\tau }}^2(\mathbf{z}))$, D₁(z) and D₂(z) are given in Equations (A.1)–(A.3) in Appendix A.3.

If the solution to Equation (9) is a negative number, we set $\widehat{\text{Var}}({\widehat{\tau }}^2(\mathbf{z}))=0$. The risk of the event occurring by time t₀ is estimated using Equation (6), with CI given by Equation (7), substituting ρ̂(z) from Equation (8) and σ̂²(z) from Equation (10) into both equations.

2.3 Key summary statistics

The patient-specific meta-analysis risk assessment can be made for any future patient with arbitrary covariate vector z using the following key summary statistics:

1. The baseline cumulative hazard estimates ${\widehat{\mathrm{\Lambda }}}_0^k(t_0)$, k = 1, 2, …, K.

2. The estimated variances of the baseline cumulative hazard estimates $\widehat{\text{Var}}\{{\widehat{\mathrm{\Lambda }}}_0^{(k)}(t_0)\}$.

3. The proportional hazards regression parameter estimate vectors β̂_k and their estimated covariance matrices V̂_k.

4. The vectors γ_k defined by Equation (2).

2.4 Martingale extension estimate of the baseline cumulative hazard

The estimate of the baseline cumulative hazard becomes unstable near the end of patient follow-up when the risk set is small. In case a particular study has few patients followed up through the time t₀ at which we are estimating the risk, we can consider extrapolating the cumulative hazard from a time t_S = t₀ − δ at which patient follow-up is sufficient to produce a reliable Breslow estimate. There are various ways to do this, but if the hazard appears to be constant over time near t_S (as could be assessed by plotting the baseline cumulative hazard estimate as a function of time, as in Figures 1 and 2), a simple way is to assume that the hazard in the interval [t_S, t₀] is the same as the hazard in the interval [t_S − δ, t_S]. An estimate of the baseline cumulative hazard at time t₀ is then given by

Figure 1.

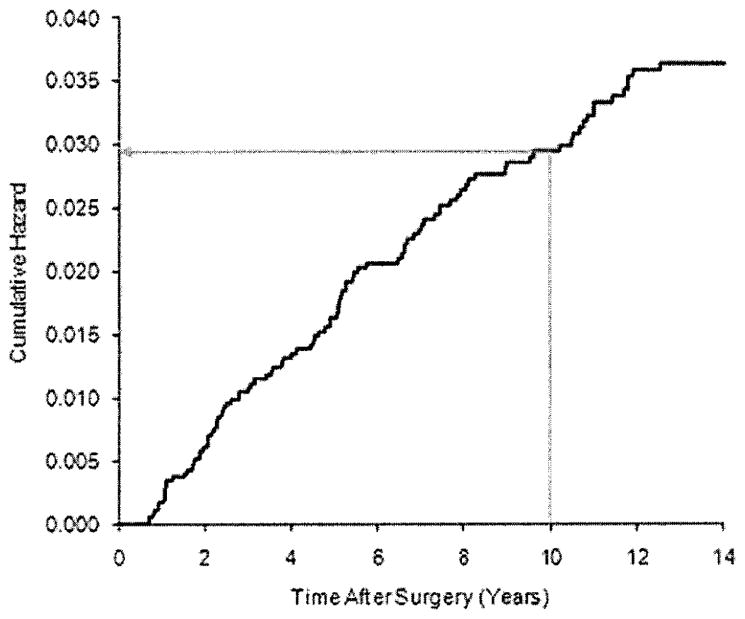
Baseline cumulative hazard estimate for NSABP B-14. The black line is the Breslow baseline hazard function estimate. The arrow shows the estimated cumulative hazard at 10 years.

Figure 2.

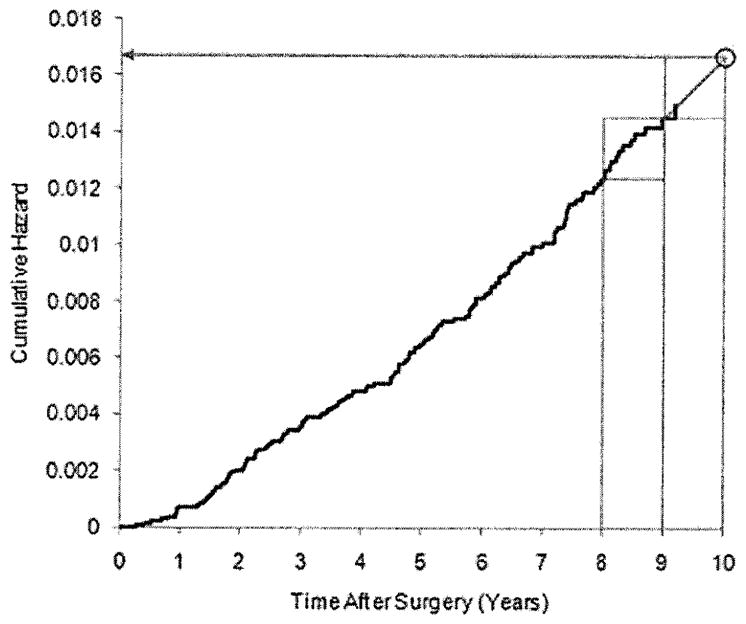
Baseline cumulative hazard estimate for TransATAC. The black line is the Breslow baseline hazard function estimate. The two rectangles in the upper right corner are of identical dimension. The arrow shows the martingale extension estimate of the cumulative hazard at 10 years.

$${\widehat{\mathrm{\Lambda }}}_0^{\ast (k)}(t_0)={\widehat{\mathrm{\Lambda }}}_0^{(k)}(t_S)+\{{\widehat{\mathrm{\Lambda }}}_0^{(k)}(t_S)-{\widehat{\mathrm{\Lambda }}}_0^{(k)}(t_S-\delta )\}={\widehat{\mathrm{\Lambda }}}_0^{(k)}(t_S-\delta )+2\{{\widehat{\mathrm{\Lambda }}}_0^{(k)}(t_S)-{\widehat{\mathrm{\Lambda }}}_0^{(k)}(t_S-\delta )\}.$$

As illustrated in Figure 2, this procedure linearly extends the cumulative hazard function from the estimated value at t_S to time t₀. Using the counting process formulation of survival analysis, we can write

$${\widehat{\mathrm{\Lambda }}}_0^{\ast (k)}(t_0)={\int }_0^{t_S-\delta }\frac{\mathrm{d}{\overline{N}}^{(k)}(t)}{{\sum }_{i=1}^{n_k}{Y}_i^{(k)}(t)exp({\widehat{\mathbf{\beta }}}_k^{\mathrm{T}}{\mathbf{z}}_i^{(k)})}+2{\int }_{t_S-\delta }^{t_S}\frac{\mathrm{d}{\overline{N}}^{(k)}(t)}{{\sum }_{i=1}^{n_k}{Y}_i^{(k)}(t)exp({\widehat{\mathbf{\beta }}}_k^{\mathrm{T}}{\mathbf{z}}_i^{(k)})}.$$

The difference between the right-continuous event counting process N̄^(k)(t) and the cumulative hazard is a martingale over the filtration generated by the histories of the counting process and the at-risk processes $Y_i^{(k)}(t)$, i = 1, 2, …, n [17]. Since martingale increments are uncorrelated, the variance of the cumulative hazard estimate is consistently estimated by

$$\widehat{\text{Var}}\{{\widehat{\mathrm{\Lambda }}}_0^{\ast (k)}(t_0)\}={\int }_0^{t_S-\delta }\frac{\mathrm{d}{\overline{N}}^{(k)}(t)}{{\left\{{\sum }_{i=1}^{n_k}{Y}_i^{(k)}(t)exp({\widehat{\mathbf{\beta }}}_k^{\mathrm{T}}{\mathbf{z}}_i^{(k)})\right\}}^2}+4{\int }_{t_S-\delta }^{t_S}\frac{\mathrm{d}{\overline{N}}^{(k)}(t)}{{\left\{{\sum }_{i=1}^{n_k}{Y}_i^{(k)}(t)exp({\widehat{\mathbf{\beta }}}_k^{\mathrm{T}}{\mathbf{z}}_i^{(k)})\right\}}^2}.$$

The log cumulative hazard at time t₀ can then be estimated by ${\widehat{\rho }}_k(\mathbf{z})=ln{\widehat{\mathrm{\Lambda }}}^{\ast (k)}(t_0;\mathbf{z})=ln{\widehat{\mathrm{\Lambda }}}_0^{\ast (k)}(t_0;\mathbf{z})+{\widehat{\mathbf{\beta }}}_k\mathbf{z}$, with estimated variance ${\widehat{\sigma }}_k^2(\mathbf{z})=\widehat{\text{Var}}\{{\widehat{\mathrm{\Lambda }}}^{\ast (k)}(t_0;\mathbf{z})\}/{\{{\widehat{\mathrm{\Lambda }}}^{\ast (k)}(t_0;\mathbf{z})\}}^2$, where $\widehat{\text{Var}}\{{\widehat{\mathrm{\Lambda }}}^{\ast (k)}(t_0;\mathbf{z})\}=exp(2{\mathbf{\beta }}_k^{\mathrm{T}}\mathbf{z})\{\widehat{\text{Var}}\{{\widehat{\mathrm{\Lambda }}}_0^{\ast (k)}(t_0)\}+{({\widehat{\mathrm{\Lambda }}}_0^{\ast (k)}(t_0)\mathbf{z}-{\mathit{\gamma }}_k^{\ast })}^{\mathrm{T}}{\widehat{\mathbf{V}}}_k({\widehat{\mathrm{\Lambda }}}_0^{\ast (k)}(t_0)\mathbf{z}-{\mathit{\gamma }}_k^{\ast })\}$ and

$${\mathit{\gamma }}_k^{\ast }={\int }_0^{t_S-\delta }\frac{{\sum }_{i=1}^{n_k}{\mathbf{z}}_i^{(k)}{Y}_i^{(k)}(t)exp({\widehat{\mathbf{\beta }}}_k^{\mathrm{T}}{\mathbf{z}}_i^{(k)})\mathrm{d}{\overline{N}}^{(k)}(t)}{{\left\{{\sum }_{i=1}^{n_k}{Y}_i^{(k)}(t)exp({\widehat{\mathbf{\beta }}}_k^{\mathrm{T}}{\mathbf{z}}_i^{(k)})\right\}}^2}+2{\int }_{t_S-\delta }^{t_S}\frac{{\sum }_{i=1}^{n_k}{\mathbf{z}}_i^{(k)}{Y}_i^{(k)}(t)exp({\widehat{\mathbf{\beta }}}_k^{\mathrm{T}}{\mathbf{z}}_i^{(k)})\mathrm{d}{\overline{N}}^{(k)}(t)}{{\left\{{\sum }_{i=1}^{n_k}{Y}_i^{(k)}(t)exp({\widehat{\mathbf{\beta }}}_k^{\mathrm{T}}{\mathbf{z}}_i^{(k)})\right\}}^2}$$

(see Appendix A.2).

2.5 Risk assessment when not all studies have the same patient subpopulations

Until now, we have assumed that all K studies have samples of patients from a common population. We now allow the possibility that some of the K studies also have patients from special subpopulations. For example, if we have a set of cancer studies, all studies might have cancer stage 1 patients, but some studies might have stage 2 patients as well. We will refer to the subpopulation that all the studies have in common as the ‘common subpopulation’ and subpopulations that only some of the studies have as the ‘special subpopulations’.

We can use the data from all the patient subpopulations to estimate the risk for patients in the common subpopulation if we make the following assumption:

Assumption A

Within each study, the multivariate relationship between the covariates and clinical outcome is the same in each of the subpopulations (that is, there is no interaction between the covariates and subpopulation). 

This assumption can be tested in the studies with special subpopulations using a likelihood ratio test comparing a model that allows for covariate-by-subpopulation interaction to one that does not. A meta-analysis test of this assumption can be made by summing the likelihood ratio chi-square statistics across studies and referring the sum to a chi-square distribution with the summed degrees of freedom. If the test of interaction of covariates with subpopulation gives no indication of a violation of Assumption A, we can include patients from all the subpopulations in the meta-analysis calculations using indicator variables that take a value of 0 for patients in the common subpopulation and 1 for patients in the special subpopulations. We then estimate the risk for any specific patient who belongs to one of the common subpopulation by setting all the indicator function values equal to 0.

As long as at least one study enrolled patients from all the subpopulations of interest, we can also make use of all the studies in estimating risk for patients in the special subpopulations if we make the following additional assumption:

Assumption B

If patients from all the subpopulations had been enrolled in all the studies, the hazard for the event in question would have been related to subpopulation the same way in all the studies. 

Assumption B cannot be tested using the data; rather, it must be argued on grounds of clinical and biological considerations, for example, on the basis of study inclusion and exclusion criteria, enrollment period, or patient characteristics. If Assumption B is reasonable, then the risk assessment calculation can be done for patients in the special subpopulations using the key summary statistics described in Section 2.3. Suppose that among the p covariates, there are q that are indicators for special subpopulations and c = p − q that are common to all studies. Let S₁ be the subset of studies that have only the common subpopulation of patients and S₂ be the subset of studies that have one or more special subpopulations, so that S₁ ∪ S₂ = {1, 2, …, K}. Consider a specific patient whose c × 1 vector of the common covariates is z_C and whose vector of indicator variables for the special subpopulations is I = (I₁, I₂, …, I_q)^T. Write the covariate vector as ${\mathbf{z}}^{\mathrm{T}}={({\mathbf{z}}_C^{\mathrm{T}},I_1,I_2,\dots ,I_q)}^{\mathrm{T}}$, where z_C = (z₁, z₂, …, z_c)^T, and define ${\mathbf{z}}_{C0}={({\mathbf{z}}_C^{\mathrm{T}},{\mathbf{0}}_q^{\mathrm{T}})}^{\mathrm{T}}$, where 0_q denotes a q × 1 vector of zeroes. Then, as shown in Appendix A.4, the log cumulative hazard accounting for membership in the special subpopulations as specified by I₁, I₂, …, I_q is consistently estimated by 

$$\widehat{\rho }(\mathbf{z})=\sum _{k\in S_1}{w}_k{\widehat{\rho }}_k({\mathbf{z}}_{C0})+\sum _{k\in S_2}{w}_k{\widehat{\rho }}_k({\mathbf{z}}_k^{†}),$$ (11)

where ${\mathbf{z}}_k^{†}={({\mathbf{z}}_C^{\mathrm{T}},w_k^{†}{I}_1/w_k,w_k^{†}{I}_2/w_k,\dots ,w_k^{†}{I}_q/w_k)}^{\mathrm{T}}$, for the fixed-effects meta-analysis $w_k^{†}=\{1/{\widehat{\sigma }}_k^2({\mathbf{z}}_{C0})\}/{\sum }_{j\in S_2}1/{\widehat{\sigma }}_j^2({\mathbf{z}}_{C0})$ and $w_k=\{1/{\widehat{\sigma }}_k^2({\mathbf{z}}_{C0})\}/{\sum }_{j=1}^{K}1/{\widehat{\sigma }}_j^2({\mathbf{z}}_{C0})$, and for the random-effects meta-analysis

$$w_k^{†}=\frac{1/\{{\widehat{\tau }}^2({\mathbf{z}}_{C0})+{\widehat{\sigma }}_k^2({\mathbf{z}}_{C0})\}}{{\sum }_{j\in S_2}1/\{{\widehat{\tau }}^2({\mathbf{z}}_{C0})+{\widehat{\sigma }}_j^2({\mathbf{z}}_{C0})\}}\text{and}{w}_k=\frac{1/\{{\widehat{\tau }}^2({\mathbf{z}}_{C0})+{\widehat{\sigma }}_k^2({\mathbf{z}}_{C0})\}}{{\sum }_{j=1}^{K}1/\{{\widehat{\tau }}^2({\mathbf{z}}_{C0})+{\widehat{\sigma }}_j^2({\mathbf{z}}_{C0})\}}.$$

Similar to Equations (1) and (3), the variance of ${\widehat{\rho }}_k({\mathbf{z}}_k^{†})$ is consistently estimated by

$${\widehat{\sigma }}_k^2({\mathbf{z}}_k^{†})=\frac{{\mathrm{e}}^{2{\widehat{\mathbf{\beta }}}_k^{\mathrm{T}}}\{\widehat{\text{Var}}\{{\widehat{\mathrm{\Lambda }}}_0^{(k)}(t_0)\}+{({\widehat{\mathrm{\Lambda }}}_0^{(k)}(t_0){\mathbf{z}}_k^{†}-{\mathit{\gamma }}_k)}^{\mathrm{T}}{\widehat{\mathbf{V}}}_k({\widehat{\mathrm{\Lambda }}}_0^{(k)}(t_0){\mathbf{z}}_k^{†}-{\mathit{\gamma }}_k)\}}{{\{{\widehat{\mathrm{\Lambda }}}^{(k)}(t_0;{\mathbf{z}}_k^{†})\}}^2}.$$

For the fixed-effects meta-analysis, the variance of ρ̂(z) is consistently estimated by ${\widehat{\sigma }}^2(\mathbf{z})={\sum }_{k\in S_1}{w}_k^2{\widehat{\sigma }}_k^2({\mathbf{z}}_{C0})+{\sum }_{k\in S_2}{w}_k^2{\widehat{\sigma }}_k^2({\mathbf{z}}_k^{†})$. For the random-effects meta-analysis, without accounting for the variability in τ̂²(z_C0), the variance of ρ̂(z) is approximately ${\widehat{\sigma }}_c^2(\mathbf{z})={\sum }_{k\in S_1}{w}_k^2\{{\widehat{\tau }}^2({\mathbf{z}}_{C0})+{\widehat{\sigma }}_k^2({\mathbf{z}}_{C0})\}+{\sum }_{k\in S_2}{w}_k^2\{{\widehat{\tau }}^2({\mathbf{z}}_{C0})+{\widehat{\sigma }}_k^2({\mathbf{z}}_k^{†})\}$. Accounting for the variability in τ̂²(z_C0) using the second-order delta method gives the estimate 

$${\widehat{\sigma }}^2(\mathbf{z})={\widehat{\sigma }}_c^2(\mathbf{z})+D_1^2(\mathbf{z})\widehat{\text{Var}}({\widehat{\tau }}^2({\mathbf{z}}_{C0}))+\frac{D_2^2(\mathbf{z}){\{\widehat{\text{Var}}({\widehat{\tau }}^2({\mathbf{z}}_{C0}))\}}^2}{2},$$ (12)

where now D₁(z) and D₂(z) are the first and second derivatives of ρ̂(z) with respect to τ̂²(z_C0). Closed form expressions for D₁(z), D₂(z) and $\widehat{\text{Var}}\{{\widehat{\tau }}^2({\mathbf{z}}_{C0})\}$ are given in Equations (A.4)–(A.6) in Appendix A.4.

The risk of an event occurring by time t₀ can be estimated by r̂(z) = 1 − exp[− exp {ρ̂(z)}] with asymptotic 100(1 − α)% CI (1 − exp[− exp{ρ̂(z) − Φ⁻¹(1 − α/2)σ̂(z)}], 1 − exp[− exp{ρ̂(z) + Φ⁻¹(1 − α/2)σ̂(z)}]). When estimating the risk for a patient in the common subpopulation, all of the special subpopulation indicators are 0, so this estimate and its CI reduce to the previous calculations (6) and (7).

2.6 Application to other types of endpoints and analysis methods

Patient-specific meta-analysis methods can be applied in analysis settings other than proportional hazards regression of a time-to-event endpoint.

2.6.1 Logistic regression

For a binary outcome analyzed using multivariate logistic regression, let the log odds estimator from study k for a patient with covariate vector z be denoted by ${\widehat{\rho }}_k(\mathbf{z})={\widehat{\mathbf{\beta }}}_k^{\mathrm{T}}\mathbf{z}$, where z includes the intercept term, and its estimated variance by ${\widehat{\sigma }}_k^2(\mathbf{z})={\mathbf{z}}^{\mathrm{T}}{\widehat{\mathbf{V}}}_k\mathbf{z}$, where V̂_k is the estimated covariance matrix of the regression parameter estimate vector β̂_k. The meta-analysis estimate of the log odds ρ̂(z) and its estimated variance σ̂²(z) are computed from Equation (8). The patient-specific meta-analysis risk estimate is r̂(z) = 1/[1 + exp {−ρ̂(z)}] with level α CI (1/[1 + exp{−ρ̂(z) − Φ⁻¹(1 − α/2)σ̂(z)}], 1/[1 + exp{−ρ̂(z) + Φ⁻¹(1 − α/2)σ̂(z)}]). The key summary statistics needed to estimate the risk for any future patient are each study’s regression parameter estimate vector β̂_k and its estimated covariance matrix V̂_k.

2.6.2 Linear models

For a continuous numeric response variable y analyzed by linear regression or the analysis of covariance, let ${\widehat{y}}_k={\overline{y}}_k+{\widehat{\mathbf{\beta }}}_k^{\mathrm{T}}\mathbf{z}$ be the estimated response variable value for a patient with covariate vector z, where ȳ_k is the mean response variable in study k, with estimated variance ${\widehat{\sigma }}_k^2(\mathbf{z})={\widehat{\sigma }}_{\epsilon }^2/n_k+{(\mathbf{z}-{\overline{\mathbf{z}}}_k)}^{\mathrm{T}}{\widehat{\mathbf{V}}}_k(\mathbf{z}-{\overline{\mathbf{z}}}_k)$, where ${\widehat{\sigma }}_{\epsilon }^2$ is the residual error variance and z̄_k is the mean covariate vector in study k. The patient-specific meta-analysis estimate of the response variable is $\widehat{y}(\mathbf{z})=\{{\sum }_{k=1}^K{\widehat{y}}_k(\mathbf{z})/({\widehat{\sigma }}_k^2(\mathbf{z})+{\widehat{\tau }}^2(\mathbf{z}))\}/{\sum }_{k=1}^{K}1/({\widehat{\sigma }}_k^2(\mathbf{z})+{\widehat{\tau }}^2(\mathbf{z}))$, where τ̂²(z) is estimated as above. A level α CI for y is (ŷ(z) − Φ⁻¹(1 − α/2)σ̂(z), ŷ(z) + Φ⁻¹(1 − α/2)σ̂(z)).

3. Simulation studies

Much of the method derivation above is based on asymptotics. In particular, the delta method estimate of the variance of the meta-analysis estimate accounting for the variability in the inter-study variance estimate τ̂²(z) is asymptotically valid as the number of studies becomes large. There are usually only a few studies in a meta-analysis. Accordingly, we conducted a simulation study to evaluate the performance of the estimates and CIs with smaller sample sizes and numbers of studies.

We simulated data for three covariates z = (z₁, z₂, z₃)^T having a multivariate normal distribution with mean vector μ_z = (0,0,0)^T and covariance matrix

$${\mathbf{\sum }}_{\mathbf{z}}=\left[\begin{array}{ccc}1& -0.3& 0\\ -0.3& 1& -0.3\\ 0& -0.3& 1\end{array}\right].$$

Time-to-event data were simulated using the exponential distribution. The distribution for patient i having simulated covariate vector z_i had intensity parameter (hazard) equal to β^Tz_i, where β = (0.2, −0.3, 0.4)^T. Random censoring of event times was introduced using independent, exponentially distributed censoring times. To achieve specified expected numbers of events N_E with a total sample size N, the intensity parameter for the censoring time distribution was set to λ_C = {(1 − r)/r}λ_E, where r = N_E/N and λ_E is the time-to-event exponential distribution intensity. Tsiatis’ [18] regularity condition for consistency of the Breslow estimator and its variance estimator is clearly satisfied for the multivariate normal covariates (see Appendix A.5). The simulations considered a total of 12 studies with the following expected number of events/total sample sizes (using martingale extension of the specified percentage of time): 100/1000, 70/500 (10%), 80/700, 30/300, 60/600, 80/800 (20%), 40/400, 90/900, 45/550 (10%), 40/350, 75/750 (10%) and 60/650. Simulations were conducted for scenarios of 2–12 studies taken in order from the preceding list.

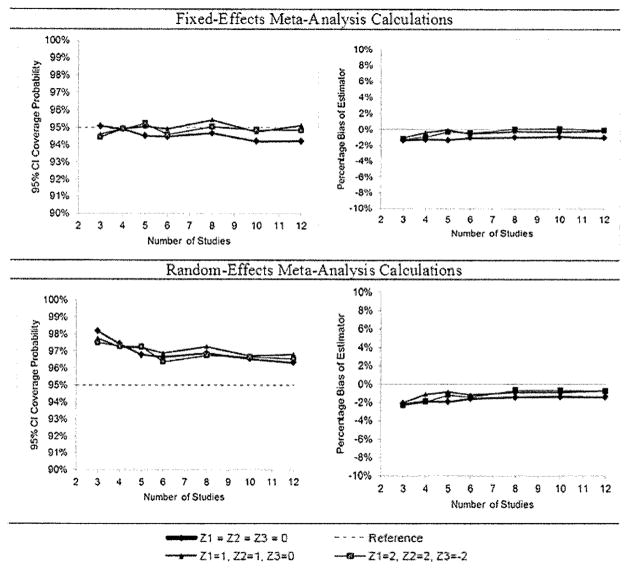
First, 10,000 simulations were performed for each scenario, without inter-study variation in the baseline log hazard. Using both the fixed-effects patient-specific meta-analysis and random-effects patient-specific meta-analysis calculations, we estimated the risk at a specific time for covariate vector values (0,0,0), (1,1,0), and (2,2,−2) and computed 95% CIs. The first vector value is typical of the sampling distribution N(μ_z, Σ_z), with all values at the population mean; the second is unusual, with the values of two covariates each set at 1 standard deviation (SD) above the mean although they are negative correlated; the third is highly unusual. The probability of coverage of the true risk by the 95% CI and the median bias of the estimator as a percentage of the true risk were computed.

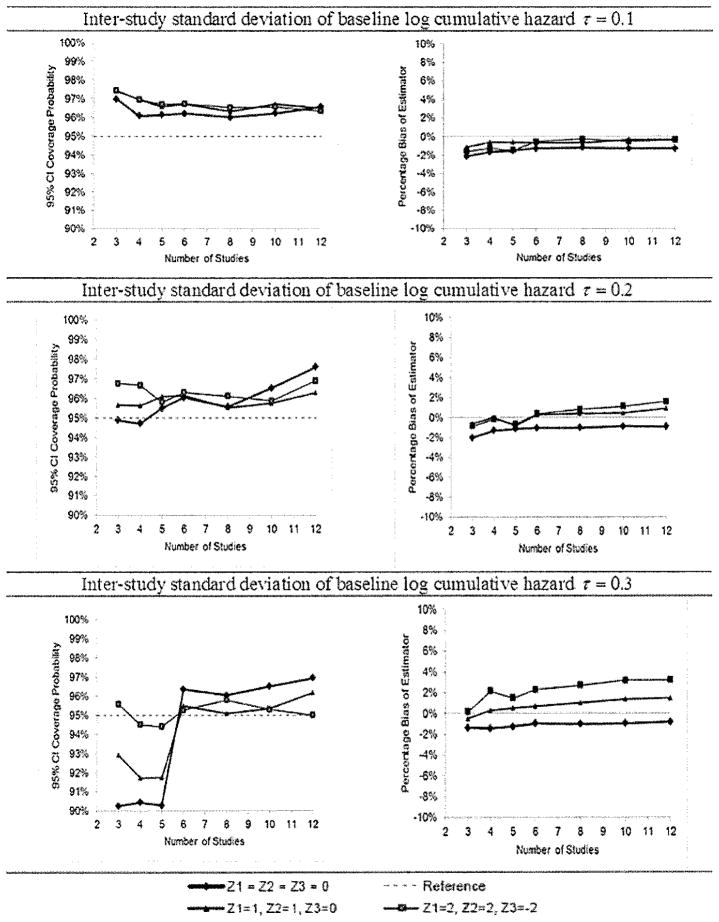
Next, inter-study variation in the log hazard was introduced by adding a normally distributed random variable p_k ~ N(0, τ²) to the baseline log hazard in study k in each iteration of the simulation. We ran 10,000 simulations for τ =0.1, 0.2 and 0.3 and each number of studies. In each iteration, the risk at a specific time was estimated and a 95% CI computed using the random-effects patient-specific meta-analysis, and the coverage probability and median percentage bias of the estimator were computed. The values of τ = 0.1, 0.2 and 0.3 represent 3–4%, 6–9% and 9–13%, respectively, of the true log cumulative hazard at the covariate values (0,0,0), (1,1,0) and (2,2,−2). With 10,000 iterations, the standard error of the estimated coverage probability when the true coverage probability is 95% is 0.2%, so the coverage probability estimates are accurate to within ±0.4% (95% CI).

The results for the simulations without inter-study variation (Figure 3) show coverage probabilities very close to the nominal 95% for the fixed-effects patient-specific meta-analysis calculations and little bias in the estimator (within ±2%). Applying the random-effects patient-specific meta-analysis in this setting gives slightly conservative CIs. Bias is small (again within 2%) and tended to be negative.

Figure 3.

Results of simulation study without inter-study variation. Results for the fixed-effects meta-analysis calculations are in the first row; results for the random-effects meta-analysis calculations are in the second row. Coverage probabilities of 95% CIs (left column) and median bias of the risk estimator as the percentage of the true risk (right column). Simulations for various covariate values, numbers of studies.

In the results for the simulations incorporating inter-study variation (Figure 4), coverage probabilities were close to the nominal 95%, and slightly higher than nominal when inter-study variation was small, when six or more studies were included in the meta-analysis calculations. However, when there were five or fewer studies, coverage probabilities were sometimes notably lower than the nominal value for larger values of inter-study variation. Bias remained within the ±2% range.

Figure 4.

Results of simulation study for random-effect meta-analysis calculations. Coverage probabilities of 95% CIs (left column) and median bias of the risk estimator as the percentage of the true risk (right column) for various covariate values, numbers of studies and amounts of inter-study variation.

4. Example application

We now give an example application of patient-specific meta-analysis methods. In this application, the objective was to estimate individual node-negative, estrogen receptor (ER)-positive breast cancer patients’ risk of distant recurrence of cancer within 10 years after surgery. The covariates were the Oncotype DX^® Recurrence Score^® (RS, a tumor tissue genomic assay), tumor grade (well, moderately or poorly differentiated), tumor size in cm and the patient’s age. These covariates were pre-specified; these were chosen because they are known prognostic factors for breast cancer. Data were available from two studies of RS as a prognostic score in ER-positive breast cancer patients treated with hormonal therapy: National Surgical Adjuvant Breast and Bowel Project (NSABP) clinical trial B-14 [11] and the TransATAC study [7]. The primary endpoint in both studies was time from surgery to distant recurrence of breast cancer. Patients in NSABP B-14 were node-negative (N0) and treated with tamoxifen; patients in TransATAC were randomized to receive either tamoxifen or anastrozole. TransATAC included N0 patients, patients with one to three positive nodes (N1–3) and patients with four or more positive nodes (N4+). There were 102 primary endpoint events among 647 patients from NSABP B-14 and 137 events among 1088 patients from TransATAC. RS was included in the multivariate analysis using a two degree-of-freedom natural spline described by Royston and Parmar [14].

The patient population in this analysis had one common subpopulation consisting of N0 tamoxifen patients, and five special subpopulations: (1) N0 anastrozole patients, (2) N1–3 tamoxifen patients, (3) N1–3 anastrozole patients, (4) N4+ tamoxifen patients and (5) N4+ anastrozole patients. Likelihood ratio tests using the TransATAC data showed no evidence of interaction of either randomized treatment or nodal status with the covariates RS, tumor grade, tumor size or age, so the data from both treatment groups and all three nodal status subpopulations were used in the analysis of TransATAC.

Recurrence risk at 10 years was to be assessed, but patient follow-up in the TransATAC study was limited after 9 years. Therefore, the martingale extension estimate of the baseline cumulative hazard at 10 years for TransATAC was computed, assuming that the hazard between 9 and 10 years was the same as the hazard between 8 and 9 years. The 10-year baseline cumulative hazard estimate for NSABP B-14 is shown in Figure 1; the calculation of the martingale extension estimate at 10 years for TransATAC is shown in Figure 2. The calculation appears reasonable, as the observed hazard is approximately constant starting at 6 years.

Results of the multivariate Cox regression analysis are shown in Table 1. Patient-specific meta-analysis cumulative hazard estimates were computed using the fixed-effects meta-analysis estimator. Estimates of the log cumulative hazard from the individual studies and the patient-specific meta-analysis for hypothetical patients with various covariate values are shown in Table 2. The relative precision of the individual study estimates vary with the covariate values, influencing the weight of each study in the calculation. The precision of the estimate from each study is determined by where the specified patient covariate values fall in the joint distribution of the covariates in each study. Of course, the meta-analysis variance is always lower than the individual study variances. The patient-specific meta-analysis estimate of risk and its CI are also shown in Table 2.

Table 1.

Results of multivariate Cox regression analysis of NSABP B-14 and TransATAC.

Covariate		NSABP B-14 (n = 647)		TransATAC (n = 1088)
		Hazard ratio	Wald test p-value	Hazard ratio	Wald test p-value
RS linear component		5.344 (3Q/1Q)a	<.001	2.766 (3Q/1Q)a	0.020
RS non-linear component
Tumor poorly differentiated		2.845	0.008	2.477	0.012
Tumor moderately differentiated		1.223	0.50	1.625	0.14
Tumor size		1.266 per 1-cm increase	0.006	1.720 per 1-cm increase	<.001
Age at surgery		0.892 per 10-year increase	0.22	0.933 per 10-year increase	0.53
Treatment (anastrozole versus tamoxifen)		–	–	0.886	0.48
1–3 nodes		–	–	1.429	0.083
4+ nodes		–	–	4.548	<.001

Note:

^aHazard ratio for RS expressed in terms of the ratio of the hazards at third and first quartiles of RS (distribution from NSABP B-14), estimated using both the linear and non-linear components.

Table 2.

Patient-specific meta-analysis estimates of log cumulative hazard and risk of distant recurrence at 10 years. Hypothetical patients of age 60.

Tumor grade	Tumor size (cm)	RS	NSABP B-14		TransATAC		Patient-specific meta-analysis
			Log cumulative hazard estimate (variance)	Meta-analysis weight	Log cumulative hazard estimate (variance)	Meta-analysis weight	Log cumulative hazard estimate (variance)	Risk estimate (95% CI)
Well	2	24	−2.179 (0.076)	60.8%	−2.390 (0.117)	39.2%	−2.262 (0.046)	9.9% (6.6%, 14.7%)
Well	4	40	−1.447 (0.112)	60.1%	−0.846 (0.169)	39.9%	−1.207 (0.067)	25.9% (16.5%, 39.2%)
Moderate	2	9	−2.841 (0.070)	42.4%	−2.520 (0.051)	57.6%	−2.656 (0.030)	6.8% (4.9%, 9.4%)
Poor	4	40	−0.401 (0.051)	58.8%	0.061 (0.073)	41.2%	−0.211 (0.030)	55.5% (43.8%, 68.0%)
Poor	0.5	40	−1.226 (0.071)	44.5%	−1.836 (0.057)	55.5%	−1.565 (0.031)	18.9% (13.7%, 25.6%)
Poor	4	9	−1.525 (0.105)	50.8%	−1.014 (0.108)	49.2%	−1.273 (0.053)	24.4% (16.3%, 35.6%)

Note: Hypothetical patients of age 60.

Assumption B (Section 2.5) seemed reasonable for the relative efficacy of tamoxifen versus anastrozole treatment based on the similarity between studies of the enrollment criteria and patient population characteristics. In particular, since both studies were in early stage, ER-receptor positive breast cancer, it seemed reasonable that if eligible B-14 patients had been randomized to anastrozole or tamoxifen, a similar treatment effect would have been observed in B-14 and TransATAC. Accordingly, the risk of distant recurrence was estimated for some hypothetical N0 patients with planned anastrozole treatment. The results, including a comparison to the risk assessment with planned tamoxifen treatment, are shown in Table 3. The CIs with anastrozole treatment are slightly wider than with tamoxifen treatment since in total there are fewer anastrozole- than tamoxifen-treated patients, and thus less information for the risk assessment.

Table 3.

Patient-specific meta-analysis risk estimates for hypothetical node-negative patients of age 50 with moderately differentiated tumors treated with tamoxifen or anastrozole.

Tumor size (cm)	RS	Tamoxifen		Anastrozole
		Risk estimate	95% CI	Risk estimate	95% CI
0.5	9	4.1%	(2.7%, 6.1%)	3.6%	(2.3%, 5.8%)
	24	8.5%	(6.1%, 11.8%)	7.5%	(5.0%, 11.4%)
	40	11.8%	(8.4%, 16.5%)	10.6%	(6.9%, 16.0%)
2	9	7.2%	(5.0%, 10.3%)	6.4%	(4.2%, 9.8%)
	24	14.5%	(11.1%, 18.9%)	13.0%	(8.9%, 18.7%)
	40	19.8%	(15.1%, 25.8%)	17.8%	(12.2%, 25.5%)
4	9	14.8%	(9.8%, 21.9%)	13.2%	(8.2%, 20.8%)
	24	27.1%	(19.7%, 36.5%)	24.4%	(16.3%, 35.6%)
	40	35.5%	(26.2%, 47.0%)	32.2%	(21.8%, 46.0%)

5. Discussion

The simulation results suggest that the random-effects meta-analysis calculation based on asymptotics can be safely used if there are at least six studies in the analysis. With five or fewer, the coverage probabilities may be lower than nominal for some covariate values if inter-study variation is substantial.

We used all the available studies in early stage ER-positive breast cancer that had the end-point distant recurrence, the specified covariates and sufficient endpoint events to support the multivariate analysis (at least 10 events per covariate). As with any meta-analysis, using all available relevant studies helps to reduce bias. We kept all the pre-specified covariates in the model for each study, even though some were not statistically significant when the models were fit to the study data. Retaining all the pre-specified covariates produces valid CIs and generally more accurate predictions than dropping non-significant covariates or using step-wise selection procedures [1,13].

We prefer to use log cumulative hazard estimates for proportional hazards regression (or log odds ratio estimates for logistic regression) rather than risk estimates for the inverse-variance meta-analysis calculation because the variance of the log cumulative hazard estimators does not depend on the value of the estimate. The risk estimator’s variance does depend on the value of the risk estimate, so the inverse-variance principle would inappropriately weight small risk estimates more heavily than large ones, producing a biased estimate.

Access to the full data set from each study is not required to perform the patient-specific meta-analysis calculations: the key summary statistics listed in Section 2.3 suffice for proportional hazards regression (as do those listed in Section 2.6.1 for logistic regression and Section 2.6.2 for linear models). However, because not all these statistics are commonly reported in the literature, a limitation of the patient-specific meta-analysis method is that it normally requires the cooperation of the owners of the data from the various studies in order to compute the key summary statistics. No pooling of study data is required, though, as the summary statistics are computed separately for each study. Once calculated, the key statistics can be used to compute the patient-specific meta-analysis risk estimate for any future patient without recourse to the original study data.

Although the calculations could be done, the effectiveness of these method for assessing risk would be diminished if the same important prognostic covariates were not available across all the studies used in the patient-specific meta-analysis (apart from indicators for special populations as discussed in Section 2.5). We recommend using these methods primarily when the same covariates are available across all the studies.

Finally, although we have developed the patient-specific meta-analysis method for risk assessment, the same methodology can be used to construct patient-specific meta-analysis estimates of any asymptotically normally distributed quantity assessed across several studies. For example, the magnitude of a treatment effect in an individual patient as measured by, depending on the endpoint, a treatment effect log hazard ratio from a proportional hazards regression, a treatment effect log odds ratio from a logistic regression or a treatment effect estimated from a linear model, could be estimated using patient-specific meta-analysis. The key principle of combining estimates across studies based on the amount of patient-specific information in each study still applies.

Appendix

A.1 Asymptotic variance of Λ̂^(k) (t₀; z)

Tsiatis’s [18] consistent estimate of the variance of the estimated cumulative hazard Λ̂^(k) (z; t₀) for an individual patient with covariate vector z is

$$\widehat{\text{Var}}\{{\widehat{\mathrm{\Lambda }}}^{(k)}(t_0;\mathbf{z})\}=exp(2{\widehat{\mathbf{\beta }}}_k^{\mathrm{T}}\mathbf{z})\widehat{\text{Var}}\{{\widehat{\mathrm{\Lambda }}}_0^{(k)}(t_0)\}+{\mathbf{q}}_k^{\mathrm{T}}{\widehat{\mathbf{V}}}_k{\mathbf{q}}_k,$$

where

$${\mathbf{q}}_k=exp({\widehat{\mathbf{\beta }}}_k^{\mathrm{T}}\mathbf{z}){\int }_0^{t_0}\{\mathbf{z}-{\overline{\mathbf{z}}}^{(k)}(t)\}\frac{\mathrm{d}{\overline{N}}^{(k)}(t)}{{\sum }_{i=1}^{n_k}{Y}_i^{(k)}(t)exp({\widehat{\mathbf{\beta }}}_k^{\mathrm{T}}{\mathbf{z}}_i^{(k)})}$$

and ${\overline{\mathbf{z}}}^{(k)}(t)={\sum }_{i=1}^{n_k}{\mathbf{z}}_i^{(k)}{Y}_i^{(k)}(t)exp({\widehat{\mathbf{\beta }}}_k^{\mathrm{T}}{\mathbf{z}}_i^{(k)})/{\sum }_{i=1}^{n_k}{Y}_i^{(k)}(t)exp({\widehat{\mathbf{\beta }}}_k^{\mathrm{T}}{\mathbf{z}}_i^{(k)})$. Defining

$${\mathit{\gamma }}_k={\int }_0^{t_0}\frac{{\sum }_{i=1}^{n_k}{\mathbf{z}}_i^{(k)}{Y}_i^{(k)}(t)exp({\widehat{\mathbf{\beta }}}_k^{\mathrm{T}}{\mathbf{z}}_i^{(k)})\mathrm{d}{\overline{N}}^{(k)}(t)}{{\left\{{\sum }_{i=1}^{n_k}{Y}_i^{(k)}(t)exp({\widehat{\mathbf{\beta }}}_k^{\mathrm{T}}{\mathbf{z}}_i^{(k)})\right\}}^2},$$

the vector q_k can be rewritten as

$$\begin{array}{l}{\mathbf{q}}_k=exp({\widehat{\mathbf{\beta }}}_k^{\mathrm{T}}\mathbf{z})\left\{\mathbf{z}{\int }_0^{t_0}\frac{\mathrm{d}{\overline{N}}^{(k)}(t)}{{\sum }_{i=1}^{n_k}{Y}_i^{(k)}(t)exp({\widehat{\mathbf{\beta }}}_k^{\mathrm{T}}{\mathbf{z}}_i^{(k)})}-{\int }_0^{t_0}\frac{\overline{\mathbf{z}}(t)\mathrm{d}{\overline{N}}^{(k)}(t)}{{\sum }_{i=1}^{n_k}{Y}_i^{(k)}(t)exp({\widehat{\mathbf{\beta }}}_k^{\mathrm{T}}{\mathbf{z}}_i^{(k)})}\right\}\\ =exp({\widehat{\mathbf{\beta }}}_k^{\mathrm{T}}\mathbf{z})\left[{\widehat{\mathrm{\Lambda }}}_0^{(k)}(t_0)\mathbf{z}-{\int }_0^{t_0}\frac{{\sum }_{i=1}^{n_k}{\mathbf{z}}_i^{(k)}{Y}_i^{(k)}(t)exp({\widehat{\mathbf{\beta }}}_k^{\mathrm{T}}{\mathbf{z}}_i^{(k)})\mathrm{d}{\overline{N}}^{(k)}(t)}{{\left\{{\sum }_{i=1}^{n_k}{Y}_i^{(k)}(t)exp({\widehat{\mathbf{\beta }}}_k^{\mathrm{T}}{\mathbf{z}}_i^{(k)})\right\}}^2}\right]=exp({\widehat{\mathbf{\beta }}}_k^{\mathrm{T}}\mathbf{z})\{{\widehat{\mathrm{\Lambda }}}_0^{(k)}(t_0)\mathbf{z}-{\mathit{\gamma }}_k\}.\end{array}$$

Thus we have

$$\widehat{\text{Var}}\{{\widehat{\mathrm{\Lambda }}}^{(k)}(t_0;\mathbf{z})\}=exp(2{\widehat{\mathbf{\beta }}}_k^{\mathrm{T}}\mathbf{z})\{\widehat{\text{Var}}\{{\widehat{\mathrm{\Lambda }}}_0^{(k)}(t_0)\}+{({\widehat{\mathrm{\Lambda }}}_0^{(k)}(t_0)\mathbf{z}-{\mathit{\gamma }}_k)}^{\mathrm{T}}{\widehat{\mathbf{V}}}_k({\widehat{\mathrm{\Lambda }}}_0^{(k)}(t_0)\mathbf{z}-{\mathit{\gamma }}_k)\},$$

which is Equation (1).

A.2 Asymptotic variance of the martingale extension estimate Λ̂*^(k) (t₀; z)

Using the martingale extension estimate ${\widehat{\mathrm{\Lambda }}}_0^{\ast (k)}(t_0)={\mathrm{\Lambda }}_0^{(k)}(t_S-\delta )+2\{{\widehat{\mathrm{\Lambda }}}_0^{(k)}(t_S)-{\widehat{\mathrm{\Lambda }}}_0^{(k)}(t_{S-\delta })\}$, the variance of Λ̂*^(k) (t₀; z) is estimated consistently by

$$\widehat{\text{Var}}\{{\widehat{\mathrm{\Lambda }}}^{\ast (k)}(t_0;\mathbf{z})\}=exp(2{\widehat{\mathbf{\beta }}}_k^{\mathrm{T}}\mathbf{z})\widehat{\text{Var}}\{{\widehat{\mathrm{\Lambda }}}_0^{\ast (k)}(t_0)\}+{\mathbf{q}}_k^{\ast \mathrm{T}}{\widehat{\mathbf{V}}}_k{\mathbf{q}}_k^{\ast },$$

where

$${\mathbf{q}}_k^{\ast }=exp(2{\widehat{\mathbf{\beta }}}_k^{\mathrm{T}}\mathbf{z})\{{\int }_0^{t_S-\delta }[\mathbf{z}-{\overline{\mathbf{z}}}^{(k)}(t)]\frac{\mathrm{d}{\overline{N}}^{(k)}(t)}{{\sum }_{i=1}^{n_k}{Y}_i^{(k)}(t)exp({\widehat{\mathbf{\beta }}}_k^{\mathrm{T}}{\mathbf{z}}_i^{(k)})}+2{\int }_{t_S-\delta }^{t_S}[\mathbf{z}-{\overline{\mathbf{z}}}^{(k)}(t)]\frac{\mathrm{d}{\overline{N}}^{(k)}(t)}{{\sum }_{i=1}^{n_k}{Y}_i^{(k)}(t)exp({\widehat{\mathbf{\beta }}}_k^{\mathrm{T}}{\mathbf{z}}_i^{(k)})}\}=exp({\widehat{\mathbf{\beta }}}_k^{\mathrm{T}}\mathbf{z})\{{\widehat{\mathrm{\Lambda }}}_0^{\ast (k)}(t_0)\mathbf{z}-{\mathit{\gamma }}_k^{\ast }\}$$

and

$${\mathit{\gamma }}_k^{\ast }={\int }_0^{t_S-\delta }\frac{{\sum }_{i=1}^{n_k}{\mathbf{z}}_i^{(k)}{Y}_i^{(k)}(t)exp({\widehat{\mathbf{\beta }}}_k^{\mathrm{T}}{\mathbf{z}}_i^{(k)})\mathrm{d}{\overline{N}}^{(k)}(t)}{{\left\{{\sum }_{i=1}^{n_k}{Y}_i^{(k)}(t)exp({\widehat{\mathbf{\beta }}}_k^{\mathrm{T}}{\mathbf{z}}_i^{(k)})\right\}}^2}+2{\int }_{t_S-\delta }^{t_S}\frac{{\sum }_{i=1}^{n_k}{\mathbf{z}}_i^{(k)}{Y}_i^{(k)}(t)exp({\widehat{\mathbf{\beta }}}_k^{\mathrm{T}}{\mathbf{z}}_i^{(k)})\mathrm{d}{\overline{N}}^{(k)}(t)}{{\left\{{\sum }_{i=1}^{n_k}{Y}_i^{(k)}(t)exp({\widehat{\mathbf{\beta }}}_k^{\mathrm{T}}{\mathbf{z}}_i^{(k)})\right\}}^2}.$$

A.3 Estimate σ̂²(z) of variance of patient-specific meta-analysis estimate ρ̂(z) accounting for variation in the estimate of inter-study variability τ̂²(z)

The partial derivative of the objective function F with respect to ρ̂_k(z) is

$$\frac{\partial F({\tau }^2)}{\partial {\widehat{\rho }}_k(\mathbf{z})}=2W_k({\tau }^2)\{{\widehat{\rho }}_k(\mathbf{z})-{\rho }_W(\mathbf{z})\}\left(1-\frac{W_k({\tau }^2)}{{\sum }_{j=1}^K{W}_j({\tau }^2)}\right).$$

Since the ρ̂_k(z) are stochastically independent of each other, we can apply the delta method to estimate the variance of F(τ̂²(z)) by

$$\begin{array}{l}\widehat{\text{Var}}\{F({\widehat{\tau }}^2(\mathbf{z}))\}=\sum _{k=1}^K{\left\{\frac{\partial F({\widehat{\tau }}^2(\mathbf{z}))}{\partial {\widehat{\rho }}_k(\mathbf{z})}\right\}}^2{\widehat{\sigma }}_k^2(\mathbf{z})\\ =4\sum _{k=1}^K{\left\{\frac{W_k({\widehat{\tau }}^2(\mathbf{z})){\sum }_{j\ne k}{W}_j({\widehat{\tau }}^2(\mathbf{z}))}{{\sum }_{j=1}^K{W}_j({\widehat{\tau }}^2(\mathbf{z}))}\right\}}^2{\{{\widehat{\rho }}_k(\mathbf{z})-{\rho }_W(\mathbf{z})\}}^2\{{\widehat{\sigma }}_k^2(\mathbf{z})+{\widehat{\tau }}^2(\mathbf{z})\}.\end{array}$$

Rukhin et al. [15] showed that the derivative of the objective function F(τ²) with respect to τ² is $F^{\prime }({\tau }^2)=-{\sum }_{k-1}^K{\{W_k({\tau }^2)\}}^2{\{{\widehat{\rho }}_k(\mathbf{z})-{\rho }_W({\tau }^2)\}}^2$. Since τ̂²(z) is the solution to F(τ²) = 0, a consistent estimate of the variance of τ̂²(z) is thus given by

$$\begin{array}{l}\widehat{\text{Var}}\{{\widehat{\tau }}^2(\mathbf{z})\}=\frac{\widehat{\text{Var}}\{F({\widehat{\tau }}^2(\mathbf{z}))\}}{{\{F^{\prime }({\widehat{\tau }}^2(\mathbf{z}))\}}^2}\\ =\frac{4{\sum }_{k=1}^K{\{W_k({\widehat{\tau }}^2(\mathbf{z})){\sum }_{j\ne k}{W}_j({\widehat{\tau }}^2(\mathbf{z}))/{\sum }_{j=1}^K{W}_j({\widehat{\tau }}^2(\mathbf{z}))\}}^2{\{{\widehat{\rho }}_k(\mathbf{z})-\widehat{\rho }(\mathbf{z})\}}^2\{{\widehat{\sigma }}_k^2(\mathbf{z})+{\widehat{\tau }}^2(\mathbf{z})\}}{{\left[{\sum }_{k=1}^K{\{W_k({\widehat{\tau }}^2(\mathbf{z}))\}}^2{\{{\widehat{\rho }}_k(\mathbf{z})-\widehat{\rho }(\mathbf{z})\}}^2\right]}^2}.\end{array}$$

If we obtain τ̂²(z) = 0 because the solution of the estimating equation is a negative number, we set $\widehat{\text{Var}}\{{\widehat{\tau }}^2(\mathbf{z})\}=0$. The first derivative of ρ̂(z) with respect to the estimate τ̂²(z) is

$$\begin{array}{l}{D}_1(\mathbf{z})=\frac{-{\sum }_{k=1}^K\frac{1}{{\widehat{\sigma }}_k^2(\mathbf{z})+{\widehat{\tau }}^2(\mathbf{z})}{\sum }_{k=1}^K\frac{{\widehat{\rho }}_k(\mathbf{z})}{{\{{\widehat{\sigma }}_k^2(\mathbf{z})+{\widehat{\tau }}^2(\mathbf{z})\}}^2}+{\sum }_{k=1}^K\frac{{\widehat{\rho }}_k(\mathbf{z})}{{\widehat{\sigma }}_k^2(\mathbf{z})+{\widehat{\tau }}^2(\mathbf{z})}{\sum }_{k=1}^K\frac{1}{{\{{\widehat{\sigma }}_k^2(\mathbf{z})+{\widehat{\tau }}^2(\mathbf{z})\}}^2}}{{\left\{{\sum }_{k=1}^K(1/({\widehat{\sigma }}_k^2(\mathbf{z})+{\widehat{\tau }}^2(\mathbf{z})))\right\}}^2}\\ =\frac{\left\{{\sum }_{k=1}^K{W}_k({\widehat{\tau }}^2(\mathbf{z})){\widehat{\rho }}_k(\mathbf{z}){\sum }_{k=1}^K{W}_k^2({\widehat{\tau }}^2(\mathbf{z}))-{\sum }_{k=1}^K{W}_k({\widehat{\tau }}^2(\mathbf{z})){\sum }_{k=1}^K{W}_k^2({\widehat{\tau }}^2(\mathbf{z})){\widehat{\rho }}_k(\mathbf{z})\right\}}{{\left\{{\sum }_{k=1}^K{W}_k({\widehat{\tau }}^2(\mathbf{z}))\right\}}^2}\\ =\frac{\left\{\widehat{\rho }(\mathbf{z}){\sum }_{k=1}^K{W}_k^2({\widehat{\tau }}^2(\mathbf{z}))-{\sum }_{k=1}^K{W}_k^2({\widehat{\tau }}^2(\mathbf{z})){\widehat{\rho }}_k(\mathbf{z})\right\}}{{\sum }_{k=1}^K{W}_k({\widehat{\tau }}^2(\mathbf{z}))}\\ =\frac{{\sum }_{k=1}^K{W}_k^2({\widehat{\tau }}^2(\mathbf{z}))\left\{\widehat{\rho }(\mathbf{z})-{\widehat{\rho }}_k(\mathbf{z})\right\}}{{\sum }_{k=1}^K{W}_k({\widehat{\tau }}^2(\mathbf{z}))}.\end{array}$$

Dropping, for the moment, the indications of dependence on z and τ̂(z), rewrite D₁ as

$$D_1=\frac{\widehat{\rho }{\sum }_{k=1}^K{W}_k^2}{{\sum }_{k=1}^K{W}_k}-\frac{{\sum }_{k=1}^K{W}_k^2{\widehat{\rho }}_k}{{\sum }_{k=1}^K{W}_k}.$$

The second derivative of ρ̂ is thus

$$\begin{array}{l}{D}_2=D_1\frac{{\sum }_{k=1}^K{W}_k^2}{{\sum }_{k=1}^K{W}_k}+\widehat{\rho }\frac{{\sum }_{k=1}^K{W}_k{\sum }_{k=1}^K(-2)W_k^3-{\sum }_{k=1}^K{W}_k^2{\sum }_{k=1}^K(-1)W_k^2}{{\left\{{\sum }_{k=1}^K{W}_k\right\}}^2}-\frac{{\sum }_{k=1}^K{W}_k{\sum }_{k=1}^K(-2)W_k^3{\widehat{\rho }}_k-{\sum }_{k=1}^K{W}_k^2{\widehat{\rho }}_k{\sum }_{k=1}^K(-1)W_k^2}{{\left\{{\sum }_{k=1}^K{W}_k\right\}}^2}\\ =-\frac{{\sum }_{k=1}^K{W}_k^2({\widehat{\rho }}_k-\widehat{\rho })}{{\sum }_{k=1}^K{W}_k}\frac{{\sum }_{k=1}^K{W}_k^2}{{\sum }_{k=1}^K{W}_k}-\frac{{\sum }_{k=1}^K{W}_k^2({\widehat{\rho }}_k-\widehat{\rho }){\sum }_{k=1}^K{W}_k^2-2{\sum }_{k=1}^K{W}_k{\sum }_{k=1}^K{W}_k^3({\widehat{\rho }}_k-\widehat{\rho }){\sum }_{k=1}^K{W}_k}{{\left\{{\sum }_{k=1}^K{W}_k\right\}}^2}\\ =2\frac{{\sum }_{k=1}^K{W}_k^2(\widehat{\rho }-{\widehat{\rho }}_k){\sum }_{k=1}^K{W}_k^2-{\sum }_{k=1}^K{W}_k^3(\widehat{\rho }-{\widehat{\rho }}_k){\sum }_{k=1}^K{W}_k}{{\left\{{\sum }_{k=1}^K{W}_k\right\}}^2}.\end{array}$$

We will assume that the distribution of τ̂², which is the solution to the estimating Equation (9) in the main text, is approximately normal. Using the second-order Taylor expansion of ρ̂ as a function of τ̂² about the true inter-study variance τ²

$$\widehat{\rho }({\widehat{\tau }}^2)\doteq \widehat{\rho }({\tau }^2)+({\widehat{\tau }}^2-\tau )D_1({\tau }^2)+\frac{{({\widehat{\tau }}^2-\tau )}^2{D}_2({\tau }^2)}{2},$$

the variance of ρ̂ due to the variability of the estimator τ̂² can be approximated by

$$\text{Var}\left\{({\widehat{\tau }}^2-{\tau }^2)D_1+\frac{{({\widehat{\tau }}^2-{\tau }^2)}^2{D}_2}{2}\right\}=E{\left\{({\widehat{\tau }}^2-{\tau }^2)D_1+\frac{{({\widehat{\tau }}^2-{\tau }^2)}^2{D}_2}{2}\right\}}^2-{\left[E\left\{({\widehat{\tau }}^2-{\tau }^2)D_1+\frac{{({\widehat{\tau }}^2-{\tau }^2)}^2{D}_2}{2}\right\}\right]}^2.$$

By the symmetry of the normal distribution, and since the kurtosis of a normal variate with variance σ² is 3σ⁴, this equals

$$\begin{array}{l}E\{{({\widehat{\tau }}^2-{\tau }^2)}^2\}{D}_1^2({\tau }^2)+\frac{E\{{({\widehat{\tau }}^2-{\tau }^2)}^4\}{D}_2^2({\tau }^2)}{4}-{\left[\frac{E\{{({\widehat{\tau }}^2-{\tau }^2)}^2\}{D}_2({\tau }^2)}{2}\right]}^2=D_1^2({\tau }^2)\text{Var}({\widehat{\tau }}^2)+\left(\frac{3}{4}\right)D_2^2({\tau }^2){\{\text{Var}({\widehat{\tau }}^2)\}}^2-\left(\frac{1}{4}\right)D_2^2({\tau }^2){\{\text{Var}({\widehat{\tau }}^2)\}}^2\\ =D_1^2({\tau }^2)\text{Var}({\widehat{\tau }}^2)+\frac{D_2^2({\tau }^2){\{\text{Var}({\widehat{\tau }}^2)\}}^2}{2}.\end{array}$$

Approximating the first and second derivatives D₁ and D₂ by their values at τ̂², we have the delta method approximation

$$D_1^2({\widehat{\tau }}^2)\widehat{\text{Var}}({\widehat{\tau }}^2)+\frac{D_2^2({\widehat{\tau }}^2){\{\widehat{\text{Var}}({\widehat{\tau }}^2)\}}^2}{2}$$

for the portion of the variance of ρ̂ that is due to the variability in the estimate τ̂².

Since τ̂²(z) is the estimator of inter-study variation, it is asymptotically uncorrelated with the estimator of the mean value ρ̂(z). Hence, applying the delta method, we can estimate the variance of ρ̂(z) accounting for the variation in the estimate τ̂²(z) by

$${\widehat{\sigma }}^2(\mathbf{z})={\widehat{\sigma }}_c^2(\mathbf{z})+\widehat{\text{Var}}({\widehat{\tau }}^2(\mathbf{z}))D_1^2(\mathbf{z})+\frac{D_2^2(\mathbf{z}){\{\widehat{\text{Var}}({\widehat{\tau }}^2(\mathbf{z}))\}}^2}{2},$$

which is Equation (10). From the derivations above, we have

$$\widehat{\text{Var}}({\widehat{\tau }}^2(\mathbf{z}))=\frac{4{\sum }_{k=1}^K{\left\{W_k({\widehat{\tau }}^2(\mathbf{z})){\sum }_{j\ne k}{W}_j({\widehat{\tau }}^2(\mathbf{z}))/{\sum }_{j=1}^K{W}_j({\widehat{\tau }}^2(\mathbf{z}))\right\}}^2{\{{\widehat{\rho }}_k(\mathbf{z})-\widehat{\rho }(\mathbf{z})\}}^2\{{\widehat{\sigma }}_k^2(\mathbf{z})+{\widehat{\tau }}^2(\mathbf{z})\}}{{\left[{\sum }_{k=1}^K{\{W_k({\widehat{\tau }}^2(\mathbf{z}))\}}^2{\{{\widehat{\rho }}_k(\mathbf{z})-\widehat{\rho }(\mathbf{z})\}}^2\right]}^2},$$ (A.1)

$$D_1(\mathbf{z})=\frac{{\sum }_{k=1}^K{W}_k^2({\widehat{\tau }}^2(\mathbf{z}))\{\widehat{\rho }(\mathbf{z})-{\widehat{\rho }}_k(\mathbf{z})\}}{{\sum }_{k=1}^K{W}_k({\widehat{\tau }}^2(\mathbf{z}))}$$ (A.2)

and

$$D_2(\mathbf{z})=\frac{2\left\{{\sum }_{k=1}^K{W}_k^2({\widehat{\tau }}^2(\mathbf{z}))(\widehat{\rho }(\mathbf{z})-{\widehat{\rho }}_k(\mathbf{z})){\sum }_{k=1}^K{W}_k^2({\widehat{\tau }}^2(\mathbf{z}))-{\sum }_{k=1}^K{W}_k^3({\widehat{\tau }}^2(\mathbf{z}))(\widehat{\rho }(\mathbf{z})-{\widehat{\rho }}_k(\mathbf{z})){\sum }_{k=1}^K{W}_k({\widehat{\tau }}^2(\mathbf{z}))\right\}}{{\left\{{\sum }_{k=1}^K{W}_k({\widehat{\tau }}^2(\mathbf{z}))\right\}}^2}.$$ (A.3)

A.4 Risk assessment when not all studies have the same patient subpopulations

Write the covariate vector as ${\mathbf{z}}^{\mathrm{T}}={({\mathbf{z}}_C^{\mathrm{T}},I_1,I_2,\dots ,I_q)}^{\mathrm{T}}$ where z_C = (z₁, z₂, …, z_c)^T, and decompose the regression parameter estimate vector β̂_k for study k into ${\widehat{\mathbf{\beta }}}_k={({\widehat{\mathbf{\beta }}}_C^{(k)\mathrm{T}},{\mathbf{0}}_q^{\mathrm{T}})}^{\mathrm{T}}$ for k ∈ S₁ and ${\widehat{\mathbf{\beta }}}_k={({\widehat{\mathbf{\beta }}}_C^{(k)\mathrm{T}},{\widehat{\mathbf{\beta }}}_S^{(k)\mathrm{T}})}^{\mathrm{T}}$ for k ∈ S₂, where 0_q denotes a q x 1 vector of zeroes. First, compute the patient-specific meta-analysis log cumulative hazard estimate for a patient with the same values of the common covariates z_C and all the special subpopulation indicator functions set to 0, that is, I₁= I₂ = ··· = I_q = 0. Write out this estimate as $\widehat{\rho }({\mathbf{z}}_{C0})={\sum }_{k=1}^K{w}_k{\widehat{\rho }}_k({\mathbf{z}}_{C0})={\sum }_{k=1}^K{w}_k\{ln{\widehat{\mathrm{\Lambda }}}_0^{(k)}(t_0)+{\sum }_{i=1}^c{\widehat{\beta }}_{Ci}^{(k)}{z}_i\}$, where ρ̂_k(z_C0) is the log cumulative hazard estimate for study k, having estimated variance ${\widehat{\sigma }}_k^2({\mathbf{z}}_{C0})$, and the w_k are the meta-analysis weights for this configuration of covariates. For the fixed-effects meta-analysis, the weights are $w_k=\{1/{\widehat{\sigma }}_k^2({\mathbf{z}}_{C0})\}/{\sum }_{j=1}^{K}1/{\widehat{\sigma }}_j^2({\mathbf{z}}_{C0})$, and for the random-effects meta-analysis

$$w_k=\frac{W_k({\widehat{\tau }}^2({\mathbf{z}}_{C0}))}{{\sum }_{j=1}^K{W}_j({\widehat{\tau }}^2({\mathbf{z}}_{C0}))}=\frac{1/\{{\widehat{\tau }}^2({\mathbf{z}}_{C0})+{\sigma }_k^2({\mathbf{z}}_{C0})\}}{{\sum }_{j=1}^{K}1/\{{\widehat{\tau }}^2({\mathbf{z}}_{C0})+{\widehat{\sigma }}_j^2({\mathbf{z}}_{C0})\}},$$

where τ̂²(z_C0) is the estimate of inter-study variation in the log cumulative hazard when the covariate vector is z_C.

Next, determine the relative weights $w_k^{†}$ among the subset S₂ of studies that have special subpopulations. For the fixed-effects meta-analysis we have $w_k^{†}=\{1/{\widehat{\sigma }}_k^2({\mathbf{z}}_{C0})\}/{\sum }_{j\in S_2}1/{\widehat{\sigma }}_j^2({\mathbf{z}}_{C0})$, and for the random-effects meta-analysis

$$w_k^{†}=\frac{W_k({\widehat{\tau }}^2({\mathbf{z}}_{C0}))}{{\sum }_{j\in S_2}{W}_j({\widehat{\tau }}^2({\mathbf{z}}_{C0}))}=\frac{1/\{{\widehat{\tau }}^2({\mathbf{z}}_{C0})+{\widehat{\sigma }}_k^2({\mathbf{z}}_{C0})\}}{{\sum }_{j\in S_2}1/\{{\widehat{\tau }}^2({\mathbf{z}}_{C0})+{\widehat{\sigma }}_j^2({\mathbf{z}}_{C0})\}}.$$

Finally, combine the estimated additional contributions to the log cumulative hazard due to the special subpopulations with the ‘baseline’ cumulative hazard estimate based on the common covariates. The log cumulative hazard accounting for membership in the special subpopulations as specified by I₁, I₂,…_, I_q is consistently estimated by

$$\begin{array}{l}\widehat{\rho }(\mathbf{z})=\sum _{k=1}^K{w}_k\left\{ln{\widehat{\mathrm{\Lambda }}}_0^{(k)}(t_0)+\sum _{i=1}^c{\widehat{\beta }}_{Ci}^{(k)}{z}_i\right\}+\sum _{k\in S_2}{w}_k^{†}\sum _{i=1}^q{\widehat{\beta }}_{Si}^{(k)}{I}_i\\ =\sum _{k\in S_1}{w}_k{\widehat{\rho }}_k({\mathbf{z}}_{C0})+\sum _{k\in S_2}{w}_k\left\{ln{\widehat{\mathrm{\Lambda }}}_0^{(k)}(t_0)+\sum _{i=1}^c{\widehat{\beta }}_{Ci}^{(k)}{z}_i+\sum _{i=1}^q{\beta }_{Si}^{(k)}{I}_i\frac{w_k^{†}}{w_k}\right\}\\ =\sum _{k\in S_1}{w}_k{\widehat{\rho }}_k({\mathbf{z}}_{C0})+\sum _{k\in S_2}{w}_k{\widehat{\rho }}_k({\mathbf{z}}_k^{†}),\end{array}$$

where ${\mathbf{z}}_k^{†}={({\mathbf{z}}_C^{\mathrm{T}},w_k^{†}{I}_1/w_k,w_k^{†}{I}_2/w_k,\dots ,w_k^{†}{I}_q/w_k)}^{\mathrm{T}}$. This is Equation (11).

For the estimate of log cumulative hazard for patients in one of the special subpopulations, rewrite

$$\widehat{\rho }(\mathbf{z})=\sum _{k=1}^K\frac{W_k({\widehat{\tau }}^2({\mathbf{z}}_{C0}))}{{\sum }_{j=1}^K{W}_j({\widehat{\tau }}^2({\mathbf{z}}_{C0}))}{\widehat{\rho }}_k({\stackrel{\sim }{\mathbf{z}}}_k),$$

where

$${\stackrel{\sim }{\mathbf{z}}}_k=\{\begin{array}{ll}{\mathbf{z}}_{C0}\hfill & \text{if}k\in S_1,\hfill \\ {\mathbf{z}}_k^{†}={({\mathbf{z}}_C^{\mathrm{T}},w_k^{†}{I}_1/w_k,w_k^{†}{I}_2/w_k,\dots ,w_k^{†}{I}_q/w_k)}^{\mathrm{T}}\hfill & \text{if}k\in S_2.\hfill \end{array}$$

Note that

$$\frac{w_k^{†}}{w_k}=\frac{W_k({\widehat{\tau }}^2({\mathbf{z}}_{C0}))/{\sum }_{j\in S_2}{W}_j({\widehat{\tau }}^2({\mathbf{z}}_{C0}))}{W_k({\widehat{\tau }}^2({\mathbf{z}}_{C0}))/{\sum }_{j\in S_1\cup S_2}{W}_j({\widehat{\tau }}^2({\mathbf{z}}_{C0}))}=\frac{{\sum }_{j\in S_1\cup S_2}{W}_j({\widehat{\tau }}^2({\mathbf{z}}_{C0}))}{{\sum }_{j\in S_2}{W}_j^{†}({\widehat{\tau }}^2({\mathbf{z}}_{C0}))}$$

is the ratio of the weight for study k in the subset S₂ to its weight in the full set of studies S₁ ∪ S₂. This ratio should be relatively stable, so dependence of ${\mathbf{z}}_k^{†}$ on τ̂²(z_C0) and ${\widehat{\tau }}_2^2(\mathbf{z})$ should be minor. Thus, similar to the result above, the first derivative of ρ̂(z) with respect to τ̂²(z) is approximately

$$\begin{array}{l}{D}_1(\mathbf{z})=\frac{\begin{array}{l}[-{\sum }_{k=1}^{K}1/\{{\widehat{\sigma }}_k^2({\mathbf{z}}_{C0})+{\widehat{\tau }}^2({\mathbf{z}}_{C0})\}{\sum }_{k=1}^K{\widehat{\rho }}_k({\stackrel{\sim }{\mathbf{z}}}_k)/{\{{\widehat{\sigma }}_k^2({\mathbf{z}}_{C0})+{\widehat{\tau }}^2({\mathbf{z}}_{C0})\}}^2\\ +{\sum }_{k=1}^K{\widehat{\rho }}_k({\stackrel{\sim }{\mathbf{z}}}_k)/\{{\widehat{\sigma }}_k^2({\mathbf{z}}_{C0})+{\widehat{\tau }}^2({\mathbf{z}}_{C0})\}{\sum }_{k=1}^{K}1/{\{{\widehat{\sigma }}_k^2({\mathbf{z}}_{C0})+{\widehat{\tau }}^2({\mathbf{z}}_{C0})\}}^2]\end{array}}{{\left\{{\sum }_{k=1}^{K}1/{\widehat{\sigma }}_k^2({\mathbf{z}}_{C0})+{\widehat{\tau }}^2({\mathbf{z}}_{C0})\right\}}^2}\\ =\frac{{\sum }_{k=1}^K{W}_k^2({\widehat{\tau }}^2({\mathbf{z}}_{C0}))\{\widehat{\rho }(\mathbf{z})-{\widehat{\rho }}_k({\stackrel{\sim }{\mathbf{z}}}_k)\}}{{\sum }_{k=1}^K{W}_k({\widehat{\tau }}^2({\mathbf{z}}_{C0}))},\end{array}$$ (A.4)

the second derivative is approximately

$$D_2(\mathbf{z})=\frac{2\{{\sum }_{k=1}^K{W}_k^2({\widehat{\tau }}^2({\mathbf{z}}_{C0}))(\widehat{\rho }(\mathbf{z})-{\widehat{\rho }}_k({\stackrel{\sim }{\mathbf{z}}}_k)){\sum }_{k=1}^K{W}_k^2({\widehat{\tau }}^2({\mathbf{z}}_{C0}))-{\sum }_{k=1}^K{W}_k^3({\widehat{\tau }}^2({\mathbf{z}}_{C0}))(\widehat{\rho }(\mathbf{z})-{\widehat{\rho }}_k({\stackrel{\sim }{\mathbf{z}}}_k)){\sum }_{k=1}^K{W}_k({\widehat{\tau }}^2({\mathbf{z}}_{C0}))\}}{{\left\{{\sum }_{k=1}^K{W}_k({\widehat{\tau }}^2({\mathbf{z}}_{C0}))\right\}}^2},$$ (A.5)

and the variance of τ̂²(z_C0) can be approximated by

$$\text{Var}\{{\widehat{\tau }}^2({\mathbf{z}}_{C0})\}=\frac{\left[4{\sum }_{k=1}^K{\{W_k({\widehat{\tau }}^2({\mathbf{z}}_{C0})){\sum }_{j\ne k}{W}_j({\widehat{\tau }}^2({\mathbf{z}}_{C0}))/{\sum }_{j=1}^K{W}_j({\widehat{\tau }}^2({\mathbf{z}}_{C0}))\}}^2\times {\{{\widehat{\rho }}_k({\mathbf{z}}_{C0})-\widehat{\rho }({\mathbf{z}}_{C0})\}}^2\{{\widehat{\sigma }}_k^2({\mathbf{z}}_{C0})+{\widehat{\tau }}^2({\mathbf{z}}_{C0})\}\right]}{{\left[{\sum }_{k=1}^K{\{W_k({\widehat{\tau }}^2({\mathbf{z}}_{C0}))\}}^2{\{{\widehat{\rho }}_k({\mathbf{z}}_{C0})-\widehat{\rho }({\mathbf{z}}_{C0})\}}^2\right]}^2}.$$ (A.6)

These are the closed form expressions for the terms in Equation (12).

A.5 Regularity condition for simulation study distributions

For a single covariate, Tsiatis’ [18] regularity condition for the consistency of the Breslow estimator and its variance estimator is that E{z exp(zβ)} is bounded in a neighborhood of β. The covariates in the simulation studies are normally distributed. For a standard normal variate z, we have

$$\begin{array}{l}E\{zexp(\beta z)\}={\int }_{-\infty }^{\infty }zexp(\beta z)\frac{1}{\sqrt{2\pi }}exp\left(-\frac{1}{2}{z}^2\right)\mathrm{d}z\\ ={\int }_{-\infty }^{\infty }z\frac{1}{\sqrt{2\pi }}exp\left\{-\frac{1}{2}{(z-\beta )}^2\right\}exp\left(\frac{1}{2}{\beta }^2\right)\mathrm{d}z=\beta exp\left(\frac{1}{2}{\beta }^2\right),\end{array}$$

which is uniformly bounded in any finite interval. The generalization to a normal deviate with mean μ and SD σ follows by considering the linear transformation z′ = σz + μ. Completing the square as above, we have

$$\begin{array}{l}E\{z^{\prime }exp(\beta z^{\prime })\}={\int }_{-\infty }^{\infty }(\sigma z+\mu )exp\{\beta (\sigma z+\mu )\}\frac{1}{\sqrt{2\pi }}exp(-\frac{1}{2}{z}^2)\mathrm{d}z\\ =(\mu +\beta {\sigma }^2)exp\left(\beta \mu +\frac{1}{2}{\beta }^2{\sigma }^2\right),\end{array}$$

which is still bounded over any finite interval of β. The multivariate case with K covariates having arbitrary mean vector and covariance matrix follows by conditioning on the each subset of K − 1 covariates, after which the remaining covariate is univariate normal.