Computational analysis of drug transport in tumor microenvironment as a critical compartment for nanotherapeutic pharmacokinetics

Abstract

Over the last decade nanotherapeutics gained increasingly important role in drug delivery because of their frequently beneficial pharmacokinetics (PK) and lower toxicity when compared to classical systemic drug delivery. In view of therapeutic payload delivery, convective transport is crucial for systemic distribution via circulatory system, but the target domain is tissue outside vessels where transport is governed by diffusion. Here, we have computationally investigated the understudied interplay of physical transports to characterize PK of payload of nanotherapeutics. The analysis of human vasculature tree showed that convective transport is still 5 time more efficient than diffusion suggesting that circulating and payload releasing drug vectors can contribute mostly to systemic delivery. By comparing payload delivery using systemic circulation and drug vectors to microenvironment, internalized vectors were the most efficient and showed Area under the Curve (AUC) almost 100 higher than in systemic delivery. The newly introduced Zone of Influence (ZOI) parameter indicated that vectors, especially internalized, lead to the largest tissue fraction covered with therapeutically significant payload concentration. The internalization to microenvironment minimizes effects of plasma domain on payload extravasation from nanotherapeutics. The computed results showed that classical PK, which mostly relies on concentration profiles in plasma, sometimes might be inadequate or not sufficient in explaining therapeutic efficacy of nanotherapeutics. These results provide a deeper look into PK of drug vectors and can help in the design of better drug delivery strategies.

Introduction

To date, several dozens of drug delivery systems are present in clinics or clinical trials which rely on liposomes, micelles or proteins as drug carriers (Norvaisas and Ziemys 2014). Drug vectors showed improvements in enhanced pharmacokinetics (PK), reduced toxicity, or improved therapeutics compared to conventional drugs (Wacker 2014). Because of their size and different surface properties, vectors generate enhanced permeability and retention (EPR) effects in tumors, leading to drug concentrations up to 10 times higher than those in plasma or normal tissues (Maeda 2001). Because of EPR, and other effects like mononuclear phagocyte system (Geissmann, Gordon et al. 2010), PK of vectors may be very different from PK of small molecule drugs. Therefore, drug molecules carried by a vector adopt the carrier’s PK profile (Simovic and Prestidge 2007).

Although nanotherapeutics can be advantageous over free chemotherapy, benefits of drug vectors and pharmacodynamics (PD) can vary from patient to patient based on differences in the tumor and organ microenvironment (Maeda, Wu et al. 2000; Davis 2008); sometimes having only modest effects (Gordon, Fleagle et al. 2001; O’Brien, Wigler et al. 2004; Jain and Stylianopoulos 2010). Although the systemic PK of drugs has been thought to be a major determinant of its utility in clinics, clinical evidences indicate that systemic PK may not be indicative of its therapeutic efficacy and does not reflect intra- and inter-tumor heterogeneity (Müller, dela Peña et al. 2004; Wolf and Presant 2004). Moreover, an excellent association between tumor-based PK and PD was shown to 5-FU (Presant, Wolf et al. 1994). Our recent in vivo and computational study has revealed that phenotypic differences of tumor microenvironment can negate enhanced PK properties of nanotherapeutics (Yokoi, Kojic et al. 2014). There, capillary collagen of type-IV can be a biophysical marker determining the extravasation of doxorubicin (DOX) by using its liposomal formulation (PLD). It was shown that the 3LL tumors having more collagen than the 4T1 tumors prevent DOX extravasation, in opposite to the 4T1 tumors.

The limited understanding of tumor microenvironment and tumor-based PK/PD relationships can be contributing to shortfalls of nanotherapeutics, which even provokes questioning the future of nanotherapeutics (Park 2013). While systemic PK/PD relationships are heavily scrutinized, tumor-based PK/PD remains an underexplored territory hiding answers to improve drug delivery. The reason this is becoming such a significant issue is the advancement of NP drug delivery systems, which have the capability to reduce the systemic circulation effects of drug compounds and the concentration effects of these particles in the tumor microenvironment, where nanotherapeutics comes to rest.

It is therefore very important to have an adequate knowledge of the mechanisms which determine the transport and kinetics of drugs from systemic circulation to tumor sites (McVie 1984). Because nanotherapeutics alters biodistribution of therapeutic payload, the most efficient drug delivery can be expected if the major payload release takes place at the location of interest, i.e. inside tumor tissue. The drug release from a vector can start immediately after an injection or once vectors meet certain conditions, e.g. get trapped into lysosomes with different pH. If payload starts leaking while vectors are circulating within blood stream, the release of drug could be subjected to a systemic circulation and, consequently, would have the PK of free drug. Therefore, nanotherapeutics and leaked drug would obey the circulation transport, unless a vector gets physically trapped on vessel wall or is internalized deeper into microenvironment. In the latter case, diffusion becomes the remaining transport mechanism in distributing payload locally among cells.

In this study, we have focused on drug payload transport and PK in tumor microenvironment by using our developed computational model. We investigate how circulation and diffusion transports could affect the delivery of payload to microenvironment from vectors at their different endpoints in circulation. This study quantifies the PK differences at systemic and microenvironment levels and emphasizes critical properties of vectors for optimal drug delivery and its interpretation.

Methods

Drug transport model

We applied a recently developed hierarchical multiscale diffusion modeling technique (Kojic, Milosevic et al. 2011; Kojic, Ziemys et al. 2011; Ziemys, Kojic et al. 2011; Kojic, Milosevic et al. 2014), which has an advantage over other approaches because it accounts for characteristics of the diffusion medium microstructure and physico-chemical properties of the diffusing molecules, including the size of the molecules or particles. Also, the model includes motion of particles within fluid which is based on a finite element solid-fluid interaction solution with large displacements of the moving solids. For simplicity, we neglect drug vector (particle) degradation and consider that drug vector releases its payload as long as the concentration within the vector is larger than in the surrounding.

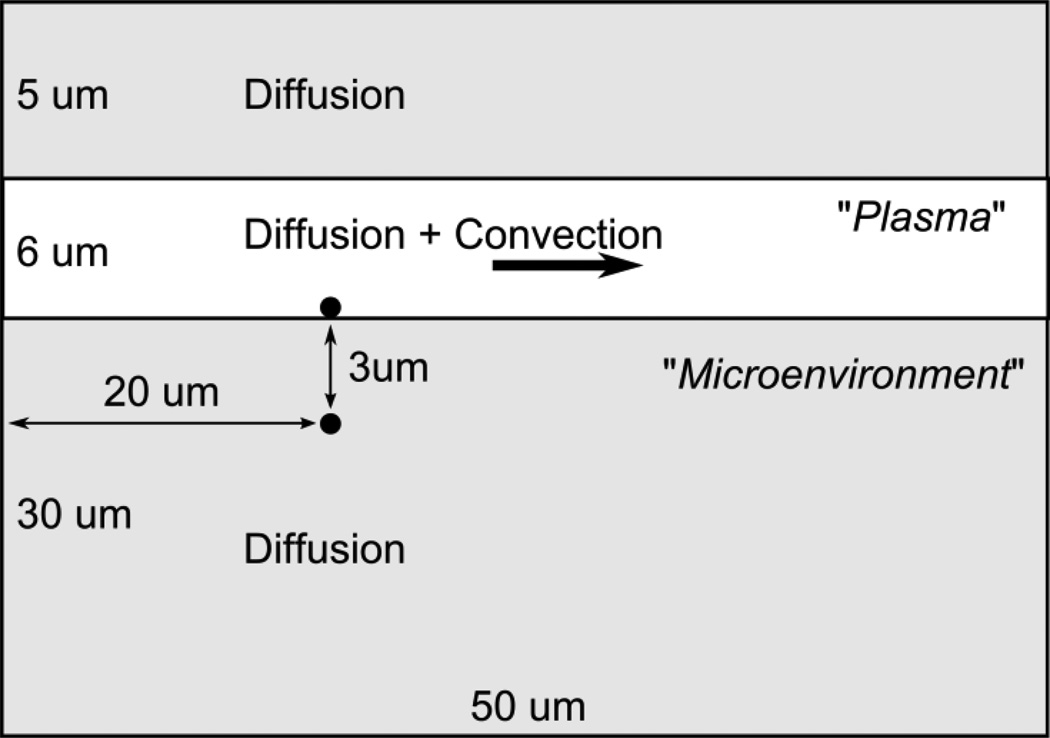
To evaluate diffusion and convective transport effects in microenvironment we have adopted a simplification of general 3D unsymmetrical conditions and developed a 2D axisymmetric FE model of capillary and its surrounding, to simulate drug release from a vector, accounting for flow and diffusion effects (Figure 1). We considered a spherical particle as a vector with 0.25 µm radius and loaded with 1 M concentration of drug. Three cases were simulated: A) the systemic example, when payload is dissolved in plasma and no drug vector is present, B) the vector is adhering to capillary wall, and C) the vector is internalized. Each model contains an equivalent mass of payload: 1 M concentration in vectors and 0.60 M in plasma before simulation starts. The following payload diffusivities were used to in the model, unless stated differently: 10⁻⁷ cm2/s in fluid (plasma), 10⁻⁹ cm2/s in vector, and 10⁻¹⁰ cm2/s in solid (tissue). Vectors were immobile during simulations. In all case, the entering concentration in fluid is zero. Area under the Curve (AUC) were calculated using mean concentration in a specific compartment (plasma or microenvironment) of interest in our model.

Figure 1.

Schematics of 2D Finite Element (FE) capillary transport domain with dimensions. Black dots mark the position of drug vectors. The third dimension (depth) is 1 µm.

Finite Element (FE) implementation

Here are summarized the fundamentals of the computational model. Considering blood (fluid) and drug vector (solid) as continuous media, the basic equations consist of the balance of linear momentum,

$$\frac{\partial {\sigma }_{ij}}{\partial x_j}+f_i^V=0$$ (1)

and incompressibility condition

$$\frac{\partial v_j}{\partial x_j}=0,\text{summ on}j:j=1,2,3$$ (2)

where σ_ij are stresses, $f_i^V$ are volumetric forces, and v_j are velocity components of a material point; as indicated, repeated index j implies summation j=1,2,3 for derivatives with respect to coordinates x_j. Constitutive laws for elastic solid include Young’s modulus E and Poisson’s ratio ϑ (equal 0.5 for incompressible material), and viscosity coefficient μ for fluid. We will consider that the drug vector does not deform and hence take for E a large number. Diffusion is governed by Fick’s law,

$$q_i=-D_{ij}\frac{\partial c}{\partial x_j},\text{summ on}j:j=1,2,3$$ (3)

so that the mass balance equation, which includes convection, can be written as

$$-\frac{\partial c}{\partial t}-\frac{\partial c}{\partial x_k}{v}_k+\frac{\partial }{\partial x_i}\left(D_{ik}\frac{\partial c}{\partial x_k}\right)+q_V=0,\text{sum on}\mathrm{i},k:\mathrm{i},k=1,2,3$$ (4)

where q_i is mass flux, c is concentration, D_ij are diffusion coefficients, and q_V is a source term. By a common implementation of the principle of virtual power and Galerkin procedure (Kojic, Filipovic et al. 2008), the above balance and continuity equations (1), (2) and (4) can be transformed into finite element incremental-iterative algebraic equations of the following form:

1. for fluid

   $$\left[\begin{array}{cc}\hfill \frac{1}{\mathrm{\Delta }t}{\mathbf{M}}^f+{\mathbf{K}}^{f(i-1)}\hfill & \hfill {\mathbf{K}}^{vp(i-1)}\hfill \\ \hfill {\mathbf{K}}^{Tvp(i-1)}\hfill & \hfill 0\hfill \end{array}\right]\left\{\begin{array}{c}\hfill \mathrm{\Delta }{\mathbf{V}}^{f(i)}\hfill \\ \hfill \mathrm{\Delta }{P}^{f(i)}\hfill \end{array}\right\}=\left\{\begin{array}{c}\hfill {\mathbf{F}}_{\mathit{\text{ext}}}^{(i-1)}\hfill \\ \hfill 0\hfill \end{array}\right\}-\left[\begin{array}{cc}\hfill {\mathbf{K}}^{f(i-1)}\hfill & \hfill {\mathbf{K}}^{vp(i-1)}\hfill \\ \hfill {\mathbf{K}}^{Tvp(i-1)}\hfill & \hfill 0\hfill \end{array}\right]\left\{\begin{array}{c}\hfill {\mathbf{V}}^{f(i-1)}\hfill \\ \hfill P^{f(i-1)}\hfill \end{array}\right\}-\left\{\begin{array}{c}\hfill \frac{1}{\mathrm{\Delta }t}{\mathbf{M}}^t({\mathbf{V}}^{f(i-1)}-{\mathbf{V}}^{f(n)})\hfill \\ \hfill 0\hfill \end{array}\right\}$$ (6)
2. for solids

   $$\left[\begin{array}{cc}\hfill \frac{1}{\mathrm{\Delta }t}{\mathbf{M}}^s+{\mathbf{K}}^{s(i-1)}\hfill & \hfill {\mathbf{K}}^{vp(i-1)}\hfill \\ \hfill {\mathbf{K}}^{Tvp(i-1)}\hfill & \hfill 0\hfill \end{array}\right]\left\{\begin{array}{c}\hfill \mathrm{\Delta }{\mathbf{V}}^{s(i)}\hfill \\ \hfill \mathrm{\Delta }{P}^{s(i)}\hfill \end{array}\right\}=\left\{\begin{array}{c}\hfill {\mathbf{F}}_{\mathit{\text{ext}}}^{(i-1)}\hfill \\ \hfill 0\hfill \end{array}\right\}-\left[\begin{array}{cc}\hfill {\mathbf{K}}^{s(i-1)}\hfill & \hfill {\mathbf{K}}^{vp(i-1)}\hfill \\ \hfill {\mathbf{K}}^{Tvp(i-1)}\hfill & \hfill 0\hfill \end{array}\right]\left\{\begin{array}{c}\hfill {\mathbf{V}}^{s(i-1)}\hfill \\ \hfill P^{s(i-1)}\hfill \end{array}\right\}-\left\{\begin{array}{c}\hfill \frac{1}{\mathrm{\Delta }t}{\mathbf{M}}^s({\mathbf{V}}^{s(i-1)}-{\mathbf{V}}^{s(n)})\hfill \\ \hfill 0\hfill \end{array}\right\}$$ (7)
3. for diffusion

   $$(\frac{1}{\mathrm{\Delta }t}{\mathbf{M}}^c+{\mathbf{K}}^{cc(i-1)}+{\mathbf{K}}^{cv(i-1)})\mathrm{\Delta }{\mathbf{C}}^{(i)}={\mathbf{Q}}^{\mathit{\text{ext}}}-({\mathbf{K}}^{cc(i-1)}+{\mathbf{K}}^{cv(i-1)}){\mathbf{C}}^{(i-1)}-\frac{1}{\mathrm{\Delta }t}{\mathbf{M}}^c({\mathbf{C}}^{(i)}-{\mathbf{C}}^n)$$ (8)

Here, ΔV^f and ΔV^s represent increments of nodal velocity vectors of fluid V^f and solid V^s within time step Δt, ΔP^f, and ΔP^s are increment of the element pressure in fluid and solid, respectively, and ΔC is increment of nodal concentration C; F^ext and F^int are external and internal nodal forces, respectively; Q^ext is external mass flux; and the upper right index “i” denotes equilibrium iteration number, while the index “n” stands for start of a time step. The expressions for the element matrices and vectors are given in Supplementary Material. In case of diffusion through porous solid there are no convective terms in equation (8). The above system of equations corresponds to one finite element. This system is further assembled and solved for the nodal quantities for time steps used to calculate evolution of the physical fields of velocity, pressure and concentration; with iterations performed for each time step until convergence is reached (Kojic, Filipovic et al. 1998, 2009).

Vascular tree analysis

Human vascular tree was analyzed based on human pulmonary artery tree data (Supplemental Material, Table S1) (Singhal, Henderson et al. 1973). We have characterized each vessel segment by the residence time t_R, and the characteristic diffusion time t_D,l:

$$t_R=L/v$$ (9)

$$t_D=R^2/4D$$ (10)

where v is the blood flow velocity a given vessel segment, L is the vessel length of the segment, R is the radius of vessels in a segment, D is the diffusion coefficient of payload outside of a drug vector. t_R characterizes the time of blood elementary volume spending within a given vasculature segment of that vessel size, while t_D = t_D,l + t_D,w – the time payload has to diffuse the longest path (the middle of vessel) through vessel lumen and wall. t_D,l was evaluated using D = 10⁻⁶ cm²/s. t_D,w was evaluated using physiological wall thickness of vessels (Supplemental Material, Figure S2) with diffusivity D = 10⁻⁸ cm²/s, because D was found up to 100 times in tissues than fluid (Nugent and Jain 1984).

Results

Considering the overall drug transport, a part corresponding to vector delivery after an injection exclusively depends on flow (convective transport), while another part related to the payload delivery is mostly associated with diffusion (diffusive transport) through microenvironment and is driven by concentration gradient: from concentrated state inside vectors to the surrounding. We analyze the interplay between convective and diffusion transports controlling payload delivery, starting from circulating vector after injection and continuing by diffusion through vessel wall and microenvironment. In our analysis, human pulmonary arterial tree serves as a general model of human vasculature and systemic delivery, which can be of interest for transport within a tumor capillary network.

Systemic circulation

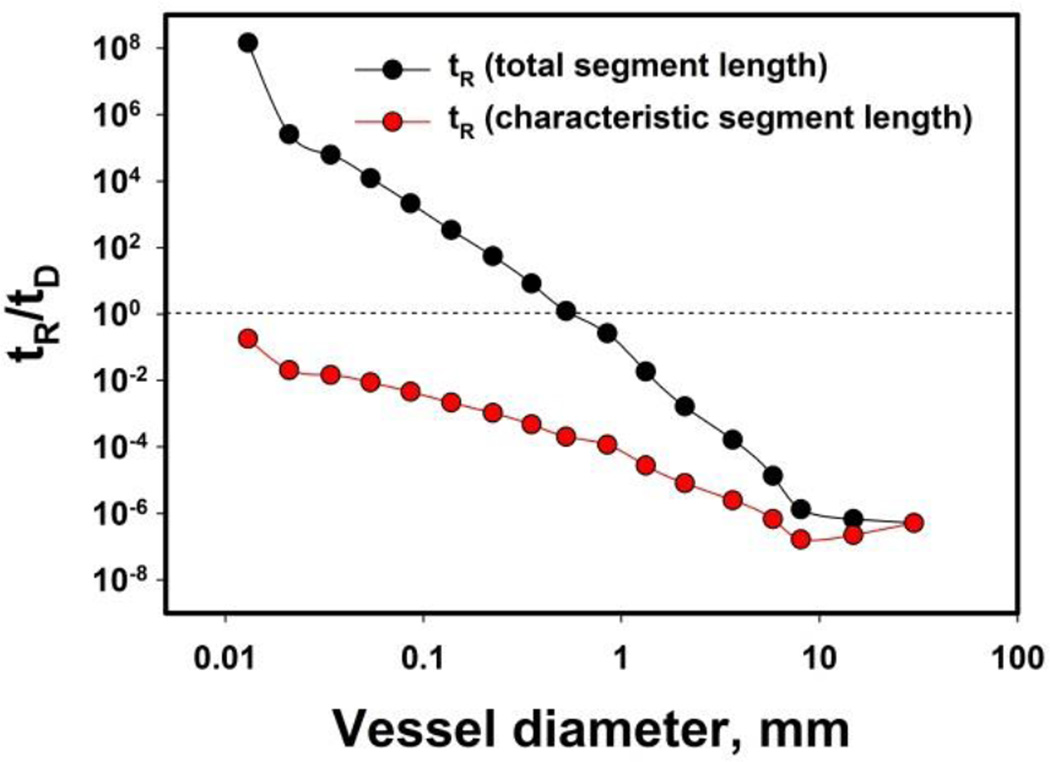
Human vascular tree can be segmented based on a vessel diameter, which has a characteristic flow rate. As estimated for human pulmonary arterial tree, the tree has 17 segments and the flow velocity decreases by decreasing a physiological diameter of human vessels d: the flow velocity dropped from 11 cm/s in aorta (d = 30 mm) down to 0.5 mm/s in capillaries (d = 10 µm) (Singhal, Henderson et al. 1973) (Supplementary Material, Table S1). Consequently, nanotherapeutics is supposed to circulate with similar velocities. In view of payload transport, the characterization of segments in human pulmonary vessel tree was accomplished by calculated the residence time t_R and the characteristic diffusion time t_D. The ratio t_R/t_D differentiates the vessels dominated by convective or diffusion transport: in vessels with t_R/t_D << 1 dominates convective flow, and in vessels with t_R/t_D >> 1 – diffusion prevails. The latter can evaluate if payload can reach the microenvironment of a local vessel by passive diffusion from circulating vector.

Figure 2 depicts the calculated t_R/t_D ratios for the human pulmonary tree. When t_R was calculated by using the total length of the segment, the t_R/t_D ratio shows that diffusion becomes increasingly important in vessels with the diameter of 0.6 mm and smaller. It also suggests that large flow velocity and relatively small fraction of vessels with d > 0.6 mm in the vascular tree eliminate those vessels in the perspective of systemic drug delivery. However, if t_R was the calculated by using a characteristic length of each segments, the t_R/t_D ratio never approaches 1 even for smallest capillaries, suggesting that microenvironment has little chance to be affected directly by the free flowing and locally present drug vector that leaks its payload. Based on physiological data, the convective transport is still 5 times more efficient than diffusion locally in the smallest capillaries of human pulmonary tree with characteristic diameter of 10 µm and length of 130 µm.

Figure 2.

Dependence of t_R/t_D (residence time vs. diffusion time) on vessel diameter in the human pulmonary artery tree. Significance of diffusion with respect to convective transport increases with a decrease of vessel diameter; dashed line marks the ratio, where convective and diffusion transport equalize, t_R/t_D = 1.

Concentration kinetics

The analysis of vascular tree showed that the release of drug from circulating vectors is not efficient to deliver payload directly to the tissue, because flow overpowers diffusion even in capillaries, where flow velocity is weakest. Most nanotherapeutics deliver payload by adhering of drug vector to a vessel wall or by being internalized into the wall or perivascular space (Ferrari 2010). Upon immobilization of a vector on vessel wall the residence time t_R becomes very large, t_R∞, because a vector particle can stay attached to the wall until it is degraded. Therefore, the ratio t_R∞/t_D becomes large and payload release relies on diffusion only. Since the smallest capillaries are dominating in the payload exchange with tissues, we have studied in our model the payload release in a capillary and surrounding microenvironment.

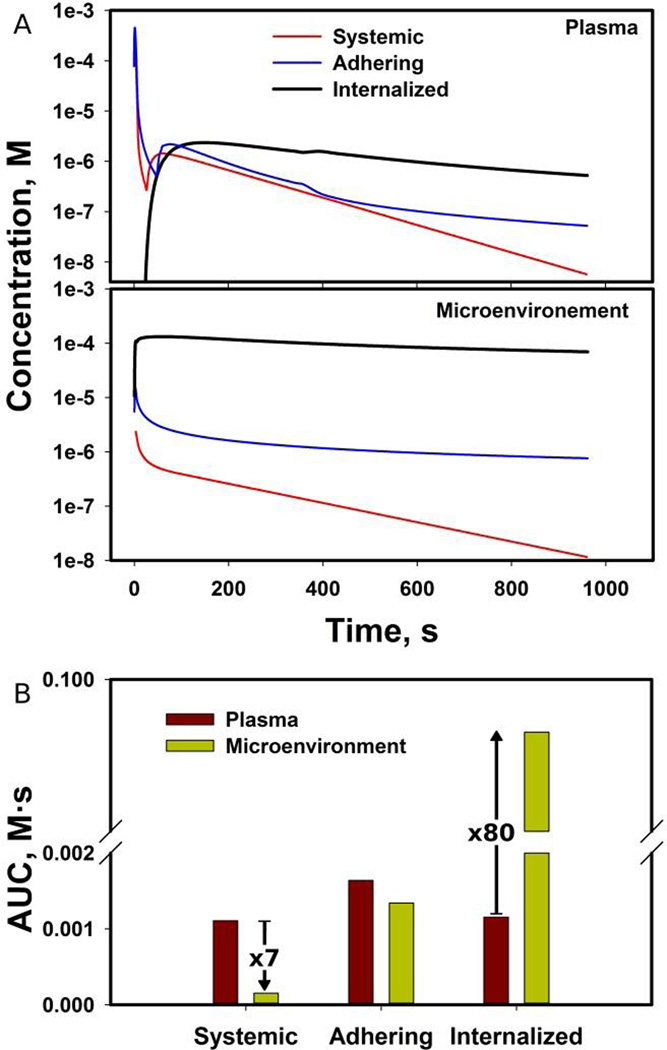
Three examples were compared in our capillary model: A) systemic circulation, B) the vector is adhering to capillary wall, and C) the vector is internalized (Figure 3). In order to compare systemic delivery with the other two cases, we have taken the mass of drug within the drug vector and equally distributed over the plasma domain shown in Fig. 1. This initial concentration of the model A) changes due to plasma flow through the domain and due to extravasation through capillary walls (initial concentration in the microenvironment is zero). In other two models, the assumption was that the initial concentration outside the drug vector was equal to zero. The calculated results revealed that the highest concentration in plasma was found in case of systemic delivery and an adhering vector, but in few hundreds of seconds the highest concentration in plasma is calculated for the internalized vector that leaks its payload out (Figure 4A). On the other hand, concentration in microenvironment was the highest when using drug vectors, especially when a vector is internalized: the concentration was by two orders of magnitude higher than in other cases. The systemic delivery among all cases showed the least payload delivered to microenvironment. Naturally, AUC in microenvironment was found to be the largest for an internalized vector, while the systemic delivery produced the largest AUC in plasma (Figure 4B).

Figure 3.

Characteristic times of payload (small green spheres) transport from drug vectors (large spheres) for three drug vector localizations within a vessel and systemic delivery: A – systemic delivery, B – vector adhered to vessel wall, C – vector internalized into vessel wall.

Figure 4.

Calculated kinetics of payload delivery in the capillary model: (A) mean payload concentration profiles in plasma and microenvironment domains, (B) comparison of calculated AUC between plasma and microenvironment.

Zone of influence (ZOI) in microenvironment

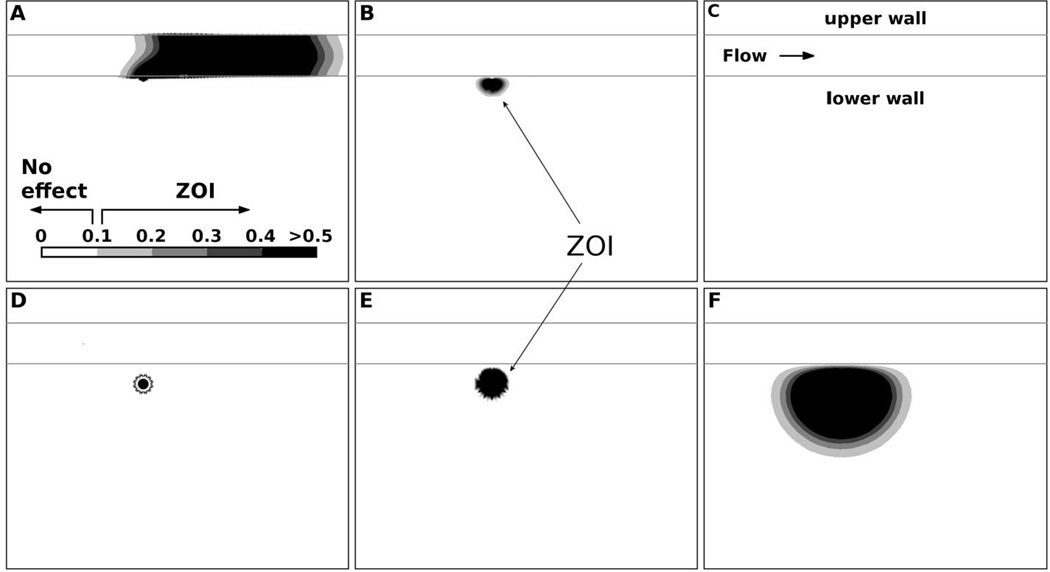
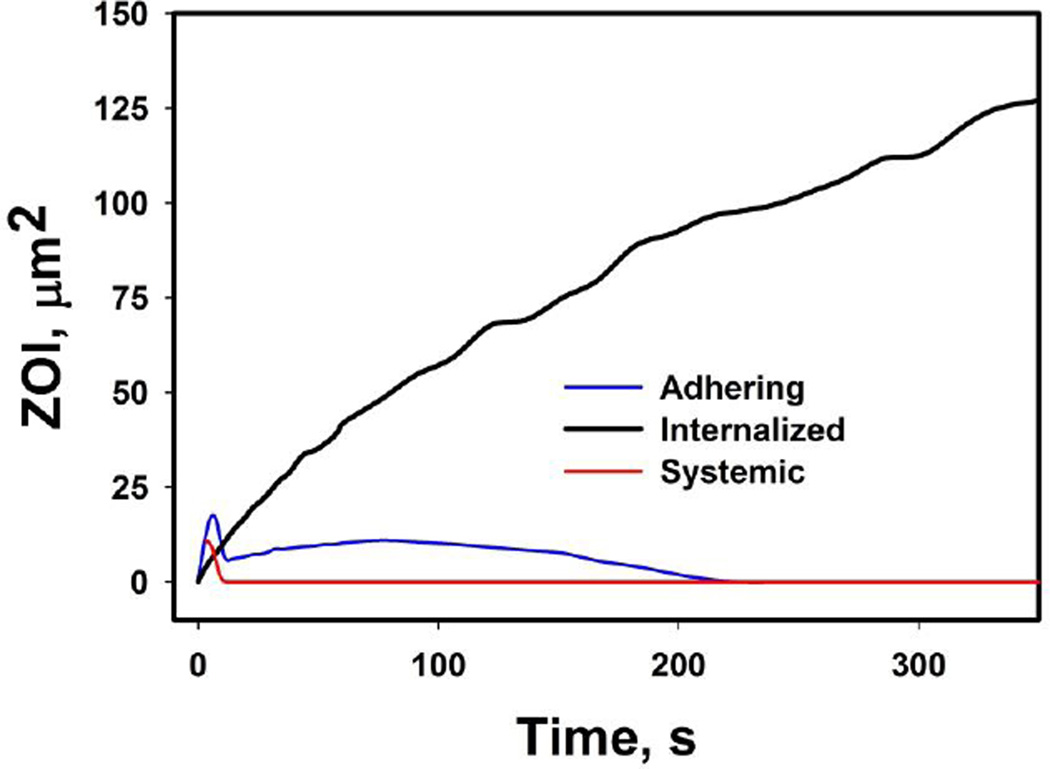
We have investigated in details the concentration fields in microenvironment produced by different endpoints of vectors, and have introduced the concept of ZOI. ZOI represents the tissue domain in microenvironment affected by the concentration, which is above an arbitrary no-effect level, i.e. having a therapeutic effect. For visually better comparison of ZOI we have used sub-physiological plasma flow velocity of 10 µm and the 0.0001 M concentration as the no-effect value. Figure 5 illustrates ZOI evolutions for adhering and internalized drug vectors. The computed results show that adhered particle delivers the payload by diffusion to microenvironment, but a substantial part of payload is removed by plasma flow in capillary at the beginning of the release (Figure 5 A–C). In opposite, the internalized drug vector develops ZOI gradually that increases in size with time as seen in Figure 5D–F. Figure 6 shows that ZOI increases all the time in case of internalized vector, while an adhered vector has therapeutic potential only in the initial phase of release until payload is cleared by plasma flow (Figure 5D–F). For the sake of better presentation, these examples used plasma flow velocity 10 times lower than physiological leading to proportionally larger ZOI within analysis window; the calculated ZOI in both cases could be lower in physiological conditions; that is especially true for the example of an adhering vector.

Figure 5.

Characteristic evolution of ZOI in microenvironment for the adhered (top row; A–C) and internalized (bottom row; D–F) drug vectors at the beginning (A,D), middle (B,E), and end of payload release (C,F). ZOI was evaluated by assuming the arbitrary concentration 0.0001 M, below which there is no therapeutic effect (the ‘no effect’ concentration); the concentration scale depicted in A has units of 10⁻³ M.

Figure 6.

Evolution of ZOI in microenvironment for different drug delivery modes: systemic, adhered vector, and internalized vector.

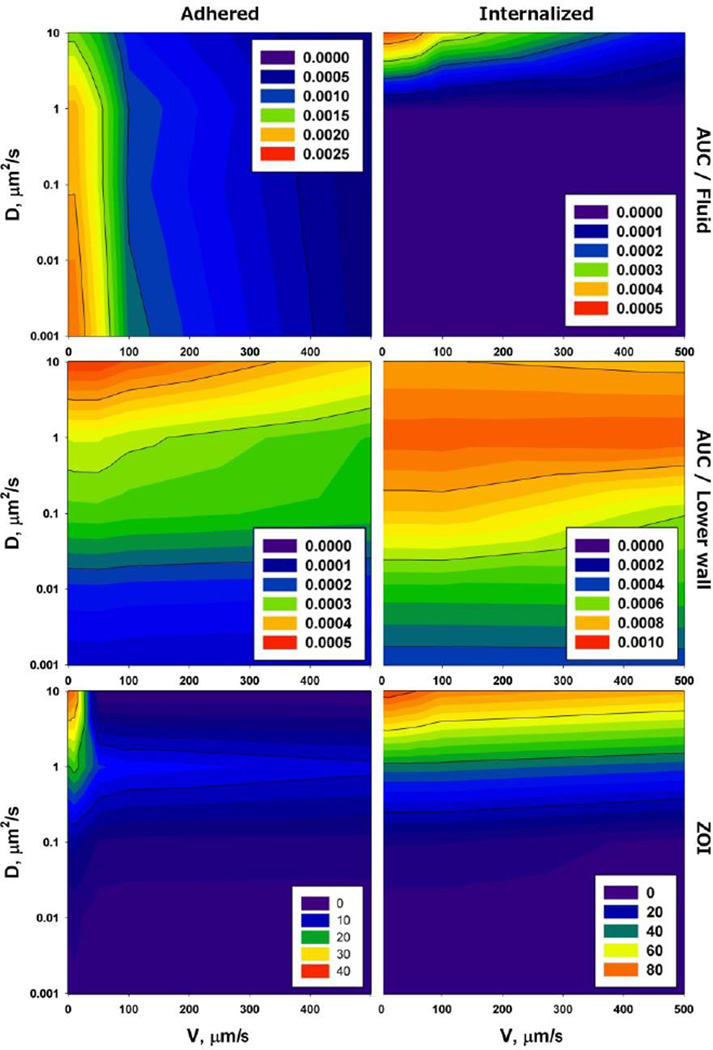
The coupling of flow and diffusion in microenvironment was further investigated by exploring AUC and ZOI at different payload diffusivities in tissue and plasma flow velocities by using same model like presented in Figure 5. The computed results show that the payload diffusivity in tissue does not modulate AUC in fluid in case of internalized or adhering vectors (Figure 7). However, AUC in fluid is 5 times lower for the internalized drug vector than adhering. On the other hand, AUC in tissue was exclusively affected by payload diffusion in microenvironment, with almost no sensitivity to the velocity of plasma flow. ZOI revealed the dependence on diffusivity similar to AUC in tissue domain, suggesting that diffusivity is crucial determining the payload penetration, and that once a vector is internalized, the plasma domain has little effect on concentration gradients inside microenvironment. However, if the payload penetration is coming from the plasma domain, the flow velocity is important for the efficacy of payload extravasation.

Figure 7.

AUC and ZOI in microenvironment and plasma in terms of payload diffusivity in tissue D and plasma flow velocity v for a drug vector adhering to vessel wall (left column) and internalized into vessel microenvironment (right column). The insets with number indicate AUC (top row – plasma; middle row - microenvironment) in M·s, and ZOI (bottom row) in µm².

Discussion

The analysis of convective and diffusion transports has provided an interesting insight into drug delivery. First, the residence time t_R calculated by using the total length of a segment in human pulmonary tree shows that vessels smaller than 0.6 mm in diameters can contribute to systemic delivery. If t_R is calculated for a characteristic length of vessel of a specific diameter, the parameters t_R and t_D quantified that a circulating vector does not have much efficiency to deliver its payload locally, because t_R is too small to ensure that payload diffuses through vessel lumen and wall to perivascular space. For example, 10 µm capillary with the characteristic length of 130 µm has a physiological velocity that is at least 5 times too high to make diffusion efficient for circulating vectors (assuming they are leaky to drugs). These results show clearly that only the domain of the smallest capillaries can be efficient in drug delivery to microenvironment. t_R and t_D also help to understand better why nanotherapeutics is not efficient from systemic drug delivery. Based on this analysis, circulating drug vectors that leak payload should have little different outcome from systemic delivery. Circulating nanotherapeutic particulates can eventually be immobilized on vessels and most frequently – on capillaries, which compose 95% of vascular tree length. The capillary segment of the vascular tree is mostly relevant to the human pulmonary tree, however our analysis provides a physics-based insight into what aspects of physiology might be important to drug delivery and nanotherapeutics.

Once drug vectors are immobilized by capillaries, the results showed major differences with respect to systemic drug delivery, and revealed an important interplay between convective and diffusion transport. As t_R becomes very large – an immobilized vector does not flow anymore, and payload delivery becomes diffusion controlled. Therefore, the condition whether vectors circulate within plasma, or are attached to the wall or internalized into tissue, becomes crucial for the drug delivery to microenvironment. It was found that the most efficient way of payload delivery is by internalization of a drug vectors into microenvironment, e.g. tumor. In this optimal scenario, payload release is controlled exclusively by diffusion in tissue and plasma may only affect the efficiency of drug delivery by a wash of the payload from microenvironment. The internalized vector also provides the largest ZOI that measures the microenvironment fraction affected by therapeutically significant drug concentration. The interesting fact in such scenario is that AUCs in plasma and tissues may be different by few orders of magnitude, suggesting that plasma concentration may not always be the adequate measure of drug exposure and efficacy in microenvironment, as it is commonly used in classical PK studies.

In case of an adhered vector, drug delivery characteristics are between systemic drug delivery and the internalized vector, as the vector is exposed at the same time to plasma flow and diffusion through the vessel wall. An adhered vector developed a short-lived ZOI that was many times smaller than the internalized vector and relatively small AUC. Although ZOI and AUC in microenvironment were not as efficient as for the internalized vector, the adhered vector provided more payload to microenvironment than systemic delivery. As expected, the systemic delivery is completely dependent on flow and the drug extravasation is almost unaffected by payload diffusivity in microenvironment. Although no significant ZOI or AUC was found for the case of the systemic delivery, ZOI and AUC could be significant upon a longer exposure. But that would also be true for the adhering and internalized vectors.

Vauper and colleagues (Vaupel, Kallinowski et al. 1989) have summarized and compared blood flow in normal tissues and tumors in different organs. Their data show that flow rate decreases from 10 to 0.02 mL/g/min (by 500 times) in healthy tissues in the following order (as an example): thyroid > kidney > liver > brain > skin > adipose tissue. At the same time, the comparison shows that tumor tissues have lower flow rate that ranges from 1 to 0.01 mL/g/min. That big range of flow rates means large differences in t_R and how efficiently payload is washed out from immobilized vectors. Also, those ranges might influence nanotherapeutic efficacy modulating payload delivery depths in tissues. The flow rate could have less than a dramatic effect for systemic circulation, because drug concentration in plasma entering and leaving a capillary is almost constant. But in case of drug vectors it is different, because the payload release is local to a capillary and its microenvironment, also with a removal of payload from the microenvironment. At this point, this analysis can draw a connection to the Enhanced Permeability and Retention (EPR) effect (Maeda 2001) helping partially in explaining why nanotherapeutics frequently provides benefits to cancer treatment over a systemic delivery.

Conclusions

The results show that diffusion and convective transports play important roles at different domains affecting the drug delivery efficiency. Considering the efficiency of payload delivery by nanotherapeutics into microenvironment, the best delivery method would be internalization of drug vectors. As drug vectors have limited diffusivity in microenvironment due to their size, the diffusion of payload will be controlling drug delivery. Based on the investigated examples, by the increasing association or internalization of drug vector into microenvironment, the payload release will be decoupled from the plasma compartment. For the same reason, plasma concentrations might be inadequate to assess the efficacy of drug delivery. In opposite to internalized or adhered vectors, circulating drug vectors (if they leak payload) conform to systemic drug delivery patterns. The results help to elucidate the transport aspect that is pertinent to PK of payload delivered by nanotherapeutics and may find use in drug delivery and nanomedicine.