A Simple Approach to Evaluate the Kinetic Rate Constant for ATP Synthesis in Resting Human Skeletal Muscle at 7 T

Abstract

Inversion transfer (IT) is a well-established technique with multiple attractive features for analysis of kinetics. However, its application in measurement of ATP synthesis rate in vivo has lagged behind the more common ST techniques. One well-recognized issue with IT is the complexity of data analysis in comparison to much simpler analysis by ST. This complexity arises, in part, because the γ-ATP spin is involved in multiple chemical reactions and magnetization exchanges, whereas Pi is involved in a single reaction, Pi → γ-ATP. By considering the reactions involving γ-ATP only as a lumped constant, the rate constant for the reaction of physiological interest, k_Pi→γATP, can be determined. Here, we present a new IT data analysis method to evaluate k_Pi→γATP using data collected from resting human skeletal muscle at 7T. The method is based on the basic Bloch-McConnell equation, which relates k_Pi→γATP with ṁ_Pi, the rate of Pi magnetization change. The k_Pi→γATP value is accessed from ṁ_Pi data by more familiar linear correlation approaches. For a group of human subjects (n = 15), the k_Pi→γATP value derived for resting calf muscle was 0.066 ± 0.017 s⁻¹, in agreement with literature reported values. In this study we also explored possible time-saving strategies to speed up data acquisition for k_Pi→γATP evaluation using simulations. The analysis indicates that it is feasible to carry out a ³¹P inversion transfer experiment in ~10 minutes or shorter at 7T with reasonable outcome in k_Pi→γATP variance for measurement of ATP synthesis in resting human skeletal muscle. We believe that this new IT data analysis approach will facilitate the wide acceptance of IT to evaluate ATP synthesis rate in vivo.

INTRODUCTION

Saturation transfer (ST) and inversion transfer (IT) are two techniques to probe the kinetics of magnetization exchange (ME) between spins at different resonance frequency (1–6). ³¹P NMR and ST have been the preferred techniques for noninvasive analysis of high energy phosphate metabolism for the last three decades (7–20). Extension of ST to high magnetic fields should be advantageous because of improved sensitivity, but implementation of prolonged saturating pulses in human subjects may be challenging because of hardware and SAR limitations, and additional data must be acquired to correct for off-resonance saturation, the so-called "spillover" effect (21,22), in spite of increased chemical shift dispersion (23). Inversion transfer may be technically simpler to implement at high fields, and it offers the advantages of low SAR, an inherently large initial labeling effect (Mz → -Mz versus Mz → 0), and insensitivity to “spillover” side effect.

Despite these potential advantages and applications in a number of kinetic studies (3–6,24–27), the inversion transfer technique is rarely used to measure the rate constant (k_Pi→ATP) for ATP synthesis in vivo while ST has been the method of choice (7–20,28–34). One reason that ST is so popular is that the prolonged saturation (5 – 9 seconds) at γ-ATP allows magnetization transfer effects to build up in Pi despite the intrinsically slow Pi ↔ γ-ATP exchange rate. Frequency-selective inversion at γ-ATP is limited by the relatively fast relaxation of the γ-ATP spin (apparent T₁ relaxation ~ 1 – 2 sec) and consequently the duration of any magnetization transfer effect is brief. At higher magnetic fields, the increased effect of chemical shift anisotropy further accelerates T₁ relaxation of ATP ³¹P spins. Our recent work has shown that the problem of fast relaxing γ-ATP can be overcome by using a band-selective inversion of multiple ³¹P resonances at 7T (35). Co-inversion of phosphocreatine (PCr) and all exchanging ATP spins results in a longer apparent T₁ relaxation of γ-ATP because the inverted magnetization is stored in the longer T₁ PCr pool (~ 5 – 6 sec). This approach leads to an increase in the magnetization transfer effect at Pi, making it suitable for quantitative evaluation of k_Pi→ATP at 7T.

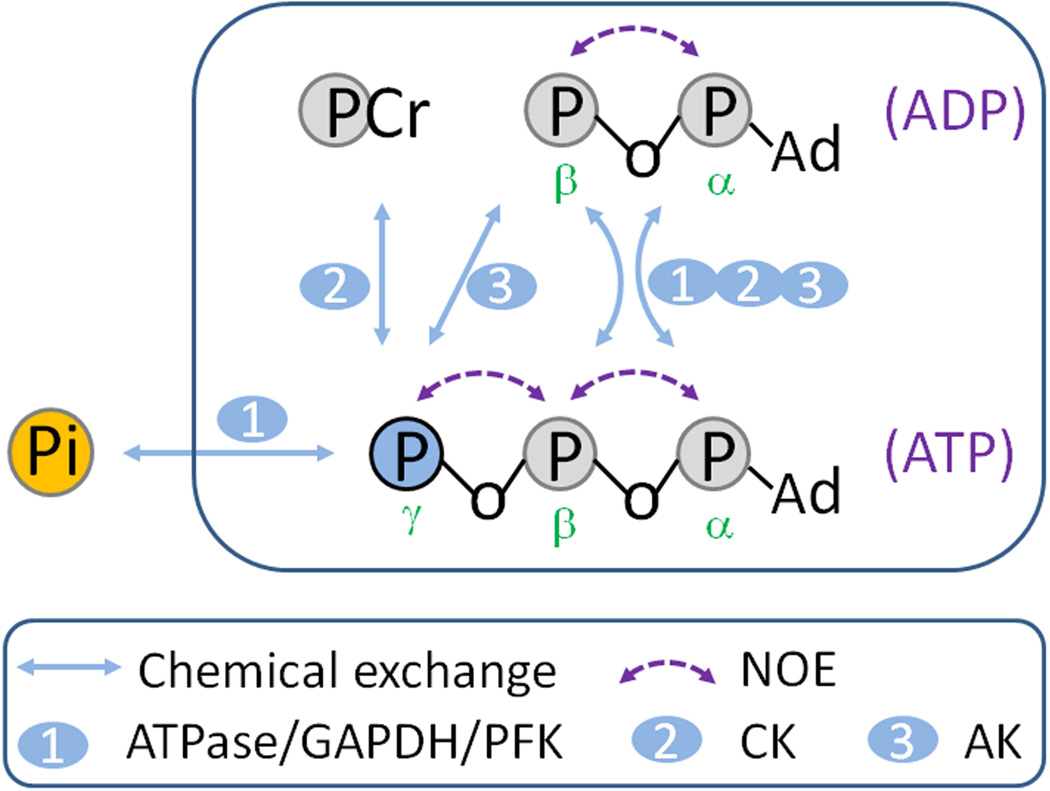
Analysis of inversion transfer data, however, is complex. The high-energy phosphate exchanges in vivo are described by a five-spin network including ³¹P in Pi, PCr, α-, β- and γ-ATP. In addition to the well-known chemical exchanges, intramolecular NOE effects have also been identified between γ-ATP ↔ β-ATP and between γ-ATP ↔ α-ATP (6,34,36). For such a complex system a full analytical solution is difficult to achieve. Instead, a numerical solution, although not intuitive, is more practical (6). In contrast to analysis of IT data, the complexity of the ³¹P spin exchange system in vivo does not affect ST data analysis because upon saturation of γ-ATP, the magnetization of Pi is uncoupled from the rest of the exchange network, resulting in a simple analytical solution to relate the Pi signal reduction and T₁ relaxation time to k_Pi→ATP (7,10,23).

In this study, we outline a new IT data analysis approach to obtain k_Pi→ATP based on a single Bloch-McConnell differential equation defined for Pi. By direct access to the rate of Pi magnetization change, it eliminates the need to solve the Bloch-McConnell differential equations for other exchange spins (PCr, α-, β- and γ-ATP) (Figure 1), thereby permitting an evaluation of k_Pi→ATP graphically by simple linear regression. The validity of this data analysis approach is demonstrated using datasets acquired from resting human calf muscle using EBIT, a band-selective inversion technique (35). We believe that this new IT data analysis approach will facilitate the wide acceptance of IT to evaluate ATP synthesis rate in vivo, a rate of fundamental importance in physiology (9–20).

FIG. 1.

Possible ³¹P magnetization exchange pathways in skeletal muscle. Abbreviations: CK, creatine kinase; AK adenylate kinase; PFK, phosphofructokinase; GAPDH, glyceraldehyde 3-phosphate dehydrogenase; NOE, nuclear Overhauser effect.

METHODS

Theory

For the chemical exchange reaction Pi ↔ γ − ATP, after applying an inversion pulse at γ − ATP either frequency-selective or band-selective, the rate of change in Pi Z-magnetization M_z (for clarity, the subscript “z” is omitted hereafter) in the inversion delay time t, can be described by the Bloch-McConnell equation as follows,

$${Ṁ}_{Pi}=\frac{M_{Pi}^o-M_{Pi}}{T_{1,Pi}}-k_{Pi\to \gamma ATP}{M}_{Pi}+k_{\gamma ATP\to Pi}{M}_{\mathrm{\gamma }\mathrm{A}\mathrm{T}\mathrm{P}}$$ [1]

where k denotes pseudo first-order kinetic rate constant, with the forward and reverse rate constants related by

$$k_{\gamma ATP\to Pi}=k_{Pi\to \gamma ATP}\frac{M_{Pi}^o}{M_{\gamma ATP}^o}$$ [2]

in which $M_{Pi}^o$ and $M_{\gamma ATP}^o$ denote the Z-magnetization at Boltzmann thermal equilibrium for Pi and γ-ATP, respectively. Substituting k_γATP→Pi in Eq [1] by Eq [2] gives:

$${ṁ}_{Pi}=\frac{1-m_{Pi}}{T_{1,Pi}}-k_{Pi\to \gamma ATP}(m_{Pi}+m_{\gamma ATP})$$ [3]

This expression can be rearranged into two different linear equations:

$$\frac{{ṁ}_{Pi}}{1-m_{Pi}}=\frac{1}{T_{1,Pi}}-k_{Pi\to \gamma ATP}\frac{m_{Pi}-m_{\gamma ATP}}{1-m_{Pi}}$$ [3a]

and

$$\frac{{ṁ}_{P\iota }}{m_{P\iota }-m_{\gamma ATP}}=\frac{1-m_{Pi}}{m_{Pi}-m_{\gamma ATP}}\frac{1}{T_{1,Pi}}-k_{Pi\to \gamma ATP}$$ [3b]

where m is the normalized Z-magnetization defined by:

$$m=M_i/M_i^o(i=\mathrm{P}\mathrm{i},\mathrm{\gamma }-\mathrm{A}\mathrm{T}\mathrm{P})$$ [4]

Eq [3] indicates that two separate terms contribute to ṁ_Pi: the first is the T₁ relaxation term, expressed as the product of 1/T_1,Pi by (1 − m_Pi), and the second is the chemical exchange term, expressed as the product of k_Pi→γATP by (m_Pi − m_γATP). Note that the quantity (1 − m_Pi) represents the exchange effect observed at Pi and that the quantity (m_Pi − m_γATP) represents the net difference in normalized magnetization between Pi and γ-ATP. Since both (1 − m_Pi) and (m_Pi − m_γATP) are experimentally measurable, those two unknowns T_1,Pi and k_Pi→γATP in Eq [3] thus can be solved by a simple linear fitting to ṁ_Pi. Alternatively, the parameters k_Pi→γATP and 1/T_1,Pi can be evaluated graphically from the intercept or slope of the linear relationship $\frac{{ṁ}_{Pi}}{1-m_{Pi}}$ versus $\frac{m_{Pi}-m_{\gamma ATP}}{1-m_{Pi}}$, or $\frac{{ṁ}_{P\iota }}{m_{P\iota }-m_{\gamma ATP}}$ versus $\frac{1-m_{Pi}}{m_{Pi}-m_{\gamma ATP}}$, as defined by Equations [3a] and [3b].

It is clear from Eqs [3, 3a and 3b] that, in order to obtain k_Pi→γATP and 1/T_1,Pi, the value of ṁ_Pi must be known. A way to obtain ṁ_Pi is first to construct the mathematical equation for the function m_Pi(t), from which ṁ_Pi(t) values can be obtained. With the boundary conditions m_Pi|_{t = 0} = 1 and m_Pi|_t→∞ = 1, the time-dependent function of m_Pi can be described by

$$m_{Pi}=1-a(e^{-{\lambda }_{1}t}-e^{-{\lambda }_{2}t})$$ [5]

where a, λ₁ and λ₂ are three constants, which can be accessed by numerical fitting the m_Pi ~ t dataset. With these three constants, it is straightforward to derive the ṁ_Pi values using the following differential equation (by applying ∂/∂t operation on Eq [5]),

$${ṁ}_{Pi}=a({\lambda }_1{e}^{-{\lambda }_{1}t}-{\lambda }_2{e}^{-{\lambda }_{2}t})$$ [6]

Based on Eq [3], one may also estimate the parameters k_Pi→γATP and T_1,Pi from the experimental m_Pi ~ t curve at a few special time points.

One example occurs when ṁ_Pi(t)=0 the transition point at which the curve m_Pi ~ t reaches a minimum and the effect of chemical exchange reaches the maximum.

$$0=\frac{1-m_{Pi}}{T_{1,Pi}}-k_{Pi\to \gamma ATP}(m_{Pi}-m_{\gamma ATP})$$

or

$$k_{Pi\to \gamma ATP}=\frac{1-m_{Pi}}{m_{Pi}-m_{\gamma ATP}}\frac{1}{T_{1,Pi}}(t=t^{\mathit{\text{min}}})$$ [7]

This particular time point is denoted by t^min. Equation [7] is equivalent to the formula given by Kuchel (1).

A second example is at t = 0, immediately after the inversion of γ-ATP, at which m_Pi = 1 but ṁ_Pi ≠ 0. At this initial time point, the T₁ relaxation term in Eq [3] becomes zero, and ṁ_Pi is given by:

$${ṁ}_{Pi}=k_{Pi\to \gamma ATP}(1-m_{\gamma ATP}(0))(t=0)$$ [8]

Equation [8] is equivalent to the formula given by Malloy et al (5).

For description of γ-ATP signal, the Bloch-McConnell-Solomon formula has to be used which contains more exchange terms contributed from five pools (Figure 1):

$${Ṁ}_{\gamma ATP}=\frac{M_{\gamma ATP}^o-M_{\gamma ATP}}{T_{1,\gamma ATP}}-k_{\gamma ATP\to Pi}{M}_{\gamma ATP}+k_{Pi\to \gamma ATP}{M}_{\mathrm{P}\mathrm{i}}-k_{\gamma ATP\to PCr}{M}_{\gamma ATP}+k_{PCr\to \gamma ATP}{M}_{\mathrm{P}\mathrm{C}\mathrm{r}}+\sigma (M_{\beta ATP}^o-M_{\beta ATP})-{\rho }_{\gamma ATP\to \beta ATP}{M}_{\gamma ATP}+{\rho }_{\beta ATP\to \gamma ATP}{M}_{\beta ATP}$$ [9]

where σ denotes the rate constant for the cross-relaxation between γ-ATP and β-ATP (NOE) and ρ denotes the rate constant for the chemical exchange between γ-ATP and β-ATP mediated by AK. If all chemical exchange and cross-relaxation effects among PCr, γ-, β-, and α-ATP are lumped in one single pool represented by γ-ATP, then a two-pool model will apply. Under the condition of band inversion with co-inversion of PCr and all ATP spins, this simplified two-pool exchange model yields:

$${Ṁ}_{\gamma ATP}=\frac{M_{\gamma ATP}^o-M_{\gamma ATP}}{T_{1\mathit{\text{app}},\gamma ATP}}-k_{\gamma ATP\to Pi}{M}_{\gamma ATP}+k_{Pi\to \gamma ATP}{M}_{\mathrm{P}\mathrm{i}}$$ [10]

where T_1app,γATP denotes the apparent T₁ relaxation time of γ-ATP, which lumps T₁ relaxation and all exchange effects together except the exchange pathway involving Pi (Figure 1). In other words, the interaction of γ-ATP with other ³¹P spins in PCr, ADP and ATP is treated as part of molecular “lattice” and is incorporated into T_1app,γATP (35). Using this approximation, the k_Pi→γATP and T_1,Pi values can be evaluated numerically by the following matrix equation:

$$M(t)=M^o-e^{At}(M^o-M(0))$$ [11]

in which $M^o=[M_{Pi}^o;M_{\gamma ATP}^o]$; M(0) = [M_Pi(0); M_γATP(0)], which is the initial Z-magnetization immediately after band inversion; and A is the exchange matrix

$$A=\left[\begin{array}{cc}\hfill -1/T_{1,Pi}-k_{Pi\to \gamma ATP}\hfill & \hfill k_{\gamma ATP\to Pi}\hfill \\ \hfill k_{Pi\to \gamma ATP}\hfill & \hfill -1/T_{1\mathit{\text{app}},\gamma ATP}-k_{\gamma ATP\to Pi}\hfill \end{array}\right]$$ [12]

Note that, unlike Eqs [3,3a,3b], Equation [11] contains an additional unknown parameter T_1app,γATP through the matrix A.

Human Subjects

The protocol was approved by the Institutional Review Board of the University of Texas Southwestern Medical Center. Prior to the MRS study, informed written consent was obtained from all participants. Fifteen subjects (9 male and 6 female), aged 27 ± 4 yr and BMI 24 ± 2, participated in the study. Spectra from 10 subjects reported elsewhere (35) were reanalyzed using the new methods, and new data from 5 subjects were acquired and analyzed. All subjects were in good general health with no history of peripheral vascular, systemic or myopathic diseases. To avoid possible exercise-associated physiological variations among subjects, all subjects were asked to refrain from any physical activity of moderate or high intensity for 24 hours prior to the study, and subjects sat at rest for 20 minutes prior to the scan. Heart rate and blood oxygen saturation level were monitored during the scan. The study was well-tolerated by all subjects.

MRS Protocol

The general MRS acquisition protocol has been described previously (35). Briefly, FID-based ³¹P spectra were acquired from calf muscle for each subject using a band-selective inversion sequence (180° – t – 90° – τ), which was comprised of an adiabatic inversion pulse, followed by a varying inversion delay time t, a hard 90° readout pulse, and a recovery period τ. The inversion time was varied from 30 to 10000 ms with 12 data points spaced logarithmically (t = 30, 626, 1253, 1923, 2641, 3414, 4252, 5167, 6174, 7294, 8556 and 10000 msec). The inversion pulse is a trapezoid-shaped adiabatic pulse with 42 ms duration and an excitation frequency band of 2500 Hz, centered at 150 Hz upfield from α-ATP, which is set to co-invert PCr and ATP spins but not Pi and PDE. Other NMR parameters were TR 30 sec, NA 4 averages, 4 K sampling points zero-filled to 8 K. The chemical shift of the ³¹P MR spectra was referenced to PCr at 0 ppm. Each ³¹P NMR spectrum was Fourier transformed, processed with Gaussian apodization (6 Hz) using the scanner software (SpectroView, Philips Healthcare), and further analyzed using Matlab (Mathworks) routines to evaluate the normalized magnetization for Pi, PCr, α-, β- and γ-ATP, based on the magnitude of the observed ³¹P peaks. The m_Pi data were fitted by Equation [5] to obtain the fitting parameters a, λ₁ and λ₂.

To evaluate the exchange rate constant k_Pi→γ-ATP and T₁ value for Pi, the ṁ_Pi values were first obtained by Eq [6]. Then these ṁ_Pi data were fit by Eq [3] against the quantities (1 − m_Pi) and (m_Pi − m_γATP). Alternatively, simpler linear relationship can be obtained to evaluate k_Pi→γ-ATP and T_1,Pi by plotting $\frac{{ṁ}_{Pi}}{1-m_{Pi}}$ versus $\frac{m_{Pi}-m_{\gamma ATP}}{1-m_{Pi}}$, or $\frac{{ṁ}_{P\iota }}{m_{P\iota }-m_{\gamma ATP}}$ versus $\frac{1-m_{Pi}}{m_{Pi}-m_{\gamma ATP}}$, as defined by Eqs [3a and 3b] respectively. Note that, since the quantity (1 − m_Pi) appears as denominator in Eq [3a], we chose to exclude the first data point with (1 − m_Pi) ~ 0 from data analysis. For comparison, the k_Pi→γ-ATP and T_1,Pi values were also obtained by solving Eq [11] numerically.

To examine the reliability of these different evaluation approaches, the k_Pi→γ-ATP and T₁ values for Pi were also analyzed from the simulated m_Pi and m_γATP datasets generated using a set of known parameters (T_1,P = 6.5 sec, T_1app,γATP = 4.0 sec, k_Pi→γ-ATP = 0.065 sec⁻¹, and M^o_γ-ATP / M^o_Pi = 2.6) at varying delay time (30 – 10000 msec, 12 data points) based on 2-site chemical exchange model. To imitate the effect of spectral background noise on small Pi signal, the m_Pi dataset was modulated by pseudo-random noise with a Gaussian distribution variance of 2% (σ ranged from −1% to 1%) generated by Box Muller transformation. A total of 1000 noise-mixed m_Pi datasets were analyzed using a self-written Matlab routine for evaluation of the variance in k_Pi→γ-ATP and T_1,Pi values.

An interesting feature embedded in Eqs [3, 3a and 3b] is the absence of T_1app,γATP in ṁ_Pi. To test this feature, simulated m_Pi and m_γATP datasets were generated at varying T_1app,γATP values (1, 2, 4, and 6 sec) to examine its effect on the outcome of k_Pi→γ-ATP and T_1,pi.

Our in vivo ³¹P study takes a total scan time of 24 minutes for collecting a series of 12 spectra at varying inversion delay times with constant TR of 30 s and 4 repeated acquisitions. Determination of k_Pi→γ-ATP and T_1,Pi as rapidly as possible is an important experimental goal, and for this reason, the following scenarios were examined by simulations. In simulation #1 (denoted as S1), the noise level was doubled (σ ranged from −2% to 2% in Gaussian distribution), corresponding to one single data acquisition for each inversion time data point, or a simulated total scan time of 6 minutes for the whole series with 12 delay times. In simulation #2 (denoted as S2), only the first 6 data points in the inversion delay series were sampled (inversion delay time = 30, 626, 1253, 1923, 2641, and 3414 msec), corresponding to a scan time of 12 minutes. In simulation #3 (denoted as S3), 6 data points were acquired at large intervals (inversion delay time = 30, 1253, 2641, 4252, 6174, and 8556 msec), which also corresponds to a reduced scan time of 12 minutes.

Statistical Analysis

All data are reported as mean ± standard deviation, calculated using standard functions in Matlab.

RESULTS

Observation of magnetization exchange between Pi and γ-ATP

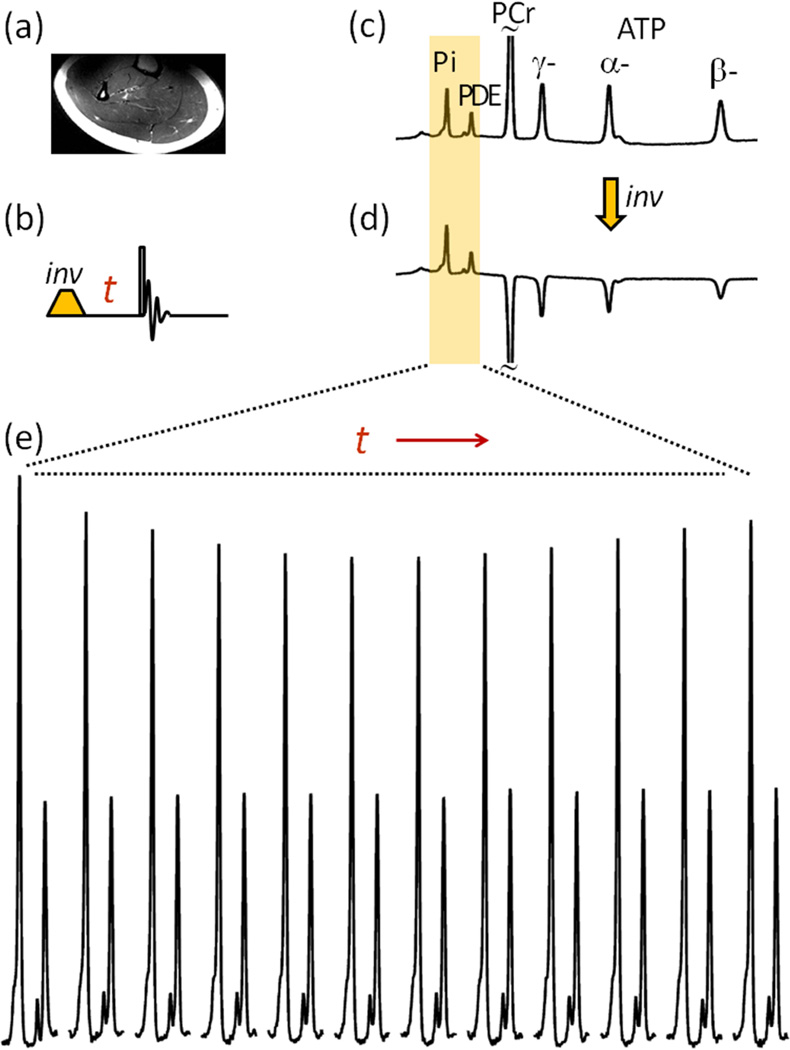
As illustrated in Figure 2, the increased chemical shift dispersion at ultra-high field 7T facilitates band-selective inversion. Upon co-inversion of ATP and PCr signals, the intensity of Pi signal in calf muscle is significantly reduced due to Pi ↔ γ-ATP exchange as shown (Figure 2e, n = 15 subjects). In contrast, there is no change in signal intensity of PDE (Figure 2e), a relatively inert metabolite not actively involved in exchange with other high energy phosphates in vivo. The absence of effect of the inversion pulse on the PDE signal illustrates the limited spillover to the Pi signal. As anticipated, the Pi signal continues to decrease as the inversion delay time t increases. After reaching a minimum in intensity, the Pi signal gradually recovers back to the equilibrium state with a further increase in t (Figure 2e). Such a biphasic feature of Pi signal change was clearly observed in the ³¹P spectra of all subjects studied (n = 15); the maximal reduction of Pi signal ranged from 13 to 21 % and typically occurred between t ~ 3.4 – 4.5 sec (Figure 3).

FIG. 2.

Image and ³¹P NMR of Human Calf Muscle. (a) T2w MR image. (b) Sequence of the band-selective inversion pulse used in the experiment. (c) and (d) ³¹P NMR spectra acquired from resting muscle before (c) and after (d) applying the band inversion sequence. (e) Evolution of the Pi signal with the inversion delay time t. The spectral data represents averages for n = 15 subjects.

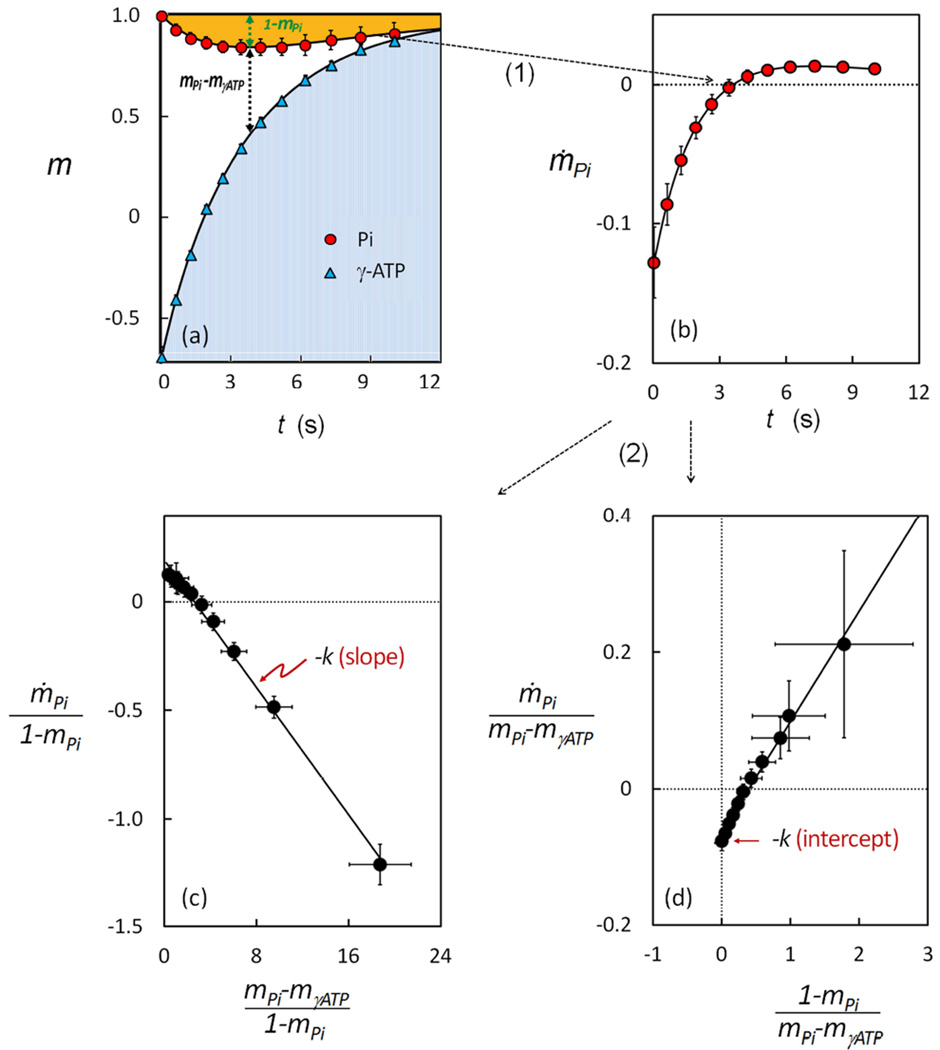
FIG. 3.

Alternative Analyses of Band Inversion-Transfer Data Sets (n = 15 subjects). (a) The m-plot, showing dependence of Pi and γ-ATP magnetization (m_Pi and m_γATP) on inversion delay time t. (b) The ṁ–plot, showing the rate of change of Pi signal with inversion delay time t. (c) The linear relationship between $\frac{{ṁ}_{Pi}}{1-m_{Pi}}$ and $\frac{m_{Pi}-m_{\gamma ATP}}{1-m_{Pi}}$, with a slope defined by - k_Pi→γATP and an intercept defined by 1/T_1,Pi. (d) The linear relationship between $\frac{{ṁ}_{P\iota }}{m_{P\iota }-m_{\gamma ATP}}$ and $\frac{1-m_{Pi}}{m_{Pi}-m_{\gamma ATP}}$, with a slope defined by 1/T_1,Pi and an intercept defined by - k_Pi→γATP.

Unlike the non-inverted ³¹P signals (Pi and PDE), all the inverted signals (PCr, α-, β- and γ-ATP) recovered exponentially with t (Figure 3 and Supplementary Figure 1S), but at varying recovery rates (PCr < γ-ATP < β-ATP < α-ATP). Notably, the recovery of γ-ATP becomes much slower than that of α- and β-ATP, and more similar to the trend observed for PCr. This yields a long period of delay time with (m_Pi − m_γATP) > 0, the driving factor for producing the ME effect at Pi (Figure 3a). As will be clear later, to be able to contribute to the net buildup of the ME effect at Pi, the exchange term k_Pi→γATP (m_Pi − m_γATP) has to be sufficiently large to overcome the draining effect of the T₁ relaxation term (1 − m_Pi)/T_1,Pi, which occurs only in the period t = 0 ~ 4 sec during which the ME effect (1 − m_Pi) is in a trend of increase (Figure 3a).

Evaluation of ṁ_Pi from m_Pi

To take advantage of the simple relationship between ṁ_Pi and k_Pi→γ-ATP, as described by Bloch-McConell equation [3] or its two simpler linear forms (Eqs [3a] and [3b]), for calculation of k_Pi→γ-ATP, the first step is to evaluate the ṁ_Pi values. These values were derived by Eq [6] using the fitting constants (a, λ1 and λ2) obtained by fitting the experimental m_Pi(t) data (Figure 3a) according to Eq [5]. As shown in Figure 3b (n = 15 subjects), with increase in inversion delay time, the ṁ_Pi values is changed from negative to positive, with transition occurring at t^min ~ 4 sec. Within t = 0 – 4 sec, the ṁ_Pi magnitude decreases with t (Figure 3b). However, a further increase in inversion delay time (t > 4 sec) leads to a rise and then fall in the ṁ_Pi magnitude, with a maximum occurring at t ~ 7.3 (Figure 3b). This feature is not visually identifiable in the curve m_Pi ~ t (Figure 3a), but becomes obvious when the ṁ_Pi value is separated into the relaxation and exchange term by Eq [3] (Figure 4b).

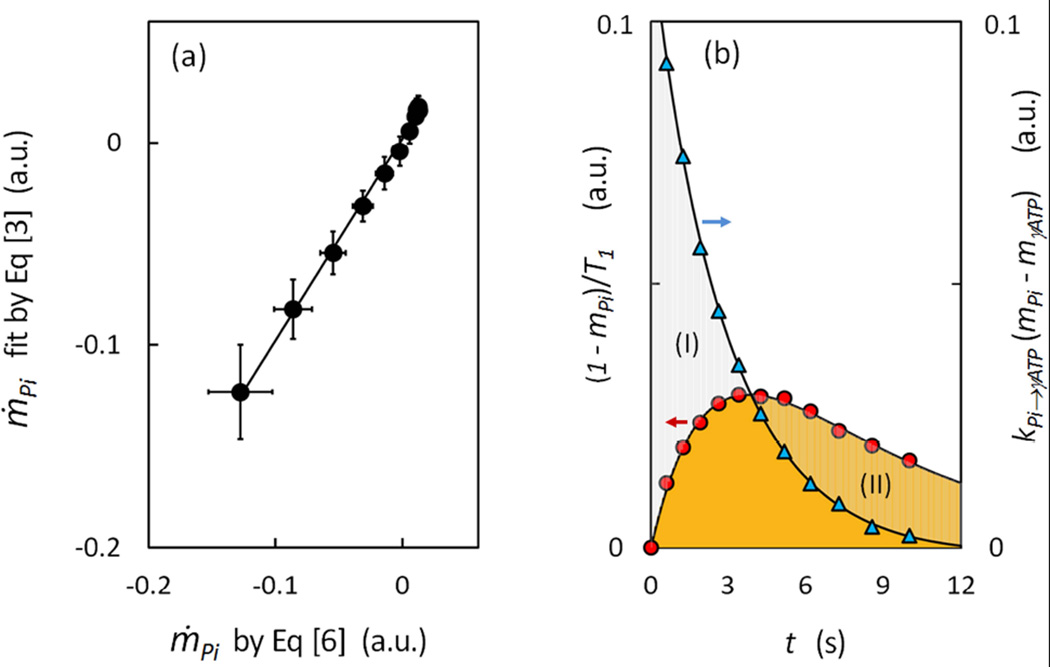
FIG. 4.

Analysis of Relaxation and Exchange Components in Rate of Change of Pi Signal. (a) Linear correlation of ṁ_Pi data derived by Eq [6] and those by fitting to Eq [3] (n = 15 subjects). The resultant fitting parameters k_Pi→γATP and T_1,Pi are presented in (b) with a multiplication factor (m_Pi − m_γATP) and (1 − m_Pi) to separate the relaxation term from the exchange term in ṁ_Pi as defined by Eq [3]. The region marked by (I) indicates the dominance of the exchange term over the relaxation term, and the opposite for the region marked by (II).

Evaluation of k_Pi→γ-ATP from ṁ_Pi

The simplest way to assess k_Pi→γ-ATP is to divide ṁ_Pi value by (m_Pi − m_γATP) at t = 0 (Eq [8]). This yielded 0.076 ± 0.014 s⁻¹ using the measurements at the first data point (t = 0.03 sec) as an approximation. The value of k_Pi→γ-ATP can also be estimated, if T_1,Pi is known, from the ratio (1 − m_Pi) / (m_Pi − m_γATP) at ṁ_Pi = 0 when t = t^min (Eq. [7]). This yielded a k_Pi→γ-ATP value in the range 0.048 – 0.096 s⁻¹ assuming a possible T_1,Pi ranging from 3.5 sec (37) to 7.0 sec (6).

To evaluate k_Pi→γ-ATP by linear graphic approach, we plotted the data $\frac{{ṁ}_{Pi}}{1-m_{Pi}}$ against $\frac{m_{Pi}-m_{\gamma ATP}}{1-m_{Pi}}$, (Figure 3c) and $\frac{{ṁ}_{P\iota }}{m_{P\iota }-m_{\gamma ATP}}$ against $\frac{1-m_{Pi}}{m_{Pi}-m_{\gamma ATP}}$ (Figure 3d), using the above-derived ṁ_Pi values (n = 15 subjects). Both datasets yielded a remarkably good linear relationship (y = −0.069 x + 0.181 and R² = 0.996 in Figure 3c, and y = 0.159 x − 0.061 and R² = 0.997), as anticipated from Eqs [3a] and [3b], respectively. More importantly, the resultant k_Pi→γ-ATP values from two different linear datasets agreed reasonably well, as summarized in Table 1. In addition, a direct ṁ_Pi fitting by Eq [3] also yielded an excellent linear correlation (y = 0.996x + 0.002 and R² = 0.996, Figure 4a), with k_Pi→γ-ATP result (Table 1) comparable to those by other two linear methods (Eqs [3a] and [3b]) and by the numeric matrix approach (Eq [11]). On average, these three different linear data analysis methods yielded a rate constant k_Pi→γ-ATP of 0.066 ± 0.017 sec⁻¹ and T_1,Pi value of 5.75 ± 1.91 sec for the group of the subjects studied (n = 15). An apparent T₁ value of 4.02 sec was also obtained by the numeric matrix approach for γ-ATP. Additionally, the fitting procedure by Eq [3] also provides a quantitative separation of ṁ_Pi into two parts distributable to relaxation- and exchange-related terms, respectively, which clearly illustrates the evolution of these two terms over the inversion delay time (Figure 4b).

Table 1.

Unidirectional rate constant for the ATP synthesis reaction Pi → γ-ATP in resting human skeletal muscle (n = 15)

kPi→γ-ATP (s−1)	Fitting equation
0.067 ± 0.012	Eq. [11]
0.068 ± 0.014	Eq. [3]
0.069 ± 0.017	Eq. [3a]
0.061 ± 0.019	Eq. [3b]

The Pi → ATP flux in resting skeletal muscle was 8.47 ± 2.18 mmol/kg wet weight, calculated by the product of the above-derived k_Pi→γ-ATP value, and the Pi concentration of 2.14 mmol/kg wet weight measured from the integral of Pi signal at 4.83 ppm in reference to that of γ-ATP (5.5 mmol/kg wet weight) in fully relaxed ³¹P MR spectrum.

Data simulation and analysis

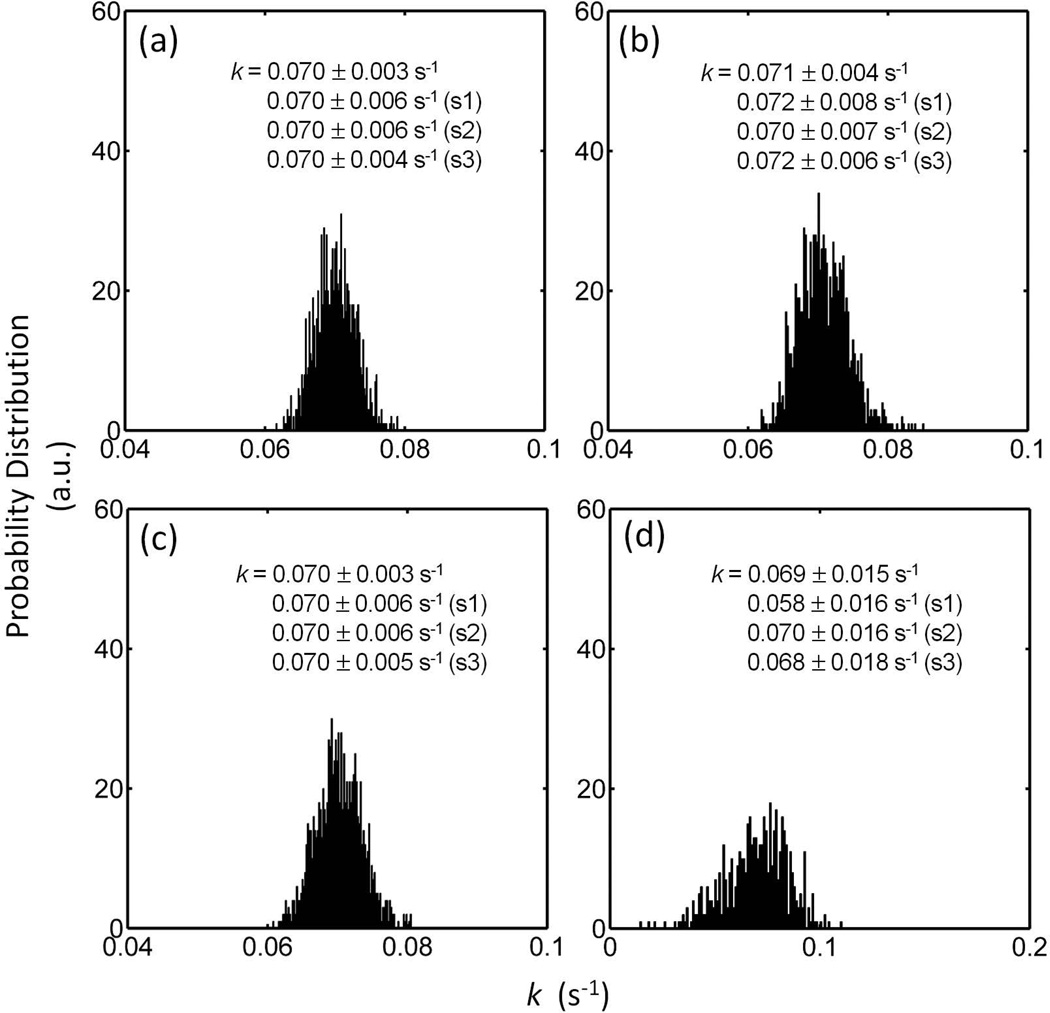
Figures 5 shows the analysis results for k_Pi→γ-ATP using the m_Pi and m_γATP datasets generated at given k_Pi→γ-ATP and T_1,Pi values and mixed with random noises. For a large number of executions (N = 1000), the mean values obtained for k_Pi→γ-ATP by these four different data analysis approaches are very similar to the input value (k_Pi→γ-ATP = 0.07 sec⁻¹), but each approach shows a different dispersion pattern, as indicated by the data histograms (Figure 5). A significant large variance in k_Pi→γ-ATP is noticed in the histogram by Eq [3b] approach, as compared to other three methods defined by Eqs [3], [3a] and [11], suggesting it may be a less favorable approach. Among the three remaining approaches with smaller variances, Eqs [3] and [11] yielded slightly better outcomes in k_Pi→γ-ATP in terms of mean and standard deviation (Figure 5). Similar features also appear in the histograms for T_1,Pi analysis results (Supplementary Figure S2).

FIG. 5.

Effects of Noise on Evaluation of k_Pi→γATP. The histograms represent the results of 1000 datasets in simulation of a scan with 12 data points at noise level ± 1%, using analysis approaches defined by Eqs [11] (a), [3] (b), [3a] (c) and [3b] (d). The derived k_Pi→γATP results are compared with those obtained for simulation at a higher noise level of ± 2% (S1), simulation of a scan collecting only the first 6 data points (S2), and simulation of a scan with 6 data points at large intervals in a wide range of delay times (S3).

For the three different time-saving acquisition strategies examined by simulation, it is found that a 100% increase in noise level (simulation S1), equivalent to a 4-fold decrease in NA and scan time, led to a 100% increase in variance in k_Pi→γ-ATP (Figures 5), as evaluated by Eqs [3], [3a] and [11]. A comparison between the two scenarios with 50% reduced data points (S2 and S3) indicates that the strategy with larger sampling intervals (S3) appears to be a better choice for k_Pi→γ-ATP determination. The T_1,Pi analysis on the same simulation datasets showed the similar findings (Supplementary Figure S2).

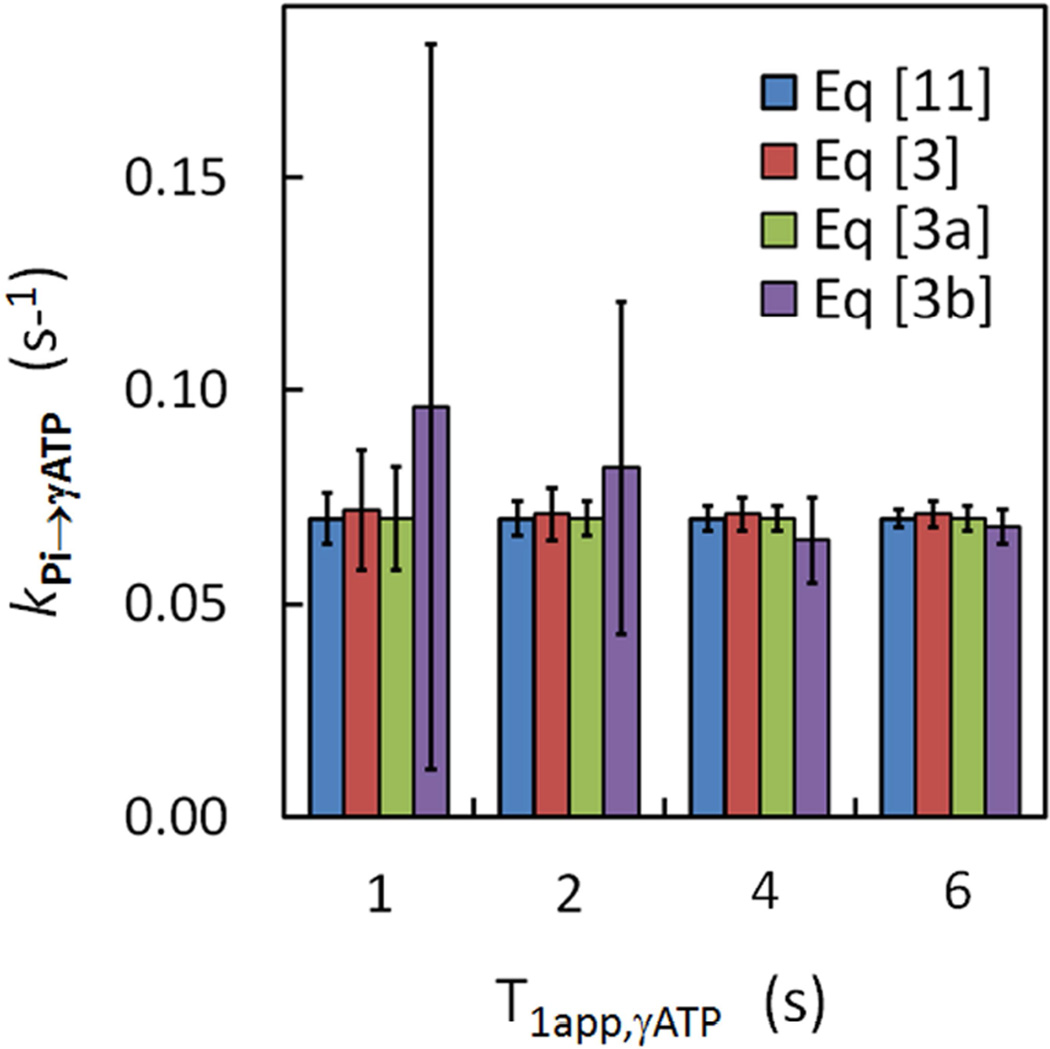
For those three linear equations (Eqs [3], [3a] and [3b]), an obvious feature is the absence of T_1app,γ-ATP, in contrast to Eq [11] in which T_1app,γ-ATP is an unknown that has to be solved in order to get k_Pi→γ-ATP. Simulations were performed to test whether a change in T_1app,γATP would affect k_Pi→γ-ATP determination. For the two linear approaches defined by Eqs. [3 and 3a], simulation results (Figure 6) indicate that there was no significant difference in mean k_Pi→γ-ATP value when T_1app,γATP was varied from 1 to 6 sec; the obtained k_Pi→γ-ATP values were comparable to that by the matrix approach defined by Eq [11] and consistent with the input value. However, the difference in k_Pi→γ-ATP between the linear approach by Eq [3b] and other approaches is noticeably large (Figure 6). Especially, the variance in k_Pi→γ-ATP by Eq [3b] was increased dramatically when T_1app,γATP was decreased from 4 to 1 sec, suggesting that Eq [3b] approach may not be reliably applicable for k_Pi→γ-ATP determination when γ-ATP relaxation is fast. At T_1app,γATP = 1 sec, which is equivalent to narrow band selective inversion, the matrix approach defined by Eq [11] yielded the best performance (Figure 6), with a variance ~2 – 3 fold smaller than those by Eqs [3] and [3a]. Similar performance was also found in T_1,Pi analysis (Supplementary Figure S3) in which a large variance in T_1,Pi was given by Eq [3b] approach, as compared to other approaches.

FIG. 6.

Effects of T_1app,γATP on analysis of k_Pi→γATP. Comparison of different fitting approaches on analysis of simulation data at different apparent T₁ values for γ-ATP.

DISCUSSION

Although the ability to probe exchange kinetics between metabolites using IT techniques has long been recognized, its use has behind alternative ST techniques for measurement of ATP synthesis rates (commentary (17) and the references therein). The added chemical shift dispersion and sensitivity of high field research scanners provide the motivation to reexamine the possible benefits of measuring such exchanges in vivo using IT methods (6). The preference of ST over IT may also have much to do with the ease of data analysis in ST, which permits the evaluation of k_Pi→ATP by a simple expression, rather than a non-intuitive way as in IT, numerically solving two or more simultaneous equations with multiple unknown parameters. Certain strategies toward simplifying IT data analysis were suggested in early kinetic studies. For example, early studies (4,5) showed that the rate constant for a two-spin system can be obtained from the initial slope of the curve M_z(t) ~ t by a formula equivalent to Eq [8]. derived directly from the basic Bloch-McConnell equation. In 1990 Kuchel (1) also proposed a simple formula, equivalent to Eq [7], to calculate the rate constant based on the inverted and non-inverted magnetizations at the time point with ṁ = 0 (for non-inverted spin).

In the current study, we suggest a method to directly utilize ṁ_Pi, as defined by the original Bloch-McConnell equation for analysis of k_Pi→γ-ATP. The ṁ_Pi data can be easily derived from the experimental m_Pi data (Eqs [5] and [6], and Figures 3a and 3b). Unlike m_Pi, which has a complex relationship with k (5), ṁ_Pi is linearly correlated to k (Eq [3]), with a simple proportional coefficient (m_Pi − m_γATP). As illustrated in Figure 3b, the trend in ṁ_Pi ~ t is governed by two counteractive terms, the exchange term k_Pi→γATP (m_Pi − m_γATP), which measures the magnitude of the net ME flux, and the relaxation term (1 − m_Pi)/T_1,Pi, which measure the magnitude of T₁ relaxation effect at Pi.

Once ṁ_Pi is derived, one can easily determine k_Pi→γATP and T_1,Pi by Eq [3, 3a or 3b], each having certain advantages and limitations. Eqs [3a and 3b] both are visually intuitive, with k_Pi→γATP and 1/T_1,Pi shown as the slope and intercept (or vice versa) of a visible line while Eq [3] provides a direct quantitative separation of relaxation and exchange terms (Figure 4b), from which one can easily understand how these two terms evolve with delay time and contribute to the observed ME effect.

Despite the difference in mathematical expression, for resting human calf muscle, the data analysis using Eqs [3, 3a and 3b] yielded comparable k_Pi→γATP results, as that by the numerical matrix approach defined by Eq [11] (Table 1). These results are also in agreement with the corresponding k_Pi→γATP value (0.050 s⁻¹) by an integrated numerical analysis method on data acquired using EKIT sequence (6). They are also consistent with the literature reported k_Pi→γATP values ranging from 0.04 to 0.12 s⁻¹ using ST approach (review (9) and the references therein). The T_1,Pi relaxation times obtained by these linear approaches are also in reasonably agreement with the literature values (6,37) at 7T.

It should be noted that, although the IT technique is not able to decouple Pi from the rest of the ³¹P exchange network in vivo as ST does through prolonged irradiation at γ-ATP, the IT data analysis method presented here requires no detailed knowledge about the various exchange reaction that the inverted γ-ATP is involved for evaluation of k_Pi→γATP. This means that, selection of IT or ST techniques depends on practical considerations such as available sequences in the MRI scanner and the required experimental time. Since IT technique does not require additional mirror irradiation to control the “spillover” effect, it is an advantage over progressive ST on this respect.

A careful analysis of the simulated datasets indicates that it is possible to get reliable rate constant k_Pi→γATP by using fewer data points or fewer acquisition averages to save scan time. One most attractive strategy is to acquire data at relatively large intervals to cover a wide range of delay times (simulation S3). It is possible that one can complete the data acquisition with ~10 minutes and still able to obtain reliable k_Pi→γATP values. While all linear approaches presented here are mathematically simpler than the numerical matrix approach, the linear data analysis approach defined by Eq [3a] offers less variance values and larger suitability range (Figures 5–6).

In summary, we demonstrated that, using simple linear fitting procedure, IT data acquired by band inversion technique can be used to derive the k_Pi→γATP parameter for evaluation of the physiologically important Pi → ATP flux. Band inversion transfer is one alternative to ST for the measurement of ATP synthesis in vivo.

Supplementary Material

Supp FigureS1-S3

FIG. S1. Evolution of PCr, α- and β-ATP signals with the inversion delay time t.

FIG. S2. Effects of Noise on Evaluation of T_1,Pi. The histograms represent the results of 1000 datasets in simulation of a scan with 12 data points at noise level ± 1%, using analysis approaches defined by Eqs [11] (a), [3] (b), [3a] (c) and [3b] (d). The derived T_1,Pi results are compared with those obtained for simulation at a higher noise level of ± 2% (S1), simulation of a scan collecting only the first 6 data points (S2), and simulation of a scan with 6 data points at large intervals in a wide range of delay times(S3).

FIG. S3. Effects of T_{1app,γ ATP} on analysis of T_1,Pi. Comparison of different fitting approaches on analysis of simulation data at different apparent T₁ values for γ-ATP.

Abbreviation used

IT

inversion transfer

ST

saturation transfer

NOE

nuclear Overhauser effect

ME

magnetization exchange

MT

magnetization transfer

SAR

specific absorption ratio

EKIT

exchange kinetics by inversion transfer

EBIT

exchange kinetics by band inversion transfer

Eq

Equation

Pi

inorganic phosphate

ATP

adenosine triphosphate

ADP

adenosine diphosphate

PCr

phosphocreatine

PDE

phosphodiesters

CK

creatine kinase

AK

adenylate kinase

PFK

phosphofructokinase

GAPDH

glyceraldehydes-3-phosphate dehydrogenase