PSHREG: A SAS macro for proportional and nonproportional subdistribution hazards regression

Highlights

• •The %pshreg SAS macro fits Fine-Gray models for competing risks.
• •The macro first modifies a given data set and then uses PROC PHREG for analysis.
• •Many useful features of PROC PHREG can now be applied to a Fine-Gray model.
• •Time-dependent effects can be accommodated by time-by-covariate interactions.
• •For small data sets, the Firth correction is available.

Abstract

We present a new SAS macro %pshreg that can be used to fit a proportional subdistribution hazards model for survival data subject to competing risks. Our macro first modifies the input data set appropriately and then applies SAS's standard Cox regression procedure, PROC PHREG, using weights and counting-process style of specifying survival times to the modified data set. The modified data set can also be used to estimate cumulative incidence curves for the event of interest. The application of PROC PHREG has several advantages, e.g., it directly enables the user to apply the Firth correction, which has been proposed as a solution to the problem of undefined (infinite) maximum likelihood estimates in Cox regression, frequently encountered in small sample analyses.

Deviation from proportional subdistribution hazards can be detected by both inspecting Schoenfeld-type residuals and testing correlation of these residuals with time, or by including interactions of covariates with functions of time. We illustrate application of these extended methods for competing risk regression using our macro, which is freely available at: http://cemsiis.meduniwien.ac.at/en/kb/science-research/software/statistical-software/pshreg, by means of analysis of a real chronic kidney disease study. We discuss differences in features and capabilities of %pshreg and the recent (January 2014) SAS PROC PHREG implementation of proportional subdistribution hazards modelling.

1. Introduction

Competing risks arise in the analysis of time-to-event data, if for some subjects the event of interest is precluded by a different type of event occurring before. Competing risks may be encountered, e.g., if interest focuses on a specific non-terminal event type such as dialysis onset. In such a situation, death before dialysis onset constitutes a competing risk.

It has frequently been pointed out that in presence of competing risks, the standard product-limit method for estimating the survival function for the event of interest yields biased results; cf., e.g., Bakoyannis and Touloumi [1]. The main assumption of this method is that any subject whose survival time is censored will experience the event of interest if followed up long enough. This does not hold if competing risks are present, as the occurrence of the event of interest is precluded or its probability of occurrence is modified by an antecedent competing event. As a remedy, the cumulative distribution function, generally denoted cumulative incidence function (CIF), proposed by Kalbfleisch and Prentice [2] can be used. While the naive product-limit estimate of CIF, treating the competing risk as an independent censoring mechanism, will reach 1 with an infinite follow-up time, the proper CIF estimate never reaches 1 as a consequence of presence of a certain proportion of subjects who will experience the competing event.

Two different ways of modelling competing risks data have been proposed. The first one analyses the cause-specific hazard of each event type separately, by applying Cox regression targeting each event type in turn, and censoring all other event types. By a complete analysis of all event types by such cause-specific Cox models, estimated cumulative incidence curves for an event of interest can be estimated using specialized software [3]. By contrast, the proportional subdistribution hazards (PSH) model proposed by Fine and Gray [4] directly aims at modelling differences in the cumulative incidence of an event of interest. Its estimation is based on modified risk sets, where subjects experiencing the competing event are retained even after their competing event. In case of censoring (which is the rule rather than the exception), a modification of this simple principle was proposed such that the weight of those subjects artificially retained in the risk sets is gradually reduced according to the conditional probability of being under follow-up had the competing event not occurred.

The two different approaches to competing risks modelling are both appropriate but have different aims: while modelling the cause-specific hazards targets aetiologic research questions by modelling the effect of covariates on event rates among subjects at risk, the PSH model is useful for medical decision making and prognosis, as it models the absolute risk of an event. Differences between these two approaches are discussed, e.g., in Wolbers et al. [5] and Andersen et al. [6]. Here we focus on the latter approach.

Programs for fitting a Fine-Gray regression model are available in R (e.g., package cmprsk by Gray [7]) and STATA (stcrreg command by StataCorp. [8]). Waltoft [9] describes a SAS macro for cumulative incidence curve estimation via Poisson regression. Zhang and Zhang [10] provide a SAS macro for the special case of computing adjusted cumulative incidence curves for two treatment groups. However, a publicly available and fairly general implementation of the Fine-Gray regression model in SAS has yet been missing. Our SAS macro %pshreg was written to fill this gap. The macro modifies an input data set by separating follow-up periods of patients with competing events into several disjoint sub-periods with declining weights, following the suggestions in Fine and Gray [4] and Geskus [11]. This allows using SAS's PROC PHREG to compute the proportional subdistribution hazards model. Thus, all options offered by PROC PHREG for verifying and relaxing the assumption of proportional subdistribution hazards can be used, including the computation and display of unscaled and scaled Schoenfeld-type residuals or extending the model by time-dependent effects of covariates.

In very small data sets with few events, monotone pseudo-likelihood may cause parameter estimates to diverge to ±∞. This phenomenon typically occurs if events are observed in only one of two levels of a binary covariate. The application of the Firth-correction [12], which is readily implemented in PROC PHREG, may be useful in such circumstances [13], [14].

In the remainder of this manuscript we first briefly review the estimation of proportional subdistribution hazards models with time-fixed and time-dependent effects, and illustrate Firth's bias correction method. Later we explain the most important macro options in detail and explain the structure of the macro code. Subsequently, a worked example illustrates different aspects of application of the macro. The manuscript closes by discussing what has been achieved and the differences in features and capabilities of %pshreg and the recent SAS implementation of PSH modelling in PROC PHREG (SAS/STAT Version 13.1, released in January 2014).

2. Methodological background

2.1. An example for competing risks

As a motivating example, we consider a study on chronic kidney disease (CKD) recently performed at the Medical University of Vienna including 273 patients, who were diagnosed with CKD between stages I and IV at their first visit of the University's outpatient department [15]. In this study, researchers were interested in modelling the time to dialysis onset, i.e., the time to progression to end stage renal disease. The continuous variables age per decade (age), log₂ of urine osmolarity (logUosm), log₂ of creatinine clearance (logCCR), log₂ of proteinuria (logProt) and the binary variables beta-blocker (bblock), diuretic therapies (diur) and type of underlying renal disease (pkd), all measured at the day of diagnosis, were considered as important in prognosis of the cumulative incidence of dialysis onset. The median follow-up time of the study was 92 months. The event of interest, dialysis onset, could be observed in 105 patients (38.46%). CKD patients are at higher risk of mortality than the normal population, and thus, in our study, death before dialysis onset constitutes a competing event (n = 35, 12.82%).

2.2. Notation

Generally, we assume observations on m covariates in n subjects, and we let x_il, t_i and ɛ_i denote subject i's (i = 1, …, n) values of covariate l (l = 1, …, m), observed survival time and follow-up status, respectively. For the latter, we consider ɛ_i = 0, ɛ_i = 1, and ɛ_i = 2 as denoting a censored time t_i, an event of interest occurred at t_i, and a competing event occurred at t_i, respectively. Furthermore, we assume that there are r distinct times at which events of interest have occurred, and that t₍₁₎, …, t_(r) denote the corresponding ordered event times.

2.3. Non-parametric cumulative incidence estimation

Without loss of generality, we assume that there is one event type of interest, dialysis onset in our example, and only one competing event, death. These two types of events are in the sequel denoted by event type 1 and event type 2. In the competing risks literature, the event types are also denoted as causes of an event. Let λ_k(t) and Λ_k(t) denote the cause-specific hazard functions and cause-specific cumulative hazard functions, respectively, for event type (cause) k, k = 1, 2. The cause-specific cumulative incidence function F₁(t), describing the cumulative probability of subjects experiencing event type 1 up to time t, is given by

$$F_1(t)={\int }_0^{t}S(s){\lambda }_1(s)ds$$

Note that S(t) is the survival function of time to the first of the two event types, given by S(t) = e^{−Λ₁(t)−Λ₂(t)}. F_k(t) has also been denoted as the ‘subdistribution’, reflecting the fact that it does not reach 1 in presence of a competing risk. In the absence of competing risks, the cumulative hazard and cumulative incidence (one minus survivor) function are connected by the relationship F(t) = 1 − e^−Λ(t). This unique correspondence is lost with competing risks, because the cumulative incidence for the event of interest depends on the cause-specific hazard of the competing event [6]. Consequently, the Kaplan-Meier estimator of the cause specific cumulative incidence function, obtained by simply censoring all observations with a competing event, is biased since 1 − S_k(t) ≥ F_k(t) (k = 1, 2) [1]. Instead, the cumulative incidence function F₁(t) at the ordered event times t_(j), j = 1, …, r, should be estimated by the non-parametric plug-in estimator [1]

$${\hat{F}}_1(t_{(j)})=\sum _{i=1}^j{\hat{\lambda }}_1(t_j)\hat{S}(t_{(j-1)})=\sum _{i=1}^j\frac{d_{1(j)}}{n_{(j)}}\hat{S}(t_{(j-1)})$$

where d_1(j) is the number of events of type 1 observed at t_(j), n_(j) is the number of patients at risk for both events just before t_(j), $\hat{S}(t)$ is the Kaplan-Meier estimator of the survival function of time to the first event at t and $\hat{S}(t_{(0)})=1$.

2.4. Proportional subdistribution hazard regression

The proportional subdistribution hazard model was proposed by Fine and Gray [4] in order to estimate the effect of covariates on the cumulative incidence of the event of interest.

2.4.1. The Fine-Gray model

We consider T as the (partly unobservable) random variable describing the time at which the first event of any type occurs in an individual, and ɛ ∈ {1, 2} as the event type related to that time. The subdistribution hazard of event type 1, h₁(t, X), is defined as

$$h_1(t,X)=\underset{\Delta t\to 0}{\lim }\frac{1}{\Delta t}\mathrm{Pr}\{t\le T\le t+\Delta t\wedge \epsilon =1|T\ge t\vee (T\le t\wedge \epsilon =2),X\}$$ (1)

with X denoting a row vector of covariates, and ' ∨ ' and ' ∧ ' denoting the logical OR and AND, respectively. Following Fine and Gray [4], the subdistribution hazard in Eq. (1) can be modelled as a function of a parameter vector β through

$$h_1(t,X)=h_{\mathrm{1,0}}(t)e^{X\beta }$$

where h_1,0 is an unspecified baseline subdistribution hazard function.

The partial likelihood of the proportional subdistribution hazards model was defined by Fine and Gray as

$$L(\beta )=\prod _{j=1}^r\frac{\exp (x_{(j)}\beta )}{\sum _{i\in ℛ(t_{(j)})}{w}_i(t_{(j)})\exp (x_i\beta )}$$

where x_(j) is the covariate row vector of the subject experiencing an event of type 1 at t_(j). For simplicity, no ties in event times are assumed here, but both the Breslow and Efron tie corrections can incorporate weights and can thus be used in this model. The risk set ℛ(t) is defined as

$$ℛ(t)=\{i;t_i\ge t\vee (t_i\le t\wedge {\epsilon }_i=2)\}$$

and includes the set of individuals who, at time t, are at risk of event type 1 as well as those who have had a competing event before t. The subject- and time-specific weights $w_i(t)$ are needed as soon as censoring occurs. Subjects who are at risk for an event of type 1 at time t, and who have not failed from an event of type 2 before t participate fully in ℛ(t) with $w_i(t)=1$, whereas $w_i(t)\le 1$ for subjects with competing events at t_i < t. Formally,

$$w_i(t)=\left\{\begin{array}{ll}1\hfill & \text{if}{t}_i\ge t\hfill \\ \frac{\hat{G}(t)}{\hat{G}(t_i)}\hfill & \text{if}{\epsilon }_i=2\wedge t_i<t\hfill \end{array}\right)$$ (2)

Here, $\hat{G}(t)$ denotes an estimator of the survival function of the censoring distribution at t, i.e., the cumulative probability of still being followed-up at t. $\hat{G}(t)$ can be estimated by the product-limit method with reverse meaning of the censoring indicator:

$$\hat{G}(t)=\prod _{t_i<t}1-\frac{{\sum }_{j=1}^{n}I(t_j=t_i\wedge {\epsilon }_i=0)}{{\sum }_{j=1}^{n}I(t_j\ge t_i)}$$ (3)

In case that there is no random censoring, i.e., every subject was followed up until a specified administrative censoring date (end of follow-up), the Fine-Gray model simplifies considerably. Then, it can be estimated by a Cox regression model in which times to competing events are replaced by times to administrative censoring and censored [1]. This simplification assumes that it would have been possible for subjects who experienced an event to follow them up until the administrative censoring date.

2.4.2. Fitting a Fine-Gray model with standard software

The proportional subdistribution hazards model can be estimated using any standard software for Cox regression that allows representation of times in counting process style, i.e., in (start, stop] syntax, and weighting [11]. In the following, we describe how to model the time to event type 1; in this case, unmodified data can be used on the subjects who either experience event type 1 or who are censored, but data of subjects who experience event type 2 has to be modified.

In particular, the event history of each subject i is represented in counting process style as one or several disjoint time intervals. For individuals who did not fail from the event of type 2 before failing from the event of type 1, these episodes, described by (start time, stop time, status indicator) are just $(0,t_i,{\epsilon }_i^{*})$, where the modified censoring indicator ${\epsilon }_i^{*}$ is 1 for event type 1, and 0 for a censored time. However, for subjects experiencing event type 2 before failing from the event of type 1 additional time intervals are created after their time to event of type 2. Assuming that the event times t_i of such subjects are such that t_(j) ≤ t_i < t_(j+1), the first time interval is given by (0, t_i, 0), the second one by (t_i, t_(j+1), 0) and further time intervals by (t_(j+1), t_(j+2), 0), (t_(j+2), t_(j+3), 0), …, (t_(r−1), t_(r), 0). These time intervals are assigned the decreasing weights 1, $w_i(t_{(j+1)}),w_i(t_{(j+2)}),\dots ,w_i(t_{(r)})$, respectively (Table 1). With this modification and weighting of the original data, the parameters of a PSH model can now be estimated using SAS's PROC PHREG.

Table 1.

Counting process representation and weighting of original survival information for a Fine-Gray model describing time to event type 1.

Subject	Observed survival time	Observed status	For Fine-Gray model
			Counting process representation	Weight
A	tA	censored	(0, tA, 0)	1
B	tB	event 1	(0, tB, 1)	1
C	tC*	event 2	(0, tC, 0)	1
			(tC, t(j+1), 0)	$\frac{\hat{G}(t_{(j+1)})}{\hat{G}(t_C)}$
			(t(j+1), t(j+2), 0)	$\frac{\hat{G}(t_{(j+2)})}{\hat{G}(t_C)}$
			etc.	etc

^*Assuming t_(j) ≤ t_C < t_(j+1) and t_A, t_B < t_C.

2.4.3. Prediction of cumulative incidence

A fitted PSH model can be used to predict the CIF of the event of interest for a new individual characterized by a covariate row vector X. Let N_i(t) = I(t_i ≤ t ∧ ɛ_i = 1) such that dN_i(t) is the increment in the counting process describing the status of subject i with respect to event type 1 in the interval [t, t + dt). (This counting process changes from 0 to 1 at the event time t_i if the event type 1 occurred at that time.) The Breslow estimator of the baseline cumulative subdistribution hazard, relating to an individual with a zero covariate vector, is given by

$${\hat{H}}_{\mathrm{1,0}}(t)=\sum _{i=1}^n{\int }_0^t\frac{1}{\sum _{a\in ℛ(s)}{w}_a(s)\exp (x_a\hat{\beta })}d{N}_i(s)$$

where $\hat{\beta }$ are the regression coefficients (covariate effect estimates) from the PSH model. With time-independent covariates X, the empirical cumulative distribution hazard for event type 1 is given by ${\hat{H}}_1(t,X)={\hat{H}}_{\mathrm{1,0}}(t)\exp (X\hat{\beta })$. The empirical cumulative subdistribution hazard estimate of the CIF can then simply be estimated by ${\hat{F}}_1(t,X)=1-\exp \{-{\hat{H}}_1(t,X)\}$.

PROC PHREG provides the possibility to compute the Breslow estimator of the baseline cumulative hazard function based on the estimates from a conventional Cox model. With appropriate data modification and weighting as described above, this baseline hazard function is exactly equal to the baseline subdistribution hazard function of a PSH model.

2.4.4. Methods of inference in proportional subdistribution hazards models

Geskus [11] discusses the use of model-based variance estimators instead of the robust ones proposed by Fine and Gray [4] in PSH models, and argues that, since subjects who experience the event type 1 are given weights of 1, and each subject appears no more than once in each risk set, the use of model-based inference, i.e., by the model-based variance or by likelihood-based methods, is asymptotically correct. Hence, both the model-based and the robust estimator of variance can be used, as in an unweighted Cox regression analysis. Both options for inference are implemented in PROC PHREG and are therefore also available in our macro. In agreement with Gray's cmprsk R‘s package [7] we use the robust covariance by default.

2.4.5. Monotone likelihood and Firth's bias correction method

In fitting a Cox regression model, the phenomenon of monotone likelihood is observed if the likelihood converges while at least one entry of the parameter estimate diverges [13]. The same may happen in a PSH model, e.g., if no events of interest are observed in one of the levels of a categorical explanatory variable.

In case of monotone likelihood, not only the parameter estimate but also its standard error diverges. Thus, inference based on standard errors becomes uninformative, even if based on values computed at the last iteration before the likelihood converged. The behaviour of the robust standard error as proposed by Lin and Wei [16], which was also proposed by Fine and Gray [4], under monotone likelihood is not yet fully understood. This standard error is based on DFBETA residuals $D_i=\hat{\beta }-{\hat{\beta }}^{(i)}$, which are one-step approximations to the Jackknife values [17], i.e., the changes in parameter estimates if each observation in turn is left out from analysis. (Specifically, with D = D₁, …, D_n, the robust variance matrix V is computed as V = D′D.) For computation of this standard error a finite estimate of $\stackrel{⌢}{\beta }$ would be needed which is not available under monotone likelihood.

By adding an asymptotically negligible penalty function to the log likelihood, the occurrence of divergent parameter estimates can be completely avoided [12], [13]. Furthermore, the penalty, suggested for exponential family models in canonical representation by Firth [12] as 1/2log|I(β)|, with I(·) denoting the Fisher information matrix, corrects the small sample bias of maximum likelihood estimates. This bias is usually low for Cox regression models unless monotone likelihood is observed. Estimation of bias-corrected PSH models can be based on modified score functions, including the weights as defined above.

In case of monotone likelihood, it was proposed that inference should be based on the profile penalized likelihood function, since the normal approximation may fail because of the asymmetry of the profile penalized likelihood [13]. Let β = (θ, γ), with θ a scalar parameter of interest, and γ a vector of nuisance parameters. With ℓ(β) denoting the log of the likelihood, and ℓ_max its maximum value, the profile log likelihood function of parameter θ is given by ℓ_θ(θ) = max_γ ℓ (β|θ = θ₀), i.e., by the log likelihood fixed at θ = θ₀ and maximized over all parameters γ. 2(ℓ _max − ℓ _θ(θ)) has a limiting χ² distribution with 1 degree of freedom [18, pp. 34-37]. Let ${\ell }_{\alpha }={\ell }_{\max }-1/2{\chi }_1^2(1-\alpha )$. Thus, a (1 − α) × 100% confidence interval for θ can be obtained by {θ_α : ℓ _θ(θ₀) ≥ ℓ _α}. Profile penalized likelihood confidence intervals are simply obtained by exchanging ℓ(β), ℓ_max and ℓ(β|θ = θ₀) by their penalized versions.

Both the Firth bias correction and the associated profile penalized likelihood confidence intervals are implemented in PROC PHREG and are thus also available for PSH models fitted by the %pshreg macro.

2.5. Nonproportional subdistribution hazards

2.5.1. Schoenfeld-type residuals

Similarly as in the Cox proportional hazards model, as a first explorative step, Schoenfeld-type residuals and weighted Schoenfeld-type residuals can be inspected in order to detect violations of the proportional subdistribution hazards assumption. Assume, that the subject that fails at the event time t_(j) has a covariate row vector x_(j), and for simplicity assume that there are no tied event times. For the event time t_(j), a row vector of Schoenfeld-type residuals is defined by ${\hat{U}}_{(j)}=x_{(j)}-\overline{x}(\hat{\beta },t)$, where $\overline{x}(\beta ,t)=S^{(1)}(\beta ,t)/S^{(0)}(\beta ,t)$, $\hat{\beta }$ is the maximum likelihood estimate of β, $S^{(0)}(\beta ,t)={\sum }_{i\in ℛ(t)}{w}_i(t)\exp (x_i\beta )$, $S^{(1)}(\beta ,t)={\sum }_{i\in ℛ(t)}{x}_i{w}_i(t)\exp (x_i\beta )$, and $w_i(t)$ is the weight of subject i at time t as defined in Eq. (2). Weighted Schoenfeld-type residuals are scaled such that the smoothed residuals can directly be interpreted as changes in β over time. They are defined as ${\hat{U}}_{(j)}^W=n_{\epsilon =1}I{(\hat{\beta })}^{-1}{\hat{U}}_{(j)}$, with n_ɛ=1 denoting the number of events of type 1.

2.5.2. Time-varying coefficients

The proportional subdistribution hazards model lends itself to accommodate non-proportional subdistribution hazards by including time-varying covariates defined by products of covariates with functions of time. The basic model is extended in the following way:

$$h_1(t,x)=h_{10}(t)e^{x\beta (t)}$$

with β(t) = f(t, β). Considering a single covariate, then, in its simplest form, f(t, β) could be defined as β₁ + β₂t, such that a covariate's effect is modelled as increasing or decreasing linearly with time. To allow for complex dependencies, flexible functions of time such as splines or fractional polynomials (β₁ + β₂t^p₁ + β₂t^p₂), with p₁, p₂ selected from a pre-defined set of values, could be used [19].

3. Working with the macro

3.1. Syntax

The most important parameters available in %pshreg are described in Table 2.

Table 2.

Definition of parameters available in %pshreg.

Parameter	Definition
data	specifies the input SAS data set. The default value is _LAST_.
cens	specifies a variable containing the censoring indicator corresponding to each observation in time. There is no default value. The censoring indicator variable is expected to assume the value 1 for a time to the event of interest, the value 2 for a time to the competing event, and 0 for censored times.
time	specifies a variable containing the times to the first event, or time to censoring. There is no default value.
admin	specifies a variable containing administrative censoring times. Use this option if there is purely administrative censoring and no random censoring. If this option is used, the Fine-Gray model can be estimated using a Cox model by replacing competing event times by administrative censoring times, and censoring competing events [1].
varlist	specifies a list of independent variables, separated by blanks. There is no default value.
class	specifies a subset of the variables of varlist, which should be interpreted as factor variables with multiple levels instead of continuous covariates.
out	specifies the output SAS data set including all covariables, the start and stop times and the weights of the observations. The default name is dat_crr.
firth=1	request the Firth penalization (default=0).
action=estimate	requests the estimation of the Fine-Gray proportional subdistribution hazards model using as covariates all variables specified in varlist (default). If action=code the PSH model is not estimated but the code needed to obtain the PSH analysis using PROC PHREG is printed in the Log window.
by	specifies a variable which can be used to define subsets of a larger data set; useful for efficient processing of multiple data sets of the same structure. This option can also be used for computing weights separately in different strata. The input data set is automatically sorted by this variable.
options	specifies options which are passed to PROC PHREG's MODEL statement. As examples, consider  - options=%str(rl=pl), which requests profile likelihood confidence limits for subdistribution hazards ratios,  - options=%str(selection=backward slstay=0.05), requesting backward variable selection at a 5% significance level, or  - options=%str(ties=efron), employing Efron's tie correction instead of the default Breslow correction. The SAS specific %str(arg) construct causes the argument arg to be used as string without evaluation. Its use is necessary to prevent SAS from interpreting arg before passing it to the MODEL statement of PROC PHREG.
id	specifies a patient identifier variable (usually not needed if each distinct patient is represented by exactly one observation in the input data set).
cuminc=1	to plot unadjusted cumulative incidence curves estimated from the empirical subdistribution hazard, stratified by the levels of the first variable specified in varlist. The default value is 0 (no cumulative incidence curve estimation).
call	specifies an output SAS data set which collects all values of macro options for later reference.
clean=1	if working data set should be cleaned (default), i.e., keeping only relevant variables mentioned in the macro call.
missing=drop	to drop missing values in the modified data set (default). To keep observations with missing values in any variable of the varlist set missing=keep.
delwork=1	to delete all working data sets on exit (default).
tiedcens=after	specifies whether censored times that are tied with event times should be interpreted as occurring slightly after the event times (the default) or slightly before the event.

Further options implemented in the macro can be used to control the interpretation of the value of the status indicator, to specify commands which are directly passed to PROC PHREG or to request subgroup-dependent estimators of the censoring distribution. The latter option may be useful if there are subgroups with different follow-up schemes, and will cause subgroup dependent estimation of the weights that are used for subjects with competing events. This option is similar to the cengroup option in the R package cmprsk. All options are described and their use is exemplified in the User's Guide of the macro, which is available at http://cemsiis.meduniwien.ac.aten/kb/science-researchsoftware/statistical-software/pshreg/.

3.2. Output of the macro

At the current output destination, the first page of output contains a list of the macro options used. In any case, the macro will also create a modified data set suitable to estimate a Fine-Gray model using PROC PHREG.

3.2.1. Immediate model estimation

With the default setting of the macro, action=estimate, PROC PHREG will be automatically invoked using the modified data set to estimate the Fine-Gray model, and its output is directly shown, without modification, in the output destination.

3.2.2. SAS code generation

If action=code, then SAS code will be written into the SAS Log window. This SAS code can be copied to the Editor window and submitted to estimate the Fine-Gray model.

In a typical analysis situation, not only one but several multivariable models will be estimated, e.g., for checking nonlinear effects, interactions or confounding. It is not necessary to repeat the macro call in this case; once the modified data set is created, the user can apply PROC PHREG with different variable lists etc. in the same manner as shown in the example code of the SAS Log. In PSH analyses of large data sets, creation of the modified data set is often the most time-consuming part of analysis. Computing time can be considerably reduced in such analyses if the modified data set is created only once by a single macro call.

3.3. Computational details

The macro code is structured as follows:

Step 1. Create a summary of all macro options in form of a SAS data set and send the data set to the current output destination.

Step 2. Estimate $\hat{G}(t)$ (cf. Eq. (3)), which serves as denominator of the time-dependent weights (cf. Eq. (2)) at event times t₍₁₎, …, t_(r), using PROC LIFETEST.

Step 3. Split the data set into two subsets: subset 1, consisting of all subjects with event indicators ɛ_i = 0 or ɛ_i = 1, and subset 2, consisting of all subjects with ɛ_i = 2.

Step 3.1. For each subject in subset 1, create a single time interval, with a _start_ time of 0. Set _stop_ time to t_i, and the censoring indicator _censcrr_ to ɛ_i. Create a weight variable _weights_, which is constantly 1.

Step 3.2. For each subject in subset 2, create the first time interval by setting _start_=0, _stop_=t_i, and _censcrr_=0. Subsequent time intervals and corresponding weights are efficiently created using PROC SQL statements:

• •Look up the weight denominator of subject i as $\hat{G}(t_i)$.
• •Extract all event times t_(j) greater than t_i.
• •For each of these event times, compute the subject- and time-specific _weights_ variable as $w_i(t_{(j)})=\hat{G}(t_{(j)})/\hat{G}(t_i)$, and create the episodes in counting process formulation as described in Table 1, setting _censcrr_=0.

Step 4. Merge subset 1 with subset 2.

Step 5. If requested by action=estimate, invoke PROC PHREG using the modified data set; otherwise (action=code), write the SAS statements of the PROC PHREG step into the Log window.

%pshreg does not do any statistical calculations besides calling PROC LIFETEST to compute survival probabilities in order to generate the time-dependent weights. All statistical computation is passed over to PROC PHREG, which employs well-validated algorithms to estimate the models. All parameters to control the iterative estimation procedure offered by PROC PHREG (convergence criteria, ridging, etc.) can be used.

4. A worked example

4.1. Example with default settings

In this section we illustrate an application of our macro %pshreg by analyzing the CKD data set described before. The primary aim of the analysis is to investigate the effects of several covariates on the cumulative incidence of dialysis in patients with chronic kidney disease. The variable Time contains the time span from diagnosis to the occurrence of the first event (dialysis or death) or end of follow-up in months. The variable status is the corresponding status indicator, it specifies whether a patient reached end stage renal disease and was started on dialysis (status=1), died (status=2) or experienced none of these events up to the last follow-up visit (status=0). Prognostic factors of interest are age in decades, osmolarity, creatinine clearance, proteinuria, beta-blocker, diuretic therapies and type of underlying renal disease (PKD). Their distribution is summarized in Table 3. Note that for further analyses, urine osmolarity, proteinuria and creatinine clearance were log₂ transformed. Thus, their subdistribution hazard ratios refer to each doubling of their values.

Table 3.

Descriptive statistics of the prognostic factors considered in the CKD study.

Prognostic factor	SAS variable name	Median (1st, 3rd quartiles) or N (%)
Age (in decades)	age	5.6 (4.2, 6.7)
Osmolarity (mOsmol/L)	logUosm*	510 (414, 622)
Proteinuria (g/L)	logProt*	0.87 (0.23, 2.35)
Creatinine clearance (ml/min)	logCCR*	47.5 (30.3, 79.0)
PKD	pkd	18 (6.59%)
Beta-blocker	bblock	119 (47.0%)
Diuretics	diur	120 (47.4%)

^*Name of log-transformed variables used in modelling.

To generate a data set dat_crr prepared for PSH regression analysis using PROC PHREG, the following code can be submitted:

%pshreg(action=code, data=CKDstudy, time=Time, cens=status, varlist=age logUosm logProt logCCR pkd bblock diur, out=dat_crr);

The Output window will show a summary of the macro options, and a frequency of the status indicator:

	The PSHREG macro: summary of macro options
Macro option	Assigned value	Remark
data	CKDstudy	Input data set
time	Time	Time variable
cens	status	Censoring variable
failcode	1	Code for event of interest
cencode	0	Code for censored observation
tiedcens	after	How censored times tied with event times should be treated
admin		Administrative censoring time variable
varlist	age	List of covariables
	logUosm
	logProt
	logCCR
	pkd
	bblocker
	diur
class		List of class variables
options		Options to be passed to PROC PHREG
firth	0	Standard ML estimation, no Firth correction
id		Subject identifier
by		BY processing variable
cuminc	0	Requests cumulative incidence curves
action	code	No output produced (see log file)
weights	0	Standard model, no weighting of risk sets
clean	1	Unnecessary variables removed
call	_pshregopt	Data set with this call's macro options
out	dat_crr	Output data set for standard Fine-Gray model
missing	drop	Delete observations with missing covariate
values
statustab	1	Summary of status variable requested
delwork	1	Temporary data sets deleted on exit
------------	-----------	------------------------------------------
macro version	2014.09
build	201409301506

The PSHREG macro: Summary of missing values in covariates and outcome variables
Remark	Covariates	Outcome (Time, status)	Total
Observations deleted in input data set because of missing values:	21	0	21

The PSHREG macro: Summary of status variable
Obs	_status	COUNT	PERCENT
1	Censored	119	47.2222
2	Events of interest	100	39.6825
3	Competing events	33	13.0952

The Log window displays the following SAS statements, which may be submitted to estimate the PSH model, or which may be further modified to include a different set of variables or change options controlling the computation or output of PROC PHREG:

PROC PHREG DATA=dat_crr covs(aggregate);

MODEL (_start_,_stop_)*_censcrr_(0)=age logUosm logProt logCCR pkd bblocker diur;

ID _id_;

WEIGHT _weight_;

RUN;

By default, %pshreg will request a robust covariance matrix by specifying covs(aggregate) in the first statement, proposed by Fine and Gray [4]. As pointed out by Geskus [11], this robust covariance matrix is not needed in a standard Fine-Gray analysis. Still, for compatibility with the R function crr, our macro will compute the robust covariance matrix.

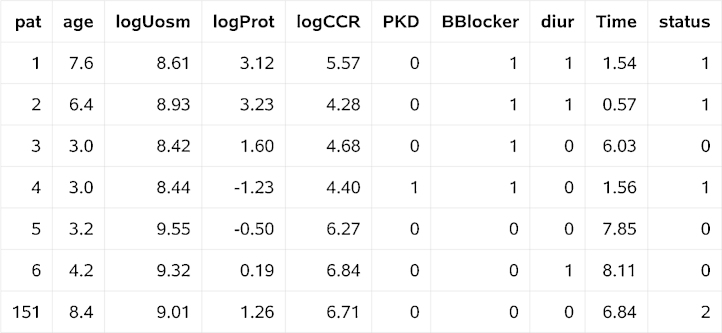
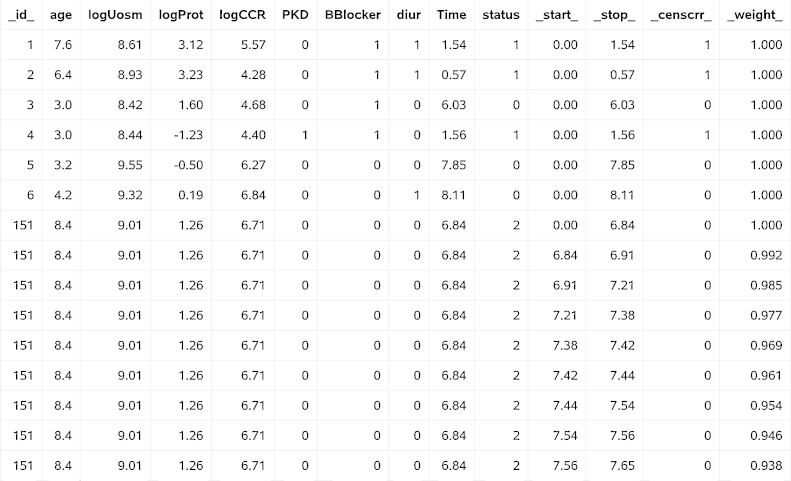
The following variables have been created by %pshreg: _start_, _stop_, _censcrr_, specifying the counting process representation, _weight_, which defines weighting by $w_i(t_{(j)})\text{,}$ and _id_, which is a subject identifier. Fig. 1, Fig. 2 show the data of some patients, before and after processing by the macro. Names of independent variables are directly carried over from the input data set. Comparing Fig. 1, Fig. 2, we learn that for patient no.151, who died after 6.84 years without earlier onset of dialysis, the macro created several disjoint episodes with time-dependent weights decreasing from 1 to 0. The juncture time points of these episodes are failure times of event type 1 greater than the time to death for patient no.151 that are observed in subjects not included in Fig. 1, Fig. 2. Because of the generation of these additional episodes, the modified data set dat_crr has 2,710 observations (multiple observations for each patient with a competing event), while the original one contains only 273 observations (exactly one observation per patient).

Fig. 1.

Extract of the input SAS data set CKDstudy.

Fig. 2.

Extract of the SAS data set dat_crr created by %pshreg.

In our exemplified macro call we did not specify a subject identifier. Therefore, the macro interprets each observation in the input data set as contributed by a different subject which is independent from all other subjects, and generates the variable _id_. Alternatively, we could also use the ID option in the call to %pshreg to define a particular variable of the input data set as the subject identifier. In this way, subjects can be traced in the output data set. The ID statement is important for the purpose of computing the robust covariance matrix (recall its construction via the change in regression coefficients D_i caused by omitting each subject i in turn), and to identify outlying or influential observations.

By copying the SAS code from the Log window into the Editor window, and submitting the code, the PSH model for time to dialysis is actually fitted. Part of the output of PROC PHREG is shown below:

The PHREG Procedure
Analysis of Maximum Likelihood Estimates
Parameter	DF	Parameter Estimate	Standard Error	StdErr Ratio	Chi-Square	Pr > ChiSq
age	1	−0.13910	0.08002	1.171	3.0219	0.0821
logUosm	1	0.71233	0.33328	1.110	4.5682	0.0326
logProt	1	0.61339	0.07247	0.955	71.6483	<.0001
logCCR	1	−1.91238	0.23115	1.033	68.4487	<.0001
PKD	1	1.23414	0.34888	1.010	12.5133	0.0004
BBlocker	1	0.42904	0.23475	1.089	3.3403	0.0676
diur	1	0.48149	0.23248	1.048	4.2895	0.0383

The PHREG Procedure
Analysis of Maximum Likelihood Estimates
Parameter	Hazard Ratio	95% Hazard Ratio Confidence Limits
age	0.870	0.744	1.018
logUosm	2.039	1.061	3.918
logProt	1.847	1.602	2.129
logCCR	0.148	0.094	0.232
PKD	3.435	1.734	6.807
BBlocker	1.536	0.969	2.433
diur	1.618	1.026	2.553

The standard errors, χ² statistics and P-values are based on the robust sandwich covariance matrix. The column labelled StdErr Ratio contains the ratio of the robust to the model-based standard error. In case of model misspecification, model-based standard errors may understate the true variability of the regression coefficients $\hat{\beta }$ if the model is not specified correctly, while robust standard errors are still appropriate [16]. Therefore, standard error ratios which are much larger than 1 may indicate problems with the assumptions of the model, such as violated linearity, additivity or proportional subdistribution hazards assumptions of model effects. In our experience standard error ratios less than 1 are less frequent than the opposite, but are possible in situations with no severe misspecifications. Such ratios less than 1 are caused by the particular covariance structure in the explanatory variables and arise by ‘chance’.

If the option rl is included as an option in the MODEL statement, then the macro will produce an additional table with subdistribution hazard ratios (exp(β)) and associated 95% confidence limits. In the PROC PHREG output, the subdistribution hazard ratios are denoted as Hazard Ratios, but they should be interpreted as subdistribution hazard ratios.

Similarly to standard hazard ratios or cause-specific hazard ratios, subdistribution hazard ratios refer to the comparison of two fictive patients who differ in only one of the covariates (e.g., in the binary variable pkd) by one unit, and who have equal values on the other covariates. Since the proportional subdistribution hazards model models differences in the CIF as effects of covariates, the subdistribution hazard ratios compare the estimated CIF between these two fictive patients by means of the ratio of their relative increments at any time point t, which are given by [F₁(t + Δt|X) − F₁(t|X)]/[1 − F₁(t|X)], with Δt → 0. The subdistribution hazard ratio of 3.435 estimated for pkd means that at any time point t, the subdistribution hazard (increase of the CIF relative to 1-CIF) estimated for patients with pkd=1 is 3.435 fold the subdistribution hazard estimated for patients with pkd=0. Although in our example data set the cause-specific hazard ratio of pkd is very similar to its subdistribution hazard ratio, this is not generally the case, as the two quantities have different interpretation [5].

For graphical visualization of the effect of osmolarity on the cumulative incidence of initiation of dialysis, one may create predicted CIF for fictive patients with different baseline urine osmolarities. Here we exemplify the necessary SAS statements to estimate and display these CIFs, using the output data set of the macro. The CIFs should be estimated for three (fictive) patients with baseline urine osmolarities of 315, 510 or 780 mOsmol/L (corresponding to the 10th, 50th, and 90th percentiles) and average values for all other covariates. We assume that the covariate values are saved in the data set datameans (Fig. 3). (The values given for logUosm are log₂(315), log₂(510), and log₂(780).)

Fig. 3.

Data set datameans.

First, we request PROC PHREG to compute estimated ‘survival’ curves for the three fictive patients, by submitting the BASELINE statement. Note that the macro does not need to be invoked again, as the modified data set dat_crr is still in the working library:

PROC PHREG DATA=dat_crr covs(aggregate);
	MODEL (_start_,_stop_)*_censcrr_(0)=age logUosm logProt logCCR pkd bblock diur/rl;
	WEIGHT _weight_;
	BASELINE out=cuminccurves covariates=datameans survival=_surv_;
RUN;

The output data set cuminccurves contains, for the three fictive patients, ‘survival’ curves estimated from the weighted Cox regression analysis. These three estimated ‘survival’ curves can be simply transformed into CIFs:

DATA cuminccurves;

SET cuminccurves;

cuminc=1 - _surv_;

RUN;

Finally, the CIFs are plotted:

SYMBOL1 v=none i=steplj line=1 c=blue width=2;

SYMBOL2 v=none i=steplj line=1 c=black width=2;

SYMBOL3 v=none i=steplj line=1 c=green width=2;

AXIS1 order=0 to 0.40 by 0.05 label=(angle=90 ‘Cumulative incidence of dialysis’);

AXIS2 order=0 to 8 by 1 value=(‘0’ ‘1’ ‘2’ ‘3’ ‘4’ ‘5’ ‘6’ ‘7’ ‘8’) label=(‘Time in years’);

LEGEND1 value=(‘315’ ‘510’ ‘780’) label=(‘Osmolarity’);

PROC GPLOT DATA=cuminccurves;

PLOT cuminc*_stop_=logUosm/vaxis=axis1 haxis=axis2 legend=legend1;

RUN;

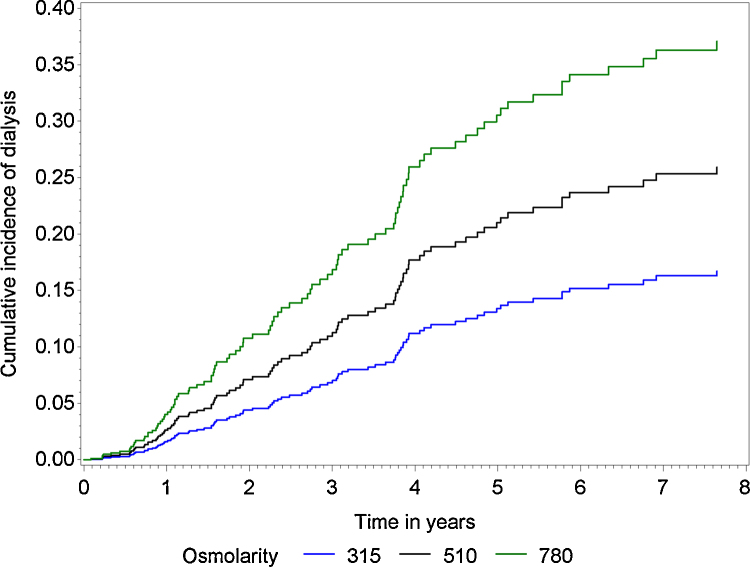
As visualised in Fig. 4, patients with increased osmolarity have a higher predicted cumulative dialysis incidence probability than patients with lower osmolarity.

Fig. 4.

Predicted cumulative incidence probabilities at the 10th, 50th and 90th percentiles of osmolarity, assuming average values for all other covariates.

4.2. An example with time-dependent effects

The following code can be used to obtain weighted Schoenfeld-type residuals for the PSH model:

PROC PHREG DATA=dat_crr covs(aggregate) outest=estimates;
	MODEL (_start_,_stop_)*_censcrr_(0)=age logUosm logProt logCCR pkd bblocker diur;
	OUTPUT out=schoenfeld_data wtressch=WSR_age WSR_logUosm WSR_logProt
	WSR_logCCR WSR_pkd WSR_bblocker WSR_diur;
	ID _id_;
	WEIGHT _weight_;
	BY _by_;
RUN;

The third line of the code shown above (the OUTPUT statement) creates a new data set, schoenfeld_data, containing the weighted Schoenfeld-type residuals for all variables in the model and all event time points. In the code below, we merge the data set of the Schoenfeld-type residuals with the data set estimates, created by PROC PHREG above, which contains the parameter estimates. For merging, it is necessary to specify a primary key variable. We can make use of the constant _by_, which is automatically generated by the macro, and which assumes the value of 1 for all observations in schoenfeld_data as well as in estimates.

DATA schoenfeld_data;
	MERGE schoenfeld_data (keep=WSR_logCCR _stop_ _by_) estimates;
	BY _by_;
	rescaled_WSR_logCCR=WSR_logCCR+logCCR;
	LABEL rescaled_WSR_logCCR=“beta(t) of log2 of creatinine clearance” _stop_=“Time in years”;
RUN;

In the fourth line of the code above, we rescale the residuals by adding the parameter estimates. Rescaled and smoothed residuals have the interpretation of time-dependent parameter estimates. Smoothing can be performed using PROC LOESS as described below, and by making use of ODS GRAPHICS the raw and smoothed time-dependent parameters along with their 95% confidence limits can be displayed:

ODS GRAPHICS on;
ODS SELECT fitplot;
PROC LOESS DATA=schoenfeld_data
	PLOTS=residuals(smooth);
	MODEL rescaled_WSR_logCCR=_stop_/clm;
RUN;
ODS GRAPHICS off;

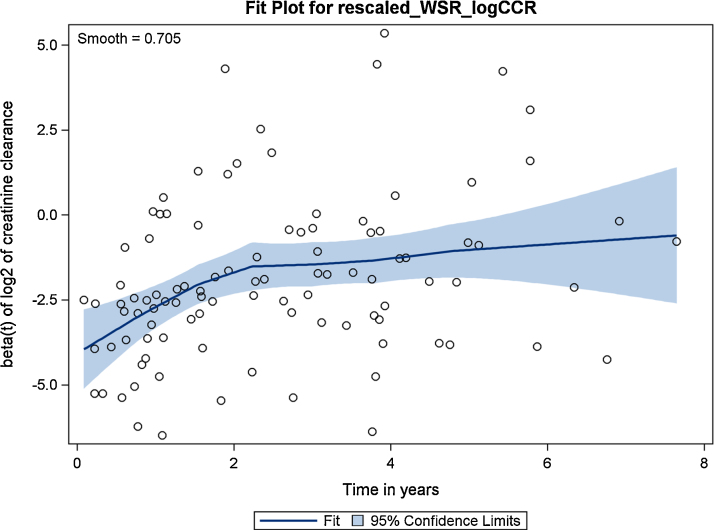
The smoothed Schoenfeld-type residuals of logCCR reveal a time-dependent effect (see Fig. 5), showing a decreasing importance of that variable in time. A formal test of this graphical impression could be obtained by assessing the correlation of the Schoenfeld-type residuals with time or a suitable transformation of time (such as the log). In the code shown below, we create a new variable logstop defined as the natural logarithm of the time variable. Then, we call PROC CORR to compute correlations of the Schoenfeld-type residuals with the original and transformed time variables.

DATA schoenfeld_data;

SET schoenfeld_data;

logstop=log(_stop_);

RUN;

PROC CORR DATA=schoenfeld_data;
	VAR _stop_ logstop;
	WITH WSR_age WSR_logUosm WSR_logProt WSR_logCCR WSR_pkd WSR_bblocker
	WSR_diur;
RUN;

Fig. 5.

Plot of weighted Schoenfeld-type residuals (95% confidence limits) for creatinine clearance.

The output of PROC CORR shown below indicates some issues with the proportionality assumption for the variable logCCR: the correlation coefficient of the weighted Schoenfeld-type residuals with log of time is 0.346 and highly significant.

The CORR Procedure
Pearson Correlation Coefficients
Prob>|r| under H0: Rho=0
Number of Observations
	_stop_	logstop
WSR_age	−0.08184	−0.04724
Standardized Schoenfeld Residual age	0.4182	0.6407
	100	100
WSR_logUosm	−0.11007	−0.15490
Standardized Schoenfeld Residual logUosm	0.2756	0.1238
	100	100
WSR_logProt	−0.12749	−0.04825
Standardized Schoenfeld Residual logProt	0.2062	0.6336
	100	100
WSR_logCCR	0.30715	0.34600
Standardized Schoenfeld Residual logCCR	0.0019	0.0004
	100	100
WSR_pkd	0.08729	0.09667
Standardized Schoenfeld Residual PKD	0.3878	0.3387
	100	100
WSR_bblocker	0.08781	0.07293
Standardized Schoenfeld Residual BBlocker	0.3850	0.4709
	100	100
WSR_diur	−0.07860	−0.08767
Standardized Schoenfeld Residual diur	0.4370	0.3857
	100	100

The obvious time-dependency of the effect of logCCR can be modelled, e.g., by including an interaction (product) term between logCCR and logstop1=log(_stop_+1). By adding a constant of 1/12 to the time variable _stop_ (corresponding to one month) before taking the logarithm we achieve a value of 0 for the interaction term logstop1*logCCR at baseline, which makes the main effect of logCCR interpretable as the effect of logCCR at baseline. PROC PHREG's HAZARDRATIO statement can be used to compute the subdistribution hazard ratios (SHR) and 95% confidence intervals at different time points, e.g., at baseline, 6 months, 1, 3 and 5 years. These times have to be supplied in the scaling of logstop1 (log(T + 1/12)), as −2.49, −0.54, 0.08, 1.13, and 1.63:

PROC PHREG DATA=dat_crr covs(aggregate);
	MODEL (_start_,_stop_)*_censcrr_(0)=age logUosm logProt logCCR pkd bblocker diur logCCR*logstop1/rl;
	logstop1=log(_stop_+1/12);
	ID _id_;
	WEIGHT _weight_;
	HAZARDRATIO logCCR/at(logstop1=-2.49 -0.54 0.08 1.13 1.63);
RUN;

The results from this call are shown below:

The PHREG Procedure
Analysis of Maximum Likelihood Estimates
Parameter	DF	Parameter Estimate	Standard Error	StdErr Ratio	Chi-Square	Pr>ChiSq
age	1	−0.12462	0.07846	1.128	2.5228	0.1122
logUosm	1	0.65759	0.31375	1.055	4.3927	0.0361
logProt	1	0.60890	0.07306	0.955	69.4532	<.0001
logCCR	1	−2.64152	0.26778	0.812	97.3099	<.0001
PKD	1	1.14126	0.33683	0.968	11.4801	0.0007
BBlocker	1	0.40915	0.22757	1.049	3.2326	0.0722
diur	1	0.47390	0.22469	1.005	4.4484	0.0349
logstop1*logCCR	1	0.83933	0.19486	0.781	18.5532	<.0001

	Analysis of Maximum Likelihood Estimates
Parameter	Hazard Ratio	95% Hazard Ratio Confidence Limits		Label
age	0.883	0.757	1.030	age
logUosm	1.930	1.044	3.570
logProt	1.838	1.593	2.121
logCCR	.	.	.
PKD	3.131	1.618	6.058
BBlocker	1.506	0.964	2.352	BBlocker
diur	1.606	1.034	2.495
logstop1*logCCR.	.	.	.	logstop1 * logCCR

	Hazard Ratios for logCCR
Description	Point Estimate	95% Wald Robust Confidence Limits
logCCR Unit=1 At logstop1=−2.49	0.009	0.002	0.033
logCCR Unit=1 At logstop1=−0.54	0.045	0.023	0.088
logCCR Unit=1 At logstop1=0.08	0.076	0.046	0.127
logCCR Unit=1 At logstop1=1.13	0.184	0.118	0.286
logCCR Unit=1 At logstop1=1.63	0.280	0.165	0.474

The interaction term has a highly significant and strong effect on the subdistribution hazard. Therefore, the subdistribution hazard ratios (denoted by Hazard Ratios by PROC PHREG) are markedly increasing from 0.009 at baseline to 0.280 at 5 years.

4.3. An example with the Firth correction

Firth's bias correction is readily available in PROC PHREG. To exemplify the effect of the Firth correction in a PSH model we extracted a random ‘smallsample’ subset of 200 patients from the original study group. Twenty-eight of these patients experienced the event of interest (dialysis) and two of them died. For simplicity and to illustrate the impact of monotone likelihood on the results, we dichotomized the variables age at 60 years (dage60), osmolarity at 500 mOsmol/L (dUosm), proteinuria at 3 g/L (dProt) and used only these variables and the log₂ transformed creatinine clearance (logCCR) as covariates. Their distribution is summarized in Table 4.

Table 4.

Descriptive statistics of the prognostic factors in the smallsample data set.

Prognostic factor	SAS variable name	Median (1st, 3rd quartiles) or N (%)
Age, binary (>60 years)	dage60	17 (8.5%)
Osmolarity, binary (>500 mOsmol/L)	dUosm*	158 (79%)
Proteinuria, binary (>3 g/L)	dProt*	26 (13%)
Creatinine clearance (ml/min)	logCCR*	91.9 (80.9, 132.86)

^*Names of binary or log-transformed variables used in modelling.

The Firth-corrected PSH model is obtained by submitting:

%pshreg(action=code, data=smallsample, time=Time, cens=status, out=small_crr,

varlist= dage60 dUosm dProt logCCR, options=%str(rl=pl), firth=1);

The option rl=pl are passed to the options of PROC PHREG's MODEL statement. Likewise, setting firth=1 will also cause the keyword firth to be included as an option to the MODEL statement. rl=pl is a standard option of PROC PHREG and produces profile likelihood confidence intervals for exp(β), in our case: the subdistribution hazard ratios. Since we request the Firth correction, these confidence intervals are computed using profile penalized likelihood, as suggested by Heinze and Schemper [13]. The action=code option will generate the following code:

PROC PHREG DATA=small_crr;
	MODEL (_start_,_stop_)*_censcrr_(0)=dage60 dUosm dProt logCCR/rl=pl firth;
	ID _id_;
	WEIGHT _weight_;
	TITLE “Firth-corrected PSH model”;
RUN;

Submission of this code leads to a bias-corrected PSH model:

Firth-corrected PSH model
The PHREG Procedure
Analysis of Maximum Likelihood Estimates
Parameter	DF	Parameter Estimate	Standard Error	Chi-Square	Pr>ChiSq
dage60	1	−2.05496	1.47804	1.9330	0.1644
dUosm	1	0.18740	0.47225	0.1575	0.6915
dProt	1	0.94149	0.49547	3.6108	0.0574
logCCR	1	−2.49539	0.66178	14.2183	0.0002

Analysis of Maximum Likelihood Estimates
Parameter	Hazard Ratio	95% Hazard Ratio Profile Likelihood Confidence Limits
dage60	0.128	0.001	0.966
dUosm	1.206	0.506	3.223
dProt	2.564	0.927	6.435
logCCR	0.082	0.021	0.275

Using the same data set small_crr, we can also compute an uncorrected PSH model by submitting:

PROC PHREG DATA=small_crr COVS(AGGREGATE);
	MODEL (_start_,_stop_)*_censcrr_(0)=dage60 dUosm dProt logCCR/rl;
	ID _id_;
	WEIGHT _weight_;
	TITLE “Uncorrected PSH model”;
RUN;

which results in:

			The PHREG Procedure
Analysis of Maximum Likelihood Estimates
Parameter	DF	Parameter Estimate	Standard Error	StdErr Ratio	Chi-Square	Pr>ChiSq
dage60	1	−15.54092	0.40801	0.000	1450.7792	<.0001
dUosm	1	0.23984	0.49566	1.037	0.2342	0.6285
dProt	1	0.91084	0.51374	1.025	3.1434	0.0762
logCCR	1	−2.58038	0.50017	0.749	26.6152	<.0001

Analysis of Maximum Likelihood Estimates
Parameter	Hazard Ratio	95% Hazard Ratio Confidence Limits
dage60	0.000	0.000	0.000
dUosm	1.271	0.481	3.358
dProt	2.486	0.908	6.806
logCCR	0.076	0.028	0.202

The parameter estimator of dage60 in the uncorrected PSH model diverges to −∞. PROC PHREG reports the parameter estimates at the iteration at which the likelihood convergence criterion is fulfilled. At that iteration, the model-based standard error for dage60 diverges, while the robust standard error collapses towards 0. Likewise, the 95% Wald confidence limits for the SHR based on the robust standard deviation collapse to [0,0], which is implausible given the small sample size. The Firth correction supplies plausible point estimates, providing a convergent value for dage60 and values similar to the uncorrected analysis for the other variables. The SHRs of those variables by the Firth-corrected analysis are just slightly closer to 1 than their uncorrected counterparts. This is expected since the Firth correction removes some of the small-sample bias from the parameter estimates, which is considered as causing some overestimation of effects. The small-sample bias is even more severe in this example as the number of events per independent variable is 14/4 = 3.5. For standard Cox regression, the Firth bias correction has recently been reported as almost unbiased even when the number of events per independent variable was only between two and six [20].

Profile penalized likelihood confidence intervals in the output of the Firth-corrected model are provided on the hazard ratio scale. For illustration we have transformed these confidence intervals to the scale of coefficients (log hazard ratios) and compare them to the corresponding normal approximated confidence intervals in Table 5. We learn that indeed, due to skewness of the profile penalized likelihood of dage60, the profile penalized likelihood confidence intervals differ from the ones based on the normal approximation, and should be preferred [13]. Their drawbacks are the increased computational effort, since for computation of each limit of each parameter an iterative optimization is needed, and their assumption of a correctly specified model (see the discussion above). Nevertheless, in situations of a diverging parameter estimate, they are certainly the best choice as both the robust and the model-based covariance will give unusable results.

Table 5.

Comparison of 95% confidence intervals for Firth-corrected coefficients estimated for the smallsample data set.

Firth-corrected analysis
Variable	Parameter estimate	Lower	Upper	Lower	Upper
		95% Wald CL		95% PPL CL
dage60	−2.06	−5.00	0.84	−6.90	−0.03
dUosm	0.19	−0.74	1.11	−0.68	1.17
dProt	0.94	−0.03	1.91	−0.08	1.86
logCCR	−2.50	−3.80	−1.20	−3.90	−1.30

Wald CL: confidence limits by normal approximation based on standard errors.

PPL CL: profile penalized likelihood confidence limits.

5. Concluding remarks

So far, data analysists working with SAS had to switch to a different statistical programming environment such as R or STATA if they needed a PSH analysis. Although using multiple environments for an analysis project may have advantages in terms of flexibility, it is often inconvenient, as workflows cannot be saved as a single program file, and thus are harder to trace in case of revisions. The new macro enables a workflow that resides entirely in the SAS environment, using as the workhorse procedure the well-validated and documented PROC PHREG. We have compared the results obtained from our macro with those obtained by R‘s cmprsk package for the data sets presented here as well as for some other data sets, and could not find any relevant differences; the maximum difference in estimated parameter estimates was negligible if the time scale was truly continuous. However, with the possibility of tied event and censoring times, there might be slight differences as in our macro we clearly interpret censoring times which are tied with event times as occurring after event times. It is not fully documented how such ties are handled in cmprsk.

For fitting standard proportional subdistribution hazards models, our SAS macro offers the same functionality as the crr function of the R package cmprsk. Moreover, we have extended the Fine-Gray model and its existing implementations in R and STATA by providing a bias correction in small samples, which effectively eliminates the occurrence of infinite parameter estimates. In addition, PROC PHREG enables the analyst to make use of several additional built-in features, such as Bayesian analysis, model assessment via martingale residuals, inclusion of frailty effects, estimation of effect contrasts, etc.; all of which not yet explored in context of the Fine-Gray model. It is also possible to apply nonlinear estimation techniques in combination with our macro, such as restricted cubic splines [21], [22] or fractional polynomials [23].

Very recently, a new SAS version 9.4 (including SAS/STAT version 13.1) has been released in which the Fine-Gray model has been made directly available in PROC PHREG, by specifying the code of the event of interest in a new option EVENTCODE of the MODEL statement. All other codes which are not contained in the list of censoring values are then treated as competing event codes. We have compared the functionality of this new option with our macro by re-analyzing our examples. Even with the new EVENTCODE option, it is not possible to:

• •apply variable selection (e.g., backward elimination),
• •compute Schoenfeld-type residuals,
• •apply the Firth correction or compute profile-likelihood based confidence intervals,
• •use the ASSESS statement for assessing model assumptions using martingale residuals,
• •include frailty effects.

All these options are possible with %pshreg as it first modifies the input data set which can then be treated as any other survival data set, making full use of the functionality of PROC PHREG.

A limitation of our current implementation of %pshreg (and of the new SAS 9.4 implementation of the Fine-Gray model) is that it does not allow for left-truncation or interval-censoring. Similarly, the macro and the SAS 9.4 implementation cannot handle time-varying predictors implemented via multiple records of follow-up time (counting process style input) per subject [24], [25]. Further information on our macro, including full documentation of its options, several examples and numerical comparisons with cmprsk can be found in a Technical Report containing some example calls and output. The macro and the Technical Report are available under the GNU GPL-2 license at http://cemsiis.meduniwien.ac.at/en/kb/science-research/software/statistical-software/pshreg/.

Conflict of interest

No benefits in any form have been received or will be received from a commercial party related directly or indirectly to the subject of this article.