MHD Stagnation-Point Flow and Heat Transfer with Effects of Viscous Dissipation, Joule Heating and Partial Velocity Slip

Abstract

The steady two-dimensional stagnation-point flow and heat transfer past a permeable stretching/shrinking sheet with effects of viscous dissipation, Joule heating and partial velocity slip in the presence of a magnetic field is investigated. The partial differential equations are reduced to nonlinear ordinary differential equations by using a similarity transformation, before being solved numerically by shooting technique. Results indicate that the skin friction coefficient and the local Nusselt number increase as magnetic parameter increases. It is found that for the stretching sheet the solution is unique while for the shrinking sheet there exist nonunique solutions (dual solutions) in certain range of parameters. The stability analysis shows that the upper branch solution is stable while the lower branch solution is unstable.

The flow and heat transfer of a viscous (Newtonian) and non-Newtonian fluid past a static flat plate is a classical problem and has been studied by many authors (see Schlichting and Gersten¹, White², Pop and Ingham³ and Bejan⁴). It seems that Crane⁵ was the first who has studied the viscous and incompressible fluid over a stretching sheet obtaining a closed form analytical solution. This paper has been extended by different authors taking into account different effect, such as, suction/injection, radiation, etc. Further, Miklavčič and Wang⁶ studied the viscous flow induced by a shrinking sheet. Existence and (non) uniqueness solutions were proven. Exact solutions, both numerical and in closed form were obtained. The industrial applications of stretching/shrinking sheets are numerous such as aerodynamic extrusion of plastic sheets, the boundary layer along a liquid film, condensation process of metallic plate in cooling bath and glass, and also polymer industries, etc. It is worth mentioning here that the shrinking sheet flow is essentially a backward flow and it shows physical phenomena quite distinct from the stretching sheet flow (Goldstein⁷).

Flow and heat transfer over a stretching/shrinking sheet near a stagnation point has attracted the interest of many researchers. Ishak et al.⁸ investigated the stagnation-point flow and heat transfer over a shrinking sheet in a micropolar fluid. Bachok and Ishak⁹ studied numerically the stagnation-point flow towards an exponentially stretching/shrinking sheet immersed in a viscous fluid. Then, an unsteady two-dimensional flow and heat trasnfer of a viscous fluid near a stagnation-point over a shrinking sheet in the presence of time-dependent free stream have been analysed by Mahapatra and Nandy¹⁰. Suali et al.¹¹ studied the similar problem but with prescribed surface heat flux. Next, Chen¹² presented the unsteady mixed convection flow over a stretching sheet in the presence of velocity and thermal slips near the stagnation-point. The steady stagnation-point flow in the presence of chemical reaction past a stretching/shrinking cylinder was done by Najib et al.¹³. Zaimi et al.¹⁴ investigated the flow and heat transfer over a stretching/shrinking sheet in a nanofluid and reported the existence of dual solutions for a certain range of parameter. Das¹⁵ considered a steady two dimensional laminar boundary layer stagnation point flow in a micropolar fluid towards a shrinking sheet in the presence of magnetic field. Nandy¹⁶ and Lok et al.¹⁷, respectively, investigated the magnetohydrodynamic (MHD) stagnation point flow past a stretching and shrinking sheets.

The aim of this study is to investigate the effects of viscous dissipation, Joule heating and partial velocity slip of a viscous, incompressible and electrically conducting fluid near the stagnation point on a stretching/shrinking sheet in the presence of magnetic field near the stagnation point when suction and injection is taken into consideration. A stability analysis is performed to investigate the stability of the dual solutions and thus determine which solution is stable and physically realiable.

Problem formulation

Consider a steady two dimensional, electrically conducting viscous and incompressible fluid over a permeable stretching/shrinking sheet coinciding with the plane , and the flow being confined to 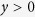. This problem also considers the effect of viscous dissipation, Joule heating and partial slip. The flow is generated by the stretching/shrinking effect along the -axis. It is assumed that the velocity of the outer (inviscid) flow is , while that of the stretching/shrinking is 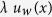with λ being a positive constant for the stretching sheet and λ a negative constant for the shrinking sheet. The constant applied magnetic field, parallel to the axis is . Also, the surface mass transfer velocity is with for suction and for injection. Further, it is assumed that the surface temperature is , while the constant ambient temperature is . Under these conditions, the governing boundary layer equations are

The boundary conditions of Eqs. (1)–(3), , are

where and are the velocity components in the and directions, respectively, 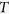is the fluid temperature, is the velocity slip length, is the thermal conductivity, is the kinematic viscosity, is the density, is the specific heat at constant pressure and is the electrical conductivity.

In order that Eqs. (1) to (3) admit similarity solutions, we assume that and , where and b are positive constants. The momentum and energy equations (2) and (3) can then be transformed into the corresponding nonlinear ordinary differential equations by the following similarity transformation

where prime denotes differentiation with respect to 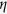. Based on Eq. (5), the mass transfer velocity is given by

where is the constant mass transfer velocity parameter with for suction and for injection.

Substituting Eq. (6) into Eqs. (2) and (3), we get the following system of nonlinear ordinary differential equations:

and the boundary conditions (4) become

where is the Prandtl number, is the Eckert number, M is the constant magnetic parameter and is the velocity slip parameter, which are defined as

Physical quantities of interest are the skin friction coefficient and the local Nusselt number , which are given by

Using variables (5), we obtain

where is the local Reynold number.

Stability of solutions

We mention that there are several papers that have performed the stability analysis to determine which solution is stable and physically reliable, such as Merkin¹⁸, Weidman et al.¹⁹, Roşca and Pop²⁰,²¹, Sharma et al.²² and Mansur et al.²³. As in these papers, in order to perform a stability analysis, we consider the unsteady problem. Equation (1) holds, while (2) and (3) are replaced by

where t denotes the time. Based on the variables (5), we introduce the following new dimensionless variables:

so that (2) and (3) can be written as

and are subjected to the boundary conditions

To test the stability of the steady flow solution f(η) = f₀(η) and θ(η) = θ₀(η) satisfying the boundary value problem (1)–(4), we write

where is an unknown eigenvalue, F(η, τ) and G(η, τ) are small relative to f₀(η) and θ₀(η). Solutions of the eigenvalue problem (16)–(18) give an infinite set of eigenvalues ; if the smallest eigenvalue is negative, there is an initial growth of disturbances and the flow is unstable but when is positive, there is an initial decay and the flow is stable. Introducing (19) into (16) and (17), we get the following linearized problem

along with the boundary conditions

The solutions f(η) = f₀(η) and θ(η) = θ₀(η) of the steady equations (6) and (7) are obtained by setting τ = 0. Hence F(η) = F₀(η) and G(η) = G₀(η) in (20) and (21) identify initial growth or decay of the solution (19). In this respect, we have to solve the linear eigenvalue problem

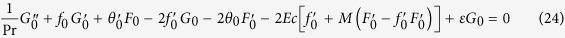along with the boundary conditions

It should be stated that for particular values of Pr and , the stability of the corresponding steady flow solutions f₀(η) and θ₀(η) are determined by the smallest eigenvalue . As it has been suggested by Harris et al.²⁴, the range of possible eigenvalues can be determined by relaxing a boundary condition on F₀(η) or G₀(η). For the present problem, we relax the condition that as and for a fixed value of λ we solve the system (23)–(25) along with the new boundary conditions .

Results and Discussion

The system of ordinary differential equations (7) and (8) subjected to the boundary conditions (9) was solved numerically using Runge-Kutta Fehlberg method with shooting technique for some values of the governing parameters. The computation was carried out until we get the velocity and temperature profiles converge and satisfy the far field boundary conditions (9) asymptotically. The numerical calculations were carried out for different values of suction/injection parameter S, magnetic parameter M, power law stretching/shrinking parameter λ, Prandtl number Pr, Eckert number Ec, velocity slip parameter γ, and their effects on the flow and heat transfer characteristics are analyzed and discussed.

Table 1 shows the comparison data with those of Aman et al.²⁵ and Wang²⁶ when M = 0 and γ = 0 for shrinking case (λ < 0). The stated data clarify the good agreement with the previous data which support the validity of our numerical results.

Table 1. Comparison with previously publish data for the values of f ″(0), when M = 0 and γ = 0 (no slip) for shrinking case (λ < 0).

λ	Present Results		Aman et al.25		Wang26
	Upper Solution	Lower Solution	Upper Solution	Lower Solution	Upper Solution	Lower Solution
−0.25	1.402241		1.4022		1.40224
−0.50	1.495670		1.4957		1.49567
−1.00	1.328817	0	1.3288	0	1.32882	0
−1.10	1.186680	0.049229
−1.15	1.082231	0.116702	1.0822	0.1167	1.08223	0.11670
−1.18	1.000449	0.178361	1.0004	0.1784
−1.20	0.932473	0.233650

Figures 1 and 2 respectively show the variation of the skin friction coefficient C_fRe_x^1/2 and the local Nusselt number Nu_x/Re_x^1/2 (heat transfer rate at the surface) for different values of the magnetic parameter M. These figures show that a unique solution exists for equations (7) and (8) with the boundary conditions (9) for the stretching case, dual (upper and lower branch) solutions are found for the shrinking case up to a critical value , and no solutions exist for . These values of are stated in Figs 1 and 2, which show that increasing the magnetic parameter M is to increase the range of λ for which the solution exists. The skin friction coefficient and the heat transfer rate at the surface increase as the magnetic parameter M increases.

Figure 1. Variation of the skin friction coefficient with λ when Pr = 1, Ec = 0.5, S = 2 and γ = 0.1 with various value of M.

Figure 2. Variation of the local Nusselt number with λ when Pr = 1, Ec = 0.5, S = 2 and γ = 0.1 with various value of M.

To test the stability of the dual solutions, the stability analysis was performed to find the eigenvalues ε (see Eq. (19)). If the smallest eigenvalue is positive, there is an initial decay and the flow is stable; while if the smallest eigenvalue is negative, there is an initial growth of disturbances and the flow is unstable. The smallest eigenvalues ε for selected values of λ are shown in Table 2. The results indicate that ε is positive for the upper branch solution and negative for the lower branch solution. So, the upper branch solution is stable and physically reliable, while the lower branch is not.

Table 2. Smallest eigenvalues ε at selected values of λ with various M when S = 2, Ec = 0.5, Pr = 1 and γ = 0.1.

M	λ	Upper Solution	Lower Solution
0	−3.2	1.1210	−1.0269
	−3.25	0.8671	−0.8104
	−3.3	0.5061	−0.4864
	−3.32	0.2500	−0.2451
0.05	−3.2	1.2201	−0.9434
	−3.25	0.9682	−0.7265
	−3.3	0.6119	−0.4051
	−3.32	0.3663	−0.1733
0.1	−3.2	1.3169	−0.8570
	−3.25	1.0664	−0.6393
	−3.3	0.7132	−0.3186
	−3.32	0.4730	−0.0913

Figures 3 and 4 present the velocity and temperature profiles for different values of λ when M = 0.1, Pr = 1, Ec = 0.5, S = 2 and γ = 0.1. From the figures we can see that the boundary layer thickness for the lower solution is thicker compared to upper solution. For a particular value of parameter, there exist two different profiles as presented in Figs 3 and 4, and thus supports the existence of dual solutions in Figs 1 and 2. Figure 5 shows the temperature profile for different values of Pr when the other parameters are fixed. It is seen that the temperature gradient at the surface increases as Pr increases, thus increase the local Nusselt number (heat transfer rate at the surface). This is because increasing Pr will cause the increasing of viscosity, then reduces the thermal conductivity, and thus increases (Ishak et al.²⁷). All velocity and temperature profiles approach the far field boundary conditions asymptotically which support the validity of the numerical results presented in Figs 1 and 2.

Figure 3. Velocity profiles for different values of λ when M = 0.1, S = 2 and γ =0.1.

Figure 4. Temperature profiles for different values of λ when M = 0.1, Pr = 1, Ec = 0.5, S = 2 and γ = 0.1.

Figure 5. Temperature profiles for different values of Pr when M = 0.1, λ = −0.5, Ec = 0.5, S = 2 and γ = 0.1.

Conclusion

We have numerically investigated how magnetic parameters influence the effects of viscous dissipation, Joule heating and partial velocity slip. The skin friction coefficient and heat transfer rate at the surface increase as magnetic parameter M increases. It was found that there exist dual solutions for the shrinking sheet while only unique solution for the stretching sheet. The stability analysis showed that there is an initial decay for the upper branch solution while there is initial growth of disturbance for the lower branch solution. Thus the upper branch is linearly stable and physically reliable while the lower branch solution is not.

Additional Information

How to cite this article: Yasin, M. H. M. et al. MHD Stagnation-Point Flow and Heat Transfer with Effects of Viscous Dissipation, Joule Heating and Partial Velocity Slip. Sci. Rep. 5, 17848; doi: 10.1038/srep17848 (2015).