Carbon-depleted outer core revealed by sound velocity measurements of liquid iron–carbon alloy

Abstract

The relative abundance of light elements in the Earth's core has long been controversial. Recently, the presence of carbon in the core has been emphasized, because the density and sound velocities of the inner core may be consistent with solid Fe₇C₃. Here we report the longitudinal wave velocity of liquid Fe₈₄C₁₆ up to 70 GPa based on inelastic X-ray scattering measurements. We find the velocity to be substantially slower than that of solid iron and Fe₃C and to be faster than that of liquid iron. The thermodynamic equation of state for liquid Fe₈₄C₁₆ is also obtained from the velocity data combined with previous density measurements at 1 bar. The longitudinal velocity of the outer core, about 4% faster than that of liquid iron, is consistent with the presence of 4–5 at.% carbon. However, that amount of carbon is too small to account for the outer core density deficit, suggesting that carbon cannot be a predominant light element in the core.

The composition of the Earth's core, particularly the light elements present, is not well constrained. Here, the authors report sound velocities of liquid iron-carbon alloy as measured at very high pressures using inelastic X-ray scattering and suggest that carbon cannot be predominant in the outer core.

Sound velocity and density are important observational constraints on the chemical composition of the Earth's core. While properties of solid iron alloys have been extensively examined by laboratory studies to core pressures (>136 GPa)1,2,3, little is known for liquid alloys because of experimental difficulties. The core is predominantly molten, and the longitudinal wave (P-wave) velocity of liquid iron alloy is the key to constraining its composition. However, previous static high-pressure and -temperature (P–T) measurements of liquid iron alloys were performed only below 10 GPa using large-volume presses4,5,6. Shock wave experiments have been carried out at much higher pressures but only along a specific Hugoniot P–T path7,8.

Carbon is one of the possible light alloying components in the core because of its high cosmic abundance and strong chemical affinity with liquid iron9. Its high metal/silicate partition coefficients indicate that thousands of parts per million to several weight percent of carbon could have been incorporated into the core during its formation9,10,11. In addition, recent experimental and theoretical studies12,13 have suggested that solid Fe₇C₃ may explain the properties of the inner core, in particular its high Poisson's ratio14,15, supporting the presence of carbon in the core.

In this study, we determine the P-wave velocity (V_P) (equivalent to bulk sound velocity, V_Φ, in a liquid) of liquid Fe₈₄C₁₆ at high P–T based on inelastic X-ray scattering (IXS) measurements. Combined with its density data at 1 bar (ref. 16) both velocity and density (ρ) profiles of liquid Fe₈₄C₁₆ along adiabatic compression are obtained. They are compared with seismological observations, indicating that both V_P and ρ in the Earth's outer core are not explained simultaneously by liquid Fe–C.

Results

Longitudinal wave velocity measurements

We collected the high-resolution IXS spectra from liquid Fe₈₄C₁₆ (4.0±0.3 wt.% carbon) at static high P–T using both resistance- and laser-heated diamond-anvil cells (Methods; Fig. 1). The starting material was synthesized beforehand as a mixture of fine-grained Fe and Fe₃C at 5 GPa and 1,623 K in a multi-anvil apparatus. Experimental P–T conditions were well above the eutectic temperature in the Fe–Fe₃C binary system (Supplementary Fig. 1). The carbon concentration in the eutectic liquid is known to be 3.8–4.3 wt.% at 1 bar to 20 GPa (ref. 17), almost identical to the composition of our sample. Above 20 GPa, we heated the sample to temperatures comparable or higher than the melting temperature of Fe₃C, a liquidus phase in the pressure range explored, assuring a fully molten sample. The molten state of the specimen was carefully confirmed, before and after the IXS measurements, by the absence of diffraction peaks from the sample (Fig. 2). We sometimes, depending on a sample volume, were also able to observe the diffuse diffraction signal typical of a liquid.

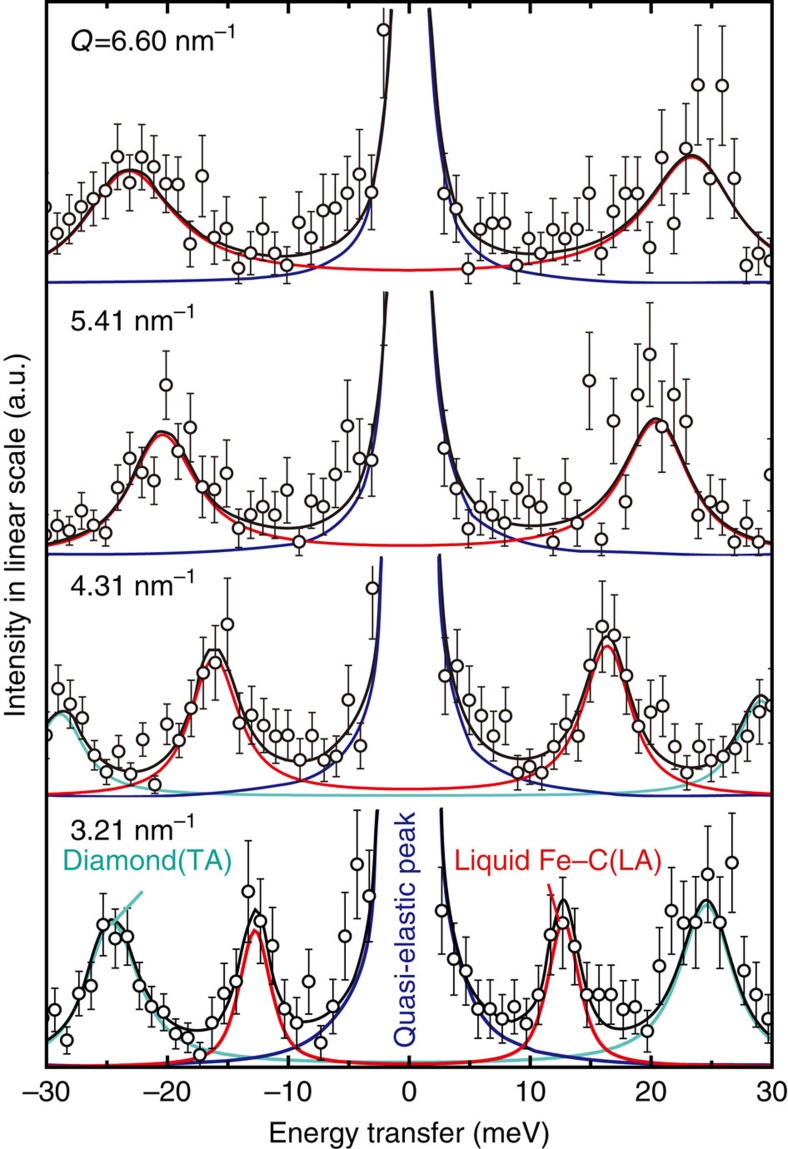
Figure 1. Typical inelastic X-ray scattering spectra.

These data were collected at 26 GPa and 2,530 K at momentum transfers Q, as indicated. The spectra include three components: a quasi-elastic peak near zero energy transfer (blue), longitudinal acoustic (LA) phonon mode of liquid Fe₈₄C₁₆ (red), and transverse acoustic (TA) phonon mode of diamond (turquoise).

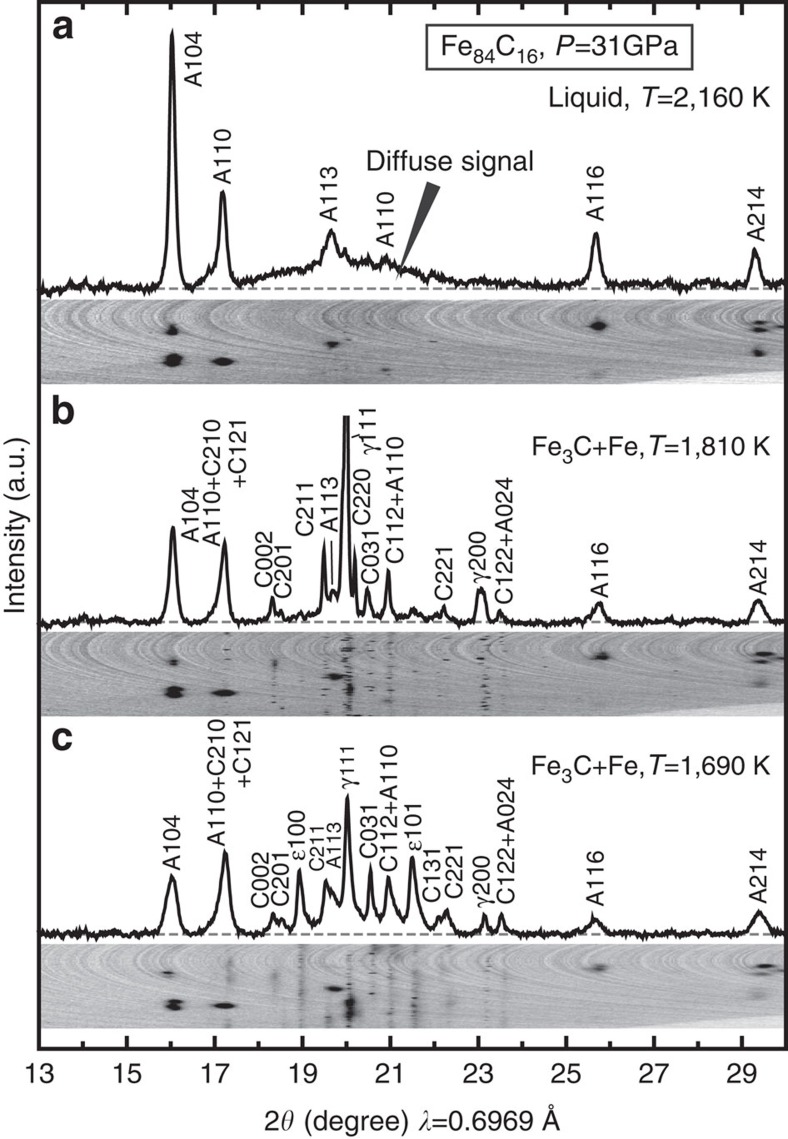
Figure 2. X-ray diffraction spectra before and after melting.

They were collected at 2,160 K (a), 1,810 K (b) and 1,690 K (c) during heating at 31 GPa. The starting material was composed of Fe (ɛ or γ) and Fe₃C (c), and the peaks of Al₂O₃ (a) were from a thermal insulator. The coexistence of ɛ- and γ-Fe phases at 1,610 K was due to a sluggish solid–solid phase transition49 and the peaks from the ɛ-phase were lost at 1,810 K. All sample peaks disappeared between 1,810 and 2,160 K. In addition, the background was enhanced slightly, indicating a diffuse scattering signal from a liquid sample.

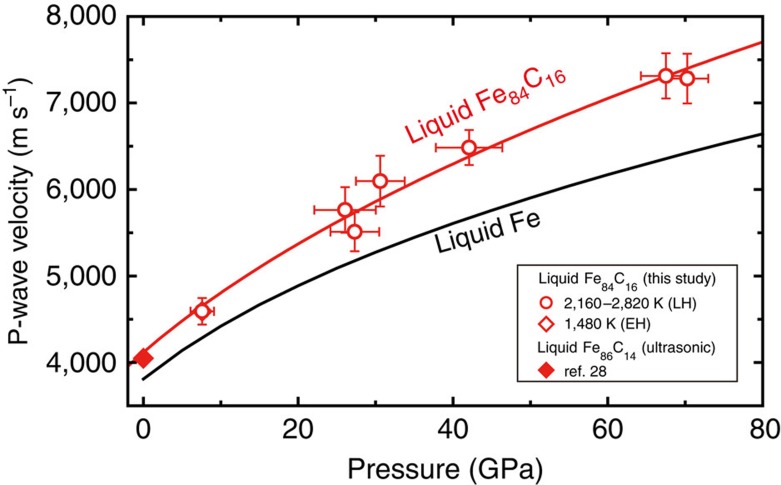
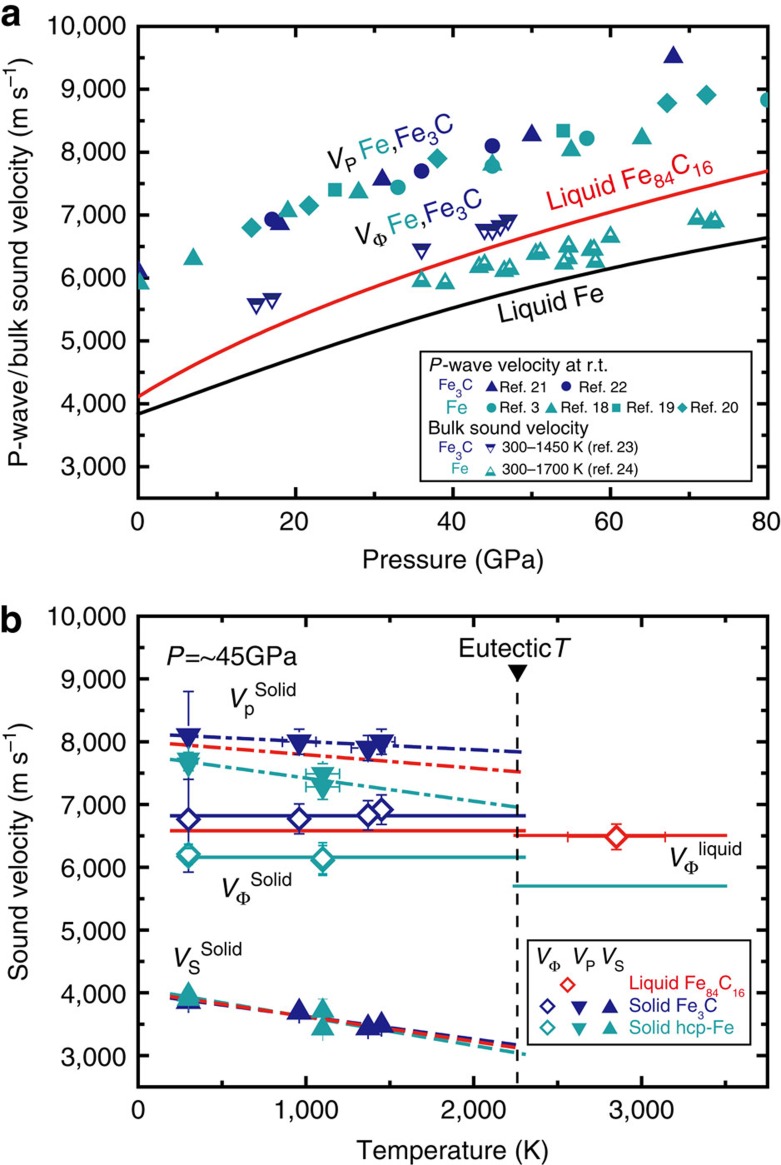
The V_P of liquid Fe₈₄C₁₆ was determined between 7.6 and 70 GPa (Fig. 3 and Supplementary Table 1) from dispersion curves for a range of momentum transfer (Fig. 4). It was found to be 15–30% smaller than that of solid Fe (refs 3, 18, 19, 20) and Fe₃C (refs 21, 22, 23; note that a starting material in the present experiments was a mixture of these solid phases) (Fig. 5), confirming that we measured a liquid sample. The velocities of a fictive solid Fe₈₄C₁₆ alloy are also estimated assuming a linear velocity change between Fe (ref. 24) and Fe₃C (ref. 23) indicating that V_P drops by 13% upon melting at 2,300 K, a eutectic temperature at 45 GPa (ref. 17). Such a velocity change is comparable to that expected for pure Fe. The difference in V_Φ between solid and liquid Fe₈₄C₁₆ is very small (1.8%). On the other hand, the V_P of our liquid Fe₈₄C₁₆ sample is 3–14% faster at 8–70 GPa than that of liquid Fe determined by shock-wave study8 (Fig. 3).

Figure 3. Compressional wave velocity of liquid Fe₈₄C₁₆.

Open circles, obtained by laser-heated DAC; open diamond, by external-resistance-heated DAC. The data at 1 bar is from ultrasonic measurements28 (closed diamond). The red curve represents a thermodynamical fitting result for liquid Fe₈₄C₁₆, compared with the velocity of liquid Fe (black curve)8.

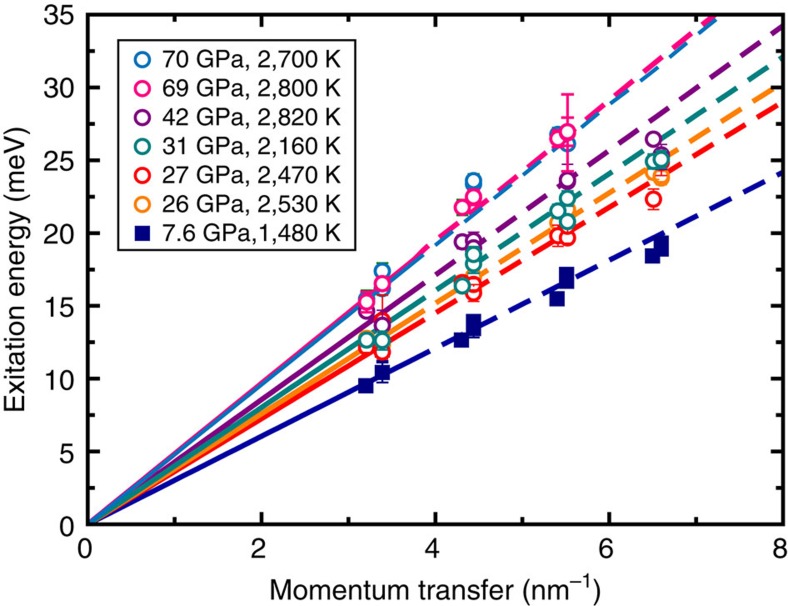
Figure 4. Longitudinal acoustic phonon dispersion of liquid Fe₈₄C₁₆.

The dispersion data were obtained at pressures from 7.6 to 70 GPa. Only data collected with the low momentum transfer (<3.5 nm⁻¹) were used to determine the velocity to avoid possible anomalous dispersion for liquid (see Methods).

Figure 5. Comparison of velocities between liquid and solid Fe–C alloys.

(a), P-wave velocities (V_P) and bulk sound velocities (V_Φ) of solid Fe (turquoise)3,18,19,20,24 and Fe₃C (blue)21,22,23 were determined by previous IXS and nuclear inelastic scattering (NIS) measurements. The V_P for liquid Fe is from shock-wave study8. (b), Temperature effects on the sound velocities of Fe–C alloys at ∼45 GPa. The V_P (= V_Φ) of liquid Fe₈₄C₁₆ and liquid Fe is from the present work at 42 GPa and shock-wave data8, respectively. The V_P, shear velocity (V_S), and V_Φ for solid Fe and Fe₃C were reported by NIS measurements23,24. Red lines for fictional solid Fe₈₄C₁₆ are estimated from a linear relationship between Fe and Fe₃C.

Earlier ultrasonic measurements performed below 10 GPa reported a change in V_P by <2–3% per 1,000 K for liquid Fe–S alloys4,5. Theoretical calculations25,26,27 and shock compression data8 on liquid Fe and Fe–S alloy demonstrated even smaller effects above 100 GPa (<0.5% by 1,000 K). It is therefore very likely that the V_P of liquid Fe₈₄C₁₆ is also not sensitive to temperature with the temperature effect much smaller than the uncertainty in the present velocity determinations (±3%).

Thermodynamical equation of state

V_P of a liquid can be described using the Murnaghan equation of state4 (Methods) as;

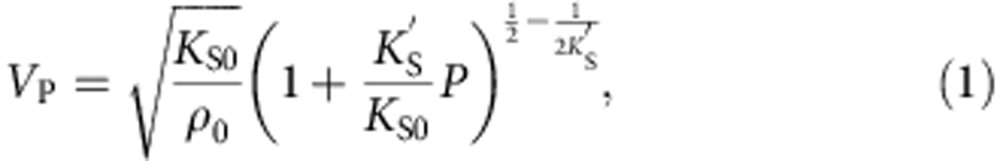where K_S and K′_S are adiabatic bulk modulus and its pressure derivative, respectively (zero subscripts denote values at 1 bar and T=T₀). Here, consistent with the discussion above, we neglect the temperature dependence of our V_P data, while ρ₀ is taken to be temperature dependent16 (Methods). We fit equation (1) to our P–V_P data for liquid Fe₈₄C₁₆ and find K_S0=110±9 GPa and K′_S=5.14±0.30 when T₀=2,500 K (Supplementary Table 2 and Supplementary Fig. 2). The choice of T₀ and, accordingly, the variation in ρ₀ practically changed K_S0 and K′_S0 as (∂K_S0/∂T)=−9.4 × 10⁻³ GPa K⁻¹ and (∂K′_S0/∂T) =−2.7 × 10⁻⁴ K⁻¹. Our value for K_S0 is similar to that for liquid iron8 but for K′_S is higher than that for pure iron, K′_S=4.7. This suggests that liquid Fe₈₄C₁₆ becomes progressively stiffer than liquid Fe with increasing pressure. We also found V_P0=4,121±177 m s⁻¹ for liquid Fe₈₄C₁₆ from K_S0 and ρ₀, in good agreement with a previous study28 of liquid Fe₈₆C₁₄ at 1 bar (4,050 m s⁻¹) and faster than V_P0=3,860 m s⁻¹ for liquid Fe (ref. 8).

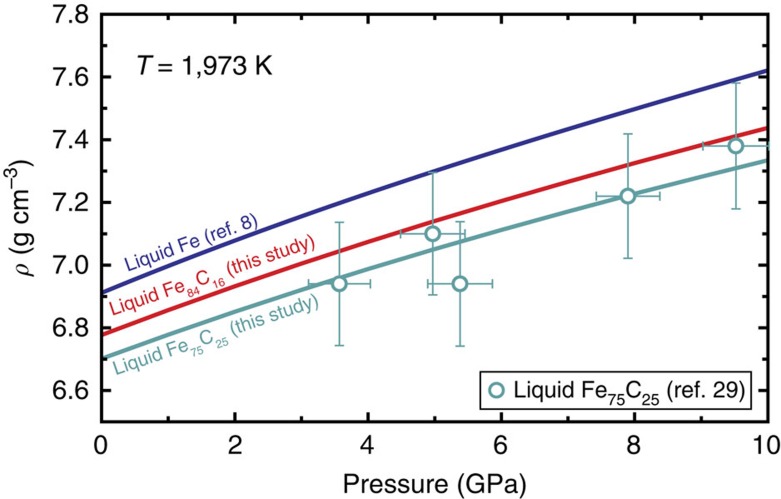
To compare the present results with earlier density measurements of liquid Fe–C alloys at high pressure29,30 the isothermal bulk modulus for liquid Fe₈₄C₁₆ is estimated to be K_T0=100 (82) GPa at 1,500 K (2,500 K) from our determination of K_S combined with Grüneisen parameter γ₀=1.74 (ref. 8) and thermal expansion coefficient16 (Methods). When applying C_P/C_V=1.125 at 1,820 K for liquid Fe₈₆C₁₄ derived from theoretical calculations31, K_T0=106–98 GPa is obtained at the same temperature range. These K_T0 values for liquid Fe₈₄C₁₆ are similar to K_T0=95–63 GPa for liquid Fe at 1,500–2,500 K (ref. 8) On the other hand, they are significantly larger than K_T0=55.4 GPa for liquid Fe₈₆C₁₄ at 1,500 K and K_T0=50 GPa for liquid Fe₇₅C₂₅ at 1,973 K from previous density measurements29,30. However, the calculated density for Fe₈₄C₁₆ using the present EoS are in reasonable agreement with the previous density measurements of Fe₇₅C₂₅ (ref. 29) (Fig. 6). The disagreement of elastic parameters with such earlier experiments may be attributed either to the limited pressure range of the previous density determinations, or to a different structure or magnetic (or electronic) change in the state of the liquid Fe–C at low pressure, as has been suggested from the change in compressional behaviour of liquid Fe₇₈C₂₂ around 5 GPa (ref. 6). Our data were collected above 7.6 GPa, so that the physical properties of liquid Fe–C obtained here should be more applicable to the Earth's core.

Figure 6. Comparison with previous density measurements.

Blue and red curves demonstrate calculated densities at 1,973 K for liquid Fe (ref. 8) and Fe₈₄C₁₆ (present study). The density of liquid Fe₇₅C₂₅ (turquoise curve) is estimated assuming linear compositional dependence between pure Fe and Fe₇₅C₂₅, which shows good agreement with the previous measurements at 1,973 K (ref. 29).

ρ of liquid Fe₈₄C₁₆ is then given, using the elastic parameters determined above, by;

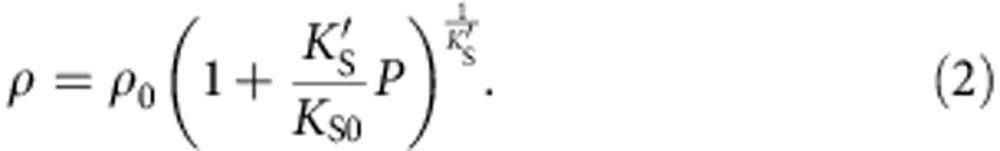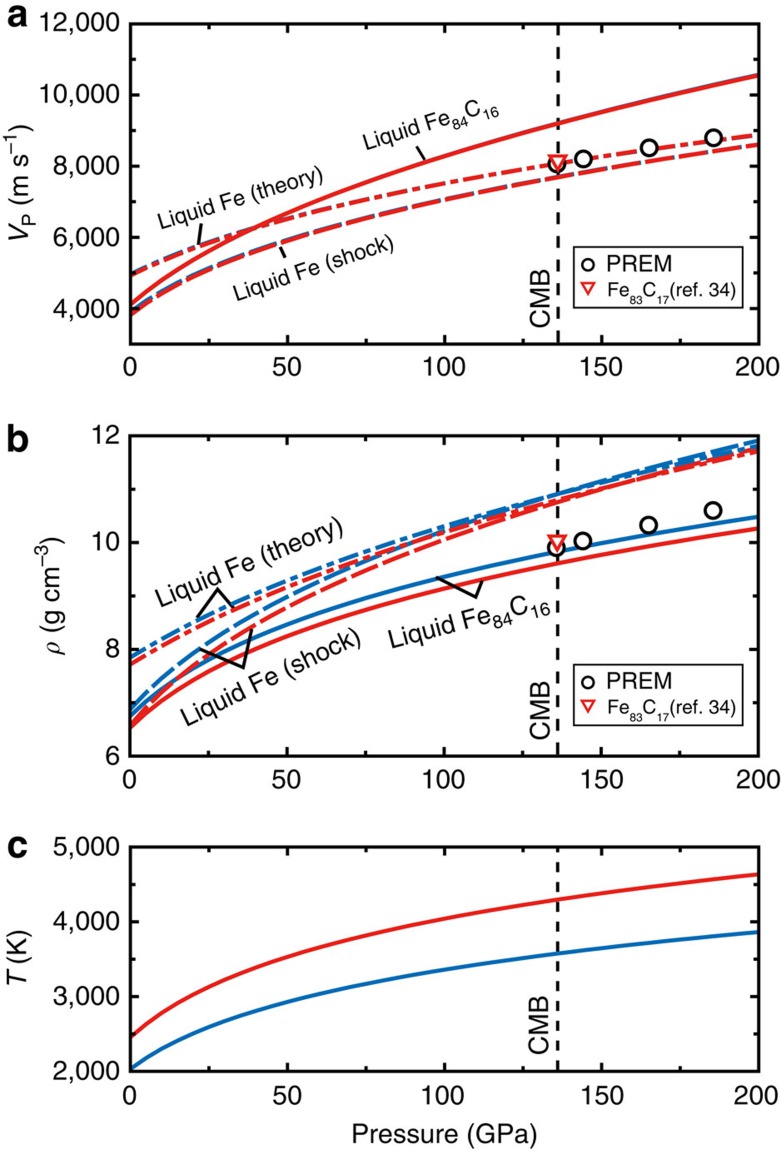
Equations (1) and (2) give the V_P and ρ profiles for adiabatic compression (Methods), assuming γ₀=1.74, the same as that of liquid Fe (ref. 8) (Fig. 7). We find V_P=9,200 m s⁻¹ and ρ=9.82–9.61 g cm⁻³ at the core-mantle boundary (CMB) for T_CMB=3,600–4,300 K (refs 32, 33) This indicates that V_P of liquid Fe₈₄C₁₆ is 19.6% faster than that of liquid Fe at the CMB8, implying that the addition of 1 at.% carbon increases the V_P of liquid Fe by 1.2%. The extrapolation of the present experimental data using the Murnaghan equation of state may overestimate the V_P by 2−4% at the CMB (Supplementary Note 1 and Supplementary Fig. 3), but, even if this is the case, 1 at.% carbon enhances the V_P of liquid Fe by as large as 0.8%. Indeed, the effect of carbon is much larger than a recent theoretical prediction of only 0.2% increase in velocity per 1 at.% carbon at 136 GPa (ref. 34). On the other hand, our data show that the incorporation of 1 at.% carbon reduces the density of liquid Fe by 0.6–0.7%, while theory suggested only 0.3% density reduction by 1 at.% carbon34.

Figure 7. Velocity and density of liquid Fe₈₄C₁₆ extrapolated to core pressures.

The P-wave velocity (a) and density (b) profiles of liquid Fe₈₄C₁₆ are calculated along two adiabatic temperature curves (c) of 3,600 K (blue) and 4,300 K (red) at the CMB. Those for liquid Fe are from shock-compression experiments8 and theoretical calculations26. The velocity and density for liquid Fe₈₃C₁₇ at the CMB (4,300 K) are by theory34. PREM denotes seismologically deduced Preliminary Reference Earth model35.

Discussion

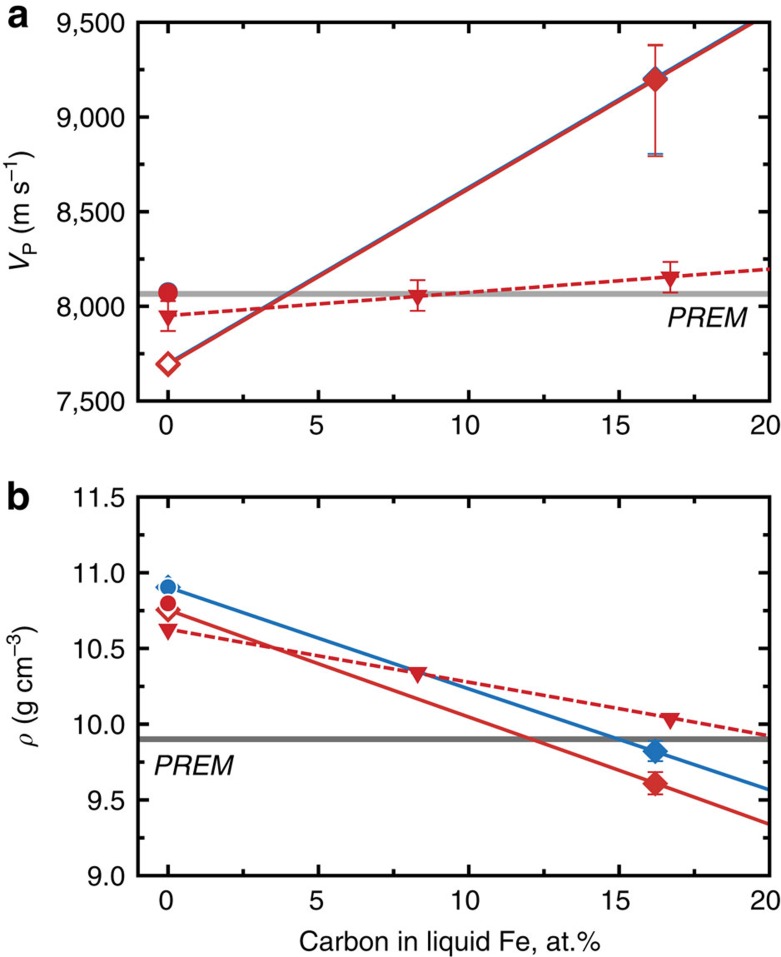
We now compare the sound velocity and density of liquid Fe₈₄C₁₆ and liquid Fe with the seismologically based PREM model35 for the outer core (Fig. 8). The V_P and ρ of liquid Fe are 4.6% slower and 10.1–8.6% denser, respectively, than the PREM at the CMB (3,600–4,300 K). To match the PREM values, considering the uncertainty of data extrapolation to higher pressures (Supplementary Note 1), only 5.2–4.0 at.% (1.2–0.9 wt.%) carbon is required to match the velocity, whereas 15.4–12.0 at.% (3.8–2.9 wt.%) carbon is necessary to account for the density. Therefore, carbon cannot be a predominant light element in the outer core.

Figure 8. Effect of carbon on the velocity and density of liquid Fe at 136 GPa.

(a) Velocity and (b) density for liquid Fe₈₄C₁₆ at T_CMB=4,300 K (red) and 3,600 K (blue). Present results (closed diamonds, solid curves) are compared with theoretical calculations34 (triangles, broken curve). The data for pure Fe are from shock compression study8 (open diamonds) and theoretical calculations26 (closed circles). PREM denotes seismological observations35 at the CMB.

These results suggest there is <5.2 at.% (1.2 wt.%) carbon in the outer core, consistent with the previous cosmochemical and geochemical arguments. In particular, the silicate portion of the Earth exhibits much higher ¹³C/¹²C isotopic ratio than that of Mars, Vesta and chondrite meteorites, as may be attributed to a strong enrichment of ¹²C in core-forming metals9. The carbon isotopic fractionation that occurred during continuous core-formation process proposed previously36,37 will give a reasonable ¹³C/¹²C ratio in the silicate Earth, and yields 1 wt.% carbon in the core9. In addition, Wood et al.9 demonstrated that carbon strongly affects the chemical activity of Mo and W in liquid metal, so that their abundance in the mantle can be explained by partitioning between silicate melt and core-forming metal with ∼0.6 wt.% carbon. It has been repeatedly suggested that the inner core may be composed of Fe₇C₃, which accounts for high Poisson's ratio observed14,15. The crystallization of solid Fe₇C₃ from a liquid outer core with <1.2 wt.% carbon may still be possible if sulfur is also included in the core38.

Methods

High P–T generation

Molten Fe–C alloy was obtained at high P–T in an external-resistance-heated (EH) or laser-heated (LH) diamond-anvil cell (DAC; Supplementary Table 1) using facilities installed at SPring-8. A disc of pre-synthesized Fe₈₄C₁₆ sample, 20–25 μm thick and 100–120 μm in diameter, was loaded into a hole of a rhenium gasket, together with two 12–17 μm thick single-crystal Al₂O₃ sapphire discs that served as both thermal and chemical insulators. The sample was compressed with 300 μm culet diamond anvils to a pressure of interest before heating.

In LH-DAC experiments, the sample was heated at high pressure from both sides by using two 100 W single-mode Yb fibre lasers (YLR-100-AC, IPG Photonics Corp.). The Gaussian-type energy distribution of the laser beam was converted into flat-top one with a refractive beam shaper (GBS-NIR-H3, Newport Corp.). A typical laser spot was 50–70 μm in diameter on the sample, much larger than X-ray beam size (∼17 μm). We determined temperature by a spetroradiometric method, and its variations within the area irradiated by X-rays and fluctuations during IXS measurements were <±10%. The pressure was obtained from the equation of state for Fe₃C (ref. 39) from the lattice constant observed before melting at 1,800–2,500 K. Its error was derived from uncertainties in both temperature and the volume of Fe₃C. A typical image of a sample recovered after the laser heating experiment at 70 GPa and 2,700 K is given in Supplementary Fig. 4.

Only run #FeC08 was conducted in an EH-DAC. The whole sample was homogeneously heated by a platinum-resistance heater placed around the diamonds. The temperature was obtained with a Pt-Rh (type-R) thermocouple whose junction was in contact with the diamond near a sample chamber. The temperature uncertainty was <20 K. We determined the pressure based on the Raman shift of a diamond anvil40 before heating at 300 K, whose uncertainty may be as much as ±20%.

IXS measurements

The sound velocity of liquid Fe–C alloy was determined in the DAC by high-resolution IXS spectroscopy at the beamline BL35XU, SPring-8 (ref. 41). Both LH- and EH-DACs were placed into vacuum chambers to minimize background scattering by air. The measurements were carried out with ∼2.8 meV energy resolution using Si (999) backscattering geometry at 17.79 keV. The experimental energy resolutions were determined using scattering from Polymethyl–methacrylate. The incident X-ray beam was focused to about 17 μm size (full width at half maximum) in both horizontal and vertical directions by using Kirkpatrick–Baez mirrors42. The X-ray beam size was much smaller than heated area (50–70 μm for LH-DAC). Scattered photons were collected by an array of 12 spherical Si analyzers leading to 12 independent spectra at momentum transfers (Q) between 3.2 and 6.6 nm⁻¹ with a resolution ΔQ ∼0.45 nm⁻¹ (full width) that was set by slits in front of the analyzer array. The energy transfer range of ±30 (or −10 to ±30) meV was scanned for 1–3 h. Before and after IXS data collections, sample melting was confirmed by X-ray diffraction data (Fig. 2) that was collected, in situ, by switching a detector to a flat panel area detector (C9732DK, Hamamatsu Photonics K.K.)43.

The IXS spectra included three (sometimes five) peaks (Fig. 1) of Stokes and anti-Stokes components of the longitudinal acoustic (LA) phonon mode from the sample (sometimes also from a diamond), and a quasi-elastic contribution near zero energy transfer. These spectra were fitted with the damped harmonic oscillator (DHO) mode44 for acoustic phonon modes and with Lorenzian function for quasi-elastic peaks convolved by experimental resolution function. The DHO model function can be described as;

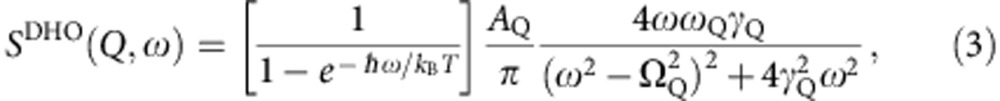where A_Q, Γ_Q, Ω_Q, k_B and ħ are the amplitude, width, and energy of inelastic modes, Boltzmann constant and Planck constant, respectively. In the fitting, temperature T was fixed at a sample temperature obtained by a spetroradiometric method or a thermocouple. The excitation energy modes appearing at both Stokes and anti-Stokes sides correspond to the phonon creation and annihilation, respectively. With increasing temperature, as given by the Bose function in equation (3), the intensities of such Stokes and anti-Stokes peaks become similar to each other. A symmetric shape of the present IXS spectra therefore assures that the IXS signals originated from a high-temperature area.

The peak at a finite energy transfer gives the frequency of each mode (Fig. 1). The excitation energies for the LA phonon mode of liquid Fe₈₄C₁₆ obtained in a pressure range of 7.6–70 GPa are plotted as a function of momentum transfer (Q) in Fig. 4. The compressional sound wave or P-wave velocity (V_P) corresponds to the long-wavelength LA velocity at Q→0 limits;

We made a linear fit to the data obtained at low Q below 3.5 nm⁻¹ to determine the P-wave velocity (Supplementary Table 1), because positive dispersion can appear at higher Q>>3 nm⁻¹ (ref. 45). For comparison, the results based on a sine-curve fit to all Q-range data, as is usually applied for polycrystalline samples in similar high-pressure IXS measurements46, are also given in Supplementary Table 1. In general, the error bars of the two determinations of V_P overlap, though the sine fit to large Q does give slightly larger V_P, as would qualitatively be expected from previous measurements on liquid iron47.

Equation of state for liquid Fe₈₄C₁₆

We constructed an equation of state (EoS) for liquid Fe₈₄C₁₆ to extrapolate the present V_P data and to estimate its density at the core pressure range. V_P of liquid can be written as;

The pressure dependence of K_S is assumed to be

where K′_S is the pressure derivative of K_S and pressure and subscript zero indicates a value at 1 bar. The adiabatic Murnaghan EoS can be described as (for example, ref. 4);

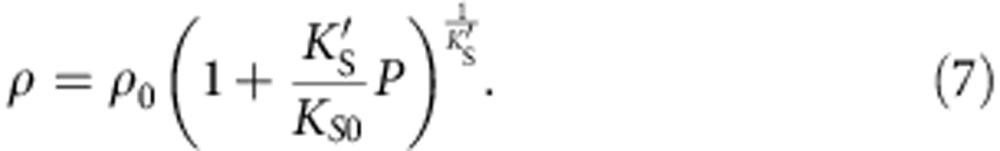Equation (5) is thus rewritten as;

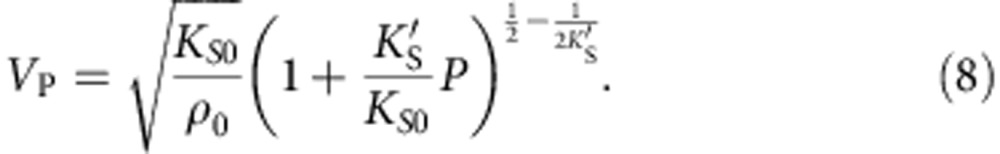The temperature effect on ρ₀ can be expressed by;

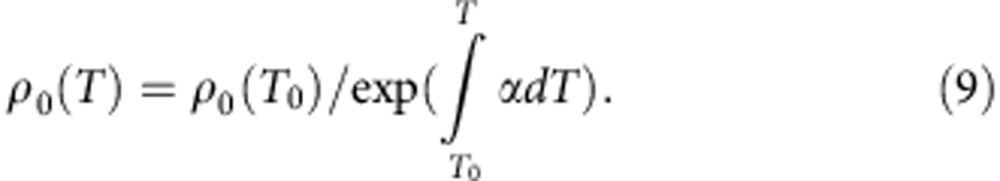The thermal expansion coefficient α is also dependent on temperature as;

where a and b are constants. Previous density measurements16 of liquid Fe–C alloys at 1 bar give a=6.424 × 10⁻⁵ K⁻¹ and b=0.606 × 10⁻⁸ K⁻² for liquid Fe₈₄C₁₆ using ρ₀=6.505 g cm⁻³ at T₀=2,500 K as a reference. The result of fitting equation (8) to the present P−V_P data is given in Fig. 3.

Isothermal bulk modulus

We estimate isothermal bulk modulus K_T from isentropic bulk modulus K_S in two ways. The relationship between these two is described as follows;

where C_P and C_V are heat capacities at constant pressure and volume, respectively. Although γ for liquid Fe–C alloys is not known, γ₀=1.74 has been reported for liquid Fe at 1 bar and 1,811 K (ref. 8) It is close to 1.58 for liquid Fe₉₀O₈S₂ estimated from the shock compression data set48.

Extrapolation of present data to core pressures

With the EoSs determined above (equations (7) and (8)), we extrapolate the P-wave velocity and density of liquid Fe₈₄C₁₆ to the core pressure range along adiabatic compression, in which temperature is given by;

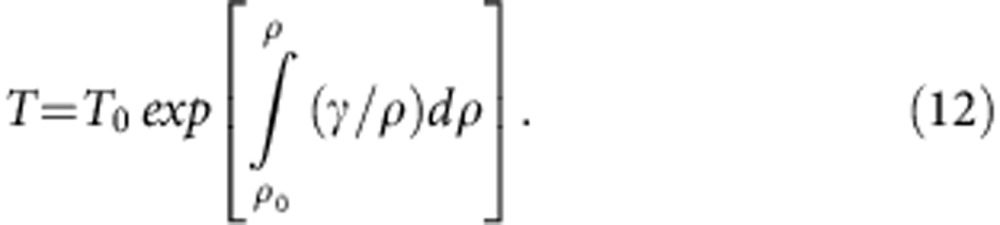Assuming γ=γ₀ × (ρ₀/ρ), temperature is simply represented as;

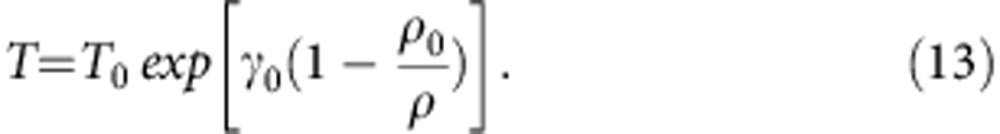γ₀ is fixed at 1.74 previously obtained for liquid Fe (ref. 8). Using the temperature dependence of K_S0 and ρ₀ shown above, we calculate density, velocity and temperature profiles along adiabatic compression with various reference temperatures at the CMB. The adiabatic compression profiles of liquid Fe₈₄C₁₆ for the low (T₀=2,045 K and T_CMB=3,600 K)32 and high (T₀=2,457 K and T_CMB=4,300 K)33 temperature cases are calculated in Fig. 7.

Additional information

How to cite this article: Nakajima, Y. et al. Carbon-depleted outer core revealed by sound velocity measurements of liquid iron–carbon alloy. Nat. Commun. 6:8942 doi: 10.1038/ncomms9942 (2015).

Supplementary Material

Supplementary Information

Supplementary Figures 1-4, Supplementary Tables 1-2, Supplementary Note 1 and Supplementary References