Cancer Mortality Among People Living in Areas With Various Levels of Natural Background Radiation

Abstract

There are many places on the earth, where natural background radiation exposures are elevated significantly above about 2.5 mSv/year. The studies of health effects on populations living in such places are crucially important for understanding the impact of low doses of ionizing radiation. This article critically reviews some recent representative literature that addresses the likelihood of radiation-induced cancer and early childhood death in regions with high natural background radiation. The comparative and Bayesian analysis of the published data shows that the linear no-threshold hypothesis does not likely explain the results of these recent studies, whereas they favor the model of threshold or hormesis. Neither cancers nor early childhood deaths positively correlate with dose rates in regions with elevated natural background radiation.

Introduction

Your body is a fine-tuned system in which billions of cells interact. Each cell has tiny receptors that enable it to sense its environment, so it can adapt to new situations.

From the poster, The Nobel Prize 2012 in Chemistry, The Royal Swedish Academy of Sciences (2012)

The sentence mentioned previously precisely reflects the capacities of our bodies to effectively defend themselves against toxic and life-threatening impacts of external and internal origin. A fraction of these threatening impacts stems from ionizing radiation, whose effects on human health are still debated with controversial arguments regarding exposures to low doses and low dose rates. One may estimate that the ratio of DNA double-strand breaks in human cells from nonradiogenic sources and from average background of ionizing radiation is close to 10³, with endogenous toxins such as reactive oxygen species playing a major role (Feinendegen et al. 2012).

There is no place on the earth without natural background radiation. This also means that life has evolved in a radiation environment that is either harmless or causes adaptation to radiation exposure and assures survival, procreation, and evolution. Indeed, background radiation has never been shown to unequivocally cause acute or latent disease, such as cancer (Hall and Ciaccia 2005). In fact, reduced cancer occurrence was reported decades ago for regions with elevated background dose rates in the United States (Frigerio et al. 1973). Similar results were found by Cohen (1995) and were confirmed by numerous studies also in other regions of the world with elevated background radiation (for instance, Aliyu and Ramli 2015; Mortazawi et al. 2005; Nair et al. 2009; Sun et al. 2000). Many epidemiological and experimental observations dedicated to investigating dose–effect relationships show the risk of late effects, such as cancer, not to be proportional to dose (for instance, Tubiana et al. 2005; Feinendegen et al. 2012; Doss 2012). Such observations are important in the light of current radiation protection which is based on the hypothetic validity of the linear-no-threshold (LNT) model, which predicts that any dose of ionizing radiation, however small, has a defined probability of causing health detriment, especially cancer (BEIR VII 2006). The articles that are selected here for reanalysis appeared during the last decade and present conclusions that rely on controversial claims regarding the validity of the LNT model. It is shown that such claims are not justified.

Natural Background Radiation and Health Risk

The level of natural background radiation on the earth varies considerably by even two orders of magnitude between geographical regions. In most places, the average value of the annual effective dose rate lies between 2 and 4 mSv. However, it may even reach several hundred mSv/year largely from terrestrial sources, for instance in Ramsar, Iran (Mortazawi et al. 2005; Hendry et al. 2009). Places with dose rates above about 10 mSv/year are usually called high natural background radiation (HNBR) regions.

When one attempts to link background radiation to the incidence of cancer in the exposed population, the potential effects from confounding factors are rarely acknowledged. However, it should be clear that there are many endogenous and exogenous causes of cancer besides radiation and that any analysis of cancer risk in different regions of the world needs appropriate control populations that ideally differ from the study population by the degree of radiation exposure only.

Natural background radiation originates from many sources. About 75% of this background comes from terrestrial radon and natural γ radiation emitted by soil and rocks. The remaining 25% come from radionuclides incorporated in the human body and from cosmic radiation (Hall and Giaccia 2005; International Atomic Energy Agency 2004).

Although various effects of dose rates and accumulated doses received by people in HNBR regions could be studied, this article focuses on the cancer mortality and early childhood death rates only. Not considered here are other relevant studies on detriment at the subcellular level, such as chromosomal aberrations or gene mutations (see eg, Wang et al. 1990; Cheriyan et al. 1999; Jiang et al. 2000; Ghassi-Nejad et al. 2004; Ohtaki et al. 2004; Zhang et al. 2003, 2004; Das and Karuppasamy 2009; Hariharan et al. 2010; Chin et al. 2008).

There is a distinct difference between the immediate responses to impacts at the subcellular and cell level on one hand and the subsequent system responses of an entire body on the other. Cell damage in the body can evolve into cancer only in case of failure of the cascade of most complex defense and protection systems. These appear to operate in ordered tiers of biological organization, when damage propagates from the subcellular and cellular level through the body to higher levels of organization. Thus, the examination of cancer incidence encompasses all responses and reactions in an exposed body with the primary radiation damage arising at the molecular and cellular level. Clinical cancer appears only when malignantly transformed cells overcome all cancer defense barriers in the body. The defenses in normal people are estimated to allow only about 1 of 10⁹ malignantly transformed cells in the body to escape and cause clinical cancer (Feinendegen et al. 2010, 2011).

In most articles on health detriment from low-dose radiation exposure, a “health risk” such as risk of cancer is considered irrespective of whether actually there is any risk. Instead of addressing risk as such, this article focuses on the relationship between level of dose and dose rates, cancer mortality, and early childhood deaths in cohorts of people spending their life in areas with elevated background radiation.

Elevated Natural Background Radiation and Health Risk, Analytical Limitations

The article by Hendry et al. (2009) reviews the possible health risks in populations living in regions with elevated background radiation (Guarapari, Brazil; Kerala, India; Ramsar, Iran; Yangjiang, China), including radon-prone areas. Since no statistically significant evidence emerges for health risk from low-level or high-level background radiation, the authors also refer to case–control studies of high-level radon exposure and lung cancer in miners. They claim that these studies provide convincing evidence of an association between disease incidence and long-term protracted radiation exposures within a certain range of dose rates. The authors use this scenario to relate cancer incidences to doses in the general population living in areas with elevated natural background radiation. Although Hendry et al. (2009) treat the case of radon exposure in miners and cancer separately from background exposures, they assume that effects from the latter can be directly compared to those in miners. However, data on cohorts of miners in the environment of underground labor need to be analyzed differently from cohorts of people who are exposed to indoor radon in dwellings (BEIR VI 1999). In this context, it is worthwhile to mention that low doses of radon can even have healing effects as discussed by Yamaoka et al. (2004).

Hendry et al. (2009), as well as recently Aliyu and Ramli (2015), discuss at length the difficulty in obtaining results with statistical significance from epidemiological observations. These must involve large cohorts, in order to succeed in overcoming the so-called “ecological fallacy” (Seiler and Alvarez 2000; Hart 2011b). This fallacy means that the average exposure in a population does not determine the average cancer risk in that population (they are not correlated). In their assessment, Mœller and Mousseau (2013) state on Hendry et al. (2009) that “Overall, these studies demonstrated no increased risks in the HNBR areas compared to control/reference populations.”

Hendry et al. (2009) state rightly that “many countries that contain HNBR areas do not have well-documented health statistics, in particular, organ-specific cancer rates.” This is another argument for focusing not on individual cancer types but on overall cancer mortality. However, even in this case, there are many confounding factors, as mentioned earlier, including smoking, social status, and environmental and climate variations, and they are difficult to control and can affect the final conclusions (Cohen 1995). The data by Hendry et al. (2009) cannot be preferably linked to any particular model in order to correlate observed cancer incidences with the dose rate in regions with elevated background radiation.

A different study pooled 28 reports on radon-induced lung cancer (Fornalski and Dobrzyński 2011). The analysis of the published data shows such a large scatter that the only statistically approved conclusion is that within a radon concentration of up to ∼800 Bq/m³, there is no statistically significant adverse effect of radon. This conclusion does not change if Cohen’s (1995) and the miners’ data are excluded from the report pool. The finding of no statistically significant adverse effect of radon is in opposition to the conclusions of United Nations Scientific Committee on the Effects of Atomic Radiation (UNSCEAR 2006), which emphasizes an elevated radiation risk even at the radon concentration of 100 Bq/m³. Also other studies, such as those by Lubin and Boice (1997), were analyzed by Fornalski and Dobrzyński (2011) in compliance with the approaches by UNSCEAR (2006). Here, too, there was no attempt to investigate the entire set of data available in the published literature. These authors relied on selected articles only. Neither did they consider beneficial health effects observed in high-radon environments, as for example, described by Becker (2003).

Natural Background Radiation in Selected Studies in Humans

The article by Mœller and Mousseau (2013) claims the existence of adverse effects as a result of exposure to ionizing radiation doses that are lower or equal to those in HNBR regions. It presents a large data set from humans, animals, and other organisms. These reanalyzed studies include human cancer deaths, stamen hair mutations among plants, or pregnancy rates among rats, with various results with borderline or no statistical power. The authors listed all data of the heterogeneous participant cohorts in table 1 in their article and reanalyzed all of them together. This type of analysis strongly increases confounding uncertainties that already exist in individual cohorts and puts in question the validity of the final conclusion of the article.

Mœller and Mousseau (2013) also try to combine information from various organisms in search for hormetic effects regarding incidence of cancer in regions with elevated background radiation. The authors argue that such effects, if present, should come to light “because of adaptation to such enhanced levels of radiation.” One of the final conclusions is “Our findings are clearly inconsistent with a general role of hormesis in adaptation to elevated levels of natural background radiation.” Moreover, the article claims that there is evidence of some adverse rather than beneficial effects of low doses and dose rates on DNA damage and DNA repair with the result of an enhancement of the incidence of cancer. Thus, the authors reject the potential of adaptation of the defense barriers against damage propagation which operate in tiers from the cellular to the whole-body level before clinical cancer evolves (Feinendegen and Neumann 2005).

Narrowing the focus in the article of Mœller and Mousseau (2013) to human cancers only, one can analyze 11 articles that are quoted in table 1 in their article. None of these quoted articles supports any significant increase in cancer mortality with dose. Also, the article of Nair et al. (1999) that is quoted by Mœller and Mousseau (2013) states no increase of health effects in HNBR regions. However, the more recent publication of Nair et al. (2009), which is omitted by Mœller and Mousseau, shows a trend to a decrease instead of an increase of cancer incidence in HNBR areas. These authors observed in Kerala, India, the relative risk of cancer at age >70 years to decline within borderline significance as absorbed dose rates increase up to more than 10 mGy/year. Mœller and Mousseau also do not consider the article of Sun et al. (2000), which shows that the excess relative risk (ERR) of some, not all, cancers in people living in areas with elevated natural background radiation in China decreases drastically. The uncertainty margins for ERR in Sun’s article, however, are very broad similar to the uncertainties in the article by Mœller and Mousseau. In table 2 of Mœller and Mousseau (2013), the mean value of the ERR for the 11 cancer studies equals 0.057 with 95% confidence intervals of (−0.017 to +0.158), and P value is .22. It is noteworthy that 7 of the 11 articles quote dose rates of <5 mSv/year, which is only 2-fold or less over the average worldwide background rate. Only 2 of the 11 articles quote exposures in the medium category of elevated background radiation (5-10 mSv/year) at 6.4 mSv/year. Another article of that group reports exposures in the low/medium categories (2.4-6.4 mSv/year).

The failure of an increased incidence of cancer to appear in regions with elevated natural background radiation discussed so far may be due not only to the limitation of the cohort size being observed at low-dose exposures and thus be of low statistical power but may also be due to an adaptation to radiation in people living in regions with higher exposures to background radiation. This is found, for instance, by Mortazavi et al. (2005). These authors also demonstrated that lymphocytes from HNBR-exposed people in the Ramsar area, Iran, have undergone an adaptive response, making the cells less sensitive to repeated high-dose irradiation. If humans adapted better to higher than lower levels of chronic irradiation, then without going into details of such mechanisms, one would have to accept that at least the higher level of radiation, as in Ramsar, is relatively well tolerated. In another HNBR study in Kerala, India, the incidence of DNA damage per person decreased with age, whereas in the control population, the incidence of DNA damage increased with age, as predicted (Kumar et al. 2012). Moreover, a recent study (Fliedner et al. 2012) reviewed the data on dogs that were kept during their entire life in an artificial high background of γ-radiation (Co-60). The dogs tolerated relatively high doses very well depending on the dose rate. The animals had a shorter life span only when the absorbed dose rate exceeded 3 mGy/d to a total accumulated dose of more than 10 Gy. A continuous exposure to 3 mGy/d of Co-60 radiation brings every cell (with the mass of 1 ng) in the dog’s body to be hit on average and stochastically by 1 energy deposition event from an electron track every 2.4 hours throughout life (Fliedner et al. 2012). At dose rates higher than 3 mGy/d, death was mainly due to hematopoietic failure. Obviously, chronic radiation exposure is not only less harmful per unit dose, than acute exposure, but it can also induce cellular responses in such a way that adaptation phenomena appear.

All data so far contradict the position taken by Mœller and Mousseau (2013), and the current state of knowledge does not allow the claim that HNBR causes adverse health effects including cancer.

Background Radiation and Cancer Mortality in Bavaria

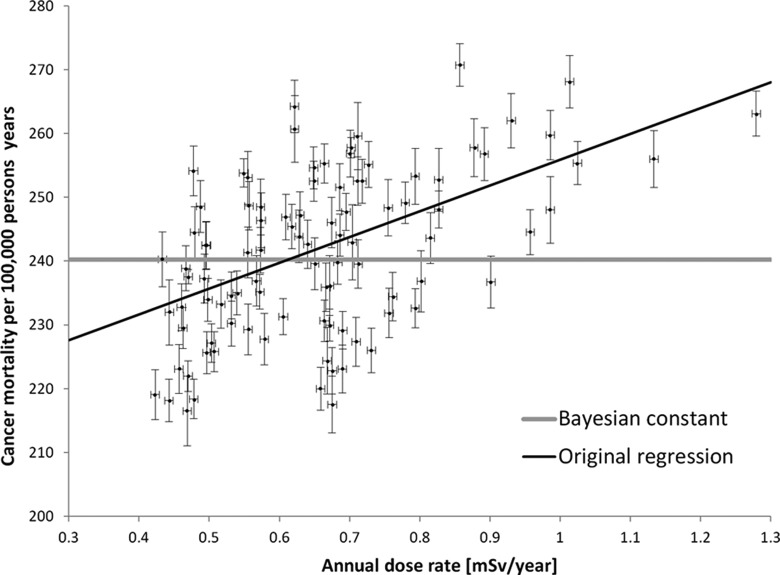
The data set of Körblein and Hoffmann (2006), which was also a part of previously described meta-analysis by Mœller and Mousseau (2013), covers a relatively large collection of observations on incidence of cancer and γ-radiation level in 96 districts of Bavaria, Germany. These studies are of great interest, as they intended to show that the risk of cancer increases even at the lowest dose rates. The individual discrete district cancer death rates per 100 000 inhabitants per year versus dose rate from terrestrial radiation exposure in mSv/year are shown in Figure 1. The authors applied multiparameter linear regression analysis and obtained a function that is graphically inserted in Figure 1, black line. Their conclusion is that an increase in the dose rate, and thus life time accumulated dose, from natural background radiation may have adverse effects on human health.

Figure 1.

Cancer deaths per 100 000 people per year in 96 districts in Bavaria, Germany, against terrestrial exposures at dose rates expressed in mSv/year (adapted from figure 1 of Körblein and Hoffmann, 2006). The authors fitted a linear function to the data, shown by the black thin line. The Bayesian fit suggests the model that the observed cancer mortality is dose independent (this is displayed by the gray horizontal line). The error bars indicate 1 standard deviation.

It is to be noted first that the data points in Figure 1 are scattered much above the uncertainties quoted by the authors in the regression analysis. Because of this discrepancy, in this article these data are subjected to a reanalysis with the Bayesian approach (see also Appendix A).

The number of possible dose–effect dependences that could be fitted to the pool of collected data is infinite. The simplest model (model 1) assumes that the cancer mortality is dose independent. The other models are linear (model 2) and linear quadratic (model 3). It turns out that all three models can be fitted to the data. However, the values of the misfit function χ² are very high, of the order of 1000, in spite of relatively many data points. This means that one can hardly conclude which of the models is better. Mathematically acceptable here is the Bayesian approach that was earlier used in the analysis of radon data (Fornalski and Dobrzyński 2011). The data to be analyzed were recovered by data digitalization from the original figures shown in the article by Körblein and Hoffmann (2006).

The Appendix explains the Bayesian approach being applied to the data in Figure 1. Allowing for improper estimation of the experimental uncertainties, one searches for a distribution of uncertainties that would characterize the data constrained to the assumed model. In the next step, one can then estimate the relative plausibility of that model. In this presentation, 3 models are tested for applicability to the data. The resulting equations with their coefficients as obtained by the Bayesian approach (see Appendix) are:

• Model 1: no dose dependence (constant mortality)

Cancer mortality per 100 000 person-years: a = 240.2 ± 1.5

• Model 2: Linear fit (mortality = a + b·Dose)

a = 218.2 ± 4.7; slope: b = 37.2 ± 5.9

• Model 3: Linear-quadratic fit (mortality = a + b·Dose + c·Dose²)

a = 205.2 ± 4.2; b = 67.4 ± 12.0; c = −17.5 ± 8.7

The comparison between the above-mentioned models shows the ordinate base line, that is, the value a to fall with increasing model complexity from 240 to 218, to 205. Conformingly, the slope that reflects relative risk, that is, the value b, increases from 0 to 37 to 67. Finally, model 3 results in an apparently inverted parabola that has no correlation to reality. Also, the slopes obtained within the scope of linear model 2 can hardly be accepted because slope 37 means that over one-third of the population should die of cancer if exposed to the dose of 1 Sv during 1 year. Such outcome does not comply with numerous experimental or epidemiological data. In addition, within the scope of the LNT approach and International Commission for Radiation Protection (ICRP; 2005) the standard of the ERR is 5%/Sv, which is still lowered by the Dose and Dose Rate Effectiveness Factor (DDREF) factor at small doses. Thus, the result obtained for the linear model 2 cannot be accepted. The analysis of the plausibility of the various models shows that model 1 is approximately 7 times more likely than model 2 and approximately 11 times more likely than Model 3.

Background Radiation and Early Childhood Death in Bavaria

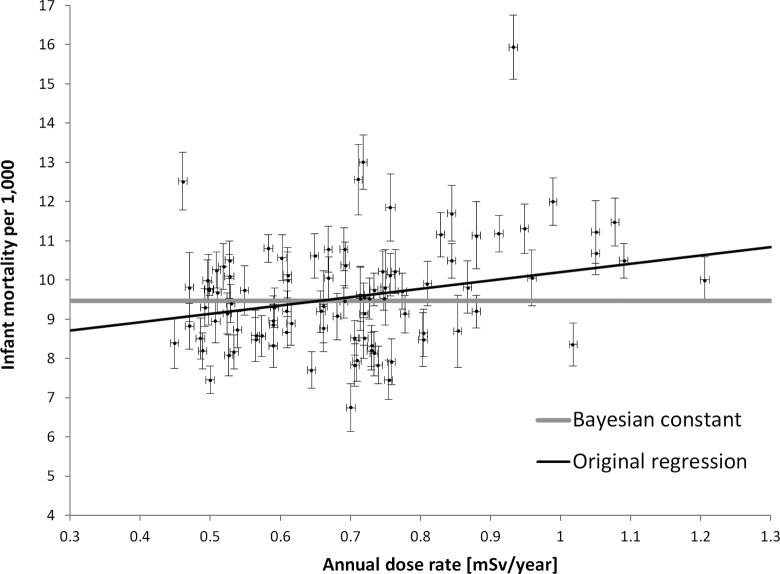
Körblein and Hoffmann (2006) included in their publication also the data on early childhood death versus γ dose rate in the 96 Bavarian districts. It appears interesting in this context that early childhood death may be viewed as a special category of consequences of basic cell damage comparable to those leading to malignancies. Figure 2 gives the individual data points that, as in the previous study from Bavaria, reflect large uncertainties.

Figure 2.

Infant mortality rates (adapted from figure 2 of Körblein and Hoffmann, 2006) plotted against dose rate in mSv/year from terrestrial background exposure. The black thin line shows the best fit of the model assuming linear no threshold (LNT), while the horizontal gray line shows the result of applying the Bayesian model conforming to the observed mortality being dose independent. The error bars indicate 1 standard deviation.

This leads to almost identical and high values of χ² (about 500), and a rational choice of the model is not possible. This in turn shows that the declared uncertainties were still heavily underestimated in the regression analysis by these authors. Using the Bayesian approach (see Appendix), again three models were tested on the data gathered for early childhood death versus dose rate.

• Model 1: a = 9.5 ± 0.1.

• Model 2: a = 7.7 ± 0.2; b = 2.5 ± 0.3.

• Model 3: a = 9.8 ± 0.7; b = −3.5 ± 1.8; c = 3.9 ± 1.3.

With the Bayesian approach, the model selection procedure again shows that the simplest model 1, that is, no dose dependence of the children’s mortality, is most likely. The linear model 2 is over 14 times and model 3 is approximately 21 times less likely than model 1. This can also be deduced from the simple fact that the huge scatter of points (Figures 1 and 2) as well as small uncertainties declared by the authors (Körblein and Hoffmann 2006) make all models but model 1 inconsistent and inappropriate for serious statistical analysis. Figure 2 includes the result of the fitting of model 1 to the original data, besides the original regression line.

Obviously, one could use still more sophisticated methods of analysis (Kaiser and Walsh 2013). However, the rather large uncertainties characterizing all the data discussed so far and the concomitant large error ranges make the use of more sophisticated statistical tools less relevant so that it is reasonable to remain with the simpler models.

Caveats in Observing and Explaining Oncogenesis in Regions With Elevated Natural Background Radiation

Since our article deals with ecological data, one should be aware of the so-called ecological fallacy argument (Seiler and Alvarez 2000; Hart 2011b), usually referred to in ecological analyses. In such studies, the dose–effect dependence in the case of, for example, cancer incidence in some geographical regions are statistically analyzed without knowing individual human exposure conditions. The statistical powers of ecological studies are, however, only a little lower than those of the case–control ones with individual exposure histories, as discussed by Hart (2011b). Ecological studies are reported widely, and our knowledge of the health effects of ionizing radiation is largely based on such studies. As an example, the much debated Cohen’s analysis of radon risk (Cohen 1995), showing a decreased lung cancer incidence with increased radon exposure, was recently confirmed in the course of case–control studies by Thompson et al. (2008). Additional ecological studies are the analyses of the cancer risk due to natural radiation in China (Sun et al. 2000), Guam (Denton and Namazi 2013), Poland (Fornalski and Dobrzyński 2012), United States (Hart 2010, 2011a), and Switzerland (Hauri 2013). Another recent study used the case–control approach (Jaikrishnan 2013) and, although not directly related to cancer, shows that the HNBR level in Kerala, India, has no influence on stillbirth and major congenital anomalies among newborns. Regardless whether it is a case–control study or an ecological study, the application of the Bayesian analysis allows the identification of essential trends of data. The application of the Bayesian analysis to the Körblein and Hoffmann (2006) article presented here is an example which overwhelmingly shows the dilemma of relating risk to low doses: Many models may be applied to the data, but the model showing no dose dependence has the highest plausibility based on the measured data. Which of the models has the highest probability of being correct appears answerable only on the basis of a holistic view of all available appropriate epidemiological and experimental data. For instance, if our analysis of the data presented in Figure 1 results in the conclusion that a no dose dependence model is 7 times more plausible than the LNT model (Model 2), one may still favor the LNT model, however, only on the assumption that the LNT model is at least 7 times more likely than model 1. There is no support for such an a priori assumption. Therefore, the aforementioned set of data from areas with elevated natural background radiation supports the current analyses and speaks in favor of a threshold and/or hormesis.

People living in elevated radiation background areas must have adapted themselves throughout history to this radiation level (Hendry et al. 2009). Some authors refer to adaptation, besides the lack of sufficiently large cohorts, to explain why no significantly elevated cancer risk was ever detected in such regions. However, this means that radiation protection recommendations could consider the level of radiation in a given environment as being the best reference level for local ruling on permissible doses or dose rates. Nevertheless, because adaptive protection (Feinendegen et al. 2011; Scott 2011) involves mechanisms that are not fully understood, the regulations on radiation protection do not take adaptive protection into account.

The ICRP admits that low and high doses and dose rates cause different responses in the exposed bodies (ICRP 2005). The DDREF of about 2 has been proposed rather arbitrarily to accommodate the decreased effectiveness of low doses or dose rates. Be it as it may, as stated by Calabrese (2005, 2011): “No person or group during the entire period of the twentieth century ever attempted to validate the capacity of the threshold dose-response to make accurate predictions in the below-threshold zone (that is, the zone where most people live for the vast majority of each day).” In fact, the studies reviewed by Calabrese and his team showed that “only the hormetic (biphasic) dose-response [model] made consistently accurate predictions” (Calabrese 2011).

Indeed, the hormetic model explains well the data from areas with elevated natural background radiation (Scott et al. 2007, 2011; Feinendegen et al. 2012), and it also encompasses the potential ability of an organism to “getting used” to higher levels of radiation. However, the published studies including those discussed here are statistically too weak to discriminate between various models for populations in a given region with elevated natural background radiation.

If one takes into account the large variations in doses which people receive in various places on the earth, and the locally measured responses of defense mechanisms in such populations, it is clear that the threshold model can hardly be defined as a unique standard. As discussed in this article, rather the hormetic model appears applicable to interpret the data from all geographic regions. This model may also explain a dose threshold as a result of the radiation-induced balance between probabilities of damage causation and prevention, as explained by the Dual Response Model (Feinendegen et al. 2012). As a consequence, if these probabilities are of the same magnitude, a threshold appears below which there is no increased incidence of cancer. Indeed, according to the model, a relatively low risk of radiogenic cancer at low doses matches the probability of a temporary prevention of spontaneous cancer at these dose ranges. This conclusion is supported by many experimental findings in single cells, tissues, and whole organisms, where acutely absorbed doses in the range up to ˜200 mGy cause a time-delayed protection not only against repeated irradiation but also against other toxic impacts (Feinendegen et al. 2012). Indeed, the experimental demonstration of hormesis also led to applying low doses for treating diseases (Sanders 2010).

The degree of temporary protection against a toxic impact in experimental studies may be expressed in percentage of protection against the development of a defined disturbance, such as DNA damage, altered enzyme reaction rate, malignant cell transformation, or cancer metastases. The degree of protection as a function of dose from acute exposure is, interestingly, similar in many different systems and at different levels of biological organization. The mean value of radiogenic reduction in detrimental effects is ∼0.6 (60%) at a dose around 100 to 200 mGy, and as absorbed doses increase beyond 500 mGy the protective effects vanish (Feinendegen et al. 2012). Protective effects also appear at higher accumulated doses provided the dose-rates are relatively low.

Regarding chronic low dose rate irradiation, as it may occur in regions with increased natural background radiation, there is clear evidence that chronically accumulated doses up to 100 times higher than ambient exposures may be beneficial (Kauffman 2003; Tanooka 2011; Takatori et al. 2013). Also, Luckey (2008) summarized that chronic irradiation can prevent much cancer irrespective of it being caused by carcinogenic chemicals or radiation. This agrees with the hypothesis that the incidence of clinical cancer comes from the difference between the incidence of oncogenesis from whatever cause on one hand and the degree of protection mainly against “spontaneous” oncogenesis on the other (Feinendegen et al. 2012). In this view, also at chronic exposure, doses below the threshold level may cause a hormetic effect, in that the radiogenically added cancer is either quantitatively overwhelmed or balanced by the prevention of developing or spontaneous cancer at that dose.

Conclusion

Risks of low doses and low dose rates, such as from elevated natural background radiation exposures, appear not to exist or be lower than such risks that one assumes by applying the LNT model in the evaluation of epidemiological data. This and the unequivocal evidence of experimental findings of adaptive protection speak against the LNT hypothesis, which should be replaced by a model that takes into consideration that low doses can induce alterations in the physiologically individual balance between cancer causation and cancer prevention. This physiological balance determines both detrimental and beneficial effects in the whole body, depending on dose and dose rate. The existing epidemiological and experimental data do not favor low dose-induced detriment but rather agree with low dose being inefficient or inducing benefits by counteracting harm, that is, with the existence of threshold or hormesis.

Claims that elevated natural background radiation levels lead to cancer or early childhood deaths are unjustified and misleading. The risk to the individual and society that is estimated by adhering to the LNT model is greater than the risk from doses and dose rates at which the LNT model cannot be validated.

The present article shows that the Bayesian analysis allows one to quantify the relative plausibility of models that are used to explain dose–risk relationships. In particular, one can appreciate the crucial consequences of accepting prior information that affects model preferences for providing highest probability values.

Appendix

A note on model selection

The Bayesian analysis used in the article was completely described and applied in practice by Fornalski and Dobrzyński (2011). The methodology covers 2 main aspects: the robust Bayesian regression analysis (a function fitted to the data points) and the model selection algorithm.

In accordance with the Bayesian approach, once we have a certain knowledge of things, that is, some experimental data, E, that made us believe in the model M, then, depending on the degree of this belief, we can describe this knowledge by a prior probability (or simply—prior) p(M|E, I), where I denotes any other information that we may have. When a new data set appears, E _new, one can test how well it corresponds with our model (hypothesis) and the old experimental data E. This is described by the so-called likelihood function, p(E _new|M, E, I). As a result, due to the Bayesian theorem, our knowledge (or degree of belief in the model—hypothesis M) changes to the so-called posterior probability given by what is named the multiplicative constant neglected:

$$P\left(M|E_{\mathrm{n}\mathrm{e}\mathrm{w}},E,I\right)\hspace{0.17em}=\hspace{0.17em}p(E_{\mathrm{n}\mathrm{e}\mathrm{w}}|M,\hspace{0.17em}E,I)p(M|E).$$ A1

In the situation of the robust Bayesian regression analysis, when the accuracy of the data is put to doubt, it is assumed that the uncertainty of any ith experimental point E_i with original uncertainty σ_0i should rather be described by the appropriate probability distribution (prior), for example, p(σ_i) = σ_0i/σ_i⁻² as proposed by Sivia and Skilling (2006). This form of prior tells that the original uncertainties (eg, shown in Figure 1) must be larger than declared, since the scatter of points in the data is much larger than the proposed uncertainties. However, the form of this probability function also guarantees that one does not give much weight to much higher overestimation of the original uncertainties. Finally, the Equation A1 takes the form:

$$P_i\hspace{0.17em}=\hspace{0.17em}{\int }_{{\mathit{\sigma }}_{0i}}^{\mathrm{\infty }}\frac{1}{{\mathit{\sigma }}_{0i}\hspace{0.17em}\sqrt{2\mathit{\pi }}}\hspace{0.17em}exp\hspace{0.17em}\frac{M_i-E_i}{{\mathrm{2}\mathit{\sigma }}_i^2}\hspace{0.17em}\times \hspace{0.17em}\frac{{\mathit{\sigma }}_{0i}}{{\mathit{\sigma }}_i^2}\hspace{0.17em}d{\mathit{\sigma }}_i$$ A2

taking the Gaussian distribution as a likelihood function. As one could check, all potential outlier points give insignificant input to the general posterior probability distribution $P\hspace{0.17em}=\hspace{0.17em}\mathrm{\Pi }{P}_i.$

$$P=\prod \hspace{0.17em}\frac{{\mathit{\sigma }}_{0i}}{(M_i-E_i\hspace{0.17em}{)}^{\mathrm{2}}\sqrt{2\mathit{\pi }}}\left[1\hspace{0.17em}-\hspace{0.17em}exp\hspace{0.17em}\left(\frac{-\hspace{0.17em}(M_i-E_i{)}^{\mathrm{2}}}{2{\mathit{\sigma }}_i^2}\right)\right],$$ A3

where the model M corresponds to the curve being fitted to existing points. This complicates the calculations as described in Fornalski and Dobrzyński (2011). However, with a simple computer program, all necessary curve parameters α_n (included in a model M) can be iteratively found by solving the set of n equations:

$${\sum }_{i\hspace{0.17em}=\hspace{0.17em}1}^N{g}_i(M_i-E_i)\hspace{0.17em}\frac{d{M}_i}{d{\mathit{\alpha }}_n}\hspace{0.17em}=\hspace{0.17em}0,$$ A4

where

$$g_i\hspace{0.17em}=\hspace{0.17em}\frac{1}{(M_i-E_i{)}_i^2}\hspace{0.17em}\left\{2\hspace{0.17em}-\frac{(M_i-E_i{)}_i^2}{{\mathit{\sigma }}_{0i}^2}\hspace{0.17em}\frac{1}{exp\hspace{0.17em}\left(\frac{(M_i-E_i{)}_i^2}{{\mathrm{2}\mathit{\sigma }}_{0i}^2}\right)\hspace{0.17em}-1}\hspace{0.17em}\right\}.$$ A5

The form of Equation A4 is essentially the same as in standard search of the minimum of χ² misfit function. However, one can see that the weights given to the points are completely different. They depend not only on the declared accuracy of an ith point, σ_0i, but also on the model which is fitted. This is just what allows to calculate relative plausibilities of models, say A and B, with conditional probabilities based on the old data set, D, on a new data set, D _new, and any earlier information, I:

$$\frac{p_A(M_A|E_{\mathrm{n}\mathrm{e}\mathrm{w}},\hspace{0.17em}E,I)}{p_B(M_B|E_{\mathrm{n}\mathrm{e}\mathrm{w}},\hspace{0.17em}E,I)}\hspace{0.17em}=\hspace{0.17em}\frac{p_A(E_{\mathrm{n}\mathrm{e}\mathrm{w}}|M_A,\hspace{0.17em}E,I)\hspace{0.17em}p(M_A|E)}{p_B(E_{\mathrm{n}\mathrm{e}\mathrm{w}}|M_B,\hspace{0.17em}E,I)\hspace{0.17em}p(M_B|E)},$$ A6

where $p_A(M_A|E)$ and $p_B(M_B|E)$ are prior degrees of beliefs in the models A and B, respectively, while the leading terms in the nominator and denominator on the right-hand side of Equation A6 are calculated in accordance with Equation A3.