Research participant compensation: a matter of statistical inference as well as ethics

Abstract

The ethics of compensation of research subjects for participation in clinical trials has been debated for years. One ethical issue of concern is variation among subjects in the level of compensation for identical treatments. Surprisingly, the impact of variation on the statistical inferences made from trial results has not been examined. We seek to identify how variation in compensation may influence any existing dependent censoring in clinical trials, thereby also influencing inference about the survival curve, hazard ratio, or other measures of treatment efficacy. In simulation studies, we consider a model for how compensation structure may influence the censoring model. Under existing dependent censoring, we estimate survival curves under different compensation structures and observe how these structures induce variability in the estimates. We show through this model that if the compensation structure affects the censoring model and dependent censoring is present, then variation in that structure induces variation in the estimates and affects the accuracy of estimation and inference on treatment efficacy. From the perspectives of both ethics and statistical inference, standardization and transparency in the compensation of participants in clinical trials is warranted.

Introduction: motivation and assumptions

In recent years, there has been increased pressure on investigators to disclose their financial stakes in clinical trials due to concerns over conflicts of interest [1]. Despite this emphasis on transparency, there are no requirements for disclosure regarding payments to research subjects or compensation of investigators for accrual and retention of trial participants. We investigate how variation in these incentives could affect statistical inference through their effect on the retention and drop-out (i.e., censoring) processes. While it is possible that incentives also affect the event time, this would likely happen to a lesser extent because the event time is often a more direct function of physiological processes. Much of our examination hinges on an assumed background of dependent censoring, i.e., an association between event and censoring times. This is a common feature of clinical trials and impedes valid time-to-event analysis. No attention has been paid in the literature to how incentive structures influence and interact with dependent censoring. However, in the case of some statistical tests, dependent censoring is not even required for an association between incentives and censoring to invalidate inference [2]. In this paper, we use the terms “incentive,” “compensation,#x0201D; and “reward” interchangeably, all in reference to the payment used to minimize participant drop-out in clinical trials. It is also important to emphasize at the outset of this investigation that while we posit that monetary compensation may be the chief source of unaccounted-for variation across trials, we can consider payment more generally. For example, it may be a psychological reward such as personal encouragement for retention and compliance from an investigator or caregiver who may be compensated, or personal satisfaction from adherence to cultural norms that are specific to study site (this is especially true for international, multi-center trials).

In this paper, we first summarize current compensation practices. We then discuss the impact of varying reward structures on cross-trial comparisons and analyses, which can refer to meta-analysis of different trials examining a common outcome and therapy or a single trial with multiple sites for which incentive heterogeneity exists. We posit one plausible censoring model that is a function of the incentive structure and other factors, and through simulation, investigate the variation in estimation of the survival distribution. We demonstrate that reward structures may influence estimated treatment efficacy and so it is important to incorporate this information in statistical analyses and disclose it in the reporting of trials. We encourage journals to add this reporting requirement along with those for conflict of interest and registration of clinical trials.

Current clinical trial compensation practices

Papers that have been published on practices of research subject inducement and compensation in clinical studies reveal variation and a lack of structure in the incentives subjects receive for procedures. Grady et al. [3] surveyed practices of subject payments in 2005 and found that of the 467 surveyed studies, 78% did not specify amount of payment per procedure in the study protocol or subject consent document, and 71% did not specify payment per hour or visit. Some procedures, such as endoscopy, showed little variation in remuneration (consistently $100), while others had considerable variation, such as MRIs ($25-$120) and venipuncture ($10-$50). When payment per visit was recorded, there was variation from $10 to $250. From a broader perspective, compensation for an entire study varied from $5 to $2000, though that variation is partly a function of the study time required and procedure invasiveness. Sixty-six of the studies surveyed were multi-site and 85% of them showed variation in payment across sites. The range of variation was as large as $1000, and the mean and median of inter-site variation were $228 and $120, respectively.

Dickert et al. [4] performed their own analysis of payment practices by investigating 32 research organizations, which spanned the academic, pharmaceutical, contract research organization (CRO), and independent institutional review board (IRB) sectors. The researchers found that only 37.5% of these organizations had specific policies in place regarding payment of research subjects, and as a result, there was no standard of compensation. Indeed, only 18.8% of organizations could even give a confident estimate of the proportion of their studies that were paid. There was also variation in how organizations viewed payment, be it as an incentive to participate (58% of organizations) or compensation for time, inconvenience, or risk. Half of the written guidelines for payment that the investigators reviewed explicitly stipulated that risk should not be compensated. One-fourth of the organizations surveyed had formulas for payment, though the level of specificity varied. When an hourly rate was specified, it varied from $4 to $10. Some organizations paid by day or visit, and payment varied from $25 to $125.

Impact of varying reward structures

If payment or some other factor altered the underlying dependent censoring mechanism, one would expect to see variation in outcomes of the placebo arms of trials of similar patient populations if incentive variation is present. Schneider and Sano [5] summarized cognitive decline as measured by Alzheimer's Disease Assessment Scale-Cognitive (ADAS-Cog) in placebo arms of phase II and III Alzheimer's drug clinical trials. They reported that even for moderate sample sizes of 107-317, the range of the mean decline over 18 months was 4.3 to 9.1 points. Although it is not possible to definitively identify the cause for the placebo group variation, differences in participant demographics across Alzheimer's drug trials does not seem to explain the observed variation since study subjects had similar ages, education levels, APOE e4 genotypes, baseline ADAS-Cog scores, and there was consistency in study eligibility criteria [5]. It would be useful to know what incentives were provided to caregivers and site investigators associated with these trials. Interestingly, two different trials of the same drug and similar design had mean cognitive placebo group declines closer to one another, suggesting that, be it through consistency of payment or other factors, trials with common features may cause similar subject behavior.

Simulation study

We illustrate through simulation how variation in research participant compensation could lead to variation in inference on the survival curve. We consider a particular model for censoring in order to encode the relationship between censoring and compensation and to investigate how that relationship might further influence the underlying dependent censoring. We estimate the survival curve using the Kaplan-Meier estimator [6] under various compensation structures and graph the results to demonstrate the variability of the curve (see Figure 1). We do not graph the true event survival distribution in any of the figures in order to emphasize the variability in estimation introduced by different incentive structures and because bias is already present when there is dependent censoring, regardless of the incentive structure. Increasing the amount of incentives may decrease bias simply by keeping more subjects on trial in some cases (which is consistent with our model below). However, this feature may not always be a characteristic of a model—there exist event-censoring models such that increasing incentives may increase bias by changing the subset of patients whose event is observed.

Figure 1. a: Survival curves under different incentive structures.

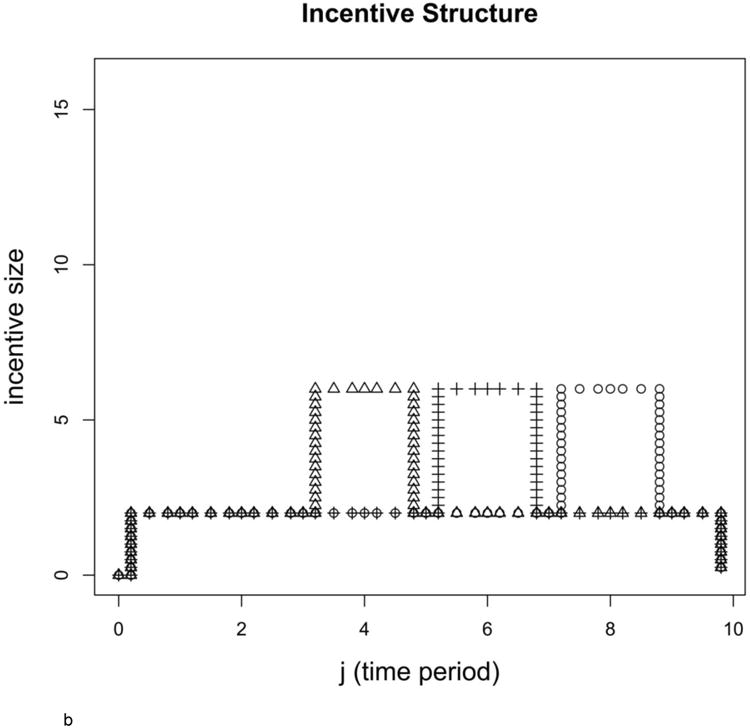
Survival curves generated under the different incentive structures shown in Figure 1b. There is a correspondence between survival curves and incentive structures by the symbols used to trace the lines (i.e., circles, triangles, and crosses).

b: Different incentive structures resulting in different estimated survival curves

Incentive structures corresponding to the survival curves shown in Figure 1a (correspondence denoted with the 3 unique symbols: circles, triangles, and crosses).

Event and censoring models

We simulated clinical trials with 40,000 subjects to limit variability in estimation and to highlight the expectation of the estimator. Half of the subjects had covariate Z_i equal to 0 and half had Z_i equal to 1. For example, Z_i might be an indicator of socio-economic status (SES), which affects both subjects' event times (since SES is associated with health) and censoring times (since those in higher SES strata may stay on the trial longer or shorter, depending on the situation). In simulations used to generate Figure 1a, the event times of those with Z_i = 0 were distributed as Gamma(6,7/12) (shape parameter 6 and rate parameter 7/12), and those with Z_i = 1 were distributed as Gamma(4,5/6). In all simulations, we rounded up the generated event times to make them discrete. The discrete event times are interpreted as the time points at which a subject was observed to have had an event.

A subject's event time was observed if it occurred prior to the minimum of the subject's randomly generated censoring time and 10 time units. The model for the discrete time hazard of censoring at time j for subject i for all simulations was

$$\mathit{\text{logit}}P({\mathit{\text{Subject}}}_i\mathit{\text{censored at time}}j|\mathit{\text{Not censored prior to time}}j,Z_i)={\alpha }_j-\mu \ast m_j+\gamma \ast Z_i+\rho \ast j,$$

where logit(p) = log(p/1 − p)), α_j helps control the overall proportion of censoring at each time period j, γ is a constant across time periods and subjects and controls to what extent the covariate Z_i influences the censoring hazard, ρ controls the degree to which subjects become “tired” of being involved in the trial and want to drop-out, μ controls the influence of the incentive m_j on the hazard of censoring, and m_j is a function of the incentive structure over the remaining time periods in the trial and the “incentive anticipation” parameter (or equivalently, decay parameter) described below. We define m_j as $m_j={\sum }_{k=j}^{\mathit{\text{tot}}}{\mathit{\text{incentive}}}_k\ast {\mathit{\text{dec}}}^{(\mathit{\text{tot}}-k)}$, where tot is the total number of follow-up periods (10 in our case), incentive_k is the incentive size at time period k, and dec is the decay or compounding parameter (0.88 in our case). Dependent censoring is present in the simulation because covariate Z_i affects the hazard-of-censoring (through γ) and the event time (because the gamma distribution parameters depend on Z_i), and we do not condition on the covariate when estimating the survival curve.

The total amount of the incentive for all of the structures shown is 28 units, but those units are distributed in three different ways for the three survival curves shown in Figure 1a. Each survival curve corresponds to a certain incentive structure, and that corresponding incentive structure is shown in Figure 1b. Under all structures, payout of the 28 units is static at a level of two in 8 of the 10 follow-up periods, but then jumps to a higher payout of six for two consecutive follow-up periods at different times during the simulated trial. A structure with an early jump represents a trial whose investigator wants quicker subject accrual, while the structure with a later jump represents a trial whose investigator desires complete follow-up. Parameter values for all simulations were α = (18.5, 16.5, 14.5, 11.5, 11.5, 11.5, 8.5, 8.5, 8.5, 8.5), μ = 1, γ =−8/3, and ρ = 1/60.

Results

Figure 1a depicts downward biased survival curves calculated with the Kaplan-Meier estimator [6] under the different incentive structures shown in Figure 1b, where there is a correspondence in symbols between the estimated survival curve and the incentive structure used in the associated censoring model. The curve denoted with circles is consistent with a median survival time of 4 time units, while median survival time for the other two curves (triangles and crosses) is 5 time units. The incentive structures represent different allocations of a set amount of incentive over time points in the simulated trial. Differences in the survival curves and median survival times shown in Figures 1a illustrate that when dependent censoring is present and the incentive structure affects the censoring model, variation in incentive structure results in variation in the curve.

Adjustment for incentives

Having established the impact of heterogeneity in incentive structure across trials, or across sites within a single trial, we turn to an examination of potential analytic adjustments that might be made. We first note that adjustment for trial or site in an analysis would not be sufficient to account for inter-trial or inter-site variation. This is because the issue invalidating inference is neither a “main effect” of trial or site, nor clustering of observations, but rather potential violation of the event and censoring time independence assumption, fundamental to most time-to-event analyses. Sensitivity analysis is a good way to assess how analysis assumptions influence inference. An Institute of Medicine (IOM) study [7] was commissioned to study the problem of missing data in clinical trials, and two associated articles have highlighted the importance of sensitivity analysis in the context of missing data, of which censored survival data is a subcategory [8,9]. The IOM report [7] recommended specific ways of conducting sensitivity analysis with time-to-event data. One such way is to use auxiliary prognostic factors to explain residual dependence between event and censoring times within strata of model covariates. If these prognostic factors are not sufficient to explain the dependence, other frameworks are suggested in which a non-identifiable censoring bias parameter that encodes residual dependence can be manipulated to investigate sensitivity of inference to it [10,7]. Regardless of the context in which sensitivity analysis is performed, both the IOM report and corresponding New England Journal of Medicine editorial state that it is important to know how robust analysis findings are to missing data assumptions [7,9].

Since it is only when the assumption of independent censoring and event times is violated that varying payment structures may lead to variation in survival curve or hazard ratio estimates, correcting for its possible violation is important. Correction for dependent censoring and analysis of sensitivity to the assumption of independent censoring can be done using a weighting scheme described in Robins [11] and Robins and Finkelstein [12]. The weight placed on any individual at time t is the inverse of the probability of not being censored by time t. Thus, those who are more likely to be censored are weighted more in a given model, the idea being that they are “stand-ins” for subjects similar to themselves who were unobserved because of a high hazard of being censored. Weights are calculated by modeling the hazard of censoring within strata of the covariates already included in the hazard or survival model of interest using additional covariates that could possibly predict censoring. Since weights calculated in this way can be very large when the probability of remaining uncensored is small, caps are sometimes used to address this instability, such as the 99^th percentile of all weights. These weights can then be used in the inverse probability weighted (IPW) analogue of the Kaplan-Meier estimator:

$$S_T(t|z)={\prod }_{\{i;X_i<t\}}[1-\frac{{\tau }_i{W}_i(X_i)I(Z_i=z)}{{\sum }_{k=1}^n{Y}_k(X_i)W_k(X_i)I(Z_k=z)}],$$

where τ_i is the event indicator for subject i, Z_i is the covariate or indicator of stratum, Y_i(t) is an indicator for presence in the risk set at time t, I() is the indicator function, and X_i is the observed event or censoring time. The weight, W_i(t), is set to 1 in the case of the typical Kaplan-Meier estimator, and is the inverse of the probability of remaining uncensored up to time t for the weighted Kaplan-Meier estimator. That probability can be estimated in different ways, including by fitting a Cox model [13] within strata of Z_i, conditional on covariates that may influence censoring. In our case, weights were obtained by first calculating the proportion of censored individuals within each stratum of the covariate at each time period j among the risk set, giving the hazard of censoring, h_j(Z_i). With this information, probability of remaining uncensored to time t given the covariate was calculated by taking the product of one minus the hazards up to t: P_i(t) = Π_{j≤t}(1 − h_j(Z_i)). Weights were calculated using W_i(t) = 1/P_i(t) so that individuals more likely to be censored by time t were weighted more than those less likely to be censored.

We see in Figure 2a that when dependent censoring is present and there are two different incentive structures, there are two corresponding and different survival curves estimated, though the underlying event model is identical for both curves. The median survival time for gray curve is 8 time units, while that for the black curve is 9 time units. These estimates are both different than the true median survival time of the underlying event model. However, after correcting for the dependent censoring using weights, we observe in Figure 2b that there is far less variation between the two estimated survival curves because the Kaplan-Meier estimator is unbiased and therefore its expectation is unaffected by incentives. Additionally, both curves are consistent with the true, underlying median survival time of 6 time units. A similar sensitivity analysis could be done with a Cox proportional hazards model [13] in which variability of effect sizes across incentive structures could be assessed after attempting to adjust for dependent censoring.

Figure 2. a: Survival curves estimated under two different incentive structures.

Survival curves calculated under two different incentive structures. There is significant variability in the curves estimated under the different structures.

b: Survival curves estimated under two different incentive structures, having corrected for dependent censoring

An inverse probability weighted analogue of the Kaplan-Meier estimator gives less variable survival curves under two different incentive structures. These survival curves are additionally not biased.

If one can correct for the dependent censoring that is present, then in theory survival curves estimated across trials within treatment strata under different payment structures should be equivalent since they estimate the same, underlying, event model. As a result, assuming that the censoring distributions differ across trials, even if dependent on event, one has the ability to check for whether the correction for dependent censoring is done well. This is an advantage afforded by the multiplicity of trials or sites within a trial, as dependence of censoring and event is generally not testable [14]. This result is a general one: if dependent censoring is present and survival curves are estimated under different censoring models (all of which are associated with the event model) so that the estimated survival curves are all different, then correcting for the dependent censoring will give unbiased estimates of the survival curves so that much less variation in those estimates should be observed. If we do not observe a decrease in the variation of the survival curves across trials after weighting and no other confounders exist, we would know that weights were not calculated effectively.

Our emphasis on payment structure and its possible effect on inference would be unnecessary if either it or dependent censoring were accounted for in analyses, though the dependent censoring itself would still invalidate inference. However, a review of a variety of terms used to describe dependent censoring in six major medical journals using PubMed and Google Scholar reveals that it is often not discussed. Using these tools to search all available archives of the New England Journal of Medicine (NEJM), Archives of Internal Medicine, Journal of the American Medical Association (JAMA), Annals of Internal Medicine, Nature Medicine, and the Lancet with terms such as “informative censoring,” “dependent censoring,” “non-informative dropout,” and permutations of them returned 65 total articles, with NEJM, JAMA, and the Lancet each contributing approximately 15 articles to the total number. Even if all these articles found appropriately addressed the possibility of informative censoring, it would still be a fraction of all time-to-event analyses described in clinical journals.

Conclusion

We have demonstrated that variation in compensation of research subjects may exacerbate the influence of dependent censoring on statistical inference in clinical trials. Through its influence on the censoring model of research subjects, different compensation patterns may result in different censoring models and thus change inference if some degree of dependent censoring is present in the trial. We have focused the context of this paper on clinical trials, but variation in compensation can affect observational studies as well. In that setting, different compensation structures would more influence which populations are attracted to participate, though this point is relevant to clinical trials, too, as participant demographics may vary with compensation, both at baseline and across time points in the trial. While some might simply advocate for more compensation of research subjects so that there is a high percentage of complete follow-up among participants, this suggestion is not feasible from both ethical and financial standpoints. For consistency across clinical trials, standardization in compensation is essential. Also, use of statistical methods that correct for dependent censoring and adjust for variable compensation structure when it is present should be emphasized more in the clinical literature. We encourage clinical journals to mandate the application of these methods, along with full disclosure of the compensation of subjects, caregivers, and investigators.