DNA on a Tube: Electrostatic Contribution to Stiffness

Abstract

Two simple models are used to estimate the electrostatic contributions to the stiffness of short DNA fragments. The first model views DNA as two strands that are appropriately parametrized and are wrapped helically around a straight cylinder radius equal to the radius of the DNA molecule. The potential energy of the DNA due to phosphate–phosphate electrostatic interactions is evaluated assuming that the charges interact through Debye–Hückel potentials. This potential energy is compared with the potential energy as computed using our second model in which DNA is viewed as two helical strands wrapping around a curved tube whose cross-section is a disk of radius equal to the radius of the DNA. We find that the electrostatic persistence length for B-DNA molecules in the range of 105–130 bp is 125.64 Å (37 bp) and 76.05 Å (23 bp) at 5 and 10 mM monovalent salt concentration, respectively. If the condensed fraction θ is taken to be 0.715 at 10 mM, then the electrostatic persistence length is 108.28 Å (32 bp), while that based on taking into account end effects is 72.87 Å (21 bp). At 5 mM monovalent salt, the total persistence length for DNA fragments in this length range is approximately 575.64 Å (171 bp), using the best estimate for nonelectrostatic contribution to persistence length. Electrostatic effects thus contribute 21.8% to DNA stiffness at 5 mM for fragments between 105- to 130-bp. In contrast, electrostatics are calculated to make a negligible contribution to the DNA persistence length at physiological monovalent cation concentration. The results are compared with counterion condensation models and experimental data.

1. Introduction

Both bending and flexibility play significant roles that allow DNA to pack into nucleosomes in eukaryotes.^1–5 In prokaryotes, gene-regulatory complexes often involve short segments of DNA that are bent into loops.^6,7 Such regulatory complexes that involve looped DNA structures are necessarily limited by the bendability and the helical twist of DNA.^6–9 In eukaryotic systems, DNA looping is increasingly seen as important, being observedorpredictedinavarietyofgene-regulatorycomplexes.^7,10

DNA is a highly charged polymer with rather high local stiffness. In fact, over a length scale of ~75 bp (one-half of the accepted value of the persistence length), DNA is essentially rodlike.^11,12 DNA fragments of 150 bp display an average deviation in end-to-end trajectory of ~60 degrees. High resistance to twisting is another characteristic of DNA. The torsion modulus for unstrained or only weakly bent DNAs lies in the range 1.7–2.3 × 10⁻¹⁹ erg cm.^13,14 The rigidity of DNA in cells is modified by a host of proteins that allow folding and looping needed for gene expression.^6–10

Approximately 146 bp of DNA is able to wrap almost twice around an octamer of histone proteins in eukaryotes. The conjecture^15,16 that part of the driving force for nuclesome folding is a result of asymmetric neutralization of the DNA phosphate charges was supported by results of a series of experiments by Maher and co-workers.^17–22 In this work, selected phosphate groups across the minor groove were chemically replaced by neutral methylphosphonate residues.^17–22 Three of these modifications were inserted on cDNA strands (6 total) so they were located as neighbors across the minor groove.^17–22 Consequently, the electrostatic repulsion among the phosphate groups was interrupted. The sites neutralized were then phased with respect to A-tracts—a strategy developed to study sequence directed bends in DNA.^23,24 Gel retardation experiments were then utilized to determine the direction and the magnitude of bending due to the asymmetric charge neutralization. Asymmetric charge neutralization of duplex DNA induced collapse toward the neutral side.^17–22

The subtle role played by decrease or increase of local interphosphate repulsive forces was also investigated by Hard-widge et al.^25–27 Specifically, the experiments probed how the distribution of cationic or anionic amino acids in the yeast basic zipper (bZip) binding protein GCN4 induced DNA bending.²⁵ DNA bending by six ammonium ions attached to flexible propyl linkers and tethered to one face of the duplex DNA was also studied.²⁶ If rigid linkers were used, then there was no DNA bending. These authors also studied how the insertion of an additional anionic phosphonic acid group within the major groove affected DNA bending.²⁷ Two negative charges were introduced into the major groove, and the DNA responded to this charge imbalance by bending away from the hypercharged face. In a study by Williams et al., single cations are tethered to thymine analogs. They found that a single cation did not induce a detectable bend, but cations on the same face did induce a bend.²⁸

Cyclization assays were exploited to measure the relative intramolecular end-to-end concentration (j-factor), a quantity directly related to flexibility, for 89-bp to 105-bp DNAs with various sequences.^29,6 A notable result, though controversial,³⁰ was that 89-bp DNA appeared over 200 times easier to twist than predicted by linear elastic theories.^6,29,30 Experimental values for the j-factor for random and nucleosome positioning sequence exceed that predicted by linear elasticity theories.^6,29 However, other cyclization studies using a different experimental protocol, and for a DNA of comparable length, tend to support the predictive capabilities of the worm-like chain model with ordinary bending rigidity.³⁰

It must be appreciated that cells contain activities that dramatically enhance the apparent flexibility of DNA relative to what is observed in vitro. For example, Maher and co-workers^31–33 discovered that relative helical phasing of the activator binding sites and the basal promoter did not significantly perturb in vitro transcription activation in HeLa cell nuclear extract. This led to the understanding that heat-resistant HMGB proteins in HeLa cell nuclear extract enhance the apparent flexibility of DNA.^31–33

The energy of cyclization of a uniformly charged thin strand and electrostatic effects on the flexibility of a short DNA fragment have been studied analytically both for straight and circularly bent strands.³⁴ A model that accounts for the effects of charge discreteness on DNA bending persistence and of DNA rod wrapping around the histone core has been investigated recently.³⁵ The electrostatic energy for wrapping of uniformly charged helical strands on the surface of oppositely charged cylinder³⁶ as well as the contribution of the phosphate–phosphate screened interactions on the DNA twist rigidity has been theoretically investigated.³⁷

In the present theoretical work, we study the flexibility of short DNA fragments. We seek to understand and quantify the relative contributions to DNA stiffness (persistence length) of electrostatic stretching forces between backbone phosphates versus nonelectrostatic forces including base stacking. Our model for DNA is designed so as to take into account the double helical nature of the strands and the resulting geometries for the phosphate–phosphate electrostatic interactions. Our model of linear DNA has the two strands wrapped around a straight cylinder; while in the model for bent DNA, the two strands are wrapped around a tube that resembles a bicycle tire. The extent to which electrostatic effects contribute to the persistence length of short DNA fragments is determined by comparing the total electrostatic energy of the circular conformer with that of the linear conformer, and using the assumption that the phosphate charges interact via the Debye–Hückel potential. Predictions of our model are compared with counterion condensation models and with experimental data. Note that our model is designed so as to avoid the weak bending approximation inherent in continuum elastic theory of DNA stiffness.^38–44 A model for a large torus, which is the uniformly charged version of the present discretely charged model, has been investigated.⁴⁵

2. Theoretical Methods

We model linear DNA as two strands, labeled H1 and H2, that are first wrapped around a straight cylinder of radius a and length L. The center of the cylinder stretches along the x-axis from x = 0 to x = L. The helical strands are modeled as lines drawn on the cylinder. The first helix, H1, is parametrized by φ → u⃗(φ), where

$$\overrightarrow{u}=(x=(b/2\pi )\phi ,y=asin(\phi ),z=acos(\phi ))$$ (1)

Thus, a change of 2π of φ takes the strand once around the circle in the (y,z) plane and b Angstroms along the x-axis. The second strand, H2, is parametrized by φ → v⃗(φ) where

$$\overrightarrow{v}=\left(x=(b/2\pi )\phi ,y=asin\left(\phi -\frac{12}{b}2\pi \right),z=acos\left(\phi -\frac{12}{b}2\pi \right)\right)$$ (2)

Consequently, while strand H1 first hits the z = a point on the cross sectional circle at x = 0, the strand H2 first hits this point when x = 12 Å. This is approximately the separation of the minor groove.

As there are α base pairs per turn, the separation between the phosphates on either strand should be Δφ = 2π/α. The coordinates of phosphate i, on strand H1, are labeled by u⃗_i = u⃗(φ_i), where φ_i = (2π/α)(i − 1), and i is an integer that runs through the set {1,…,N}. Observe that the length of the cylinder is L = (b/α)N. Since strand H2 is running in the reverse direction from H1, we place the last phosphate on H2 at the end of the cylinder, thus at x = (b/α)N, and the first one at x = b/α. This requires that the phosphate i on H2 has coordinates v⃗_i = v⃗(φ_i), where φ_i = (2π/α)(N + 1 −i).

Next, we model a double-stranded DNA that is wrapped around a circular tube that resembles a bicycle tire (Figure 1). The tube is obtained by drawing a circle of radius a about point (x = r + a, z = 0) in the (x,z) plane, and then rotating this circle around the z-axis. The resulting circle of revolution is parametrized by the pair of angles, (θ, φ), such that (x = (r + a + a sin(φ))cos(θ), y = (r + a + a sin(φ))sin(θ), z = a cos(φ)). Observe that changing φ → φ + 2π draws a circle cross section of the tube, while θ → θ + 2π draws a circle that winds once around the z-axis, thus parallel to the central axis.

Figure 1.

A double stranded DNA is wrapped around a circular tube.

We model strand H1 on the tube as a curve that winds some number, n, times around the cross sectional circle while winding once around the z-axis. Such a curve is obtained by using the relation θ = φ/n. Thus φ → φ + 2πn completes one traverse of this curve. This traverse should see N equally spaced base pairs, where the spacing is given by Δφ = 2π/α. Thus, n = N/α implying that N must be divisible by α. If the helix is overcoiled or undercoiled relative to α, then N need not be divisible by α. Strands H1 and H2 are parametrized respectively by φ → u⃗ (φ) and φ → v⃗ (φ) where

$$\begin{array}{l}\overrightarrow{u}(\phi )=((r+a+asin(\phi ))cos((\alpha /N)\phi ),(r+a+asin(\phi ))sin((\alpha /N)\phi ),acos(\phi ))\\ \overrightarrow{v}(\phi )=((r+a+asin(\phi -(\alpha /N)\pi ))cos((\alpha /N)\phi ),(r+a+asin(\phi -(\alpha /N)\pi ))sin((\alpha /N)\phi ),acos(\phi -(\alpha /N)\pi ))\end{array}$$ (3)

As before, the positions of the phosphates are given by taking the i^th phosphate at the points φ_i → u⃗(φ_i) and φ_i → v⃗(φ_i) on strands H1 and H2, respectively. The parametrization of the strands assume that the minor and major grooves are compressed by the same fraction on the inside of the bicycle tube and expanded by the same fraction on the outside of the tube.

The potential energy of the double stranded DNA that is due to phosphate–phosphate electrostatic interactions is given by

$$\begin{array}{l}V/k_{\mathrm{B}}T=\frac{q^2}{\epsilon k_{\mathrm{B}}T}\{\sum _{1\le i\le N-1}\sum _{i<j\le N}{\mid {\overrightarrow{u}}_i-{\overrightarrow{u}}_j\mid }^{-1}\times \\ exp(-\kappa \mid {\overrightarrow{u}}_i-{\overrightarrow{u}}_j\mid )+\sum _{1\le i\le N-1}\sum _{i<j\le N}{\mid {\overrightarrow{v}}_i-{\overrightarrow{v}}_j\mid }^{-1}\times \\ exp(-\kappa \mid {\overrightarrow{v}}_i-{\overrightarrow{v}}_j\mid )+\sum _{1\le i}\sum _{j\le N}{\mid {\overrightarrow{u}}_i-{\overrightarrow{v}}_j\mid }^{-1}\times \\ exp(-\kappa \mid {\overrightarrow{u}}_i-{\overrightarrow{v}}_j\mid )\}\end{array}$$ (4)

where T is the absolute temperature, k_B is the Boltzmann constant, and ε is the dielectric constant of the solvent (water). This charge discreteness of DNA phosphates can become particularly important for short fragments and small circles, and it is considered in the model explicitly.

3. Results and Discussion

For B-DNA, the charge spacing of the phosphates is 3.37 Å, while the charge density parameter ξ, defined as the ratio of the Bjerrum length to the charge spacing, is 4.22.⁴³ The radius a of the double helix B-DNA is taken to be 9.33 Å. The Debye screening parameter in monovalent salt solution is κ = (√I/3)Å⁻¹, where I is the ionic strength in units of molarity.⁴³

Let ΔV denote the difference in potential energy due to phosphate–phosphate electrostatic interactions of the double-stranded DNA that is wrapped around the circular tube and straight cylinder. In our calculation of ΔV, we assumed that each charge q is divided by the charge density parameter ξ to approximately account for counterion condensation effects.⁴³

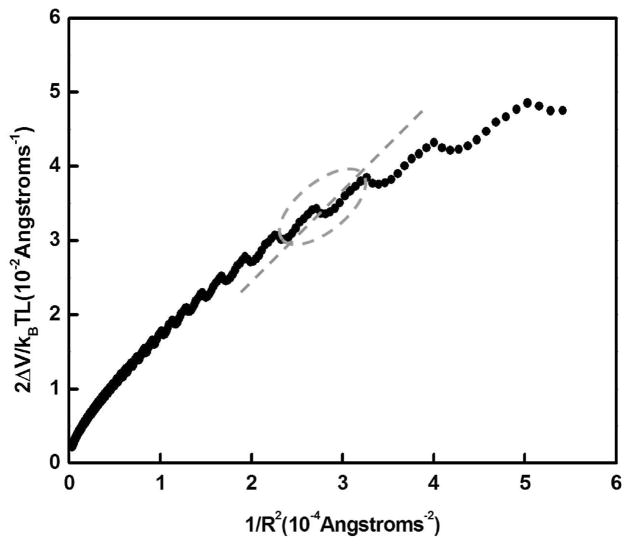
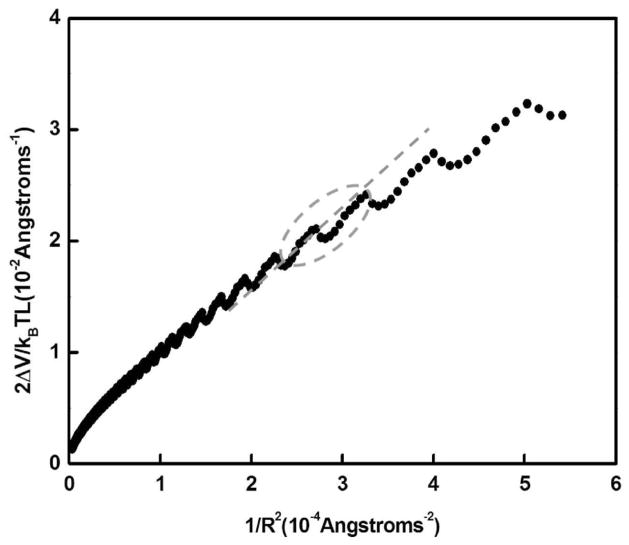
The energy to bend a segment of DNA of contour length L, assuming a restoring force obeying Hooke’s law, is ΔV/k_BT = PL/2R², where R is the radius of curvature and P is the persistence length. Thus, the slope of 2ΔV/k_BTL versus 1/R², would yield the electrostatic persistence length of the DNA.^39,44

Figures 2–3 show a plot of 2ΔV/k_BTL versus 1/R² for salt concentrations at 5 and 10 mM for the DNA tube model. Observe that 2ΔV/k_BTL versus 1/R² (Figure 2–3) is not linear in certain range of radius of curvature investigated. The nonlinearity in the plot stems from the fact that the helix on the tube is overcoiled or under-coiled relative to α, where α is the number of base pairs per turn; in this case, the number of phosphates is not divisible by α.

Figure 2.

Plot (filled circles) of 2ΔV/k_BTL versus 1/R². The salt concentration is 5 mM (monovalent). The slope of the straight line through the origin (dashed line) for DNA of length between 105 and 130 bp is 125.64 Å (37 bp), which is an estimate of the electrostatic persistence length.

Figure 3.

Plot (filled circles) of 2ΔV/k_BTL versus 1/R². The salt concentration is 10 mM. The slope of the straight line through the origin (dashed line) for DNA of length between 105 and 130 bp is 76.05 Å (23 bp), which is an estimate of the electrostatic persistence length.

The slope of the straight line though the origin (see Figure 2) at 5 mM salt for DNA of lengths between 85 and 105 bp and between 105 and 130 bp is 104.83 Å (31 bp) and 125.64 Å (37 bp), respectively. The corresponding slope at 10 mM for DNA of lengths between 85 and 105 bp and between 105 and 130 bp is 65.12 Å (19 bp) and 76.05 Å (23 bp), respectively. For DNA fragments between 300 and 1000 bp, the electrostatic persistence length is 119.6 Å (36 bp) at 10 mM.

Published results of ligase-mediated DNA cyclization were utilized to measure the persistence length of random DNA sequences and DNA nucleosome-positioning sequences of lengths between 89 to 105 bp DNAs.^6,29 T4 DNA ligase-catalyzed DNA cyclization experiments are typically performed under low salt conditions and measure the apparent intramolecular end-to-end concentration (j-factor). The j-factors for the two nucleosome-positioning sequences exceed those for the three DNA random sequences.⁶ Furthermore, the j-factor for all sequences examined exceeded that predicted by elastic theories of bending for all DNA constructs.⁶ If the cyclization data are fitted to the entire range of DNA lengths between 89 and 105 bp, for all sequences this yields a value P = 113 bp and C = 7.4 × 10⁻²⁰ erg • cm.⁶

Inclusion of sharp kinks into the wormlike chain (WLC) bending model was shown to account for the higher-than-expected j-factors for DNA and its flexibility at short lengths (~105 bp).³⁰ However, such a modification leads to overestimation of the j-factors for longer DNAs where the WLC model was known to perform well.³⁰ Consequently, Du et al. carried out additional measurements of j-factors for four sets of DNA fragments that were selected from phage lambda DNA to avoid sequences known to be especially curved or anisotropically flexible and which spanned the range from 105–199 bp.³⁰ The experimental results, for even short DNA fragments, were consistent with WLC model provided T4 DNA ligase concentration was reduced to avoid an artifact that had affected previous experiments. The best fit to the experimental data led to helical repeat and persistence length values of 10.54 bp/turn and 470 Å (138 bp) respectively for DNA of generic sequences.³⁰

To compare the prediction of our model with such experimental cyclization data, we need an estimate of the nonelectrostatic contribution to the persistence length. There is a suggestion in the literature that value is around 300 Å (~89 bp).^41a However, there is a wealth of experimental evidence^41b that the nonelectrostatic contribution to DNA stiffness in monovalent salt is between 450 and 500 Å for most, if not all, DNAs. For 0.01 M NaCl, there is general consensus that P_tot equals or exceeds 500 Å. For a majority of DNA samples, the total persistence length is found to be nearly constant at ~450–500 Å between 0.01 and 1.0 M monovalent salt, and that is taken to be the intrinsic (nonelectrostatic) persistence length of DNA under those conditions.

Given this estimate, the total persistence length P predicted by our DNA tube model for short DNA fragments (85–105 bp) is 554.83 Å (165 bp) and 515.12 Å (153 bp) at 5 and 10 mM monovalent salt concentration, respectively (Table 1). These results suggest that electrostatic effects contribute between 18.9 and 12.6% to stiffness at these monovalent cation concentrations and DNA fragments of length 85–105 bp.

TABLE 1.

Prediction of the Electrostatic Persistence Length of DNA Based on the Tube Model Described Here at 5 mM and 10 mM (Monovalent) Salt Solution^a

DNA length (bp)	5 mM monovalent cation			10 mM monovalent cation
	electrostatic persistence length	total persistence length	% electrostatic	electrostatic persistence length	total persistence length	% electrostatic
85–105	104.83Å(31 bp)	554.83Å(165bp)	18.9%	65.12Åb(19bp)	515.12Å(153bp)	12.6%
105–130	125.64Å(37 bp)	575.64Å(171bp)	21.8%	76.05Åc(23bp)	526.05Å(156bp)	14.5%
300–1000	356.20Å(106bp)	806.20Å(239bp)	44.2%	119.6 Åd(36bp)	569.6 Å(169bp)	20.0%

^aThe condensed fraction is taken to be θ = 1 – 1/ξ, where ξ is the charge density parameter. The non-electrostatic contribution to DNA stiffness in monovalent salt is taken to be 450 Å.^55–64

^bIf the condensed fraction θ is taken to be 0.715 at 10 mM monovalent salt,⁴⁸ then the electrostatic persistence length is 99.96 Å (30 bp), while that based on taking into account end effects as described in text to be 68.34 Å (20 bp). The percentage electrostatic contribution would respectively vary between 18.2 and 13.1%.

^cIf the condensed fraction θ is taken to be 0.715 at 10 mM monovalent salt,⁴⁸ then the electrostatic persistence length is 108.28 Å (32 bp), while that based on taking into account end-effect as described in text to be 72.87 Å (21 bp). The percentage electrostatic contribution would respectively vary between 19.4 and 13.9%.

^dIf the condensed fraction θ is taken to be 0.715 at 10 mM monovalent salt,⁴⁸ then the electrostatic persistence length is 337.66 Å (100 bp), while that based on taking into account end effects as described in text to be 134.82 Å (40 bp). The percentage electrostatic contribution would respectively vary between 42.9 and 23.1%.

For DNA fragments between 105 to 130 bp, the total persistence length obtained form the tube model is 575.64 Å (171 bp) and 526.05 Å (156 bp) at 5 and 10 mM monovalent salt concentration. Thus, the electrostatic effects contribute 14.5% to DNA stiffness at 10 mM for fragments between 105 to 130-bp. Overall summaries of calculations based on our DNA tube model are provided in Table 1.

In the DNA tube model, the electrostatic contribution to the persistence length at 150 mM (~physiological) salt concentration for DNA fragments between 85 and 105 bp is approximately 5.9 Å (~2 bp). This result can be contrasted with the study by York et al. who estimated that 30% of energy cost of deforming DNA into the curvature in the nucleosome is due to electrostatics at physiological salt.⁴⁶ Direct comparison with this result is not possible since these authors do not compute the electrostatic contribution to persistence length. In another study, Hardwidge et al. compared the electrostatic energies of two 71-bp DNA having identical sequences; one of the DNA is bent while the other is straight.²⁷ These authors find that the penalty in electrostatic energy for bending DNA can be attributed to crowding of phosphates which are separated over a stretch of 4–17 Å.²⁷ In other words, the excess electrostatics of the curved conformation is due to local phosphate–phosphate stretching forces rather than distant forces.²⁷

Recently, Manning has proposed an alternative treatment of DNA bending in terms of a null isomer.⁴¹ We have compared the predictions of our model with Manning’s counterion condensation models.^39,42,43 In the line model due to Manning, the difference in free energy between a straight DNA and a weakly bent DNA of identical contour length is³⁹

$$\mathrm{\Delta }G/N{k}_{\mathrm{B}}T=\frac{{(1-\theta )}^2\xi b^2}{R^2}f(\kappa b)$$ (5)

where b is the charge spacing between the phosphate charges, N is the number of phosphate charges, θ the number of counterions per charge of DNA, and f(κb) is defined as³⁹

$$f(\kappa b)=\frac{e^{-\kappa b}}{24{(1-e^{-\kappa b})}^3}[1+\kappa b-e^{-\kappa b}(1-\kappa b)]$$ (6)

The electrostatic contribution to the persistence length based on Manning’s infinite line and double helix models of B-DNA is 101.8 Å (30 bp) and 113.8 Å (34 bp) respectively at 10 mM monovalent cation concentration. The results tabulated in Table 2 are similar to those resulting from our model (Table 1) under comparable monovalent cation concentrations. Although this model provides a decent agreement with the weak bending of infinitely long charged wire model of Manning, the two models give different results at low salt and for finite length oligomers; the latter case cannot be addressed within the framework of Manning’s model.

TABLE 2.

Prediction of the Electrostatic Persistence Length of DNA Based on Counterion Condensation Models Due to Manning^35,38,39 at 10 mM (Monovalent) Salt Solution^a

DNA	salt concentration	electrostatic persistence length	total persistence length	% electrostatic
line model	10mM	101.8Å(30bp)	551.8Å(118bp)	18.4%
line model	5mM	203.5Å(60bp)	653.5Å(194bp)	31.1%
double helix model	10mM	113.8Å(34bp)	563.8Å(167bp)	20.2%
double helix model	5mM	221.2Å(66bp)	671.2Å(199bp)	33%

^aThe non-electrostatic contribution to DNA stiffness in monovalent salt is taken to be 450 Å.^55–64

A recent calculation by Schurr and Fujimoto used extension of counterion condensation theory that takes into account the effects of finite salt concentrations and nonlinear geometries.⁴⁹ Their work indicates that for a long double-helical array of discrete intrinsic charges, θ = 0.715 in 10 mM and θ = 0.45 in 100 mM salt for DNA. This model yields condensed fractions that agree at low and at high salt with the predictions based on nonlinear Poisson–Boltzmann (NLPB) theory, for long uniformly charged cylinders with parameters characteristic of DNA.⁴⁸ NLPB theory gives θ = 0.76 for salt concentrations below 3 mM. At salt concentrations above approximately 3 mM, extended counterion condensation theory and NLPB theory yield values lower than the Manning fraction.⁴⁸ We have provided the results of our calculations using these somewhat lower condensed fractions in Table 1 at 10 mM monovalent salt.

Linear DNA is susceptible to end effects.^49–52 The condensed fraction and the electrostatic free energy per intrinsic charge of an ionic oligomer are lower near the ends of the polyelectrolyte chain than in the middle.^49–52 In 10 mM salt, this end-effect extends over 30 bp. In contrast, the circle has no end-effect. As the length of DNA is decreased, the end-effect will increase the difference in electrostatic free energy per bp between the circular and the linear DNAs of the same length over that in the absence of the end effect. This would lead to overestimation of electrostatic persistence length P_el for the shorter DNAs. In experiments on small circles, the contributions from end effects cancel out. This is because the j-factor is defined as the ratio of the rate of formation of monomer circles to that of linear dimers plus circular dimers. A more accurate approximation of P_el is obtained by calculating the electrostatic energy per bp of a very much longer linear DNA, and multiplying that by the number of bp in the linear control DNA, and then subtracting that from the electrostatic free energy of the circular DNA. These results are also presented in Table 1.

Although the model presented here is an improvement in regard to its treatment of the discreteness of the intrinsic charges, it is nevertheless approximate in its electrostatic potentials and free energies of the individual species. Counterion condensation theory accounts for the electrostatic potential near a uniformly charged cylindrical polyion and the associated electrostatic free energy in an approximate fashion.⁴³ However, differences in free energies between differently curved forms of the same polyion that are predicted by counterion condensation theory could be more accurate than the free energies of the individual species. In fact, nonlinear Poisson–Boltzmann (NLPB) calculations of P_el by Le Bret and Fixman for long, but weakly curved, cylindrical species with uniformly charged surfaces at 10 mM monovalent salt yielded P_el = 168 Å.^45,47 In contrast, we obtain for the electrostatic persistence length of DNAs between 300–1000 bp at 10 mM to be 134.8 Å for condensed fraction θ = 0.715. This result suggests that calculations based on the model for the computed differences in electrostatic free energies and P_el has reasonable validity.

For DNA circles of infinite radii there is a finite energy penalty for cyclization, the closure energy that describes the electrostatic cost of approach of two ends of the DNA chain into a circular conformation as compared to the energy of a straight piece of a finite length. We have extended our calculations for both linear and circular DNAs to encompass the long-chain limit by treating chains up to 2000 bp. At both 5 and 10 mM monovalent salt concentrations and for chain lengths up to 2000 bp, we find that electrostatic persistence length scales as N.

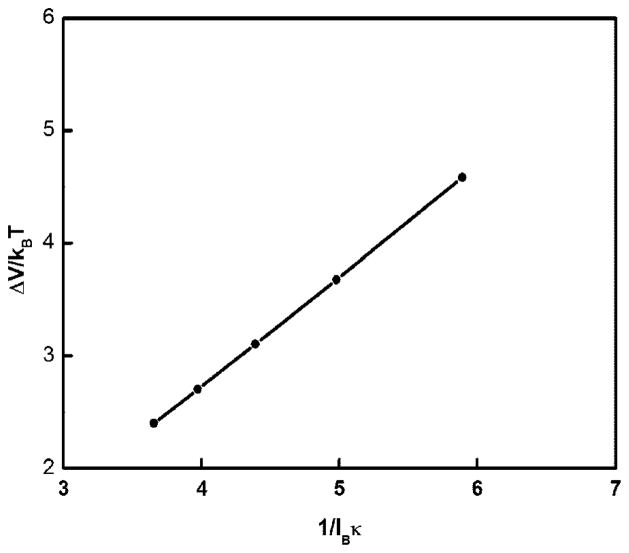
To explain the N dependence of the persistence length, we need to consider the energy of ring closure. The ring closure energy is the electrostatic energy to connect the two ends of a rod to a closed circle.³⁷ Assuming the charges interact by Debye–Huckel potentials and in the limit the length of the rod is larger than 1/κ, one obtains an approximate expression for the electrostatic energy to connect two rods to a single rod of length L³⁷

$$F_{\text{closure}}/k_{\mathrm{B}}T\approx 1/\kappa l_{\mathrm{B}}$$ (7)

Here, l_B is the Bjerrum length. Several comments are in order. First, one can show the energy of ring closure leads to an increase of P_el in proportion to N. Second, we have calculated ΔV/k_BT for a large circular DNA of length 10 000 bp at various salt concentrations and plotted it as a function of 1/l_Bκ (Figure 4). The results are in agreement with predictions based on eq 7. Third, in calculating the persistence length one subtracts the energy of ring closure from the total energy of electrostatic interactions. Otherwise, this finite energy enters in the total energy and when the ring radius increases there is no other way to get the finite number in the left-hand-size of the equation for the bending energy as to increase the persistence length, also infinitely, in the right-hand-side. Indeed, on subtracting this closure term, the persistence length saturates for large DNA rings.

Figure 4.

Plot (filled circles) of electrostatic ring closure energy ΔV/k_BT for circular DNA of length 10 000 bp, as a function of 1/l_Bκ, at various monovalent salt concentrations. The continuous line is a straight line through the filled circles.

We have examined the electrostatic persistence length at a number of different monovalent salt concentration. In Figure 5, the electrostatic persistence length is plotted as a function of 1/κ², where κ is the Debye screening parameter, for DNA fragments of lengths 100 and 300 bp. We find that at low salt, P_el scales as (1/κ)²; the result is in agreement with the 1/κ² law known from the Odijk–Skolnik–Fixman theory.^38,53

Figure 5.

Plot of electrostatic persistence length (in Å) versus 1/κ² in units of Ų, where κ is Debye screening parameter.

We have assumed that Manning’s counterion condensation theory applies equally to both circular and linear DNAs. In the case of the circular DNA, the charge density is greater on the inner surface and lesser on the outer surface. The extent of counterion condensation should differ for those two surfaces. For very large circles, where the curvature is slight, this effect is negligible. However, for circles of ~100 bp, such as those considered here, the average condensed fraction could differ significantly from that of the linear DNA. This assumption of uniform and equal condensed fractions is therefore explicit in the model. Furthermore, we have neglected the entropic penalty upon confinement of cations onto a ring is larger than for straight DNA fragments.

As mentioned above, the effects of counterion condensation are taken into account in the model by assuming Manning-like renormalization of the DNA phosphate charges. However, the cations can occupy different positions on DNA surface such as in the major groove (like many trivalent cations), in the minor groove (like Na⁺), and along the DNA strands (like Mg²⁺ and Ca²⁺).^54,55 In the current model, the effects of the different partitioning of ions on DNA surface upon the persistence length have not been assessed.

In 5 mM monovalent salt, the Debye length is approximately 42 Å. The diameter of a DNA circle with ~100 bp is ~100 Å. Consequently, there is some contribution from all parts of the ring, including the opposite side of the ring, to the total electrostatic free energy per bp of any given intrinsic charge. The cross-ring contributions could be viewed as arising from excluded volume interactions rather than persistence length per se.

In summary, we have proposed a model for double-stranded DNA wrapped on a tube that allows quantitative estimation of the electrostatic contribution to the persistence length. Using the consensus value for the nonelectrostatic contribution (134 bp), we find that the total persistence length for a tightly bent DNA of fragment lengths between 105 to 130 bp that takes into account end-effects is around 171 bp, and electrostatic effects make a contribution of 21.8% to this persistence length at 5 mM monovalent salt concentration. In contrast, this model predicts that the contribution of electrostatics to persistence length at 150 mM monovalent salt (physiological conditions) is negligible.