A new dynamic null model for phylogenetic community structure

Abstract

Phylogenies are increasingly applied to identify the mechanisms structuring ecological communities but progress has been hindered by a reliance on statistical null models that ignore the historical process of community assembly. Here, we address this, and develop a dynamic null model of assembly by allopatric speciation, colonisation and local extinction. Incorporating these processes fundamentally alters the structure of communities expected due to chance, with speciation leading to phylogenetic overdispersion compared to a classical statistical null model assuming equal probabilities of community membership. Applying this method to bird and primate communities in South America we show that patterns of phylogenetic overdispersion – often attributed to negative biotic interactions – are instead consistent with a species neutral model of allopatric speciation, colonisation and local extinction. Our findings provide a new null expectation for phylogenetic community patterns and highlight the importance of explicitly accounting for the dynamic history of assembly when testing the mechanisms governing community structure.

Introduction

Ecological communities are assembled according to processes operating over a vast range of spatial and temporal scales, from local niche-based interactions (e.g. competition) to long-distance biogeographic dispersal events and allopatric speciation (Ricklefs 1987; Hubbell 2001; Vellend 2010; HilleRisLambers et al. 2012). Inferences regarding these different processes, and in particular the importance of niche-based assembly mechanisms relative to more stochastic historical factors, therefore typically relies on the comparison of observed patterns to those expected under a null model in which assembly occurs at random with respect to species identity or ecological traits (Williams 1947; Connor & Simberloff 1979; Gotelli & Graves 1996).

First applied to test for evidence of non-randomness in local species-genus ratios (Williams 1947), ecological null models have since come to underpin almost all hypothesis testing in biogeography and community ecology (Gotelli & Graves 1996). Over the last decade, intense interest has focused on applying this approach to examine the phylogenetic structure of communities, on the basis that phylogenetic relatedness provides a convenient proxy for similarity in functional traits mediating community assembly (Webb 2000; Cavender-Bares et al. 2004; Kembel & Hubbell 2006; Kraft et al. 2007; Cooper et al. 2008; Graham & Fine 2008; Gomez et al. 2010; Barnagaud et al. 2014). According to this framework, evidence that co-occurring species are more closely (clustered) or distantly (overdispersed) related than expected by chance may indicate the importance of trait-based assembly mechanisms in promoting (e.g. environmental filtering) or inhibiting (e.g. competition) coexistence amongst closely related and ecologically similar species. In contrast, failure to reject a null model of random community membership may imply a largely stochastic (i.e. species neutral) assembly process, dictated primarily by extrinsic biogeographic events that are independent of species traits (Webb et al. 2002).

This potentially powerful approach has been criticised because the phylogenetic patterns arising from any particular ecological process need not conform to this simplified conceptual framework. For instance, phylogenetic distance may provide a poor proxy for niche similarity (Cavender-Bares et al. 2004), and competitive exclusion can also lead to phylogenetic clustering if closely related species have similar fitness (Mayfield & Levine 2010; HilleRisLambers et al. 2012). However, another key concern is that any biological interpretation of phylogenetic structure also critically relies on the null model against which observed patterns are compared (Colwell & Winkler 1984). Yet, despite this central importance, the basic assumptions underlying null models of phylogenetic community structure have received comparatively little scrutiny (Kraft et al. 2007; Hardy 2008; Kembel 2009).

Most null models are based on algorithms that randomise community structure (Gotelli & McGill 2006), either by drawing species at random from a regional species pool (for a single community) or by shuffling species occurrences across sites (for multiple communities) (Fig.1a) (Kraft et al. 2007; Hardy 2008; Kembel 2009). While these models produce communities that are random in a statistical sense they do not actually model the historical process through which communities are assembled (Gotelli & McGill 2006; Vellend 2010). In particular, while new species arise through speciation and are added to and lost from communities through colonisation and local extinction, traditional null models exclude all of these fundamental processes (MacArthur & Wilson 1967; Hubbell 2001).

Figure 1.

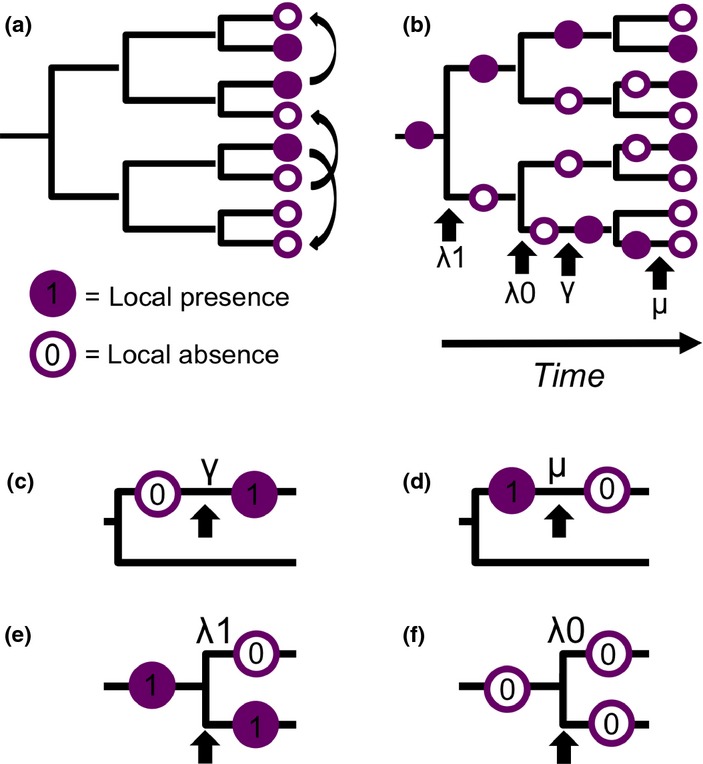
Alternative null models of community assembly (a) a statistical null model in which species presence (state = 1, filled circles) and absence (state = 0, unfilled) values are shuffled across the tips of the phylogenetic tree equivalent to a ‘random-draw’ model. (b) a dynamic null model (DAMOCLES) in which the local community evolves over time by speciation (λ), colonisation (γ) and local extinction (μ). States (i.e. presence/absence) of interior branches are shown to illustrate the historical sequence of community assembly, with key events highlighted for the bottom branch. (c–f) illustrate the four possible events in the model (c) colonisation, (d) local extinction, (e) speciation of a locally present species (λ1) giving rise to one daughter that is present and one that is absent and (f) speciation of a locally absent species (λ0) giving rise to two locally absent daughters.

This disconnect between existing null models and the dynamics of community assembly is problematic, particularly for systems influenced by processes over large spatial and temporal scales, where ecological and historical effects may leave almost identical present day signatures (Bell 2001; Hubbell 2001; Warren et al. 2014). For instance, a pattern in which closely related and ecologically similar species rarely co-occur may arise due to strong negative species interactions (e.g. competition) (Diamond 1975), but could also arise due to recent stochastic extinction or limited dispersal following speciation in allopatry (Connor & Simberloff 1979; Warren et al. 2014). In this case, disentangling trait-based assembly mechanisms from purely historical explanations may benefit from a dynamic modelling approach that explicitly incorporates the processes through which communities are assembled over time.

Here, we address this by developing a dynamic null model of community assembly based on the fundamental processes of colonisation, local extinction and speciation, or ‘DAMOCLES’ (Dynamic Assembly Model Of Colonisation, Local Extinction and Speciation). In this model, we consider the assembly of a single local community from a clade of species as it diversifies over time (Fig.1b). At any given time, species can exist in one of two geographic states: locally present (state = 1) or locally absent (state = 0). Species are added to the local community via colonisation, modelled as the transition from state 0 to 1 (Fig.1c), and lost from the local community through extinction, modelled as the transition from state 1 to 0 (Fig.1d). This model is thus closely aligned with MacArthur & Wilson's (1967) equilibrium theory of island biogeography (ETIB) in which the number of species on an island is set by a balance between rates of colonisation from the mainland and local extinction. In accordance with the ETIB, we assume that per lineage rates of colonisation (γ) and local extinction (μ) are equal across species (i.e. the model is neutral at the species level). However, while the original ETIB excludes speciation and assumes that the mainland species pool is static over time, in DAMOCLES the species pool is dynamic according to the speciation or global extinction of species within the clade. We assume that speciation (λ) occurs in allopatry and that the area of the local community is sufficiently small that in-situ speciation is negligible (Hubbell 2001). As a result when a species present in the local community speciates (λ1) only one daughter species will be locally present (Fig.1e). In contrast, when a locally absent species undergoes speciation (λ0) both daughters will also be locally absent (Fig.1f). These historical effects of speciation, together with the dynamics of colonisation and local extinction acting over time, thus combine to determine community composition at the present day (Fig.1).

In this study we use this new model to address three key aims. First, using simulations we explore the phylogenetic patterns expected due to chance under a dynamic process of community assembly. Second, implementing DAMOCLES as a null model we assess the power to correctly infer when community assembly is dependent or independent of species traits, evaluating both phylogenetic and trait-based metrics. To do this, we develop a likelihood-based method to estimate colonisation and extinction rates from presence-absence data given a phylogeny and then simulate null communities under these empirically derived rates. We compare DAMOCLES’ power to that of a statistical null model in which species are drawn with equal probability and without replacement from the tips of the phylogenetic tree until observed local richness is reached. This widely used ‘random-draw’ model provides the appropriate comparison because it also assumes species equivalence but, in contrast to DAMOCLES, ignores the historical context of community assembly (Gotelli & McGill 2006). Finally, we illustrate the application of DAMOCLES with three case studies of large Neotropical vertebrate radiations; the hummingbirds (Trochilidae), ovenbirds (Furnariidae) and New World Primates (Platyrrhini). In these groups competition on the basis of ecological trait similarity has been implicated in driving phylogenetic overdispersion (Cooper et al. 2008; Graham et al. 2012) but we hypothesise that a dynamic null model of community structure accounting for speciation may suffice to explain their community structure.

Methods

Our methodology consists of four main stages. First, we develop the likelihood approach to estimate γ and μ from presence-absence data given a phylogeny. Second, we simulated multiple phylogenies and along each of these simulated communities under (1) an Equal-Rates scenario in which γ and μ are independent of species traits and (2) a Trait-Dependent scenario in which γ depends on the distribution of species traits and their variation through time. For both scenarios, we evolve multiple quantitative traits according to a Brownian or Conserved model of evolution (note that traits our simulated in the Equal-Rates scenario for use in trait-based hypothesis testing). In the Trait-Dependent scenario we explore two widely studied assembly mechanisms: (1) ‘trait filtering’ in which local environmental suitability differs across species (Webb et al. 2002) and (2) ‘trait repulsion’ in which residents exclude immigrants with similar traits (i.e. niche incumbency through competition). Third, we quantify the structure of simulated communities using phylogenetic and trait-based metrics. Fourth, we apply DAMOCLES as a null model to our simulated data sets and evaluate its power, relative to that of a random-draw null model, to correctly identify the true assembly process (i.e. Equal-Rates or Trait-Dependent). We compare power for different metrics of community structure (phylogenetic and traits) and assess the effects of different Trait-Dependent scenarios (filtering or repulsion), levels of trait dimensionality and trait phylogenetic conservatism, species sampling and rates of community dynamics.

Estimating rates of colonisation and local extinction

We derived the exact likelihood of species' presences and absences in a community under DAMOCLES given the phylogeny, γ and μ (Box 1) and used likelihood optimisation to estimate γ and μ. To ensure that this approach is able to reliably and precisely infer rates of colonisation γ and local extinction μ we conducted extensive simulation tests on communities generated under known parameter values (see Table S1). All code to implement the likelihood optimisation and simulations are available in the R package DAMOCLES.

Box 1 The likelihood of a community under DAMOCLES

Our procedure for obtaining the exact likelihood of a community (i.e. binary vector of species presence and absence) bears resemblance to the Felsenstein pruning algorithm (Felsenstein 1981). We track each lineage back in time where we use presence/absence as the state of the lineage. We define p_if (t) as the probability that the subclade subtending from the lineage is in state f at time 0 (the present) given that it is in state i at time t (before the present). The (Kolmogorov backward) equation for the change in this probability with time on a branch reads:

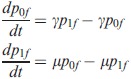(1)

The solution can be calculated analytically when the rates do not depend on time:

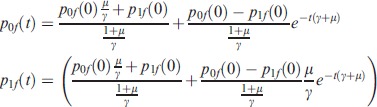(2)

At a node we need to combine the probabilities of the two lineages:

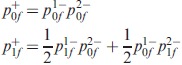(3)

where the+ denotes the state just after the speciation event (remember that we are working backwards in time, so deeper in history) and the -just before the speciation event; the 1 and 2 denote the left and the right branch (or top and bottom branch, depending on how you view the tree).

The algorithm to calculate the likelihood then proceeds as follows:

1. Look for the two branches that will coalesce first. We assume that the initial condition for a tip is p_if = 0 or 1 depending on whether the tip is present or absent in the local community, but note that uncertainty can be accounted for by replacing the binary vector of presence/absences with probabilities of presence/absence. The initial condition for internal nodes is the probability obtained so far (after step 3).

2. For each branch integrate equation the set of ODEs, eqn 1, until we reach a node.

3. At a node change the probabilities according to eqn 3.

4. Repeat 1–3 until there are no branches to coalesce.

5. The likelihood can be computed as any combination of p_0f and p_1f at the root depending on our prior distribution on the state of the system at the root. We used the sum of the two probabilities to reflect complete ignorance. Alternatively, one could use the observed frequencies of the states, which implies an assumption of equilibrium, or one could introduce a new parameter for the weight of one of the two states at the root (the other is obviously 1-this weight).

Simulating assembly under an Equal-Rates scenario

We explored phylogenetic structure expected under DAMOCLES by first generating phylogenies and then simulating local communities along the branches of these trees (this is identical to simulating diversification and assembly simultaneously, assuming assembly does not affect diversification). Phylogenies were simulated according to a pure birth model (λ = 0.1) using the TreeSim package in R v 3.02 (Stadler 2013), conditioned on a clade size of N = 100 and crown age = 39 (i.e. expected age given λ = 0.1). We assigned the root a state of 1 or 0 with equal probability and simulated communities in continuous time using the Gillespie algorithm (Gillespie 1977), whereby waiting times (δ) to the next colonisation or local extinction event were drawn from an exponential distribution with mean 1/γ and 1/μ respectively.

Simulating trait evolution

Along each phylogeny we modelled the evolution of a quantitative trait according to a Brownian motion model (ancestral trait value = 0). Specifically, following each event we added a random normal deviate to species trait values with a standard deviation given by the variance of the normal distribution (variance = 0.01) multiplied by δ. A time-independent variance [which we refer to as the Brownian Random (BR) model] produces moderate phylogenetic signal in trait values and an expected value of K = 1 according to the K statistic (Blomberg et al. 2003). To assess the effects of increased phylogenetic signal we simulated an exponential decline in the variance through time [Brownian Conserved (BC) model], selecting parameter values (variance = 0.1, decline parameter = −0.1) giving biologically realistic values of K (K = 3.1 ± 0.05) (Blomberg et al. 2003). Finally, because the number of independent niche dimensions describing species interactions is debated (Eklof et al. 2013) we simulated different numbers of traits, ranging from 1 to 32 (code to simulate trait evolution is implemented in DAMOCLES).

Simulating assembly under a Trait-Dependent scenario

We simulated assembly in which γ was dependent on species traits using the modified Gillespie algorithm for non-constant rates (Allen & Dytham 2009). Specifically, we used the maximum values of γ at time t to determine δ with the probability of a colonisation or local extinction event occurring dependent on the ratio of the actual rates at time t + δ and the maximum rates, which may differ if species' traits have evolved. We modelled a process of filtering, in which γ declines at an exponential rate (Φ) with the Euclidian distance (D) of a colonist species (i) from a trait optimum according to the following equation,

(4)

To ensure substantial filtering we used preliminary simulations to identify trait optima expected to occupy the edge of trait space (95% quantile of species distances from the ancestral trait value) given rates of trait evolution (see Kraft et al. 2007). We modelled a process of repulsion by allowing γ to increase as a function of the Euclidian distance in trait space (D) between a colonist (i) and local residents (j) according to the following equation,

(5)

where Ψ denotes the value of D at which γ is half its maximum value and z controls the shape of this increase (Fig. S1). To ensure substantial repulsion we used a value of z = 10 resulting in a sigmoidal increase in γ with D (Fig. S1).

Simulation scenarios

To assess power under DAMOCLES and the random-draw model we first examined the effects of changing γ and thus the percentage of locally present species (0.011 = 10%, 0.045 = 30%, 0.1 = 50%, 0.23 = 70%, 0.9 = 90%). Holding local richness constant (n ∼ 50), we then varied the (1) rate of community turnover by increasing both μ (0, 0.2, 0.4, 0.9, 1.8) and γ (0.1, 0.25, 0.5, 1, 2), (2) number of independent trait dimensions (1, 4, 8, 16 and 32), (3) phylogenetic signal in traits (K = 1, 3.1) and the level of sampling of both the (4) regional pool and (5) community. To simulate incomplete sampling of the regional pool we generated clades of different sizes (N = 100, 500 and 1000) and randomly pruned locally absent species until each tree contained only 100 species. To explore a scenario in which local communities represent a subsample from a larger community assembled under low extinction, we simulated communities of different richness (n ∼ 50, 70 and 90) and then randomly sampled 50 species from each (i.e. 100, 71, 56% sampling). Finally, for our Trait-Dependent scenario we selected combinations of Ψ, Φ and γ giving rise to substantial filtering and repulsion defined as conditions in which 50% of species are expected to locally co-occur compared to ≥ 90% in the absence of these mechanisms (see Table S2 for a complete list of parameter combinations used in the simulations).

Quantifying community structure

We quantified phylogenetic structure of cooccurring species using two standard metrics (e.g. Webb 2000; Kraft et al. 2007; Kembel 2009): the Mean Phylogenetic Distance (MPD) and the Mean Nearest taxon Distance (MNTD), which is the mean phylogenetic distance between pairs of closest relatives (Webb 2000; Kraft et al. 2007). We calculated trait dispersion using two widely used indices: the Mean Nearest Neighbour Distance (MNND), which is the mean Euclidian distance between species which are closest neighbours in trait space, and the variance in trait values (VAR) calculated as the sum of the variances along each trait axis (e.g. Kraft et al. 2008; Graham et al. 2012; Swenson et al. 2012). We report metric standardised effect sizes (SES_Metric) which compare the value for a community to the mean expected under a random-draw null model correcting for the standard deviation. SES_Metric values were multiplied by −1, with values greater and less than 0 indicating clustering and overdispersion respectively (Eq. S1).

Statistical analysis

We assessed the power of each metric to correctly identify the true assembly process by simulating 200 communities under both an Equal-Rates and Trait-Dependent scenario and then counting how many of these exhibited non-random structure (i.e. occurred in the lower or upper 2.5% of the null distribution of expected values) according to DAMOCLES and the random-draw model. We define Type I and Type II errors as the frequency that an Equal-Rates and Trait-Dependent scenario is incorrectly rejected respectively. For the random-draw model we created 100 null communities by reshuffling presence/absence across the tips of the tree. For DAMOCLES we generated null communities using parametric bootstrap. Specifically, for each simulated community we estimated values of γ and μ via maximum likelihood and used these to simulate a further 100 null assemblages under an Equal-Rates scenario.

Application to empirical data

We selected three speciose and geographically coincident vertebrate radiations for which well sampled and highly resolved phylogenies were available: ovenbirds (Furnariidae: N = 285) (Derryberry et al. 2011), hummingbirds (Trochilidae: N = 294) (McGuire et al. 2014) and New World Primates (Platyrrhini: N = 94) (Springer et al. 2012). For each clade we modelled community assembly within the Manu Biosphere Reserve in south-eastern Peru, where local richness is high (Furnariidae: n = 74, Trochilidae: n = 66 and Platyrrhini: n = 14) and thoroughly surveyed (Solari et al. 2006; Walker et al. 2006). This system is appropriate for our analysis because allopatric speciation is the predominant mode of speciation in these groups (Bolnick & Fitzpatrick 2007) and while the area of the reserve is large (c. 18 000 km²) in-situ speciation is likely to be negligible if not completely absent (see Kisel & Barraclough 2010). For each clade, we calculated the phylogenetic structure expected under DAMOCLES by using our likelihood method to estimate γ and μ and then using these empirically derived rates to simulate 1000 null assemblages under an Equal-Rates scenario. Finally, we calculated SES_MNTD and SES_MPD for observed and simulated communities relative to the random-draw model.

Results

Community phylogenetic structure under DAMOCLES

Under the Equal-Rates scenario the probability of community membership (p₁) is not equal across species but varies due to differences in the historical pattern of speciation (Figs2a, S2). Each speciation event halves the probability p₁ that a descendent lineage will be locally present and following speciation, p₁ then increases towards an equilibrium probability of community membership (p_eq) set by a balance between the rates of colonisation γ and local extinction μ (p_eq = γ/γ + μ) (see Fig. S2). Thus, species derived from branches undergoing slow diversification and with more time available for colonisation have a higher probability of being locally present (Figs2a, S2). This non-random variation in community membership translates into non-random patterns of phylogenetic structure, with communities more overdispersed than expected under a random-draw model (Fig.2b, c). As μ increases, the probability p₁ of community membership becomes increasingly decoupled from speciation history and is instead largely governed by the relative rates of colonisation γ and local extinction μ (Figs2d, S2). This has the effect of equalising species probabilities p₁ of community membership, leading to a phylogenetic structure that converges on that expected under the random-draw model (Fig.2e, f).

Figure 2.

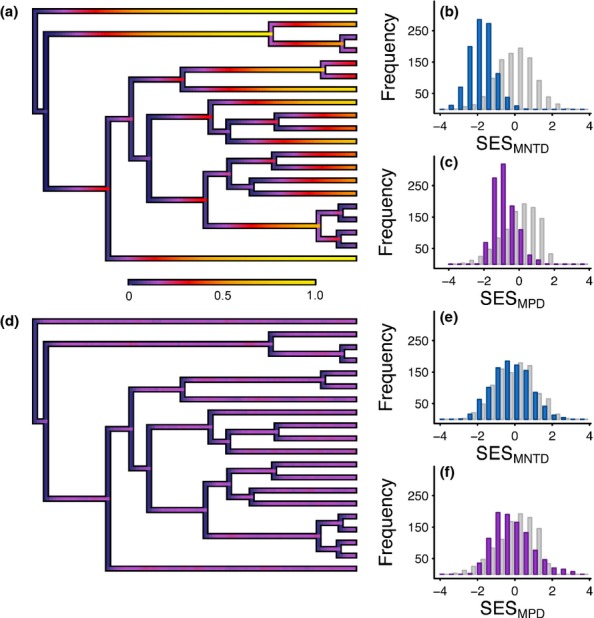
Community phylogenetic structure expected under a constant rate of colonisation and local extinction. Phylogenies show the probabilities of community membership over time under (a) low and (d) high rates of local extinction produced using code modified from the phytools package (Revell 2012). Histograms show the corresponding (b, e) mean nearest taxon distance and (c, f) mean phylogenetic distance (SES_MNTD and SES_MPD), under DAMOCLES (coloured bars) compared to the random-draw null model (grey bars). Results show values from 1000 replicate simulations.

Distinguishing neutral-and niche-assembly mechanisms

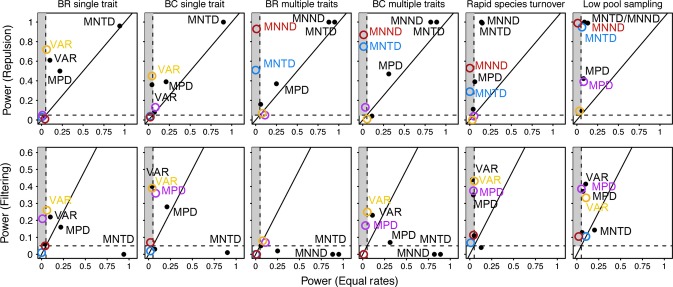
Type I error rates under DAMOCLES are generally low, correctly rejecting a Trait-Dependent scenario when the colonisation rate γ is equal across species (Fig.3, Table S2). Power to detect trait dependence varies with the metric used, ecological scenario (repulsion or filtering), trait phylogenetic signal and dimensionality (Fig.3, Table S2). For repulsion acting on few trait dimensions that are weakly conserved, phylogenetic metrics have almost no power, and repulsion is best detected using trait metrics (VAR) (Fig.3). In contrast, with more strongly conserved traits, and in particular with multiple trait dimensions, the power of phylogenetic metrics (MNTD) increases towards that of trait metrics (MNND) (Fig.3).

Figure 3.

Power of each phylogenetic and trait metric to infer a Trait-Dependent assembly (filtering or repulsion) scenario under DAMOCLES (colours) and the random-draw model (black) and for different simulation scenarios (left to right). The solid 1 : 1 line indicates equal power under the Equal-Rates (x-axis) and Trait-Dependent (y-axis) scenarios (N.B differences in scale across plots). Dashed lines indicate 0.05 significance levels. Metrics falling inside the grey box have acceptable Type I error (i.e. < 5%). Ideal tests would fall in the upper left corner of the plot exhibiting high power to reject the null model for the Trait-Dependent scenario but low power for the Equal-Rates scenario. See Methods for details of metrics and Table S2 for parameter values used in simulations.

In contrast to DAMOCLES, the random-draw model has high Type I error, inferring a process of trait repulsion when the colonisation rate γ is equal across species (Figs4, Table S2). This strong bias applies to both phylogenetic and trait metrics and arises because the pattern of overdispersion caused by allopatric speciation is mistaken for strong repulsion (Fig.2). We note that Type I errors under the random-draw model (but not DAMOCLES) increase with colonisation rate γ due to higher local richness and thus power to detect overdispersion (Fig.4a) and, for trait metrics (MNND), increase with both trait dimensionality and phylogenetic signal (Fig.3, 4b). Thus, while the random-draw model appears to have high power to detect repulsion, tests using this method are unable to reliably infer the correct assembly scenario (Figs4).

Figure 4.

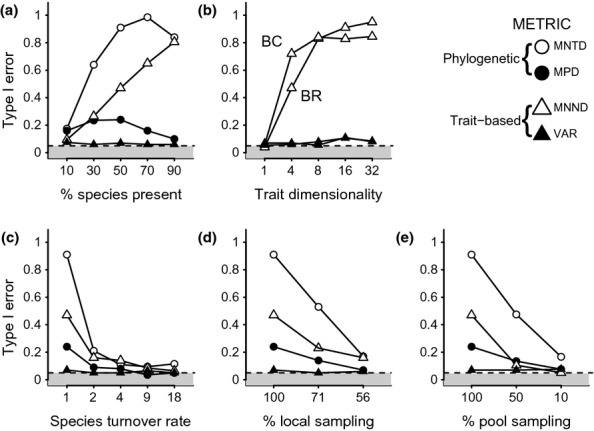
Type-1 error rates under the random-draw null model for different metrics (symbols). Type-1 error depends on (a) the % of species locally present, (b) trait conservatism (BR = Brownian Random, BC = Brownian Conserved) and dimensionality (c) rates of community turnover (shown as rate of local extinction relative to speciation), (d) the % of species in the local community that have been sampled and (e) the % of the species pool included in the phylogenetic tree. Plots (a, c, d, e) show results under a BR model of trait evolution for 4 trait dimensions. See Methods for details of metrics and Table S2 for parameter values used in simulations. Dashed black line and grey box shows acceptable Type 1 error rates (i.e. < 5%).

When communities assemble via filtering this can rarely be detected by the random-draw model (high Type II error) because the effects of speciation mask the trend towards greater clustering (Fig.3). Power to detect filtering using phylogenetic metrics is higher under DAMOCLES, but remains lower than for repulsion (Fig.3). This is because filtering decouples the relationship between species age and the probability of being locally present p₁, which under an Equal-Rates model is thus inferred as arising from elevated local extinction μ. When null communities are then simulated under high local extinction μ, the expected phylogenetic structure converges on that expected under the random-draw model, thus reducing power to detect filtering (Fig.2d). Under DAMOCLES, power to detect filtering is highest for the MPD or VAR but declines rapidly with increasing trait dimensionality because the distribution of species distances from the environmental trait optimum becomes increasingly platykurtotic, equalising probabilities of colonisation (Fig.3).

When species are subject to high rates of local extinction (i.e. μ > 5 × speciation rate), the effect of speciation on the probability of community membership, and thus phylogenetic structure, is erased so that Type I errors of the random-draw model are reduced to acceptable levels, while power to detect filtering increases (Figs3, 4c, Table S2). Thus, under conditions of rapid community turnover, the random-draw model has equal (filtering) or greater (repulsion) power than DAMOCLES to infer the correct assembly process (Fig.3). However, our results also show that when local species represent a random sample from a larger community, which has been assembled according to low extinction, then the Type I error rate of the random-draw model remains unacceptably high (Fig.4d, Table S2). Finally, we find that incomplete sampling of the regional pool, by eroding the signature of speciation history on community membership, reduces Type I error for a random-draw model (Figs3, 4e). Although incomplete phylogenetic sampling (i.e. < 50%) increases Type I error rates under DAMOCLES, power to correctly detect trait-dependent colonisation remains high (Fig.3, Table S2).

Empirical community assembly dynamics and phylogenetic structure

We find that vertebrate communities in Manu are governed by extremely slow rates of colonisation and local extinction (Fig.5). For ovenbirds and hummingbirds we estimate a colonisation rate of γ = 0.083 (0.067 : 0.106, values are 75% CI) and γ = 0.080 (0.062 : 0.102) per lineage per million years and a rate of local extinction of μ = 0.11 (0.064 : 0.178) and μ = 0.12 (0.055 : 0.188) respectively. For primates, colonisation is even slower (γ = 0.04, 0.036 : 0.061) and a model without local extinction cannot be rejected (μ = 0, 0 : 0.575). Compared to the random-draw model all communities appear strongly phylogenetically overdispersed according to the MNTD (Fig.5), with ovenbirds also overdispersed according to the MPD (Fig. S4). However, when these data are reanalysed using DAMOCLES an Equal-Rates scenario cannot be rejected. Thus, the phylogenetic distances amongst species co-occurring within Manu are consistent with that expected under a null model of allopatric speciation and slow but equal rates of colonisation and local extinction across species (Fig.5).

Figure 5.

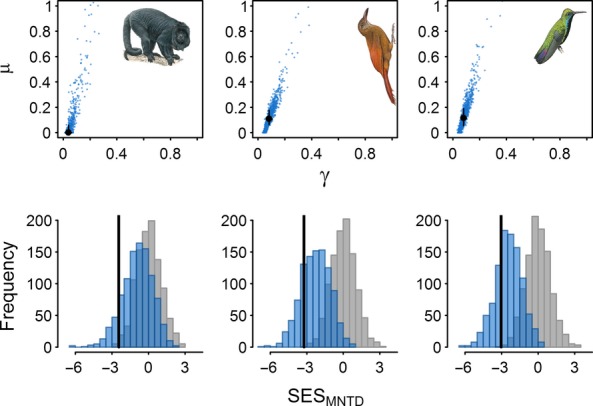
The dynamics and phylogenetic structure of community assembly for New World primates (left), ovenbirds (middle) and hummingbirds (right) in Manu. Maximum likelihood rate estimates (black points) of colonisation (γ) and local extinction (μ) with uncertainty in estimates (black lines 75% CI) quantified from 1000 bootstrap replicates (blue points). Community phylogenetic structure according to the Mean Nearest Taxon Distance (SES_MNTD) showing the observed patterns (black lines), the expectation under the random-draw null model (grey) and the expectation under DAMOCLES given estimated rates (from 1000 replicate simulations).

Discussion

Most null models in community ecology are random in a purely statistical sense and assume that in the absence of ecological differences, species have an equal probability of being present within a local community (Gotelli & Graves 1996; Webb 2000; Cavender-Bares et al. 2009). By constructing communities under a realistic assembly process incorporating the dynamics of speciation, colonisation and extinction, we show that this is not the case. In particular, because allopatric speciation reduces the probability that a descendent lineage will be present within any given local community, older species with more opportunity for colonisation or those descended from more slowly diversifying branches are more likely to be locally present. This non-random variation in the probability of community membership translates into non-random phylogenetic structure, with co-occurring species less closely related than expected if species were randomly sampled from across the tips of the tree. Thus, even when species have been governed by identical colonisation and extinction dynamics, communities will not be randomly structured but will instead tend to be strongly phylogenetically overdispersed compared to a random draw of species from the present day regional pool.

A pattern of overdispersion in traits (e.g. Ingram & Shurin 2009; Swenson et al. 2012; Belmaker & Jetz 2013) or phylogeny (e.g. Cooper et al. 2008; Gomez et al. 2010; Graham et al. 2012; Barnagaud et al. 2014) has been widely reported and often interpreted as evidence for competition in limiting species coexistence or, more rarely, the environmental filtering of species with convergent niches (Cavender-Bares et al. 2004). Our results show that this pattern is also expected simply due to the effects of speciation, and that failure to account for differences in species phylogenetic history may lead to a null model of random community assembly being incorrectly rejected. These results are complementary to those of Hardy (2008) and Kembel (2009) who showed that, when colonisation probabilities vary with species abundance, null models which fail to account for differences in abundance (e.g. random-draw model) may lead to biased inferences. Here, we demonstrate that even when species do have identical (instantaneous) probabilities of colonisation and local extinction, null models assuming species equivalence are likely to be unreliable and subject to elevated Type I error rates. Importantly we show that the high Type I error of the random-draw model persists even when colonisation occurs rapidly relative to speciation and is only ameliorated when the local community is formed under high rates of local extinction. While this latter finding may imply that accounting for assembly history is unnecessary for localised assemblages subject to rapid turnover, our results caution against this interpretation. In particular, we show that assemblages sampled from a larger community, where rates of extinction have been slower, may still retain the phylogenetic signature of speciation and thus remain biased towards incorrectly inferring a model of trait repulsion.

The possibility that allopatric speciation may provide an alternative explanation to niche-based models for patterns of overdispersion has been acknowledged but until now methods to separate these processes have been unavailable (Webb et al. 2002; Graham & Fine 2008; Vamosi et al. 2009; Warren et al. 2014). By modelling the historical dynamics of community assembly DAMOCLES overcomes this problem and provides a more robust framework for hypothesis testing. For instance, our empirical analysis of birds and primates in Manu showed that while previous studies have interpreted overdispersion in these clades as evidence of competition (Cooper et al. 2008; Graham et al. 2012) the phylogenetic structure of these communities do not in fact differ from that expected under a null model of allopatric speciation, colonisation and extinction. These results do not preclude the possibility that species interactions or other niche-based mechanisms may also structure community membership in these clades but suggest that these processes will not be easily distinguished using phylogenetic data alone.

The limitations of relying on phylogenetic patterns when testing community assembly hypotheses have increasingly been highlighted, leading to a renewed focus on analyses based on functional traits (Cadotte et al. 2013). Our results add caution to a reliance on phylogenetic data alone, but also demonstrate that biases arising from the failure of traditional null models to account for assembly history may also compromise trait-based tests. Intriguingly, we find that for trait-based tests the tendency to incorrectly infer a process of repulsion increases dramatically with trait dimensionality, because under these conditions trait similarity becomes more strongly correlated with phylogenetic distance and thus sensitive to the effects of allopatric speciation (Fig. S5). Analyses of functional trait diversity should therefore also account for the effects of speciation before attempting to infer the mechanisms underlying community assembly.

A corollary of our finding, that speciation drives communities towards greater overdispersion, is that a random-draw model should rarely detect a pattern of phylogenetic clustering. Yet, such a pattern has commonly been detected in empirical systems (Vamosi et al. 2009). One explanation for this, is that many studies have focused on highly localised systems where; the regional species pool is itself formed through colonisation rather than allopatric speciation, rates of local extinction may be high, and the regional pool may be incompletely sampled (e.g. Webb 2000; Kembel & Hubbell 2006). All these factors are expected to erase the phylogenetic signature of allopatric speciation and thus increase power to detect filtering. While this may partly account for the widespread observation of phylogenetic clustering, our results also suggest that the importance of environmental filtering is likely to have been greatly underestimated using traditional null models that fail to account for the opposing effects of speciation on community structure.

The model we introduce here is a step towards a more dynamic theory of community phylogenetic structure but we acknowledge a number of important simplifying assumptions. While we assessed the statistical performance of our model to a variety of assembly processes and sampling regimes, further investigation across a broader parameter space is warranted. For instance, our model treats the dynamics of speciation, colonisation and extinction independently (for an alternative approach see Goldberg et al. 2011) and ignores the effects of geographic space (i.e. our model is spatially implicit). Thus, although our approach can be applied across multiple communities, it assumes independent dynamics across these units which may be compromised by spatial non-independence. Addressing this will require a realistic spatially explicit model of community assembly against which traditional multi-sample approaches that randomise species co-occurrence across sites (Hardy 2008; Kembel 2009), but that ignore speciation, can then be tested.

The dynamic modelling approach we advocate may hold a number of advantages over traditional randomisation techniques, not least the greater transparency of the underlying assumptions. For instance, our dynamic model shows that the assumption of equal probabilities of community membership across species actually only corresponds to a species neutral assembly scenario when rates of community turnover are rapid relative to speciation. Furthermore, we expect that the fitting of dynamic assembly models to phylogenetic data will move beyond hypothesis testing and ultimately enable deeper mechanistic questions to be addressed, such as; ‘what are the typical rates of colonisation and local extinction underlying community assembly?’, ‘how do these rates depend on environmental conditions, traits or geographic area?’, ‘do rates of colonisation slow-down through time as niches are filled?’. Given the recent advances that have taken place in the phylogenetic modelling of species diversification and trait evolution (Morlon 2014), we see many exciting opportunities to now extend these dynamic models to address fundamental questions in the assembly of ecological communities.

Author contributions

ALP and RSE developed conceptual framework and devised analytical approach, ALP performed analyses, ALP and RSE wrote the manuscript.

SUPPORTING INFORMATION

Additional Supporting Information may be downloaded via the online version of this article at Wiley Online Library (http://www.ecologyletters.com).