Predicting changes in the distribution and abundance of species under environmental change

Abstract

Environmental changes are expected to alter both the distribution and the abundance of organisms. A disproportionate amount of past work has focused on distribution only, either documenting historical range shifts or predicting future occurrence patterns. However, simultaneous predictions of abundance and distribution across landscapes would be far more useful. To critically assess which approaches represent advances towards the goal of joint predictions of abundance and distribution, we review recent work on changing distributions and on effects of environmental drivers on single populations. Several methods have been used to predict changing distributions. Some of these can be easily modified to also predict abundance, but others cannot. In parallel, demographers have developed a much better understanding of how changing abiotic and biotic drivers will influence growth rate and abundance in single populations. However, this demographic work has rarely taken a landscape perspective and has largely ignored the effects of intraspecific density. We advocate a synthetic approach in which population models accounting for both density dependence and effects of environmental drivers are used to make integrated predictions of equilibrium abundance and distribution across entire landscapes. Such predictions would constitute an important step forward in assessing the ecological consequences of environmental changes.

“Distribution from place to place and abundance at different times are two aspects of the one fundamental problem.” (L.C. Birch ¹⁹⁵³)

Introduction

Ecology has been defined as the study of the factors governing the distributions and abundances of species (Krebs 1972). Understanding those factors is a fundamental scientific aim in its own right, but in a world highly influenced by human-caused environmental changes, ecology must also rise to the applied challenge of predicting how distributions and abundances will respond to environmental change. Distributions are the fundamental unit of biogeographical study, providing information about where a species is present and may interact with other species. Distributions have also been the focus of most studies examining historical responses to environmental changes (e.g. Parmesan et al. ¹⁹⁹⁹; Moritz et al. ²⁰⁰⁸; Lenoir et al. ²⁰⁰⁸). However, predicting future abundance is as important as, if not more important than, predicting future distribution. Abundance is a far better measure of the effects a species has on its local ecosystem than simply whether it is present. For species of value to humans, estimates of future abundance will be essential for regulating current and future harvests. For species of conservation concern, their future numbers will be an important determinant of their extinction risk. Finally, abundance will be a much stronger indicator than presence alone of the carry-on effects that one species will have upon interacting species in the community.

Unfortunately, work to date predicting the effects of environmental changes has focused disproportionately on changes in species' distributions, likely for two reasons. First, simple methods to predict distributions – without considering abundance – exist that can be parameterised with only readily available information about collection locations and abiotic variables, and that are readily linked to future climate predictions. Second, information about current distributions needed to validate distribution models is more often available than is information about abundances.

Simultaneously, the smaller but growing number of detailed studies assessing the influence of environmental changes on the growth rates of, and abundance in, single populations has largely ignored how those changes are associated with changes in distributions. Thus, we are currently in a situation resembling the proverbial blind men examining different parts of an ele-phant (http://en.wikisource.org/wiki/The_Blindmen_and_the_Elephant), in which researchers are each addressing only separate parts of a larger question (i.e. what are the ecological effects of environmental changes?).

Here, we argue that it is time for the field of ecology to begin to make integrated predictions about how environmental changes will simultaneously alter both the geographical distributions of species and the patterns of abundance across those distributions. We begin by describing what we view to be the most achievable next step towards making such integrated predictions, we continue by reviewing steps that have recently been taken in this direction, and we end by describing our view of what remains to be done.

The full approach and a more achievable alternative

The full approach to forecasting both distribution and abundance would start by predicting the actual abundance of a species at all points across an entire landscape at a specified future time (Fig.1). If we knew abundance, we would automatically know the distribution, defined as the set of locations where abundance is above zero. To make such detailed predictions, we would need to know: (1) the initial condition, i.e. the current abundance of the focal species at all locations in the landscape; (2) the drivers, relevant abiotic and biotic factors at all locations and times during the investigated time interval (e.g. derived from downscaled climate models and spatially explicit population models for the interacting species); (3) how abiotic and biotic drivers plus intraspecific density of the focal species jointly determine its vital rates (i.e. survival, individual growth, reproduction and recruitment) and (4) dispersal ability of the focal species (to assess the probability of future colonisation and effects on established populations of emigration and immigration). With this information, we would start from the initial abundances, predict annual vital rates given the changing drivers and intraspecific density, use the vital rates to update population sizes at each location, add stochastic dispersal and repeat until we reach the desired future time horizon, and then use the predicted abundance to identify the distribution (Fig.1, arrow 2).

Figure 1.

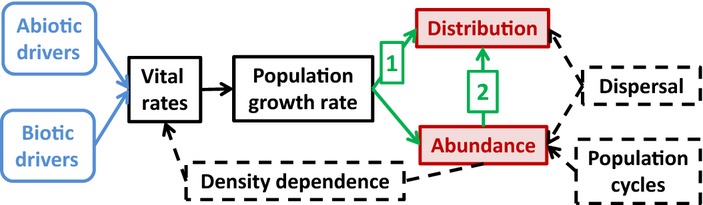
Components of population-based approaches to predicting abundance or distribution of organisms under environmental change. Blue = input drivers; solid black = intermediate state variables; red = prediction goals; dashed boxes = important processes. Demographic range models (Table 1) use the intrinsic population growth rate to predict the distribution (arrow 1). We advocate as a next step incorporating density-dependent feedback to the vital rates to calculate the population growth rate at all densities, and using it to compute equilibrium local abundance at all sites and thus the distribution (locations where equilibrium local abundance is positive; arrow 2). The full approach would add: (1) dispersal, which modifies local abundance (through migration), alters local density-dependent feedback and allows dispersal limitations and source-sink dynamics and (2) population cycles, which may cause local abundance to deviate from equilibrium. The full approach would also require knowing initial abundances of the focal species at all sites.

In practice, we will rarely – perhaps never – have all of this information in the quantity and quality that would be needed to make reliable predictions about actual abundance. Quantifying dispersal rates and distances and the initial abundances of the focal species (and interacting species) at all points in space will be particularly challenging. A more achievable goal would be to predict the equilibrium abundance of the focal species at all points across the future landscape in the absence of dispersal, which we refer to here as the ‘equilibrium local abundance’. Specifically, once we had quantified how drivers and intraspecific density jointly determine the vital rates and thus the population growth rate, we would apply the density- and driver-dependent population models to the future landscape of abiotic and biotic drivers, and identify the equilibrium for each location as the abundance at which the finite population growth rate is 1. With this approach, we would identify the distribution as the set of locations where equilibrium local abundance is positive (Fig.1, arrow 2).

Many authors (including Pulliam ²⁰⁰⁰; Holt ²⁰⁰⁹; Schurr et al. ²⁰¹²; Diez et al. ²⁰¹⁴) have emphasised, in diverse contexts, that multiple factors will frequently cause the actual abundance at a location to deviate from the equilibrium local abundance. Dispersal limitations may prevent or delay a species from reaching locations where populations could grow, causing the equilibrium local abundance to overestimate actual abundance. Populations at newly colonised locations may not yet have reached their equilibrium abundance. Persistent life stages, such as long-lived adults or seeds in a seed bank, or slow life histories may introduce time lags between environmental change and population responses. Such time lags may cause the equilibrium to over- or under-estimate the actual abundance (e.g. it would give an underestimate for ‘living dead’ populations that have not yet gone extinct despite inadequate long-term growth, and an overestimate for new populations that have not had time to grow to a new, higher equilibrium). Actual abundance may also be positive where equilibrium local abundance is zero due to dispersal into sink habitats. Gains and losses to local populations due to migration will produce discrepancies between actual and equilibrium local abundance. Finally, while strong effects of intraspecific competition will often rapidly bring actual and equilibrium abundances close together, populations may cycle around an (unstable) equilibrium abundance due to over-compensatory density-dependent feedbacks or interactions with other species, causing the actual abundance to deviate (positively or negatively) from the equilibrium abundance.

These complications make the task of predicting the actual abundance quite problematic, even if we knew the initial abundances of all species. Nevertheless, the equilibrium local abundance would be a useful ‘first cut’ at predicting future abundance. For the many species with limited dispersal, migration is likely to be less important than local demography in determining abundance in established populations, and the local equilibrium may convey a reasonably accurate picture of how abundance will respond to environmental change. Because it remains unclear whether making accurate predictions about the actual abundance in the future will ever be an attainable goal for most species, and because predictions of the equilibrium local abundance will likely be more attainable yet still useful for guiding both management and basic ecological understanding, we think that predicting local equilibria across the landscape should be the primary goal for the next phase of research on anticipating effects of environmental change.

Distribution could also be predicted by considering the population growth rate rather than abundance. Following Birch (1953), many authors (e.g. Maguire ¹⁹⁷³; Hutchinson ¹⁹⁷⁸; Pulliam ²⁰⁰⁰; Holt ²⁰⁰⁹) have defined the area where long-term persistence is possible in the absence of migration (or, in environmental space rather than geographical space, the fundamental niche) as the set of locations where the intrinsic population growth rate of the species is positive, the logic being that for a location to be within the species' range, populations must be able to establish there and increase from low density. If the population experiences strictly negative density dependence, the intrinsic growth rate is approached as population density approaches zero. However, with positive density dependence at low density and negative density dependence at high density, the zero-density population growth rate may no longer be the relevant indicator of the distribution (Holt 2009), as the growth rate may be negative at near-zero density but positive at higher density (i.e. above the Allee threshold). In this case, we would require that the population growth rate is positive at the density at which it is maximised (cf. fig.1C in Holt ²⁰⁰⁹) for a site to lie within the region where persistence is possible (recognising that the initial population must exceed the threshold for the local population to grow). Once we have connected the vital rates to the drivers and integrated them into the intrinsic population growth rate, it would be straightforward to modify that machinery by incorporating the effects of intraspecific density on the vital rates to predict the equilibrium local abundance. Thus, the ability to predict the distribution based on the intrinsic population growth rate does advance us towards being able to predict abundance, even if it does not get us all the way there.

In the remainder of this study, we evaluate how far we have come, and how far we have yet to go, towards achieving the goal of predicting equilibrium local abundance in the face of environmental change. We begin by reviewing recent work aimed at predicting future distributions, where there has been a growing realisation that incorporating processes influencing abundance may lead to better predictions about distribution. Second, we review the largely independent recent literature that has attempted to understand how changing environmental drivers influence demography and, often only by implication, abundance. We summarise the key features of the approaches we review in Table 1. While none of these approaches has fully realised the ideal – or even the more realistic alternative – that we have described above, different approaches have yielded good understanding of parts of the larger problem, i.e. parts of ‘the elephant’. We end with a summary of what still needs to be done to understand the whole elephant.

Table 1.

Summary of nine key approaches to predicting distribution and abundance under environmental change. Some of these approaches have been applied to empirical data, but others have only been suggested. Columns categorise the different methods with respect to prediction goals, required data inputs, and complexities taken into account and provide a reference to an example of each method. Table entries are discussed in more detail in Appendix S1 in the online supporting information

	Prediction goals		Required data inputs						Complexities taken into account
Approach	Distribution	Abundance	Known occurrences	Values of abiotic and biotic drivers	Vital rates at low density	Effect of intraspecific density on vital rates	Initial abundances at all sites	Dispersal	Living dead populations	Source/sink dynamics	Effects of dispersal on local abundance	Effects of dispersal on distribution	Population cycles	Examples
Classical SDMs	Yes	No	Yes	Yes	No	No	No	No	No	No	No	No	No	Elith & Leathwick (2009)
Abundance-based SDMs (including Poisson process models)	Yes	Yes	Yes	Yes	No	No	No	No	No	No	No	No	No	Fithian & Hastie (2013)
Hybrid SDMs	Yes	Yes	Yes	Yes	Yes	Yes/No	No	Yes/No	Unclear	Unclear	Yes	Yes/No	Yes/No	Dullinger et al. (2012)
Phenology models	Yes	No	No	Yes	No	No	No	No	No	No	No	No	No	Chuine & Beaubien (2001)
Population-based ‘mechanistic’ models	Yes	Yes/No	No	Yes	Yes	Yes/No	No	No	Yes	No	No	No	No	Buckley (2008)
Dynamic range models	Yes	Yes	Yes	Yes	No	No	Yes	No	Unclear	Yes	Yes	Yes	Yes	Schurr et al. (2012)
Demographic range models	Yes	No	No	Yes	Yes	No	No	No	Yes	No	No	No	No	Diez et al. (2014)
Demographic equilibrium abundance models	Yes	Yes	No	Yes	Yes	Yes	No	No	Yes	No	No	No	No	None (suggested in this paper)
Full approach	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes	None

SDM, species distribution models.

Recent developments in predicting changes in species distributions

Background

As background to our review of recent work to predict changing distributions, we note that most such work in the past has been based on species distribution models or SDMs, also known by many other names such as climate envelope models, habitat suitability models, niche models and resource selection functions (Elith & Leathwick ²⁰⁰⁹; Elith et al. ²⁰¹¹; Araújo & Peterson ²⁰¹²). SDMs typically combine information about known locations where a species occurs (and sometimes where searches have not found the species) with data about abiotic variables (climate, soil, elevation, etc.) from those locations to predict the probability of occurrence of that species at other sites or times given the abiotic environment. Distributions in an altered future climate are predicted by linking SDMs fitted to current species occurrence and climate data to future temperature and precipitation predicted by climate models forced by anthropogenic CO₂ inputs to Earth's atmosphere. Studies that have used SDMs for this purpose, or to predict future geographical ranges of exotic species introduced into new areas, now likely number in the hundreds.

The principal advantage of the most used SDMs is that they require only the map coordinates of collection or survey sites and the abiotic variables across the reference landscape to infer the species' abiotic niche. However, the limitations of such ‘classical’ SDMs for predicting actual distributions in the face of environmental change have been reviewed by many authors (e.g. Guisan & Thuiller ²⁰⁰⁵; Thuiller et al. ²⁰⁰⁸; Wiens et al. ²⁰⁰⁹; Araújo and Peterson ²⁰¹²; Higgins et al. ²⁰¹²; Schurr et al. ²⁰¹²). In particular, all these authors have discussed the problems of ‘living dead’ populations and dispersal limitation causing SDMs to misrepresent future distributions. Other published criticisms concern lack of attention to biotic interactions and to effects of source-sink dynamics, population genetic differentiation and evolutionary responses. Recent modifications of classical SDMs have attempted to incorporate information about population growth to circumvent the ‘living dead’ problem (Dullinger et al. ²⁰¹²), or information about dispersal (Cabral et al. ²⁰¹³), but these remain fundamentally attempts to predict distribution, not abundance. We now ask: which of this recent work advances the cause of predicting equilibrium local abundance?

Process-based approaches

Much recent work to predict changing distributions has done away entirely with the use of SDMs. However, very few studies have yet made combined predictions of abundance and distribution. Buckley (2008) is perhaps the only study to date that adopted the approach of first predicting the equilibrium abundance across space and then using it to predict distribution under climate change. To predict distribution of fence lizards in North America, Buckley used a bioenergetic model to make reproduction depend on the net rate of energy gain, which depended on body temperature, determined by ambient temperature and thermoregulation. Her model predicts local carrying capacity (K) – the density at which each lizard has only enough space to gain sufficient energy to produce one offspring before dying – given prey abundance and temperature; locales with K above zero defined the distribution. Her carrying capacity maps (her Fig.1) also clearly show equilibrium local abundance across space in a warmer climate. While it produced perhaps the most comprehensive prediction of future equilibrium abundance to date, Buckley's model used a simplified representation of demography by making a single vital rate (fecundity) sensitive to environmental drivers and by omitting age structure (but see Buckley et al. ^2010a).

Crozier & Dwyer (2006) used the intrinsic population growth rate (Fig.1, arrow 1) to predict changes in the distribution of a skipper butterfly. Specifically, they predicted where future summer and winter temperatures would allow the intrinsic rate of population growth to be positive. In their model, overwinter survival depended on winter temperature and the number of summer generations depended on the temperature-dependent rate of larval development. Similarly, Buckley & Kingsolver (2012) modelled temperature-dependent flight time for two alpine butterflies to predict oviposition rate and fecundity. Combining temperature-dependent fecundity and egg viability with constant egg, larval and adult survival, they predicted that the intrinsic population growth rate of the higher elevation species would decline at low elevation but increase at high elevation due to climate warming. Both of these papers focused on the intrinsic population growth rate. With knowledge of how density affects the vital rates they could be modified to predict how abundance would change in a warmer climate.

Models such as those of Crozier & Dwyer (2006), Buckley (2008) and Buckley & Kingsolver (2012) have been labelled ‘mechanistic’ or ‘process-based’ models (Helmuth et al. ²⁰⁰⁵; Kearney & Porter ²⁰⁰⁹) in that they use underlying processes to predict how vital rates, such as lizard fecundity or the number of butterfly generations per year, would respond to abiotic drivers, and then used those vital rates in a comprehensive population model (Table 1). As a result, these models get us closer to predicting abundance given environmental change. Other mechanistic models predicting distributions do not link the underlying process to a full population model, making prediction of abundance difficult. For example, Chuine & Beaubien (2001) and Chuine (2010) have argued that for plants, phenology (e.g. dates of flowering, leafing, fruit maturation and leaf senescence) is a key individual-level trait that provides a mechanistic link between climate and distribution (Table 1). In predicting the distributions of two trees, Chuine & Beaubien (2001) assumed that the probability that a species would be present at a site is the product of the probabilities of survival and of fruit maturation, which depend on the timing of phenological events and the temperatures and precipitation between those events. The logic of this index for predicting geographical range limits is clear: populations cannot persist where either existing individuals cannot survive or reproductive failure precludes recruitment. However, the product of survival and fruit production cannot be translated into abundance, without also considering other vital rates and density dependence.

Dynamic range models

A recent proposal for predicting changes in actual abundance and distribution, the so-called dynamic range model (DRM), would use abundance and driver data from multiple sites and years to simultaneously estimate driver-dependent vital rates, density dependence and dispersal rates (Pagel & Schurr ²⁰¹²; Schurr et al. ²⁰¹²). Specifically, one would first collect data on: (1) presence/absence at many sites at two or more times; (2) abundances at fewer sites more frequently and (3) climate data at all sites each year. Hierarchical Bayesian methods would then be used to exploit the information in the changing site abundances and distribution in response to climatic variation to simultaneously estimate the parameters of a climate-driven density-dependent population model and a dispersal kernel. The fitted model could then be linked to climate forecasts to predict future abundances and distribution. Schurr et al. (2012) also argue that vital rate data could be used along with other information in fitting DRMs, although this has not yet been demonstrated. The advantage of the DRM approach is that it simultaneously estimates population dynamics (and its link to drivers) and dispersal. However, the method has not yet been applied to real data and the data requirements may be quite high, especially if climate and abundance change slowly and establishment of new populations is rare. In addition, as pointed out by Schurr et al. (2012), capturing the climate responses of multiple vital rates needed to accurately represent the demography of species with more complex life histories would require even more data than the unstructured model used by Pagel and Schurr, as would dealing with model uncertainty (Pagel and Schurr fit the same model that was used to generate the data). The strengths and weaknesses of this approach need to be compared to those of the demographic approach we describe below, in which shorter-term data on performance of individuals in response to environment is used to build links between vital rates and environmental drivers. But the DRM approach does clearly illustrate the advantages of linking abundance and distribution, and may be a practical way to predict changes in both for species with simple, rapid life histories, high vagility and large amounts of data (e.g. univoltine insect pests of agricultural crops).

‘Hybrid’ models and other approaches allied with SDMs

Other recent work has attempted to incorporate population dynamics into SDMs to better predict distributions, but it is not clear that these approaches will be useful for predicting abundance. For example, explicitly motivated by the possibility that ‘living dead’ populations might make SDM predictions unreliable, Dullinger et al. (2012) constructed ‘hybrid models' (sensu Thuiller et al. ²⁰⁰⁸) for 150 alpine plant species. Specifically, they made each species' vital rates and carrying capacity functions of the occurrence probability predicted by an SDM given each site's soil and climate variables each year (eqn 1 in their supporting information). Assuming that each currently occupied site starts at carrying capacity, and using species-specific seed dispersal kernels, they used the changing vital rates and carrying capacities (driven by changes in occurrence probability from the SDM governed by changing climate) to predict the abundance of each species across multiple sites (including newly colonised ones) into the future. Although their model tracks abundance, they present results only about changing distribution. Setting aside the issue of whether many of the assumptions used to tie vital rates and carrying capacities to occurrence probability are valid, the abundance predictions one would obtain by this indirect method would not necessarily yield the same values one would obtain by correlating demographic rates with environmental drivers and density directly. Why both vital rates and carrying capacity (which is a function of the vital rates) should be driven separately by occurrence probability remains unclear, as is what would be gained by tying vital rates to the SDM-predicted occurrence probability to predict abundance if we actually knew the relationship between vital rates, climate and density. Keith et al. (2008) also assumed that carrying capacity is proportional to an SDM-derived occurrence probability, although they assumed density dependence of a ceiling type, so that vital rates in their model were independent of both climate and density below the carrying capacity. Cabral & Schurr (2010) and Cabral et al. (2013) used high-quality data on the landscape abundance of Protea species, combined with a mechanistic dispersal model, to estimate the parameters of a density-dependent unstructured population model, which they then linked to an SDM predicting changes in the distribution of suitable habitat due to climate change. While the resulting hybrid model predicts landscape abundance, the underlying demographic rates are assumed to be independent of climate or other drivers, which is unlikely to be true. Indeed, none of these ‘hybrid’ approaches allow vital rates to respond idiosyncratically to climate variation, despite evidence that they do (Doak & Morris ²⁰¹⁰; Villellas et al. ^2013a,b). A general problem with hybrid models is that they continue to rely on SDMs to predict vital rates, carrying capacity or suitable habitat.

Other approaches allied to SDMs may allow prediction of abundance. Some (e.g. Maravelias et al. ²⁰⁰⁰; Rouget & Richardson ²⁰⁰³) have correlated abundance (or proxies of it, such as percent cover) directly with environmental variables. Poisson process models estimate a ‘rate of occurrence’ as a correlate of climate which may in some cases be proportional to abundance (Fithian & Hastie ²⁰¹³). Thuiller et al. (2014), in an approach conceptually similar to the one we advocate but with important differences, fit a density-dependent population model (the Ricker model) to changes in tree basal area, allowed r and K to be functions of environmental variables, and computed equilibrium abundance. A caveat with using only biomass indices such as basal area to predict abundance is that it confounds individual and population growth; for example, basal area may increase due to tree growth in a living-dead population that is destined for extinction (also a concern for the correlative approaches above). The probability of occurrence from standard SDMs sometimes correlates with aspects of abundance, such as maximum observed abundance (VanDerWal et al. ²⁰⁰⁹), but such correlation is not universal (Thuiller et al. ²⁰¹⁴). The overarching question is whether more mechanistic models based on population processes, such as those we advocate here, would do a better job than the correlative approaches in this paragraph at predicting abundance; at present, we lack the data needed to answer this question.

Recent developments in demographic modelling

Simultaneous with, but largely independent of, recent developments in predicting effects of environmental changes on distributions, demographic models for single populations have increasingly sought to link vital rates and population growth rates to abiotic and biotic environmental drivers (Fig.1, leftmost arrows). These new models have opened the possibility to more firmly establish the values and combinations of environmental parameters that can sustain positive population growth rates, and could be adapted to predict equilibrium local abundance across entire landscapes. The relationships between environmental factors and vital rates can be parameterised by ‘capitalising on natural variation’, i.e. spatial and temporal variability in organisms' performance along gradients of environmental conditions (Ibáñez et al. ²⁰¹³; Frederiksen et al. ²⁰¹⁴). Given some previous knowledge of study systems and putative drivers, relationships between vital rates and drivers can also be determined by direct experimental manipulation of drivers. Below, we review recent developments of demographic modelling, primarily from plant studies, that are potentially important for understanding and predicting abundances and distributions in changing environments.

Identifying environmental drivers of demography

Links between demography and environmental drivers have most often been forged with the aid of one of three types of variation: spatial, temporal or spatio-temporal. Studies using spatial (i.e. among-site) variation have identified relationships between vital rates and abiotic environmental factors, including light availability (Alvarez-Buylla ¹⁹⁹⁴; Horvitz et al. ²⁰⁰⁵; Metcalf et al. ²⁰⁰⁹; Diez et al. ²⁰¹⁴), soil nutrients (Gotelli & Ellison ²⁰⁰²; Brys et al. ²⁰⁰⁵; Colling & Matthies ²⁰⁰⁶; Dahlgren & Ehrlén ^{2009, 2011}), soil moisture (Diez et al. ²⁰¹⁴) and fire (e.g. Menges & Quintana-Ascencio ²⁰⁰⁴; Weekley & Menges ²⁰¹²; Mandle & Ticktin ²⁰¹²). Variation in vital rates and population growth rates have also been linked to spatial variation in biotic interactions, including interspecific competition (e.g. Ramula & Buckley ²⁰⁰⁹), herbivory (Maron & Crone ²⁰⁰⁶) and seed predation (Kolb et al. ²⁰⁰⁷).

Studies using temporal variation have mostly linked variation in vital rates to among-year variation in climate (Altwegg et al. ²⁰⁰⁵; Pfeifer et al. ²⁰⁰⁶; Lucas et al. ²⁰⁰⁸; Hunter et al. ²⁰¹⁰; Toräng et al. ²⁰¹⁰; Dalgleish et al. ²⁰¹¹; Nicolè et al. ²⁰¹¹; Bucharová et al. ²⁰¹²; Salguero-Gómez et al. ²⁰¹²; Jenouvrier ²⁰¹³; Sletvold et al. ²⁰¹³), but other factors, such as prey availability, have also been investigated (e.g. Miller et al. ²⁰¹¹). Linking temporal variation in vital rates directly to specific drivers is essential for predicting how trends in environmental conditions might influence species abundances and distributions. In contrast, demographic models such as stochastic matrix models usually treat temporal variation in vital rates as directly stochastic, i.e. characterised only by means and variances and caused by unknown factors, and are thus unable to predict the effects of changes in environmental drivers. Moreover, having established the relationship between vital rates and climate, we can use independent historical data on the frequency distribution of climate conditions to achieve a better understanding of current and past population dynamics (e.g. Åberg ¹⁹⁹²; Toräng et al. ²⁰¹⁰; Vanderwel et al. ²⁰¹³; Merow et al. ^2014a).

Several studies have been carried out in multiple populations over multiple years (e.g. Doak & Morris ²⁰¹⁰; Eckhart et al. ²⁰¹¹). Such spatio-temporal data allow us to partition variation in vital rates into components due to yearly variation in environmental conditions vs. relatively fixed environmental differences across space, and also enable us to examine interactive effects of drivers operating at different spatial scales. For example, Nicolè et al. (2011) showed that region-wide increases in summer temperatures had a negative effect on population growth rates of a perennial herb, but that the effects were much more severe on steeper slopes, presumably because faster runoff of precipitation exacerbated the effects of high temperatures. Knowledge about such effects of the interactions between climate variables and local habitat is important to downscale regional climate change scenarios to effects on local populations. Moreover, in many habitats indirect effects of environmental change, via competitive or facilitative relationships, are important (Brooker et al. ²⁰⁰⁶; Adler et al. ²⁰¹²; De Frenne et al. ²⁰¹³). Interactions between climate variables and biotic factors, such as interspecific competition, are therefore fundamental to understand and predict the effects of climate change at a local scale (e.g. Sletvold et al. ²⁰¹³).

An obvious advantage of correlative approaches is that effects of environmental factors on vital rates and population growth rate are estimated under realistic conditions. However, many potentially important factors might be correlated and causal relationships difficult to disentangle. Moreover, using only natural variation it might be difficult to get enough sites or years to cover a sufficiently broad range of environmental factors. Lastly, assessments of effects of environmental factors on vital rates based on correlative studies are likely to be biased if they do not account for differences in intraspecific densities (see below). Ideally, causal relationships between environmental factors and vital rates suggested by correlations should therefore be corroborated by manipulative experiments. Experimental manipulations could also push variables beyond the current range of natural variation, allowing better predictions for conditions that have not yet occurred. Such experiments can (1) manipulate the environmental factors in existing populations, e.g. using artificial warming, watering or exclusion of interacting species (Alatalo & Totland ¹⁹⁹⁷; Gotelli & Ellison ²⁰⁰⁶; Miller et al. ²⁰⁰⁹; Dahlgren & Ehrlén ²⁰¹¹; Mandle & Ticktin ²⁰¹²; Sletvold et al. ²⁰¹³), (2) transplant the species into new driver parameter spaces (e.g. Griffith & Watson ²⁰⁰⁶; Meineri et al. ²⁰¹³) or (3) grow the species in a greenhouse or common garden where environmental conditions are under experimental control (Radchuk et al. ²⁰¹³). By using common garden or reciprocal transplant experiments we can also disentangle genetic and environmental effects on vital rates.

Incorporating intraspecific density dependence

If density dependence is weak and populations are of similar age, then population growth rate might be a good predictor of local abundance. For example, Merow et al. (2014a) found that the population growth rate predicted by a climate-driven density-independent model for a perennial shrub correlated with local abundance. However, we know from the simple logistic model that intrinsic growth rate (r) and equilibrium abundance (K) need not be related to one another. Thus, in general, we must quantify density dependence to predict abundance. Yet, most recent demographic models linking vital rates to environmental drivers have not simultaneously accounted for the effects of intraspecific density. Because for logistical ease demographic studies are often, consciously or unconsciously, conducted where individuals are fairly abundant, the average density in those populations is likely to be at (or even slightly above; Buckley et al. ^2010b) the carrying capacity and the population nearly stable (r = 0 or λ = 1). In these cases, the effects of environmental drivers on vital rates, and thus on population growth rate, provide useful information about whether the population is likely to increase or decline from its current density in a changed environment. But it does not necessarily indicate how the intrinsic population growth rate will be affected by those drivers. Thus, the vital rates and population growth rate from these studies, uncorrected for density, cannot be used to predict the distribution (Diez et al. ²⁰¹⁴) or equilibrium local abundance.

Even the relationship between vital rates and environmental factors cannot be assessed accurately without taking density dependence into account, as spatial and temporal variation in environmental drivers may be confounded with variation in density. The effects of environmental factors and intraspecific density on vital rates therefore need to be assessed simultaneously, and omitting one can yield erroneous estimates of the effects of the other. Several studies of birds and mammals have assessed the simultaneous effects of temporal variation in climate and density in single populations (Berryman & Lima ²⁰⁰⁶; Hone & Clutton-Brock ²⁰⁰⁷; Coulson et al. ²⁰⁰⁸; Simard et al. ²⁰¹⁰; Brown ²⁰¹¹; Pelletier et al. ²⁰¹²; Jenouvrier ²⁰¹³). However, studies intentionally using spatial variation in environmental factors and intraspecific density to explore their simultaneous effects on among-site demographic variation are still rare (but see Diez et al. ²⁰¹⁴; Dahlgren et al. ²⁰¹⁴). We thus still know little about how spatial variation in abiotic and biotic environmental factors interacts with local population densities in determining vital rates and population dynamics in natural systems, and how much observed relationships with environmental factors are biased by differences in density.

Linking demographic information to species abundances and distributions under environmental change

Once we have quantified how environmental drivers and intraspecific density jointly influence the vital rates, we could predict equilibrium local abundance (i.e. the density at which population growth is zero) across the landscape, and therefore distribution, under a changing environment (see section “The full approach and a more achievable alternative”). The studies that perhaps have come closest to this approach are Vanderwel et al. (2013), Diez et al. (2014) and Merow et al. (2014a). This is also essentially the approach taken by Buckley (2008), but she used an underlying mechanistic model rather than correlations between vital rates and environmental drivers. Although their aim was not to predict responses to environmental change, Diez et al. used data on how the vital rates of an orchid respond to light and soil moisture availability to parameterise a population model [an integral projection model (IPM); see next paragraph] and predict the current distribution of the species, following the approach in Fig.1, arrow 1. Importantly, they also assessed whether each vital rate was sensitive to local intraspecific density, and used the zero-density population growth rate to predict the distribution. Only two steps (making vital rates density-dependent, and predicting future changes in the drivers) would be needed to enable their model to generate predictions of future equilibrium local abundance. Similarly, Merow et al. (2014a) used an IPM in which vital rates were correlated with abiotic variables, but in addition they linked their model to predictions from climate models to generate predicted future distributions (i.e. locations with λ > 1). Making the vital rates in their model density-dependent is all that would be needed to enable it to predict future abundance. Vanderwel et al. (2013) used an individual-based simulation to assess the importance of climate-dependent vital rates and competition, and to predict how changes in climate would affect abundance (basal area) and distribution of trees. Even though they did not distinguish between intra- and interspecific competition and parameterised models for functional types rather than species, their study illustrates how a demographic framework and existing data can be used to predict abundances and distributions of multiple interacting species under changing environmental conditions.

The modelling framework we employ to predict equilibrium abundance will depend on the species' biology and the type of data in hand. For species with simple life cycles, unstructured population models may often be sufficient to link drivers to abundance and distribution (e.g. Crozier & Dwyer ²⁰⁰⁶). Use of unstructured models is also the only available option if the data are the numbers of individuals. However, for species with long lifespans, large variation in size, or multiple life states, structured models provide more accurate measures of population growth rate and abundance as well as an assessment of the contributions that different vital rates (e.g. adult survival vs. recruitment of juveniles) make to population growth, which may be informative when different drivers do not affect all these rates equally. Structured models may also be required to represent phenomena such as living-dead populations and other time lags between environmental change and population response. Once established, the relationships between vital rates and both environmental variables and intraspecific density can be integrated using demographic models to assess the overall relationship between environmental variables and abundance. The most common types of structured population models are projection matrix models and IPMs (Easterling et al. ²⁰⁰⁰; Caswell ²⁰⁰¹; Morris & Doak ²⁰⁰²; Ellner & Rees ²⁰⁰⁶; Rees & Ellner ²⁰⁰⁹; Merow et al. ^2014b; Rees et al. ²⁰¹⁴). The former type uses a limited number of discrete classes, whereas the latter is based on continuous state variables (although it is usually implemented by using a large number of discrete classes, i.e. converted to a matrix). A main difference is that while the former is based on observed state transitions and does not assume any specific relationship between vital rates and state, the latter is based on functions statistically fitted to the observations. This statistical fitting procedure reduces the number of parameters to be estimated and enables the inclusion of multiple state variables and the effects of abiotic and biotic environmental drivers, as well as intraspecific density, on vital rates. While studies using structured population models typically have been density-independent, it is straightforward to incorporate the effects of intraspecific density (for a description of how to do so in a projection matrix model, see Caswell ²⁰⁰¹ or Morris & Doak ²⁰⁰²). To construct a density-dependent structured model (based on either a projection matrix or an IPM), the vital rates are first modelled as functions of intraspecific density, perhaps integrated over a subset of the size distribution, as well as external drivers. Current intraspecific density in the model affects vital rates and the model is iterated until stable population densities, corresponding to equilibrium abundance, are reached (Ellner & Rees ²⁰⁰⁶; Rebarber et al. ²⁰¹²; Dahlgren et al. ²⁰¹⁴). Lastly, if we have the data to determine how microenvironment or interactions with neighbours influence the fates of individuals, spatially explicit individual-based models may be appropriate to assess how environmental change influences abundance and distribution.

Establishing relationships between environmental drivers and vital rates will often involve a large number of candidate variables while the number of years or sites with independent data is limited. This may create problems with model over-fitting and identification of the relevant drivers. One suggested way to partly alleviate such problems is to use penalised regressions (e.g. Dahlgren ²⁰¹⁰). Moreover, relationships between drivers and vital rates may take many different forms, and effects on one factor might depend on the level of others. It is therefore important to use statistical methods that can identify nonlinear relationships (Dahlgren et al. ²⁰¹¹; González et al. ²⁰¹³) and interactive effects.

Using demographic information to model distributions and abundances as functions of climate and environmental factors constitutes an important advance, from a conservation perspective, compared with deterministic or stochastic but stationary models. It enables us to model and predict population growth trends and abundances, not only in constant or stochastically varying environments but also in the non-stationary environments that are the result of anthropogenic impacts, and which are likely to constitute the major threat to biodiversity currently on Earth. Moreover, because conservation efforts usually seek to ameliorate environmental conditions rather than population viability per se, framing population viability as a function of environmental factors provide important guidance for management.

Recommendations and ongoing challenges

Distributions are ultimately determined by the establishment and persistence of populations, which are determined, respectively, by the capacity for positive population growth at low density and the ability to maintain at least moderate abundance (and of course dispersal). We therefore cannot expect to make reliable predictions about how environmental changes will alter distributions without accounting for effects on population processes. Moreover, distribution and abundance are inseparable aspects of ‘the one fundamental problem’ (Birch 1953). If predictions about abundance would be more useful than predictions about presence/absence only, as we believe they would be, then we should begin to construct the machinery to predict abundance across space and use predicted abundance to predict distribution. As an alternative to SDMs (including ‘hybrid’ models), phenology models and Poisson process models (Table 1), we therefore advocate the direct use of population models with vital rates linked to abiotic and biotic drivers and to intraspecific density as a more mechanistic way to predict the locations where conditions allow populations to flourish, and where they are doomed to extinction. In our view, connecting demography directly to environmental drivers, either with process-based submodels (e.g. Buckley ²⁰⁰⁸) or with correlative links (e.g. Diez et al. ²⁰¹⁴; Merow et al. ^2014a), is a more straightforward, parsimonious and defensible way to predict equilibrium local abundance than by interposing the output of an SDM between the drivers and demography, as in some hybrid SDM models. Simultaneously, we would glean far more useful information about where the species could be expected to be abundant.

Important steps have already been taken towards the goal of predicting equilibrium local abundance. Nevertheless, significant work remains to be done to fully achieve this goal. We already have the quantitative tools we need to link drivers and density to vital rates, abundance and distribution. What is particularly needed is improved and expanded empirical inputs to existing quantitative models. We now know a great deal about how both abiotic and biotic drivers influence vital rates, but demographic studies to date have mostly considered only single environmental drivers or have assumed that multiple drivers influence vital rates in an additive and linear fashion (but see Dahlgren & Ehrlén ²⁰⁰⁹; Miller et al. ²⁰⁰⁹; Nicolè et al. ²⁰¹¹; Mandle & Ticktin ²⁰¹²; Diez et al. ²⁰¹⁴). Fully understanding how complex environmental changes will influence abundance and distribution also requires us to understand nonlinear effects, and interactive effects of multiple drivers on vital rates, e.g. temperature affecting plant survival more in dry years.

A particular challenge is the fact that detailed demographic studies and SDMs focus on very different spatial scales. Importantly, the relative importance of local demography vs. migration may vary with spatial scale. Moreover, upscaling predictions from demographic models to landscapes needs to acknowledge that different environmental factors might explain variation in vital rates over different spatial scales. Given that the drivers determining vital rates are often very heterogeneous locally, appropriately downscaling regional variation in climate is also challenging. For example, regional climate might affect demography differently depending on microtopography or soil type. Even though we have the tools to identify and model the interactive demographic effects of multiple drivers acting over different spatial scales, our understanding of those interactive effects remains in its infancy because of a lack of relevant data. We also know how to account for the simultaneous effects of environmental drivers and intraspecific density (e.g. Diez et al. ²⁰¹⁴; Dahlgren et al. ²⁰¹⁴), but the joint effects of these two factors on vital rates have been little explored. Once we know how drivers and intraspecific density affect vital rates, we know how to model population growth and identify the equilibrium abundance across the landscape, but this step has rarely been taken (but see Buckley ²⁰⁰⁸). For example, we are not aware of any studies that have used observed correlations between vital rates and both environmental drivers and intraspecific density to predict equilibrium local abundance at the landscape scale (Table 1). Using knowledge of underlying physiological mechanism to model the dependence of some of the vital rates on environmental drivers (e.g. Buckley ²⁰⁰⁸) represents an alternative to using only observed vital rate/driver correlations. Virtually all existing mechanistic models that include an intermediate population model treat some of the vital rates as external inputs to the model, rather than predicting them from an underlying mechanistic model of within-individual processes. Thus, the ‘holy grail’ of predicting all vital rates from first principles of how environment shapes individual performance has yet to be achieved for any species. With such knowledge, multi-year, multi-site demographic studies might be unnecessary.

Even without tackling the challenges of estimating dispersal, equilibrium local abundance may not be easily estimated or most relevant in some situations, and alternatives may be better. Forms of density dependence that produce population cycles may make it difficult to compute the equilibrium for a structured population (Caswell 2001). If so, we might use stage abundances averaged across the cycle in place of the equilibrium. For fugitive species, local populations may quickly die out, such that the equilibrium without dispersal is zero. In this case, we might use the average abundance while populations are extant, weighted by the population lifetime relative to the time between disturbances.

Certainly, the approach we advocate of using population models directly to predict future abundance and, from it, distribution requires much more – and a different type of – data than the current, simpler SDM approaches (but perhaps not more than for approaches such as DRMs or hybrid SDMs). Multi-site demographic studies involve very large data requirements and logistical challenges. Moreover, we still need the spatially detailed predictions that SDMs also require about the relevant drivers of demography. We thus may face a trade-off between quality and quantity of predictions. If we want good predictions then short-cuts likely would not work, and we will need demographic information. However, we likely will not be able to get these data for all or even the majority of species of concern. We suggest that collection of relevant demographic data is not an insurmountable problem for species of key interest. Moreover, detailed knowledge of variation in demography and environmental drivers over large spatial scales from a limited number of model systems can tell us much about how predictions from standard SDMs and demographic models differ, and thus about the importance of the factors incorporated in the latter but not the former.

Even with perfect knowledge about how environmental drivers influence vital rates, the limitations of climate models, and of predictions about changes in land use and other drivers, will restrict how well we can predict abundance and distribution. Important challenges in predicting the effects of environmental change are that multiple factors are likely to change, in their means, variabilities and extremes, and in the correlations between them. However, these are problems that all attempts to predict changing abundance and distribution face, and some of them must be solved by others (e.g. climate modellers and public planners), not ecologists.

We have advocated improving our ability to make predictions about equilibrium local abundance (and thus distribution) as a worthy next step in assessing the ecological consequences of environmental changes. That does not mean we think we should abandon entirely the quest to predict actual abundance and distribution. But we must be realistic about the challenges involved in making this subsequent step. We would need much better information about current abundances across the landscape and a much better understanding of dispersal abilities, of the impact of biotic interactions, and of expected changes in abundance of interacting species (Araújo & Luoto ²⁰⁰⁷). But as we improve our understanding of these additional complexities, we should not delay improving our ability to predict equilibrium abundance, especially as doing so will be part of the solution for predicting actual abundance in the future.

SUPPORTING INFORMATION

Additional Supporting Information may be downloaded via the online version of this article at Wiley Online Library (http://www.ecologyletters.com).