The Behavior of Water in Collagen and Hydroxyapatite Sites of Cortical Bone: Fracture, Mechanical Wear, and Load Bearing Studies

Abstract

The mechanical properties of cortical bone, which is largely comprised of collagen, hydroxyapatite, and water, are known to hinge on hydration. Recently, the characteristics of water in bone have drawn attention as potential markers of bone quality. We report on the dynamics, diffusion, population, and exchange of water in cortical bone by NMR relaxation and diffusion methodologies. Relaxation measurements over timescales ranging from 0.001 to 4.2 s reveal two distinguishable water environments. Systematic exposure to ethylenediaminetetraacetic acid or collagenase reveals one peak in our 2D relaxation map belonging to water present in the hydroxyapatite rich environment, and a second peak with shorter relaxation times arising from a collagen rich site. Diffusion-T₂ measurements allowed for direct measurement of the diffusion coefficient of water in all observable reservoirs. Further, deuterium relaxation methods were applied to study cortical bone under an applied force, following mechanical wear or fracture. The tumbling correlation times of water reduce in all three cases, indicating that water dynamics may be used as a probe of bone quality. Lastly, changes in the relative populations and correlation times of water in bone under an applied force suggest that load bearing occurs largely in the collagen rich environment and is reversible.

Introduction

Bone is a composite biomaterial comprised of collagen which is surrounded by hydroxyapatite crystals ^1,2. Water is the third major component of bone and contributes approximately 20% to its wet weight³. Collagen provides elasticity⁴, the mineral component confers strength⁵, and water is believed to impart shock absorbing capacity¹. Because of this unique makeup, the fracture toughness of bone is 3 to 10 times higher than silicon⁴. Early bone mineral density (BMD) tests were considered a standard method for accessing bone quality and risk of fracture⁶. In the last three decades, however, studies have shown that BMD tests alone are not a good predictor of fracture risk^7,8. Hence, there has been an ongoing need for additional parameters to assess bone quality.

The strength, toughness, and stiffness of bone is known to be associated to the degree of hydration⁹. Solid state nuclear magnetic resonance (SSNMR) spectroscopy has proved to be a popular technique to study bone structure as it can probe both hard (mineral, mineralized collagen) and soft matter (water) unlike X-ray methodologies^10–16. Water and its role in bone has been extensively studied by NMR spectroscopy and relaxation methodology^12,16–21. Many studies have been performed to observe or distinguish bone water (i.e., mobile or bound)^16,18 or have addressed the presence of different water layers¹⁹ or reservoirs^12,16,17,21 in cortical bone. SSNMR has also been applied to indirectly measure the thickness of a water layer in bone to be 9Å, by measuring the distance of the organic and inorganic components¹⁰. Apart from these approaches, NMR relaxation methods have allowed for the study of bone porosity and to determine the pore size distribution in bone^21–25. Recently, it has been shown that NMR relaxation can also be employed to study bone quality by measuring the mobile and bound water components¹⁸. The diffusion characteristics of exchangeable water in cortical bone have also been measured and the results point to the presence of two different water environments, i.e. mobile and tightly bound water³.

Water should not be considered an isolated component of bone as it interacts with collagen and inorganic apatite and influences both macroscopic and microscopic characteristics²⁶. SSNMR studies have shown that water may deeply influence the orientation of apatite crystals by forming an amorphous layer outside crystals¹³ and plays a key role in triple helical assembly of native collagen²⁶. The total water concentration in bone was recently shown to exhibit a correlation with bone stiffness followed by BMD measurements, bone volume/trabecular volume and trabecular number in rat trabecular bones²⁷. Recent NMR studies showed that bound water shows a strong correlation with bone fracture properties^28,29. Although there have been studies elucidating mobile water, bound water and bound water associated with collagen, many questions remain relating to the differentiation of water related to collagen and hydroxyapatite, their associated diffusion coefficients, and how the dynamics and population of water in each reservoir are altered following fracture, mechanical wear or when bone is placed under a mechanical load.

In the present study, we have measured the diffusion, exchange, and tumbling correlation times of water in intact cortical bone. ²H two dimensional T₁ – T₂, T₂ – T₂, D–T₂ experiments have been performed, based on an inverse Laplace transform (ILT)^30–33. These two dimensional relaxation methods have been previously applied to characterize water in multisite systems such as elastin ³⁴, silk³⁵, poly(N-substituted α/β-asparagine) derivative ³⁶, potato tissue³⁷, cement pastes³⁸ and saturated sedimentary rocks³⁹. The bone matrix was systematically modified by either collagenase or EDTA (ethylenediaminetetraacetic acid) to follow the changes in water dynamics and its distribution in each resolvable reservoir observed in the two dimensional relaxation data. These experiments allowed for identifying different water reservoirs present in the bone extracellular matrix (i.e., collagen and mineral apatite). Diffusion-T₂ experiments by pulsed gradient field NMR methods were also performed and the molecular diffusion coefficients of different water reservoirs were directly measured in fractured cortical bone. Our studies of bone under a mechanical load, following fracture or mechanical wear indicate that the largest changes in dynamics and population of water occur in the organic component (collagen) of cortical bone and are reversible.

Materials and Methods

Sample Preparation

Cortical bone from goat femora were collected from a local slaughter house. The bone was cut into a right-angled parallelepiped weighed approximately 40±5 mg. Bone samples were demineralized or deproteinized following the procedures detailed below.

EDTA (ethylenediaminetetraacetic acid) Treatment

A small piece of intact bone with a dimension of approximately 6.0 mm × 3.0 mm × 1.0 mm was immersed in a 0.1M EDTA solution and incubated for about 1 week at 37 °C. After the treatment the bone was washed several times in water and subsequently dried.

Collagenase Treatment

Collagenase from Clostridium histolyticum was purchased from Sigma Aldrich (St. Louis, MO). A solution was prepared using PBS (Phosphate Buffer Saline) and 20 mg/ml collagenase. A sample of the bone having approximate dimensions 5.0 mm × 3.0 mm × 2.0 mm was immersed in the collagenase solution and incubated at 37 °C for approximately 1 week. Afterward, the sample was washed and dried as in the EDTA treatment.

Prior to the NMR experiments each specimen (untreated, EDTA and collagenase treated) was immersed into 99.9 atom % D₂O (Sigma Aldrich,USA) and sonicated for 20 min. During sonication the temperature did not exceed 40°C. For the untreated bone the soaking time was 50 days while for collagenase and EDTA treated samples the soaking time was 8 days. Fractured bone samples were prepared by striking the samples with a hammer under liquid nitrogen and consisted of several small fragments of bone. ²H T₁ – T₂ measurements were performed on three different goat femurs and were reproducible (results from only one measurement are shown). Studies that involved mechanical loading, fracture, and mechanical wear were performed on a sample from one goat femur, twice.

Mechanical Wear and Application of an External Force

To perform mechanical wear, a small piece of intact bone with dimensions of approximately 4.5 mm × 3.0 mm × 2.0 mm was used. The sample was mechanically worn on the surface by a scalpel by carving a hole approximately 1 mm wide × 1 mm thick. Prior to the NMR experiments the sample was immersed in D₂O for 17 days. To apply an external force on the bone sample the following procedure was performed. A cylinder machined from delrin having dimensions 7 mm in diameter and 2 cm in length was tapped through to accommodate an 8-32 screw. A bone sample approximately 6.5 mm × 1.5 mm × 2.0 mm was placed in the cylinder and compressed using nylon screws. The torque on the screws was measured using a digital torque wrench and the force applied was then estimated knowing the lever arm length on the torque wrench; the applied force was estimated to be approximately 10 to 25N. Before applying the force the sample was immersed in D₂O for 24 days. Experiments on samples under an applied force made use of a magic angle spinning probe with a stator that can accommodate the delrin cylinder (samples were static).

¹H, ²H Relaxation Measurements

All the ²H (¹H) 2D T₁ – T₂ and ²H 2D T₂ – T₂ NMR experiments were carried out at a magnetic field strength of 4.699 T using a Varian Unity NMR spectrometer at a frequency of 30.716 (200.093) MHz with a Varian liquids NMR probe and DOTY MAS (magic angle spinning) probe. The experiments were performed at room temperature unless otherwise stated. The variable temperature T₁ – T₂ experiments were carried out in the temperature range between 2 to 40 °C and controlled by an FTS systems TC-84 Air Jet temperature controller to within ± 1 °C. The pulse sequences^31,40,41 used for T₁ – T₂ and T₂ – T₂ experiments are shown in supplementary figure S1. The 90° pulse length of 24 μs was used for all experiments and calibrated at every temperature studied. The recycle delay used was 10 s (20s) which is more than five times the largest relaxation time measured at the magnetic field used in this study. For the 2D T₁–T₂ experiments, the delay t₁ (supplementary figure S1) was logarithmically incremented from 1 ms to 10 s in 100 steps (1.5 ms to 20 s). In the pulse sequence for T₁ – T₂ experiments, the initial 180° pulse inverts the magnetization and then it recovers to thermal equilibrium by T₁ relaxation during the variable delay time t₁. After the 180° pulse, the 90° pulse following the delay t₁ transforms the magnetization into the transverse plane and the NMR signal is detected by a Carr-Purcell-Meiboom-Gill (CPMG) pulse train with τ =0.350 ms⁴². The CPMG pulse train refocuses field inhomogeneity effects, and averages out any heteronuclear dipolar interactions (e.g. ²H-¹H) in the T₂ domain. The T₂ – T₂ experiment allows for probing the exchange time of water molecules between different water reservoirs resolved. Referring to supplementary figure S1, the 90° pulse applied after the first CPMG pulse train stores the magnetization along the azimuthal axis for variable mixing time t_m. The second CPMG pulse train is applied after the time period t_m and the T₂ time is again measured. In the 2D ILT map a cross peak in this experiment corresponds to water molecules exchanging between different water reservoirs during time t_m. In the T₁ – T₂ and T₂ – T₂ experiments n = 6000 points were collected to measure T₂ in each dimension.

Diffusion-relaxation Measurements

In addition to the relaxation correlation experiments, diffusion-relaxation correlation experiments were performed. The experiments were carried out at a magnetic field of 4.214 T and ²H resonance frequency of 27.546 MHz using a homemade probe equipped with magnetic field gradients for solid state studies. The gradient coil was composed of a superposition of Maxwell coils and was capable of delivering a gradient along the azimuthal axis of the sample of up to 90G/cm· A for a sample with a diameter of 2.1 mm⁴³. These strong magnetic field gradients allow for measuring diffusion during time intervals where the magnetization decay is dominated by strong quadrupolar relaxation as discussed later in the text. The pulse sequence used in this work is shown in supplementary figure S2 and is composed of a bipolar gradient stimulated echo pulse sequence⁴⁴ in the indirect dimension for encoding diffusion and a CPMG train in the direct dimension for T₂ encoding. Trapezoidal bipolar gradient pulses with duration of 300 μs were used for phase encoding and decoding as well as to mitigate Eddy currents and ring down effects. Referring to supplementary figure S2, the pre and post gradient delay τ=100μs, Δ=4ms, δ_c=120μs, and the amplitude of the crushing gradient was approximately 12G/cm. The π pulses had duration of 20 μs and were used to refocus any background gradients⁴⁵. The maximum gradient strength in the experiment was 1120G/cm using approximately 12A. The gradient strength was calibrated using D₂O, a substance with a known diffusion coefficient⁴⁶. The kernel for the signal attenuation due to diffusion differs from that provided in the work by Wu⁴⁴ due to the presence of trapezoidal pulses and was derived explicitly for the pulse sequence shown in supplementary figure S2 using the cumulant expansion^47,48. In the T2 dimension, the delay τ′=300 μs and 1280 echoes were acquired. For all diffusion-relaxation measurements the temperature was set to 22°C and was regulated digitally to within 0.5 °C.

¹³C MAS NMR

The ¹H-¹³C CP spectra at magic angle spinning were recorded on solid-state Avance Bruker NMR spectrometer operating at 600.156 MHz for ¹H and 150.924 MHz for ¹³C frequencies with a 3.2 mm DVT probe. All the experiments were performed at 10 kHz Magic Angle Spinning (MAS). A Bruker MAS pneumatic unit controlled the spinning speed with accuracy of ± 2 Hz. The ¹H 90° pulse length was 2.28 μs. For the cross-polarization measurements we used a 1.0 ms contact time with 10k transients and a 5s recycle delay.

Inverse Laplace Transformation

All 2D correlation maps were obtained by a 2D inverse Laplace transform (ILT) using an algorithm described elsewhere ³¹. In this study we used the BRD method⁴⁹ for determining a converged regularization parameter (α). Additionally, we checked that the results obtained which include the T₁, T₂, and relative signal intensities did not change significantly with the value of α. In supplementary materials figure S3 we show the resulting ILT on one ²H T₁ – T₂ 2D data set for different values of α ranging from 0.5 to 0.0005. While the resolution in the map is reduced with large value of α, the T₁, T₂, and relative signal intensities did not vary significantly. The converged value of α in all our ²H, ¹H T₁ – T₂ and D – T₂ 2D data sets was approximately 10⁻⁴. Lastly, when documenting the measured T₁ and T₂ times we included the half-width of the peak of the peak observed in the ILT map and reported this in Tables 1 and 2.

Table 1.

Measured T₁, T₂, correlation times (τ_c), and relative populations of water reservoirs obtained from the untreated or treated (collagenase or EDTA) intact bone. The numbers shown after the ± symbol for any of the T₁ and T₂ relaxation times represent the half-width of the peak observed in the 2D ILT maps and have been propagated to the correlation times.

Assignments		untreated intact bone	EDTA treated intact bone	collagenase treated intact bone
Peak A	T1 [ms]	475 ± 22.1	413 ± 19.2	433 ± 20.1
	T2 [ms]	147 ± 15.4	81.1 ± 5.6	86.9 ± 6.0
	τc [s] ×10−8	0.75 ± 0.11	1.09 ± 0.1	1.07 ± 0.1
	Relative population	0.62	0.23	0.54
Peak B	T1 [ms]	413 ± 19.2	305 ± 21.3	394 ± 18.3
	T2 [ms]	13.6 ± 1.4	13.2 ± 1.8	9.3 ± 1.3
	τc [s] ×10−8	3.19 ± 0.27	2.75 ± 0.34	3.8 ± 0.41
	Relative population	0.23	0.19	0.37
Peak C	T1 [ms]	385 ± 26.9	183 ± 12.8	376 ± 17.5
	T2 [ms]	2.9 ± 0.5	3.1 ± 0.3	2.4 ± 0.5
	τc [s] ×10−8	6.85 ± 0.95	4.48 ± 0.43	7.33 ± 1.1
	Relative population	0.15	0.58	0.09

Table 2.

Measured T₁, T₂, correlation times (τ_c), relative populations and diffusion coefficients obtained from fractured bone, intact bone following mechanical wear, under an applied force and after releasing pressure. As discussed in the text, the estimated applied force to the bone was approximately 10 to 25 N. The numbers shown after the ± symbol for any of the T₁ and T₂ relaxation times or diffusion coefficients represent the half-width of the peak observed in the 2D ILT maps.

Assignments		Fractured Bone	Following mechanical wear	Under an applied force	After releasing pressure
Peak A	T1 [ms]	385 ± 26.9	404 ± 28.2	377 ± 35.0	433 ± 20.1
	T2 [ms]	116 ± 24.2	128 ± 22.4	104 ± 18.0	73.1 ± 7.6
	τc [s] ×10−8	0.77 ± 0.22	0.73 ± 0.18	0.83 ± 0.21	1.2 ± 0.13
	Relative population	0.51	0.43	0.26	0.50
	Diffusion Coefficient [μm2/ms]	2.10 ± 0.07	-	-	-
Peak B	T1 [ms]	291 ± 20.3	351 ± 24.5	115 ± 18.8	360 ± 16.7
	T2 [ms]	22.4 ± 3.9	22.4 ± 3.9	16.3 ± 1.7	12.3 ± 0.8
	τc [s] ×10-8	2.0 ± 0.31	2.2 ± 0.34	1.4 ± 0.25	3.1 ± 0.19
	Relative population	0.27	0.34	0.23	0.30
	Diffusion Coefficient [μm2/ms]	1.76 ± 0.06	-	-	-
Peak C	T1 [ms]	215 ± 10	285 ± 13.2	41.5 ± 4.8	298 ± 13.9
	T2 [ms]	5.1 ± 0.5	4.6 ± 0.32	4.3 ± 0.6	3.1 ± 0.3
	τc [s] × 10-8	3.8 ± 0.30	4.6 ± 0.28	1.7 ± 0.28	5.8 ± 0.45
	Relative population	0.22	0.23	0.51	0.20
	Diffusion Coefficient [μm2/ms]	0.62 ± 0.07	-	-	-

Results and Discussion

This section is organized as follows: we first describe our two dimensional T₁ – T₂ relaxation experiments that were performed in deuterium hydrated cortical bone and following EDTA and collagenase treatments. Second, we highlight results from relaxation exchange experiments, by T₂ – T₂ methodology, which provide insight to the connectivity of the sites resolved in our T₁ – T₂ data. Lastly, we discuss findings from our diffusion-relaxation measurements and T₁ – T₂ measurements on bone under an applied force, following fracture, or mechanical wear.

T₁ – T₂ Experiments on ²H Hydrated Untreated, EDTA, and Collagenase Treated Bone Samples

The ²H 2D ILT T₁ – T₂ map of ²H₂O hydrated untreated intact bone acquired at 22°C is shown in figure 1. In the 2D ILT map of untreated intact bone, apart from the bulk water (T₁ and T₂ value of about 464 ms and 433 ms), three water peaks (labeled A, B and C) are observed each pointing to environments where water molecules experience different dynamical characteristics distinguishable over the time scale ranging from approximately 1ms to 4.2s (range of values probed in the T₂ dimension). Similar findings were observed with the same number of reservoirs in a ¹H 2D T₁ –T₂ experiment, with cortical bone hydrated in H₂O (data shown in the supplementary materials figure S4). Measurements on either ¹H or ²H preclude the observation of water molecules having a relaxation time T₂ less than our sampling time which was 0.35 ms for ²H and 1.5 ms for ¹H. The ²H relaxation measurements, as we discuss in detail below, allow for a probe of the rotational correlation times as the relaxation pathway for ²H nuclei is quadrupolar in origin. Furthermore, as this work focuses on investigating the dynamics of water only, ²H detection allows us to readily separate the signal from ¹H nuclei which relax by ¹H-¹H dipolar coupling (note that ¹H relaxation would be mediated by ¹H nuclei in the surrounding water as well as that of the neighboring protein nuclei ⁵⁰).

Figure 1.

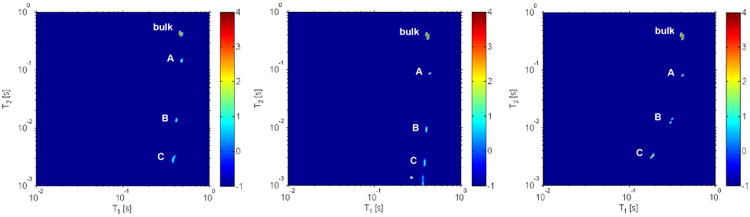
2D ILT map of the ²H T₁ – T₂ experiment performed on untreated (left), collagenase (middle), and EDTA (right) treated intact bone at 22 °C. In all three measurements four peaks are observed. Note that in the middle figure the peak denoted with a * is likely an artifact. In this figure the color bar to the right, denoting signal intensity in arbitrary units, is on a logarithmic scale.

Bone has a complex composite structure allowing for different environments for water, which include pores in between the mineral and collagen matrix. The peak denoted A, with T₁ and T₂ values of 475 ms and 147 ms respectively was assigned to the water molecules which are present at the surface of the bone sample. To support our assignment an additional experiment was performed by removing the bulk water from the sample tube (supplementary figure S5). This measurements revealed that peak A is greatly suppressed leaving peaks B and C and some residual bulk water (likely from water on the surface the NMR tube). The observation that the relaxation times are shifted with the bulk water removed is described below, and is due to exchange that occurs over times scales longer than 10 ms. Table 1 summarizes the relaxation times observed as well as the relative peak intensity of peaks B, C, and A relative to the sum of their combined intensity.

For ²H nucleus of ²H₂O the ²H-¹H and ²H-²H dipolar interactions are negligible and the NMR relaxation times are dominated by the quadrupolar interaction. The T₁ and T₂ are given by

$$\frac{1}{T_1}=\frac{3{\pi }^2}{20}{C}_{Q_{\mathit{\text{eff}}}}^2[2J({\omega }_0)+8J(2{\omega }_0)]$$ (1)

$$\frac{1}{T_2}=\frac{3{\pi }^2}{20}{C}_{Q_{\mathit{\text{eff}}}}^2[3J(0)+5J({\omega }_0)+2J(2{\omega }_0)]$$ (2)

In the above equation, ω₀ is the Larmor frequency of the deuterium nucleus and $C_{Q_{\mathit{\text{eff}}}}=\frac{e^2{q}_{\mathit{\text{eff}}}Q}{h}\mathrm{\Gamma }$ is the effective quadrupolar coupling constant where, Γ is a motional averaging parameter. The spectral density in these equations is defined by $J(m\omega )=\frac{{\tau }_c}{1+{(m\omega {\tau }_c)}^2}$, where τ_c denotes the correlation time of the nuclear spin and surrounding electric field gradient. For ²H nucleus of ²H₂O, this correlation time is intramolecular in origin and allows for a probe of the rotational motion of a given water molecule. In the above formalism it is assumed that the molecular motion of the D₂O exhibits fast oscillatory motion and slower diffusional process⁵¹. According to Lang et al., in the short time, reorientational motion of a given water molecule consists of fast librations about an equilibrium orientation in a random network of surrounding water molecules. In the present system the network includes the collagen protein or apatite mineral. In longer time scales, the slow diffusive motion will lead to changes in the orientation of the water molecule and thereby it will rearrange with respect to the surrounding network which includes collagen and hydroxyapatite. In this model, one assumes the cross-correlation between the two relaxation pathways is separable, as fast librational motion occurs on a much shorter time scale compared to diffusive motion⁵¹.

Using the theoretical formalism described above, the correlation time of the water molecules were determined by the ratio of the two relaxation times T₁ and T₂ and are summarized in Table 1. The observed relaxation times for peaks B and C are characteristic of anisotropic tumbling as T₁ > T₂. Additionally, the correlation time for water molecules in reservoir C (6.85 ± 0.95 × 10⁻⁸s) is approximately a factor of 2 greater than that of water molecules in reservoir B (3.19 ± 0.27 × 10⁻⁸s). We point out that the correlation time for the bulk water was not reported, as the method for determining a correlation time via the ratio of T₁ and T₂ is inapplicable when T₁=T₂. To obtain information about the activation energy for tumbling motion of different water reservoirs (i.e., peak B and C) inside the bone matrix, additional T₁ – T₂ experiments were carried out in the temperature range from 2 to 40 °C (data not shown). We found that the trend observed in these variable temperature experiments appeared to indicate a reduction in the correlation time of peak B with increasing temperature, whereas the data for peak C were quite scattered. Although we attempted to fit an Arrhenius expression to these data, the fit was poor and suggestive of a phase change.

Previous studies showed that water present in bone can be both mobile and tightly bound^{3,16,17,21,52}. Horch et al. performed a¹H 2D T₁ – T₂ experiment on human cortical bone and they observed several peaks¹⁷. Their work highlighted two short lived T₂ components with T₂ values of 60 and 400 μs at 4.7 T arising from collagen side chain or methylene protons and collagen bound water, respectively, whereas the long T₂ component arises from pore water. They also carried out T₂ – T₂ relaxation exchange spectroscopy (REXSY) and observed a cross peak between the short relaxing T₂ components with a mixing time of 200 ms but they remain isolated from the long lived protons. Unal et al. recently employed Raman spectroscopy to study bound and unbound bone water following drying and exchange of water by ethanol or deuterium ⁵². By analyzing the different Raman–OH stretch bands they were able to identify different water compartments i.e., unbound water and water bound to either the collagen or mineral sites. Their work suggested that water molecules are mainly bound to the collagen and a small portion to the mineral phase. Previous NMR studies on bone water have allowed for differentiating the details of collagen bound and mobile water¹⁶, and in addition, water in proximity to the mineral matrix⁵³.

To provide further insight into the environments of the different water reservoirs in cortical bone we systematically exposed the samples to EDTA or collagenase. It is expected that collagenase will partially digest the collagen and EDTA treatment will demineralize the bone and thereby affect the population of water in these respective reservoirs that are observable and distinguishable on the NMR time scale. Without EDTA or collagenase treatment we find an almost equal intensity of water in sites B and C (0.23 and 0.15 respectively). The observation of almost equal concentration of water in the two sites appears to correlate with the concentration of collagen and mineral in bone which is known to be approximately equal (reported % by volume) ²⁹.

Similar to the untreated bone sample (figure 1), four water peaks are observed including the bulk water signal in the EDTA or collagenase treated samples. Due to this treatment, a change is observed in the relative population of the different peaks resolved in the T₁-T₂ map (Table 1). Compared to the population present in untreated bone sample, when the collagenase treatment is performed the relative intensity of peak C is reduced by 40 %, whereas the EDTA treatment decreases the population of peak B 17.4 %. This observation indicates that the peaks denoted B and C result from water present in mineral rich and collagen rich environments, respectively. Additionally, the EDTA treatment modified the surface of the outer surface of the bone sample as well (this was observable macroscopically with the naked eye) and changes were observed for both the correlation times and populations for peak A. Furthermore, ¹³C MAS NMR spectra of collagenase and EDTA treated bone samples (supplementary figure S6) verified that the collagenase treatment worked well as the intensity of all the spectroscopically resolvable ¹³C peaks are greatly reduced after collagenase treatment. Though the cross-polarization experiment is not quantitative, the intensity of the carboxylic carbon is reduced by 20 % compared to the EDTA treated bone sample. Our measurements also indicate changes in the T₁ and T₂ relaxation times following EDTA or collagenase treatment. We suspect that this may be due to the additional crystallites or collagen fragments in the reservoirs denoted A, B, and C following each respective treatment and as a consequence should not be interpreted quantitatively.

T₂ – T₂ Experiments on Untreated Bone Samples

Figure 2 represents the 2D ILT maps of T₂ – T₂ exchange experiments that were performed using mixing times ranging from 100 μs to 10 ms at 22 °C. Similar to the T₁ – T₂ experiments, three peaks (A, B and C) and bulk are observed. This experiment allows the study of exchange between the various water sites and the appearance of cross peaks in the T₂ – T₂ map is a signature of exchange during the mixing time. However, no cross peaks are observed indicating no exchange over the time scales probed. Additionally, the T₂ values measured here appear slightly larger than that observed in T₁ – T₂ experiments —this could be due to slow exchange with the bulk D₂O. However, the ability to measure the exchange at longer time scales beyond 10 ms is challenging due to the short T₂ relaxation times.

Figure 2.

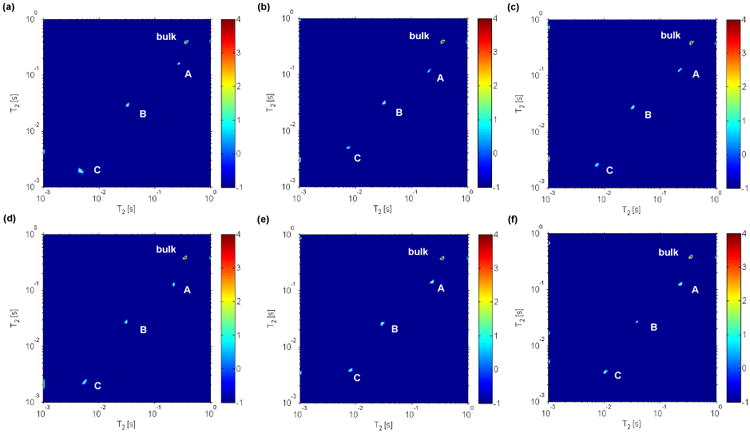
2D ILT map of ²H T₂ – T₂ exchange experiments performed on untreated intact bone at 22 °C. In the experiments the mixing time t_m (supplementary figure S1) was experimentally varied as follows (a) 100 μs, (b) 500 μs, (c) 1 ms, (d) 2 ms, (e) 3 ms and (f) 10 ms. No cross peaks are observed over the times probed which would indicate slow or little exchange between different sites. In this figure the color bar to the right, denoting signal intensity in arbitrary units, is on a logarithmic scale.

T₁–T₂ and D-T₂ Measurements: Fracture, Mechanical Wear, and Load Bearing Studies

T₁ – T₂ experiments were performed on fractured bone and similar to the intact bone sample four water peaks were visible in the 2D ILT map (figure not shown). The observed T₁ and T₂ values and the correlation times (τ_c) are tabulated in table 2. A reduction in correlation time for peak B and C is observed compared to that of the intact bone sample. Because the correlation time appearing in equations 1 and 2 is intramolecular in origin, the reduction in τ_c indicates that the water tumbling motion increases when the bone is fractured. Fracturing of bone may decrease the interaction of water molecules to the collagen and mineral matrix and thereby increase water mobility. However, no change in τ_c is observed for peak A, which again strengthens our interpretation that peak A corresponds to surface water. We note that the population of peak A decreases slightly following fracture from 0.62 to 0.51. The changes in the relative populations in fractured bone should not be interpreted quantitatively as the size of the fractured fragments we used were smaller than that of the intact bone studied (we expect that the relative population should increase as the surface area of the fragments following fracture are greater than the initial size of the sample).

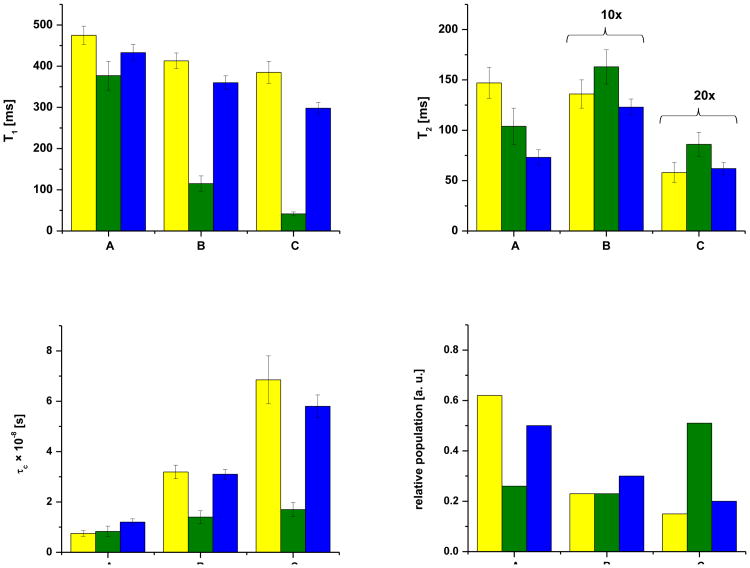
Additional T₁ – T₂ experiments were performed after inducing mechanical wear on the bone with a scalpel and when the bone sample was placed under an applied load. The observed T₁ and T₂ values, correlation times, and the relative population of the peaks deduced from these measurements are tabulated in Table 2. We note that the damage induced by mechanical wear with a scalpel is likely not a realistic model of wear that occurs physiologically, but probes the effects of acute wear or damage. As in the case of fractured bone, following mechanical wear on the surface a reduction in correlation time is observed for peak B and C compared to that of the intact bone sample. The findings resulting from measurements of bone under an applied load are highlighted graphically in Figure 3; the correlation times of peak B and C decrease (Table 2 and Figure 3). However, the reduction in τ_c for peak C is much higher compared to fracturing the bone or after mechanical wear. This behavior would suggest that when bone is exposed to an external force the collagen is more significantly altered or deformed. This deformation may lead to the breaking of hydrogen bonds between water molecules and collagen which result in changes in the tumbling motion of localized water. An additional key finding of these measurements is that the population of water in the collagen rich site increases from 0.15 to 0.51 when bone is placed under a mechanical load, whereas the population of the mineral rich site does not change. The same measurement revealed, as expected, that the population of surface water is altered (decreases from 0.62 to 0.26) when a force was applied. This observation resulted from the fact that two nylon screws were used to compress the bone which altered its surface area.

Figure 3.

T₁, T₂, τ _c, and relative populations of the water reservoirs denoted A, B and C (see figure 1) in bone without an applied force (yellow), under an applied load (green) and when the applied force was removed (blue).

A T₁ – T₂ experiment was also performed on the bone sample 23 days after releasing pressure (Table 2 or Figure 3). We observed that changes in the correlation times and populations of water were somewhat reversible to their initial values without an applied force. The finding that the populations and dynamics of water are altered more so at the collagen rich site under mechanical load suggest that much of the load bearing occurs therein, and not at the mineral rich sites. This behavior is reversible and indicates that the flexibility of bone is largely due to collagen.

It is known that dehydration significantly affects the mechanical properties of bone^9,10,18,54. Water in bone may form hydrogen bonds with the collagen or mineral matrix or hydrogen bonded water bridges. The role of water in fracture resistance of dentin, a bio-composite with structure comparable with bone, has been studied⁵⁵. Following chemical dehydration with different solvents (e.g., acetone, ethanol, methanol which form weaker hydrogen bonds), Nalla et al. suggested the hydrogen bonded network or hydration states and may increase the material strength, stiffness, and fracture properties. However, the hydrogen bonding of water plasticizes collagen leading to lower strength, stiffness, and fracture resistance⁵⁵. To follow the strain level in bone (tissue, fibrils and mineral particle) Gupta et al. used in situ tensile testing with combined synchroton X-ray diffraction and scattering⁵⁶. Their work showed that the structural arrangement at the nanoscale leads to deformation and that the collagen matrix plays an important role in strain transfer to mineral platelets⁵⁶. Our study shows that fracture and/or mechanical wear increases the mobility of water molecules inside the bone as the correlation times of peak B and C are observed to decrease. Thus, this study provides additional insight that water mobility in bone may be used as a local probe of microscopic fracture which may be challenging to observe with current methods. For example, one might envision applying these methods in a spatially resolved two dimensional ¹H T₁-T₂ measurement to probe local microscopic fracture and mechanical wear in bone.

Two dimensional diffusion–T₂ experiments were performed on the fractured bone at 22 °C. Figure 4 shows the 2D ILT map, where four water peaks are visible as observed in previous experiments. The observation of four peaks with diffusion coefficients on the order of μm²/ms eliminates the possibility that any of the peaks observed in the T₁ – T₂ and T₂ – T₂ experiments raised from ²H exchange with ¹H protein nuclei. As the diffusion–T₂ experiment was carried out in a different magnetic field a slightly different T₂ is observed compared to T₁ – T₂ experiments. The measurement of diffusion for short T₂ components e.g., peak C (T₂ = 5 ms in fractured bone) is experimentally challenging as it requires strong gradient pulses to encode and decode the grating to track diffusion. Fernandez et al. studied the dynamics of osteoid water exchange (i.e., exchange of water by D₂O) by NMR and reported the apparent diffusion coefficient of water in cortical bone of rabbit to be (3.56 ± 0.78) × 10⁻⁷ cm²/s at 25 °C³. In bone, the diffusion of water presumably takes place through the pores, i.e., Haversian canals, lacunae, canaliculi etc. However, in their study they observed a significant amount of water with slower diffusion than that of the major water fraction passing through the pores mentioned above, monitored from the slow exchange rate. The water molecules with slow apparent diffusion coefficients are associated to the collagen or mineral sites and diffuse along the micropores present in collagen-hydroxyapatite matrix. Diffusion of water molecules associated with the mineral rich environment is faster compared to that of the collagen rich environment (peak B, D=1.76 ± 0.06 μm²/ms and peak C, D=0.62 ± 0.07 μm²/ms). A possible reason for the reduction in transport may arise from diffusion being hindered due to the strong affinity between water and collagen. Given these diffusion coefficients it is worthwhile to provide a spatial dimension probed by the T₁ – T₂ measurements. For peak B the diffusion coefficient is approximately 1.76 μm²/ms and over a time scale of T₂ (T₂ = 13.6 ms) the spatial dimension we probe is $\mathrm{\Delta }\mathrm{r}=\sqrt{6\mathit{\text{Dt}}}\simeq 12\mu \mathrm{m}$. For peak C the diffusion coefficient was lower, D = 0.62 μm²/ms, and over a time scale of T₂ (T₂ = 2.9 ms) the spatial dimension probed is approximately Δr (≃) 3μm.

Figure 4.

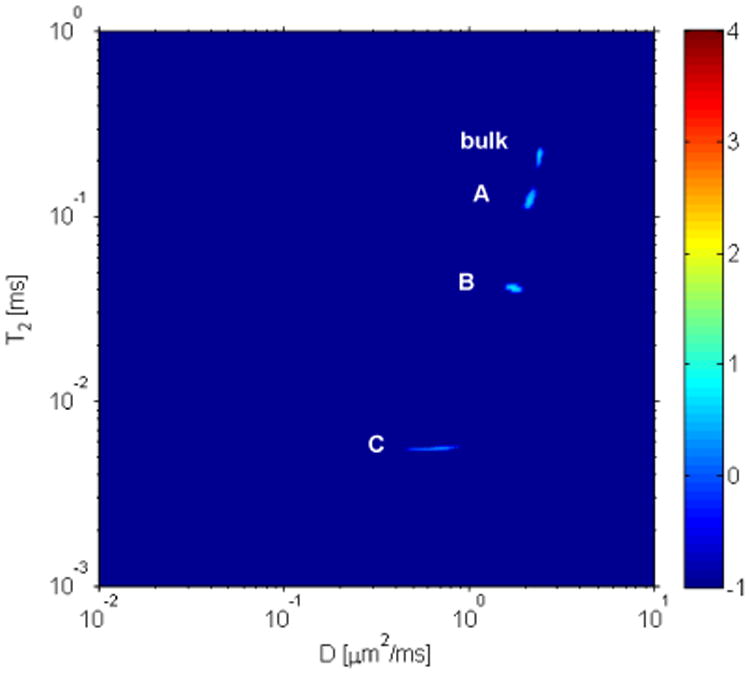
2D diffusion-T₂ correlation map of fractured bone soaked in D₂O for 30 days. As discussed in the text, four distinguishable components of water were observed. Note that the measured T₂ values are slightly different than that in the T₁ – T₂ and T₂ – T₂ as the Larmor field was slightly different. The measured diffusion coefficients are tabulated in table 2. In this figure the color bar to the right, denoting signal intensity in arbitrary units, is on a logarithmic scale.

Water, arguably the most ubiquitous molecule found in biological tissue, is known to mediate macromolecular ordering via hydrogen bonding or electrostatic interactions, especially in collagen. Recently, Fathima et al. showed that the extent of cross linking in collagen samples modified by different chemical agents alter significantly the dynamics of bound water on the NMR time scale⁵⁷. Libonati et al.⁵⁸ performed molecular dynamic simulations in a collagen-hydroxyapatite nanocomposite (in both dry and wet cases). Their work showed that the hydrogen bonds between collagen and hydroxyapatite play an important role in fracture resistance. In their model, they showed that confinement leads to breaking of intramolecular hydrogen bonding, whereas inter-molecular hydrogen bonds undergo continuous formation and breakage. In their simulation, water present in bone forms a network of hydrogen bonds, and in the confined state, the progressive formation and breakage of hydrogen bonds acts as an energy dissipation mechanism. The observation that the NMR T₂ relaxation times of water may be used to study the volume of bound and pore water in cortical bone and report on fracture characteristics has been reported recently elsewhere²⁸. In our study, we have observed the changes in localized water dynamics and relative populations in bone due to fracture or mechanical wear, and when bone is under an applied force. Our observations suggest that water dynamics can be used to follow structural changes of collagen as bone undergoes alteration or deformation under stress, fracture, or mechanical wear.

Conclusions

In this work we have measured the tumbling correlation times, diffusion coefficients, population and exchange of water in goat cortical bone by 2D ²H T₁ – T₂, T₂ – T₂, and diffusion–T₂ NMR methods. Collagenase or EDTA treatment allowed for assigning the different water reservoirs revealed in our relaxation measurements to a collagen or a mineral rich environment of the bone matrix. Our T₂ – T₂ correlation measurements indicate these sites are relatively isolated as no exchange was observed over time scales from 1 ms to 10 ms. Lastly, T₁ – T₂ experiments were performed on fractured bone, bone under mechanical wear, and under applied force revealing dynamical and population changes of the various sites. These measurements revealed that load bearing occurs largely in the collagen rich site, and that the changes in relative populations and dynamics of water may serve as a local probe of microscopic fracture which may be challenging to probe with other methods. While this study focused on goat cortical bone, we believe the findings would be the same across cortical bones from other mammalian subjects as the bone structures are similar⁵⁹.