Powerful set-based gene-environment interaction testing framework for complex diseases

Abstract

Identification of gene-environment interaction (GxE) is important in understanding the etiology of complex diseases. Based on our previously developed Set Based gene EnviRonment InterAction test (SBERIA), in this paper we propose a powerful framework for enhanced set-based GxE testing (eSBERIA). The major challenge of signal aggregation within a set is how to tell signals from noise. eSBERIA tackles this challenge by adaptively aggregating the interaction signals within a set weighted by the strength of the marginal and correlation screening signals. eSBERIA then combines the screening-informed aggregate test with a variance component test to account for the residual signals. Additionally, we develop a case-only extension for eSBERIA (coSBERIA) and an existing set-based method, which boosts the power not only by exploiting the G-E independence assumption but also by avoiding the need to specify main effects for a large number of variants in the set. Through extensive simulation, we show that coSBERIA and eSBERIA are considerably more powerful than existing methods within the case-only and the case-control method categories across a wide range of scenarios. We conduct a genome-wide GxE search by applying our methods to Illumina HumanExome Beadchip data of 10,446 colorectal cancer cases and 10,191 controls and identify two novel interactions between NSAIDs and MINK1 and PTCHD3.

Introduction

Common diseases such as cancer, diabetes and cardiovascular diseases result from a complex interplay of genetic (G) and environmental (E) factors. For most of these diseases, several environmental factors and a rapidly increasing number of genetic factors have been identified [Hindorff et al., 2009]. However, so far there have been very few findings of gene-environment interactions (GxE). Some exceptions include an observed interaction between smoking and the GSTM1 deletion and a tag SNP in NAT2 in bladder cancer [Garcia-Closas et al., 2005; Rothman et al., 2010], ADH7 variants and alcohol consumption in upper aerodigestive cancers [Hashibe et al., 2008], GRIN2A variants and coffee consumption in Parkinson's disease [Hamza et al., 2011] and our recent finding of GATA3 variants and processed meat consumption in colorectal cancer [Figueiredo et al., 2014]. Several aspects could contribute to the lack of GxE findings, including, for the environmental factors, measurement error and lack of optimal data harmonization across studies. In addition, the statistical power to detect an interaction is much smaller than to detect a main effect, requiring approximately four times as many subjects are needed to detect a main genetic effect of comparable size [Smith and Day, 1984].

To enhance the power to detect GxE, many methods have been proposed and can be broadly categorized into two groups. The first, which encompasses most existing methods, is focused on increasing the power to detect GxE for a single variant. These methods include the case-only test [Chatterjee and Carroll, 2005; Piegorsch et al., 1994], the empirical Bayes method [Mukherjee and Chatterjee, 2008], and the Bayesian Model Averaging method [Li and Conti, 2009]. Within this category, two types of screening methods have also been proposed to reduce the multiple testing burden in genome-wide GxE search: correlation-based screening [Murcray et al., 2009] and marginal association-based screening [Kooperberg and LeBlanc, 2008].

Toward this end, several recent methods have been developed to use and combine existing screening and testing approaches, such as the hybrid method [Murcray et al., 2011], Cocktail method [Hsu et al., 2012] and EDGx [Gauderman et al., 2013].

The second group of methods aims at increasing power by performing a set-based GxE test. A set-based test can enhance the power not only by aggregating multiple GxE signals in the same set, but also by greatly reducing the multiple-testing burden. As large-scale sequencing studies are increasingly being conducted, there is a great interest in testing GxE on rare variants, which makes set-based methods necessary. Tzeng et al. (2011) developed a method to test for interaction between a set of variants and an environmental variable for a continuous outcome using the set-based genetic similarity method [Tzeng et al., 2011]. Lin et al. (2013) proposed a set-based GxE test called GESAT by extending the SNP-set Kernel Association Test (SKAT) to the GxE setting for both continuous and categorical outcomes [Lin et al., 2013]. GESAT assumes random GxE effects following a mean 0 distribution with variance t². Testing GxE for a set of variants is equivalent to testing a zero variance of t².

When aggregating signals in a set-based test, it is a thorny issue to determine which are the signals and what are the directions of the signals, as not all variants in a set have GxE and if those that have GxE, the directions can be positive or negative. Differing from a typical set-based association test, the set-based GxE tests have the advantage that there exist screening statistics that are informative in revealing the strength and direction of interaction signals but still independent of the interaction test. In an earlier work, we proposed SBERIA to take advantage of this desirable feature of GxE by exploiting the established correlation and marginal screening to determine which variants to choose and the direction of their effects, while aggregating genotypes within a variant set [Jiao et al., 2013]. As the screening statistics are independent of the interaction test, conventional logistic regression can be used to test the hypothesis without resorting to permutation to adjust for the data adaptive weight.

Although we showed that SBERIA provided attractive power compared to benchmark methods, it also has limitations. SBERIA requires specifying a p-value threshold to determine which variants to include in the aggregation. In practice, it can be difficult to find a cutoff that achieves optimal power. In addition, SBERIA gives each variant a weight of 1, −1 or 0, which does not take into account the difference in signal strengths among variants. Furthermore, SBERIA excludes the variants that are not selected based on screening. However, since the screening is not perfect, those variants can still contain useful information. Hence, power could potentially be increased by combining SBERIA with other tests to retrieve some or all of the remaining signals.

In this paper, we aim to address the aforementioned limitations of SBERIA. We propose a new method, enhanced SBERIA (eSBERIA), using more nuanced variant weights instead of 1, −1, and 0 and combining SBERIA with the variance component test to achieve a more powerful and robust performance. In addition, we propose a case-only version of the new test (coSBERIA). In the single variant GxE test, the case-only test has been shown to be more efficient than the conventional case-control test by exploiting the G-E independence assumption [Chatterjee and Carroll, 2005]. In set-based GxE tests, the case-only analysis is even more advantageous because it not only exploits the G-E independence assumption, but also avoids the need to include a large number of G's as main effects. We compared eSBERIA and coSBERIA with existing methods through extensive simulations under a wide range of scenarios. We also applied our methods to Illumina HumanExome Beadchip data with 10,446 colorectal cancer cases and 10,191 controls from the Genetics and Epidemiology of Colorectal Cancer Consortium (GECCO) to identify novel genome-wide gene-based interactions.

Methods

Notation and Models

Suppose there are N subjects and their disease status is denoted by D_i (=0 or 1) for subject i, i=1, ..., N. Assume E_i is the environmental factor X_i = (X_i1,...X_iq)is a vector of q potential confounder covariates, and G_i = (G_i1,...G_ip) is a vector of p genetic variants. The interaction model between the set of p variants and the environmental factor is:

$$logit\left({\pi }_i\right)={\alpha }_0+E_i{\alpha }_1+{\mathbf{G}}_{\mathbf{i}}{\alpha }_2+{\mathbf{X}}_{\mathbf{i}}{\alpha }_3+E_i{\mathbf{G}}_{\mathbf{i}}\beta ,$$ (1)

where logit(.) is a logit link function, π_i = P(D_i = 1), α₀ is the intercept, α₁ is the coefficient for the main effect of E_i, α₂ is the px1 vector of coefficients for G_i, α₃ is the qx1 vector of coefficients for X_i, E_iG_i = (E_iG_i1,...E_iG_ip), and β = (β₁,...,β_p)^T is the px1 vector of interaction coefficients. The null hypothesis for interaction effects is H₀ : β = 0.

SBERIA

SBERIA uses the screening statistics (G and E correlation screening or marginal association screening of G with disease risk, whichever is more significant) as a guide to aggregate the genotypes. Specifically, SBERIA first selects variants for which the strength of the screening signal is greater than a threshold. For the selected variants, a weighted sum of their interaction terms is computed, where the weight=1 if the screening statistic is positive and −1 otherwise. As the screening statistics, both marginal association [Dai et al., 2012] and G and E correlation [Murcray et al., 2009] are independent of the interaction test, conventional logistic regression can be used to test the interaction without requiring permutation [Jiao et al., 2013].

eSBERIA

As described in the Introduction, SBERIA can be improved in several aspects. Suppose E_i is a binary variable (we will focus on binary environment variables in this paper; the extension to a continuous E is trivial). First we test the marginal association of each variant in the set G_ij (j=1 to p) with D_i and the correlation between each variant with E_i using logistic regression without conditioning on other variants and GxE interactions. Note that covariates can be straightforwardly adjusted for in the logistic regression model. Depending on the context of the studies, investigators may want to adjust for covariates such as study, age, sex, and principal components to account for population sub-structure when calculating the screening statistics. For each variant j, we denote the marginal-screening statistic by M_j and the correlation-screening statistic by C_j. Then we fit the following logistic regression:

$$logit\left({\pi }_i\right)={\alpha }_0+{\alpha }_1{E}_i+{\mathbf{G}}_{\mathbf{i}}{\alpha }_2+{\mathbf{X}}_{\mathbf{i}}{\alpha }_3+\rho E_i{\mathbf{G}}_{\mathbf{i}}\widehat{\mathbf{w}},$$ (2)

where ŵ = (ŵ₁,...ŵ_p)^T is the weight vector and ŵ_j = M_j if |M_j |>| C_j and otherwise ŵ_j = C_j. The hypothesis of interest is H₀ : ρ = 0 and the Wald statistic to test this hypothesis is $\widehat{\rho }∕se\left(\widehat{\rho }\right)$, where $\widehat{\rho }$ is the maximum likelihood estimator. It can be seen that the larger the magnitude of the screening statistics, the higher is the weight assigned to the corresponding variant. This weighting scheme is inspired by the previous findings that marginal and correlation screening statistics are good indicators for the strength of interaction signals [Hsu et al., 2012; Kooperberg and LeBlanc, 2008; Murcray et al., 2011; Murcray et al., 2009]. In addition, the direction of the screening statistics can also inform the direction of the interaction signals [Jiao et al., 2013]. As the screening statistics are independent of the interaction test, the regular Wald test is valid without requiring permutation [Jiao et al., 2013].

However, these screening statistics may not capture the signals of all the interaction effects, because various factors such as the type of interaction (qualitative vs. quantitative), limited sample size and rare variants could make the signals for the interaction sometimes difficult to capture. To account for residual effects that may have been missed by (2), we adopt a similar idea to that in Sun et al. (2013) to test for the remaining signals [Sun et al., 2013]. Specifically, we used the following variance component SKAT statistic:

$$\sum _{j=1}^{p}w{t}_j{\left\{\sum _{i=1}^n{E}_i{G}_{ij}(D_i-{\widehat{\pi }}_i)\right\}}^2,$$ (3)

where wt_j is the weight for the jth variant and ${\widehat{\pi }}_i$ is the predicted value for D_i from model (2). The weight wt_j can be equal or different for each variant. SKAT sets the default weight to be the density of a Beta distribution with shape parameters 1 and 25 for a given MAF, which is denoted by Beta(MAF;1, 25). This weight function is powerful when the effect of the variant is inversely proportional to the MAF. For simplicity of presenting the main idea of eSBERIA, we use the SKAT default weight, Beta(MAF;1, 25), in the simulation and the real data application, nothing that investigators can easily plug in a different weight function. As the aggregated interaction effect ρ in (2) has been adjusted for in (3), the SKAT statistic and the Wald test for H₀ : ρ = 0 are independent (see the proof in Appendix) so the p-values from the two tests can be combined via Fisher's method.

coSBERIA

As mentioned before, the case-only GxE test for a single variant boosts the power by exploiting the gene-environment independence assumption. Thus, it is expected that the case-only test would also increase power for a set-based GxE test. Another unique advantage of the case-only test for set-based GxE is that it does not require specifying main effects for G. As pointed out above, including main effects for a large number of variants can potentially lead to convergence issues [Lin et al., 2013], which is particularly an issue for rare variants and usually requires sophisticated statistical methods such as regularization or variance component tests to solve. Because case-only test does not estimate the main effects for G, it naturally circumvents the issue.

Similar to eSBERIA, we propose to combine the SBERIA and SKAT tests for the case-only test. First, we fit the following case-only model:

$$logit\left\{P(E_i=1\mid D_i=1)\right\}={\alpha }_0+{\mathbf{X}}_{\mathbf{i}}{\alpha }_1+\tau {\mathbf{G}}_{\mathbf{i}}M,$$ (4)

where M = (M₁,...M_p)^T is the weight vector and M_j is the marginal association screening statistic. The hypothesis of interest is H₀ : τ = 0. Note that we do not include the correlation screening here in the weight because it is not independent from the case-only interaction test [Dai et al., 2012; Hsu et al., 2012], and the inclusion of correlation screening will lead to an inflated type I error.

Then we use the following SKAT to test for the remaining interaction effects within cases:

$$\sum _{j=1}^{p}w{t}_j^E{\left\{\sum _{i=1}^n{G}_{ij}(E_i-{\widehat{\pi }}_i^{E\mid D=1})\right\}}^2$$ (5)

where $w{t}_j^E$ is the default SKAT weight for the jth variant and ${\widehat{\pi }}_i^{E\mid D=1}$ is the predicted value for E_i in cases from model (4). Again, the p-values from the SBERIA test and SKAT test are combined by Fisher's method.

Methods for comparison

We will compare the performance of eSBERIA with SBERIA [Jiao et al., 2013] and GESAT [Lin et al., 2013], both of which have been shown to be more powerful than the benchmark methods such as the likelihood ratio test and the minimum p-value method under a wide range of scenarios. Thus, we do not include those benchmark methods in the comparison in this paper. We also evaluate the performance of the case-only tests. The case-only approach essentially tests the association between the binary E variable and the set of genetic variants in cases. Therefore, previous set-based methods such as Sun et al. (2013) for testing the association between disease risk and a set of variants can be applied without additional modification. We have shown previously that the burden test does not perform well in GxE settings because it is not reasonable to assume the interaction effects of all the variants in a set are in the same direction [Jiao et al., 2013]. Hence, in addition to coSBERIA, we will consider the case-only version of SKAT-O test [Lee et al., 2012] and denote it by coSKAT-O. SKAT-O test was a popular test proposed for set-based marginal association test of rare variants. Like coSBERIA, coSKAT-O is also a combination of the burden test and the SKAT variance component test. By taking advantage of the screening statistic, we expect coSBERIA to be more powerful than coSKAT-O.

Simulation

The increasing popularity of set-based methods is driven mainly by the need for increasing power when testing the associations between rare variants from sequencing studies and outcomes of interest. Thus, in this paper we focus on evaluating the performance of various set-based GxE methods in the rare variant setting.

In the simulation, the disease status was generated based on the following model:

$$logit\left\{P(D_i=1)\right\}={\alpha }_0+\gamma E_i+\sum _{j=1}^p{\alpha }_j{G}_{ij}+\sum _{j=1}^p{\beta }_j{E}_i{G}_{ij},i=1,\dots n;$$ (6)

where α₀ = exp(−5) denoting a relatively rare disease; γ = log(1.2) is the effect size for the environmental factor E_i; E_i is assumed to be a binary variable with frequency 0.3; p is the number of variants in the set; G_ij is the genotype of variant j in sample i; α_j's and β_j's are the main effects and interaction effects, respectively. For each simulated dataset, we generated a large population based on model (6) and randomly selected 2000 cases and 2000 controls. All parameters and variables were randomly generated for each simulated dataset. For each scenario, we generated 2,000 simulated datasets.

Type I error rate

We generated datasets under the null model of no interaction between any variant in the set and E. Specifically, we generated p (=10, 20, 40) variants G_ij (j=1 to to p) with MAF_j ~Uniform(0.001, 0.05) under Hardy-Weinberg equilibrium. The main genetic effects α_j in (6) were generated as α_j ~ Normal(0,log(1.5) / 2) β_j's in (6) were set to 0. All five methods (SBERIA, eSBERIA, GESAT, coSBERIA, coSKAT-O) were used to test the interaction between the set of variants and E based on the generated dataset and the results (p-values) were recorded. The type I error was estimated based on significance level α =0.05. Case-only approaches are known to yield inflated type I error when the gene-environment independence assumption is violated. Hence, we also conducted simulations where E_i and G_ij's are correlated: $\mathrm{logit}\left(P(E_i=1)\right)=\mathrm{logit}\left(0.3\right)+{\sum }_{j=1}^p{\lambda }_j(G_{ij}-2MA{F}_j)$, where λ_j = Normal(0,log(1.5)/2)* Bernoulli(0.5)

Power

We used five models to generate datasets for the evaluation of power.

1. Model 1: p (=10, 20, 40) variants G_ij (j=1 to p) were generated with MAF_j ~ Uniform (0.001, 0.05) under Hardy-Weinberg equilibrium. We set a background main effect for each variant as α_j ~ Normal(0,log(1.5) / 2). The interaction effects β_j's in (6) were generated as c*|log10(MAF_j)|* Bernoulli(P_causal) *{1-2* Bernoulli(P_negative)} where P_causal =0.2, 0.5, 0.8 and P_negative =0.5, 0.5. In other words, every variant had probability P_causal of having interaction effect, and if the variant had the interaction, the direction of the interaction effect had probability P_negative of being negative. IN addition the rarer variants had larger effect sizes [Wu et al., 2011]. For the variants with an interaction effect, the main effects were set as 0, representing a synergistic interaction model. In order to see differences among methods, c was chosen such that the resulting power was neither too high nor too low. Hence the value of c can be different for different scenarios and the actual power is not comparable across scenarios but for each scenario the methods are directly comparable.

2. Model 2: The same simulation settings were used as in Model 1 except that for the variants with interaction effects (β_j ≠ 0), the corresponding main effects were set to be −0.5β_j, which represents a qualitative interaction model because the main effect is in opposite direction to the interaction effect.

3. Model 3: The same simulation settings and a synergistic interaction model were used as in Model 1 except that the MAF_j's were generated from the MAF distribution observed in the GECCO HumanExome Beadchip data (see the next section for a detailed description). We limited the range of the MAF distribution to 0.001 - 0.05, as in Model 1.

4. Model 4: The same simulation settings and a qualitative interaction model were used as in Model 2 except that the MAF_j's were generated from the exomechip MAF distribution.

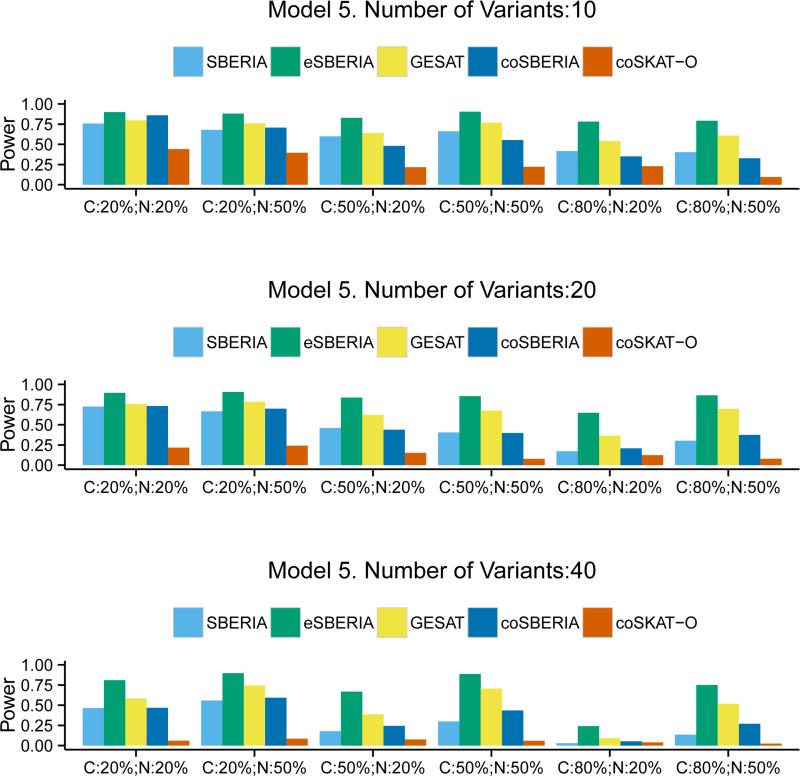
5. Model 5: The same simulation setting was used as in Model 1 except that E_i and G_ij's are correlated: $\mathrm{logit}\left(P(E_i=1)\right)=\mathrm{logit}\left(0.3\right)+{\sum }_{j=1}^p{\lambda }_j(G_{ij}-2MA{F}_j)$ where λ_j = 0.5β_j. We intended to use this simulation scenario to show that the case-only approach can also lose power when there is a correlation between G and E in the direction opposite to the interaction effect.

For each model, SBERIA, eSBERIA, GESAT, coSBERIA, and coSKAT-O were applied to perform the set-based GxE test and their power was estimated based on significance level 2.5×10⁻⁶, which is the significance level when 20,000 genes are tested.

Real data application

We applied all five methods to the Illumina HumanExome Beadchip data in the Genetics and Epidemiology of Colorectal Cancer Consortium (GECCO) to conduct a genome-wide GxE search for three environmental factors: NSAID usage (yes/no), smoking (ever/never), and postmenopausal hormone use (PMH, yes/no). The participants are of European descent and from seven nested case-control and five case-control studies (Supplemental Table I). Each study is described in detail in the Supplementary Materials. CRC cases were defined as colorectal adenocarcinoma and confirmed by medical records, pathologic reports, or death certificates. All participants gave written informed consent and each study was approved by their respective Institutional Review Boards. Study samples were genotyped on the Illumina HumanExome BeadChip using standard protocols. The quality control (QC) procedure is described in detail in the Supplemental Materials. After QC, a total of 10,446 cases, and 10,191 controls were used in the analysis. The environmental factors were harmonized across studies and the harmonization procedure is described in the Supplemental Materials.

We aggregated variants within genes according to the annotation provided by SeattleSeq134 (http://snp.gs.washington.edu/SeattleSeqAnnotation134/). The total number of genes was 17,986. Within each gene, we used variants with MAF<0.05 and minor allele count no less than 10 for the set-based GxE testing. We implemented this lower bound for minor allele count to avoid convergence issues when including very rare variants in the main effect. We also filtered out genes with fewer than three variants or an aggregated MAF less than 0.5%. There were 7,600 genes left after the filtering. We applied all five methods to the 7,600 genes for each of the three environmental variables to identify potential GxE. All analyses were adjusted for study, sex, age, and the first principal components to account for population substructure. We did not adjust for more potential environmental confounders because unless the confounders also interact with the same G, they will not bias the interaction estimate [Vanderweele et al., 2013].

Results

Type I error rate

The results are summarized in Table I. When G and E are independent, all tests maintain the correct type I error. When G and E are correlated, the type I error rates for the two case-only methods (coSBERIA, coSKAT-O) are inflated as expected while the case-controls methods (SBERIA, eSBERIA, GESAT) maintain the correct type I error.

Table I.

Type I error for set-based GxE tests.

	SBERIA	eSBERIA	GESAT	coSBERIA	coSKAT-O
G and E independent
p=10	0.040	0.046	0.050	0.044	0.048
p=20	0.046	0.050	0.053	0.041	0.053
p=40	0.050	0.056	0.054	0.048	0.048
G and E correlated
p=10	0.045	0.046	0.043	0.270	0.150
p=20	0.054	0.053	0.047	0.340	0.216
p=40	0.048	0.054	0.060	0.375	0.302

Power

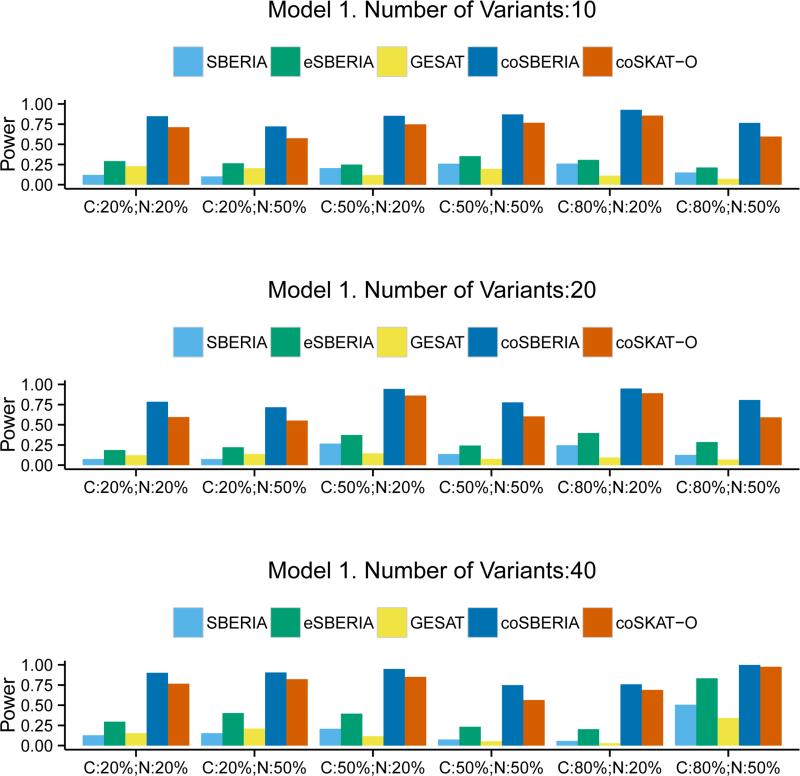
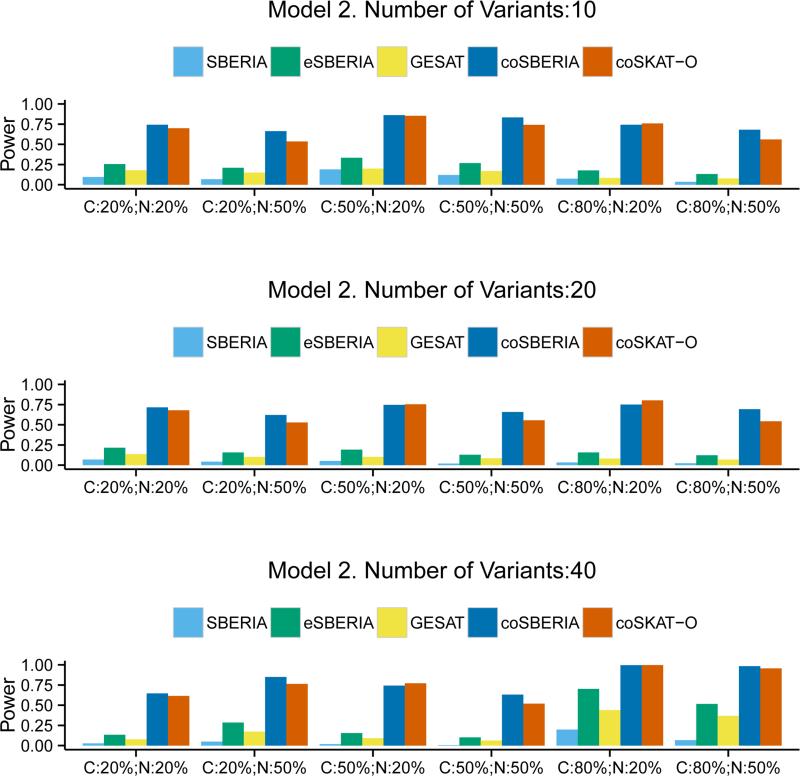
The power comparison results under Model 1 are summarized in Figure 1. The case-only tests are generally much more powerful than the case-control tests. Within the case-controls tests, eSBERIA is always the most powerful test for all scenarios. Compared to GESAT the power gain ranges from 27.7% to 600%. Among the case-only tests, coSBERIA is always more powerful than coSKAT-O. When the interaction model is qualitative (Model 2), Figure 2 shows the clear advantage of eSBERIA in the case-control tests; however the advantage of the case-only test coSBERIA over coSKAT-O is somewhat reduced compared to Model 1. This is because coSBERIA uses marginal screening to guide the aggregation of interaction signals and the marginal signal under a qualitative interaction model is generally weak. In contrast, eSBERIA uses both the marginal and the correlation screening, the latter of which performs well under a qualitative interaction model. Nevertheless, coSBERIA is still more powerful than coSKAT-O under most scenarios.

Figure 1.

Power of SBERIA, eSBERIA, GESAT, coSBERIA, coSKAT-O under Model 1. Different proportion of causal variants (C= P_causal) and proportion of causal variants with negative effects (N= P_negative) were used.

Figure 2.

Power of SBERIA, eSBERIA, GESAT, coSBERIA, coSKAT-O under Model 2. Different proportion of causal variants (C= P_causal) and proportion of causal variants with negative effects (N= P_negative) were used.

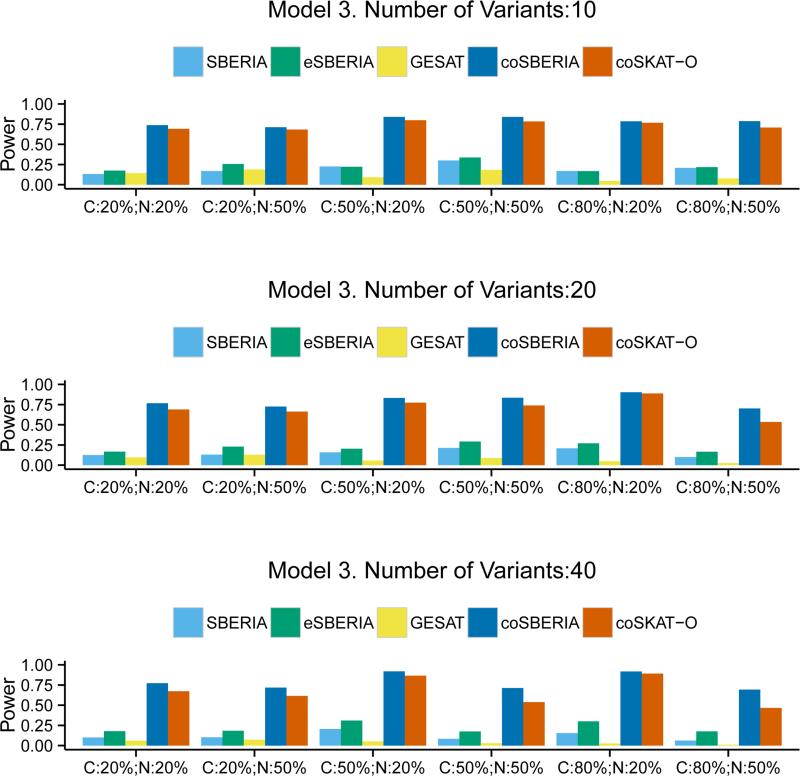
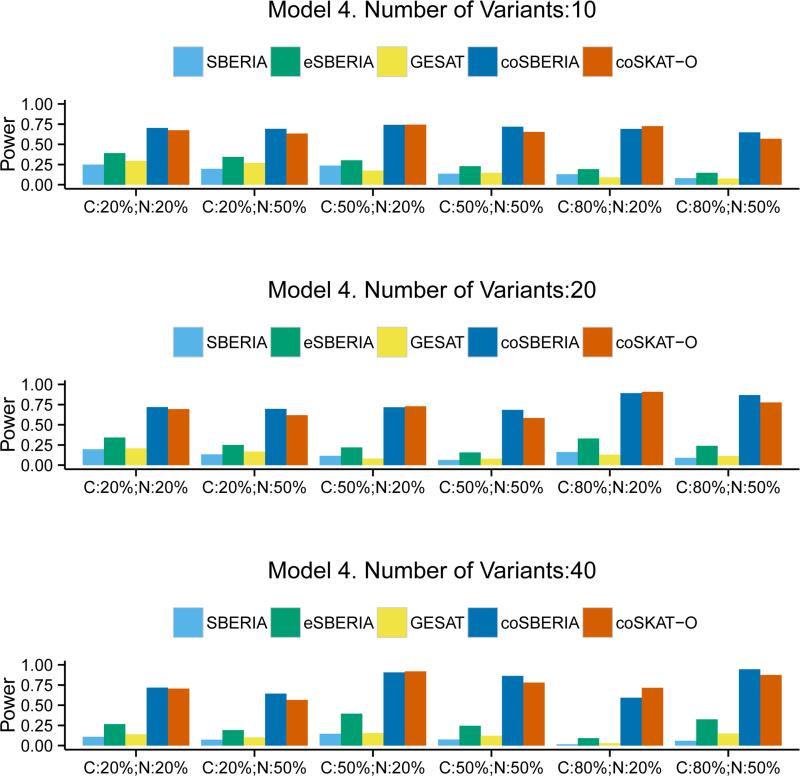
In Models 3 and 4, we mimic the MAF distribution that was observed from the exomechip variants. As shown in the Supplemental Figure 1, the frequency of rare variants is higher than less rare ones. Thus it can be expected that the power of SBERIA methods would be affected because the screening methods do not work as efficiently for very rare variants. Figure 3 confirms that the advantage of SBERIA methods is indeed reduced, especially when the number of variants is small (=10). However, the overall conclusion is still the same: eSBERIA is the most powerful among the case-control methods and coSBERIA is more powerful than coSKAT-O. The power gain ranges from 1.6% to 48.7%. Figure 4, where the interaction model is qualitative, shows that the performance of the two case-only tests becomes similar. eSBERIA still takes a relatively large lead in power compared to the other two case-control tests. When there is an inverse G-E correlation, Figure 5 shows that case-only tests become less powerful than the case-control tests. Regardless, eSBERIA and coSBERIA are still the most powerful tests within their respective categories.

Figure 3.

Power of SBERIA, eSBERIA, GESAT, coSBERIA, coSKAT-O under Model 3. Different proportion of causal variants (C= P_causal) and proportion of causal variants with negative effects (N= P_negative) were used.

Figure 4.

Power of SBERIA, eSBERIA, GESAT, coSBERIA, coSKAT-O under Model 4. Different proportion of causal variants (C= P_causal) and proportion of causal variants with negative effects (N= P_negative) were used.

Figure 5.

Power of SBERIA, eSBERIA, GESAT, coSBERIA, coSKAT-O under Model 5. Different proportion of causal variants (C= P_causal) and proportion of causal variants with negative effects (N= P_negative) were used.

Real data application

First, we constructed the quantile-quantile (QQ) plots for the interaction test p-values from each method against their expected values (Supplemental Figures 2-4). All QQ plots align very well with the 45 degree line indicating the type I error is generally controlled. There is also no overall departure of G and E independence for the three environmental factors; otherwise, the QQ plots for the case-only tests would have been deviated from the 45 degree line.

In the genome-wide NSAIDs x gene interaction tests, we observe two interactions that reach genome-wide significance = 6.6 × 10-6 = 0.05/7600 for any of the five methods (Table II). The first interaction is between NSAIDs and PTCHD3 at 10p12.1 for which eight variants are included in the analysis. Out of 10,446 cases and 10,191 controls, the minor allele counts of these eight variants range from 8 to 1,564 with a total minor allele count of 2,235 (Supplemental Table II). The most significant p-value 2.7×10⁻⁷ is given by eSBERIA. Supplemental Table II shows that eSBERIA gives a large weight to a variant (chr10:27688101) with a strong interaction signal. eSBERIA also gives a very small weight to a variant (chr10:27687775) with the largest number of minor alleles in the set but no interaction signal, which is important because this null variant would otherwise dominate the whole set. We also find that the variant chr10:27688101 with the strongest interaction signal has a significant correlation (p= 1.26e-5) with E but in the opposite direction of the interaction effect. Based on the simulation results from Model 5, this explains why the two case-only tests give less significant values but still reasonably small p-values. The second significant interaction is with the gene MINK1 at 17p13.2 which has four variants. The minor allele counts for the four variants range from 13 to 673 with a total minor allele count of 861 (Supplemental Table III). As it can be seen from Table II, coSKAT-O gives significant results. The p-value for coSBERIA is also very small although not as significant as coSKAT-O. This can be explained by the fact that the variant (chr17:4797910) with the strongest signal in MINK1 was given a small marginal screening weight by coSBERIA (Supplemental Table III). Further investigation shows that the main effect of that variant is in the opposite direction to the interaction effect, which leads to weak marginal signal. Nonetheless, coSBERIA still gives a small p-value because it uses SKAT to account for the residual signals that are missed by the non-informative weighting in this special case. All three case-control tests also give reasonably small p-values with eSBERIA being the most significant. There is no significant GxE finding for PMH and smoking.

Table II.

Significant gene-based GxE results from HumanExome Beadchip data in GECCO

Gene	SBERIA	eSBERIA	GESAT	coSBERIA	coSKAT-O
(x NSAIDS)
PTCHD3	9.67E-01	2.13E-07	1.40E-03	6.86E-03	7.98E-03
MINK1	7.22E-03	2.01E-03	4.60E-03	2.41E-05	5.65E-06

Discussion

In this paper, we have proposed a powerful test framework for detecting set-based GxE (eSBERIA). eSBERIA takes advantage of the correlation or marginal screening for interaction tests by using the strength of the screening signals as adaptive weight to aggregate the interaction signals in a set. Though screening signals for individual rare variants provide limited information, collectively as a set of rare variants these screening signals have been shown to be able to increase power considerably especially when the number of variants increases. Furthermore, eSBERIA uses SKAT variance component to account for the signals that may have been missed by the screening-informed interaction test. Unlike other data-adaptive weights, eSBERIA maintains the correct type I error without requiring permutation because the screening statistics are independent of the interaction test. We have also extended the case-only approach from the single variant to a set of variants. We showed, through extensive simulation, that eSBERIA and coSBERIA have appealing power compared with existing methods.

eSBERIA tests a set of rare variants for interaction with an environmental risk factor. Therefore, as long as the overall aggregated frequency of the variants in a set is not too rare, eSBERIA should perform adequately. However, we may encounter non-convergence from calculating the screening statistics, because we calculate these statistics for each variant. If a variant occurs only a few times in the sample, these screening statistics can be unstable. Under this situation, one may consider to set the weight for these extremely rare variants to some constant (e.g., the mean or median of the weights for variants that converge) to reflect the lack of screening information, instead of up- or down-weighting the variants according to their screening statistics.

In a real data application, we found two novel GxE interactions with NSAIDs use for colorectal cancer risk. MINK1 encodes a serine/threonine kinase belonging to the germinal-center kinase family; it has been found to be significantly misregulated in colorectal cancer tumors [Capra et al., 2006]. MINK1 has also been shown to interact with Wnt/ β-catenin signaling pathways, long established to be associated with colorectal cancer risk [Daulat et al., 2012; Fearon, 2011]. PTCHD3, on the other hand, has been less well studied but one study showed evidence that PTCHD3 is a tumor suppressor for colorectal cancer [Smith et al., 2013]. Independent studies are needed to replicate the identified interactions.

We can see from the simulation that the advantage of coSBERIA is more obvious when the number of variants in the set is large. In the HumanExome Beadchip application, ~80% of the genes used in the analysis have fewer than 10 variants, which partially explains why coSBERIA do not show a notable power gain over coSKAT-O. However, we expect coSBERIA to show its advantage when applied to denser marker panels or sequencing data.

It is well known that case-only approaches boost the power in detecting interactions compared with conventional case-control methods. However, as pointed out in Wu et al. 2013 and also in the current paper, case-only approaches can also lose power when there is an inverse G-E correlation compared to the interaction effect [Wu et al., 2013]. Thus, it is important to not rely entirely on case-only approaches even though the power gain can be substantial when G and E are independent.

In summary, eSBERIA and coSBERIA showed promising performance compared to existing methods in both simulations and a real data application.

Appendix

The independence between $\widehat{\rho }$ and SKAT statistic

Let Z_i = (1,E_i,G_i,X_i,S_i) and η (α₀,α₁,α^T₂,α^T₃,ρ)^T where S_i = E_iG_iŵ is the SBERIA-aggregated interaction term. Under model (2), $\widehat{\rho }$, the maximum likelihood estimator of ρ satisfies

$$n^{-1∕2}(\widehat{\rho }-\rho )=H^{-1}U,$$

where U = n^−1/2S^T{D – g⁻¹(Zη)} and H = n⁻¹S^Tdiag(V)S; diag(V) is a n x n diagonal matrix with the ith diagonal element V_i = exp(Z_iη) / (1+ exp(Z_iη))²; g(.) is the logit link function. On the other hand, the SKAT statistic we used can be written as

$$\sum _{j=1}^{p}w{t}_j{\left\{\sum _{i=1}^n{G}_{ij}(D_i-{\widehat{\pi }}_i)\right\}}^2={\{\mathbf{D}-g^{-1}\left(\mathbf{Z}\widehat{\eta }\right)\}}^T{\mathbf{GWW}}^{\mathbf{T}}{\mathbf{G}}^{\mathbf{T}}\{\mathbf{D}-g^{-1}\left(\mathbf{Z}\widehat{\eta }\right)\},$$

where $\widehat{\eta }$ is the maximum likelihood estimator for η; W is a diagonal matrix with jth diagonal element wt^1/2_j Using Taylor expansions, we have

$$\mathbf{D}-g^{-1}\left(\mathbf{Z}\widehat{\eta }\right)\approx \mathbf{D}-\{g^{-1}\left(\mathbf{Z}\eta \right)+diag\left(\mathbf{V}\right)\mathbf{Z}(\widehat{\eta }-\eta )=\mathbf{D}-\{g^{-1}\left(\mathbf{Z}\eta \right)+diag\left(\mathbf{V}\right)\mathbf{Z}{\left\{{\mathbf{Z}}^{\mathbf{T}}diag\left(\mathbf{V}\right)\mathbf{Z}\right\}}^{-1}{\mathbf{Z}}^{\mathbf{T}}\{\mathbf{D}-g^{-1}\left(\mathbf{Z}\eta \right)\}=\{\mathbf{I}-diag\left(\mathbf{V}\right)\mathbf{Z}{\left\{{\mathbf{Z}}^{\mathbf{T}}diag\left(\mathbf{V}\right)\mathbf{Z}\right\}}^{-1}{\mathbf{Z}}^{\mathbf{T}}\}\{D-g^{-1}\left(\mathbf{Z}\eta \right)\}$$

As Z^T{I − diag(V)Z{Z^Tdiag(V(Z}⁻¹Z^T} = 0 and S is a part of Z, it implies that

$${\mathbf{S}}^{\mathbf{T}}\{\mathbf{I}-diag\left(\mathbf{V}\right)\mathbf{Z}{\left\{{\mathbf{Z}}^{\mathbf{T}}diag\left(\mathbf{V}\right)\mathbf{Z}\right\}}^{-1}{\mathbf{Z}}^{\mathbf{T}}\}=0$$

Similar to Sun et al. 2013, this shows that $\widehat{\rho }$ is independent of the SKAT statistic.