Abstract
The viscoelastic nature of axons plays a key role in their selective vulnerability to damage in traumatic brain injury (TBI). Experimental studies have shown that although axons can tolerate 100% strain under slow loading rates, even strain as small as 5% can rupture microtubules (MTs) during the fast loading velocities relevant to TBI. Here, we developed a computational model to examine rate-dependent behavior related to dynamic interactions between MTs and the MT-associated protein tau under varying strains and strain rates. In the model, inverted pairs of tau proteins can dynamically cross-link parallel MTs via the respective MT-binding domain of each tau. The model also incorporates realistic thermodynamic breaking and reformation of the bonds between the connected tau proteins as they respond to mechanical stretch. With simulated stretch of the axon, the model shows that despite the highly dynamic nature of binding and unbinding events, under fast loading rates relevant to TBI, large tensile forces can be transmitted to the MTs that can lead to mechanical rupture of the MT cylinder, in agreement with experimental observations and as inferred in human TBI. In contrast, at slow loading rates, the progressive breaking and reformation of the bonds between the tau proteins facilitate the extension of axons up to ∼100% strain without any microstructural damage. The model also predicts that under fast loading rates, individual MTs detach from MT bundles via sequential breaking of the tau-tau bonds. Finally, the model demonstrates that longer MTs are more susceptible to mechanical rupture, whereas short MTs are more prone to detachment from the MT bundle, leading to disintegration of the axonal MT ultrastructure. Notably, the predictions from the model are in excellent agreement with the findings of the recent in vitro mechanical testing of micropatterned neuronal cultures.
Introduction
Traumatic brain injury (TBI) has recently become recognized as a major health issue, affecting over 1.7 million individuals each year in the United States (1). As a biomechanical injury, TBI is characterized by head rotational acceleration at the moment of impact, resulting in rapid deformation of the brain tissue (2). Axons in the white matter are particularly susceptible to damage under these dynamic loading conditions. Indeed, diffuse axonal injury (DAI) is one of the most common and important pathologies of TBI and is thought to be the predominant pathological substrate of mild TBI or concussion (3). Although axons rarely disconnect at the time of injury, TBI induces a spectrum of evolving pathological changes to axons that can lead to their degeneration or dysfunction, which can last for several years after trauma (2, 4, 5).
Historically, little has been known about how the mechanical insult during TBI triggers axon injury. However, recent in vitro studies in our laboratory have indicated that dynamic stretch injury to axons using parameters based on human TBI causes mechanical breaking of axonal microtubules (MTs) (6, 7, 8, 9). In turn, this damage results in transport interruption at the level of individual MTs, inducing periodic swellings or varicosities that are very similar to what is seen in human TBI (10).
The MT-associated protein tau plays a crucial role in stabilizing and organizing MTs in a parallel arrangement along axons. In particular, cross-linking of tau proteins can provide uniform spacing between adjacent MTs and block or mitigate MT depolymerization (11, 12, 13, 14, 15). tau proteins are also essential to protect MTs from severing proteins (16, 17) and avert the collapse of the MT bundles in the axons (18). To study the mechanical properties of the tau protein, experimental techniques such as atomic force microscopy (AFM) can provide information on the distribution and strength of the intramolecular interactions in the coiled and folded states. The force-elongation curve obtained by AFM is a saw-tooth-shaped curve containing numerous force peaks relevant to the breaking of individual molecular bonds. In a recent study, Wegmann et al. (19) identified three major force peaks (corresponding to the release of three intramolecular folds) for the tau protein in the relaxed state. By repeating their experiments at various pulling velocities, they also derived the unfolding (transition) rate and the energy barrier distance associated with each force peak. This information can be used to derive the intrinsic viscoelastic properties of the tau protein and can be incorporated in the multiscale models of brain injury.
Using a computational model, we recently demonstrated that under normal physiological stretching of axons, tau proteins can unfold from their relaxed state, thereby permitting differential sliding of adjacent MTs while maintaining stability during axon extension (20). We further showed that owing to their intrinsic viscoelasticity, tau proteins behave more stiffly under the dynamic loading conditions of axon stretch encountered in TBI. In turn, the restricted extension of tau protein inhibits sliding of the MTs during rapid axon stretch, which results in primary breaking of the MTs, as is found experimentally for axon stretch injury in vitro.
Although the viscoelasticity of the tau proteins is a key factor that successfully predicts the characteristic vulnerability of the axons to fast loading velocities, the previous model assumed that tau proteins do not dislodge from the MTs. However, experimental studies have shown that binding and unbinding of the tau proteins to the MTs is highly dynamic. Indeed, fluorescence microscopy studies have measured a dwell time of ∼4 s for tau proteins on the MTs (21), during which they can bind to other nearby tau proteins and promote cross-linking of the MTs (12).
These observations suggest that both the rates of binding and unbinding and the strength of the formed tau dimers could directly influence estimations of the ability of tau proteins to rupture MTs during injury. Alternatively, failure of the bonds between the connected tau proteins facilitates sliding of the MTs and leads to the disintegration of MT bundles. Although the former case was predicted in our previous model, disintegration of the MT bundle is an unexplored scenario where the intact MTs lose their connectivity to the bundle and survive trauma. Thus, failure of the tau-tau bond appears to be an important consideration in further development of the computational model.
Here, we present a comprehensive model where, in addition to the viscoelastic behavior, we incorporate the failure of bonds between paired tau proteins, which can lead to translocation and dissociation of the MTs, as is observed after TBI. In particular, the model and governing equations are based on the ultrastructure of the axon and load transfer mechanisms. At different loading rates, we identify the spatial regions along the MTs where the connections between tau proteins have failed. In this regard, the importance of this study is in part to identify the conditions that lead to either rupture of the MTs or detachment of MTs from the bundle. Among the different parameters that determine this outcome, we find that the rate of applied stretch and the lengths of the MTs play the most crucial roles.
Materials and Methods
The axonal cytoskeleton consists of MTs, neurofilaments, and microfilaments interacting through proteins associated with these filamentous structures (22). Among the three, MTs that are 25 nm in diameter and have a Young’s modulus of ∼2 GPa (23) are the largest and stiffest constituent, making the largest contribution to the axon mechanical stiffness (24). MTs in the axon undergo periods of polymerization (growth) and depolymerization (shrinkage) regulated by tau proteins (15). tau protein interacts with α-tubulin and β-tubulin and stabilizes the assembly of the MTs. Following previous work from our group and others, we exclude neurofilaments, microfilaments, and the non-tau MT-associated proteins, since their roles in the mechanics of TBI are believed to be minimal (24).
Human tau proteins have six isoforms of varying length, from 352 amino acids for the shortest to 441 amino acids for the longest version. In the MT binding domain, the 441-amino-acid tau possesses four positively charged repeats, each capable of making electrostatic ties with the negatively charged surface of the MTs. Preceding the MT binding domain, tau protein contains a positively charged proline-rich region (∼100 amino acids long) and a negatively charged N-terminus (∼100 amino acids long). As argued by Rosenberg et al. (12), the proline-rich region of a tau protein and the N-terminus of another tau can form an electrostatic zipper bond, leading to the assembly of a dimer of tau proteins. Cross-linking of the MTs with MT-associated proteins such as the tau protein has also been previously observed both in vitro (25, 26) and in vivo (27, 28). By incorporating this configuration for the tau-tau connection, we construct an axon model composed of a bundle of MTs linked by tau proteins that create an electrostatic zipper-bond dimer.
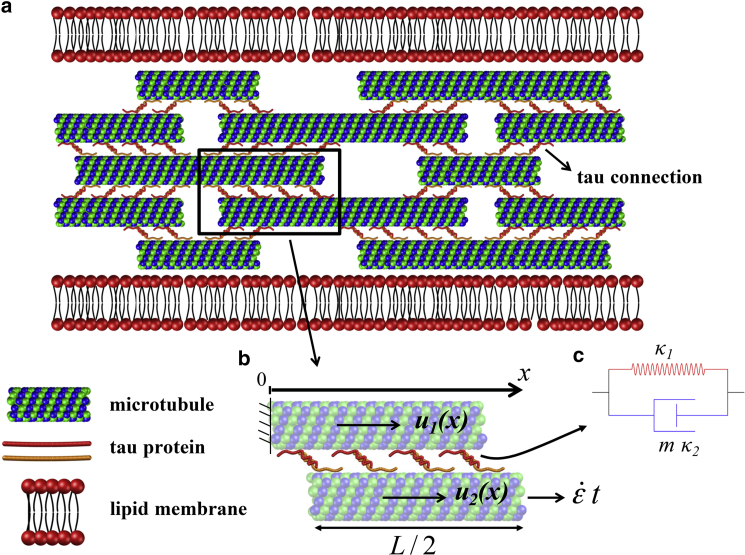
As shown in Fig. 1, our axon model consists of a staggered array of MTs (with length and outer and inner radii nm and nm), with tau proteins spaced at a distance of nm. The reference coordinate system is placed at the center of the MTs, with the x axis oriented along the length of the axon. For a periodic arrangement of MTs, we can define a unit cell consisting of two neighboring segments of MTs and their associated tau proteins as a representative of the whole model and perform simulations on this unit cell (Fig. 1 b). Mimicking tensile loading of the axon during TBI, we apply a uniaxial tensile strain at a rate to the ends of the MTs in the unit cell.
Figure 1.
(a) The axon model consists of MTs of length to which tau proteins bind and are linked to tau proteins on nearby MTs through an electrostatic zipper bond. (b) The unit cell used in this study consists of two adjacent half-length MTs and their associated tau proteins. (c) A mechanical element representing the tau protein, which is made up of a spring placed in parallel to a nonlinear dashpot. The red spring, with stiffness , represents the stiffness of the tau backbone, and the dashpot, with stiffness , represents the additional resistance resulting from the viscoelastic response of the intramolecular bonds within the tau structure. To see this figure in color, go online.
In our axon model, MTs are modeled as elastic elements with Young’s modulus GPa. However, for the tau proteins, the elastic model (with fixed stiffness) cannot capture the rate-dependent mechanical response observed in recent experiments. Within the structure of the tau protein, intramolecular binding interactions between polypeptide regions promote a highly coiled structure composed of folded segments. By pulling the tau protein at high rates, these bonds resist the applied force and create substantial mechanical stiffness. On the other hand, at slow pulling velocities, thermal fluctuations facilitate the breaking of the bonds and release the folded segments without any significant force (19). To include this rate-dependent behavior, we modeled the tau protein using a parallel spring and dashpot (Fig. 1 c). Here, the spring with stiffness represents the backbone stiffness of the tau protein and can be obtained by approximating a freely-jointed-chain model at small extensions. Next (18, 29), by assuming a persistence length of nm and a total length of nm for the tau dimer zipper bond, the stiffness of the first spring, , can be obtained from
| (1) |
where J.
The dashpot with stiffness represents the stiffness that arises from the intramolecular bonds at fast pulling rates. As noted in the introduction, to measure the strength and unfolding rate of the intramolecular bonds within the tau protein, we used the results of the AFM study performed by Wegmann et al. (19). In this study, three major force peaks (corresponding to the release of three intramolecular folds) and their associated unfolding (transition) rates were identified and measured. We used the force, elongation, and probability of the observed peaks and obtained pN/nm as a weighted average for the stiffness (defined as force/elongation) of the second spring. Also, we apply a factor of , indicative of the broken or intact status of the intramolecular bonds associated with this spring. At small pulling velocities, where the thermal fluctuations facilitate easy breaking of the bonds, we use , whereas at fast pulling rates, varies from 1 to 0, depending on the applied force magnitude and velocity. To relate the force acting on an intramolecular bond to the bond status , we used Bell’s equation (30),
| (2) |
where is the intrinsic rate of the bond breaking and is the distance between the potential energies of the intact and broken states. Bell’s equation states that an applied force can increase the chance of bond breakage exponentially. Both and have been calculated for each intramolecular bond in Wegmann et al. (19). By taking a weighted average of the three intramolecular bonds, we obtain s−1 and nm for the parameters in Eq. 2. With the parallel spring and dashpot defined, the applied force to a tau protein and the resulting elongation can be related as
| (3) |
The connection between the two tau proteins (shown in Fig. 1) can also break at a critical elongation. Here, similar to Bell’s equation used for the breaking of the intramolecular bonds (Eq. 2), we employ an exponential relation to describe the elongation of a tau-tau connection and its bonded status :
| (4) |
where is the intrinsic binding rate of the tau connections and and are the elongation and the stretched dimer length ( nm), respectively. tau proteins dynamically bind and unbind to the MTs and an average duration of ∼4 s has been measured for the dwell time of the tau proteins on MTs (21). We use this dwell time (or the rate s) as the rate at which the connection between the proteins is formed, and as described in the Discussion, we will predict how longer and shorter durations can affect the final mechanical response of the axon. Also, in Eq. 4 is the identifier for the tau-tau connection state and can vary between 0 and 1. Further, we define a threshold of 0.5, where for we assume that the tau proteins are connected, whereas for , the tau proteins are free. Here, we use the term connected to refer to a tau protein that is connected to a nearby tau protein and the term free to refer to a tau protein that is disassembled from a connection with another tau protein.
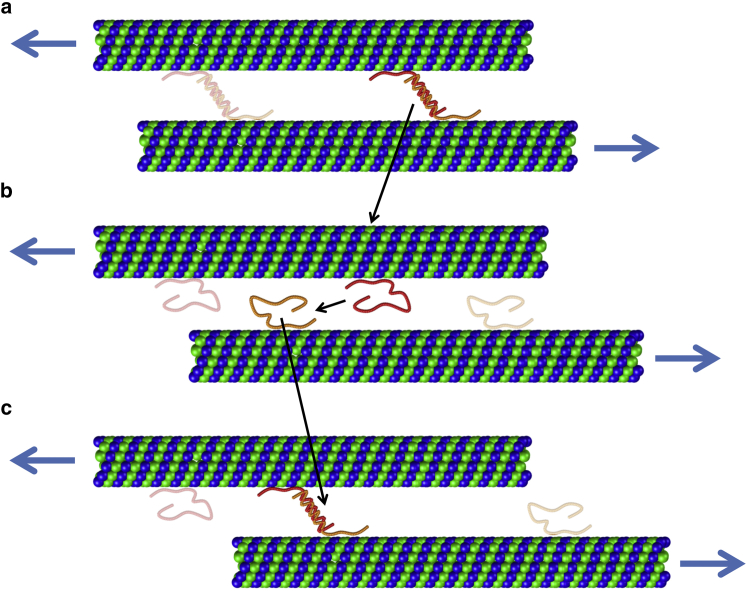
Although the connection between the two tau proteins can break at a certain force, governed by Eq. 4, the floating end of a free tau protein can still reattach to the tail of the next available tau protein and reengage in the load-transfer mechanism if the applied loading rate is sufficiently slow (or quasistatic). As illustrated in Fig. 2, under quasistatic loading rates, the broken end of a free tau protein has enough time to reattach to the closest tau protein and revive its load-bearing capacity. This recruitment of the free tau proteins, herein called reformation process, can be repeated until the ends of the adjacent MTs pass each other.
Figure 2.
The reformation process. Recruitment of free tau proteins after breaking is incorporated in our model when the loading rate is sufficiently slow (quasistatic loading). (a) By pulling an axon, tau proteins are stretched and the probability of the failure of the tau-tau bond grows exponentially (Eq. 4). (b)The bond connecting the two tau proteins breaks eventually. (c) The broken tail of a free tau protein can reattach to the next available tau and revive its load-transferring role. To see this figure in color, go online.
By defining the longitudinal displacements and for two neighboring MTs shown in Fig. 1 b, the governing equations can be obtained from the mechanical force balance:
| (5) |
The righthand side of Eq. 5 is the force ( from Eq. 3) transmitted through the tau protein connecting points and , and the lefthand side is the force exerted on each MT.
Also,
| (6) |
is the shear lag length, characterizing the length at the ends of the MTs where the sliding of the MTs is the dominant load-transfer mechanism. The boundary conditions used to solve Eq. 5 are
| (7) |
where the first two terms define the prescribed displacements at the ends and the last two correspond to the force-free ends of the MTs in the unit cell (Fig. 1 b). As for the initial conditions, the MTs are assumed to be placed at zero displacement and the tau proteins connect the points with the same -coordinate, thus . For the quasistatic loading rates, when in the reformation process the tau proteins can connect the points with different -coordinates, in the subsequent time steps, , whereas for the dynamic loading rates, where the reformation is not plausible, the broken connection between the attached tau proteins is permanent and is maintained throughout the simulation.
Equation 5 contains a system of nonlocal partial differential equations with coupling between points at different coordinates in space ( -coordinates). To solve this equation, we implemented the Livelink with Matlab feature of Comsol (v. 4.4) and created an iterative finite-element-based algorithm where the whole simulation was divided into sufficiently small time steps and the governing equations were solved for each step. By completion of each time step, we computed the status of each tau-tau bond using Eq. 4 and replaced the broken connections with new bonds as described in Fig. 2 for the subsequent steps. We also varied the length of the MTs from 2 to 200 μm to cover the range of the reported values in past studies (31). The simulations are performed for quasistatic loading (incorporating a reformation process) and dynamic loading (strain rate 1–50 s−1) relevant to the loading rates observed in TBI (8, 9, 32). In each simulation, we monitored the maximum force exerted on each MT, which can be related to the chance of MT rupture at different loading rates. In addition, we calculated the ratio of the connected tau proteins (defined as the ratio of the number of connected tau proteins to the total number of tau proteins) and identified the conditions leading to the disintegration of the MT bundle.
Results
MT rupture is more sensitive to strain rate compared to strain
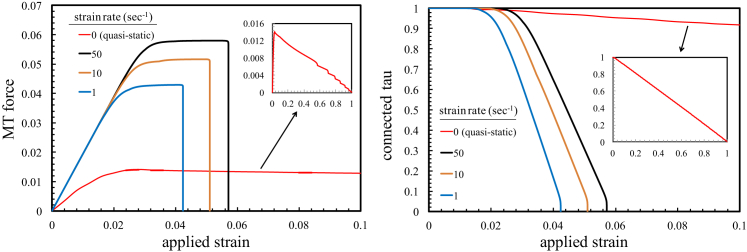
In the first study, we applied tensile strain at different strain rates ranging from quasistatic to dynamic (1–50 s−1) and obtained the force exerted on the MTs as well as the ratio of the connected tau proteins with strain. As shown in Fig. 3, under dynamic loading rates (1–50 s−1), despite the progressive breaking of the tau-tau connections, MTs experience larger forces (almost three to four times larger) compared to the quasistatic rate. In this case, the large force can rupture the MTs and lead to subsequent interruption of the cargo transport, similar to experimental observations of axons injured by TBI (7, 8, 9). With increasing strain, the bonds between the paired tau proteins start to break and the force-strain curve shows a plateau region starting at ∼2–3% strain. Eventually, by the breaking of the majority of the tau connections, intact MTs detach from the MT bundle and the force-strain curve displays a rapid drop as the axon loses its load-bearing capacity and the MT bundle disintegrates completely. Our model shows that at the onset of the MT bundle disintegration, the force exerted on the MTs and, correspondingly, the chance of MT rupture is in proportion to the strain rate. This fact is also verified by experimental studies showing that the frequency of the MT rupture depends on strain rate rather than on strain (8, 9).
Figure 3.
(Left) The maximum force exerted on the MTs at different strain rates. An axon under quasistatic loading can resist ∼100% strain, whereas at dynamic strain rates (1–50 s−1), due to the breaking of the tau-tau bonds, the axon loses its load-bearing capacity at small strains. (Right) The ratio of the connected tau proteins at different strain rates. The insets in both figures show the curves for the quasistatic loading over a larger time span. The MT length is 200 μm in both figures. The MT force is normalized by . To see this figure in color, go online.
For quasistatic loading, the mechanical response of the axon is considerably different. Although the force exerted on the MTs is significantly small compared to the case of dynamic loading, with the help of the reformation process (explained in Fig. 2), the free tau proteins can still reengage in the load-transfer mechanism and avert the drop of the force. As a result, we observe a slow decline in the force, as well as the ratio of the connected tau proteins, with strain. In this case, the axon maintains its load-bearing capacity up to large tensile strains close to 100% and eventually loses its tensile stiffness as the ends of the MTs pass each other. This fact is also consistent with the experimental results, which show that the axon can resist a large tensile strain of ∼100% without any evidence of MT rupture when the duration of the applied loading is on the order of a few minutes (9).
The pattern of MT bundle disintegration depends on the strain rate
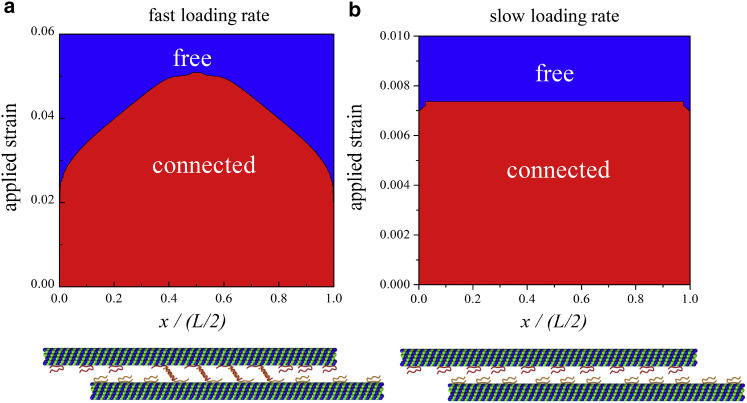
In the previous section, we observed that with increasing strain, the intact MTs eventually detach from the MT bundle, and as a result, a sharp drop appears in the stiffness of the axon. In this section, by applying fast (50 s−1) and slow (quasistatic) loading rates to an axon with a fixed MT length (L = 50 μm), we identify the onset of the breaking of the tau connection at various points along the MT and examine the process of bundle disintegration. For the purpose of this section, we ignore the reformation process occurring at slow loading rates and assume that all the bond breakings are unrecoverable.
In Fig. 4, we plot the status of the tau proteins (connected or free) for the fast and slow loading rates with strain. The model predicts that under the fast loading rate, the breaking of the tau-tau bonds starts from the ends of the MTs and progresses sequentially toward the interior points. In contrast, under slow loading rates, these bonds break simultaneously.
Figure 4.
Breaking of the tau-tau connections at (a) fast (50 s−1) and (b) slow (quasistatic) loading rates. The abscissa is the x-coordinate of the connection. The red region represents connections that are intact, and the blue region denotes the broken ones. At fast loading rates, the breaking of the tau-tau bonds occurs sequentially, whereas under slow loading, this process occurs simultaneously, as evidenced by the flat boundary between the red and blue regions. The MT length is taken to be 50 μm. To see this figure in color, go online.
This different pattern of MT bundle disintegration can be understood in the context of the shear-lag model we developed earlier (20). Under slow loading rates, due to significant MT relative sliding, the majority of tau proteins bonded to different locations along the MT undergo stretching that depends weakly on spatial coordinates, and as a result, all of the bonds break simultaneously. Conversely, under fast loading rates, and with large MT stretching, the tau proteins experience different elongations depending on their location relative to the ends of the MT. As a result, the breaking of the tau-tau bonds occurs sequentially starting from the tau proteins located near the ends of the MTs. This behavior predicts that during TBI the intact MTs in the axon will detach from the MT bundle by sequential breaking of the connected tau proteins.
Following TBI, the long MTs inside the axon break while the short MTs detach from the MT bundle
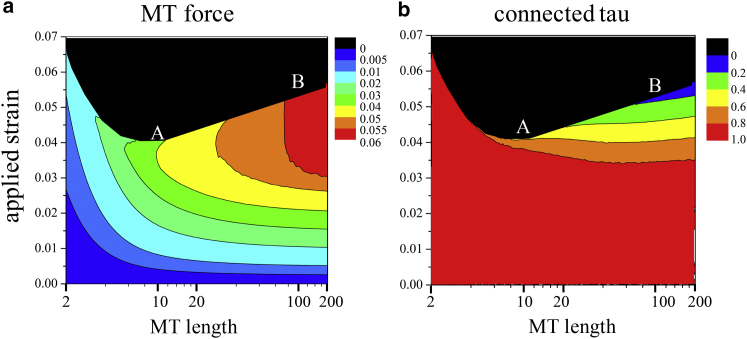
It is well-known that the MTs in the axon have different lengths. Although the long MTs are considered to be stationary, the short MTs are mobile and undergo rapid translocation driven by motor proteins (17, 33). In this section, focusing on the fast strain rates relevant to TBI, we examine how MTs of different lengths are affected by the dynamics of the tau connections. To this end, we apply a tensile strain rate of 50 s−1 to an axon containing various MT lengths (2–200 μm) and derive the force exerted on each MT, as well as the associated ratio of the connected tau proteins with strain.
We find that at the onset of MT bundle disintegration, long MTs in the axon experience large tensile forces, whereas short MTs undergo large relative sliding without any significant force. As a result, the large forces on the long MTs eventually break the MTs, whereas the large sliding of the short MTs results in MT detachment from the rest of the MTs by breaking of the bonds between the tau proteins.
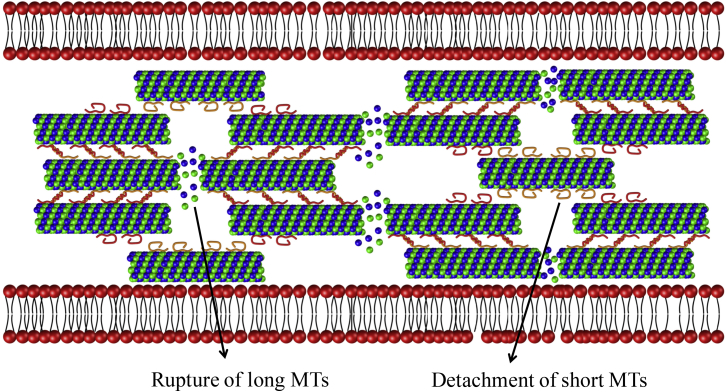
The above observations can be understood from Fig. 5, where the forces exerted on MTs of varying length and the associated ratio of the attached tau proteins are plotted. Here, we examine two MT lengths, namely, μm for the short MT (denoted by A) and μm for the long MT (denoted by B) and compare their deformation at the same rate of loading. The model predicts that at the onset of total detachment (points A and B), the force exerted on MT B is almost twice the force exerted on MT A. This indicates a greater chance of MT rupture after TBI for MT B. On the other hand, MT A experiences small forces followed by detachment from the MT bundle. Although in the former case the MT rupture would hinder protein-driven cargo transport and create swellings along the length of the axon, consistent with experimental findings, in the latter case, MTs remain intact while dislodging from the MT bundle. This predicted behavior for the response axon with varying MT lengths is also illustrated schematically in Fig. 6.
Figure 5.
Response of MTs of different lengths to loading at rapid rates (strain rate 50 s−1), predicted by the model. Points A and B correspond to MT lengths μm and μm, respectively, at the onset of detachment. Color-coded plots represent (a) the normalized force (normalized by ) acting on the MTs and (b) the fraction of tau proteins that remain connected. The model predicts the rupture of the long MTs (B) and detachment of the short MTs (A). To see this figure in color, go online.
Figure 6.
Predicted damage evolution in the axon after TBI: long MTs in the axon break and cause interruption of cargo transport followed by the appearance of axonal swelling, whereas short MTs detach from the MT bundle and remain intact. To see this figure in color, go online.
Discussion
Axons show significant ability to stretch under slow loading rates and peculiar vulnerability characterized by the rupture of the MTs under fast rates. To investigate the axonal damage, micropatterned cell culture has been used extensively to mimic the tensile deformation experienced by the axons in human TBI (6, 7, 8, 9, 32, 34). These experimental studies have shown that under slow tensile loading with a duration of seconds, axons can be stretched up to ∼100% strain and recover to their initial state without any change in morphology (9). Alternatively, under the fast strain rates of >50 s−1 relevant to TBI, components of the axons become stiffer and do not tolerate even low strain. Indeed, 5% or more tensile strain causes various MT ruptures at the microstructural level (8). These studies also confirmed that near the broken end of the MTs, axonal swellings start to appear, a definite indication that the swellings are due to the rupture of the MTs as the tracks for chemical cargo transport.
The vulnerability of the axon to high strain rates is indicative of a viscoelastic mechanical behavior (rate-dependent) that can arise from a series of dissipative events occurring at the level of the axonal cytoskeleton. In the past, different viscoelastic models composed of a combination of springs and dashpots have been proposed to fit the macroscopic viscoelastic behavior of the axon (35, 36, 37). These models are successful in predicting the overall stiffness of the axon, the relaxation behavior, and the electrophysiological changes after injury, although the connection between the internal structure and the observed macroscopic response have not been explained explicitly.
Under tensile loading, the MTs in the axon undergo relative sliding, which is regulated by tau proteins. In our previous model, we showed that due to their viscoelastic behavior, tau proteins resist the relative sliding and rupture the MTs during the axonal injury. Although interconnecting of the MTs with viscoelastic tau proteins can explain the rupture of the MTs during TBI, failure of the bonds between the connected tau proteins to resist the sliding of the MTs was unpredicted in our previous model. Indeed, by failure of the cross-linkers, the MT bundle starts to disintegrate and the MTs lose their connectivity and slide freely.
Our model predicts that despite the progressive breaking of the bonds between the connected tau proteins, faster stretching of the axon causes larger force acting on the MTs, which facilitates the rupture of the MTs, in agreement with experimental observations. On the other hand, under slow loading rates and while the force exerted on the MTs is small, the reengagement of the free tau proteins after the failure, implemented through the reformation process (Fig. 2), can explain the large extensibility of the axon up to ∼100% strain without any microstructural damage. The breaking of the tau connections is a progressive process that eventually leads to the detachment of the MTs from the MT bundle. Although the large forces acting on the MTs under fast loading can increase the chance of MT rupture, the intact MTs eventually detach from the MT bundle and survive the injury. Our model shows that under dynamic loading, breaking of the tau-tau bonds starts from the tau proteins located near the ends of the MTs and progresses toward the interior points. Under faster loading rates, we observe a sequential failure for all the tau proteins located along the length of the MTs, whereas under slower loading rates, this process is more simultaneous for all the tau proteins. In addition, MTs of various lengths are affected differently: whereas the long MTs undergo a large force that can eventually cause rupture, the short MTs are more prone to large sliding and detachment from the MT bundle.
Interestingly, this rate-dependent detachment pattern is not exclusive to axons and has been reported for other biological systems as well. As an example, in the structure of the α-helix, one of the secondary structures of many proteins, it has been shown that the hydrogen bonds that stabilize helical turns break simultaneously under slow pulling rates and sequentially at fast rates (38, 39). Although these findings are obtained by means of atomistic simulation techniques, here, by making an analogy of each helical turn as a fiber and each hydrogen bond as a cross-linker, our model is capable of reproducing the same result while presenting a rigorous mathematical description of the behavior.
In our previous model (20), the tau-protein linking between the neighboring MTs was assumed to be permanent, and as a result, the simulation could only be carried out on short MTs (2–10 μm) where the extension of the tau proteins was below the critical rupture length. Compared to that model, the strength of the model presented here is its ability to account for realistic breaking of the connections between the tau proteins, which enables us to model MTs∼200 μm in length. Also incorporating the reformation of the broken cross-linkers provides a mechanism to explain the large extensibility of the axon under slow loading rates.
The intrinsic binding/unbinding rate of the connections between the tau proteins, , plays a central role in determining the rupture of the MTs versus the detachment of the MT bundle. It has been shown that the tau proteins exist in both static and diffusive states on the MTs, and various factors determine their propensity to be in a given state. Different types of MTs (depending on the stabilizing agents during polymerization) and the concentration of the tau proteins and the ionic solution are among the key factors that alter the binding/unbinding rates of the tau connections in our model (40, 41, 42). For s−1 (or for tau dwell time on MTs of <∼4 s), tau proteins show reduced affinity for the MTs. In this case, due to the weaker binding strength between the tau proteins, the dynamic stretching of the axon results in an immediate breaking of the tau connections and the detachment of the MT bundle without any significant force applied to the MTs. An example relevant to this case is phosphorylated tau protein, which is known as one of the main mechanisms of tau disintegration from the MTs and the aggregation implicated in disease (43). On the other hand, with s−1, the tau proteins have a longer dwell time on the MTs. In this case, due to the stronger connection between the tau proteins, rupture of the MTs is more likely compared to the detachment of the MT bundle. This case can be relevant to the tau proteins that were present during the assembly of the MTs and penetrate the lumen of the MTs, leading to strong attachments to the MTs (42).
The microscale predictions of the axonal injury from our model can be linked to macroscale strain fields of the brain tissue in multiscale models of TBI. The threshold tissue-level strain in the white matter to cause axonal injury is determined to be 14% (at strain rates in the range 30–60 s−1) (44). Alternatively, available in vivo measurements of the strain field during mild accelerations of the head show strains of 2–5% in the brain tissue (45, 46, 47). Although these measurements of the strain are at the tissue level, transition of the strain from the macroscale to the axonal level and the evaluation of the axonal injury strain are still the focus of multiscale computational studies (48, 49). As an example, reconstruction of the TBI-related translational and angular accelerations experienced by athletes by means of finite-element simulations showed that during the injury, brain tissue undergoes strains as high as ∼28%, from which 5–7% (with strain rate ∼5 s−1) is the maximum strain transmitted to the axons (50). This study indicates that the tissue-level strain is an overprediction of the axonal strain and that based on the orientation and relative distance of the axons to the inclusions and boundaries, axonal strain can be different (51).
In our model, the load-transfer mechanism between the MTs is solely mediated by the tau proteins, and the potential role of the other cytoskeletal components, such as the neurofilaments and actin filaments, is not dismissed, but is excluded at this stage for simplicity. Notably, however, these structures have been shown to be modified after trauma. Neurofilaments are flexible polymers, the lengths of which are aligned parallel to the MTs, with perpendicular side arms that are thought to help with spacing and organization of the axon ultrastructure. After axonal injury, dephosphorylation of the side-arm domains causes them to collapse, thereby inducing neurofilament compaction. As with MT rupture, neurofilament compaction is believed to play a role in axonal transport interruption and swelling after injury (2, 52, 53, 54). Regarding the actin filaments, recent experimental observations with superresolution fluorescence microscopy have identified periodic rings of actin filaments surrounding the circumference of the axonal shaft, which are interconnected by spectrin tetramer (55). This network provides the axon with mechanical support and stability against various deformations, and axons lacking spectrin break easily under mechanical insult (56). Given the implication of neurofilaments and actin filaments in maintaining the structural integrity of the axon, the interplay between the MTs and other components can be included in our model in future studies.
Our new axon model can be improved further to incorporate other physiological phenomena observed in experimental studies. In the model presented here, the load transfer is mediated through the tau proteins, which form dimer structures, and failure is attributed to the breaking of the zipper bond within the dimer. Although the binding between two tau proteins has been shown to be weaker than the binding between a tau protein and an MT (12), a more rigorous approach can be adopted where these two binding scenarios are considered separately. In this case, depending on the magnitude of the applied loading rate relative to each binding/unbinding rate, breaking of the tau-MT bonds can precede the breaking of the tau-tau bonds and cause release of the tau protein dimer. Furthermore, the main assumptions made in the reformation process (Fig. 2) can be improved in future models. Here, it is assumed that upon breaking of the tau connections, there is enough tau protein bound to the neighboring MT available to reattach to the free tau protein and revive its load-bearing capacity, whereas in realistic systems, the tau proteins undergo conversion between the bound and free states (42) as well as the stationary and mobile phases along the MT lattice (40, 41). An additional simplifying assumption present in the model is the constant length of the MTs throughout the simulation. Experimental studies have shown that MTs undergo polymerization and depolymerization with respective rates of ∼1.5 mm/min and 0.088 mm/min in the presence of the tau proteins (57). Given the length of 200 μm for the MTs of our model, during the quasistatic loadings and when the duration of the simulations is on the order of a few minutes, MT dynamics may affect the response of the model, which is an interesting focus for further investigation. For simplicity, we have also ignored the variation in the concentration of tau proteins caused by diffusion of the tau protein on the MT lattice or through the cytosol (58, 59).
Author Contributions
H.A., V.B.S., and D.H.S conceived the model. H.A. and V.B.S. formulated the mathematical framework. H.A. carried out the computations. H.A., D.H.S., and V.B.S. wrote the manuscript.
Acknowledgments
This study was supported by the National Institute of Biomedical Imaging and Bioengineering of the National Institutes of Health under award number R01EB017753, and by U.S. National Science Foundation grant CMMI-1312392 (to V.B.S.), National Institutes of Health grants R01-NS038104, R01 NS092389, and P01-NS056202, and U.S. Department of Defense grant PT110785 (to D.H.S.).
Editor: Jennifer Ross.
References
- 1.Faul M., Xu L., Coronado V.G. Centers for Disease Control and Prevention, National Center for Injury Prevention and Control; Atlanta, GA: 2010. Traumatic Brain Injury in the United States: Emergency Department Visits, Hospitalizations and Deaths, 2002–2006. [Google Scholar]
- 2.Smith D.H., Meaney D.F. Axonal damage in traumatic brain injury. Neuroscientist. 2000;6:483–495. [Google Scholar]
- 3.Meaney D.F., Smith D.H. Biomechanics of concussion. Clin. Sports Med. 2011;30:19–31. doi: 10.1016/j.csm.2010.08.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Smith D.H., Johnson V.E., Stewart W. Chronic neuropathologies of single and repetitive TBI: substrates of dementia? Nat. Rev. Neurol. 2013;9:211–221. doi: 10.1038/nrneurol.2013.29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Johnson V.E., Stewart J.E., Stewart W. Inflammation and white matter degeneration persist for years after a single traumatic brain injury. Brain. 2013;136:28–42. doi: 10.1093/brain/aws322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Smith D.H., Wolf J.A., Meaney D.F. High tolerance and delayed elastic response of cultured axons to dynamic stretch injury. J. Neurosci. 1999;19:4263–4269. doi: 10.1523/JNEUROSCI.19-11-04263.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Tang-Schomer M.D., Johnson V.E., Smith D.H. Partial interruption of axonal transport due to microtubule breakage accounts for the formation of periodic varicosities after traumatic axonal injury. Exp. Neurol. 2012;233:364–372. doi: 10.1016/j.expneurol.2011.10.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Yuen T.J., Browne K.D., Smith D.H. Sodium channelopathy induced by mild axonal trauma worsens outcome after a repeat injury. J. Neurosci. Res. 2009;87:3620–3625. doi: 10.1002/jnr.22161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Tang-Schomer M.D., Patel A.R., Smith D.H. Mechanical breaking of microtubules in axons during dynamic stretch injury underlies delayed elasticity, microtubule disassembly, and axon degeneration. FASEB J. 2010;24:1401–1410. doi: 10.1096/fj.09-142844. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Johnson V.E., Stewart W., Smith D.H. Axonal pathology in traumatic brain injury. Exp. Neurol. 2013;246:35–43. doi: 10.1016/j.expneurol.2012.01.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Chen J., Kanai Y., Hirokawa N. Projection domains of MAP2 and τ determine spacings between microtubules in dendrites and axons. Nature. 1992;360:674–677. doi: 10.1038/360674a0. [DOI] [PubMed] [Google Scholar]
- 12.Rosenberg K.J., Ross J.L., Israelachvili J. Complementary dimerization of microtubule-associated τ protein: Implications for microtubule bundling and τ-mediated pathogenesis. Proc. Natl. Acad. Sci. USA. 2008;105:7445–7450. doi: 10.1073/pnas.0802036105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ross J.L., Santangelo C.D., Fygenson D.K. τ induces cooperative Taxol binding to microtubules. Proc. Natl. Acad. Sci. USA. 2004;101:12910–12915. doi: 10.1073/pnas.0402928101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Shahpasand K., Uemura I., Hisanaga S. Regulation of mitochondrial transport and inter-microtubule spacing by τ phosphorylation at the sites hyperphosphorylated in Alzheimer’s disease. J. Neurosci. 2012;32:2430–2441. doi: 10.1523/JNEUROSCI.5927-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Conde C., Cáceres A. Microtubule assembly, organization and dynamics in axons and dendrites. Nat. Rev. Neurosci. 2009;10:319–332. doi: 10.1038/nrn2631. [DOI] [PubMed] [Google Scholar]
- 16.Qiang L., Yu W., Baas P.W. τ protects microtubules in the axon from severing by katanin. J. Neurosci. 2006;26:3120–3129. doi: 10.1523/JNEUROSCI.5392-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Baas P.W., Karabay A., Qiang L. Microtubules cut and run. Trends Cell Biol. 2005;15:518–524. doi: 10.1016/j.tcb.2005.08.004. [DOI] [PubMed] [Google Scholar]
- 18.Sendek A., Fuller H.R., Cox D.L. Simulated cytoskeletal collapse via τ degradation. PLoS One. 2014;9:e104965. doi: 10.1371/journal.pone.0104965. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Wegmann S., Schöler J., Muller D.J. Competing interactions stabilize pro- and anti-aggregant conformations of human τ. J. Biol. Chem. 2011;286:20512–20524. doi: 10.1074/jbc.M111.237875. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ahmadzadeh H., Smith D.H., Shenoy V.B. Viscoelasticity of τ proteins leads to strain rate-dependent breaking of microtubules during axonal stretch injury: predictions from a mathematical model. Biophys. J. 2014;106:1123–1133. doi: 10.1016/j.bpj.2014.01.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Konzack S., Thies E., Mandelkow E. Swimming against the tide: mobility of the microtubule-associated protein τ in neurons. J. Neurosci. 2007;27:9916–9927. doi: 10.1523/JNEUROSCI.0927-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Brady S., Siegel G., Price D. Academic Press; New York: 2005. Basic Neurochemistry: Molecular, Cellular and Medical Aspects. [Google Scholar]
- 23.Suresh S. Biomechanics and biophysics of cancer cells. Acta Biomater. 2007;3:413–438. doi: 10.1016/j.actbio.2007.04.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Ouyang H., Nauman E., Shi R. Contribution of cytoskeletal elements to the axonal mechanical properties. J. Biol. Eng. 2013;7:21. doi: 10.1186/1754-1611-7-21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Aamodt E.J., Culotti J.G. Microtubules and microtubule-associated proteins from the nematode Caenorhabditis elegans: periodic cross-links connect microtubules in vitro. J. Cell Biol. 1986;103:23–31. doi: 10.1083/jcb.103.1.23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Hirokawa N., Shiomura Y., Okabe S. τ proteins: the molecular structure and mode of binding on microtubules. J. Cell Biol. 1988;107:1449–1459. doi: 10.1083/jcb.107.4.1449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Hirokawa N. Cross-linker system between neurofilaments, microtubules, and membranous organelles in frog axons revealed by the quick-freeze, deep-etching method. J. Cell Biol. 1982;94:129–142. doi: 10.1083/jcb.94.1.129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Lewis S.A., Ivanov I.E., Cowan N.J. Organization of microtubules in dendrites and axons is determined by a short hydrophobic zipper in microtubule-associated proteins MAP2 and τ. Nature. 1989;342:498–505. doi: 10.1038/342498a0. [DOI] [PubMed] [Google Scholar]
- 29.Phillips R., Kondev J., Garcia H. Garland Science; New York: 2012. Physical Biology of the Cell. [Google Scholar]
- 30.Bell G.I. Models for the specific adhesion of cells to cells. Science. 1978;200:618–627. doi: 10.1126/science.347575. [DOI] [PubMed] [Google Scholar]
- 31.Bray D., Bunge M.B. Serial analysis of microtubules in cultured rat sensory axons. J. Neurocytol. 1981;10:589–605. doi: 10.1007/BF01262592. [DOI] [PubMed] [Google Scholar]
- 32.Dollé J.-P., Morrison B., 3rd, Yarmush M.L. An organotypic uniaxial strain model using microfluidics. Lab Chip. 2013;13:432–442. doi: 10.1039/c2lc41063j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Baas P.W., Buster D.W. Slow axonal transport and the genesis of neuronal morphology. J. Neurobiol. 2004;58:3–17. doi: 10.1002/neu.10281. [DOI] [PubMed] [Google Scholar]
- 34.Fournier A.J., Rajbhandari L., Ramesh K.T. In vitro and in situ visualization of cytoskeletal deformation under load: traumatic axonal injury. FASEB J. 2014;28:5277–5287. doi: 10.1096/fj.14-251942. [DOI] [PubMed] [Google Scholar]
- 35.Dennerll T.J., Lamoureux P., Heidemann S.R. The cytomechanics of axonal elongation and retraction. J. Cell Biol. 1989;109:3073–3083. doi: 10.1083/jcb.109.6.3073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Rajagopalan J., Tofangchi A., A Saif M.T. Drosophila neurons actively regulate axonal tension in vivo. Biophys. J. 2010;99:3208–3215. doi: 10.1016/j.bpj.2010.09.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Jérusalem A., García-Grajales J.A., Peña J.M. A computational model coupling mechanics and electrophysiology in spinal cord injury. Biomech. Model. Mechanobiol. 2013;13:883–896. doi: 10.1007/s10237-013-0543-7. [DOI] [PubMed] [Google Scholar]
- 38.Ackbarow T., Chen X., Buehler M.J. Hierarchies, multiple energy barriers, and robustness govern the fracture mechanics of α-helical and β-sheet protein domains. Proc. Natl. Acad. Sci. USA. 2007;104:16410–16415. doi: 10.1073/pnas.0705759104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Ackbarow T., Keten S., Buehler M.J. A multi-timescale strength model of α-helical protein domains. J. Phys. Condens. Matter. 2009;21:035111. doi: 10.1088/0953-8984/21/3/035111. [DOI] [PubMed] [Google Scholar]
- 40.Hinrichs M.H., Jalal A., Scholz T. τ protein diffuses along the microtubule lattice. J. Biol. Chem. 2012;287:38559–38568. doi: 10.1074/jbc.M112.369785. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.McVicker D.P., Hoeprich G.J., Berger C.L. τ interconverts between diffusive and stable populations on the microtubule surface in an isoform and lattice specific manner. Cytoskeleton (Hoboken) 2014;71:184–194. doi: 10.1002/cm.21163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Makrides V., Massie M.R., Lew J. Evidence for two distinct binding sites for τ on microtubules. Proc. Natl. Acad. Sci. USA. 2004;101:6746–6751. doi: 10.1073/pnas.0400992101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Morris M., Maeda S., Mucke L. The many faces of τ. Neuron. 2011;70:410–426. doi: 10.1016/j.neuron.2011.04.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Bain A.C., Meaney D.F. Tissue-level thresholds for axonal damage in an experimental model of central nervous system white matter injury. J. Biomech. Eng. 2000;122:615–622. doi: 10.1115/1.1324667. [DOI] [PubMed] [Google Scholar]
- 45.Bayly P.V., Cohen T.S., Genin G.M. Deformation of the human brain induced by mild acceleration. J. Neurotrauma. 2005;22:845–856. doi: 10.1089/neu.2005.22.845. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Sabet A.A., Christoforou E., Bayly P.V. Deformation of the human brain induced by mild angular head acceleration. J. Biomech. 2008;41:307–315. doi: 10.1016/j.jbiomech.2007.09.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Feng Y., Abney T.M., Bayly P.V. Relative brain displacement and deformation during constrained mild frontal head impact. J. R. Soc. Interface. 2010;7:1677–1688. doi: 10.1098/rsif.2010.0210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Wright R.M., Post A., Ramesh K.T. A multiscale computational approach to estimating axonal damage under inertial loading of the head. J. Neurotrauma. 2013;30:102–118. doi: 10.1089/neu.2012.2418. [DOI] [PubMed] [Google Scholar]
- 49.Giordano C., Kleiven S. Evaluation of axonal strain as a predictor for mild traumatic brain injuries using finite element modeling. Stapp Car Crash J. 2014;58:29–61. doi: 10.4271/2014-22-0002. [DOI] [PubMed] [Google Scholar]
- 50.Cloots R.J.H., van Dommelen J.A.W., Geers M.G.D. Multi-scale mechanics of traumatic brain injury: predicting axonal strains from head loads. Biomech. Model. Mechanobiol. 2013;12:137–150. doi: 10.1007/s10237-012-0387-6. [DOI] [PubMed] [Google Scholar]
- 51.Tamura A., Nagayama K., Hayashi S. Variation in nerve fiber strain in brain tissue subjected to uniaxial stretch. Stapp Car Crash J. 2007;51:139–154. doi: 10.4271/2007-22-0006. [DOI] [PubMed] [Google Scholar]
- 52.DiLeonardi A.M., Huh J.W., Raghupathi R. Impaired axonal transport and neurofilament compaction occur in separate populations of injured axons following diffuse brain injury in the immature rat. Brain Res. 2009;1263:174–182. doi: 10.1016/j.brainres.2009.01.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Siedler D.G., Chuah M.I., King A.E. Diffuse axonal injury in brain trauma: insights from alterations in neurofilaments. Front. Cell. Neurosci. 2014;8:429. doi: 10.3389/fncel.2014.00429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Chen X.-H., Meaney D.F., Smith D.H. Evolution of neurofilament subtype accumulation in axons following diffuse brain injury in the pig. J. Neuropathol. Exp. Neurol. 1999;58:588–596. doi: 10.1097/00005072-199906000-00003. [DOI] [PubMed] [Google Scholar]
- 55.Xu K., Zhong G., Zhuang X. Actin, spectrin, and associated proteins form a periodic cytoskeletal structure in axons. Science. 2013;339:452–456. doi: 10.1126/science.1232251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Hammarlund M., Jorgensen E.M., Bastiani M.J. Axons break in animals lacking β-spectrin. J. Cell Biol. 2007;176:269–275. doi: 10.1083/jcb.200611117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Drechsel D.N., Hyman A.A., Kirschner M.W. Modulation of the dynamic instability of tubulin assembly by the microtubule-associated protein τ. Mol. Biol. Cell. 1992;3:1141–1154. doi: 10.1091/mbc.3.10.1141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Scholz T., Mandelkow E. Transport and diffusion of τ protein in neurons. Cell. Mol. Life Sci. 2014;71:3139–3150. doi: 10.1007/s00018-014-1610-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Kuznetsov I.A., Kuznetsov A.V. A comparison between the diffusion-reaction and slow axonal transport models for predicting τ distribution along an axon. Math. Med. Biol. 2014;32:263–283. doi: 10.1093/imammb/dqu003. [DOI] [PubMed] [Google Scholar]