Response Times to Gustatory–Olfactory Flavor Mixtures: Role of Congruence

Abstract

A mixture of perceptually congruent gustatory and olfactory flavorants (sucrose and citral) was previously shown to be detected faster than predicted by a model of probability summation that assumes stochastically independent processing of the individual gustatory and olfactory signals. This outcome suggests substantial integration of the signals. Does substantial integration also characterize responses to mixtures of incongruent flavorants? Here, we report simple response times (RTs) to detect brief pulses of 3 possible flavorants: monosodium glutamate, MSG (gustatory: “umami” quality), citral (olfactory: citrus quality), and a mixture of MSG and citral (gustatory–olfactory). Each stimulus (and, on a fraction of trials, water) was presented orally through a computer-operated, automated flow system, and subjects were instructed to press a button as soon as they detected any of the 3 non-water stimuli. Unlike responses previously found to the congruent mixture of sucrose and citral, responses here to the incongruent mixture of MSG and citral took significantly longer (RTs were greater) and showed lower detection rates than the values predicted by probability summation. This outcome suggests that the integration of gustatory and olfactory flavor signals is less extensive when the component flavors are perceptually incongruent rather than congruent, perhaps because incongruent flavors are less familiar.

Introduction

Although the flavors of foods and beverages are often perceived as coherent, the stimuli that produce most flavors typically activate neural signals in multiple sensory modalities, including olfaction and gustation. Recently, we reported evidence of substantial integration of signals arising from gustatory and olfactory components of flavor mixtures (Veldhuizen et al. 2010). In that study, using our automated taste delivery system (Ashkenazi et al. 2004), we asked subjects to respond as quickly as possible when they detected any of 3 possible flavorants: the gustatory flavorant sucrose, the olfactory flavorant citral, or their mixture (but not respond to a fourth possible stimulus, water). Response times (RTs) to the sucrose–citral mixture were smaller than RTs predicted by a model of probability summation that assumes statistically independent processing of responses to the gustatory and olfactory components. This outcome suggests relatively early and substantial integration of gustatory and retronasal olfactory signals in the flavor system, in agreement with observations of super-additive neural responses to congruent gustatory and olfactory flavors in various regions of the brain (de Araujo et al. 2003; Small et al. 2004; Eldeghaidy et al. 2011).

In our earlier study, we used sucrose and citral because subjects generally perceive and report them to be congruent and/or harmonious in combination (e.g., Murphy and Cain 1980). Congruence is generally defined as “the extent to which 2 stimuli are appropriate for combination in a food product” (Schifferstein and Verlegh 1996). Presumably, congruence arises between sweet and citrus flavors because most people have experienced citrus flavorants together with sweet tastes (e.g., fruit, soda, and lemonade). Experience may play an important role in the integration of gustatory and olfactory flavorants. Co-occurrence of gustatory and olfactory flavors increases their perceptual similarity (Stevenson et al. 1995, 1998, 1999; Prescott 1999), and perceptual similarity has also been shown to be critical to reports of enhancement of taste intensity by olfactory stimuli (Frank et al. 1989; Schifferstein and Verlegh 1996).

Two observations conform with the view that experience and congruence are important to sensory integration in flavor perception. Small et al. (2004) observed that incongruent salty and vanilla mixtures gave subadditive neural responses in the same regions of the brain that gave superadditive responses to congruent sweet and vanilla mixtures. And Dalton et al. (2000) showed that a sniffed odor (cherry-scented benzaldehyde) enhanced the detectability of a congruent taste stimulus in the mouth (sweet saccharin), but not the detectability of an incongruent one (savory monosodium glutamate, MSG). It is noteworthy, however, that judgments of perceived intensity of suprathreshold flavorants showed comparable degrees of summation regardless of the congruity, pleasantness, or (presumably) familiarity of the combination of flavorants (Murphy et al. 1977; Murphy and Cain 1980).

Here, we expand on our earlier observation that “congruent” mixtures (sucrose and citral) are detected faster than predicted by a model that assumes independent stochastic processing of the signals (Veldhuizen et al. 2010). In the present study, we measured RTs to detect “incongruent” mixtures (MSG and citral) as well as RTs to detect the separate components.

There are 3 possible outcomes: 1) RTs to an incongruent gustatory–olfactory mixture, like RTs to a congruent mixture, will be smaller than the values predicted by probability summation—congruence being irrelevant to the rapid, superadditive integration of gustatory and olfactory signals; 2) RTs to an incongruent mixture will equal the values predicted by probability summation—integration of incongruent gustatory and olfactory signals being neither subadditive nor superadditive relative to a model of independence, although weaker than the superadditive integration previously found with a congruent mixture; or 3) RTs to an incongruent mixture will be greater than the values predicted by probability summation, showing subadditive integration, as well as less integration than previously found with a congruent mixture. Subadditive rather than superadditive integration in the detection of congruent versus incongruent mixtures, as measured by RT, would accord in particular with evidence indicating the critical role of congruence to neural integration of gustatory and olfactory flavor signals (e.g., Small et al. 2004).

Materials and methods

Subjects

Each of 11 healthy, right-handed subjects (4 men and 7 women), aged 19–35 years (mean 22.75±9.20 [SD]), received $10 per hour to participate in all sessions (baseline plus 6 test sessions). All were students or employees at Yale University. In addition, another 11 subjects participated in baseline tests, but were excluded from the study because one was not available to complete the study, whereas the other 10 produced excessive proportions, >30%, of false positive responses to water and/or failed to detect the MSG or citral on at least 90% of trials.

The research complied with the “Declaration of Helsinki” for medical research involving human subjects, and all subjects gave informed consent under protocols approved by Yale University’s Human Subjects Committee. All subjects were nonsmokers with no taste or smell impairments, including seasonal allergies or common colds. Each subject was instructed to refrain from eating or drinking anything except water for 1h prior to the each experimental session.

Materials

To create an incongruent flavor mixture, we combined the gustatory flavorant MSG (Aldrich, CAS#142-47-2 C5H9NO4) (generally described as “savory”) with the olfactory flavorant citral (International Flavors and Fragrances, CAS#5392-40-5, chemical characterization: 3,7-dimethyl-2,6 octadienal, mixture of cis- and trans-isomers). For baseline testing, MSG was dissolved in deionized water to concentrations of 0.003M and 0.005M. The citral component started as a stock solution of 3% citral, dissolved in 97 parts ethyl alcohol (200 Proof, CAS#64-17-5). This stock solution was then diluted to 0.02% and 0.03% (0.647% and 0.97% ethanol) with deionized water for baseline testing. All of the stimuli in the baseline and experimental conditions were made fresh every 2 days, stored in a refrigerator, and then allowed to come to room temperature (74.3°F, 23.5°C) prior to each session.

Detectability of citral by retronasal olfaction alone

Although the concentrations of citral fell above retronasal olfactory threshold, we sought to ensure that the citral was perceived wholly through retronasal olfaction and not through taste or oral chemesthesis. We also wanted to ensure that no gustatory or chemesthetic sensation could be detected from the added ethyl alcohol. To this end, we first asked each subject to plug his/her nose and sample 5mL of the solution. If the subject did not perceive a tingling or burning sensation and could not taste anything, we inferred that the citral and ethyl alcohol were effectively below both the taste and trigeminal thresholds and, therefore, that the stimulus was suitable for experimental testing (Wilson et al. 1973; Cometto-Muñiz and Cain 1990; Cerf-Ducastel and Murphy 2004).

Procedure

Following the procedure of Veldhuizen et al. (2010), we measured simple RTs to citral, MSG and citral–MSG mixtures with our automated taste delivery system (Ashkenazi et al. 2004), modified to operate at low pressure and present stimuli through titanium nozzles (Veldhuizen et al. 2010). At the beginning of the sessions, the subjects were seated in an adjustable chair so they could comfortably rest their tongue on a Teflon guide located just below the metal casing of the oral interface. Subjects were asked to rinse thoroughly with deionized water and wait for the “Ready” prompt on the computer monitor. At this point, the subjects positioned their nose on a medical gauze pad, placed their tongue onto the Teflon guide (3cm below the nozzle) and placed their right thumb directly over the handheld response button.

After a foreperiod of ~3–4 s (exact duration randomized from trial to trial), the delivery device released 0.5mL of solution onto the tip of the subjects’ tongue. The subjects were instructed to pull away from the device, pull their tongue back into the mouth and swallow the solution, as quickly as possible. Subjects were to push the response button as soon as they detected any of the target stimuli, but to refrain from responding to the non-target (water) stimulus. The subjects had 5 s to respond. After 5 s, regardless of whether the subject had responded, the word “Rinse” appeared on the monitor, prompting the subject to rinse with the deionized water, expectorate into the sink and wait for the next trial to begin, ~30 s later. The experimenter was present during the entire baseline session, providing feedback on technique to ensure that each subject developed a consistent method for executing the task.

Baseline

The baseline condition consisted of 2 blocks of 60 presentations. On each trial, the subject received 1 of 5 possible stimuli, in random sequence: 0.02% citral, 0.03% citral, 0.003M MSG, 0.005M MSG, or deionized water. Each of the 4 non-water stimuli was presented equally often (20 trials apiece) and water was presented on the remaining 40 trials, making a total of 120 trials. There were also 6 practice trials at the beginning of each block; responses on these practice trials were not included in the data analysis. On each trial, the subject received a brief pulse (0.5 s duration/0.5mL volume) of 1 of the 5 possible stimuli. Subjects were instructed to press a button as soon as they perceived any of the 4 flavorants but to refrain from responding to water. Including water in the set of stimuli helps minimize false positive responding while also making it possible to calculate rates of false-positive responses.

At the end of the baseline session, the concentrations of citral and MSG that produced the greatest overlap in the distributions of RTs were selected to use in the main experiment. Subjects ran in the main experiment only if baseline performance exceeded 90% detection on at least 1 concentration of MSG and at least 1 concentration of citral (i.e., the subjects responded on at least 18 of 20 the trials containing each flavorant) and produced less than 30% false positives (responded on fewer than 12 of the 40 water trials). Table 1 gives the concentrations of citral and MSG presented to each subject in the main experiment.

Table 1.

Volume percent (%) of citral and molarity (M) of MSG used with each subject in the main experiment

Subject no.	Citral (%)	MSG (M)
1	0.03	0.005
2	0.03	0.003
3	0.03	0.005
4	0.03	0.003
5	0.03	0.005
6	0.03	0.003
7	0.02	0.003
8	0.03	0.005
9	0.03	0.003
10	0.03	0.003
11	0.03	0.005

Main experiment

The main experiment comprised 6 sessions (~1.25h each, including short breaks), held on different days over a 2–3 week period. Each session in turn comprised 4 blocks of trials. In 1 block of 60 trials (interleaved condition), all 4 stimuli (MSG, citral, MSG + citral, and water) appeared in a randomly ordered interleaved fashion, each stimulus presented a total of 15 times. In the other 3 blocks (control conditions, 20 trials each), 15 trials of 1 of the 3 flavorants were randomly interleaved with 5 trials of water. Thus, there were 120 trials in all, with each of the 3 flavorants presented 30 times (15 times in the interleaved condition and 15 times in its control condition) and water presented 30 times (15 times in the interleaved condition and 5 times in each of the 3 control conditions).

We obtained RTs to single flavorants and mixtures in both the main (interleaved) stimulus conditions and the control (blocked) conditions, in order to test for possible effects of selective attention; if subjects can attend selectively to only the gustatory or only the olfactory component of the mixture, then summation could appear to be greater when different stimuli are interleaved rather than blocked because, with stimuli interleaved, subjects could sometimes attend the “wrong” single-component flavor stimuli. Blocks were counterbalanced so that the interleaved condition came first on alternate sessions, and the 3 blocks of the control condition were counterbalanced so that each block came first, second and third twice in the set of 6 sessions.

Data analysis

Model of probability summation

According to the model of probability summation, a person detects a flavor mixture (M) containing a gustatory component (G) and an olfactory component (O) when the person detects either G or O, assuming the processing of the 2 components proceeds independently. Both P _G and P _O are the high-threshold probabilities that the gustatory channel detects G (e.g., MSG or sucrose) and the olfactory channel detects O (e.g., citral), respectively, when each stimulus is presented alone. Probability summation posits that because M contains both G and O, presenting M affords the subject 2 independent opportunities to detect the stimulus, and M will fail to be detected only when neither G nor O is detected. The probability that M will be detected with probability, P _M, is therefore given by the equation:

$$P_{\text{M}}=\text{ 1}-(\text{1}-P_{\text{G}})\times (\text{1}-P_{\text{O}})=P_{\text{G}}+P_{\text{O}}-P_{\text{G}}\times P_{\text{O}}$$ (1a)

For example, if G and O are both presented at their threshold concentrations (P _G = P _O = 0.5), then equation (1a) predicts that the probability of detecting M will equal 0.75. In this conventional formulation, probability summation applies to conditions in which there is no constraint on the time available for detection and response. Probability summation also applies, however, to conditions in which responses are speeded, that is, to the detection of stimuli within limited periods of time. As the time, t, for detecting G, O, and M increases, the corresponding probabilities of detection, P _G(t), P _O(t), and P _M(t), also increase. By analogy to equation (1a):

$$P_{\text{M}}(t)=P_{\text{G}}(t)+P_{\text{O}}(t)-P_{\text{G}}(t)\times P_{\text{O}}(t)$$ (1b)

A conventional study of flavor detection yields a single value giving the probability of detecting each stimulus, G, O, and M. A study like the present one that encourages rapid responding, however, produces, for each stimulus, a corresponding distribution of detection probabilities over time, t, where t = RT. Differences among the distributions of times (RTs) are readily assessed by cumulating the probabilities within each distribution and comparing the resulting cumulative distributions.

Critical is comparing the empirical cumulative distribution of probabilities for detecting the mixture to the theoretical cumulative distribution predicted by probability summation. Deriving cumulative distributions is a 3-step process. The first step generates the distributions of RTs. The empirical distributions of RTs to G, O, and M come directly from the data; the theoretical distribution of RTs to M comes by concatenating the distributions of RTs to the gustatory and the olfactory flavorants presented alone, choosing from each possible pair the smaller RT (Veldhuizen et al. 2010). The second step cumulates each of the probability distributions. The resulting cumulative distribution functions (CDFs) then reveal differences in the probabilities of (proportions of) fast and slow responses (short and long RTs). And the third step quantifies the differences in the shapes of the CDFs. The Cumulative distribution functions section details these steps.

Cumulative distribution functions

The present analysis of RTs largely follows that of Veldhuizen et al. (2010), with a few adjustments. Each empirical CDF gives the cumulative probability of responding to a given stimulus as a function of RT. An empirical CDF was created for each stimulus using the following procedure. Raw RTs were first sorted by stimulus (citral, MSG, and MSG + citral). Then, each set of RTs was ordered from smallest to largest. Unlike the analysis in Veldhuizen et al. (2010), we did not bin the observations at this point but deferred binning to later. As in Veldhuizen et al., “misses” (trials on which a subject failed to respond to a flavorant) were coded as an RT of 5 s (longest RT possible) in order to include all trials within each CDF.

From the CDFs obtained for the single components, we also generated a predicted (theoretical) CDF for the MSG–citral mixture, based on the assumptions of probability summation (race model: Raab 1962), which treats RTs to MSG and to citral as stochastically independent random variables. By equation (1b), each point along the theoretical CDF for the mixture gives the probability, to that point in time, of detecting either one of the components. This is equivalent to assuming that the RT to the mixture on a given trial will equal the smaller of the empirical RTs to the separate components. Given, for each subject, 90 RTs to MSG alone and 90 RTs to citral alone, we generate 8100 possible pairs of RTs, which, according to the race model, serve to predict RTs to the MSG–citral mixture. The model predicts that, for each pair, the RT will be the smaller of the 2 values in each pair. Subsequently, by binning, we reduce the number of values from 8100 to 90 and thereby produce a predicted CDF for that subject that is directly comparable with the observed CDF, each containing 90 RTs. RTs in the control conditions were analyzed in the same way.

We then transformed all of the RTs for each CDF logarithmically. We did this because the skewness of the RTs >1 across all conditions in the data of 11 of the 25 subjects (in 3 of the 11 subjects in the present study and in 8 of the 14 in the study of Veldhuizen et al. 2010). Average skewness equaled 1.27±1.09. Next, after log transformation, we used the trapz function of Matlab (R2013a, Mathworks) to calculate the area-under-the-curve (AUC) for each CDF, thereby characterizing each distribution by a single measure. Because the CDFs related integrated probability of detection to RT, the AUCs have units of probability weighted by the proportions of faster versus slower responses: The greater the proportion of fast responses (small RTs), the larger the AUC. And finally, we applied the entire procedure just described to the data reported by Veldhuizen et al. (2010), thereby allowing us to compare directly the present findings with MSG and citral to the earlier findings with sucrose and citral. Comparison of results obtained in the blocked and interleaved conditions makes it possible to assess possible effects of selective attention to the gustatory and olfactory components.

Analysis of variance of AUCs

We subjected the AUCs, just described, to analysis of variance (ANOVA), using the repeated measures, general linear model in IBM SPSS Statistics (Version 19, SPSS, Inc.). To address the first of 2 questions—whether congruence affected the rapid integration of gustatory and olfactory signals—we entered all of the individual AUCs for the mixtures into a 2×2 × 2 ANOVA, with experiment as a between-subjects factor (congruent mixtures in previous study vs. incongruent mixtures in present study) and with source (observed vs. predicted) and condition (interleaved vs. control) as within-subjects factors. If congruence matters, then we should observe a significant interaction between experiment and source. To address the second question—whether focusing attention (blocked conditions) versus dividing attention (interleaved condition) affects the apparent magnitude of mixture summation, we entered the AUCs for all flavorants into a 2×3 × 2 ANOVA, with experiment again as a between-subjects factor, but now with flavorant (gustatory, olfactory, and mixture) and condition as within-subjects factors. If subjects can attend fully at any time to only the gustatory signal or the olfactory signal but not both, then requiring subjects to attend to all 3 flavorants (interleaved condition) should impair performance on single-component trials, which on half the trials the subject will inadequately attend, but not on mixture trials, as the mixture always contains an attended component. By way of contrast, subjects presumably can attend fully to all 3 flavorants in the blocked condition. This inability to attend fully in the interleaved condition would show itself as an interaction between flavorant and condition.

In both ANOVAs, when sphericity of the data was violated (as determined by Mauchly’s test), we used the adjusted values of df (Greenhouse-Geisser correction) to calculate significance, and we used post hoc planned t-tests to compare results obtained at different levels of the factors in the ANOVAs. In all analyses, we set alpha at 0.05.

False positive responses

The model of probability summation assumes that any responses made in the absence of a stimulus (flavorant) reflect a tendency or bias for subjects to guess. This tendency may vary over the duration of a trial or over the course of a session, but in any case may be assessed from the CDF to water, where guesses produce false positive responses. By incorporating into the model of probability summation a parameter that characterizes the average rate of guessing over time, we can modify the predicted CDFs to take account of false positives—assuming, of course, that the guessing model is appropriate. Unfortunately, because there were proportionally few false positives per subject (~20% of all water presentations), it was not possible to estimate false positives for individual subjects. Consequently, we pooled false positives across subjects before sorting and binning the RTs. Over linear portions of the average observed CDFs, we could then estimate a pooled guessing parameter, P _FP, which in turn made it possible to correct the average predicted CDFs [the method is described in detail in Veldhuizen et al. (2010) and Marks et al. (2012)].

Because it was not possible to obtain estimates of P _FP for individual subjects, we could not apply ANOVA to the results, but instead simply compare, numerically and graphically, the predictions of the probability-summation model when applied to the original observed RTs (as described in Model of probability summation) and to the RTs after “correcting” for false positives. The correction procedure follows.

Given the guessing model of false positive responses, the observed probability of responding to a given flavor stimulus, S, within a given period of time after stimulus onset, P′_S(t), is given by

$${P^{\prime }}_{\text{S}}(t)=P_{\text{S}}(t)+(\text{1}-P_{\text{S}}(t))\times P_{\text{FP}}(t)$$ (2)

where P _S represents the probability of detecting S and (1 − P _S) × P _FP represents the probability of making a false positive response on that fraction of the trials in which S is not detected. From equation (2), we can calculate P _S as

$$P_{\text{S}}(t)=\frac{{P^{\prime }}_{\text{S}}(t)-P_{\text{FP}}(t)}{\text{1}-P_{\text{FP}}(t)}$$ (3)

Analogous equations apply to the probabilities of detecting single-component flavorants and their mixture. By correcting the observed distributions of RTs for false positives, it is possible to eliminate differential rates of guessing when we compare the observed RTs for detecting the mixture to the values predicted from the observed RTs to components presented alone.

Given equations (2) and (3), Veldhuizen et al. (2010) showed mathematically that the presence of false positive responses, if not corrected, will exaggerate the predicted degree of probability summation between the components. And exaggerating probability summation means, in turn, underestimating the magnitude of inferred (sensory) integration because inferred integration is calculated relative to the prediction from probability summation. Accordingly, failing to account for false positives can lead to underestimating the magnitude of inferred gustatory–olfactory integration.

Probability of detection

When comparing RTs across conditions, we need to consider the possibility that subjects might deploy different response strategies in different conditions, and hence use different response criteria. By setting a relatively laxer or stricter response criterion in different conditions, a subject will require less or more sensory information before responding. Requiring relatively less information can improve response speed (i.e., reduce time to respond), but at the cost of increasing errors—here, the rate of false positive responding. Changes in criterion across conditions can lead, therefore, to a speed-accuracy tradeoff (Luce 1986). To assess whether subjects traded overall accuracy for speed, we also analyzed performance by calculating the probability of detecting each flavorant (for each subject in each condition of each experiment) by the end of each 5-s trial. For this analysis, we combined 2 measures: the overall probability of a “hit” (the probability of responding during the trial to the flavorant) and the overall probability of a “false alarm” (the probability of responding during the trial to water).

Again, we assume that, over trials, RTs to the gustatory and olfactory components are stochastically independent random variables. We then can apply the model of probability summation, incorporating estimates of false positives as described previously, analogous to the predictions from equations (2) and (3) (Marks et al. 2012):

$$P_{\text{G}}=\frac{{P^{\prime }}_{\text{G}}-P_{\text{FP}}}{\text{1}-P_{\text{FP}}}$$ (4)

$$P_{\text{O}}=\frac{{P^{\prime }}_{\text{O}}-P_{\text{FP}}}{\text{1}-P_{\text{FP}}}$$ (5)

$$P_{\text{M}}=\frac{{P^{\prime }}_{\text{G}}-P_{\text{FP}}}{\text{1}-P_{\text{FP}}}+\frac{{P^{\prime }}_{\text{O}}-P_{\text{FP}}}{\text{1}-P_{\text{FP}}}-\frac{{P^{\prime }}_{\text{G}}-P_{\text{FP}}}{\text{1}-P_{\text{FP}}}\times \frac{{P^{\prime }}_{\text{O}}-P_{\text{FP}}}{\text{1}-P_{\text{FP}}}$$ (6)

where P _G, P _O, and P _M are the predicted overall probabilities of responding to the gustatory component alone, the olfactory component alone and the mixture, respectively. All 3 measures are now corrected for false positives. The resulting probabilities, P _G, P _O, and P _M were entered again into 2 ANOVAs: a 2×2 × 2 ANOVA with factors of experiment, source and condition (results for mixtures only) and a 2×3 × 2 ANOVA with factors of experiment, stimulus, and condition. If we observe a similar pattern of results for these probabilities as for the RTs, then we would infer that subjects did not trade speed for accuracy.

Results

RTs to mixtures: role of congruence

CDFs obtained in the interleaved conditions of the present study appear in Figure 1. Figure 1A shows the average CDFs for MSG alone, citral alone, and the incongruent MSG–citral mixture, as well as the pooled CDF for false positives and the predicted CDF for the MSG–citral mixture. Figure 1B shows the observed CDF for the mixture and the corresponding predicted CDF individually for each subject. For comparison, Figure 2 presents the analogous results derived from findings of Veldhuizen et al. (2010) for sucrose, citral and the congruent sucrose–citral mixture.

Figure 1.

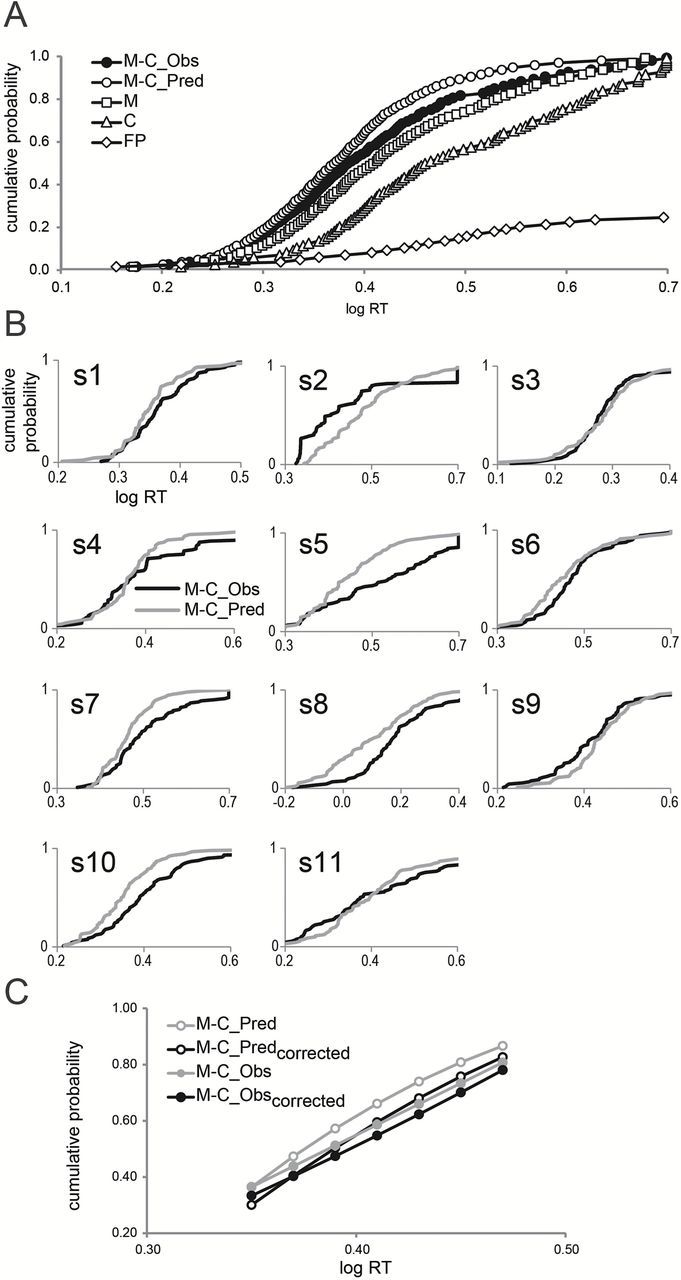
CDFs for subjects in the present study, who responded to MSG, citral, and the incongruent mixture of MSG + citral. (A) The pooled CDF obtained for the MSG–citral mixture (M-C_Obs, filled circles); the CDF predicted from a model of stochastic independence (probability summation model: M-C_Pred, open circles); the CDF for the MSG alone (M, open squares); the CDF for citral (C, open triangles); and the CDF for false positive responses to water (FP, open diamonds). (B) CDFs to the MSG–citral mixture for each of the 11 individuals subjects. Black and gray lines represent observed and predicted CDFs, respectively. (C) Predicted (open circles) and observed (filled circles) CDFs over a linear portion of the pooled distribution of RTs to the mixture, before correcting (gray) and after correcting (black) for false positive responding. Values on the abscissa are given as log RT (seconds).

Figure 2.

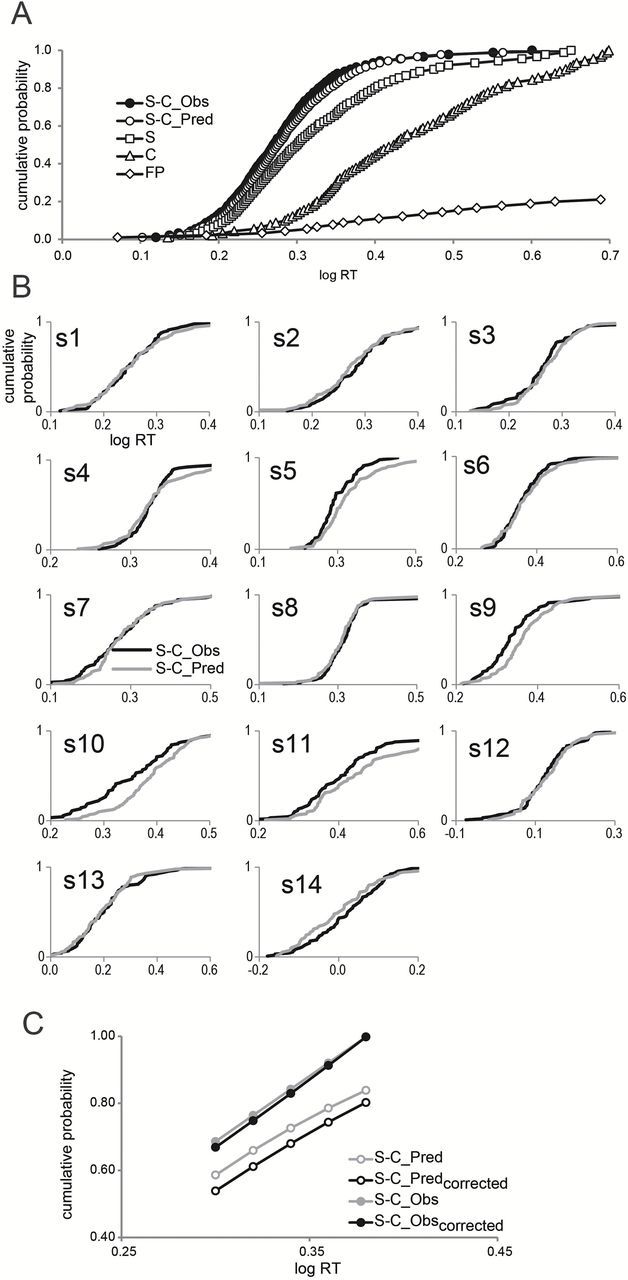
CDFs for subjects, in the study by Veldhuizen et al. (2010), who responded to sucrose, citral, and the congruent mixture of sucrose + citral. (A) The pooled CDF obtained for the sucrose–citral mixture (S-C_Obs, filled circles); the CDF to the mixture predicted from a model of stochastic independence (probability summation model: S-C_Pred, open circles); the CDF for sucrose (S, open squares); the CDF for citral (C, open triangles); and the CDF for false positive responses to water (FP open diamonds). (B) CDFs to the sucrose–citral mixture for each of the 14 individuals subjects. Black and gray lines represent observed and predicted CDFs, respectively. (C) Predicted (open circles) and observed (filled circles) CDFs over a linear portion of the pooled distribution of RTs to the mixture, before correcting (gray) and after correcting (black) for false positive responding. Values on the abscissa are given as log RT (seconds).

As Figure 1A shows, responses to the incongruent mixture of MSG + citral are faster than responses to either of the individual flavorants, MSG or citral, but slower than the values predicted by probability summation. By way of contrast, Figure 2A shows that responses to the congruent mixture of sucrose + citral are not only faster than responses to either of the components presented separately but also faster than the values predicted by probability summation.

The results of the ANOVA show a significant main effect of experiment (F[1, 23] = 6.987, P = 0.015), in that the incongruent mixture (present experiment) produced smaller AUCs (slower responses, meaning greater RTs] than did the congruent mixture. This difference may simply reflect greater responsiveness to the sucrose component than the MSG component of the mixture. There was also a significant main effect of source (F[1, 23] = 4.991, P = 0.035), the AUCs predicted by probability summation being greater (reflecting faster responses/smaller RTs) than the observed AUCs. Finally, there is a marginally significant effect of condition (F[1, 23] = 4.210, P = 0.052), with responses marginally faster/RTs smaller in the blocked, control conditions compared with the interleaved condition.

Critical to our main research question, however, is the interaction between experiment and source, and this interaction is significant (F[1, 23] = 11.326, P = 0.003), in that the AUCs for the incongruent mixture are significantly smaller (i.e., responses slower) than predicted (post hoc P = 0.001), whereas the AUCs for the congruent mixture are not smaller (post hoc P = 0.403), and, in fact, are numerically slightly larger (i.e., responses are faster). None of the other interactions is significant: experiment × condition (F[1, 23] = 0.045, P = 0.833), source × condition (F[1, 23] = 1.584, P = 0.221) or experiment × source × condition (F[1, 23] = 0.068, P = 0.797).

RTs to mixtures: role of attention

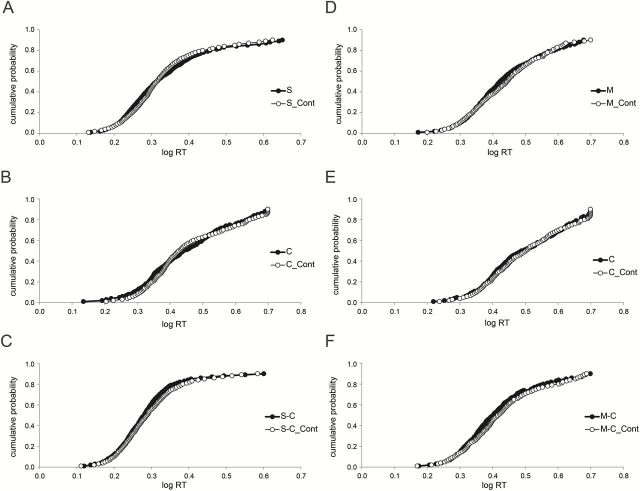
To assess the possible contribution of attention, both the earlier study (Veldhuizen et al. 2010) and the present one included 3 sets of control conditions, in each of which the subjects received, and therefore needed to attend to, just 1 of the 3 flavorants within a block of trials: sucrose or MSG, citral, or the mixture. Figure 3 shows CDFs for each flavorant in the main (interleaved) and the control (blocked) conditions of both studies. Panels A and D shows the difference between conditions for the gustatory flavorant, panels B and E the difference for the olfactory flavorant, and panels C and F the difference for the mixture. The CDFs in the main and control conditions largely overlap for all flavorants in both studies.

Figure 3.

CDFs to sucrose (S), citral (C), and their mixture (S-C) (left-hand panels A–C, data of Veldhuizen et al. 2010) and to monosodium glutamate (M), citral (C), and their mixture (M-C) (right-hand panels, D–F), data of present study. Data in each panel show results obtained when all conditions were interleaved (filled circles) and when conditions were run separately as controls (open circles, labeled “Cont”) for possible effects of distributing attention.

As above, results of the ANOVA show a significant main effect of experiment (F[1, 23] = 7.533, P = 0.012), in that the incongruent mixture (present experiment) produced smaller AUCs (slower responses, meaning greater RTs) than did the congruent mixture, again possibly reflecting greater responsiveness to the sucrose component than the MSG component. There is also significant main effect of flavorant, F(2, 46) = 25.303, P < 0.001, reflecting faster responses to the mixture relative to both the gustatory component (post hoc P = 0.003) and the olfactory component (post hoc P < 0.001), and faster responses to the gustatory component relative to olfactory component (post hoc P = 0.001), regardless of experiment. Critical to the question whether focusing attention (blocked conditions) versus dividing attention (interleaved condition) affected the apparent magnitude of mixture summation, we did not observe a significant interaction between flavorant and condition (F[2, 46] = 1.212, P = 0.307). Nor did we observe a significant main effect of condition (F[1, 23] = 1.907, P = 0.181) or a significant interaction: experiment × flavorant, F[2, 46] = 2.824, P = 0.070, experiment × condition, F[1, 23] = 0.209, P = 0.652, or experiment × flavorant × condition, F[2, 46] = 0.223, P = 0.801.

RTs to mixtures: accounting for false positive responses

Figure 1C compares the average predicted and observed CDFs to incongruent mixtures of MSG and citral before and after correcting for false positives pooled across subjects. The observed CDF falls below the predicted CDF both before and after the correction, but the difference between observed and predicted is smaller after the correction. In contrast, as shown in Figure 2C, in the earlier study, which tested mixtures of sucrose and citral (Veldhuizen et al. 2010), the observed CDF exceeds the predicted CDF before correction for false positives, and correcting for false positives actually increases the extent to which the observed CDF exceeds the prediction of probability summation. With the congruent flavorants sucrose and citral, therefore, there is a benefit to processing both components in a mixture, greater than the benefit predicted by a model that assumes statistical independence. Failing to account for false positives can underestimate this benefit. With the incongruent flavors MSG and citral, however, there is no benefit, and there may even be a cost associated with processing both components of the mixture.

Detection of mixtures: effect of congruence

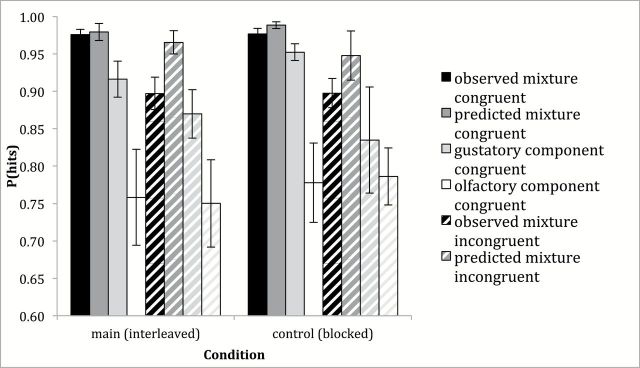
Figure 4 shows observed and predicted probabilities (corrected for false positive rates) for congruent mixtures (sucrose and citral) and incongruent mixtures (MSG and citral) in the main (interleaved) condition. The results of the ANOVA show a significant main effect of experiment (F[1, 23] = 9.591, P = 0.005), in that the hit rates were lower in the present experiment with incongruent flavorants compared with the previous experiment with congruent flavorants. The ANOVA also gave a significant main effect of source (F[1, 23] = 14.433, P = 0.001), in that hit rates predicted by probability summation are higher than observed hit rates to the mixtures. The effect of condition, however, did not reach significance (F[1, 23] = 0.073, P = 0.789). The interaction between experiment and source is significant (F[1, 23] = 8.481, P = 0.008): the probability of responding correctly to the incongruent mixture is significantly smaller than predicted by probability summation (post hoc P = 0.001), whereas the probability of responding correctly to the congruent mixture does not differ from prediction (post hoc P = 0.510). None of the other interactions is significant: experiment × condition (F[1, 23] = 1.056, P = 0.315), source × condition (F[1, 23] = 0.125, P = 0.727) or experiment × source × condition (F[1, 23] = 0.848, P = 0.367). This pattern of results for accuracy very closely follows that of RTs.

Figure 4.

Probability of detecting the mixture (hits, corrected for false alarms) observed (black) and predicted by the model for probability summation (dark gray), as well as the gustatory (light gray) and olfactory (white) components when the flavorants were congruent (solid bars, data of Veldhuizen et al. 2010) or incongruent (striped bars, data of present study). Results for the main, interleaved conditions appear on the left and results for the control, blocked conditions appear on the right.

Detection of mixtures: role of attention

Figure 4 also shows observed probabilities (corrected for false positive rates) for the mixture, the gustatory component, and olfactory component in the 2 studies in the main (interleaved) and control (blocked) conditions. The results of the ANOVA show a significant main effect of flavorant (F[2, 46] = 14.857, P < 0.001), reflecting higher hit rates for the mixture relative to the gustatory component (post hoc P = 0.027) and the olfactory component (post hoc P < 0.001), and higher hit rates for the gustatory component relative to the olfactory component (post hoc P = 0.004). Neither the main effect of experiment (F[1, 23] = 2.418, P = 0.134) nor of condition (F[1, 23] = 0.692, P = 0.414) is significant.

Critical to the question whether focusing attention (blocked conditions) versus dividing attention (interleaved condition) affected the apparent magnitude of mixture summation, there the interaction between flavorant and condition was not significant (F[2, 46] = 0.709, P = 0.498). None of the remaining interactions was significant: experiment × flavorant (F[2, 46] = 1.046, P = 0.359), experiment × condition (F[1, 23] = 0.628, P = 0.436) or experiment × flavorant × condition (F[2, 46] = 1.556, P = 0.222).

Discussion

The present study asked how congruence affects flavor integration. Previously, we found that RTs to sucrose + citral, a congruent gustatory–olfactory mixture, were substantially smaller (speed of response was greater) than the values predicted by a model of probability summation (Veldhuizen et al. 2010). If congruence enhances the integration of gustatory and olfactory flavorants, then we predicted that RTs to the incongruent MSG + citral should show less summation than did RTs to the congruent sucrose + citral; indeed, perhaps RTs to MSG + citral would be greater, not smaller, than the values predicted by probability summation. The results showed that RTs to the MSG + citral were indeed greater (responses were slower) than predicted from RTs to the components. This outcome suggests that congruence is important to gustatory–olfactory flavor integration, and this is the case even when we correct for false positive responses (assumed by the model of probability summation to reflect guesses). Given that rates of detection (accuracy) as well as speed of response were lower with the incongruent mixtures compared with congruent mixtures, the effects of congruence do not simply reflect a speed-accuracy trade off.

Although it is plausible that the difference between the outcomes obtained with MSG + citral and with sucrose + citral reflect the difference in congruence of the 2 mixtures, a caveat is in order: It is also possible that the difference between outcomes reflects differences in pleasantness, which tend to correlate with congruence (e.g., Schifferstein and Verlegh 1996), or perhaps with familiarity. Or, for unknown reasons (perhaps umami’s complex taste quality/profile), olfactory flavorants may simply integrate less well with MSG than with sucrose. Nevertheless, an explanation in terms of congruence is plausible to account for the difference between the findings of Veldhuizen et al (2010) and those of the current study.

Critically, we did not observe a significant main effect of condition, which refers to interleaving versus blocking the different stimuli within an experiment; nor was there a significant interaction between condition and any of the other variables. This outcome implies little if any cost to response speed associated with attending to all 3 flavorants in the interleaved condition. If, early in processing, subjects could attend fully to only one modality, then we would expect RTs to single flavorants to be greater in the interleaved compared with the blocked condition, because with flavorants varying over trials, subjects would sometimes attend to the “wrong” flavorant. This asymmetry would not occur (or would be smaller) on trials containing the mixture, which contains both flavorants.

Note that the model of probability summation used here treats false positive responses as guesses, and therefore assumes that noise is too small in magnitude to affect performance. This is the conventional assumption of probability summation. Perhaps, however, following signal-detection theory (Green and Swets 1966), noise is more substantial, and, consequently, false positive responses do not reflect guessing but arise instead when the level of the noise surpasses the subject’s criterion for responding. Pertinent here are the outcomes of both the present study and that of Veldhuizen et al. (2010) suggesting similar results when the single-component flavorants and their mixtures are interleaved and when they are blocked. These 2 outcomes imply that the flavor system operates, in tasks requiring rapid detection, as a “single channel,” that is, as a perceptual channel having a single source of noise, which affects responses to all flavorants equivalently. If so, then the presence or magnitude of the noise, and hence of false positive responses, should not affect the observed difference between sensitivity to mixtures and sensitivity to their individual gustatory and olfactory components (Marks et al. 2012, pp. 267–269). In any case, we anticipate further development of theories of flavor processing that are grounded in decision-theoretic frameworks (e.g., Brewer et al. 2013).

The findings that congruence is critical to the integration of gustatory and olfactory flavorants, as measured by speed of responding, agree with observations that incongruent taste-olfaction mixtures, compared with congruent mixtures, produce subadditive rather than superadditive neural responses (Small et al. 2004) and similar levels of detection sensitivity, compared with control, rather than enhanced sensitivity (Dalton et al. 2000). The present findings appear inconsistent, however, with the evidence that judgments of perceived intensity of suprathreshold flavorants show comparable degrees of mixture summation regardless of congruence (Murphy et al. 1977; Murphy and Cain 1980). As stimulus concentrations increase, both response speed and perceived intensity generally increase with gustatory stimuli (Bonnet et al. 1999) and with flavor stimuli (Veldhuizen et al. 2005). Thus, one might expect congruence to affect RTs and perceived intensity in similar ways, that is, RT may serve as a good surrogate for perceived intensity. Yet it is noteworthy that, in other sensory systems, RT and perceived intensity sometimes dissociate. To give 2 examples in vision, increasing the duration of a flash of light leads to changes in brightness without concomitant changes in RT (Raab et al. 1961), and the brightness of a flash of light may be reduced by a subsequent, spatially adjacent masker (metacontrast) with little or no corresponding effect on RT (Fehrer and Raab 1962). In both of these examples, the dissociation between perceived intensity and RT takes place as the processing of intensity proceeds over time (spatio-temporal contrast, temporal integration). In these cases, overt behavioral responses appear to be established rapidly, before the sensory experiences reach their final levels of perceived intensity. It is at least plausible that a similar dissociation arises in flavor perception, with rapid overt responses to mixtures established before perceived flavor intensity unfolds fully.

In conclusion, the present results, together with those of Veldhuizen et al. (2010), imply that gustatory and olfactory flavorants integrate their effects in producing rapid responses, but only if, or especially when, the flavorants are congruent. This observation accords with the view that sensory systems act in concert within the perceptual flavor system, which evolution has presumably shaped to deal with ecological information relevant to the perception of foods and thereby to guide food consumption (Gibson 1966; Auvray and Spence 2008; Small 2008). We chose MSG and citral for the present study because they are generally perceived in combination to be incongruent and/or inharmonious. Congruence is generally defined as “the extent to which 2 stimuli are appropriate for combination in a food product” (Schifferstein and Verlegh 1996). Congruence presumably arises when people frequently experience 2 or more flavorants together, as they do citrus flavorants, such as citral, with a sweet-tasting flavorants, such as sucrose—combinations found, for example, in fruits, soft drinks, and lemonade. Conversely, most people are unlikely to have experienced foods containing both citrus flavorants and MSG. One caveat in the current study is that we did not explicitly ask subjects to indicate how congruent or harmonious they perceived the mixtures. Nevertheless, subjects’ spontaneous comments about disliking the MSG–citral mixture suggest that the subjects indeed perceived it to be incongruent.

Funding

This work was supported by the National Institute on Deafness and Other Communication Disorders of the National Institutes of Health (NIH) [R01 DC011823-03 and R01 DC009021-03 to L.E.M.].