Abstract
To segregate chromosomes during cell division, microtubules that form the bipolar spindle attach to and pull on paired chromosome kinetochores. The spindle assembly checkpoint (SAC) is activated at unattached and misattached kinetochores to prevent further mitotic progression. The SAC is silenced after all the kinetochores establish proper and stable attachment to the spindle. Robust timing of SAC silencing after the last kinetochore-spindle attachment herein dictates the fidelity of chromosome segregation. Chromosome missegregation is rare in typical somatic cell mitosis, but frequent in cancer cell mitosis and in meiosis I of mammalian oocytes. In the latter cases, SAC is normally activated in response to disruptions of kinetochore-spindle attachments, suggesting that frequent chromosome missegregation ensues from faulty SAC silencing. In-depth understanding of how SAC silencing malfunctions in these cases is yet missing, but is believed to hold promise for treatment of cancer and prevention of human miscarriage and birth defects. We previously established a spatiotemporal model that, to the best of our knowledge, explained the robustness of SAC silencing in normal mitosis for the first time. In this article, we take advantage of the whole-cell perspective of the spatiotemporal model to identify possible causes of chromosome missegregation out of the distinct features of spindle assembly exhibited by cancer cells and mammalian oocytes. The model results explain why multipolar spindle could inhibit SAC silencing and spindle pole clustering could promote it—albeit accompanied by more kinetochore attachment errors. The model also eliminates geometric factors as the cause for nonrobust SAC silencing in oocyte meiosis, and instead, suggests atypical kinetochore-spindle attachment in meiosis as a potential culprit. Overall, the model shows that abnormal spindle-pole formation and its aberrant coordination with atypical kinetochore-spindle attachments could compromise the robustness of SAC silencing. Our model highlights systems-level coupling between kinetochore-spindle attachment and spindle-pole formation in SAC silencing.
Introduction
As a key foundation of eukaryotic life, chromosome segregation during cell mitosis passes complete copies of all nuclear genetic information equally to each of two daughter cells (1). The chromosome segregation process is mediated by a bipolar spindle comprising microtubules. Each chromosome consists of two duplicate sister chromatids to be segregated; before separating sister chromatids, spindle microtubules must first establish stable connections with each chromatid via its outer centromere layer, the kinetochore. Otherwise, chromosome loss or lagging could occur and lead to aneuploidy—aberrancy in chromosome number; and aneuploidy can lead to a plethora of pathological conditions (2, 3, 4). Normally, unattached and misattached kinetochores activate the mitotic spindle assembly checkpoint (SAC)—a robust surveillance mechanism that prevents mitotic progression and chromosome segregation until each chromosome establishes a stable, bipolar attachment with the spindle microtubules (5). Evidently, accurate chromosome segregation hinges on the robust timing of SAC silencing after the last kinetochore attachment. With such stringent control of SAC signaling, chromosome missegregation is rare in normal somatic cell mitosis (5, 6).
Under some conditions, however, the cell loses the stringent control by SAC and suffers high risk of chromosome segregation error. In this work we address two cases of broad biomedical significance—cancer cell mitosis and mammalian oocyte meiosis. Cancer cell mitosis is subject to frequent chromosome missegregation and aneuploidy (2, 4, 7). Consequently, most cancer cell lines suffer chromosomal instability, the result of elevated chromosome missegregation rate (2, 4, 7). Chromosomal instability is associated with poor prognosis and drug resistance (7, 8, 9). Additionally, during meiosis I (the first cycle of reduction division) in mammalian oocytes, chromosome segregation is notoriously error-prone (3, 10); the chromosomes could segregate even when one or more chromosomes are unaligned or not attached to the spindle (11, 12, 13, 14, 15). Notably, meiosis I errors account for most spontaneous miscarriages and birth defects in humans (3).
Frequent chromosome missegregation and aneuploidy in cancer cells and mammalian oocytes result from SAC malfunctioning. Proper SAC functioning relies both on SAC activation in response to disruptions of kinetochore-spindle attachments and timely SAC inactivation when all the kinetochores establish stable connection with the spindle. Problems in either of the two phases could incur faulty SAC. In cancer cells and oocyte meiosis, SAC activation is effective, as evidenced by SAC-dependent delay of mitotic/meiotic exit upon spindle disruptions in these cells (16, 17, 18, 19, 20). Therefore, chromosome missegregation likely stems from compromised robustness in the timing of SAC silencing. But exactly how and why SAC silencing becomes unreliable remains a mystery. Understanding these questions is believed to be an important step toward treatment of cancers and prevention of human miscarriage and birth defects.
In this work, we investigate through theoretical modeling how robust timing of SAC silencing could be compromised in cancer cells and mammalian oocyte meiosis I. To study nonrobust SAC silencing, we take advantage of our previously established theoretical model that specifically and uniquely accounts for the robustness of SAC silencing in normal mitosis (21). The key insight gained from the model is that the entire mitotic spindle apparatus—comprising kinetochores, spindle microtubules, and spindle poles—coordinates to encode kinetochore attachments into a highly nonlinear concentration signal at the spindle pole. A dramatic boost in spindle pole signal that only occurs upon the stable spindle attachment of the last kinetochore serves as the noise-proof trigger for SAC silencing. This signaling mechanism is in contrast to the traditional view that SAC silencing results from gradual loss of SAC activation upon each kinetochore attachment. Our model elucidates the functional role of the spatiotemporal patterns of SAC proteins evidenced in mitosis (22, 23, 24, 25): the spatiotemporal regulation mediates robust signal to time SAC silencing after and only after the last kinetochore-spindle attachment forms. Furthermore, because it delineates the whole mitotic spindle in SAC signaling, our model provides a useful platform to study the effects of spindle organization on SAC silencing.
Here, we leverage the previous model to study the origins of nonrobust SAC silencing in cancer cell mitosis and mammalian oocyte meiosis I. Within the scope of spatiotemporal regulation addressed by the model, this work focuses on how unusual features of the spindle apparatus evidenced in cancer cells and mammalian oocytes affect the SAC silencing signal. The model results explain why the multipolar spindle commonly found in cancer cells inhibits SAC silencing, whereas spindle pole clustering promotes SAC silencing (16). The model also suggests that in mammalian oocyte meiosis, nonrobust timing of SAC silencing is not likely caused by large sizes of the cell and the spindle, but is probably caused by the meiosis-specific kinetochore-spindle attachments. This theoretical study introduces a spatiotemporally based angle of view toward understanding questions of biomedical significance in cancer cell biology and oocyte biology.
Materials and Methods
Model setup
We briefly outline here the setup of our spatiotemporal model for robust SAC silencing in typical somatic cell mitosis. The model is developed in two stages: the core transport model that only concerns the spatiotemporal patterning of SAC components, and the full transport-reaction model that additionally incorporates a simplistic biochemical pathway for SAC silencing (21). While the model is built upon well-established experimental observations, it provides a systemwide perspective beyond these facts and exposes the roles of individual parts of the mitotic apparatus in SAC silencing (Fig. 1).
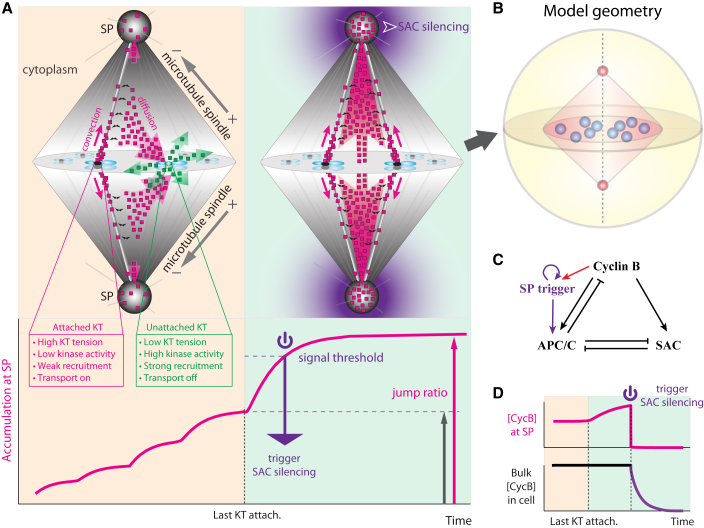
Figure 1.
Summary of spatiotemporal model for SAC silencing. (KT) Kinetochore; (SP) spindle pole. (A) Illustrative summary of the model for spatiotemporal regulation of SAC components. (Upper-left panel) Streaming of SAC components (pink square) from attached kinetochores (black ovals) is strongly diverted by any unattached kinetochore (green ovals). Unattached kinetochores channel streaming proteins to the diffusive state (green square). (Upper-right panel) After all kinetochores are attached, strong, undiverted poleward flux causes significant accumulation of SAC components at the spindle pole. The signal could serve as robust trigger for SAC silencing, which then propagates from the spindle pole throughout the cell. For clarity, fluxes of mitotic proteins are only shown for two pairs of kinetochores in the foreground. Distribution of the squares does not reflect spatial distribution of SAC components. (Translucent magenta arrows) Flux of streaming proteins. (Translucent green arrows) Flux of diffusive proteins. (Solid magenta arrows) Proteins streaming poleward along microtubules. (Black curly arrows) Streaming proteins binding/unbinding with microtubules. (Gray straight arrows) Microtubule minus-ends are organized toward the spindle pole and plus-ends away from the spindle pole. (Lower panel) Spindle pole accumulation of SAC components as a function of kinetochore-spindle attachments (magenta solid line). The last kinetochore attachment boosts the spindle pole signal above the threshold and triggers SAC silencing. Index for signal robustness, the jump ratio, is defined as the ratio between the steady-state spindle pole signals after and before the last kinetochore attachment (i.e., length of magenta arrow divided by length of gray arrow). (B) Geometry for model simulation. As a simplification, each kinetochore domain in the model represents a compartment that characterizes the status of chromosome-spindle attachment. Without loss of generality, the model geometry includes 10 kinetochore domains located at the equator of the spindle. (For brevity, we will call the kinetochore domain “kinetochore” throughout the article.) (C) Biochemical feedback among SAC components. (Black) Cyclin B, APC/C, and SAC proteins exhibit identical spatiotemporal patterns governed by the spatiotemporal model in (A). (Purple) Trigger factor constantly concentrates at the spindle pole. After threshold cyclin B level activates the trigger factor (red arrow), the factor stays active via autoactivation even after cyclin B is depleted from the spindle pole. (D) Cyclin B level at the spindle pole serves as trigger signal for SAC silencing (upper panel). After SAC silencing is triggered at the spindle pole, cyclin B is quickly depleted from the spindle pole. Degradation of cyclin B then propagates throughout the whole cell (lower panel).
The core transport-only model recapitulates the common spatiotemporal pattern of SAC components observed in mitosis. The model hinges on the differences between the unattached and attached kinetochores induced by kinetochore tension. Kinetochore tension refers to the force imposed by microtubules on an attached kinetochore. The kinetochore tension pulls the kinetochore away from the Aurora B kinase-enriched inner centromere region, and thus reduces the local mitotic kinase activities at the kinetochore (26, 27, 28). The kinase activity at the kinetochore controls recruitment and transport activation of SAC components as elaborated in the list below. In the model, specifically, changes in the corresponding rates of SAC recruitment and transport activation are used to phenomenologically characterize the kinetochore attachment and tension. The effects of kinetochore tension, together with basic cytoskeleton-mediated spatial dynamics of the SAC components, translate to the following key model assumptions that make up the simplest model retaining the essence of reality (Fig. 1 A). Detailed formulation of the model is given in Appendix A.
-
1)
The kinetochore-localized mitotic kinase activity promotes recruitment of SAC component to the kinetochore (27, 29, 30). An unattached kinetochore, associated with stronger kinase activity, thus assumes a much larger recruitment rate for SAC components than an attached kinetochore does. This assumption is in line with the observation that SAC proteins are highly concentrated at unattached kinetochores, yet depleted from attached ones (31, 32, 33, 34, 35).
-
2)
Dynein-mediated poleward streams of SAC components emanate from the attached kinetochores (22, 23, 24, 25), whereas dynein activity is inhibited by high kinase activity at the unattached kinetochores (36). To simulate this difference, the model assumes two distinct states in the SAC components: 1) diffusive proteins that emanate from the unattached kinetochores and diffuse in the cytoplasm, and 2) streaming proteins that emanate from the attached kinetochores and stream toward the spindle poles. Because the kinases and the antagonistic phosphatases that control dynein-mediated poleward streaming are concentrated at the kinetochores (36, 37), the model further assumes that conversion between the diffusive and streaming states occurs only at the kinetochores. This assumption reproduces the observation that poleward streams emanate from nowhere in the cell but the attached kinetochores (22, 23, 24, 25).
-
3)
The streaming SAC components, in the form of dynein-cargo complexes, undergo constant binding and unbinding with the microtubules; the binding rate to microtubules depends on local microtubule density. The model incorporates a microtubule density field that depicts both the spindle and astral microtubules (see Appendix A). The spindle defines a compartment that concentrates the streaming proteins through the combined effect of dense microtubule network, spindle matrix, and peri-spindle membranous structures (38, 39). Additionally, the dynein-cargo complexes that reach the spindle pole are partially sequestered through binding/unbinding dynamics.
The model predicts a step change in the concentration of SAC components at the spindle pole after the final kinetochore attachment (21). The big jump in spindle pole accumulation of SAC components could provide a noise-proof trigger for SAC silencing after and only after the final kinetochore-spindle attachment (Fig. 1 A). The big jump occurs because the poleward streaming from the attached kinetochores is strongly diverted by the unattached kinetochores (21) (green arrows in Fig. 1 A). Mechanistically, most of the dyneins (and hence the streaming SAC components) fall off the spindle before reaching the spindle pole; they could then revisit the kinetochores. The larger recruitment power of the unattached kinetochores—conferred by low kinetochore tension—strongly biases the recruitment onto the unattached kinetochores, instead of the attached ones. At the unattached kinetochores the dynein activity is turned off and the SAC components stop streaming. Taken together, the preferential recruitment onto the unattached kinetochores effectually diverts the poleward stream of SAC components, persistently preventing it from entering the spindle pole. Upon the last kinetochore-spindle attachment, the now unchallenged poleward stream results in a dramatic boost in the spindle pole accumulation of SAC components (Fig. 1 A). Heuristically, the jump ratio that characterizes the signal robustness for SAC silencing (Fig. 1 A) can be roughly estimated from the dynamic rates of protein exchange at the kinetochores (see the Supporting Note in the Supporting Material). In particular, a large jump ratio hinges on weak recruitment at the attached kinetochore.
Equipped with the large jump ratio from the transport model, the full transport-reaction model additionally incorporates a minimalist SAC silencing-pathway (Fig. 1 C and Appendix B) derived from experimental observations. The pathway consists of three key biochemical components: SAC protein, cyclin B, and APC/C. Cyclin B and APC/C follow the same spatiotemporal patterns as SAC proteins (40, 41, 42). The three mitotic players form a feedback loop. Cyclin B promotes activities of SAC proteins (43, 44, 45) and APC/C (46, 47). SAC inhibits APC/C activity (5). Active APC/C degrades cyclin B (5) and inhibits SAC activity (48, 49). When the spindle pole-localized cyclin B concentration rises above a threshold (Fig. 1, A and C), the model assumes that it irreversibly activates a trigger factor at the spindle pole. The active trigger factor then activates APC/C and initiates cyclin B degradation and SAC inactivation (Fig. 1 D). The dramatic concentration boost at the spindle pole upon the final kinetochore attachment ensures accurate and robust timing of SAC silencing.
We note that neither the specific threshold value of spindle pole accumulation nor the identity of the trigger factor has strong experimental support—they are pure model assumptions. SAC silencing cannot be triggered from the spindle pole when the threshold value is too high, whereas it occurs prematurely when the threshold value is too low. Nevertheless, we would like to emphasize that, as far as we can tell, our model proposes the first mechanism capable for robust SAC silencing. Other seminal models in the field (50, 51, 52, 53), while greatly contributing to quantitative understanding of SAC functions, do not have the capacity to account for robust SAC silencing. While providing a feasible proposal for robust SAC silencing does not validate our model, it does provide interesting predictions waiting for future experimental testing. With this perspective, we now set out to theorize the potential reasons that robust timing of SAC silencing becomes compromised in cancer cell mitosis and meiosis I of mammalian oocytes.
Results
Abnormal spindle configuration could affect SAC silencing in cancer cell mitosis
In cancer cell mitosis, SAC signaling unexpectedly responds to aberrant spindle morphology (16). Cancer cell mitosis, unlike normal somatic cell mitosis, often occurs with supernumerary centrosomes that initially form a multipolar spindle (54). Yet progression of multipolar division is hindered by active SAC signal (16). Interestingly, cancer cells manage pseudo-bipolar divisions by clustering the supernumerary centrosomes into two poles (55, 56). Such pseudo-bipolar division frequently incurs chromosome missegregation (55, 56), as multipolar spindles tend to harbor significantly more merotelic kinetochore attachments than normal bipolar spindles do (55, 56). A merotelic attachment is a defective kinetochore-spindle attachment wherein one kinetochore is attached to both spindle poles (57). Merotelic attachments mostly evade the SAC in normal mitosis (58) probably because the corresponding kinetochore tension is still sufficient to cause the depletion of SAC components from the kinetochore (57). During pseudo-bipolar divisions, chromosomes segregate while a significant number of merotelic attachments persist, causing frequent lagging chromosomes and missegregation (6, 55, 56). In a sense, the pseudo-bipolar division prevents massive, often fatal, chromosome missegregation at the price of minor missegregation caused by chromosome lagging. Therefore, forcing fatal multipolar division is a potential cancer therapy under discussion (16, 59); and effectiveness of such therapy entails SAC silencing in the multipolar spindle. Here, we aim to understand 1) the mechanisms that prevent SAC silencing in multipolar spindles even though the SAC is insensitive against the erroneous merotelic kinetochore attachment, and 2) the dependence of SAC silencing on spindle pole configurations.
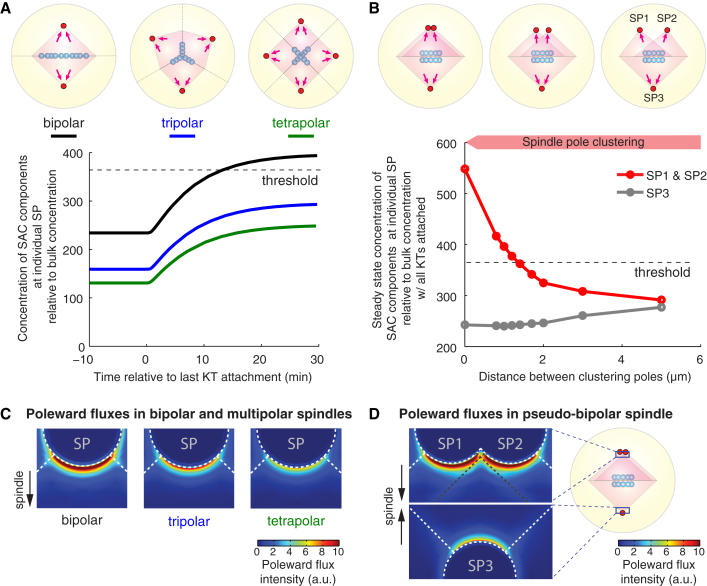
We first use our transport-only model to investigate the influence of spindle configuration on accumulation of SAC components at spindle poles. Specifically, we modify the spindle geometry in the transport-only model to reflect the initial multipolar configuration and the intermediate states en route to pseudo-bipolarity (Fig. 2, A and B), while maintaining all the other features and parameters of the model as those for normal bipolar spindles (see Tables S1 and S2). For now, we put aside the potential effect of merotelic attachments, and assume stable kinetochore-spindle attachments in all kinetochores. The model results show that each spindle pole in a multipolar spindle accumulates lesser amount of SAC components than does each pole in a bipolar spindle (Fig. 2 A). This difference emerges because multiple spindle poles diverge the poleward flux into multiple directions, and hence the flux in each direction is weakened (Fig. 2 C). The divergence of poleward flux could explain the mitotic arrest in a multipolar spindle even if all the kinetochore-spindle attachments are stable. However, clustering of spindle poles causes adjacent spindle arrays to overlap (Fig. 2 B), which leads to confluence of previously separated poleward fluxes (Fig. 2 D). Merging of poleward fluxes significantly boosts the concentration of SAC components at the clustered spindle pole and could thus trigger SAC silencing (Fig. 2 B).
Figure 2.
Poleward fluxes of SAC components diverge in multipolar spindle until spindle-pole clustering causes fluxes to converge. (KT) Kinetochore; (SP) spindle pole. (A) Spindle pole signal in multipolar spindles before and after the final kinetochore attachment. (B) Final steady-state signals at the spindle pole for each intermediate spindle configuration during spindle pole clustering. Microtubule density in the overlapped spindle area (heavier red shade) is doubled (see Appendix C). (A and B) Computations are performed on static geometries with examples given in the cartoons. (Magenta arrows on cartoons) Streaming proteins flux toward the spindle poles. (Dashed lines on plots) Signal threshold at spindle pole necessary to trigger SAC silencing. (C and D) Poleward flux intensities in multipolar spindles (C) and spindle pole clustering (D). (Color maps) Absolute flux intensity of streaming proteins at the transverse plane through the spindle poles. Flux intensity quickly decreases away from the spindle pole. The crescents right outside the spindle pole show the difference between flux intensities in different cases. In all simulations, the kinetochore positions are chosen to maximize symmetry; the geometry is then reduced according to the symmetry to improve computational efficiency. This treatment is viable because the model results barely depend on the positions of the kinetochores inside the spindle (Fig. S1).
To obtain a more realistic sense of the SAC silencing caused by centrosome clustering, we simulate the full transport-reaction model (21) with the multipolar geometries and the intermediate states en route to pseudo-bipolarity. Here we ignore the dynamic process of centrosome clustering, and simulate each intermediate state as geometrically static. This approximation could make the results of intermediate states less accurate, but it does not change the eventual outcome of the centrosome clustering process. This is because whether SAC silences critically depends upon the steady-state signal level at the spindle poles in the final spindle configuration. Besides, centrosomes cluster much more slowly (approximately subhour) than SAC components are transported in the spindle (approximately minutes). One would thus expect the signal pattern to roughly follow the sequence in Fig. 2 B during a realistic centrosome clustering process.
Following our previous work (21), we use cyclin B concentration as the readout for SAC silencing during centrosome clustering (Fig. 3 A). In a tripolar spindle that eventually remodels into a pseudo-bipolar spindle, the model predicts that the pole with two centrosomes attracts stronger poleward flux, and accumulates enough cyclin B (as spindle pole signal, see Fig. 1 C) to trigger SAC silencing (Fig. 3 A). Our finding thus sheds light on the signaling role of centrosome clustering: it pools distributed, weakened poleward flux into a strong flux, which yields a strong signal at the clustered pole to trigger SAC silencing.
Figure 3.
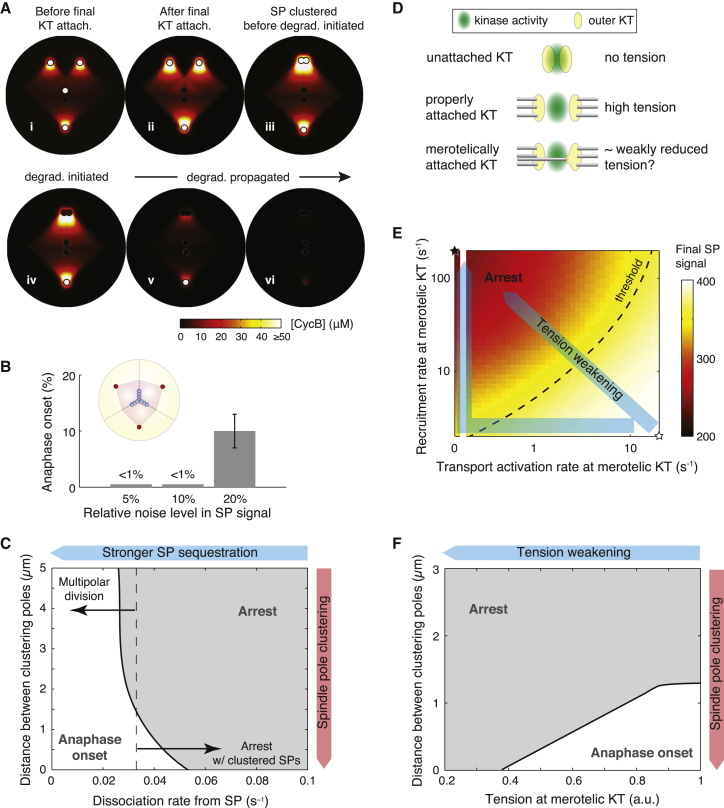
SAC silencing with asymmetric spindle pole clustering and merotelic kinetochore attachments. (KT) Kinetochore; (SP) spindle pole. (A) Spatiotemporal pattern of cyclin B during spindle pole clustering. (i and ii) Steady-state cyclin B pattern before and after the last kinetochore attachment. Cyclin B degradation is not triggered, and the patterns persist. (iii) Cyclin B pattern with two clustered spindle poles right before SAC silencing is triggered. (iv–vi) Propagation of cyclin B degradation with two clustered spindle poles. (B) Probability of SAC silencing and anaphase onset in a multipolar spindle in the presence of signal noise at the spindle pole. Results from 100 stochastic simulations. Error bars show mean ± SE estimated via the Wald method. (C) Phase diagram of mitotic fate given degrees of spindle pole clustering and dissociation rates of SAC components from the spindle pole (koffSP; see Table S1). (D) Illustration of the effect of merotelic attachment on kinetochore tension. Normal tension with amphitelic attachment pulls the outer kinetochore away from the inner centromere, where kinase activity is centered. Merotelic attachment could pull part of the outer kinetochore back toward the inner centromere region and effectively increase the kinase activity on the outer kinetochore. Kinase activity at a merotelic attachment may thus resemble that at an attached kinetochore with weakly reduced tension. (E) Effects of reduction in kinetochore tension at one merotelically attached kinetochore on the spindle pole signal in a normal bipolar spindle. Reduction in kinetochore tension promotes recruitment of SAC components onto the kinetochore and/or inhibits transport activation from the kinetochore. Exactly how the rates depend on kinetochore tension is unknown. (Translucent blue arrows) Examples of the rate-tension dependence. For simplicity, by default the reduction of kinetochore tension first reduces the transport activation rate, and then increases the recruitment rate (bent blue arrow, see Fig. S2 for details). (F) Phase diagram of mitotic fate given degrees of spindle pole clustering and kinetochore tension at one merotelically attached kinetochore. (E and F) One kinetochore out of 10 is assigned the weakened tension. (B, C, and F) The anaphase onset refers to those cases in which cyclin B is degraded within 2 h after the last kinetochore attachment; otherwise the mitotic fate is assigned as arrest.
We note that the pseudo-bipolar spindle configuration after centrosome clustering could be sufficient, but might not be necessary to trigger SAC silencing. The bottom line is: as long as one spindle pole gets sufficient accumulation, it will trigger SAC silencing. In the tripolar spindle configuration that lacks centrosome clustering, for instance, the steady-state spindle pole accumulation of SAC components is generally below the threshold value that triggers SAC silencing (Fig. 2 A), but large stochastic fluctuations (e.g., ∼20% of the steady-state level) could temporarily raise spindle pole accumulation above the threshold and trigger SAC silencing, although with only small probability (Fig. 3 B). Alternatively, if for some reason SAC components turn over at the spindle poles more slowly in the cell, the multipolar spindle could also achieve sufficient spindle pole accumulation steadily to trigger SAC silencing (Fig. 3 C), conferring multipolar cell division. More interestingly, when several but not all centrosomes cluster sufficiently to achieve a strong spindle pole signal, SAC silencing may also be triggered with some poles left unclustered. For instance, the tetrapolar spindle may successfully trigger SAC silencing with only two spindle poles clustered, amounting to a pseudo-tripolar division (Fig. S3). These predictions are in line with the experimental observations that cancer cells as well as normal cells could undergo viable multipolar divisions under certain conditions (60, 61, 62). Taken together, we suggest that the key to SAC silencing is sufficient spindle pole accumulation of SAC components, and centrosome clustering is one of the possible ways leading to sufficient accumulation in multipolar spindles.
In addition, the status of kinetochore-spindle attachment is also important for spindle pole accumulation of SAC components. According to our model, the whole mitotic spindle is the signal mediator for SAC silencing; specifically, the signal is issued by kinetochores, transmitted via spindle microtubules, and integrated at spindle poles (Fig. 1). Spindle pole accumulation of SAC components hence critically depends on the transport into and out of kinetochores controlled by the status of kinetochore-spindle attachments. In light of this analysis, a large number of aberrant, merotelic kinetochore attachments in cancer cell mitosis may also affect SAC silencing. We thus further use the model to investigate the effects of aberrant kinetochore attachments on the spatiotemporal dynamics of SAC proteins and the timing of SAC silencing in addition to the centrosome clustering process.
Kinetochore tension at an attached kinetochore controls two aspects of the transport process (Fig. 1 A): 1) it serves as a key upstream signal recruiting SAC components (26, 27, 28, 29, 30), and 2) it inhibits dynein-mediated transport of SAC components from the kinetochore (36). Therefore, merotelic spindle-kinetochore attachments, which presumably compromise kinetochore tension (Fig. 3 D), could increase SAC recruitment and/or decrease poleward transport at the kinetochore. In the model, however, the kinetochore tension is not explicitly expressed. The exact quantitative relationship between the rates and the kinetochore tension is unknown. Therefore, we simulate the effect of merotelic attachment using combination of different values for the two rates (Fig. 3 E); each rate varies between its extreme values assigned for typical attached and unattached kinetochores.
We first examine the effect of merotelic kinetochore attachment in normal bipolar division. We incorporate the corresponding variations in the SAC recruitment rate and the transport activation rate into the transport-only model while keeping all other model parameters the same as those for normal somatic cell mitosis, including the bipolar spindle configuration. The simulation results show that both increase of SAC recruitment and decrease of transport activation at one kinetochore lower the spindle pole accumulation (Fig. 3 E). Regardless of the exact quantitative relationship between the rates and the kinetochore tension, there exists some threshold kinetochore tension, above which the spindle pole signal is still sufficient to trigger SAC silencing. While the extreme case involving one unattached kinetochore expectedly leads to mitotic arrest (black star, Fig. 3 E) (63, 64), the model results suggest that small reductions in kinetochore tension from one or a few merotelically attached kinetochores are insufficient to evoke mitotic arrest. This finding is consistent with the observations on merotelic attachments in normal somatic cell mitosis: 1) merotelic attachments induce only weak, if any, reduction in kinetochore tension, because 3F3/2, a tension-sensing marker, is depleted from the kinetochore as from stably attached kinetochores (58); and 2) SAC can be silenced in the presence of merotelic attachments (58).
After examining their respective effects on SAC silencing individually, we investigate the combined effect of centrosome clustering and merotelic attachment on SAC silencing. The model results show that as long as kinetochore tension at the merotelically attached kinetochore is sufficiently high, SAC silencing in cancer cell mitosis depends only on centrosome clustering, and not on merotelic attachments (Fig. 3 F). Moreover, asymmetric clustering patterns could elevate the spindle pole signal at the more strongly clustered pole above the level in a normal bipolar spindle (Fig. 2 B); thus the signal at the this dominant pole may reach the threshold for triggering SAC silencing in the presence of more severe kinetochore attachment errors (Fig. S4). This result proposes, to our knowledge, a novel explanation for the existence of more merotelic attachments in cancer cell mitosis upon anaphase onset. Certainly, a severe reduction of kinetochore tension (Fig. 3 F) or a large number of merotelic kinetochores (Fig. S4) could further delay or even inhibit SAC silencing. Thus, mitotic exit in cancer cells with extra centrosomes requires both centrosome clustering and sufficient—but not necessarily thorough—correction of kinetochore attachment errors. These model results also suggest that while centrosome clustering could release the cell from multipolarity-induced mitotic arrest (Figs. 2 and 3 A), anaphase onset is probably delayed due to the time needed for centrosome clustering and partially correcting merotelic kinetochore attachments.
Overall, we believe that our model suggests a new role of centrosome clustering in mitotic exit of cancer cells, and underscores a novel functional coordination between spindle pole and kinetochore in SAC silencing.
Nonrobust SAC silencing in meiosis I of mammalian oocytes
Although a compromised SAC that permits deregulated proliferation could be considered advantageous for survival of cancer cells, mammalian oocytes do not gain any obvious benefits from reduced robustness of SAC silencing. Such nonrobust SAC silencing could result in aneuploid embryos that either perish in uterus or develop into organisms with severe congenital birth defects (3). What could have caused the apparently detrimental nonrobustness in SAC silencing to defy potential selection pressure and persist in oocyte meiosis? Could it be a tradeoff for other necessary functions of the meiotic process?
For mammalian oocytes, meiosis is long and complicated (3). Oocytes commit to meiosis during fetal development, during which the chromosomes undergo DNA replication and recombination. Meiosis is then arrested until sexual maturity. Upon ovulatory stimulation, some oocytes resume and complete meiosis I, during which homologs separate while cohesion between sister chromatids persists (Fig. 4 A). The second meiotic division (meiosis II) occurs only when the oocyte is fertilized. In meiosis II, cohesion between sister chromatids is dissolved, allowing separation of sister chromatids and production of haploid gametes.
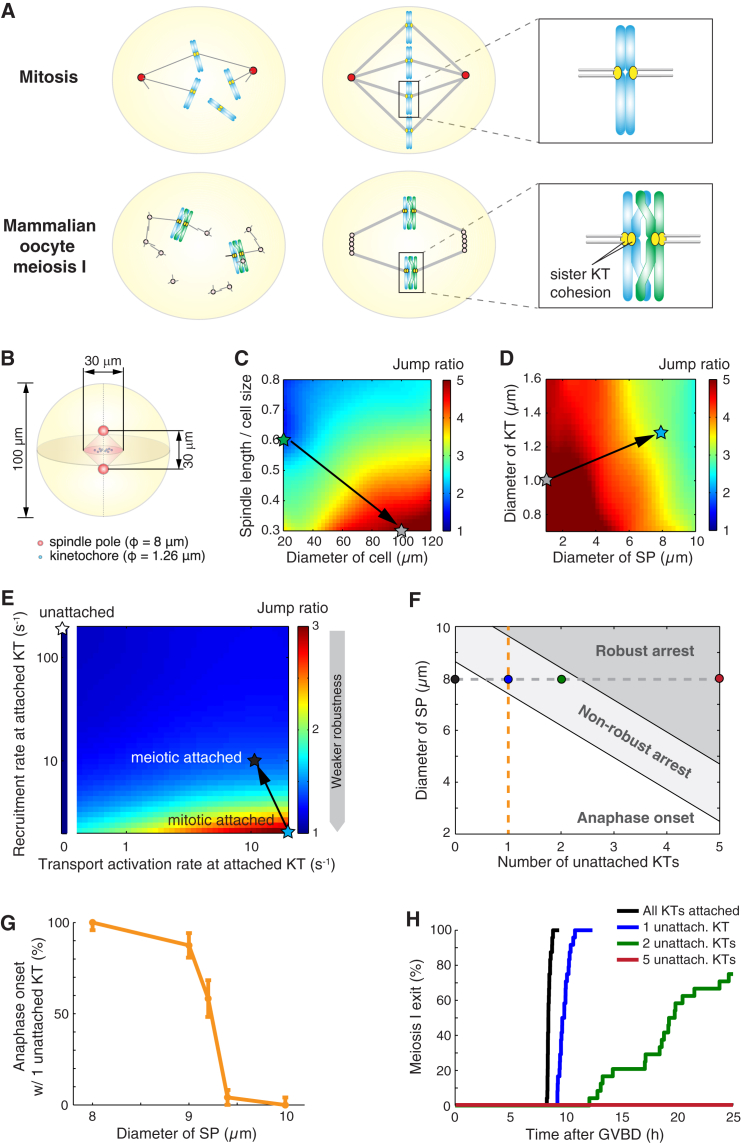
Figure 4.
Nonrobust SAC silencing in oocyte meiosis I cannot result from sizing, but could result from atypical kinetochore attachment. (A) Comparison between somatic cell mitosis and oocyte meiosis I. As opposed to mitosis, oocytes in meiosis I lack centrosomes and maintain unseparated sister kinetochores. (B) Geometric setting for oocyte meiosis I. In (C–E), robustness of the spindle pole signal is characterized by the jump ratio as defined in Fig. 1A. Color-labeled stars represent progressive adjustments of parameters for sizes and rates (details given in the following). (C) Signal robustness at various cell sizes and spindle sizes. (Green star) Sizes for somatic cells. (Gray star) Cell and spindle resized to oocyte dimensions, and the other parameters remain somatic cell values. (D) Signal robustness at various spindle pole sizes and kinetochore sizes. (Gray star) Same as in (C). (Blue star) Cell, spindle, spindle poles, and kinetochores are all resized to oocyte dimensions. (E) Signal robustness under varying recruitment rates and transport activation rates at attached kinetochores. (Blue star) Same as in (D); rates for attached kinetochores follow those in mitosis. (Black star) Increased recruitment rate and decreased transport activation rate at attached kinetochores (see Table S3). (White star) Rates for unattached kinetochores. (F) Meiotic fate with different numbers of unattached kinetochores and at various spindle pole sizes. (White region) Anaphase onset in deterministic simulations. (Light-gray region) Arrest in deterministic simulations but anaphase onset within 25 h in stochastic simulations. (Dark-gray region) Arrest within 25 h in stochastic simulations. (Solid circles) Default parameter value. (Colored dots and orange dashed line) Correspondence to cases in (G) and (H), respectively. (G) Computed frequency of premature anaphase onset with one persistently unattached kinetochore and different spindle pole sizes (parameters along orange dashed line in F). Results from 24 stochastic simulations. Error bars show mean ± SE estimated via the Wald method. (H) Cumulative distribution of time of oocyte meiosis I exit with respect to germinal vesicle breakdown (GVBD) with different numbers of persistently unattached kinetochores. For each simulation, the time for meiotic exit after GVBD = 5 h mean duration for establishing kinetochore attachments after GVBD (15, 66) plus the computed time for 90% cyclin B degradation since the last kinetochore attachment. (Line colors correspond to dot colors in F.) See Appendices D and E in the main text, and Supporting Materials and Methods for detailed procedure of stochastic simulations.
While errors can occur at any stage of mammalian oogenesis, chromosome segregation during the first meiotic division is notoriously error-prone (3, 10). The SAC functionally monitors kinetochore-spindle attachments in oocyte meiosis I (17, 18, 19, 20); nevertheless, mounting evidence indicates that the SAC is inherently defective during this division. SAC silencing and chromosome segregation can proceed even when a few chromosomes are unaligned or unattached to the spindle (11, 12, 13, 14, 15).
To identify factors that might compromise the robustness of SAC silencing in mammalian oocyte meiosis, we focus on the salient differences between the spindle apparatuses in mammalian oocyte meiosis I and in typical somatic cell mitosis. Mammalian oocytes are much larger than most somatic cells (∼100 vs. ∼20 μm in diameter) (Fig. 4 B). Unlike typical mitotic cells that have centrosomes and well-focused spindle poles, mammalian oocyte in meiosis I lack centrosomes (65) (Fig. 4 A). Consequently, the oocyte spindle is initially organized by numerous microtubule-organizing centers (MTOC) dispersed throughout a large cytoplasm (Fig. 4 A). It takes hours to form a bipolar spindle by MTOC clustering (66). The resulting bipolar meiotic spindle is longer in pole-to-pole length, larger in equatorial radius, and wider in spindle-pole diameter than the spindle in somatic cell mitosis (65) (Fig. 4 B). The persistence of cohesion between sister chromatids renders the sister kinetochores on meiosis I chromosomes a doublet that is twice as large as mitotic kinetochores. Furthermore, instead of forming end-on attachment as in normal somatic cell mitosis, the kinetochores remain laterally attached to the spindle for several hours onward (15, 66, 67). Meanwhile, depletion of SAC proteins from the attached kinetochores occurs extremely slowly (15, 67), and some key SAC components (e.g., Bub1) that respond to kinetochore tension persist at kinetochores even after homolog segregation in mammalian oocytes (68). The persistence of SAC proteins and tension-sensing molecules at the attached kinetochores indicates that kinetochore tension is likely lower in oocyte meiosis I than in somatic mitosis, constituting another oocyte meiosis I-specific feature.
Intrigued by these observations, we investigate how these distinct features affect the robustness of SAC silencing. Our original model indicates that robust SAC silencing hinges on the large jump ratio of the spindle pole accumulation of SAC components upon the final kinetochore-spindle attachment (Fig. 1 A), which essentially represents a large signal/noise. Herein we first use the transport-only model to examine the effects of oocyte-specific factors on this jump ratio.
We revise the geometric settings of the model to reflect the geometry of oocyte meiosis I after two spindle poles form via MTOC clustering. Typical dimensions in mammalian oocytes are applied: cell diameter, 100 μm; spindle length, 30 μm; and spindle pole diameter, 8 μm (Fig. 4 B). Additionally, each kinetochore domain assumes double volume to represent the functional union of sister kinetochores in oocyte meiosis I (Fig. 4 B). All other model parameters stay the same as those for normal somatic cell mitosis. We simulate the model in the meiotic geometry to determine whether these geometric factors alone could account for poor signal robustness. Notably, large cell size and relatively small spindle/cell size ratio together actually increase the jump ratio (from green star to gray star in Fig. 4 C); however, increases in spindle pole size and kinetochore volume reduce the jump ratio moderately (from gray star to blue star in Fig. 4 D). The final jump ratio resulting from these geometry changes is higher than that in mitosis (indicated by blue star in Fig. 4 D). Therefore, we conclude that geometric factors cannot account for the unstable SAC silencing in oocyte meiosis I. This size-free robustness reveals a mechanistic advantage of our model: it applies to cells of different sizes; moreover, these finding are in line with the fact that oocyte meiosis II and the first zygotic mitosis have similar cell and spindle sizes as oocyte meiosis I (69), but are not as error-prone (70).
Now that sizing differences fail to explain low signal robustness in oocyte meiosis I, we turn to the unique kinetochore-spindle attachment features in oocyte meiosis I, and examine its effect on the jump ratio of spindle pole accumulation. The meiotic kinetochores likely experience less tension than their mitotic counterparts, as suggested by kinetochore retention of Bub1 until late anaphase of meiosis I (68). Bub1 normally dissipates from the kinetochore in a tension-dependent manner upon chromosome alignment (71, 72, 73), and Bub1 mediates the association of other SAC proteins with kinetochores (74). Therefore, we reason that retention of Bub1 at attached kinetochores could result in a high recruitment rate of SAC components onto these kinetochores; such high recruitment could explain the extremely slow depletion of SAC proteins from attached kinetochores in oocyte meiosis I (15, 67). In the model, high recruitment rates at attached kinetochores (Table S3) significantly reduce the jump ratio and hence the signal robustness (from blue star to black star in Fig. 4 E). This is because SAC components are no longer preferentially recruited to the unattached kinetochores; a single unattached kinetochore therefore cannot sufficiently divert the poleward flux issued by numerous attached kinetochores. Therefore, the model suggests the atypical kinetochore-spindle attachment as the source of nonrobust SAC silencing. This theoretical finding is corroborated by a recent experimental observation that abnormal kinetochore-spindle attachments play an important role in aneuploidy in human oocyte meiosis I (75).
Having found that atypical kinetochore attachment alone could compromise the robustness of SAC silencing during meiosis I in mammalian oocytes, we next examine whether configuration of the spindle pole—the ultimate signal integrator of the spatiotemporal signaling system—interacts with the kinetochore-mediated impact on SAC silencing. Keeping the kinetochore tension reduced in oocyte meiosis I, we investigate the dependence of SAC silencing robustness on two factors: 1) spindle pole size, and 2) the number of unattached kinetochores (Fig. 4 F). Stochastic simulation results gathered from the full transport-reaction model indicate that SAC silencing is ultimately gated by the spindle pole size. That is, even after all chromosomes are properly attached to the spindle, a larger spindle pole, which effectively corresponds to the state of numerous dispersed MTOCs, could arrest oocyte meiosis I (Fig. 4, F and G). As dispersed MTOCs become sufficiently focused into spindle poles, SAC is silenced (Fig. 4, F and G). Interestingly, despite one or more unattached kinetochores, a hyperfocused spindle pole could deterministically confer SAC silencing (Fig. 4 F). This finding explains the unusually high aneuploidy rate in mutant mouse oocyte meiosis I with hyperfocused spindle poles (76). With the spindle pole size fixed at 8 μm, which is about the average size found in wild-type mammalian oocyte meiosis I, the model predicts that the response of SAC silencing to the number of unattached kinetochores becomes highly probabilistic (Fig. 4, F and H). While one or a few unattached kinetochores reduce the mean spindle pole accumulation of SAC components below the threshold for SAC silencing, such conditions fail to permanently arrest meiosis I in the presence of stochastic noise. In other words, unattached kinetochores merely delay meiotic exit; having more unattached kinetochores just leads to longer delays and a larger variation in the timing of meiotic exit (Fig. 4 H). The nonrobustness stems from the low jump ratio of spindle pole signal (Fig. 4 E). These findings propose what is, to our knowledge, a novel explanation for the inherently nonrobust SAC silencing in mammalian oocyte meiosis I (11, 12, 13, 14, 15). They also align with the observation that low-dose nocodazole treatment (76), which may produce a limited number of unattached or misattached kinetochores, delays but does not abrogate exit of mammalian oocyte meiosis I.
In sum, the model suggests that geometric factors in mammalian oocyte meiosis I are not the cause for nonrobust SAC silencing. Instead, high SAC recruitment rates at the kinetochores could jeopardize signal robustness at the spindle pole and account for nonrobust SAC silencing. The slow process of MTOC clustering (spindle pole formation) and the resulting large spindle poles could lower and delay the spindle pole signal, thus helping to reduce meiotic error. The model points out a functional coupling between kinetochore attachments and spindle pole configuration in the signaling for accurate chromosome segregation.
Discussion
Experimental research on cell division control has progressed substantially in the past three decades, and researchers have defined many if not all essential molecular interactions among key mitotic players involved in the SAC mechanism (5). Valuable knowledge obtained from experiments renders this field ripe for systems-level modeling. Theoreticians can begin to quantitatively address mechanistic questions regarding the robustness of SAC silencing. While remarkably robust in normal somatic cell division (5, 6), SAC silencing is likely compromised in other physiologically relevant scenarios, e.g., cancer cell mitosis and mammalian oocyte meiosis I, as put forward in the Introduction. This variation in robustness presents a perfect testing ground and yet remains a challenging task for modeling. A useful model should not only recapitulate the robustness of SAC silencing, but also explain how things go wrong when conditions change.
Previously, we established a theoretical model that introduced a spatial-regulation based mechanism for achieving robust SAC silencing (21). This model provides, to our knowledge, a coherent new picture of the SAC silencing process. In contrast to the conventional view that SAC is inactivated directly by depleting SAC proteins from stably attached kinetochores, the model points out the entire spindle structure as signal mediator of SAC silencing (Fig. 1). Specifically, the kinetochores mediate poleward flux that encodes the information about kinetochore-spindle attachments; the spindle poles integrate the poleward flux, and confer a noise-proof signal to initiate SAC silencing. The whole-spindle perspective of our model enables us to deduce in this work how unusual features of the division apparatus in cancer cell mitosis and mammalian oocyte meiosis I might compromise SAC silencing. In this regard, other insightful model could not be used to study effects of spindle abnormalities on SAC signaling, as they do not incorporate the spatiotemporal regulation by the spindle.
Our model study suggests that in cancer cells with supernumerary centrosomes, multiple spindle poles could dissipate poleward flux in multiple directions and consequently weaken the spindle pole signal sufficiently to cause mitotic arrest (Fig. 2, A and C). Centrosome clustering could ameliorate the spindle pole signal, and resume SAC silencing (Figs. 2, B and D, and 3 A). In addition, centrosome clustering coordinates with correction of merotelic kinetochore attachments to produce sufficient spindle pole signal for SAC silencing (Fig. 3 F). If a dominant pole arises from asymmetric clustering, it might accumulate superfluous signal, allowing more merotelic attachment errors to slip into anaphase and hence aggravating chromosome missegregation (Fig. S4). This finding underscores the importance of coordinated spindle assembly in SAC signaling. Of course, abnormalities in cancer cells extend far beyond supernumerary centrosomes and centrosome clustering. Nevertheless, the model presented here constitutes a starting point, from which we can begin to understand the role of spindle reorganization in SAC silencing.
For mammalian oocyte meiosis I, our model suggests that geometric factors are unlikely to cause nonrobust SAC silencing, and that low signal robustness could stem from increases in recruitment rate of SAC components to meiosis I kinetochores. The resulting low signal/noise in the spindle pole signal delays, instead of permanently blocks, onset of anaphase I in the presence of a few unattached kinetochores (Fig. 4). Additionally, the large meiotic spindle poles that focus slowly may have prevented some erroneous SAC silencing, whereas hyperfocused spindle poles aggravate erroneous silencing (Fig. 4, F and G). We suggest that nonrobust SAC silencing might be an adverse effect of persistent cohesion between sister chromatids. Notably, this persistent cohesion is the most important meiosis I-specific function. Protection of cohesion between sister chromatids requires shugoshins (77, 78, 79). Recruitment of shugoshins to the chromosomes and kinetochores requires Bub1 (77, 80, 81). In particular, Bub 1 keeps oocyte meiotic-specific shugoshin-2 on the centromere until metaphase II (82). Therefore, centromeric retention of Bub1 is necessary for persistent sister chromatid cohesion during meiosis I in oocytes. Unfortunately, however, because Bub1 and its ultimate target of protection, cohesin, promote SAC recruitment and activation at kinetochores (74, 83), their persistent localization at the kinetochore compromises the robustness of SAC silencing. While this reasoning could explain the error-prone nature of meiosis I in mammalian oocytes, it could not account for the remarkably low error rate in meiosis I of mammalian spermatocytes (84, 85), in which sister centromeric cohesin is also protected. This discrepancy may derive from many differences between oocyte meiosis I and spermatocyte meiosis I. For instance, spermatocytes have centrosomes, but oocytes do not (65); and the spatiotemporal dynamics of SAC components differ between spermatocytes and oocytes (86). How these differences contribute to the robustness of SAC silencing would be a subject of future study, which would certainly benefit from more detailed experimental observations on spermatocyte meiosis I. In a broader sense, different species with or without centrosomes utilize distinct spindle configurations to complete chromosome segregation. For instance, in Caenorhabditis elegans meiosis, the spindle microtubules bundle in parallel around the holocentric kinetochores to segregate chromosomes (87). Understanding how these diverse configurations of spindle apparatus affect the SAC mechanism is the subject of future work.
Our model suggests that centrosome clustering in cancer cells and spindle pole focusing in oocytes play similar functional roles: both increase the spindle pole signal and promote SAC silencing. Hyperfocused spindle pole in oocyte meiosis aggravates premature SAC silencing and chromosome missegregation, much as the dominant pole in asymmetric centrosome clustering does. But in general, the MTOCs in acentriolar oocyte meiosis significantly outnumber the centrosomes in cancer cell mitosis; this difference leads to a contrast in the extent of MTOC clustering in the two scenarios and therein quantitative deviations of the results in the two cases. For example, the jump ratio upon the final kinetochore attachment increases significantly as the spindle pole shrinks in the oocyte (Fig. 4 D), whereas it stays leveled during centrosome clustering (Fig. S5 A). This is because centrosome clustering contributes to a much smaller actual size change in the spindle pole (a fewfold change in volume) than that shown in Fig. 4 D (∼102-fold change in volume). The decrease of jump ratio with spindle pole sizes derives from the competition between the spindle pole and the unattached kinetochore: a large spindle pole sequesters greater amount of SAC components and effectively opposes the diversion of poleward flux by the unattached kinetochore. Expectedly, the dependence of jump ratio on the spindle pole size attenuates with decreasing binding affinity of SAC components to the spindle pole (Fig. S5 B).
We note that the model results depend on the signal threshold required for triggering SAC silencing. If the threshold is set sufficiently high, no SAC silencing could happen in any case. Vice versa, sufficiently low threshold initiates SAC silencing regardless of spindle disruption or unattached kinetochores. In this study, the signal threshold is assumed to remain the same for cancer cell mitosis and oocyte meiosis. Arising from some biochemical pathway, the threshold could admittedly vary with factors like mutations or cell type-specific regulations of the signaling molecules. But because the biochemical pathway for SAC in this model is highly simplified, the model at this stage is not the best tool to study the biochemical effects on SAC signaling. Rather, we choose to leverage the strength of this model and focus on the effects of spindle abnormalities on the spatiotemporally regulated signal as a starting point. Likewise, left unchanged are other model parameters that do not have evidenced relationship to the centrosome clustering process or oocyte-specific spindle assembly process. Nonetheless, the model results concerning spatiotemporal regulation alone already yield interesting physical insights into aberrancies in SAC silencing. In the future when the model is enriched with more accurate biochemical details supplied by experiments, it can then be used to dissect the intricate molecular interactions in SAC signaling in the milieu of their spatiotemporal context.
Overall, our spatiotemporal model provides a perspective on dysfunctional SAC signaling and chromosome missegregation beyond molecular pathways. It indicates that coupling between kinetochore attachments and spindle pole formation dictates the robustness of SAC silencing. Coordinated spindle assembly in every aspect of the spindle is thus important for accurate chromosome segregation. In this sense, the model highlights an interesting feature of the SAC that echoes its name: the SAC monitors not only kinetochore attachments, but also the overall spindle assembly.
Author Contributions
J.L. developed the concept; J.C. and J.L. designed the models; J.C. implemented the simulations and performed data analysis; J.C. and J.L. interpreted the data; and J.C. and J.L. wrote the article.
Acknowledgments
This work was supported by the Intramural Research Program of the National Heart, Lung, and Blood Institute at the National Institutes of Health.
Editor: Charles Wolgemuth.
Footnotes
Supporting Materials and Methods, one note, seven figures, and three tables are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(15)01073-5.
Appendix A: Formulation of Transport-Only Model
The transport-only model is formulated with compartmentalized convection-diffusion-reaction equations. Reaction terms describe the binding/unbinding of SAC components with microtubules and spindle poles. The whole system is divided into NKT kinetochore domains, NSP spindle pole domains, and NSP associated cytoplasmic domains (Figs. 1 B, 2, A and B, and 4 B). Because the model results are largely insensitive to the positions of kinetochores as long as they are inside the spindle (Fig. S1), the kinetochore positions are chosen to maximize symmetry. The symmetry allows reduction of geometry for computational efficiency. A reduced geometry usually includes one spindle pole domain and its associated cytoplasmic domain; the number of kinetochore domains also reduces according to the symmetry.
The SAC components in the cytoplasm assume either the streaming or the diffusive state. Because the streaming proteins constantly bind and unbind with the microtubules, the streaming state is represented by two variables—one for the proteins bound to the microtubule (Y1), and the other for the ones unbound but can rebind to microtubules (Y0). Interconversion between Y0 and Y1 depicts the binding/unbinding dynamics between the streaming proteins and the microtubules. In contrast, proteins in the diffusive state (Y00) do not have binding affinity to the microtubule. The spatiotemporal dynamics of the SAC components in the cytoplasm is thus governed by Eqs. 1–3 with reflective boundary conditions at the cell boundary.
In cytoplasm:
| (1) |
| (2) |
| (3) |
Meanings and values of the parameters are given in Table S1. In particular, at any given location in the cell the streaming velocity is assumed to point toward the nearest spindle pole, as indicated by the unit vector, . The binding rate of streaming proteins, konMT, is proportional to the local microtubule density ρMT (Eq. 4). The value Uext denotes the sequestration potential imposed by the spindle on the streaming proteins; it phenomenologically integrates all sequestrating factors mediated by the spindle apparatus, e.g., sequestration by spindle matrix, peri-spindle membranous networks. Here, kB is the Boltzmann constant, and T is temperature.
We treat the microtubule network as a mean density field that includes both the spindle and astral microtubules (Eq. 4). The density field concentrates towards the spindle pole:
| (4) |
where is the distance towards the nearest spindle pole. The values NMTsp and NMTast denote the numbers of microtubules inside and outside the spindle, respectively.
The mean-field treatment of the microtubule network is supported by timescale separation in the system. The microtubules in mitosis are highly dynamic with the average lifetime of 30 s or less. On much slower timescales, convection from the kinetochore to the spindle pole takes a few minutes, and the spindle pole signal in our model approaches steady state in ∼10 min in somatic cell mitosis and much longer in large oocytes. This timescale separation warrants mean-field description of the microtubule network. In the mean-field setup, the dynamics of the microtubules are essentially lumped into the binding/unbinding dynamics of the streaming proteins with the microtubules.
Binding/unbinding of protein with the spindle pole specifically occurs in the spindle pole domain. This domain thus accommodates an additional state variable for the spindle-pole bound proteins (YP). The spatiotemporal dynamics in the spindle pole domain is governed by Eqs. 5–8. Y1, Y0, and Y00 naturally assume continuity conditions at the spindle pole boundary because the spindle pole is set up as a virtual domain for these variables. The variable YP, however, lives exclusively on the spindle pole domain, and assumes the reflective boundary condition at the spindle pole boundary.
At the spindle pole:
| (5) |
| (6) |
| (7) |
| (8) |
Without knowing details of the spindle pole-binding dynamics, the model assumes one simple scenario to effectively characterize partial sequestration of the streaming proteins at the spindle pole. The streaming proteins fall off the microtubules upon entering the spindle pole ( = 1000 s−1 and = 0), bind with the spindle pole with rate konSP, and dissociate from the spindle pole with rate koffSP.
Finally, on each kinetochore domain, the variables for kinetochore-bound proteins live exclusively (Eq. 9).
At the nth kinetochore,
| (9) |
The kinetochore-binding/unbinding dynamics is characterized by the flux boundary conditions at the kinetochore boundaries.
At the boundary of unattached kinetochores, the boundary condition characterizes the strong recruitment and turnover as diffusive proteins:
At the boundary of attached kinetochores, the boundary condition characterizes the weak recruitment and issuance of streaming proteins:
In the boundary conditions, n refers to the unit vector normal to the kinetochore boundary. The Γ-values with corresponding subscripts denote the fluxes of proteins across the kinetochore boundary. The term sets the saturating limit of kinetochore-bound proteins.
The value koffKT is the turnover rate of SAC components into the cytoplasm in the diffusive state. The value konKTu is the recruitment rate of SAC components onto the unattached kinetochore. The value kDoffKT is the transport activation rate of SAC components at the attached kinetochore. Note that konKTu and kDoffKT phenomenologically characterize kinetochore tension.
In Eqs. 8 and 9, simple diffusion is applied to the spindle pole-bound (YP) and kinetochore-bound (YKn) species to homogenize the concentration of proteins in the spindle pole and kinetochore domains. This treatment takes place because our model concerns the average dynamics in these compartmentalized domains. With the homogenization, the spindle pole signal and the flux across kinetochore boundaries depend on the average concentration of SAC components in the corresponding domains.
Appendix B: Formulation of Biochemical Pathway
The full transport-reaction model further incorporates the biochemical reactions into the spatiotemporal dynamics. Because SAC proteins, APC/C, and cyclin B are assumed to undergo the same transport process, the spatial regulation terms are kept the same as in Eqs. 1–9. As the biochemical reactions occur volumetrically, no modification is needed for the boundary conditions. The general form of the equation looks like the following:
The chemical reaction fluxes for SAC proteins (M), APC/C (A), and cyclin B (C) are given in Eqs. 10–14. The fluxes carry opposite signs for the chemically active and inactive states. There is no inactive C, because cyclin B degradation is the major outcome of cyclin B during SAC silencing.
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
Please refer to Tables S1 and S2 for meanings and values of the parameters in Eqs. 10–14. In particular, SAC activation in Eqs. 10 and 11 gradually decreases with kinetochore attachments. The SAC activation term is further broken into two parts to characterize the localized activation at the kinetochore and the catalyzed activation in the cytoplasm (88, 89). Furthermore, cyclin B degradation in Eq. 14 assumes a nonlinear form to inhibit leaky degradation before the final kinetochore attachment. Please refer to Fig. S6 and Supporting Materials and Methods for the SAC activation term in Eqs. 10 and 11 and the nonlinear cyclin B degradation term in Eq. 14.
Overall, the variables of the full model result from combination of biochemical species, chemical activity states, and transport states. The whole set of state variables are given in Table 1
Table 1.
List of state variables of the model
| Active SAC | Inactive SAC | Active APC/C | Inactive APC/C | Active Cyclin B | Active Trigger Factor | Inactive Trigger Factor | |
|---|---|---|---|---|---|---|---|
| Streaming: bound with MT | Ma1 | Mi1 | Aa1 | Ai1 | Ci1 | N/A | N/A |
| Streaming: unbound with MT | Ma0 | Mi0 | Aa0 | Ai0 | Ca0 | N/A | N/A |
| Diffusive | Ma00 | Mi00 | Aa00 | Ai00 | Ca00 | Xa00 | Xi00 |
| Bound to SP | MaP | MiP | AaP | AiP | CaP | XaP | XiP |
| Inside nth KT | MaKn | M1Kn | AaKn | AiKn | CaKn | XaKn | XiKn |
. Although the full model contains ∼100 partial differential equations as given in the Supporting Materials and Methods, they are combined from far fewer basic elements (see Eqs. 1–14 above) and controlled by a limited number of parameters.
Finally, the concentration signal at the spindle pole is relayed to SAC silencing by the trigger factor X that constitutively concentrates at the spindle pole. X assumes a generic toggle switch dynamics (Eqs. 15 and 16) (90), and fires (shifted to high value state) when cyclin B concentration, Ca, at the spindle pole, exceeds a threshold. Autoactivation mechanism in X ensures irreversible activation of X (90). The threshold for activating X is chosen to be sufficiently higher than the penultimate steady-state concentration of SAC components at the spindle pole to ensure robust signaling against noise; it is also sufficiently lower than the final steady-state concentration at the spindle pole to be reached within limited time. Biochemical rates for X are adjusted to realize such a threshold:
| (15) |
| (16) |
where GK refers to the Goldbeter-Koshland function.
The spatial regulation terms for X are rather simple because X is assumed to constantly concentrate at the spindle pole. The spatial terms are thus expressed in Eqs. 17–20, as follows:
In the cytoplasm, we have
| (17) |
at the spindle pole, we have
| (18) |
| (19) |
at the nth kinetochore, we have
| (20) |
and with the flux boundary condition independent of the attachment status of the kinetochore, we have
Appendix C: Microtubule Density During Centrosome Clustering
Centrosome clustering causes spatial overlapping of the microtubule networks organized by the clustering spindle poles (Fig. 2 B, area in the spindle with a heavier shade). In this area microtubule density is doubled. For simplicity, the model does not differentiate the microtubule network to which the streaming protein is bound. The velocity of streaming protein in the overlapped region is assumed to point towards the nearest spindle pole (Fig. 2 B, schematically indicated by magenta arrows), regardless of the microtubule network to which the protein is actually bound.
Appendix D: Stochastic Simulations for Evaluation of Signal Robustness
Stochastic simulations are used to evaluate the probability of SAC silencing induced by fluctuation noises. The probability is 100% for any parameter or geometric setup that deterministically causes SAC silencing. In a stochastic simulation, SAC silencing is registered if cyclin B level drops to <10% of its maximal level within the designated simulation cutoff time—10% maximum cyclin B level roughly corresponds to the cyclin B level required for mitotic or meiotic exit. The cutoff time is 2 h for mitosis and 25 h for meiosis to match a few times their realistic durations in reality.
Because the study concerns how variations in the spatiotemporal regulation influence robustness of the spindle pole signal-triggered SAC silencing, stochastic fluctuations are specifically implemented in the spindle pole signal, i.e., cyclin B activity. Noise in the cyclin B signal results from fluctuations in cyclin B concentration and biochemical activity. A high cyclin B concentration at the spindle pole leads to very small concentration fluctuations. With ∼100 nM bulk concentration for most SAC components, a spindle pole ∼cubic micron in volume and a protein concentration several hundred times the bulk concentration accumulates at least 104 molecules of each biochemical species. The relative fluctuations in molecule number are thus no more than ∼1%. Besides, fluctuations in individual kinetochore tension are averaged and smoothed by the transport dynamics, causing much lower level of fluctuations at the spindle pole (Fig. S7). Finally, fluctuations in biochemical activities could stem from fluctuations in protein conformation, variations in protein expression level, etc. Here we simply lump all these stochastic effects into a dynamic noise in the biochemical reaction rates controlled by cyclin B.
Exclusively at the spindle pole region, a relative noise is implemented as a multiplier ξ(t) to the reaction rates that involve Ca in Eqs. 10–16, except for the degradation of cyclin B itself. For example, the APC/C dynamics at the spindle pole in Eq.12 is replaced by Eq. 21. The whole set of revised equations is given in the Supporting Materials and Methods:
| (21) |
Intracellular noises usually assume multiple timescales. Fast noises likely average out and have little effects on slow processes. But slow noises on timescales comparable to the process of interest could significantly affect the process. Because our model is mainly concerned with the ability of the transport mechanism to distinguish the number of attached kinetochores, the most important process of interest is the transduction of information from the kinetochores to the spindle pole. This process is mediated by dynein-dependent transport along the spindle microtubules, which takes time on the order of minutes. Therefore, we impose on the noise term a memory effect of 2 min. For easy implementation, the noise term ξ(t) assumes a piecewise function with segments of 2 min; random numbers with mean value 1 are assigned to each segment. Mathematically, ξ(t) = ξn, where n = floor(t/2 min). ξn ∼ N(1, q), where q characterizes noise level of (q × 100)%.
Appendix E: Geometry Reduction for Stochastic Simulations
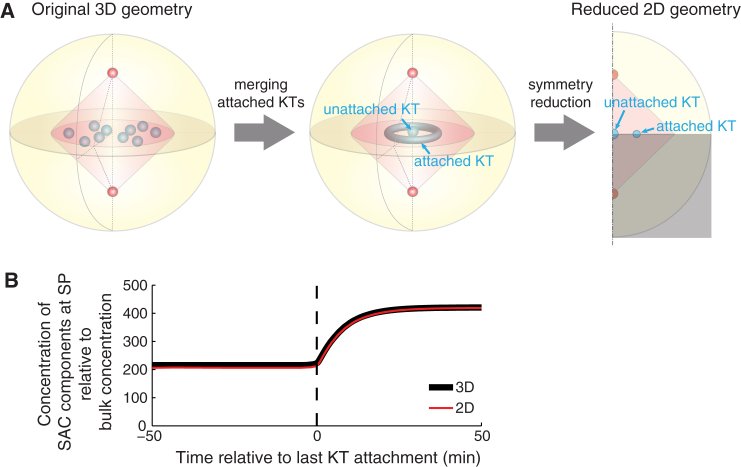
To reduce the computational cost for the lengthy stochastic simulations, we perform the simulations on 2D-axisymmetric geometry (Fig. 5 A) in replacement of the 3D geometry. Such axisymmetric geometry is characterized by two spatial variables r and z.
Figure 5.
Reduced geometry for stochastic simulation. (A) Geometry transformation and reduction. All attached kinetochores are merged into a toroid domain. The axisymmetric geometry is reduced to 2D. (Shaded area) Further reduction by mirror symmetry. (B) The spindle pole signal in the reduced 2D geometry is nearly identical to the result from the original 3D geometry.
Robust SAC silencing signal at the spindle pole stems from the competition between the total fluxes of SAC components through the attached kinetochores versus the total fluxes through the unattached kinetochores. Therefore, it is a good approximation to lump the total fluxes through the unattached kinetochores into one domain at the center of the cell, and lump those through the attached kinetochores into another toroid domain away from the central domain for the unattached kinetochores (Fig. 5 A).
To conserve the total fluxes of SAC components through the unattached kinetochores, the volume of the central spherical domain must equal the total volume of unattached kinetochores. Therefore, the radius of the central spherical domain is given by
| (22) |
where NuKT denotes the number of unattached kinetochores.
Similarly, the volume of the toroid domain must equal the total volume of attached kinetochores. Hence the tube radius of the torus is given by
| (23) |
where NaKT denotes the number of attached kinetochores and Rtorus is the circumferential radius of the torus.
As expected, the spindle pole signal computed from the 2D simulation is highly consistent with that from the 3D simulation (Fig. 5 B).
Supporting Citations
References (91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124) appear in the Supporting Material.
Supporting Material
References
- 1.Morgan D.O. New Science Press; London, UK: 2007. The Cell Cycle—Principles of Control. [Google Scholar]
- 2.Kops G.J.P.L., Weaver B.A.A., Cleveland D.W. On the road to cancer: aneuploidy and the mitotic checkpoint. Nat. Rev. Cancer. 2005;5:773–785. doi: 10.1038/nrc1714. [DOI] [PubMed] [Google Scholar]
- 3.Nagaoka S.I., Hassold T.J., Hunt P.A. Human aneuploidy: mechanisms and new insights into an age-old problem. Nat. Rev. Genet. 2012;13:493–504. doi: 10.1038/nrg3245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Gordon D.J., Resio B., Pellman D. Causes and consequences of aneuploidy in cancer. Nat. Rev. Genet. 2012;13:189–203. doi: 10.1038/nrg3123. [DOI] [PubMed] [Google Scholar]
- 5.Musacchio A., Salmon E.D. The spindle-assembly checkpoint in space and time. Nat. Rev. Mol. Cell Biol. 2007;8:379–393. doi: 10.1038/nrm2163. [DOI] [PubMed] [Google Scholar]
- 6.Thompson S.L., Compton D.A. Examining the link between chromosomal instability and aneuploidy in human cells. J. Cell Biol. 2008;180:665–672. doi: 10.1083/jcb.200712029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Holland A.J., Cleveland D.W. Boveri revisited: chromosomal instability, aneuploidy and tumorigenesis. Nat. Rev. Mol. Cell Biol. 2009;10:478–487. doi: 10.1038/nrm2718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Siegel J.J., Amon A. New insights into the troubles of aneuploidy. Annu. Rev. Cell Dev. Biol. 2012;28:189–214. doi: 10.1146/annurev-cellbio-101011-155807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.McGranahan N., Burrell R.A., Swanton C. Cancer chromosomal instability: therapeutic and diagnostic challenges. EMBO Rep. 2012;13:528–538. doi: 10.1038/embor.2012.61. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Jones K.T., Lane S.I. Molecular causes of aneuploidy in mammalian eggs. Development. 2013;140:3719–3730. doi: 10.1242/dev.090589. [DOI] [PubMed] [Google Scholar]
- 11.LeMaire-Adkins R., Radke K., Hunt P.A. Lack of checkpoint control at the metaphase/anaphase transition: a mechanism of meiotic nondisjunction in mammalian females. J. Cell Biol. 1997;139:1611–1619. doi: 10.1083/jcb.139.7.1611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Nagaoka S.I., Hodges C.A., Hunt P.A. Oocyte-specific differences in cell-cycle control create an innate susceptibility to meiotic errors. Curr. Biol. 2011;21:651–657. doi: 10.1016/j.cub.2011.03.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Kouznetsova A., Lister L., Höög C. Bi-orientation of achiasmatic chromosomes in meiosis I oocytes contributes to aneuploidy in mice. Nat. Genet. 2007;39:966–968. doi: 10.1038/ng2065. [DOI] [PubMed] [Google Scholar]
- 14.Sebestova J., Danylevska A., Anger M. Lack of response to unaligned chromosomes in mammalian female gametes. Cell Cycle. 2012;11:3011–3018. doi: 10.4161/cc.21398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Lane S.I.R., Yun Y., Jones K.T. Timing of anaphase-promoting complex activation in mouse oocytes is predicted by microtubule-kinetochore attachment but not by bivalent alignment or tension. Development. 2012;139:1947–1955. doi: 10.1242/dev.077040. [DOI] [PubMed] [Google Scholar]
- 16.Kwon M., Godinho S.A., Pellman D. Mechanisms to suppress multipolar divisions in cancer cells with extra centrosomes. Genes Dev. 2008;22:2189–2203. doi: 10.1101/gad.1700908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Wassmann K., Niault T., Maro B. Metaphase I arrest upon activation of the Mad2-dependent spindle checkpoint in mouse oocytes. Curr. Biol. 2003;13:1596–1608. doi: 10.1016/j.cub.2003.08.052. [DOI] [PubMed] [Google Scholar]
- 18.Homer H.A., McDougall A., Herbert M. Mad2 prevents aneuploidy and premature proteolysis of cyclin B and securin during meiosis I in mouse oocytes. Genes Dev. 2005;19:202–207. doi: 10.1101/gad.328105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.McGuinness B.E., Anger M., Nasmyth K. Regulation of APC/C activity in oocytes by a Bub1-dependent spindle assembly checkpoint. Curr. Biol. 2009;19:369–380. doi: 10.1016/j.cub.2009.01.064. [DOI] [PubMed] [Google Scholar]
- 20.Hoffmann S., Maro B., Polanski Z. A single bivalent efficiently inhibits cyclin B1 degradation and polar body extrusion in mouse oocytes indicating robust SAC during female meiosis I. PLoS One. 2011;6:e27143. doi: 10.1371/journal.pone.0027143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Chen J., Liu J. Spatial-temporal model for silencing of the mitotic spindle assembly checkpoint. Nat. Commun. 2014;5:4795. doi: 10.1038/ncomms5795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Howell B.J., Hoffman D.B., Salmon E.D. Visualization of Mad2 dynamics at kinetochores, along spindle fibers, and at spindle poles in living cells. J. Cell Biol. 2000;150:1233–1250. doi: 10.1083/jcb.150.6.1233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Wojcik E., Basto R., Hays T. Kinetochore dynein: its dynamics and role in the transport of the Rough deal checkpoint protein. Nat. Cell Biol. 2001;3:1001–1007. doi: 10.1038/ncb1101-1001. [DOI] [PubMed] [Google Scholar]
- 24.Howell B.J., McEwen B.F., Salmon E.D. Cytoplasmic dynein/dynactin drives kinetochore protein transport to the spindle poles and has a role in mitotic spindle checkpoint inactivation. J. Cell Biol. 2001;155:1159–1172. doi: 10.1083/jcb.200105093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Basto R., Scaerou F., Karess R. In vivo dynamics of the rough deal checkpoint protein during Drosophila mitosis. Curr. Biol. 2004;14:56–61. doi: 10.1016/j.cub.2003.12.025. [DOI] [PubMed] [Google Scholar]
- 26.Liu D., Vader G., Lens S.M. Sensing chromosome bi-orientation by spatial separation of aurora B kinase from kinetochore substrates. Science. 2009;323:1350–1353. doi: 10.1126/science.1167000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Welburn J.P., Vleugel M., Cheeseman I.M. Aurora B phosphorylates spatially distinct targets to differentially regulate the kinetochore-microtubule interface. Mol. Cell. 2010;38:383–392. doi: 10.1016/j.molcel.2010.02.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Maresca T.J., Salmon E.D. Intrakinetochore stretch is associated with changes in kinetochore phosphorylation and spindle assembly checkpoint activity. J. Cell Biol. 2009;184:373–381. doi: 10.1083/jcb.200808130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Famulski J.K., Chan G.K. Aurora B kinase-dependent recruitment of hZW10 and hROD to tensionless kinetochores. Curr. Biol. 2007;17:2143–2149. doi: 10.1016/j.cub.2007.11.037. [DOI] [PubMed] [Google Scholar]
- 30.Ditchfield C., Johnson V.L., Taylor S.S. Aurora B couples chromosome alignment with anaphase by targeting BubR1, Mad2, and Cenp-E to kinetochores. J. Cell Biol. 2003;161:267–280. doi: 10.1083/jcb.200208091. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Vigneron S., Prieto S., Lorca T. Kinetochore localization of spindle checkpoint proteins: who controls whom? Mol. Biol. Cell. 2004;15:4584–4596. doi: 10.1091/mbc.E04-01-0051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Hoffman D.B., Pearson C.G., Salmon E.D. Microtubule-dependent changes in assembly of microtubule motor proteins and mitotic spindle checkpoint proteins at PtK1 kinetochores. Mol. Biol. Cell. 2001;12:1995–2009. doi: 10.1091/mbc.12.7.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Chan G.K.T., Jablonski S.A., Yen T.J. Human BUBR1 is a mitotic checkpoint kinase that monitors CENP-E functions at kinetochores and binds the cyclosome/APC. J. Cell Biol. 1999;146:941–954. doi: 10.1083/jcb.146.5.941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Waters J.C., Chen R.H., Salmon E.D. Localization of Mad2 to kinetochores depends on microtubule attachment, not tension. J. Cell Biol. 1998;141:1181–1191. doi: 10.1083/jcb.141.5.1181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Chen R.H., Waters J.C., Murray A.W. Association of spindle assembly checkpoint component XMAD2 with unattached kinetochores. Science. 1996;274:242–246. doi: 10.1126/science.274.5285.242. [DOI] [PubMed] [Google Scholar]
- 36.Whyte J., Bader J.R., Vaughan K.T. Phosphorylation regulates targeting of cytoplasmic dynein to kinetochores during mitosis. J. Cell Biol. 2008;183:819–834. doi: 10.1083/jcb.200804114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Kasuboski J.M., Bader J.R., Vaughan K.T. Zwint-1 is a novel Aurora B substrate required for the assembly of a dynein-binding platform on kinetochores. Mol. Biol. Cell. 2011;22:3318–3330. doi: 10.1091/mbc.E11-03-0213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Zheng Y. A membranous spindle matrix orchestrates cell division. Nat. Rev. Mol. Cell Biol. 2010;11:529–535. doi: 10.1038/nrm2919. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Chen J., Lippincott-Schwartz J., Liu J. Intracellular spatial localization regulated by the microtubule network. PLoS One. 2012;7:e34919. doi: 10.1371/journal.pone.0034919. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Famulski J.K., Vos L.J., Chan G.K. Dynein/Dynactin-mediated transport of kinetochore components off kinetochores and onto spindle poles induced by nordihydroguaiaretic acid. PLoS One. 2011;6:e16494. doi: 10.1371/journal.pone.0016494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Chen Q., Zhang X., Zhang C. Cyclin B1 is localized to unattached kinetochores and contributes to efficient microtubule attachment and proper chromosome alignment during mitosis. Cell Res. 2008;18:268–280. doi: 10.1038/cr.2008.11. [DOI] [PubMed] [Google Scholar]
- 42.Acquaviva C., Herzog F., Pines J. The anaphase promoting complex/cyclosome is recruited to centromeres by the spindle assembly checkpoint. Nat. Cell Biol. 2004;6:892–898. doi: 10.1038/ncb1167. [DOI] [PubMed] [Google Scholar]
- 43.Kamenz J., Hauf S. Slow checkpoint activation kinetics as a safety device in anaphase. Curr. Biol. 2014;24:646–651. doi: 10.1016/j.cub.2014.02.005. [DOI] [PubMed] [Google Scholar]
- 44.Rattani A., Vinod P.K., Nasmyth K. Dependency of the spindle assembly checkpoint on Cdk1 renders the anaphase transition irreversible. Curr. Biol. 2014;24:630–637. doi: 10.1016/j.cub.2014.01.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Vázquez-Novelle M.D., Sansregret L., Petronczki M. Cdk1 inactivation terminates mitotic checkpoint surveillance and stabilizes kinetochore attachments in anaphase. Curr. Biol. 2014;24:638–645. doi: 10.1016/j.cub.2014.01.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Yang Q., Ferrell J.E., Jr. The Cdk1-APC/C cell cycle oscillator circuit functions as a time-delayed, ultrasensitive switch. Nature Cell Biol. 2013;15:519–525. doi: 10.1038/ncb2737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Golan A., Yudkovsky Y., Hershko A. The cyclin-ubiquitin ligase activity of cyclosome/APC is jointly activated by protein kinases Cdk1-cyclin B and Plk. J. Biol. Chem. 2002;277:15552–15557. doi: 10.1074/jbc.M111476200. [DOI] [PubMed] [Google Scholar]
- 48.Reddy S.K., Rape M., Kirschner M.W. Ubiquitination by the anaphase-promoting complex drives spindle checkpoint inactivation. Nature. 2007;446:921–925. doi: 10.1038/nature05734. [DOI] [PubMed] [Google Scholar]
- 49.Stegmeier F., Rape M., Elledge S.J. Anaphase initiation is regulated by antagonistic ubiquitination and deubiquitination activities. Nature. 2007;446:876–881. doi: 10.1038/nature05694. [DOI] [PubMed] [Google Scholar]
- 50.He E., Kapuy O., Novák B. System-level feedbacks make the anaphase switch irreversible. Proc. Natl. Acad. Sci. USA. 2011;108:10016–10021. doi: 10.1073/pnas.1102106108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Ibrahim B., Diekmann S., Dittrich P. In-silico modeling of the mitotic spindle assembly checkpoint. PloS One. 2008;3:e1555. doi: 10.1371/journal.pone.0001555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Sear R.P., Howard M. Modeling dual pathways for the metazoan spindle assembly checkpoint. Proc. Natl. Acad. Sci. USA. 2006;103:16758–16763. doi: 10.1073/pnas.0603174103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Doncic A., Ben-Jacob E., Barkai N. Evaluating putative mechanisms of the mitotic spindle checkpoint. Proc. Natl. Acad. Sci. USA. 2005;102:6332–6337. doi: 10.1073/pnas.0409142102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Nigg E.A. Centrosome aberrations: cause or consequence of cancer progression? Nat. Rev. Cancer. 2002;2:815–825. doi: 10.1038/nrc924. [DOI] [PubMed] [Google Scholar]
- 55.Ganem N.J., Godinho S.A., Pellman D. A mechanism linking extra centrosomes to chromosomal instability. Nature. 2009;460:278–282. doi: 10.1038/nature08136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Silkworth W.T., Nardi I.K., Cimini D. Multipolar spindle pole coalescence is a major source of kinetochore mis-attachment and chromosome mis-segregation in cancer cells. PLoS One. 2009;4:e6564. doi: 10.1371/journal.pone.0006564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Gregan J., Polakova S., Cimini D. Merotelic kinetochore attachment: causes and effects. Trends Cell Biol. 2011;21:374–381. doi: 10.1016/j.tcb.2011.01.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Cimini D., Howell B., Salmon E.D. Merotelic kinetochore orientation is a major mechanism of aneuploidy in mitotic mammalian tissue cells. J. Cell Biol. 2001;153:517–527. doi: 10.1083/jcb.153.3.517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Ogden A., Rida P.C.G., Aneja R. Let’s huddle to prevent a muddle: centrosome declustering as an attractive anticancer strategy. Cell Death Differ. 2012;19:1255–1267. doi: 10.1038/cdd.2012.61. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Duncan A.W., Taylor M.H., Grompe M. The ploidy conveyor of mature hepatocytes as a source of genetic variation. Nature. 2010;467:707–710. doi: 10.1038/nature09414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Yang Z., Loncarek J., Rieder C.L. Extra centrosomes and/or chromosomes prolong mitosis in human cells. Nat. Cell Biol. 2008;10:748–751. doi: 10.1038/ncb1738. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Gisselsson D., Jin Y., Mandahl N. Generation of trisomies in cancer cells by multipolar mitosis and incomplete cytokinesis. Proc. Natl. Acad. Sci. USA. 2010;107:20489–20493. doi: 10.1073/pnas.1006829107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Rieder C.L., Cole R.W., Sluder G. The checkpoint delaying anaphase in response to chromosome monoorientation is mediated by an inhibitory signal produced by unattached kinetochores. J. Cell Biol. 1995;130:941–948. doi: 10.1083/jcb.130.4.941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Rieder C.L., Schultz A., Sluder G. Anaphase onset in vertebrate somatic cells is controlled by a checkpoint that monitors sister kinetochore attachment to the spindle. J. Cell Biol. 1994;127:1301–1310. doi: 10.1083/jcb.127.5.1301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Schuh M., Ellenberg J. Self-organization of MTOCs replaces centrosome function during acentrosomal spindle assembly in live mouse oocytes. Cell. 2007;130:484–498. doi: 10.1016/j.cell.2007.06.025. [DOI] [PubMed] [Google Scholar]
- 66.Kitajima T.S., Ohsugi M., Ellenberg J. Complete kinetochore tracking reveals error-prone homologous chromosome biorientation in mammalian oocytes. Cell. 2011;146:568–581. doi: 10.1016/j.cell.2011.07.031. [DOI] [PubMed] [Google Scholar]
- 67.Gui L., Homer H. Spindle assembly checkpoint signalling is uncoupled from chromosomal position in mouse oocytes. Development. 2012;139:1941–1946. doi: 10.1242/dev.078352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Brunet S., Pahlavan G., Maro B. Functionality of the spindle checkpoint during the first meiotic division of mammalian oocytes. Reproduction. 2003;126:443–450. doi: 10.1530/rep.0.1260443. [DOI] [PubMed] [Google Scholar]
- 69.Courtois A., Schuh M., Hiiragi T. The transition from meiotic to mitotic spindle assembly is gradual during early mammalian development. J. Cell Biol. 2012;198:357–370. doi: 10.1083/jcb.201202135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Hassold T., Hunt P. To err (meiotically) is human: the genesis of human aneuploidy. Nat. Rev. Genet. 2001;2:280–291. doi: 10.1038/35066065. [DOI] [PubMed] [Google Scholar]
- 71.Taylor S.S., McKeon F. Kinetochore localization of murine Bub1 is required for normal mitotic timing and checkpoint response to spindle damage. Cell. 1997;89:727–735. doi: 10.1016/s0092-8674(00)80255-x. [DOI] [PubMed] [Google Scholar]
- 72.Skoufias D.A., Andreassen P.R., Margolis R.L. Mammalian mad2 and bub1/bubR1 recognize distinct spindle-attachment and kinetochore-tension checkpoints. Proc. Natl. Acad. Sci. USA. 2001;98:4492–4497. doi: 10.1073/pnas.081076898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Taylor S.S., Hussein D., Morrow C.J. Kinetochore localisation and phosphorylation of the mitotic checkpoint components Bub1 and BubR1 are differentially regulated by spindle events in human cells. J. Cell Sci. 2001;114:4385–4395. doi: 10.1242/jcs.114.24.4385. [DOI] [PubMed] [Google Scholar]
- 74.Johnson V.L., Scott M.I.F., Taylor S.S. Bub1 is required for kinetochore localization of BubR1, Cenp-E, Cenp-F and Mad2, and chromosome congression. J. Cell Sci. 2004;117:1577–1589. doi: 10.1242/jcs.01006. [DOI] [PubMed] [Google Scholar]
- 75.Holubcová Z., Blayney M., Schuh M. Human oocytes. Error-prone chromosome-mediated spindle assembly favors chromosome segregation defects in human oocytes. Science. 2015;348:1143–1147. doi: 10.1126/science.aaa9529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Kolano A., Brunet S., Verlhac M.H. Error-prone mammalian female meiosis from silencing the spindle assembly checkpoint without normal interkinetochore tension. Proc. Natl. Acad. Sci. USA. 2012;109:E1858–E1867. doi: 10.1073/pnas.1204686109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Leland S., Nagarajan P., Venkatachalam S. Heterozygosity for a Bub1 mutation causes female-specific germ cell aneuploidy in mice. Proc. Natl. Acad. Sci. USA. 2009;106:12776–12781. doi: 10.1073/pnas.0903075106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Kitajima T.S., Hauf S., Watanabe Y. Human Bub1 defines the persistent cohesion site along the mitotic chromosome by affecting Shugoshin localization. Curr. Biol. 2005;15:353–359. doi: 10.1016/j.cub.2004.12.044. [DOI] [PubMed] [Google Scholar]
- 79.Kitajima T.S., Kawashima S.A., Watanabe Y. The conserved kinetochore protein shugoshin protects centromeric cohesion during meiosis. Nature. 2004;427:510–517. doi: 10.1038/nature02312. [DOI] [PubMed] [Google Scholar]
- 80.Tang Z., Sun Y., Yu H. Human Bub1 protects centromeric sister-chromatid cohesion through Shugoshin during mitosis. Proc. Natl. Acad. Sci. USA. 2004;101:18012–18017. doi: 10.1073/pnas.0408600102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Kawashima S.A., Yamagishi Y., Watanabe Y. Phosphorylation of H2A by Bub1 prevents chromosomal instability through localizing shugoshin. Science. 2010;327:172–177. doi: 10.1126/science.1180189. [DOI] [PubMed] [Google Scholar]
- 82.Lee J., Kitajima T.S., Watanabe Y. Unified mode of centromeric protection by shugoshin in mammalian oocytes and somatic cells. Nat. Cell Biol. 2008;10:42–52. doi: 10.1038/ncb1667. [DOI] [PubMed] [Google Scholar]
- 83.Tachibana-Konwalski K., Godwin J., Nasmyth K. Spindle assembly checkpoint of oocytes depends on a kinetochore structure determined by cohesin in meiosis I. Curr. Biol. 2013;23:2534–2539. doi: 10.1016/j.cub.2013.10.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Nicklas R.B., Waters J.C., Ward S.C. Checkpoint signals in grasshopper meiosis are sensitive to microtubule attachment, but tension is still essential. J. Cell Sci. 2001;114:4173–4183. doi: 10.1242/jcs.114.23.4173. [DOI] [PubMed] [Google Scholar]
- 85.Martin R.H., Ko E., Rademaker A. Distribution of aneuploidy in human gametes: comparison between human sperm and oocytes. Am. J. Med. Genet. 1991;39:321–331. doi: 10.1002/ajmg.1320390315. [DOI] [PubMed] [Google Scholar]
- 86.Kallio M., Eriksson J.E., Gorbsky G.J. Differences in spindle association of the mitotic checkpoint protein Mad2 in mammalian spermatogenesis and oogenesis. Dev. Biol. 2000;225:112–123. doi: 10.1006/dbio.2000.9818. [DOI] [PubMed] [Google Scholar]
- 87.Wignall S.M., Villeneuve A.M. Lateral microtubule bundles promote chromosome alignment during acentrosomal oocyte meiosis. Nat. Cell Biol. 2009;11:839–844. doi: 10.1038/ncb1891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Simonetta M., Manzoni R., Ciliberto A. The influence of catalysis on mad2 activation dynamics. PLoS Biol. 2009;7:e10. doi: 10.1371/journal.pbio.1000010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.De Antoni A., Pearson C.G., Musacchio A. The Mad1/Mad2 complex as a template for Mad2 activation in the spindle assembly checkpoint. Curr. Biol. 2005;15:214–225. doi: 10.1016/j.cub.2005.01.038. [DOI] [PubMed] [Google Scholar]
- 90.Tyson J.J., Chen K.C., Novak B. Sniffers, buzzers, toggles and blinkers: dynamics of regulatory and signaling pathways in the cell. Curr. Opin. Cell Biol. 2003;15:221–231. doi: 10.1016/s0955-0674(03)00017-6. [DOI] [PubMed] [Google Scholar]
- 91.Doxsey S. Re-evaluating centrosome function. Nat. Rev. Mol. Cell Biol. 2001;2:688–698. doi: 10.1038/35089575. [DOI] [PubMed] [Google Scholar]
- 92.Wühr M., Chen Y., Mitchison T.J. Evidence for an upper limit to mitotic spindle length. Curr. Biol. 2008;18:1256–1261. doi: 10.1016/j.cub.2008.07.092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Jorgensen P., Edgington N.P., Futcher B. The size of the nucleus increases as yeast cells grow. Mol. Biol. Cell. 2007;18:3523–3532. doi: 10.1091/mbc.E06-10-0973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Neumann F.R., Nurse P. Nuclear size control in fission yeast. J. Cell Biol. 2007;179:593–600. doi: 10.1083/jcb.200708054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Wang Z., Shah J.V., Cleveland D.W. In vivo quantitative studies of dynamic intracellular processes using fluorescence correlation spectroscopy. Biophys. J. 2006;91:343–351. doi: 10.1529/biophysj.105.077891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Wang Z., Sheetz M.P. One-dimensional diffusion on microtubules of particles coated with cytoplasmic dynein and immunoglobulins. Cell Struct. Funct. 1999;24:373–383. doi: 10.1247/csf.24.373. [DOI] [PubMed] [Google Scholar]
- 97.Ross J.L., Wallace K., Holzbaur E.L.F. Processive bidirectional motion of dynein-dynactin complexes in vitro. Nat. Cell Biol. 2006;8:562–570. doi: 10.1038/ncb1421. [DOI] [PubMed] [Google Scholar]
- 98.Heald R., Tournebize R., Hyman A. Spindle assembly in Xenopus egg extracts: respective roles of centrosomes and microtubule self-organization. J. Cell Biol. 1997;138:615–628. doi: 10.1083/jcb.138.3.615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.King S.J., Schroer T.A. Dynactin increases the processivity of the cytoplasmic dynein motor. Nat. Cell Biol. 2000;2:20–24. doi: 10.1038/71338. [DOI] [PubMed] [Google Scholar]
- 100.Reck-Peterson S.L., Yildiz A., Vale R.D. Single-molecule analysis of dynein processivity and stepping behavior. Cell. 2006;126:335–348. doi: 10.1016/j.cell.2006.05.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Howell B.J., Moree B., Salmon E.D. Spindle checkpoint protein dynamics at kinetochores in living cells. Curr. Biol. 2004;14:953–964. doi: 10.1016/j.cub.2004.05.053. [DOI] [PubMed] [Google Scholar]
- 102.Shah J.V., Botvinick E., Cleveland D.W. Dynamics of centromere and kinetochore proteins; implications for checkpoint signaling and silencing. Curr. Biol. 2004;14:942–952. doi: 10.1016/j.cub.2004.05.046. [DOI] [PubMed] [Google Scholar]
- 103.Famulski J.K., Vos L., Chan G. Stable hZW10 kinetochore residency, mediated by hZwint-1 interaction, is essential for the mitotic checkpoint. J. Cell Biol. 2008;180:507–520. doi: 10.1083/jcb.200708021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104.Lippincott-Schwartz J., Snapp E., Kenworthy A. Studying protein dynamics in living cells. Nat. Rev. Mol. Cell Biol. 2001;2:444–456. doi: 10.1038/35073068. [DOI] [PubMed] [Google Scholar]
- 105.Swaminathan R., Hoang C.P., Verkman A.S. Photobleaching recovery and anisotropy decay of green fluorescent protein GFP-S65T in solution and cells: cytoplasmic viscosity probed by green fluorescent protein translational and rotational diffusion. Biophys. J. 1997;72:1900–1907. doi: 10.1016/S0006-3495(97)78835-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 106.Tang Z., Bharadwaj R., Yu H. Mad2-Independent inhibition of APCCdc20 by the mitotic checkpoint protein BubR1. Dev. Cell. 2001;1:227–237. doi: 10.1016/s1534-5807(01)00019-3. [DOI] [PubMed] [Google Scholar]
- 107.Fang G. Checkpoint protein BubR1 acts synergistically with Mad2 to inhibit anaphase-promoting complex. Mol. Biol. Cell. 2002;13:755–766. doi: 10.1091/mbc.01-09-0437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108.Deibler R.W., Kirschner M.W. Quantitative reconstitution of mitotic CDK1 activation in somatic cell extracts. Mol. Cell. 2010;37:753–767. doi: 10.1016/j.molcel.2010.02.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109.Ciliberto A., Shah J.V. A quantitative systems view of the spindle assembly checkpoint. EMBO J. 2009;28:2162–2173. doi: 10.1038/emboj.2009.186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 110.Dick A.E., Gerlich D.W. Kinetic framework of spindle assembly checkpoint signalling. Nat. Cell Biol. 2013;15:1370–1377. doi: 10.1038/ncb2842. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 111.Mistry H.B., MacCallum D.E., Davidson F.A. Modeling the temporal evolution of the spindle assembly checkpoint and role of Aurora B kinase. Proc. Natl. Acad. Sci. USA. 2008;105:20215–20220. doi: 10.1073/pnas.0810706106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 112.Brito D.A., Rieder C.L. Mitotic checkpoint slippage in humans occurs via cyclin B destruction in the presence of an active checkpoint. Curr. Biol. 2006;16:1194–1200. doi: 10.1016/j.cub.2006.04.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 113.Oliveira R.A., Hamilton R.S., Nasmyth K. Cohesin cleavage and Cdk inhibition trigger formation of daughter nuclei. Nat. Cell Biol. 2010;12:185–192. doi: 10.1038/ncb2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 114.Luo X., Tang Z., Yu H. The Mad2 spindle checkpoint protein has two distinct natively folded states. Nat. Struct. Mol. Biol. 2004;11:338–345. doi: 10.1038/nsmb748. [DOI] [PubMed] [Google Scholar]
- 115.Lang I., Scholz M., Peters R. Molecular mobility and nucleocytoplasmic flux in hepatoma cells. J. Cell Biol. 1986;102:1183–1190. doi: 10.1083/jcb.102.4.1183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 116.Wojcieszyn J.W., Schlegel R.A., Jacobson K.A. Diffusion of injected macromolecules within the cytoplasm of living cells. Proc. Natl. Acad. Sci. USA. 1981;78:4407–4410. doi: 10.1073/pnas.78.7.4407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 117.Seksek O., Biwersi J., Verkman A.S. Translational diffusion of macromolecule-sized solutes in cytoplasm and nucleus. J. Cell Biol. 1997;138:131–142. doi: 10.1083/jcb.138.1.131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 118.Luca X., Martínez E.A., Alabart J.L. Relationship between antral follicle size, oocyte diameters and nuclear maturation of immature oocytes in pigs. Theriogenology. 2002;58:871–885. doi: 10.1016/s0093-691x(02)00699-4. [DOI] [PubMed] [Google Scholar]
- 119.Griffin J., Emery B.R., Carrell D.T. Comparative analysis of follicle morphology and oocyte diameter in four mammalian species (mouse, hamster, pig, and human) J. Exp. Clin. Assist. Reprod. 2006;3:2. doi: 10.1186/1743-1050-3-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 120.Otoi T., Yamamoto K., Suzuki T. Bovine oocyte diameter in relation to developmental competence. Theriogenology. 1997;48:769–774. doi: 10.1016/s0093-691x(97)00300-2. [DOI] [PubMed] [Google Scholar]
- 121.Tomari H., Honjou K., Horiuchi T. Relationship between meiotic spindle characteristics in human oocytes and the timing of the first zygotic cleavage after intracytoplasmic sperm injection. J. Assist. Reprod. Genet. 2011;28:1099–1104. doi: 10.1007/s10815-011-9634-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 122.Hu Y., Betzendahl I., Eichenlaub-Ritter U. Effects of low O2 and ageing on spindles and chromosomes in mouse oocytes from pre-antral follicle culture. Hum. Reprod. 2001;16:737–748. doi: 10.1093/humrep/16.4.737. [DOI] [PubMed] [Google Scholar]
- 123.Guo X., Gao S. Pins homolog LGN regulates meiotic spindle organization in mouse oocytes. Cell Res. 2009;19:838–848. doi: 10.1038/cr.2009.54. [DOI] [PubMed] [Google Scholar]
- 124.Lane S.I., Jones K.T. Non-canonical function of spindle assembly checkpoint proteins after APC activation reduces aneuploidy in mouse oocytes. Nat. Commun. 2014;5:3444. doi: 10.1038/ncomms4444. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.