Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2015 Oct 21;15(12):7987–7993. doi: 10.1021/acs.nanolett.5b03161

Lead Telluride Quantum Dot Solar Cells Displaying External Quantum Efficiencies Exceeding 120%

Marcus L Böhm †, Tom C Jellicoe †, Maxim Tabachnyk †, Nathaniel J L K Davis †, Florencia Wisnivesky-Rocca-Rivarola ‡, Caterina Ducati ‡, Bruno Ehrler #, Artem A Bakulin †, Neil C Greenham †,*
PMCID: PMC4676030  PMID: 26488847

Abstract

graphic file with name nl-2015-031618_0005.jpg

Multiple exciton generation (MEG) in semiconducting quantum dots is a process that produces multiple charge-carrier pairs from a single excitation. MEG is a possible route to bypass the Shockley-Queisser limit in single-junction solar cells but it remains challenging to harvest charge-carrier pairs generated by MEG in working photovoltaic devices. Initial yields of additional carrier pairs may be reduced due to ultrafast intraband relaxation processes that compete with MEG at early times. Quantum dots of materials that display reduced carrier cooling rates (e.g., PbTe) are therefore promising candidates to increase the impact of MEG in photovoltaic devices. Here we demonstrate PbTe quantum dot-based solar cells, which produce extractable charge carrier pairs with an external quantum efficiency above 120%, and we estimate an internal quantum efficiency exceeding 150%. Resolving the charge carrier kinetics on the ultrafast time scale with pump–probe transient absorption and pump–push–photocurrent measurements, we identify a delayed cooling effect above the threshold energy for MEG.

Keywords: Lead telluride quantum dots, solar cells, multiple exciton generation, pump−push photocurrent spectroscopy

Charge-carrier multiplication processes where an initial hot exciton is converted into multiple electron–hole pairs are considered promising mechanisms in photovoltaic devices to bypass efficiency losses due to thermalization of carriers generated by above-bandgap photons.1−3 While carrier multiplication in inorganic bulk semiconductors is inefficient and only significant at very high photon energies (e.g., hν > 4Eg in silicon),4 the same process is significantly amplified in semiconducting quantum dots (QDs) where the process is termed multiple exciton generation (MEG).5 It is believed that this phenomenon is due to the quantum confinement in QDs that provides a strong coulomb matrix element for the generation of multiple excitons from a hot single exciton and valence band electrons.6−8 Furthermore, the restricted spatial extent of the crystal weakens the requirement for crystal momentum conservation, thereby reducing the photon energy that is necessary to drive MEG.9,10

In a simple picture, the early time yield of multiple-exciton states is determined by a competition between the MEG process and rapid cooling of the photogenerated state.11−14 The multiple-exciton state may then decay by an Auger process, which in lead chalcogenide QDs is found to occur on 20–200 ps time scales,15,16 and it is this process that is typically used as the signature of multiple excitons in spectroscopic measurements of MEG yields.11,16,17 In a device, charge carrier separation must outcompete this decay process. While this competition will be highly sensitive to the interparticle charge transfer rate, the competing Auger rate has been found not to depend systematically on the choice of material within the PbS, PbSe, and PbTe series.13,18 On the other hand, the early time yield of MEG has been found to increase from PbS to PbSe to PbTe.13,14,19 One reason for this may be the decreased frequency of the longitudinal optical (LO) phonons20−22 that participate in the cooling process, leading to reduced carrier cooling rates.

Despite the prospect of utilizing MEG in PbTe QD-based solar cells, it has proved challenging to achieve working photovoltaic devices based on these particles, presumably due to the high susceptibility of PbTe to oxidation.23,24 Here, we present a solar cell based on PbTe QDs and show that charges produced by MEG can be efficiently harvested with external quantum efficiencies exceeding 120%. Furthermore, employing ultrafast transient absorption and two-pulse ultrafast photocurrent spectroscopy we confirm delayed intraband relaxation of hot carriers at early times and estimate the threshold energy necessary to extract charge carriers generated by MEG.

Lead telluride QDs with a band gap of 0.95 eV were synthesized following methods reported previously25 (see Methods). Narrow size distributions comparable with published literature values were confirmed by absorbance spectroscopy (UV/vis) and transmission electron microscopy (TEM; see Supporting Information S1).25−27 The valence band edge of the QDs was determined by ultraviolet photoelectron spectroscopy (UPS) to be −4.7 ± 0.1 eV (see Supporting Information S2). Adding the optical band gap measured by absorption spectroscopy gives an estimate of the conduction band edge energy of −3.8 ± 0.1 eV.

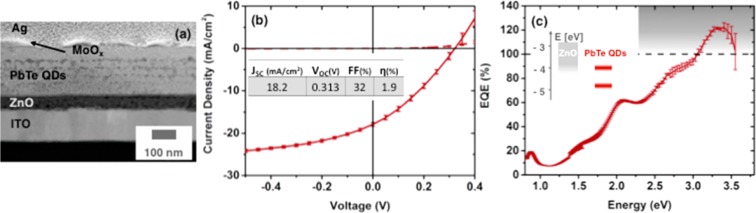
Solar cells were fabricated by depositing a dense array of PbTe CQDs on sol–gel processed ZnO films. The CQDs were applied following a layer-by-layer spin-coating approach where the native ligand oleic acid (OA) is replaced by the short organic molecule 3-mercaptopropionic acid (MPA). Further fabrication details are provided in Methods. Current–voltage characteristics and photovoltaic performance of optimized photovoltaic devices are shown in Figure 1b. Using smaller-bandgap QDs or changing the electron extraction layer from ZnO to TiO2 reduced the solar cell performance (see Supporting Information S3 and S4). In Figure 1c, the spectrally resolved photocurrent under short-circuit conditions normalized by the incident photon flux (i.e., external quantum efficiency (EQE)) shows a maximum value of 122 ± 4% at high photon energies (ca. 3.3 eV) that provides clear evidence for the extraction of charge carriers generated by MEG.28 The drop in quantum efficiency at energies greater than 3.5 eV is due to parasitic absorption by ZnO. Integration of the EQE over the AM1.5G solar spectrum results in a calculated short-circuit current that is ca. 3% larger than the value obtained from white-light measurements (see Supporting Information S5). This small discrepancy arises from a slight intensity dependence of the quantum efficiency (see Supporting Information S6 and S7).

Figure 1.

Figure 1

Open in a new tab

(a) Cross-sectional transmission electron microscopy image illustrating the device architecture. (b) Current–voltage charactersitics of solar cells fabricated from PbTe QDs (Eg = 0.95 eV) under AM1.5G conditions (solid line) and in the dark (dashed line). The inset shows the common photovoltaic parameters. (c) The corresponding EQE of solar cells displaying quantum efficiencies greater than 100% at high photon energies. The band energy alignment across the metal oxide QD heterojunction as determined by absorbance spectroscopy and UPS is shown as an inset.

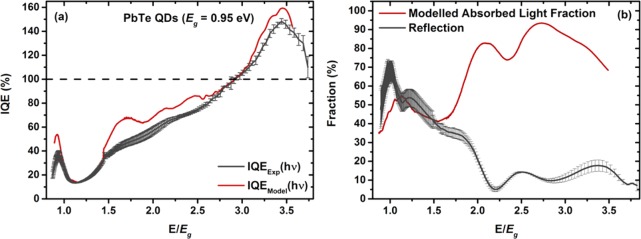
To study the efficiency of exciton dissociation and charge carrier extraction, we consider the absorbance-corrected quantum efficiency (i.e., the internal quantum efficiency (IQE)). Measuring the spectrally resolved reflected light fraction, R(hν) using calibrated germanium and silicon photodiodes (see Supporting Information S8)28 allows the calculation of IQEExp(hν) following the expression IQEExp(hν) = (EQE(hν))/(1 – R(hν)). In a second independent approach, we determine the absorbed light fraction A through an optical transfer matrix model (see Supporting Information S9)29,30 and calculate the IQEModel(hν) according the equation IQEModel(hν) = ((EQE(hν))/(A(hν)). Figure 2a presents the IQE curves from the two methods, which both show peak values above 150% at high photon energies. Note that we consider the determined IQEExp(hν) as the lower bound for the IQE as the measured R(hν) neglects parasitic absorbance and diffuse light scattering.28 In the low-energy region, we note a significant decrease in the IQE slightly above the QD bandgap, as has been seen in many other QD-based solar cells.28,31−34

Figure 2.

Figure 2

Open in a new tab

(a) IQE of devices consisting of PbTe QDs (Eg = 0.95 eV). IQEExp(hν) and IQEModel(hν) were determined using reflectance measurements and optical modeling respectively (see experimental details). (b) Experimentally determined reflectance (red curve) and modeled absorbed light fraction (gray curve).

Comparing the quantum yield of solar cells based on PbSe and PbTe QDs of comparable size reveals a significant increase in the latter system (ca. 90%28 and >150% in PbSe and PbTe QDs respectively). A similar material-dependent trend in initial MEG yield has been observed in spectroscopic experiments conducted on PbS, PbSe, and PbTe QDs in dispersion.13,14,17,19 These reports suggest that at comparable confinement energies the material-dependence of the quantum yield arises predominantly from ultrafast energy loss processes, which compete with the initial MEG process. Indeed, there is clear spectroscopic evidence of material-dependent cooling rates for near-band-edge states with relative cooling rates of 7.4:2.9:1 for PbS, PbSe, and PbTe QDs, respectively.13 Carrier cooling in lead chalcogenides is mainly mediated by a polar coupling to LO phonon modes.17 As the LO phonon frequency decreases in heavier lead chalcogenides,20−22 it can become smaller than the transition energy between individual quantum-confined electronic states. As a result the carrier cooling process is likely to require slow multiphonon instead of fast single-phonon mechanisms, which reduces the carrier cooling rate.35 However, the photogenerated states relevant to MEG are at much higher energies, and, considering the more continuum-like density of states higher up in the energy manifold,36 it remains unclear if these near-band-edge kinetics are relevant for the “hot regime” (see Figure 3). We therefore study the intraband relaxation kinetics of these “hot” carriers employing ultrafast pump–probe transient absorption spectroscopy where we excite a film of PbTe QDs (Eg = 0.93 eV) at 3.1 eV and probe with a white light pulse in the energy range between 1.9 and 3.1 eV (see Figure 4a).

Figure 3.

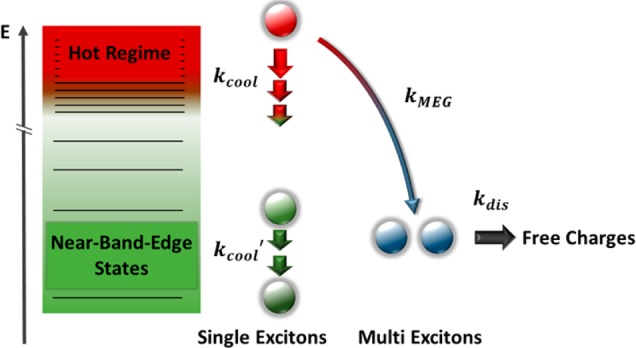
Figure 3

Open in a new tab

Schematic of the relaxation pathways of a photoexcited, hot single exciton.

Figure 4.

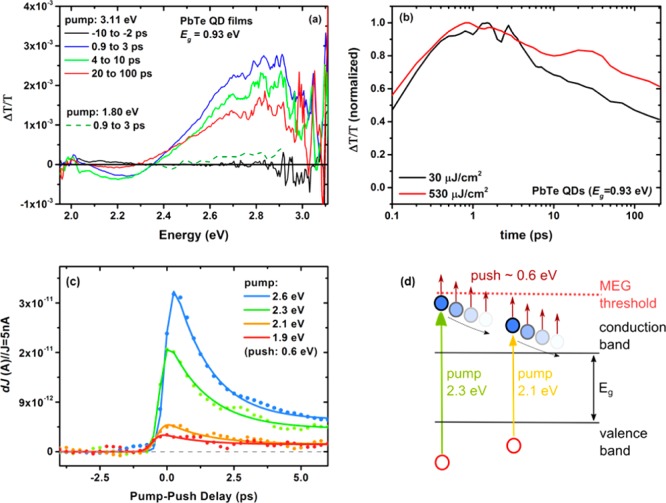
Figure 4

Open in a new tab

(a) Pump–probe transient absorption experiment where a film of PbTe QDs (Eg = 0.93 eV) is excited with a pump pulse of 3.11 eV (30 μJ/cm2) and 1.80 eV (60 μJ/cm2, green dashed line). The transient absorption was probed with a time-tunable white-light pulse. The full raw spectrum after an excitation at 1.80 eV can be found in the Supporting Information S11. (b) Kinetic traces for PbTe QD films, which were excited at 3.11 eV. To increase the signal-to-noise ratio, we integrated the signal between 2.96 and 2.40 eV. The black line indicates an excitation fluence of 30 μJ/cm2 and the red line a fluence of 530 μJ/cm2. (c) Photocurrent response as a function of time delay between pump and push pulse. The fluence of the pump excitation was adjusted to produce 5 nA for each excitation energy. The transients were corrected for the response at negative delay times. Lines are guide-to-the-eye exponential fits convolved with the 100 fs Gaussian response function of the setup. (d) Illustration of the pump–push photocurrent experiment in a schematic band diagram.

Interestingly, we find a prominent bleaching feature (positive ΔT/T) in the transient absorption spectrum at 2.8 eV, which we assign to a ground-state bleach (GSB) arising from state filling effects. This signal decays on a time scale of tens of picoseconds in a nonexponential manner, while maintaining its spectral shape. There is also evidence of a buildup of this signal at times below 1 ps. We note that this GSB is not present when a pump excitation of 1.8 eV is chosen (i.e., energies which are lower than the GSB signal; see Supporting Information S10) and find that the decay is fluence-dependent, showing slower decay dynamics at higher fluences (see Figure 4b). The observed behavior is different from the rapid spectral shift to lower energies that might be expected for conventional carrier cooling, and suggests a “bottleneck” in cooling high in the density of states. Geiregat et al. reported a similar behavior in PbS and PbSe QDs in solution and interpreted this finding with a phonon scattering bottleneck at high-energy points in the Brillouin zone (e.g., the Σ or Δ point).37 Specifically, the authors argue that at these points the change in phonon wave vector as a function of carrier energy for each LO phonon emission event is maximal. It follows that in order to cool charge carriers through these points the required number of phonons per energy interval is also increased, leading to a delayed carrier relaxation around this point in the energy manifold. Furthermore, the material dependence of this effect in PbS and PbSe QDs has been explained by the smaller LO phonon frequency in PbSe20,21 which requires more phonon emission events for a given amount of energy, leading to a decrease in cooling rate. Because in PbTe QDs the trend of a decreasing LO phonon frequency is continued,22 we suggest that an even slower hot carrier cooling rate than in PbS and PbSe QDs reduces the competition with MEG and is therefore likely to contribute to a more efficient generation of multi excitons in PbTe QDs, consistent with spectroscopic measurements of initial MEG yields and with the device data presented here.

To obtain further information about cooling dynamics and MEG threshold behavior in devices, we implement an ultrafast pump–push photocurrent spectroscopy measurement. First, carriers are generated with an above-bandgap excitation “pump” pulse (1.9–2.6 eV). Then, after a controlled delay we impulsively increase the energy of the photoinduced charge carriers using a ca. 0.6 eV photon-energy “push” pulse. The effect of the additional energy provided by the push pulse to the charge carriers is observed through the lock-in detected increase in device photocurrent.38 Keeping the push photon energy constant (ca. 0.6 eV), we use a variety of different pump photon energies (1.9–2.6 eV) and investigate the efficiency and kinetics of the MEG process by changing the time delay between the arriving pump and push pulses.

Figure 4c shows the increased photocurrent due to the push as a function of pump–push pulse delay. At negative delays, the IR push leads to minimal photocurrent (<20 pA) due to the resonant excitation into tail states of the QD absorption and activation of long-lived charge carriers39 (see Supporting Information S1 and S11). We note that the contribution of potential two-photon excitation from the push pulse was minimized by limiting the push intensity.39 At time zero, where pump and push pulse overlap, we find significant photocurrent contribution for pump energies of 2.6 and 2.3 eV, but only a small increase in extractable charge carriers for lower pump energies. The additional photocurrent response for high pump energies decays with increasing delay between pump and push pulses on a time scale of ∼900 ± 200 fs (see Supporting Information S12). We attribute this push-induced photocurrent response to additional carriers generated via MEG. The additional photocurrent response appears at total (pump + push) energies above 2.8 ± 0.1 eV. This is consistent with an MEG threshold at around 2.9Eg, corresponding to the energy at which the IQE exceeds 100% (see Figure 2a). While the state produced by pump–push excitation is not necessarily the same as that produced by single-photon excitation,13,40,41 the total (pump + push) energy provides a robust upper limit for the MEG threshold. Furthermore, we note that the kinetics observed in the pump–push experiment represent the cooling dynamics of the intermediate state formed by the pump only. It is interesting that these kinetics are considerably faster than the above-threshold dynamics observed in transient absorption measurements described in Figure 4a,b. This is consistent with the phonon-scattering bottleneck model discussed above. We therefore argue that direct excitation at energies above the bottleneck leads to slow cooling and efficient MEG, whereas in the pump–push measurements presented here the pump produces a state below the bottleneck energy, which cools rapidly, and efficient MEG only takes place when the push pulse takes the system above the bottleneck (see Figure 4d).

In conclusion we have successfully implemented PbTe QDs as the photoactive layer in working solar cells and demonstrate external quantum efficiencies exceeding 120%, thereby proving unambiguously an efficient photocurrent contribution from MEG. Furthermore, we identify a high-energy ground-state bleach signal that indicates a delayed intraband cooling process of the initial hot single exciton. As this mechanism is believed to directly compete with MEG at early times we argue that the time for converting single excitons into multiple charge carrier pairs is extended. We measure the MEG threshold energy hνth under operating solar cell conditions using ultrafast pump–push photocurrent spectroscopy. The MEG onset energy of around 2.9Eg can be considered as a robust upper limit for the MEG threshold in PbTe QD-based solar cells. Together with a calculated IQE of more than 150% at around 3.3Eg, this demonstrates the potential of QD solar cells to recover significant above-bandgap energy that would normally be lost to thermalization.

Methods

PbTe Quantum Dot Synthesis

PbTe QDs were synthesized following a modified version of previously reported methods.25 All chemicals were purchased from Sigma-Aldrich if not stated otherwise and were anhydrous if available. Briefly, 1.138 g Pb(OAc)2·3H2O (3 mmol), 1.4 mL oleic acid (OA; 38 mmol; 1.25 g) and 20 mL squalane (4.41 mmol; 16.2 g) were combined and degassed at 90 °C under vacuum (10–2 mbar or better) for 2 h. Subsequently the reaction flask was flushed with nitrogen and heated to either 180 °C (for a QD bandgap, Eg, of 0.75 eV) or 160 °C (Eg = 0.95 eV). A solution of 31.9 mg tellurium (4 mmol) in 4.0 mL tri-n-octylphosphine (TOP; 9 mmol; 3.32 g) was rapidly injected into the lead precursor solution. The reaction was quenched after 5 min (Eg = 0.78 eV) or 30 s (Eg = 0.95 eV) by adding 20 mL of ice cold n-hexane and by placing the reaction flask in an ice-water bath. QDs were isolated from the reaction mixture by flocculating to turbidity using a 1-buthanol/ethanol/hexane solvent system.

Quantum Dot Analysis

Absorption spectra of QD solutions were measured by dispersing the PbTe QDs in tetrachloroethylene (TCE) at a concentration of ca. 1 mg/mL and using a PerkinElmer Lambda 9 UV–vis-IR spectrometer. Film absorption spectra were measured by depositing PbTe QDs on Spectrosil quartz substrates in the same fashion as described in Photovoltaic Device Fabrication, with a similar encapsulation technique. Optical bandgap was determined as reported elsewhere.42 Transmission electron microscopy samples were prepared by drop casting ca. 1 mg/mL QD solutions in TCE on a TEM Grid (200 Mesh Cu, Agar Scientific) in a nitrogen-filled glovebox. TEM images without elemental mapping (see Supporting Information S1) were taken on a FEI Philips Tecnai 20 TEM at an electron acceleration of 200 keV in bright-field mode. For imaging the cross section of operational devices with TEM, a cross-sectional lamellar specimen was fabricated employing a FEI Helios dual beam FEG SEM/FIB microscope, fitted with an Omniprobe micromanipulator for in situ lift-out. The thinning step of the lamellar specimen was performed with decreasing beam current to reduce sample damage and to improve the sputtering of the protective Pt layer. The cross-sectional specimen was analyzed through high-angle annular dark-field scanning transmission electron microscopy (HAADF-STEM), using a Fischione detector. Both HAADF-STEM and HR TEM images were acquired on a FEI Tecnai Osiris TEM/STEM, operated at 200 kV. For ultraviolet photoelectron spectroscopy (UPS) measurements, 3 nm chromium and 80 nm of gold was evaporated on precleaned silicon substrates and the QD film was deposited in a layer-by-layer fashion as described above. The samples were transferred into an ultrahigh vacuum (UHV) chamber (ESCALAB 250Xi) with minimal exposure to ambient conditions. Measurements were performed using a double-differentially pumped He gas discharge lamp emitting He I radiation (hν = 21.2 eV) with a pass energy of 2 eV.

Photovoltaic Device Fabrication

Solar cells were prepared on ITO-patterned glass substrates cleaned in an ultrasonic bath with ethanol, acetone, and isopropanol successively. TiO2 compact layers were deposited on top of the ITO layer using atomic layer deposition (ALD) from titanium tetrachloride (TiCl4) and H2O precursors at 200 °C.43 Subsequently, the substrates were annealed at 350 °C for 30 min under inert atmosphere. PbTe QDs were deposited following a sequential layer-by-layer spin-coating technique in a nitrogen-filled glovebox (<1 ppm of O2 and H2O).44 The QDs were dispersed in octane at 25 mg/mL and 3-mercaptopropionic acid (MPA; 20 mmol in acetonitrile) was used as ligand. The samples were transferred into a thermal evaporator and MoOx (7 nm) and Ag (80 nm) were deposited through a shadow mask at 3 × 10–6 mbar or better. The solar cells were encapsulated by attaching a glass slide on top of the contacts using transparent epoxy glue. For external quantum efficiency (EQE) measurements without background illumination, a 100 W tungsten halogen lamp (1500–500 nm) and a 120 W xenon lamp (500–350 nm) dispersed through a monochromator was used as the light source and a Keithley 2635 source measure unit (SMU) was employed to measure the short-circuit current at various wavelengths. For wavelengths between 1500 and 800 nm, a set of Ge detectors (ThorLabs SM05PD6A) was employed, and for wavelengths between 900 and 350 nm a set of silicon diodes (ThorLabs SM05PD1A) was used. The incident light was focused to a spot size of ca. 1 mm2 using a set of lenses to illuminate the individual pixel of size 5.5 mm2. The irregularity in the spectrum around 1.5 eV shown in Figure 1c arises from different UV exposure times leading to a different photoconductivity in the ZnO.45 Current–voltage characteristics were measured under AM 1.5G conditions using an Abet Sun 2000 solar simulator at an intensity equivalent to 100 mW cm–2 after correcting for spectral mismatch. Both the dark and light current–voltage characteristics were measured using the Keithley 2635 SMU. EQE measurements under various background illumination followed previous work of Brenner et al.46,47 Briefly, we used a ring of six white Lumiled LUXEON V LXHL-NWE7 LEDs as tunable white light source that light intensity was tunable through adjustments of the LED current. In order to distinguish between the monochromatic probe beam and the white background illumination, the monochromatic light was chopped employing a Thorlabs MC 2000 mechanical chopper with the modulated current recorded using a Femto LIA-MVD- 200 lock-in amplifier in conjunction with a Stanford Research SR 570 current preamplifier. White-light bias intensity was calibrated using a reference cell and comparing its current to the current under the AM1.5G solar simulator mentioned above. The background light was varied between 0 and 0.3 suns. The intensity of the chopped incident monochromatic light was monitored in parallel using a beam splitter, reference photodiode, and a separate lock-in amplifier.

Ellipsometry

The individual samples (ZnO, PbTe film, and MoOx) were prepared on silicon substrates as described in Photovoltaic Device Fabrication. ITO was measured on glass as received from Psiotec. Values for the refractive index n and the extinction coefficient k of silver have been taken from ref (48). The test samples were measured on a Woollam Vase VB-400 ellipsometry in reflection mode (ITO in transmission mode) using monochromatic light from a xenon lamp guided through a monochromator. The data for the quantum dot samples was fitted using a combination of a Cauchy and a Gaussian model. The ITO data was fitted with a combination of a Drude and a Lorentz oscillator and the MoOx was fitted with a Lorentz oscillator.

Determination of the IQE

The IQE was determined via two independent methods. For the IQEExp(hν) the absorbed light fraction R was recorded by measuring the reflectivity of a device at almost normal incidence using a set of photodiodes. A 100 W tungsten lamp was used in the spectral region from 500 to 1500 nm and we employed a 120 W xenon lamp between 350 and 500 nm. For photodiodes between 800 and 1500 nm a set of Ge detectors (ThorLabs SM05PD6A) and for wavelengths between 350 and 350 nm a set of silicon diodes (ThorLabs SM05PD1A) were employed. The respective diode calibration curves are shown in the Supporting Information S8. The IQEExp(hν) was calculated following the equation IIQEExp(hν) = ((EQE(hν))/(1 – R(hν))) . The IQEModel(hν) was calculated via transfer matrix approach where the reflectance was modeled according published literature procedures.29,30 The required values for the refractive index n and the extinction coefficient k have been determined via ellipsometry (see above and Supporting Information S9). The field profile, exciton generation profile, and generated current from the wavelength dependent complex indices of refraction in the device are determined assuming the light source to be located in air (n = 1) and the first layer (glass) to be thick compared to all other layers. It follows that incoherent reflection at the air/glass interface is taken into account that enabled an accurate description of the coherent interference of the remaining layers. Film thicknesses were determined using cross-sectional TEM (see Figure 1a in the main text) and ellipsometry.

Transient Absorption Spectroscopy

A pump pulse generates photoexcitations in the film and their dynamics are studied at some later time using a broadband probe pulse. For the pump pulse, a portion of the output of a Ti:sapphire amplifier system (Spectra-Physics Solstice) operating at 1 kHz was used to pump an in-house-built noncollinear optical parametric amplifier (NOPA), to generate (40 nm fwhm) pulses centered at 630 nm. For experiments with a pump excitation at 400 nm, the Ti:sapphire output was directed through a barium borate crystal (BBO) for second harmonic generation. For the broad band probe pulse, another portion of the NOPA output was directed through a sapphire crystal. The probe was delayed using a mechanical delay stage (Newport) and every second pump pulse was omitted using a mechanical chopper. Data acquisition at 1 kHz was enabled by a custom-built board from Stresing Entwicklunsbüro. The differential transmission (ΔT/T) was calculated after accumulating and averaging 500 “pump on” and “pump off” events for each data point.

Pump–Push–Photocurrent Spectroscopy

The output of a regenerative 1 kHz Ti:sapphire amplifier system (Coherent, Legend Elite Duo, 800 nm, 40 fs pulse duration, 7 mJ per pulse) was split into two parts. One part was used to pump a broadband noncollinear optical amplifier (Clark) to generate visible pump pulses (100 fs pulse duration, 1.8 eV photon energy). Another part was used to generate mid-IR probe/push pulses by pumping a two-stage home-built optical parametric amplifier (100 fs pulse duration, 0.5 eV photon energy).

In the pump–push photocurrent experiments, all devices were measured at short-circuit conditions. Pump pulses (in the order of 10 nJ) and ∼1 μJ push pulses were focused onto an ∼0.5 mm2 spot on the device. The reference photocurrent induced in the studied device by the pump was detected at the laser repetition frequency of 1 kHz by a lock-in amplifier. The pump power was adjusted to keep the reference current equal to 5 nA. The push beam was mechanically modulated at ∼380 Hz, and its effect on the photocurrent was detected by a lock-in amplifier locked to the chopper frequency. The polarization of the pump beam was set by an achromatic half-wave plate and thin-film polarizer (1:200 extinction) to 54° (magic angle) with respect to the polarization of the push beam.

Acknowledgments

The authors thank Dr. Frederick Morgenstern and Dr. Arjen Houtepen for useful discussion. M.L.B. thanks the German National Academic Foundation (Studienstiftung) for funding. This work was supported by the EPSRC (Grants EP/M005143/1, EP/G060738/1, EP/G037221/1) and the ERC (Grant 259619 PHOTO-EM). M.T. thanks the Gates Cambridge Trust and the Winton Programme for Sustainability for financial support. N.J.L.K.D. thanks the Cambridge Commonwealth European and International Trust, Cambridge Australian Scholarships and Mr. Charles K. Allen for financial support. F.W.R.R. thanks financial support from CNPq (Grant 246050/2012-8). C.D. acknowledges financial support from the EU under Grant 312483 ESTEEM2. A.A.B. is a Royal Society Research Fellow.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.nanolett.5b03161.

  • A summary of UV–vis absorption spectra, TEM figures, UPS raw data, additional figures of device I–V characteristics, ellipsometry data, white light bias EQE measurements as well as supporting figures on transient absorption and pump–push–photocurrent spectroscopy. (PDF). The data underlying this publication are available at https://www.repository.cam.ac.uk/handle/1810/252376.

Author Contributions

The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

The authors declare no competing financial interest.

Supplementary Material

nl5b03161_si_001.pdf (1.1MB, pdf)

References

  1. Beard M. C.; Midgett A. G.; Hanna M. C.; Luther J. M.; Hughes B. K.; Nozik A. J. Nano Lett. 2010, 10, 3019–3027 10.1021/nl101490z. [DOI] [PubMed] [Google Scholar]
  2. Robbins D. J. Phys. Status Solidi B 1980, 97, 9. 10.1002/pssb.2220970102. [DOI] [Google Scholar]
  3. Beard M. C.; Luther J. M.; Nozik A. J. Nat. Nanotechnol. 2014, 9, 951–954 10.1038/nnano.2014.292. [DOI] [PubMed] [Google Scholar]
  4. Beard M. C.; Luther J. M.; Semonin O. E.; Nozik A. J. Acc. Chem. Res. 2013, 46, 1252–1260 10.1021/ar3001958. [DOI] [PubMed] [Google Scholar]
  5. Schaller R. D.; Klimov V. I. Phys. Rev. Lett. 2004, 92, 186601. 10.1103/PhysRevLett.92.186601. [DOI] [PubMed] [Google Scholar]
  6. Beard M. C. J. Phys. Chem. Lett. 2011, 2, 1282–1288 10.1021/jz200166y. [DOI] [PubMed] [Google Scholar]
  7. Nozik A. J. Chem. Phys. Lett. 2008, 457, 3–11 10.1016/j.cplett.2008.03.094. [DOI] [Google Scholar]
  8. Smith C.; Binks D. Nanomaterials 2014, 4, 19–45 10.3390/nano4010019. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Ellingson R. J.; Beard M. C.; Johnson J. C.; Yu P.; Micic O. I.; Nozik A. J.; Shabaev A.; Efros A. L. Nano Lett. 2005, 5, 865–871 10.1021/nl0502672. [DOI] [PubMed] [Google Scholar]
  10. Pietryga J. M.; Zhuravlev K. K.; Whitehead M.; Klimov V. I.; Schaller R. D. Phys. Rev. Lett. 2008, 101, 1–4 10.1103/PhysRevLett.101.217401. [DOI] [PubMed] [Google Scholar]
  11. Schaller R. D.; Petruska M. A.; Klimov V. I. Appl. Phys. Lett. 2005, 87, 253102. 10.1063/1.2142092. [DOI] [Google Scholar]
  12. Allan G.; Delerue C. Phys. Rev. B: Condens. Matter Mater. Phys. 2009, 79, 195324. 10.1103/PhysRevB.79.195324. [DOI] [Google Scholar]
  13. Stewart J. T.; Padilha L. A.; Bae W. K.; Koh W. K.; Pietryga J. M.; Klimov V. I. J. Phys. Chem. Lett. 2013, 4, 2061–2068 10.1021/jz4004334. [DOI] [PubMed] [Google Scholar]
  14. Stewart J. T.; Padilha L. A.; Qazilbash M. M.; Pietryga J. M.; Midgett A. G.; Luther J. M.; Beard M. C.; Nozik A. J.; Klimov V. I. Nano Lett. 2012, 12, 622–628 10.1021/nl203367m. [DOI] [PubMed] [Google Scholar]
  15. Nootz G.; Padilha L. A.; Levina L.; Sukhovatkin V.; Webster S.; Brzozowski L.; Sargent E. H.; Hagan D. J.; Van Stryland E. W. Phys. Rev. B: Condens. Matter Mater. Phys. 2011, 83151–7 10.1103/PhysRevB.83.155302. [DOI] [Google Scholar]
  16. McGuire J. A.; Sykora M.; Joo J.; Pietryga J. M.; Klimov V. I. Nano Lett. 2010, 10, 2049–2057 10.1021/nl100177c. [DOI] [PubMed] [Google Scholar]
  17. Midgett A. G.; Luther J. M.; Stewart J. T.; Smith D. K.; Padilha L. A.; Klimov V. I.; Nozik A. J.; Beard M. C. Nano Lett. 2013, 13, 3078–3085 10.1021/nl4009748. [DOI] [PubMed] [Google Scholar]
  18. Padilha L. A.; Stewart J. T.; Sandberg R. L.; Bae W. K.; Koh W.; Pietryga J. M.; Klimov V. I. Acc. Chem. Res. 2013, 46, 1261–1269 10.1021/ar300228x. [DOI] [PubMed] [Google Scholar]
  19. Colloidal Quantum Dot Optoelectronics and Photovoltaics; Konstantatos G., Sargent E. H., Eds.; Cambridge University Press: Cambridge, 2013. [Google Scholar]
  20. Dalven R. Phys. Rev. B 1971, 3, 3359. 10.1103/PhysRevB.3.3359. [DOI] [Google Scholar]
  21. Habinshuti J.; Kilian O.; Cristini-Robbe O.; Sashchiuk A.; Addad A.; Turrell S.; Lifshitz E.; Grandidier B.; Wirtz L. Phys. Rev. B: Condens. Matter Mater. Phys. 2013, 88, 1–7 10.1103/PhysRevB.88.115313. [DOI] [Google Scholar]
  22. Wu H.; Cao C.; Si J.; Xu T.; Zhang H.; Wu H.; Chen J.; Shen W.; Dai N. J. Appl. Phys. 2007, 101, 103505. 10.1063/1.2714682. [DOI] [Google Scholar]
  23. Bae W. K.; Joo J.; Padilha L. A.; Won J.; Lee D. C.; Lin Q.; Koh W.; Luo H.; Klimov V. I.; Pietryga J. M. J. Am. Chem. Soc. 2012, 134, 20160–20168 10.1021/ja309783v. [DOI] [PubMed] [Google Scholar]
  24. Bode D.; Levinstein H. Phys. Rev. 1954, 96, 259. 10.1103/PhysRev.96.259. [DOI] [Google Scholar]
  25. Murphy J. E.; Beard M. C.; Norman A. G.; Ahrenkiel S. P.; Johnson J. C.; Yu P.; Mićić O. I.; Ellingson R. J.; Nozik A. J. J. Am. Chem. Soc. 2006, 128, 3241–3247 10.1021/ja0574973. [DOI] [PubMed] [Google Scholar]
  26. Pan Y.; Bai H.; Pan L.; Li Y.; Tamargo M. C.; Sohel M.; Lombardi J. R. J. Mater. Chem. 2012, 22, 23593. 10.1039/c2jm15540k. [DOI] [Google Scholar]
  27. Urban J. J.; Talapin D. V.; Shevchenko E. V.; Murray C. B. J. Am. Chem. Soc. 2006, 128, 3248–3255 10.1021/ja058269b. [DOI] [PubMed] [Google Scholar]
  28. Semonin O. E.; Luther J. M.; Choi S.; Chen H.-Y.; Gao J.; Nozik A. J.; Beard M. C. Science 2011, 334, 1530–1533 10.1126/science.1209845. [DOI] [PubMed] [Google Scholar]
  29. Burkhard G. F.; Hoke E. T.; McGehee M. D. Adv. Mater. 2010, 22, 3293–3297 10.1002/adma.201000883. [DOI] [PubMed] [Google Scholar]
  30. Tabachnyk M.; Ehrler B.; Bayliss S.; Friend R. H.; Greenham N. C. Appl. Phys. Lett. 2013, 103, 153302 .10.1063/1.4824420. [DOI] [Google Scholar]
  31. Hillhouse H. W.; Beard M. C. Curr. Opin. Colloid Interface Sci. 2009, 14, 245–259 10.1016/j.cocis.2009.05.002. [DOI] [Google Scholar]
  32. Fuke N.; Hoch L. B.; Koposov A. Y.; Manner V. W.; Werder D. J.; Fukui A.; Koide N.; Katayama H.; Sykora M. ACS Nano 2010, 4, 6377–6386 10.1021/nn101319x. [DOI] [PubMed] [Google Scholar]
  33. Law M.; Luther J. M.; Beard M. C.; Choi S.; Nozik A. J. Conf. Rec. IEEE Photovolt. Spec. Conf. 2009, 002068–002073 10.1109/PVSC.2009.5411446. [DOI] [Google Scholar]
  34. Davis N. J. L. K.; Böhm M. L.; Tabachnyk M.; Wisnivesky-Rocca-Rivarola F.; Jellicoe T. C.; Ducati C.; Ehrler B.; Greenham N. C. Nat. Commun. 2015, 6, 8259. 10.1038/ncomms9259. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Schaller R. D.; Pietryga J. M.; Goupalov S. V.; Petruska M. A.; Ivanov S. A.; Klimov V. I. Phys. Rev. Lett. 2005, 95, 1–4 10.1103/PhysRevLett.95.196401. [DOI] [PubMed] [Google Scholar]
  36. Mukherjee A.; Ghosh S. Phys. E 2014, 64, 234–239 10.1016/j.physe.2014.08.004. [DOI] [Google Scholar]
  37. Geiregat P.; Delerue C.; Justo Y.; Aerts M.; Spoor F.; Thourhout D.; Van Siebbeles L. D. A.; Allan G.; Houtepen A. J.; Hens Z. ACS Nano 2015, 9, 778–788 10.1021/nn5062723. [DOI] [PubMed] [Google Scholar]
  38. Bakulin A. A.; Rao A.; Pavelyev V. G.; van Loosdrecht P. H. M.; Pshenichnikov M. S.; Niedzialek D.; Cornil J.; Beljonne D.; Friend R. H. Science 2012, 335, 1340–1344 10.1126/science.1217745. [DOI] [PubMed] [Google Scholar]
  39. Bakulin A. A.; Neutzner S.; Bakker H. J.; Ottaviani L.; Barakel D.; Chen Z. ACS Nano 2013, 7, 8771. 10.1021/nn403190s. [DOI] [PubMed] [Google Scholar]
  40. McGuire J. A.; Joo J.; Pietryga J. M.; Schaller R. D.; Klimov V. I. Acc. Chem. Res. 2008, 41, 1810–1819 10.1021/ar800112v. [DOI] [PubMed] [Google Scholar]
  41. Kang I.; Oh J.; Wise F. W.; Chang K.; Ihm G.; Lee S. Phys. Rev. B 1996, 14, 1632. [Google Scholar]
  42. Ehrler B.; Musselman K. P.; Böhm M. L.; Friend R. H.; Greenham N. C. Appl. Phys. Lett. 2012, 101, 153507. 10.1063/1.4757612. [DOI] [Google Scholar]
  43. Saberi Moghaddam R.; Huettner S.; Vaynzof Y.; Ducati C.; Divitini G.; Lohwasser R. H.; Musselman K. P.; Sepe A.; Scherer M. R. J.; Thelakkat M.; Steiner U.; Friend R. H. Nano Lett. 2013, 13, 4499–4504 10.1021/nl4024275. [DOI] [PubMed] [Google Scholar]
  44. Ehrler B.; Walker B. J.; Böhm M. L.; Wilson M. W. B.; Vaynzof Y.; Friend R. H.; Greenham N. C. Nat. Commun. 2012, 3, 1019. 10.1038/ncomms2012. [DOI] [PubMed] [Google Scholar]
  45. Jin Y.; Wang J.; Sun B.; Blakesley J. C.; Greenham N. C. Nano Lett. 2008, 8, 1649–1653 10.1021/nl0803702. [DOI] [PubMed] [Google Scholar]
  46. Brenner T. J. K.; Vaynzof Y.; Li Z.; Kabra D.; Friend R. H.; McNeill C. R. J. Phys. D: Appl. Phys. 2012, 45, 415101. 10.1088/0022-3727/45/41/415101. [DOI] [Google Scholar]
  47. Brenner T. J. K.; Li Z.; McNeill C. R. J. Phys. Chem. C 2011, 115, 22075–22083 10.1021/jp208466t. [DOI] [Google Scholar]
  48. Winsemius P.; Kampen F. F. Van; Lengkeek H. P.; Went C. G. Van. J. Phys. F: Met. Phys. 1976, 6, 1583–1606 10.1088/0305-4608/6/8/017. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nl5b03161_si_001.pdf (1.1MB, pdf)

Articles from Nano Letters are provided here courtesy of American Chemical Society

RESOURCES