Ether Cleavage Re-Investigated: Elucidating the Mechanism of BBr₃-Facilitated Demethylation of Aryl Methyl Ethers

Abstract

One of the most well-known, highly utilized reagents for ether cleavage is boron tribromide (BBr₃), and this reagent is frequently employed in a 1:1 stoichiometric ratio with ethers. Density functional theory calculations predict a new mechanistic pathway involving charged intermediates for ether cleavage in aryl methyl ethers. Moreover, these calculations predict that one equivalent of BBr₃ can cleave up to three equivalents of anisole, producing triphenoxyborane [B(OPh)₃] prior to hydrolysis. These predictions were validated by gas chromatography analysis of reactions where the BBr₃:anisole ratio was varied. Not only do we confirm that sub-stoichiometric equivalents may be used for ether demethylation, but the findings also support our newly proposed three cycle mechanism for cleavage of aryl methyl ethers.

Introduction

Boron tribromide is a versatile reagent utilized in diverse areas ranging from polymer chemistry to natural product synthesis.¹ Owing its high reactivity to the Lewis acidic boron center, BBr₃ reactions include haloborylation,² boron–silicon exchange,³ and rearrangement of 7,7-diphenylhydromorphone derivatives.⁴ While there is no shortage in the diversity of BBr₃-mediated reactions, many of the mechanisms for these transformations have not been fully elucidated. In this report we investigate the mechanism of ether cleavage by BBr₃^5–10 in anisole.

Conceptually, demethylation of anisole is initiated by the formation of an ether adduct 1 followed by the loss of bromide. Free bromide nucleophilically attacks the methyl group of the cationic intermediate (2) cleaving the C–O bond and producing PhOBBr₂, which undergoes hydrolysis upon aqueous work-up. While this pathway (Scheme 1) at first appears to be viable, we calculated that the formation of 2 and bromide in dichloromethane is thermodynamically inaccessible (ΔG = +38.9 kcal/mol).

Scheme 1.

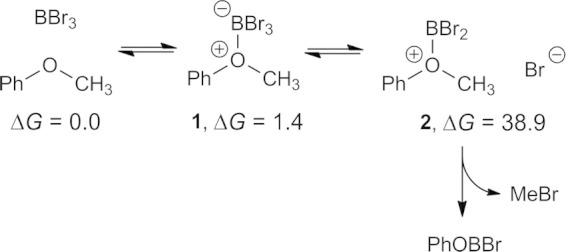
Conceptual reaction mechanism for demethylation of anisole is thermodynamically inaccessible due to formation of 2 and bromide. Gibbs energies are in kcal/mol.

Recently, alternative mechanisms for ether cleavage were proposed by Sousa and Silva that involve unimolecular or bimolecular rate-determining steps that circumvent formation of bromide in solution (Scheme 2).¹¹ While a unimolecular process is kinetically favored for ethers containing one or more substituents (e.g. branched alkyl) that stabilize carbocation character in an S_N1-like transition state, this barrier for demethylation of primary C atoms, like in the methyl group of anisole, lies too high on the potential energy surface to be accessible under reported reaction conditions. They found that a bimolecular process (Scheme 2, bottom) decreases the kinetic barrier for anisole demethylation significantly. During this reaction pathway, one of the bromides of the first ether adduct nucleophilically attacks the methyl group of the second ether adduct. This is analogous to an S_N2 reaction with 180^o attack of the methyl group by a bromide in the nucleophilic ether adduct. However, this bimolecular pathway produces two highly charged intermediates 2 and 3 that Sousa and Silva did not investigate. Their computational investigation stopped with the calculation of the initial kinetic barrier.¹¹ We speculate that these charged intermediates may undergo a similar bimolecular reaction to yield two equivalents of PhOBBr₂ and MeBr. Moreover, if charged intermediates are formed then we believe an important set of mechanistic pathways may have been overlooked, namely, those where Lewis acidic BBr₃ abstracts bromide from the ether complex to form BBr₄^– in a mechanism related to the pathway introduced in Scheme 1.

Scheme 2.

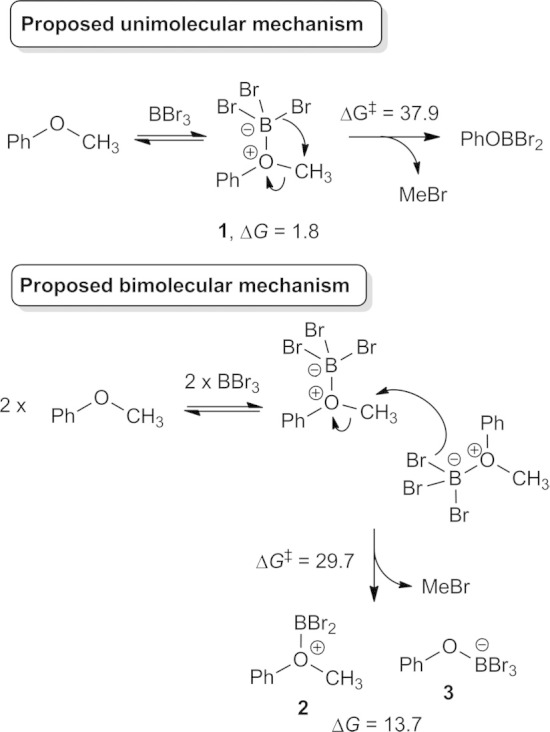
Previously proposed unimolecular and bimolecular pathways proposed by Sousa and Silva.¹¹ Gibbs energies are in kcal/mol.

In this manuscript, we re-investigate the mechanisms of anisole ether cleavage proposed by Sousa and Silva and compare them to new mechanisms involving charged intermediates using density functional theory coupled to a continuum solvation model. The kinetically favored pathway explains mechanistic intricacies regarding the reactivity of all three bromides on BBr₃, a finding that we confirm with ¹H NMR and GC experiments run with different stoichiometries. Our proposed mechanism rationalizes the key observation of 0.33:1 BBr₃:ether stoichiometry reported in the original methodology paper⁵ and is supported by additional experimental findings.

Results and Discussion

The computational investigation began by replicating the uni- and bimolecular pathways proposed by Sousa and Silva for the demethylation of anisole. Our methodology differs slightly from their method because we did not use a pseudopotential for Br, did not scale computed frequencies when evaluating zero-point and thermal corrections, and we assumed a temperature of 298 K vs. 250 K (though this difference has a negligible impact). We also avoided mixed basis sets in our triple-zeta energy refinements by employing 6-311+G(d,p) for all elements. Our method reproduces well their geometry (Figure S1 in the Supporting Information) and kinetic barrier (ΔG^‡ = 37.9 kcal/mol vs. 38.8 kcal/mol) for the unimolecular pathway. We were also able to replicate a similar geometry for the bimolecular pathway (Figure S2 in the Supporting Information), however, we were unable to replicate their low barrier of 13.3 kcal/mol. Formation of the ether adduct is only slightly uphill in Gibbs energy (ΔG = 1.4 kcal/mol) and therefore anisole, BBr₃, and the ether adduct are predicted to be in equilibrium in solution. The loss of translational entropy due to two of the ether adducts coming together at the bimolecular transition state suggests that ca. 10 kcal/mol of this barrier is entropic.¹² Consequently, nucleophilic attack of the methyl group must only invoke a ca. 3 kcal/mol enthalpic barrier based on their reported value, a finding that we struggled to rationalize. We calculated an enthalpic barrier (relative to two ether adducts) of 14.9 kcal/mol and an entropic barrier of 12.0 kcal/mol for an overall Gibbs energy barrier of 26.9 kcal/mol (or 29.7 kcal/mol vs. free BBr₃ and anisole). This transition state leads to MeBr and two charged intermediates, 2 and 3, that are uphill by 13.7 kcal/mol. Thus, while this bimolecular pathway is a significant improvement over the unimolecular pathway, its kinetic barrier is high enough to warrant the investigation of alternative mechanisms based on the experimental conditions. Three important concepts from the Sousa and Silva bimolecular mechanism are: (i) ether adduct formation makes bromide a nucleophile without generation of free bromide, (ii) ether adduct formation makes the methyl group more susceptible to nucleophilic attack, and (iii) the local geometry of the methyl group at the transition state is S_N2-like.

A New Demethylation Mechanism

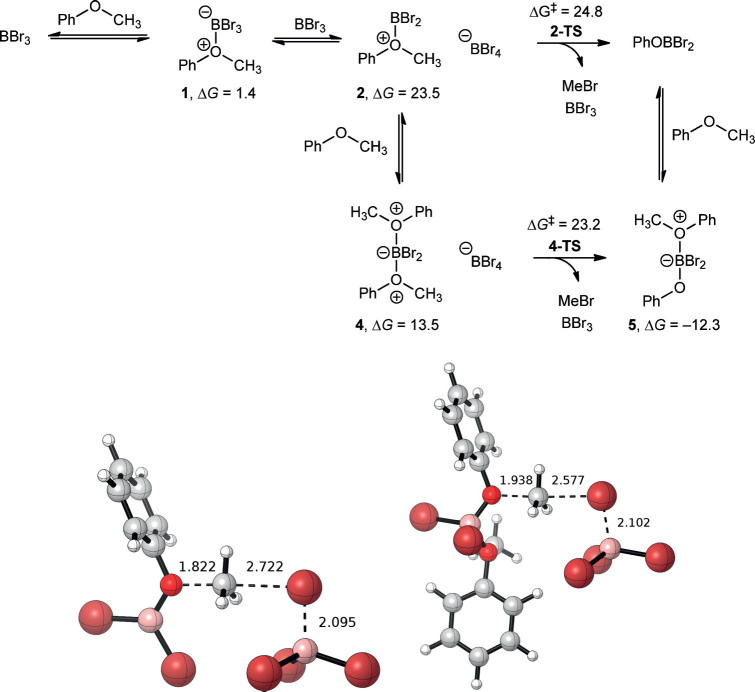
Using the key insights from Sousa and Silva’s mechanism, we envisioned that BBr₃ could abstract bromide from an ether adduct to afford 2 and BBr₄^– (Scheme 3, top). These charged intermediates are computed to be thermodynamically unfavorable compared to formation of two ether complexes (23.5 kcal/mol vs. 2.8 kcal/mol) but still accessible under the experimental conditions. Importantly, this energy is below the previously proposed bimolecular kinetic barrier by ca. 6 kcal/mol. Because boron tetrabromide is less stable, this masked bromide should be a more potent nucleophile than the bromide in 1. The barrier for nucleophilic attack of the methyl group in 2 by BBr₄^– is found to be only 1.3 kcal/mol higher in energy than these intermediates, or 24.8 kcal/mol (2-TS, Scheme 3 bottom left). This reaction produces MeBr, BBr₃, and PhOBBr₂ with an overall reaction energy of –21.8 kcal/mol. The critical feature of our mechanism is the dynamic equilibrium at the boron center that stabilizes bromide until it is needed for nucleophilic attack.

Scheme 3.

Top: calculated mechanism for demethylation of anisole. Bottom left: transition state (2-TS) for demethylation of mono-ether adduct 2. Bottom right: transition state (4-TS) for demethylation of di-ether adduct 4. Gibbs energies are in kcal/mol and bond lengths are listed in Å.

This idea of dynamic equilibrium at boron made us consider further possibilities for stabilization of the charged intermediates. Boron is coordinatively-saturated in BBr₄^–, however, three-coordinate boron in 2 could be stabilized by an additional Lewis base. Thus, we evaluated the thermodynamics of Lewis base stabilization of 2 by anisole to afford 4, which is favorable by 10.0 kcal/mol (+13.5 kcal/mol vs. reactants). Demethylation of 4 by BBr₄^– is predicted to have a slightly lower kinetic barrier (4-TS, Scheme 3 bottom right) of 23.2 vs. 24.8 kcal/mol for 2 and generates MeBr, BBr₃, and 5 with an overall reaction energy of –12.3 kcal/mol. PhOBBr₂ may be formed via this pathway upon disassociation of anisole from 5 (–9.5 kcal/mol). Within the intrinsic errors of our computational methodology one cannot predict whether the barrier involving 2 or 4 is preferred and both may be operative. However, both pathways are favored over the previously proposed bimolecular mechanism. The transition state structures for the mono- and di-ether adduct pathways are shown at the bottom of Scheme 3. Both feature S_N2-like geometries with a trigonal bipyramidal carbon center. 2-TS is earlier than 4-TS, as evidenced by the shorter C–O bond length of 1.82 vs. 1.94 Å and longer C–Br bond length of 2.72 vs. 2.58 Å. This finding is consistent with the stability of the cation adducts 2 and 4; the more reactive intermediate 2 has an earlier transition state. 2-TS and 4-TS are much earlier than the bimolecular transition state reported by Sousa and Silva that had C–O and C–Br bond lengths of 2.09 and 2.42 Å (Figure S2 in Supporting Information), respectively.¹¹

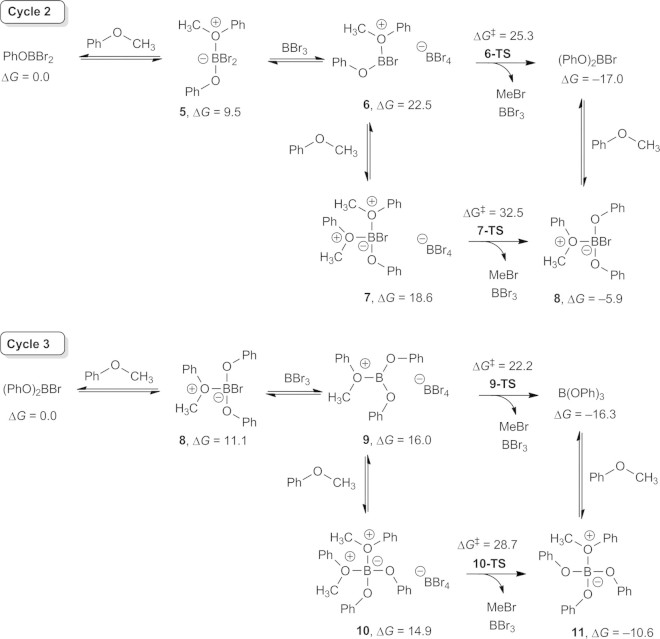
Bromide loss from the ether adduct should become more accessible with more stabilizing substituents on boron, like phenoxide. Thus, while we computed 5 to be slightly uphill in energy relative to PhOBBr₂, this adduct is still thermodynamically accessible and features a tetracoordinate boron center containing two bromides. The loss of bromide from 5 to BBr₃ yields BBr₄^– and 6. 6 may either undergo demethylation facilitated by BBr₄^– to produce (PhO)₂BBr or may coordinate an additional anisole to generate intermediate 7 prior to demethylation to form 8 (Scheme 4, top). One could envision similar reactivity occurring until all bromides are lost from the boron center. This concept of multiple demethylation cycles per BBr₃ equiv. is consistent with the original methodology paper that reported a 3:1 ether:BBr₃ stoichiometry.⁵ Because the reverse barrier from PhOBBr₂ to 2 is disfavored by 44.9 kcal/mol, we now reference our thermodynamics to PhOBBr₂, anisole, and BBr₃. Bromide abstraction from 5 to produce 6 and BBr₄^– is computed to be uphill by 22.5 kcal/mol. Similar to the first reaction cycle that we considered (Scheme 3, top), 6 can be stabilized by anisole to generate 7. This reaction is only downhill by 3.9 kcal/mol (+18.6 kcal/mol vs. PhOBBr₂) as compared to the stabilization of 2 to form 4 by 10.0 kcal/mol. Already we see a marked difference from the first cycle; 6 is much more stable, as compared to 2, due to the π-donor ability of the phenoxide substituent. The transition state involving 6 is 25.3 kcal/mol (6-TS) while the transition state for 7 is 32.5 kcal/mol (7-TS). Thus, the mono-ether adduct pathway is kinetically favored in this second reaction cycle. 6-TS produces MeBr, BBr₃, and (PhO)₂BBr with a reaction energy of –17.0 kcal/mol. A summary of this reaction mechanism is shown in Scheme 4 (top) and the rate-limiting transition state is shown in Figure1. The C–O and C–Br bond lengths in 6-TS of 1.87 and 2.64 Å, respectively, are intermediate between those of the transition states in the first cycle and further highlight the stability provided by the phenoxide substituent.

Scheme 4.

Cycles 2 and 3 for proposed mechanism for BBr₃-facilitated ether cleavage. Gibbs energies are in kcal/mol.

Figure 1.

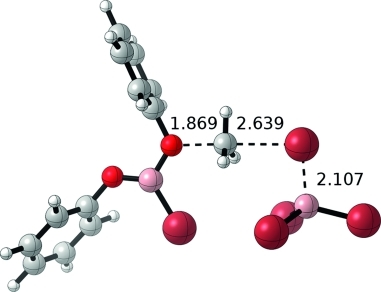
Optimized structure for 6-TS. Bond lengths are listed in Å.

One can further envision a third cycle that would react the remaining bromide in (PhO)₂BBr (Scheme 4, bottom). Because the reverse reaction from the product of cycle 2 to form 6 is uphill by 36.4 kcal/mol, all energies are referenced to (PhO)₂BBr, anisole, and BBr₃ in cycle 3. Formation of 8 from (PhO)₂BBr and anisole is uphill by 11.1 kcal/mol. Abstraction of bromide from 8 by BBr₃ generates 9 and BBr₄^– and is further uphill by 4.9 kcal/mol [16.0 kcal/mol vs. (PhO)₂BBr]. Intermediate 9, which features a three-coordinate boron center, may bind anisole to form 10 and become coordinatively saturated. This adduct formation only slightly stabilizes 9 by 1.1 kcal/mol [14.9 kcal/mol vs. (PhO)₂BBr]. Similar to the second cycle, the kinetic barrier for the mono-ether adduct intermediate 9 is much lower than the di-ether adduct intermediate 10 (22.2 vs. 28.7 kcal/mol for 9-TS and 10-TS). The favored kinetic pathway 9-TS generates MeBr, BBr₃, and B(OPh)₃, and is calculated to be exergonic by 17.6 kcal/mol. The C–O and C–Br bond lengths in 9-TS of 1.92 and 2.60 Å, respectively, indicate a later transition state than cycle 2 with bond lengths nearly equal to that of 4-TS in cycle 1. Two questions come to mind from these calculations: (i) why does the third cycle have the lowest barrier and (ii) why does the di-ether adduct pathway (4-TS, 7-TS, and 10-TS) become kinetically disfavored after cycle 1? (Figure2).

Figure 2.

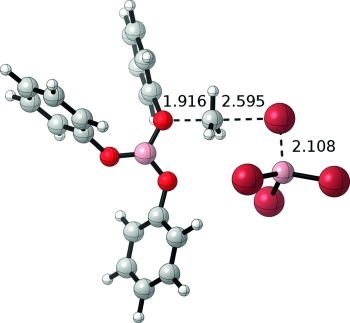
Optimized structure for 9-TS. Bond lengths are listed in Å.

Analysis of Reaction Barrier Heights

To answer the first question, we decomposed the rate-limiting barrier for the mono-ether adduct pathways for all three cycles in terms of the individual reaction steps. The first step towards demethylation is formation of the Lewis acid/base adduct in each cycle (Table1, column 1). Our calculations predict that this reaction becomes increasingly unfavorable as bromides are substituted with phenoxides, as evidenced by the increasing reaction energy of 1.4 < 9.5 < 11.1 kcal/mol. This trend can be rationalized by the π-donor capability of phenoxide that reduces the Lewis acidity of the boron center. Next, each of these mono-ether adducts (1, 5, and 8) loses bromide to BBr₃. Additional phenoxide substituents bound to the boron center that loses bromide should stabilize the cationic boron species formed in this reaction (2, 6, and 9). This prediction is observed in the reaction free energies of 22.1, 13.0, and 4.9 kcal/mol for cycles 1, 2, and 3, respectively (Table1, column 2). Finally, these cationic intermediates react with boron tetrabromide in the rate-limiting steps 2-TS, 6-TS, and 9-TS to form MeBr, BBr₃, and (PhO)_xBBr_3–x. This rate-limiting barrier increases with the number of phenoxide substituents because a less Lewis acidic boron center will make the oxygen of the coordinated anisole less positive, thereby disfavoring demethylation (Table1, column 3). While each of these individual steps are easily rationalized by the ratio of bromide:phenoxide substituents at the boron center, the overall barrier trend of 24.8, 25.3, and 22.2 kcal/mol for cycles 1, 2, and 3, does not dominantly arise from one of the three fundamental reaction steps (i.e. none of these individual reaction steps govern the rate for each cycle).

Table 1.

Breakdown of rate-limiting barrier free energies for the mono-ether adduct pathways of cycles 1, 2, and 3 in terms of the fundamental reaction free energies leading to that barrier. All energies are in kcal/mol.

Anisole binding		Bromide loss		Demethylation		Total
A + PhOMe ↔ B		B + BBr3 ↔ C + BBr4–		C + BBr4– → C-TS		ΔG‡
A = BBr3, B = 1	+1.4	C = 2	+22.1	2-TS	+1.3	24.8
A = PhOBBr2, B = 5	+9.5	C = 6	+13.0	6-TS	+2.8	25.3
A = (PhO)2BBr, B = 8	+11.1	C = 9	+4.9	9-TS	+6.2	22.2

To answer the second question, we decomposed the binding energy of the second barrier starting from the cationic intermediates 2, 6, and 9, whose thermodynamics are already summarized in the first two columns of Table1. The subsequent steps are summarized in Table2. Adduct formation between the cationic intermediates and a second equivalent of anisole steadily decreases in exergonicity from –10.0 to –1.1 kcal/mol as the number of phenoxide substituents at the boron center increases (Table2, column 1). The kinetic barrier, as measured from these di-ether adduct intermediates 4, 7, and 10, increases slightly for cycles 2 and 3. This finding suggests that additional phenoxide substituents are counterproductive to demethylation, as evidenced by the demethylation energies in Table2 (+9.7 to +13.8 kcal/mol) vs. Table1 (+1.3 to +6.2 kcal/mol). One can rationalize this based on the reduced Lewis acidity with increasing numbers of phenoxides and with increasing of the coordination number at boron from three to four. The trend in binding of the first anisole and formation of the charged species (Table1, sum of columns 1 and 2) results in energies of 23.5, 22.5, and 16.0 kcal/mol for cycles 1–3, respectively. When combined with the second equivalent of anisole (Table2, column 1), one observes overall energies of 13.5, 18.6, and 14.9 kcal/mol to reach 4-TS, 7-TS, and 10-TS. The more costly energetic penalties for 7-TS and 10-TS (13.8 kcal/mol) increases the gap for the di-ether adduct barrier in cycles 2 and 3 as compared to cycle 1. One might ask why 10-TS is not higher in energy? While 10 maintains a weakly coordinated anisole, both 10-TS and 11 dissociate the additional anisole to form a weak van der Waal complex. Thus, while cycle 1 has competitive kinetics for the mono- and di-ether adduct pathways, the boron center with phenoxide substituents in cycles 2 and 3 is not sufficiently Lewis acidic for the di-ether adduct pathway to be viable because decreased Lewis acidity (i) disfavors binding of the second ether equivalent and (ii) raises the barrier height for the demethylation step.

Table 2.

Breakdown of rate-limiting barrier free energies for the di-ether adduct pathways of cycles 1, 2, and 3 in terms of the fundamental reaction free energies leading to that barrier. All energies are in kcal/mol.

Second anisole binding		Demethylation		Total
C + PhOMe ↔ E		E + BBr4– → E-TS		ΔG‡
C = 2, E = 4	–10.0	4-TS	+9.7	23.2
C = 6, E = 7	–3.9	7-TS	+13.8	32.5
C = 9, E = 10	–1.1	10-TS	+13.8	28.7

Experimental Validation

In order to validate our computational predictions, we aimed to reproduce and expand the findings disclosed in the original methodology report by varying the BBr₃:anisole ratio. We began our investigation using standard conditions¹⁰ for this reaction: CH₂Cl₂ as the reaction solvent, near ambient temperature, and a reaction time of ca. 18 h. However, the reaction solvent was varied from CH₂Cl₂ to CDCl₃ for NMR analysis and to o-dichlorobenzene for the high temperature reactions.

Table3 shows the quantitative GC results of varied the molar equivalence of BBr₃:anisole. Not surprisingly a 1:1 ratio results in near quantitative conversion to phenol after hydrolysis. Decreasing the ratio to 0.66:1 only decreases the efficiency of the reaction from 99.8 to 95.8 %, which is within our experimental error and demonstrates more than one cycle must be operative. Monitoring the reaction by ¹H NMR shows disappearance of the methoxy resonance at 3.6 ppm and formation of the MeBr resonance at 2.6 ppm after 18 h at room temperature (Figure S3 in Supporting Information). However, when the ratio is decreased further to 0.33:1 a marked decrease in the conversion to 56.9 % is observed. Our GC data demonstrates that this inefficiency is due to unreacted anisole rather than formation of byproducts. Our computational mechanism predicts that we should observe full conversion at 0.33:1 because the second cycle had the highest barrier of 25.3 kcal/mol, and if there is sufficient energy to overcome the second barrier then the third cycle, with a lower barrier of 22.2 kcal/mol, should be easier to traverse. Unfortunately, conversion of anisole to phenol does not surpass 67 % even when run at slightly elevated temperatures (50 °C in CH₂Cl₂). This finding suggests that only cycles 1 and 2 are accessible, which contradicts our computational prediction.

Table 3.

Gas chromatography analysis of product mixture run in CH₂Cl₂ after hydrolysis.

BBr3 [equiv.]	Temp. [°C]	Anisole [%]	Phenol [%]
1.0	30	0.20	99.8
0.66	30	4.23	95.8
0.33	30	43.1	56.9
0.33	50	33.2	67.8

Is this simply a failure of density functional theory or is there additional chemistry missing from our computational model? In recent years there has been an increasing interest in the dynamic covalent chemistry of boron–oxygen bonds.¹³ One relevant pathway to consider is the output of each individual cycle [PhOBBr₂, (PhO)₂BBr, and B(OPh)₃] equilibrating with BBr₃. Roy reported that MeOBBr₂ and (MeO)₂BBr can be synthesized by equilibrating different ratios of BBr₃/B(OMe)₃.¹⁴ With the well-established dynamic nature of boron–oxygen bonding, we envisioned similar equilibria may impact our proposed reaction mechanism. The first possible equilibrium would be between BBr₃ and the product of cycle 1, PhOBBr₂ (Scheme 5, top). Even if this reaction occurs it does not complicate our mechanism because: (i) the reaction is thermoneutral and (ii) it does not generate new species. The second equilibrium between BBr₃ and the product of cycle 2, (PhO)₂BBr (Scheme 5, bottom), potentially complicates our mechanism by generating two equivalents of PhOBBr₂. Our computational model predicts this reaction to be exergonic by 4.8 kcal/mol, thus any (PhO)₂BBr generated in the presence of BBr₃ will comproportionate to form PhOBBr₂. With this in mind, an additional energetic penalty should be factored into the barrier height of cycle 3 because two equivalents of PhOBBr₂ must disproportionate to form BBr₃ and (PhO)₂BBr. In turn, the barrier rises from 22.2 to 27.0 kcal/mol and makes cycle 3 the least kinetically accessible. Therefore, additional thermal energy may make full conversion through cycle 3 possible. We tested this hypothesis by switching solvents from CH₂Cl₂ to o-dichlorobenzene, which allowed for this reaction to be run at 100 °C. Under this set of reaction conditions using 0.33:1 we observed full conversion of anisole to phenol as measured by GC. This result not only supports our mechanism, but also confirms the results disclosed in the original report of full conversion with a 0.33:1 ratio at elevated temperatures.⁵

Scheme 5.

Possible dynamic covalent equilibria between BBr₃ and products of cycles 1 and 2.

One may ask: why can anisole not be demethylated through cycle 2 once PhOBBr₂ is generated (Scheme 5, bottom)? A critical feature of our mechanism is that catalytic BBr₃ is required for each of the cycles. In the 1:1 and 0.66:1 experiments the possibility of demethylating through cycle 2 multiple times is viable because excess BBr₃ remains after the comproportionation equilibrium has consumed the (PhO)₂BBr generated from cycle 2. However, the 0.33:1 reaction would consume all of the BBr₃ by the time the comproportionation reaches equilibrium, thereby disabling cycle 2.

Conclusions

While the cleavage of highly branched aliphatic ethers most likely proceeds through the unimolecular process proposed by Sousa and Silva, we believe our alternative bimolecular mechanism for demethylation in aryl methyl ethers, which differs from the classical mechanism of bromide attack in terms of the bromide source, is operative. Our computational predictions indicate that demethylation of anisole proceeds through a three-cycle mechanism that is underpinned by previously reported and new experimental findings. The results of this study show that sub-stoichiometric amounts of BBr₃ can be used in place of one full equivalent and may enable the use of BBr₃ in total synthesis when multiple moieties are susceptible to attack. However, there are a number of lingering questions that require further investigation. (i) Does the new mechanism for ether cleavage extend to alkyl methyl ethers and, if so, are all three cycles operable? (ii) Is the multi-cycle mechanism proposed for aryl methyl ether cleavage general for BX₃ reagents (X = Br, Cl)? The reaction of BCl₃ with ethers and alcohols suggests that two- and three-cycle mechanisms are accessible under the reported conditions.^15,16 (iii) Can a multi-cycle extension of Sousa and Silva’s unimolecular mechanism be viable for branched ethers? Work is ongoing in our laboratories to answer these and related questions about BX₃ reactivity.

Computational Methods

Geometry optimizations were performed in the Gaussian09 program (G09.D01)¹⁷ at the B3LYP/6-31G(d) level of theory.^18–22 The effect of implicit solvation was included during geometry optimization using the SMD model for dichloromethane.^23,24 Stationary points on the potential energy surface were characterized as minima or first-order saddle points (transition states) by evaluating harmonic frequencies at the optimized geometries.²⁵ From these frequency calculations performed with a double-zeta basis set, electronic energies [E(SCF)_DZ] and Gibbs free energies [G(sol)_DZ] based on standard thermodynamic approximations were tabulated.²⁶ Single-point energy refinements with the 6-311+G(d,p) basis set, implicit solvation, and Grimme’s empirical dispersion corrections (with Becke–Johnson damping)^27,28 allowed for improved triple-zeta electronic energies [E(SCF)_TZ]. For select species, single point energy refinements with aug-cc-pVTZ produced similar results (see Supporting Information) and the more efficient 6-311+G(d,p) basis was therefore employed. Approximate triple-zeta free energies were obtained by G(sol)_TZ ≈ G(sol)_DZ – E(SCF)_DZ + E(SCF)_TZ. Visualizations were made with GaussView 5.0.9²⁹ and CylView.³⁰

Experimental Methods

General: Anisole was purchased from Acros Organics and used without additional purification. BBr₃ was purchased from Aldrich as a 1 m solution in CH₂Cl₂ and used only for two weeks after opening to ensure purity. Dry CH₂Cl₂ was obtained from a PureSolv solvent purification system that passes solvent over two columns of neutral alumina. ¹H NMR were taken on a 300 MHz JEOL OXFORD spectrometer in CDCl₃ that was stored over 4 Å molecular sieves. Spectra were referenced to the deuterated solvent. Gas chromatography was performed on Thermo Scientific GC-Focus Series instrument which was fitted with a Supelco MDN-5 column. The injector (Thermo Scientific AL3000) temperature was set at 185 °C. An initial column temperature of 80 °C was held for four minutes and ramped at a rate of 10 °C per minute until a final temperature of 280 °C was reached. The detector temperature was set to 280 °C.

Representative Experimental Procedure: To a dry 5.00 mL thick walled vial equipped with a stir bar and septum was added anisole followed by the addition of dry dichloromethane (1 mL per 1 mL of BBr₃ solution). The vial was allowed to purge under nitrogen for approximately 5 min, after which BBr₃ was added slowly through the septum with stirring. The reaction was left to stir overnight before the contents were poured into ca. 1 mL of deionized H₂O. The organic layer was separated and an aliquot was analyzed by GC using dichloromethane as the solvent.

Supporting Information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re-organized for online delivery, but are not copy-edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.