Application of Markov chain Monte Carlo analysis to biomathematical modeling of respirable dust in US and UK coal miners

Abstract

A biomathematical model was previously developed to describe the long-term clearance and retention of particles in the lungs of coal miners. The model structure was evaluated and parameters were estimated in two data sets, one from the United States and one from the United Kingdom. The three-compartment model structure consists of deposition of inhaled particles in the alveolar region, competing processes of either clearance from the alveolar region or translocation to the lung interstitial region, and very slow, irreversible sequestration of interstitialized material in the lung-associated lymph nodes. Point estimates of model parameter values were estimated separately for the two data sets. In the current effort, Bayesian population analysis using Markov chain Monte Carlo simulation was used to recalibrate the model while improving assessments of parameter variability and uncertainty. When model parameters were calibrated simultaneously to the two data sets, agreement between the derived parameters for the two groups was very good, and the central tendency values were similar to those derived from the deterministic approach. These findings are relevant to the proposed update of the ICRP human respiratory tract model with revisions to the alveolar-interstitial region based on this long-term particle clearance and retention model.

1. Introduction

A biomathematical model was previously developed to describe the long-term clearance and retention of particles in the lungs of coal miners, which included separate evaluations of model structure and model parameter calibration¹ in two data sets, one from the United States (US) and one from the United Kingdom (UK) (Kuempel et al., 2001a,b; Tran and Buchanan, 2000). The model structure consists of deposition of inhaled particles in the pulmonary (alveolar) region, clearance from the alveolar region to the tracheo-bronchial region or translocation to the lung interstitium, and irreversible sequestration of interstitialized material. Each of these processes was described as first order. The structure of this three-compartment sequestration model describes additional processes that were not captured in a simple one-compartment model (Kuempel, 2000). Previous analyses also showed that the process of dose-dependent overloading of lung clearance as observed in rats did not adequately fit the coal miner data (Kuempel, 2000; Kuempel et al., 2001a; Tran and Buchanan, 2000). This three-compartment sequestration model has been shown to best predict the long-term retention behavior observed in US and UK coal miners and (more recently) in workers with relatively low exposure to radioactive cobalt or plutonium (Gregoratto et al., 2010, 2011). In contrast, other first-order human lung clearance models (NCRP, 1997; ICRP, 1994) were shown to underpredict the human retained lung particle burden data (Kuempel and Tran, 2002). In addition, a rat-based model (extrapolated to humans) with normal first-order clearance followed by dose-dependent impairment of clearance (overloading) (Hsieh and Yu, 1998) both underestimated the human retained lung dose at low exposures and overestimated the lung dose at higher exposures (Kuempel and Tran, 2002).

The model structure in Kuempel et al. (2001a) was recently adopted by the International Commission on Radiological Protection (ICRP) to describe the long-term clearance and retention of inhaled particles in the alveolar-interstitial region of the human respiratory tract model (HRTM) (Bailey et al., 2007, 2008) [draft revision of the ICRP (1994) model and comments on the draft available at: http://www.icrp.org/page.asp?id = 155)]. This model structure is considered to be physiologically more realistic and provides a simpler model that adequately represents the long-term retained lung dose in humans in several studies (described in Gregoratto et al., 2010). The initial model development and parameter estimates were based on a US coal miner autopsy study (Kuempel, 2000), and the model structure was independently evaluated and validated using UK coal miner data (Tran and Buchanan, 2000). The model calibration was also performed separately, and different point estimates of the optimal parameters were obtained for each of these data sets.

To facilitate implementation in the HRTM update, it is of interest to examine whether these differences in the US and UK parameter estimates are systematic, or whether these best-fit point estimates are consistent with a single distribution of values for each parameter in the larger population. The optimal point estimates of the model parameters were originally estimated separately in each data set by identifying those parameter values that minimizing the mean squared error (MSE) in fitting the model to the data (Kuempel, 2000; Kuempel et al., 2001a; Tran and Buchanan, 2000). In addition to point estimates, the current analysis provides estimates of the distributions of parameter values, which are needed to characterize the variability in predicted lung burdens in the human population.

For the current analysis, Bayesian population analysis using Markov chain Monte Carlo (MCMC) simulation is considered an appropriate method for calibrating this particle clearance and retention model. This approach permits parameters to be simultaneously calibrated for multiple data sets using uninformative prior parameter distributions that minimize bias (Bernillon and Bois, 2000; Lunn et al., 2009; Jonsson and Johanson, 2003; Hack, 2006; Hack et al., 2006). Distributions were estimated for the parameters in this three-compartment model, rather than point estimates, to provide information on variability in the lung dose estimates in the population. This analysis also helps to reduce uncertainty in human lung dose estimation by better characterizing the distribution in the parameters influencing the long-term clearance and retention of inhaled particles in the lungs.

2. Materials and methods

2.1. Key data sets and model structure

The US data are from a study by the late Werner Laqueur, M.D., who systematically collected approximately 600 cases from consecutive autopsies at Beckley Appalachian Regional Hospital in West Virginia. Lung dust burden was measured for 141 of these coal miners, who were autopsied between 1962 and 1968. Of the 141 miners, 128 miners had the minimal information specified in the original model parameter calibration, which included (in addition to the lung dust burden), the duration of employment in mining, the mining job history (to assign job-specific exposure concentration), and the dates and/or ages at retirement and death (to compute the post-exposure duration) (Kuempel et al., 2001a). Of these, 57 miners also had data on the lung-associated lymph node dust burden. The work histories were derived from questionnaires provided to the next-of-kin, clinical records, and mine company records (Kuempel et al., 2001a). In the current analysis, an additional 8 individuals were omitted due to discrepancies in tabulated values for ages, work experience, and death, which resulted in 120 US coal miners with lung burden, and 54 with lymph node data, for this MCMC-based parameter estimation.

The miners in the UK study were participants in the British National Coal Board's Pneumoconiosis Field Research program, which was set up in the 1950s, with lung autopsy dust burden data becoming available in the 1970s (Tran and Buchanan, 2000). Usable data (i.e., information on exposure, lung burden, age) was available for 514 individuals in the British study. For 115 of these individuals, lymph node dust burden data were also available (Tran and Buchanan, 2000).

Briefly, the model structure (illustrated in Fig. 1) consisted of the deposition of inhaled dust in the alveolar (gas-exchange) region; the competing processes of either particle clearance from the alveolar region (rate: KT) or particle translocation to the interstitial region (rate: KI); and the very slow (irreversible) translocation of interstitialized material in the hilar (lung-associated) lymph nodes (rate: KLN) The original parameter estimation for this model was performed using a systematic grid search within biologically plausible ranges of KT, KI, and KLN (identified from human and animal studies in the literature; Table 4 of Kuempel et al., 2001a). In addition, a fixed value of the average alveolar deposition fraction (ICRP, 1994) was estimated on the reported airborne coal mine particle size data (Jones et al., 1988a; Burkhart et al., 1987). The clearance parameters were then iteratively varied to determine the best fit of the model to the data (Kuempel et al., 2001a). The optimal parameter values were estimated as those that minimized the MSE in fitting the model to the data. Evaluation of the evidence for possible dose-dependent KT was a focus of the original model development (Kuempel, 2000; Kuempel et al., 2001a). In the best-fitting model, each of these processes is described as first-order because the inclusion of biomathematical equations describing varying degrees of dose-dependent impairment of alveolar clearance (KT) did not improve the model fit to either the US or the UK data (Kuempel, 2000; Tran and Buchanan, 2000). The equations describing the model and parameters (both original and updated) are provided in Appendix A.

Fig. 1.

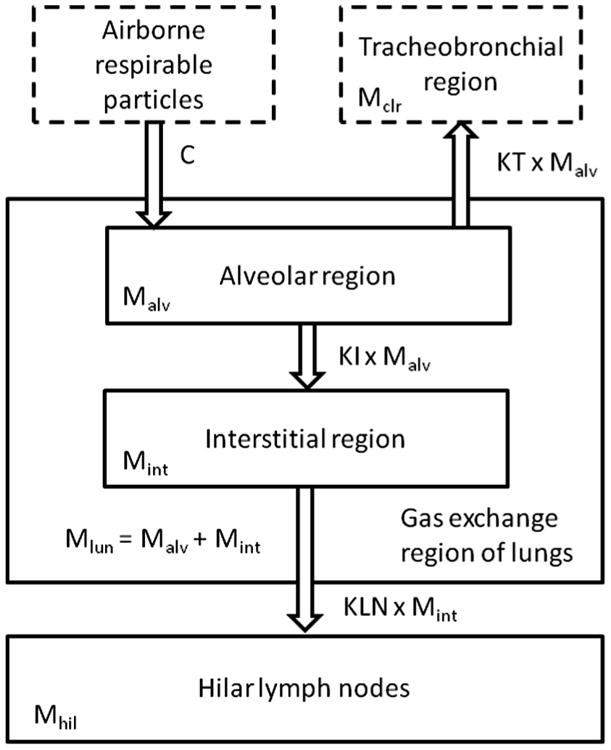
Structure of the three-compartment biomathematical model for long-term clearance and retention of particles in the lungs of coal miners.

2.2. Model implementation/model calibration

The previously used model code (Kuempel et al., 2001a,b) was adapted to the conventions for MCSim (version 5.3.1). Extensive reformatting was conducted on the input files. The UK files in particular required extensive preprocessing because of greater detail in the exposure histories (i.e., several changes in exposure concentration throughout individuals' employment). The reported concentrations were converted to adjusted concentrations based on a standardized work schedule (per the format of the US data, with respect to numbers of hours per day and per year; i.e., from estimated average of 1740 h/yr in UK data to 2000h/yr in US data, assuming 8 h/d, 5 d/wk, 50 wk/yr).

To facilitate the MCMC analysis, a statistical model was generated in order to implement a Bayesian approach. Bayesian modeling draws from two types of knowledge to derive model parameter estimates: prior knowledge, as described in initial parameter distributions, and information that can be deduced from measured data, if appropriately analyzed (Gelman et al., 1996; Bernillon and Bois, 2000). In the case of toxicokinetic data, the measured data generally consist of measurements from blood, breath, urine, and tissues, while the desired information may be values of parameters that describe the absorption, distribution, biotransformation, and elimination of the compounds of interest. Initial assumptions about the data and the parameters are tested against the available data sets. Using a sampling algorithm, such as the Metropolis Hastings algorithm, the proposed distributions are tested and thinned to yield distributions that provide the best agreement to the data. That is, the MCMC simulations are stochastic simulations where the selection of subsequent random values is influenced by the current parameter values (Bois and Maszle, 2009). The goal is that improved agreement between model and data will result as the simulation progresses. Each chain should be inspected to establish that “equilibrium” has been achieved, and further, multiple chains with different starting points (i.e., seed values) should be executed to test for consistency among chains.

The statistical model parameters are summarized in Table 1. The parameters to be sampled and optimized (KTdivKI, KI, and KLN) were transformed so that they would be described by distributions of the means of the natural logarithm of the parameter value (M_lnParam) and the associated variances (V_lnParam).

Table 1.

Statistical model parameters for disposition of lung coal dust in US and UK miners.

Data description
Measurement			Distribution			Geometric mean			Variance
Mlun			Lognormal			Mlun (prediction)			Ve Mlun
Mhil			Lognormal			Mhil (prediction)			Ve_Mhil
Subject level error distributions
Measurement	Distribution		Prior			Posterior
			Minimum	Maximum		Group	Mean	Variance	R
Ve_Mlun	Loguniform		0.01	3.3		US	0.473	0.00395	1.00
						UK	0.835	0.00263	1.00
Ve_Mhil	Loguniform		0.01	3.3		US	0.855	0.0315	1.01
						UK	1.07	0.0210	1.00

Model parameters
Variable	Distribution	Mean	Prior			Posterior
			Minimum	Maximum	Variance	Group	Mean	Variance	R
lnKTdivKI	Truncated normal	M_lnKTdivKI	−10	10	V_lnKTdivKI	US	0.806	0.00886	1.02
						UK	1.02	0.00575	1.12
lnKI	Truncated normal	M_lnKI	−10	10	V_lnKI	US	−1.39	0.755	1.14
						UK	−1.95	0.938	1.13
lnKLN	Truncated normal	M_lnKLN	−10	10	V_lnKLN	US	−5.53	0.0186	1.06
						UK	−5.19	0.0200	1.12

Population level parameters
Variable	Distribution	Mean	Prior			Posterior
			Minimum	Maximum	Variance	Mean		Variance	R
M_lnKTdivKI	Truncated normal	0	−10	10	4	0.922		0.116	1.00
M_lnKI	Truncated normal	0	−10	10	4	−1.64		0.819	1.14
M_lnKLN	Truncated normal	0	−10	10	4	−5.32		0.112	1.05
		Variance shape		Variance scale
V_lnKTdivKI	Inverse gamma	2.25		0.3125		0.215		0.0363	1.00
V_lnKI	Inverse gamma	2.25		0.3125		0.331		0.175	1.00
V_lnKLN	Inverse gamma	2.25		0.3125		0.209		0.0361	1.02

Parameter units: KTdivKI was dimensionless, KI and KLN were expressed in units of per year.

MCMC analysis further requires assumptions about the data that were measured (the mass of coal dust in the lung [Mlun] and the mass of coal dust in the hilar lymph nodel [Mhil]) and that were the ultimate source of information about the distributions of parameters that cannot be directly measured. The variance of the measurement error for these measured covariates was designated Ve_Meas.

Bayes' theorem specifies that the posterior probability distribution of the model unknowns (ψ, in this case, toxicokinetic parameters), given experimentally measured data (y, in this case, amounts of coal dust in lymph nodes and lung) is proportional to the product of the priors for the means (μ), variance (Σ), and error (σ²); measurements, given the toxicokinetic parameters and error model; and the population model (the toxicokinetic parameters, given the prior means and variance of the toxicokinetic parameters (Bernillon and Bois, 2000). Mathematically, this theorem is expressed as follows (per Bernillon and Bois, 2000, Eq. (9)):

$$p(\psi ,\mu ,\sum ,{\sigma }^2|\mathrm{y})\propto \mathrm{p}(\mu )\times \mathrm{p}(\sum )\times \mathrm{p}({\sigma }^2)\times \mathrm{p}(y|\psi ,{\sigma }^2)\times \mathrm{p}(\psi |\mu ,\sum ).$$

For the present analysis, ψ= {lnKTdivKI, lnKI, lnKLN},

μ = {M_lnKTdivKI, M_lnKI, M_lnKLN},

Σ = {V_lnKTdivKI, V_lnKI, V_lnKLN},

σ² = {Ve_Mhil, Ve_Mlun},

and y = {Mhil, Mlun}, as defined in Table 1.

In an MCMC analysis, multiple “levels” can be considered. For each parameter, separate distributions of that parameter are developed at the “study” level, but in combination, these study-level distributions must be consistent with the distribution for the parameter as defined at the higher “population” level (i.e., same shape). In this case, the UK and US studies were each considered to be a different subpopulation. This formulation is consistent with the way the data were previously analyzed and is also typical in treatment of data from different studies, even in the absence of differences with respect to national origin. The distributions for M_lnParam were truncated normal distributions, while the V_lnParam values were assumed to follow an inverse gamma distribution. The Ve_Meas distributions were characterized as log uniform. The distribution shapes are consistent with those used for parameters for biokinetic processes in other MCMC analyses (U.S. EPA, 2009; Evans et al., 2009; Chiu et al., 2009) and are typically used in Bayesian population modeling (Hack et al., 2006).

As noted above, the outputs of a Bayesian analysis are derived from the prior assumptions and information that is inherent in the data. Highly uninformative prior parameter distributions were used to avoid bias, so that the posteriors were determined by the data alone. Upper and lower limits for the priors were selected to encompass previously derived deterministic values with ample range for determination of alternative optimal values (U.S. EPA, 2009). The use of uninformative priors is considered a more robust, less biased approach to parameter estimation and strengthens the confidence that the parameter values represent a global optimum rather than a local optimum.

Multiple chains of MCMC optimizations (2000 iterations per chain, results reported for every fifth iteration) were produced by using different seed values for the MCMC algorithm. The outputs from the last 1000 iterations (only each 5th iteration is used, so 200 of the final 1000 iterations are used per chain) are used to compute the parameter descriptors for each chain. The results of three chains are used to determine convergence. The average of these three values is reported in Table 1 as the posterior value. Occasionally chains produced fatal errors; when this happened, such events typically occurred early in the chain and the results were discarded. We attribute these occurrences to the selection of broad, highly uninformative prior parameter estimates which initially include parameter values that were more likely to be incompatible with successful simulation of the data than values selected after multiple iterations have narrowed the range of values. Preliminary analyses of the chains consisted of evaluating the progress of the chain by viewing the changes in the log likelihood function (LLF) as the iterations progressed (the objective of the optimization process is to maximize the LLF). This inspection ensured that the chain was sufficiently stable that the last 1000 iterations would yield an acceptable set of “optimal” parameter values from the chain. Once three or more acceptable chains had been produced, an initial assessment of the consistency of the results was made by comparing the average of the LLFs. If one chain appeared to be an outlier (with substantially lower average LLF), additional chains were initiated, until a third chain with a comparable average LLF was produced.

Initial optimizations with KT, KI, and KLN as the varied parameters were attempted, using MCMC simulation. The first three successful chains did not converge (per the criterion described below in Section 2.3.1, “Convergence of Model Parameter Estimates”). A fourth chain was completed, and it was noted that three of these chains produced KLN estimates similar to the values previously determined (Kuempel et al., 2001a,b; Tran and Buchanan, 2000). The KI and KT values did not converge when the subset of chains with similar KLN values were evaluated (results not shown). It was noted, however that the difference between the mean values of M_lnKT and M_lnKI was consistent in multiple trials, but the individual values of M_lnKT and M_lnKI were different from trial to trial (note that lnKT – lnKI = ln(KT/KI) = constant, therefore the ratio KT/KI would be constant). The parameterization of the model was altered such that the parameter KT was redefined as KT = KI × KTdivKI, where KTdivKI is the ratio of KT to KI. This reformulated model produced convergent model parameter estimates, as described below in Section 3.

2.3. Evaluation of model output

2.3.1. Convergence of model parameter estimates

The convergence (similarity) of results among chains was analyzed by comparing the means and variances of the parameter estimates through the use of the “R” statistic, where R = 1 indicates perfect convergence (Gelman and Rubin, 1992; Gelman, 1996; Gelman et al., 1996). Gelman et al. (1996) indicated that PBPK model parameter value estimates demonstrated acceptable convergence if √R < 1.2.

2.3.2. Visualization of output

MCSim does not provide for the automated generation of plots, etc. Output files were analyzed in Microsoft Excel spreadsheets. The M_lnParam estimates were converted back to deterministic estimates of central tendency for the parameter values. These values were used to generate plots wherein the model predictions could be compared to the calibration data.

2.3.3. Agreement between model and measured amounts of dust in the lungs and lung-associated lymph nodes

The mean bias and mean squared error of the model predictions were calculated as described in the following equations (also as reported earlier (Kuempel et al., 2001a,b; Tran and Buchanan, 2000)).

$$\text{Bias}=\frac{1}{n}\sum _{i=1}^n({\mathit{\text{Observed}}}_i-{\mathit{\text{Predicted}}}_i)$$

$$\text{Mean squared error}(\text{MSE})=\frac{1}{n}\sum _{i=1}^n{({\text{Observed}}_i-{\text{Predicted}}_i)}^2$$

The fold error was calculated as the observation/prediction or prediction/observation, whichever was greater.

2.3.4. Sensitivity analysis

A sensitivity analysis was conducted wherein each parameter value was increased by 1 percent and the corresponding change in output was determined. Sensitivity coefficients were normalized to the output value and parameter value to yield a normalized sensitivity coefficient (NSC) equal to the fractional change in output divided by the fractional change in input. A positive value indicates that the output increased when the input parameter was increased while a negative value indicates that the output decreased when the input parameter value was increased. The scenario that was simulated was for a worker exposed to a constant concentration for 36 years followed by 0 or 10 years of retirement. These values were selected as being the average years worked in mining and the average post-exposure duration in the US coal miner data (Kuempel et al., 2001a). NSCs were calculated for dust accumulations in the lung and lung associated lymph nodes.

3. Results

3.1. Parameter estimates

All of the parameters to be optimized (Table 1) converged. The final parameter values were not near the upper or lower ends of the initial ranges; therefore the priors were demonstrated to have been sufficiently broad, so as to not bias the results. The central tendency estimates are similar to those of Kuempel et al. (2001a) and Tran and Buchanan (2000) (Table 2). The KT/KI ratio demonstrated the greatest consistency between groups (US vs. UK) and across the analyses (current, Kuempel et al., 2001; Tran and Buchanan, 2000). The KI values showed the greatest differences in central tendency values, but also the greatest variation within groups, suggesting that the seeming differences between groups are due to overall uncertainty regarding this parameter. The KLN values were intermediate in their consistency across groups and analyses.

Table 2.

Comparisons of model parameter estimates for human lung coal particle disposition.

	Rate of particle translocation to the interstitial region (KI) (per year)	Ratio of the clearance rate to tracheobronchial region (KT) to KI (KTdivKI)	Clearance rate to the tracheobronchial region (KT) (per year)	Sequestration rate to lymph nodes (KLN) (per year)
Population value (GSD) (this analysis)	0.194 (1.78)	2.51 (1.59)	0.488a	0.00489 (1.58)
US group (GSD) (this analysis)	0.249 (2.38)	2.24 (1.10)	0.558a	0.00397 (1.15)
US group (Kuempel et al., 2001a)	0.172	2.12b	0.365	0.00365
UK group (GSD) (this analysis)	0.142 (2.63)	2.77 (1.08)	0.393a	0.00557 (1.15)
UK group (GSD) (Tran and Buchanan, 2000)	0.172c	2.76b	0.475	0.00584

^aCalculated as KI × (KTdivKI).

^bCalculated as KT/KI.

^cAssumed equal to value of Kuempel et al. (2001a).

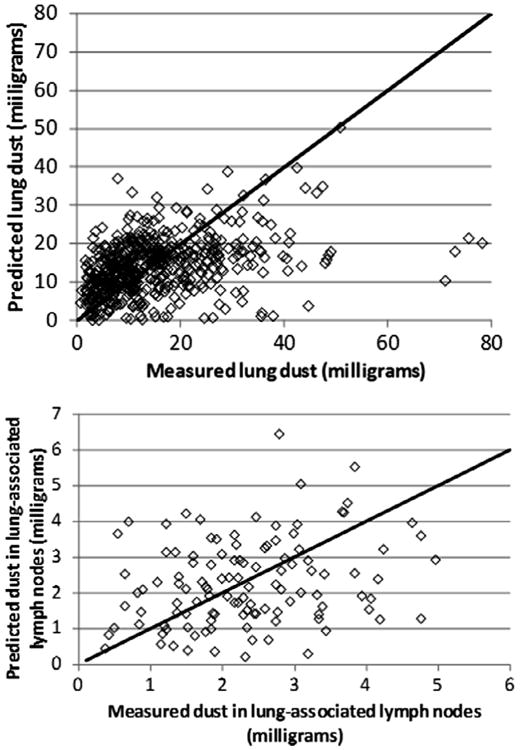
Fig. 2 shows the observed and predicted values for the combined data of US and UK miners based on the population central tendency estimates of the parameter values (Table 2). (US and UK data are separately compared to both central tendency and group estimates in figures found in Appendix B.) Residuals were compared to observed lung and lymph node burdens for simulations using the group-specific values (Figs. 3 and 4). For miners with low lung and lymph node dust burdens, the model tended to over predict the dust burden, while for miners with higher observed dust burdens, the model tended to underpredict what was observed. This same trend was observed in earlier analyses of the US coal miner data (Kuempel et al., 2001a,b).

Fig. 2.

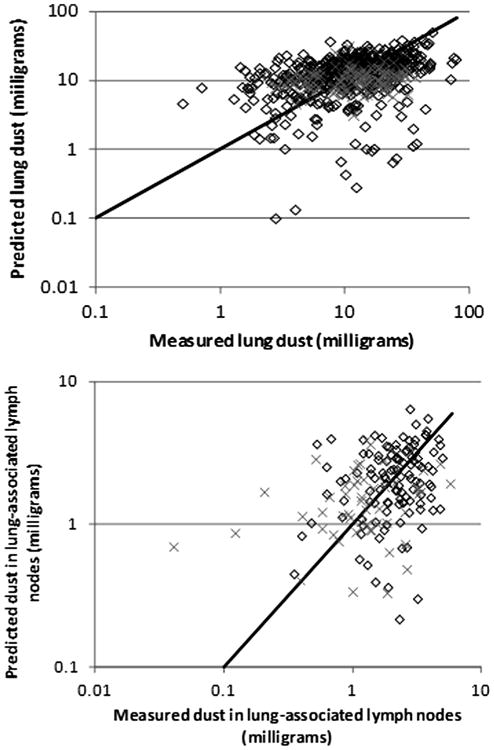
Observed and predicted values for UK miners (diamond) and US miners (×), using the population central tendency estimates of parameter values. Diagonal line indicates perfect agreement.

Fig. 3.

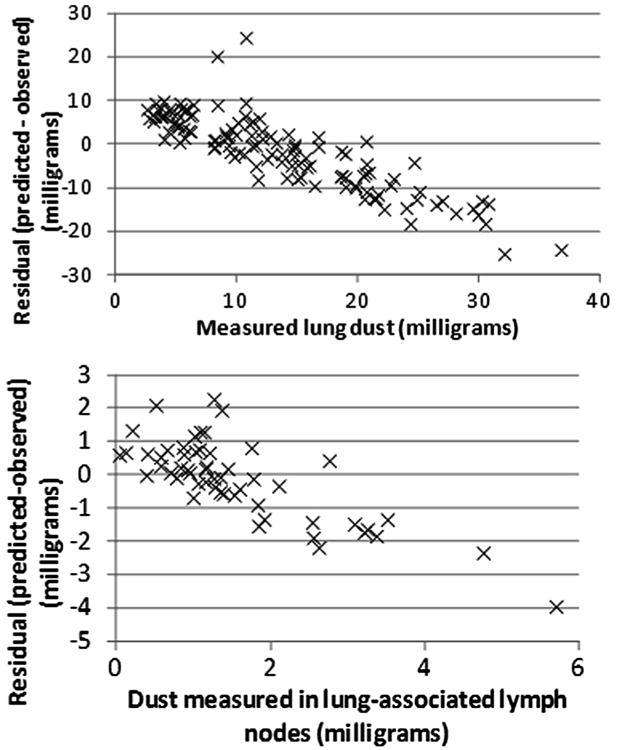
Residual (predicted-observed) values for US miners, using the subpopulation-specific central-tendency estimates of parameter values.

Fig. 4.

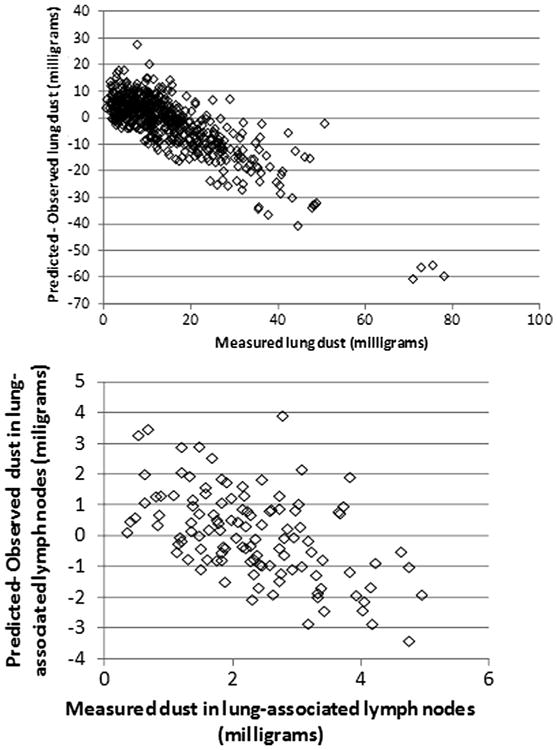
Residual (predicted-observed) values for UK miners, using the subpopulation-specific central-tendency estimates of parameter values.

3.2. Quantitative assessment of the agreement between the modeled and predicted values

The model tended to underpredict the lung data of both the US and UK miners, as indicated by the bias values (Table 3). The average lung dust underprediction was less for the UK miners than the US miners, when population model parameter values were used, and roughly equal when group-specific model parameter values were used. The direction of bias of the lymph node dust predictions different between the simulations with population and group values for both US and UK miners, and the bias was generally less than for the lung. On average, the model predictions were within a factor of just less than 2 of the experimentally measured amounts of dust in lungs and lymph nodes. Almost all of the predictions for miners were within 10-fold of the measured values; most of the instances with the largest fold errors were in the UK miners. Of the 15 cases where the lung dust predictions for UK miners were in error by 10-fold or greater, 14 of these cases had measured concentrations that were higher than predicted. This suggests an underestimation of the total coal mine dust exposure among those miners, a greater particle deposition fraction, and/or reduced clearance of particles than predicted on average.

Table 3.

Comparisons of deterministic model predictions and experimental data.

Location	US data				UK data
Tissue (n)	Lung (120)		Lymph node (54)		Lung (514)		Lymph node (115)
	Pop.	Group	Pop.	Group	Pop.	Group	Pop.	Group
Bias (mg) (% of average experimental value)	−2831 (21%)	−1675 (12%)	9 (0.64%)	−138 (8.9%)	−811 (5.5%)	−1299 (13%)	−24 (1.0%)	54 (2.4%)
Square root of MSE (mg) (% of average experimental value)	8764 (64%)	8563 (63%)	1219 (78%)	1193 (77%)	10951 (74%)	10985 (74%)	1369 (60%)	1400 (61%)
Fold error: geometric mean	1.8	1.7	2.0	2.0	1.9	1.9	1.7	1.7
Fold error: median	1.7	1.7	1.8	1.7	1.7	1.6	1.5	1.6
Fold error: % < 3	95%	90%	85%	81%	85%	84%	89%	89%
Fold error: percent < 10	100%	100%	98%	98%	97%	97%	97%	98%
Fold error: maximum	5.1	4.6	17	16	44	48	11	10

3.3. Sensitivity analysis

An analysis was conducted to evaluate the sensitivity of the lung and lymph coal dust estimates to the values of the model parameters. For this analysis, the deterministic model (i.e., a model with unique, rather than distributed, parameter values) with the mean population parameter values was used, and the tissue coal dust content was simulated for a worker exposed to 3 mg/m³ coal dust for 36 years (average values in US coal miner group (Kuempel et al., 2001a), starting at age 22 (until age 58), followed by either zero or 10 years (to age 68 years) with no additional exposure. The predicted time course of the dust content of the lungs and associated lymph nodes are depicted in Fig. 5. The predicted lung and lymph node dust content had a linear relationship to the values of C (concentration), FD (fractional deposition in the alveolar region), DE (days exposed per year), and VI (volume inhaled per day) at both times. The sensitivity coefficients for the kinetic parameters are summarized in Table 4. The value of KLN has only a modest impact on the amount of coal dust in the lung, but is a key determinant of the predicted amount in the lymph nodes (as expected). By contrast, KTdivKI has almost the same impact on predictions in both tissues at both times. That is, a change in KTdivKI (e.g., 10 percent increase) would change the levels of dust in both the lung tissue and the lymph node equally (e.g., a 6% to 7% decrease). Thus, the optimized values of the KT/KI ratio determine the total lung plus lymph node burden, while the value of KLN determines the fraction of the total tissue burden which is located in the lymph nodes. KI had little impact on the tissue dust burdens in these scenarios, but the sensitivity of the model predictions to KI was observed to be greater at retirement than at autopsy. Thus, while limited information on KI can be derived from samples in which the gap between retirement is longer, when the gap is shorter, information on KI, independent of KT or the KT/KI ratio, can also be discerned.

Fig. 5.

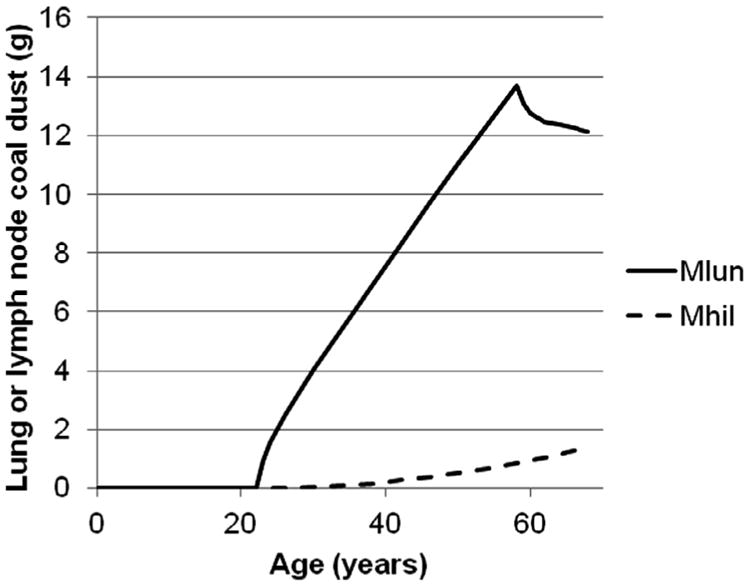
Predicted time course of coal dust in the lung (Mlun) and lung-associated (hilar) lymph nodes of a miner exposed to 3 mg/m³ coal dust for 36 years, from age 22 to 58 years old, until death at age 68 years old.

Table 4.

Sensitivity coefficients for predicted burden of coal dust in the lungs and lung-associated lymph nodes of miners.

Parameter	Normalized sensitivity coefficient
	Lung coal dust		Lymph node coal dust
	At retirement	10 years after retirement	At retirement	10 years after retirement
KTdivKI	−0.67	−0.69	−0.64	−0.66
KI	−0.08	0.00	0.07	0.04
KLN	−0.08	−0.13	1.20	1.18

The fractional deposition in the alveolar region (FD) was considered “fixed” in this analysis. Kuempel et al. (2001a) used an MMAD of 5.0 μm (GSD 2.1) for respirable coal mine dust based on studies published at that time, and the ICRP (1994), Table F.2 estimate of FD = 0.12 for heavy work and mouth breathing. More recent characterizations of respirable coal dust yield smaller median particle sizes. A study in which a total of 83 underground samples were taken at 13 mines reported respirable particle sizes ranging from the lowest MMAD of 0.9 μm (GSD 2.32) to the highest MMAD of 3.6 μm (GSD 1.32), with the median of the medians being 2.1 μm (GSD 1.65) (Page, 2003). Estimates of FD for various particle size distributions corresponding to ranges reported by Page (2003) and previously used by Kuempel et al. (2001a) were calculated using different breathing scenarios in the currently available version of MPPD (MPPD 2.11, 2009) (Table 5) with two combinations of breathing frequency and tidal volume that yield the same ventilation rate. Within this set of FD estimates, the values vary by almost seven fold. The choice of tidal volume had a modest impact (∼1.3-fold higher deposition at the higher tidal volume) for a constant particle size and same mode of breathing. For a given mode of breathing, variability in particle size and distribution could produce as much as a 2.3-fold change in the alveolar deposition estimate. The mode of breathing had less impact at the smaller (0.9 and 2.1 μm) particle sizes, but the greatest variability at the 3.6 μm particle size (as much as a 4.5-fold difference in deposition for oral vs. nasal breathing).

Table 5.

MPPD entire lung alveolar region deposition fraction output for different breathing scenarios by particle size.

Breathing scenario	Particle size MMAD (GSD)
	0.9 μm (GSD 2.32)	2.1 μm (GSD 1.65)	3.6 μlm (GSD 1.32)	5.0 μm (GSD 2.1)
Tidal volume = 1607 ml, 17.5 breaths per minute
Nasal or Oronasal (normal augmenter)	0.0899	0.0910	0.0754	0.0495
Oral	0.1452	0.2406	0.3389	0.1879
Oronasal (mouth breather)	0.1326	0.2036	0.2707	0.1551
Tidal volume = 1143 ml, 24.6 breaths per minute
Nasal or Oronasal (normal augmenter)	0.0701	0.0712	0.0612	0.0395
Oral	0.1135	0.1906	0.0612	0.0395
Oronasal (mouth breather)	0.1038	0.1614	0.2226	0.1238

Calculated using MPPD 2.11 (2009).

If the FD value used in the simulations is not representative of the central tendency experienced by the subjects (as a group), values of KT are likely to be erroneous. The process of tracheobronchial clearance removes mass that has not penetrated into the interstitium and lymph nodes. If the model value of FD is, for example, an overestimate, then the optimal value of KT could be altered to compensate for the larger mass of coal dust that must be cleared from the alveolar region (within biologically reasonable set of parameter values, e.g., Table 4 in Kuempel et al. (2001a)). To the extent that any errors in FD are likely to be equally applicable to the two mining populations, there is not likely to be any alteration to the interpretation that the US and UK miners' lung and lymph node burdens can be described by a common set of parameters. However, values of the other parameters (KT and KLN) may not be “true” values for these processes if other key parameters are not accurately specified. For this reason, if external information is available to estimate the true value of any of these parameters, it provides a basis for fixing that measured value and estimating the other parameters. In the best-fitting model in Kuempel et al. (2001a) (using a systematic grid search within biologically plausible ranges of KT, KI, and KLN identified from human and animal studies in the literature), KT was identified as 0.001 per day, which is equal to the measured clearance rate coefficient in a study of workers 200 days after inhalation of radiolabeled tracer particles (Bailey et al., 1985). Estimation of KI was also estimated in the systematic search, starting with that KT value and fitting the model (by minimizing the mean squared error) to the measured lung and lymph node data. Similarly, additional information on the variability of FD or other factors affecting coal dust deposition (within or between groups) could allow a refined estimate of the variability of KT (or KTdivKI) to be derived.

4. Discussion

Data from the two previously-identified studies of US and UK coal miners (Kuempel, 2000; Tran and Buchanan, 2000) were used in these analyses. Initial simulations with the US data alone were conducted in which optimizations of KT, KI, and KLN were attempted, using MCMC simulation. It was determined that only the ratio of KT and KI was consistent, and that the parameter estimates failed to converge even when subsets of chains with similar KI estimates were evaluated. In subsequent simulations, the parameters were regrouped such that the ratio of KT to KI (KIdivKI) was to be estimated instead of KT. The reformulated parameterization led to a successful MCMC parameterization. The central tendency values were similar to those derived from the previous deterministic approaches.

The structure of this three-compartment human long-term clearance and retention model was developed based on biologically-relevant pathways, and the transfer rate coefficients were determined to be first-order (i.e., not dose-dependent) (Kuempel, 2000). This model structure was found to provide the best fit to several human data sets (Kuempel et al., 2001a; Tran and Buchanan, 2000; Gregoratto et al., 2010, 2011). Earlier simple first-order (one compartment) models provided poorer fit to the human lung burden data (as discussed in Kuempel, 2000; Kuempel et al., 2001a; Kuempel and Tran, 2002). Evaluations of possible dose-dependent impairment of alveolar macrophage-mediated clearance (non-first order) as observed in rats (i.e., “overloading”) (Morrow, 1988; Bellmann et al., 1990) was not found to improve the model fit of the three-compartment sequestration model (Kuempel, 2000; Tran and Buchanan, 2000; Kuempel and Tran, 2002). However, accounting for particle sequestration substantially improved the model fit to the data and the prediction of the long-term retained lung burden of insoluble particles in humans (Kuempel et al., 2001a; Tran and Buchanan, 2000; Gregoratto et al., 2010).

Mathematically, this model consists of a series of differential equations that are integrated over time to predict individuals' lung and lymph node particle burdens (Kuempel et al., 2001a). Previously, Kuempel et al. (2001a) iteratively varied the clearance parameters (using a systematic grid search approach) to determine the best fit of the model to the data. Biologically plausible ranges in which to search for alternatives to the initial parameter values were based on data from the literature (Table 4 of Kuempel et al. (2001a)). Variability in the clearance rate coefficients was characterized in the US coal miner population using a multivariate optimization approach (Kuempel et al., 2001a). In the current analysis, MCMC analyses permitted simultaneous estimation of the distribution of parameter values.

Gregoratto et al. (2010) adapted this model (Kuempel et al., 2001a) into a simplified form using exponential decay functions, which is consistent with the expression of radioactivity in the lungs as described by ICRP (1994). The model structure was retained, although the model parameters were renamed; thus, K_T and m_T; K_I and m_I; and K_LN and m_LN (in Kuempel (2000) and Gregoratto et al. (2010), respectively). In addition, Gregoratto et al. (2010) introduced the terms AIseq and m, as follows:

$$\mathit{\text{AIseq}}=m_I/(m_T+m_I)$$

$$m=m_T+m_I$$

AIseq is the proportion of the inhaled particle mass deposited in the alveolar region that is not cleared from the lungs (i.e., sequestered. The complementary fraction (1 – AIseq) clears with an overall rate m. Gregoratto et al. (2010) uses these terms to define an equivalent model of the total retention in the alveolar-interstitial region and lung-associated lymph nodes. Based on the best-fitting model parameters in Kuempel et al. (2001a), “default” values of AIseq = 0.32 and m = 0.0015/day were estimated in Gregoratto et al. (2010). Similar (but slightly higher) values were estimated by Gregoratto et al. (2010) as best fits to three additional human data sets: (1) 900-day follow-up in 10 volunteers inhaling gold-labeled Teflon particles (Philipson et al., 1996); (2) 15-year follow-up of 7 workers who inhaled radioactive Co (⁶⁰Co) in the same incident (Davis et al., 2007); and (3) up to 30-year measurements of 9 workers who received an accidental inhalation exposure to plutonium oxides at the US Rocky Flats Plant (ORAUT 2007). The best estimates to those three data sets (averaged) were: AI_seq = 0.37 and m = 0.0027/day.² In addition the rate coefficients were estimated as: m_T = 1.7 × 10⁻³/day; m_I = 1.0 × 10⁻³/day; and m_LN = 3 × 10⁻⁵/day (Gregoratto et al., 2010, 2011).

The comparable values in the US coal miner data were: K_T = 1.0 × 10⁻³/day; K_I = 4.7 × 10⁻⁴/day; and K_LN = 1 × 10⁻⁵/day (Kuempel et al., 2001a). Thus, it can be seen that the clearance rate coefficients in Gregoratto et al. (2010) are approximately 2–3 times higher. Given that KT and KI are correlated and that the lung clearance process represented by the rate coefficient K_T is competitive to interstitial-sequestration process represented by K_I, higher values of K_T would require higher values of K_I in order to fit the lung burden data (thus, either set of parameters may adequately fit the coal dust data). Likewise, the model calibration and coal dust (non-quartz) parameter estimates in UK coal miners gave slightly different (but consistent) parameter estimates: K_T = 1.3 × 10⁻³/day; K_I = 3 × 10⁻⁴/day (fixed); and K_LN = 1.6 × 10⁻⁵/day (geometric mean) (Tran and Buchanan, 2000, Table 2.7). The arithmetic mean estimates (K_T and K_LN) were up to 50% higher (Tran and Buchanan, 2000), Table 2.7. In the current paper, the MCMC analyses show that the best-fitting parameter estimates in the US and UK coal miner data are consistent with a single distribution in a combined population.

All of these analyses have shown that accounting for sequestration of some portion of the inhaled dose is necessary to adequately predict the long-term lung burden of insoluble particles in several human data sets. This sequestration process was found to be first-order (i.e., not dose-dependent). Thus, even at low exposures, the current lung models based on simple (one compartment) first-order clearance would underpredict the human long-term retained lung dose – including the rat lung overload model structure at low exposure (since the rat lung overload model is first-order at non-overloading doses). The ICRP (1994) HRTM also underpredicts the long-term lung burden although not as much since it actually consists of three one-compartment alveolar models.

The current analysis and previous human studies provide consistent evidence in support of the proposed revision of the alveolar-interstitial region of the ICRP (1994) HRTM (Bailey et al., 2007, 2008; Gregoratto et al., 2010) to adopt the sequestration model structure developed in Kuempel (2000), Kuempel et al. (2001a). This model structure has been shown to improve the estimates of the long-term retained lung burdens of poorly-soluble particles in humans, including those with relatively low inhaled particle exposures (Gregoratto et al., 2010, 2011; Avtandilashvili et al., 2012). This sequestration model also improves the biological basis of the particle retention description in the alveolar region, and increases the parsimony of the model structure and parameters. These are the reasons the original model structure (Kuempel, 2000; Kuempel et al., 2001a), as fit to several other human data sets, was proposed for the pending update of the ICRP (1994) HRTM (Bailey et al., 2007; Gregoratto et al., 2010). The current analysis provides further support for this pending update by providing estimates of the distribution of parameter values in the US and UK coal miner data in addition to estimates of the best-fit parameter values to the combined data (Kuempel, 2000; Kuempel et al., 2001a; Tran and Buchanan, 2000). The lack of a clear difference in quality of the model agreement to the data when optimized values for group-specific or population values were used (e.g., Fig. B1 vs. Fig. B2, and Fig. B3 vs. Fig. B4) support the use of a common set of distributed model parameter estimates. These distribution estimates provide useful information to further characterize the variability in lung burden predictions in worker populations. The distributions of parameter values estimated in the current analysis are consistent with those reported in other human studies (Gregoratto et al., 2010, 2011; Avtandilashvili et al., 2012), and as such would be expected to provide similar estimates of the long-term retained lung burden at similar exposure conditions.

Concerning particle type, the Tran and Buchanan (2000) study – which included data on individual coal miners' exposures and lung and lymph node burdens to respirable quartz, as well as to non-quartz dust) – showed differences in the estimated clearance rate coefficients for these two dusts. The rate of alveolar-macrophage mediated clearance (Kt) was estimated to be lower for quartz than for non-quartz fraction of dust in miners' lung, and the rate of translocation to the lymph nodes was estimated to be higher for quartz (Tran and Buchanan, 2000). These findings are consistent with those reported by Seaton and Cherrie (1998) showing increased translocation of quartz to the hilar (lung-associated) lung nodes. Subsequent model development (e.g., HRTM) would be needed to differentiate the rate coefficients for high toxicity (quartz) and lower toxicity (e.g., coal) particles. Another area of model development that is needed is the evaluation of clearance and retention of nanoparticles relative to larger respirable particles (MacCalman et al., 2009).

5. Conclusions

The two data bases (US and UK miners) can be reasonably described by a common set of parameter values, an interstitialization rate (KI) of 0.194/year, a translocation/insterstitialization ratio (KTdivKI) of 2.51, and a lymph node sequestration rate (KLN) of 0.00489/year. The central tendency values of the parameters differ only modestly (75 percent difference for KI, 23 percent for KTdivKI, and 40 percent difference for KLN) between the two groups. Overall, the model tends to underpredict both lung and lymph node dust burdens, although on average the model predicted burdens are within a factor of two of the measured values. Simulations of alveolar deposition of dust based on different reported coal particle size estimates (MMAD and GSD) for different breathing scenarios (nasal, oral, or oronasal) indicate the potential for variability in fractional deposition, which was a “fixed” parameter in the model. The extent to which the value of fractional deposition used in the model is not representative of what any individual miner experienced cannot be determined. However, because the discrepancy is likely to be similar between the groups, the conclusion that the general structure of the model is appropriate and central tendency parameter values are similar between groups remains robust.

Appendix A

A.1. Base model equations and initial parameter values.

State parameters
Mdep – mass of dust deposited in lung (mg)
Malv – mass of dust in alveolar portion of lung (mg)
Mint – mass of dust in interstitial portion of lung (mg)
Mhil – mass of dust in hilar lymph nodes associated with lung (mg)
Mclr – mass of dust cleared from lung gas exch region to tracheobronichal region (mg)
Additional model output
Mlun – mass of dust in alveolar and insterstitial interstitial portions of lung (mg)
Input
C – dust conc in air (mg/m3) (Described as step function with the value changing at specified set points.)
Constants
FD = 0.12 – fractional deposition particle mass in alveolar region of lungs (dimensionless)
DE = 250 – days exposed per year (days)
VI = 13.5 – volume inhaled per working day (m3/day)
Optimized parameters (initial model)
KTy –alveolar clearance rate to tracheobronchial region (per year)
KLNy – transfer rate from interstitium into lymph node (per year)
KIy – transfer rate from alveolar tissue to interstitium (per year)
Sampled parameters
lnKIy
lnKTy
lnKLNy
Statistical model parameters
Mean values
M_lnKTy
M_lnKIy
M_lnKLNy
Variance
V_lnKTy
V_lnKIy
V_lnKLNy
Error distributions
Ve_Mlun
Ve_Mhil
Model equations
dMdep/dt = FD × C × DE × VI	mass deposition in lung (mg/year)
dMclr/dt = KTy × Malv	clearance to tracheobronchial region (mg/yr)
RI = KIy × Malv	first order transfer from alveolar region to interstitium (mg/yr)
dMalv/dt = dMdep/dt – dMclr/dt – RI	mass balance for alveolar region (mg/yr)
dMhil/dt = KLNy×Mint	accumulation in hilar lymph nodes (mg/yr)
dMint/dt = RI – dMhil/dt	Mass balance for interstitium (mg/hr)
Output
Mlun = Malv + Mint
Revised Model Equations and Initial Parameter Values
State parameters
Mdep – mass of dust deposited in lung (mg)
Malv – mass of dust in alveolar portion of lung (mg)
Mint – mass of dust in interstitial portion of lung (mg)
Mhil – mass of dust in hilar lymph nodes associated with lung (mg)
Mclr – mass of dust cleared from lung gas exch region to tracheobronichal region (mg)
Additional model output
Mlun – mass of dust in alveolar and insterstitial interstitial portions of lung (mg)
Input
C – dust conc in air (mg/m3) (Described as step function with the value changing at specified set points.)
Constants
FD = 0.12 – fractional deposition particle mass in alveolar region of lungs (dimensionless)
DE = 250 – days exposed per year (days)
VI = 13.5 – volume inhaled per working day (m3/day)
Optimized parameters (initial model)
KTdivKI –ratio of alveolar clearance rate to tracheobronchial region to the transfer rate from alveolar tissue to interstitium
KLNy – transfer rate from interstitium into lymph node (per year)
KIy – transfer rate from alveolar tissue to interstitium (per year)
Sampled parameters
lnKIy
lnKTdivKI
lnKLNy
Statistical model parameters
Mean values
M_lnKTdivKI
M_lnKIy
M_lnKLNy
Variance
V_lnKTdivKI
V_lnKIy
V_lnKLNy
Error distributions
Ve_Mlun
Ve_Mhil
Model equations
dMdep/dt = FD × C × DE × VI	mass deposition in lung (mg/year)
dMclr/dt = KTdivKI × KI × Malv	clearance to tracheobronchial region (mg/yr)
RI = KIy × Malv	first order transfer from alveolar region to interstitium (mg/yr)
dMalv/dt = dMdep/dt – dMclr/dt – RI	mass balance for alveolar region (mg/yr)
dMhil/dt = KLNy × Mint	accumulation in hilar lymph nodes (mg/yr)
dMint/dt = RI – dMhil/dt	Mass balance for interstitium (mg/hr)
Output
Mlun = Malv + Mint

Appendix B

Plots of observed vs. expected values each data set using the mean values for KT and KLN for both the population– and group-specific estimates are provided in Figs. B1–B4).

Fig. B1.

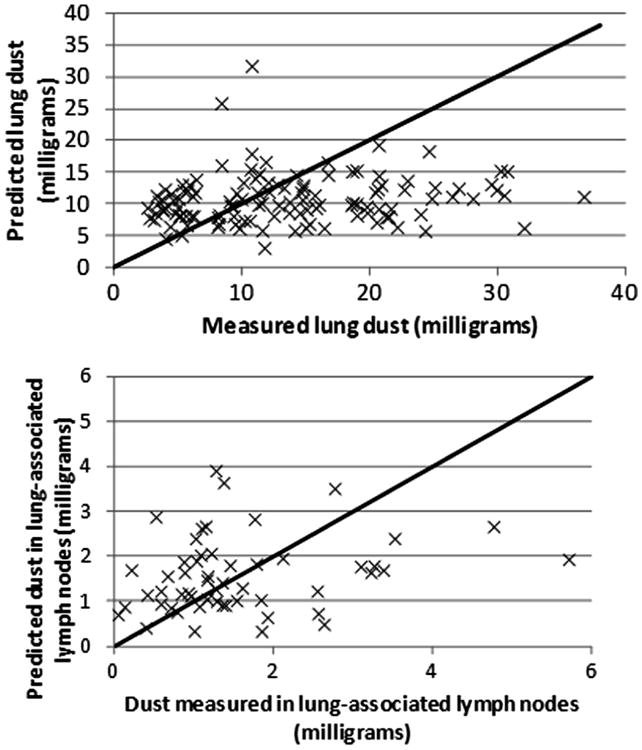
Observed and predicted values for US miners, using the population central-tendency estimates of parameter values.

Fig. B2.

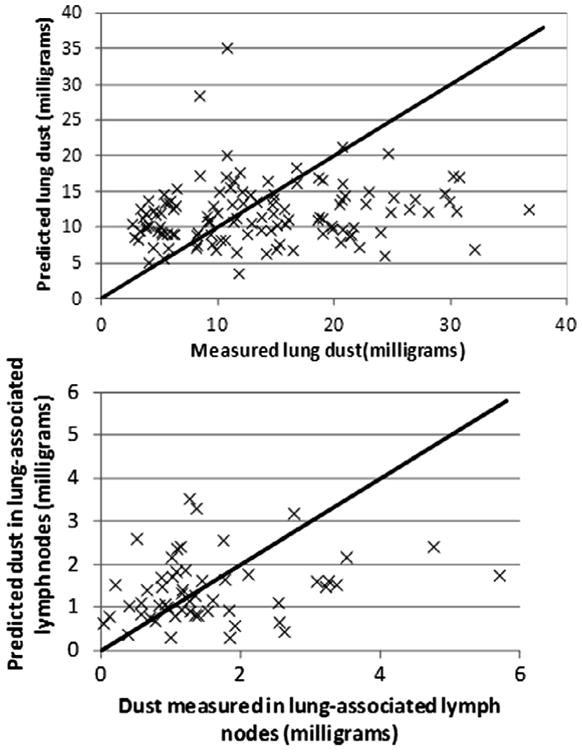
Observed and predicted values for UK miners, using the population central-tendency estimates of parameter values.

Fig. B3.

Observed and predicted values for UK miners, using the population central-tendency estimates of parameter values.

Fig. B4.

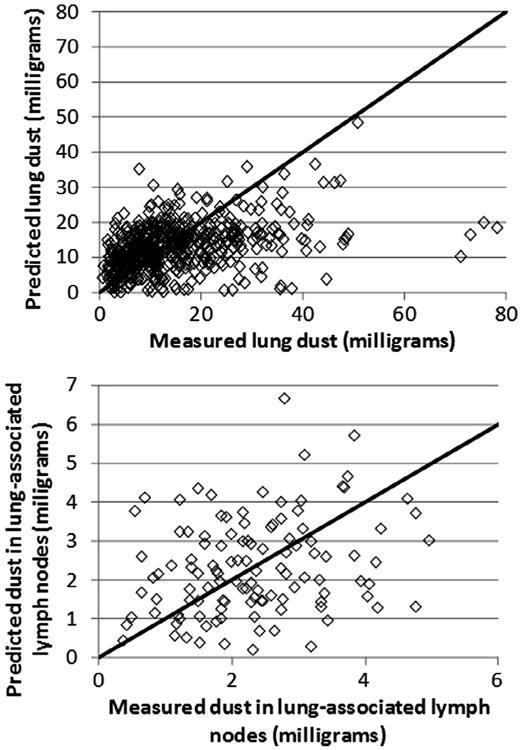
Observed and predicted values for UK miners, using the subpopulation-specific central-tendency estimates of parameter values.