Ensemble Properties of Network Rigidity Reveal Allosteric Mechanisms

Abstract

The distance constraint model (DCM) is a unique computational modeling paradigm that integrates mechanical and thermodynamic descriptions of macromolecular structure. That is, network rigidity calculations are used to account for nonadditivity within entropy components, thus restoring the utility of free energy decomposition. The DCM outputs a large number of structural characterizations that collectively allow for quantified stability/flexibility relationships (QSFR) to be identified. In this review, we describe the theoretical underpinnings of the DCM and introduce several common QSFR metrics. Application of the DCM across protein families highlights the sensitivity within the set of protein structure residue-to-residue couplings. Further, we have developed a perturbation method to identify putative allosteric sites, where large changes in QSFR upon rigidification (mimicking ligand-binding) detect sites likely to invoke allosteric changes.

1. Introduction

Static glimpses of proteins provided by x-ray crystal structures routinely shown in biochemistry textbooks do not convey how proteins flex and wiggle over a spectrum of timescales that can span more than 12 orders of magnitude (1). In fact, dynamical motions associated with conformational changes on long timescales are generally paramount to protein function. These motions are modulated by thermodynamic and environmental conditions that a protein is subjected to, where pH and other environmental conditions are determined by the cellular environment. A given protein will slosh around in a mixture of other proteins, complex polymers, and myriad small molecules in the midst of tens of thousands of chemical reactions taking place. Being in thermal contact with a heat reservoir (the cell), proteins are subject to thermal fluctuations that give rise to statistical interactions, and, yet, they perform a wide range of functions with exquisite precision. For example, enzymes catalyze chemical reactions with a remarkable degree of specificity, control and efficiency (2). Decades of painstaking structure/function biochemical and structural biology studies have uncovered many physiochemical principles that consist of the interplay of a large number of different types of interactions. Typically, proteins have thousands of atoms that interact through covalent bonding, hydrogen bonding and salt bridges, and weak non-bonding forces (3).

An open challenge is to develop a computational method that accurately predicts protein thermodynamics and flexibility for specified solvent and thermodynamic conditions in computing times fast enough for high-throughput applications. We review here crucial theoretical aspects that enable new types of algorithms to be successfully developed to accurately predict protein thermodynamics. Despite considerable complexity, we will describe how progress has been made in predicting protein properties and behavior by focusing on the essential physics, which subsequently greatly simplifies model details and calculations. Central to this task is to reconcile conformational flexibility as a critical link relating structure to stability. After discussing key properties of mechanical networks, which our approach is based upon, a Distance Constraint Model (DCM) (4, 5) is defined based on a paradigm that combines constraint theory with free energy decomposition. With the theoretical framework laid out, the DCM is solved using an efficient graph-rigidity algorithm in conjunction with a hybrid Monte Carlo and mean field approximation (6). The consequence of this approach is the ability to calculate a large number mechanical network properties in a thermodynamically meaningful way, including pairwise residue-to-residue couplings intrinsic to the native structure ensemble (7-11) and putative allosteric sites via a perturbation method (12).

2. Generating Protein Ensembles

Generating conformational ensembles is a necessary first step to describe protein stability, dynamics and function, including allosteric mechanisms. Molecular dynamics (MD) simulation is the most common approach used to explore protein dynamics and investigate detailed atomic mechanisms (13). Unfortunately, MD is severely limited when trying to describe thermodynamic properties because robust and statistically significant sampling of atomic configurations is required to accurately estimate conformational entropy. Even in the next decades to come, there is little hope that an all-atom brute force MD simulation will be able to robustly explore conformational space to make free energy calculations meaningful. However, this is not to say that MD cannot be used, quite the contrary. One realizes that much of the motion of a protein is organized though cooperative behavior and local constraints that restrict much of the motion. When this information is incorporated into a model, then the simulation time can be greatly reduced by effectively working with less number of degrees of freedom (DOF). Multiscale modeling is such an approach, allowing much more efficient sampling through a hierarchical characterization of protein structure and dynamics (14). Combined with advance sampling algorithms (15), free energy calculations using MD simulations are tractable (16), although they will probably remain prohibitively expensive for a high throughput workflow. Moreover, the free energy estimates will always have statistical errors associated with the limited and/or biased sampling, and systematic errors are introduced through specific coarse-graining approximations made within the multiscale model (17).

Proteins exhibit a high degree of fidelity in function, and their ensemble of conformations cluster into well-defined thermodynamic states (18). Consequently, conformational sampling can be localized into key regions in configuration space, characterized by sub-ensembles. A multiscale approach deals with the process of coarse graining to reduce the number of dynamical variables in order to accurately describe a system within the most relevant sub-ensembles. That said, a coarse grained description should be able to reduce sampling errors to a point where they pose no concern, and the model approximation becomes the only relevant factor. With this appreciation, an alternate computational strategy emerges when considering tradeoffs between statistical sampling error (controlled by CPU time) and systematic error (controlled by model approximations).

Two alternative methods that explore the dynamics of proteins within their native basin are the elastic network model (ENM) (19) and the Framework Rigidity Optimized Dynamics Algorithm (FRODA) (20). Both methods rely on a known 3D structure as the primary determinate of characterizing the essential dynamics of a protein. The ENM approach (on its own) is not suitable for generating conformations that deviate far from the starting point, and this poses too great of a limitation for further discussions here. In contrast, FRODA is in principle able to generate conformations that deviate far from the native basin. Recently, pathways have been generated between conformational states as demonstrated with a new improved version called FRODAN (21), which is no longer an acronym. Both FRODA and FRODAN are based on a specific type of coarse-grained molecular mechanics potential, and they use Monte Carlo sampling rather than propagating dynamical equations of motion to more efficiently generate conformational ensembles. The most relevant features pertinent to our discussions here is that they are an all atom-based model that runs much faster than MD (perhaps 10⁴ times faster) by employing concepts of rigidity to naturally coarse grain the protein structure into rigid sub-units based on chemical bonding and atomic packing. The tremendous gain in speed derives from a reduction in DOF and because of the method of geometrical simulation, where the potentials are greatly simplified. It is prudent at this point to briefly highlight some properties about network rigidity, which is the central concept that enables us to estimate conformational entropy and restore the utility of free energy decomposition, as will be discussed below.

2.1. Network Rigidity

Classical mechanics textbooks define a “rigid body” as a set of material points with positions, whose mutual separations are fixed. There is no room for an ensemble of conformations in a rigid system, rather it can only execute trivial motions: translations and rotations. In other words, there can be no internal motions within a rigid object. A very simple but powerful approach is to realize that constant separations between atoms result from chemical bonds. In mechanical models, bonds are represented by distance constraints, connected at atoms, which are treated as universal pivot joints. The bars and atoms define a graph consisting of vertices (atoms) connected by edges (bars). Rigidity theory determines how the number of internal independent DOF depends on the number of edges (bars) and their distribution within the network.

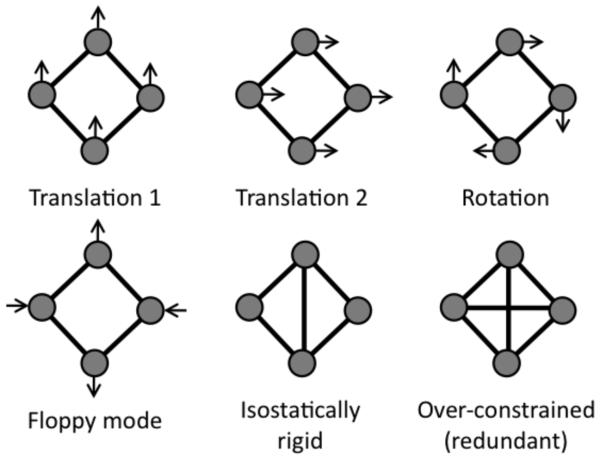
An analysis of network rigidity allows the determination of all continuous deformations of the network that are possible by checking if relative atomic motions are allowed while all bar lengths are fixed. A brute force mathematical procedure of counting the DOF is similar to normal mode analysis in molecular systems (22). If a system is simple, intuition can be used to determine whether it is rigid or not. For purpose of discussion and defining terms, we will consider a quadrangle in two dimensions. It can be seen by inspection that a quadrangle is flexible having one internal DOF in two dimensions. The allowed displacements of the particles are shown in Fig. 1 by arrows. Using this example, we work through the important exercise of constraint counting. If there are no constraints, the total number of DOF is the number of particles, N, times the number of independent displacements of each particle, which is equal to dimensionality, d. Each distance constraint eliminates a single DOF. This implies that the constraints are all independent, which is the case for the quadrangle shown in Fig. 1 (redundant constraints will be discussed later). Having K constraints, the total number of DOF is given by: N_t = d·N – K, which is equal to N_t = 2·4 – 4 = 4 for a quadrangle in a two dimensional plane.

FIGURE 1.

Examples of floppy modes in a quadrangle network. In two dimensions, all networks posses the three trivial modes (two translations + rotation), which are indicated by the arrows. A quadrangle also has one deformable floppy mode. Addition of a crosslinking constraint fixes the distance between the connected vertices, thus freezing out the floppy mode. This marginally rigid network is referred to as isostatic, indicting N_f = N_t − G = 0. Adding a second crosslinking constraint, which over-constrains the network, does not affect the number of floppy modes because the structure was already rigid, meaning it is redundant. Removal of a redundant constraint has no effect of the number of floppy modes.

Not all of the four DOF describe continuous deformation of the network because any body in a plane can be displaced in two orthogonal directions, say x and y. It can also be rotated around the z-axis that is perpendicular to the plane. Under these global translations and rotations all the particle separations remain the same. These global motions always contribute to the total number of DOF of a constrained network, N_t. In particular, the global motions are the only available DOF for a rigid body. Thus, in order to get the number of internal DOF that describes the intrinsic flexibility of a network, we need to subtract the number of global motions from the total number of DOF. In a d dimensional space, a body can rotate in d(d − 1)/2 independent planes. It can also be translated in d independent directions. The number of global motions is therefore given by G = d + d(d −1)/2 = d(d + 1)/2. For d=2, G=3. The number of internal DOF governing the conformation of the quadrangle in a plane is therefore N_f = N_t − G = 4 − 3 = 1, corresponding to only one possible mode for continuous (no energy cost) deformation shown in Fig. 1. For a triangle in the plane, the same counting gives N_t = 2 × 3 − 3 = 3, and the number of conformational DOF is N_f = 3 − 3 = 0, meaning a triangle is rigid.

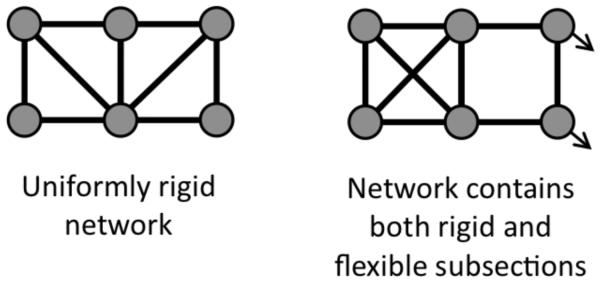
Adding an additional constraint along one of the diagonals removes the final DOF (locking the angle), and results in a rigid quadrangle, N_f = N_t − G = 4 − 4 = 0. Whenever there are just enough constraints in a network to make it rigid, then the network is said to be marginally rigid, or isostatic. Adding a second distance constraint along the other diagonal leads to an over-constrained network with one redundant constraint. That is, there are more constraints present than possible internal DOF, resulting in some constraints being redundant. Since the distance constraints are modeling atomic interactions in the physical system, strain energy will reside in any region within a network identified as over-constrained by constraint counting. In other words, some distances will have to stretch or compress to accommodate adding a distance constraint between a pair of atoms in which the distances between the atoms are already predefined based on network rigidity. A redundant constraint can be removed from the network without affecting the number of DOF, cf. Fig. 1. When all constraints are uniformly distributed, the number of DOF is given by N_f = max[N_t – G, 0], which is called Maxwell counting based on his profound insight (23). While Maxwell constraint counting can be quite powerful as a mean field approximation, the method fails when constraint density is not uniform, which can be seen clearly by inspection in Fig. 2. In general, a network will consist of regions that are rigid that interconnect through flexible mechanisms. It is possible to decompose a network into a set of rigid substructures (or clusters), and identify rigid clusters as isostatic or over-constrained. In large networks counting the available conformational DOF is possible using graph-rigidity algorithms to identify the independent and redundant constraints in practical computing times.

FIGURE 2.

Two example face-sharing quadrangle networks. The example on the left is isostatically rigid with no redundant constraints, whereas the example on the right is more complicated. That is, based on a heterogeneous constraint distribution, it possesses both a redundant constraint and an internal degree of freedom. While it is possible to identify the redundant constraints and internal degrees of freedom by inspection in this case, sophisticated graph rigidity algorithms are needed as networks become more complicated.

For a protein consisting of thousands of atoms, an algorithm to count the internal DOF is required, for which a number of methods can be employed (24). The pebble game is one such algorithm (25), which quickly and accurately calculates network rigidity properties by implementing combinatorial constraint counting by visualizing the DOF as pebbles. Each pebble corresponds to a single DOF of each atom. By tracking pebble movements according to simple rules, the pebble game determines how DOF are lost to constraints, and it exactly identifies all rigid clusters, redundant constraints and over-constrained regions. The program FIRST (Floppy Inclusion and Rigid Substructure Topography) (26) analyzes a protein structure, and maps out all rigid and flexible regions. In performing this analysis, it should be noted that the calculation is valid for a given set of constraints, and furthermore, the way in which distance constraints model interactions is not unique. This FIRST approach has proven to be a powerful tool to describe protein rigidity and flexibility.

When thermal fluctuations are taken into account, some interactions will break while others will form. In the implementation of FIRST, native contacts were diluted (removed) in the order from weakest to strongest, which simulated the process of protein unfolding (27). Moreover, FRODA also only considers native contacts. In both cases, the primary criticism of using network rigidity is that thermal fluctuations are not modeled. The important point that is critical for obtaining a robust description of protein stability and calculating free energy is to find a way to model protein ensembles that span the range from folded to unfolded states, as well as any intermediate states (or partially unfolded states) and the transition state. In terms of rigidity, this means the number of constraints must be allowed to fluctuate. When many constraints are present, the protein motions are greatly restricted, and as distance constraints are removed, motion is increased. FRODAN improves upon this problem, but in doing so, it has dramatically rendered its dependence on FIRST as a pre-processing step. Our approach to modeling the process of constraints breaking and forming is through an Ising-like model. Ising-like models have been employed with great success to capture the gross features of protein thermodynamics and kinetics (28).

2.2. Ising-like models and native contacts

The Ising model was originally created to study ferromagnetism based on discrete spin variables that can be in one of two states (spin up or down) representing magnetic moments. The spins interact with one another, and with an external magnetic field. The Ising model has become a hallmark paradigm to describe phase transitions for all kinds of phenomena, including protein folding. The first example of this goes back to the classic Zimm-Bragg (29) and Lifson-Roig models (30) for the helix-coil transition. In the Zimm-Bragg model, backbone hydrogen bonds (H-bonds) are considered as formed (spin up) or broken (spin down). In the helix state, almost all H-bonds are formed, while in the coil state almost all of the H-bonds are missing. In the Lifson-Roig model the residues are considered as being in a helical conformation (spin up) or coil conformation (spin down). The nature of the polypeptide is completely described by the spin configuration at a coarse grained level. These two models differ from one another in terms of details, but they both apply free energy decomposition (FED). That is, as more native interactions form (either H-bonds along the backbone, or a consecutive sequence of residues in an alpha-helix state), both enthalpy and entropy is lowered. The entropy reduction is a critical part of the contribution.

With respect to the original Ising-model that only represented the Hamiltonian (energy) of the system, there is a fundamental departure using Ising models for the helix-coil transition or protein folding. Now, the local spin variables represent local conformational states that add certain amounts of free energy that consist of both enthalpy and entropy contributions. For a given spin configuration of the system, the total enthalpy and entropy contributions are simply added together. Despite this difference, a partition function is calculated as a sum over all Boltzmann factors as done in the original Ising-model, where one should in principle include all spin configurations (microstates). However, these spin configurations actually represent macrostates of a protein because they describe atomic conformations at a coarse grained level. Taken together, all spin configurations define the complete ensemble from which all thermodynamic properties can be calculated, including metastable states, if present.

As applied to proteins, the three-dimensional structure of the protein is assumed known, and residues are assigned as being folded or unfolded. When neighboring residues are in a folded-state, the native contacts that connect these two residues form, otherwise they are broken. Two popular Ising-like models are COREX (31, 32) and the Wako-Saitô-Muñoz-Eaton (WSME) model (33), which have been reviewed recently (34) in the context of methods that generate protein ensembles. The important aspect that we mention here is both models assume additivity within the FED, just as do the Zimm-Bragg and Lifson-Roig models. The meaning of additivity in the context used here is mathematically precise. It means for a given spin configuration, the total free energy is the sum over all parts, where both the enthalpy and entropy contributions are individually additive. It is worth noting that once the partition function is calculated, the thermodynamic entropy will always be a non-additive function that reflects all the spin configurations within the ensemble, or sub-ensemble of interest.

What is often overlooked is that a given spin configuration represents a sub-ensemble of a protein, and the process of adding free energy contributions from each spin variable implies each local state acts independently from each other. If each component operates independently from one another, then, cooperativity between the local units is lost by definition! Cooperativity can be built into an Ising-like model through spin-spin coupling terms, as done in the Zimm-Bragg, Lifson-Roig and WSME models, or through an external field using 1-body interactions by relating the solvation of residues to solvent accessible surface area (SASA) as done in COREX. In general, long-range cooperativity within a given spin-configuration is lost whenever an additive model is employed. As recently discussed in the context of the helix-coil transition (35, 36), cooperativity can also be explicitly calculated using the properties of network rigidity. Network rigidity is essential for restoring the utility of a FED because of the fundamental problems that occur with free energy reconstitution, next reviewed.

2.3. Free Energy Decomposition and Reconstitution

The free energy of a protein determines its thermodynamic state. Accurate calculation of the free energy for a protein, consisting of hundreds of amino acids connected by covalent bonds and other types of chemical bonds and weak interactions is formidably difficult. One reason for persistent inaccuracies in these calculations is the assumption of additivity. Therein, it is assumed that the free energy of a protein can be obtained as a sum of free energies of each individual amino acid. Unfortunately, while additivity models have been applied to proteins for decades, they are fundamentally flawed (37). In their seminal 1989 paper (38), Karplus and co-workers coined the tantalizing term “hidden thermodynamics,” reflecting the observation that some aspect or key element of the FED scheme was missing. Nevertheless, it was at this point absolutely clear that some essential physics was not being accounting for, leading to the search for better FED schemes that somehow included the missing physics.

Attempts to analyze protein thermodynamics have revealed that additivity principles applied to a FED scheme in terms of specific interactions breakdown when cooperativity is present in the system. In view of the fact that most proteins exhibit some level of cooperativity, Mark and van Gunsteren (39) write: “In Regard to the detailed separation of free energy components, we must acknowledge that the hidden thermodynamics of a protein will, unfortunately, remain hidden.” Further, Hallerbach and Hinz (40) analyzed the cold denaturation and found inconsistencies in heat capacity predictions. They conclude that models that assume additivity in the conformational entropy due to hydration effects violate the second law of thermodynamics. These and many other studies point to inconsistencies that arise when additivity principles are applied to the FED approach. Ken Dill notes (37): “Perhaps some of our models in computational biology are based on flawed assumptions. Thermodynamic additivity principles are the foundations of chemistry, but few additivity principles have yet been found successful in biochemistry.” The best way to understand why additive models are unlikely to succeed is to write the consequence of such a condition whenever it is found to be true. Given that the k-th component of free energy is given by G_k , and assuming the total free energy is indeed additive over all components, such that $G_{tot}={\sum }_k{G}_k$ then it follows that the total partition function is a product of individual partition functions, where $Z_{tot}={\prod }_k{Z}_k$ and the standard relations follow: $G_k=-RT\text{ln}\left(Z_k\right)\text{and}{G}_{tot}=-RT\text{ln}\left(Z_{tot}\right)$, where R is the ideal gas constant and T is absolute temperature. This complete factorization of the Z_k partition functions can only be true when there is strictly no coupling between any of the subsystems. Said another way, a set of generalized coordinates must be determined that are separable across all subsystems. As it routinely happens, because of the well-separated types of forces involved in chemical bonding contributing to vibrational motions in bond-lengths, bond-angles and dihedral angle rotations, this factorization approximately holds in small molecules, where additive models are found to work markedly well (but never exactly).

In general, the enthalpy and entropy contributions are never exactly additive due to coupling terms that arise in part due to local variation in micro-environments. In macromolecules such as proteins, the nonadditivity in the entropy is much more significant than that found in enthalpy. The main reason for this is the formation of loop connections in the otherwise chain-like structure of these molecules. Once a protein starts to collapse into its native structure from a (hypothetical) completely extended state, even a single H-bond can dramatically reduce the entropy of the chain. The situation is not too bad with only a few cross-linking H-bonds, but additivity becomes problematic when there is a high density of cross-linking interactions. As the cross-links are added, more constraints are imposed on the motions of the atoms within the various parts of the protein that have been identified as subunits or components. The source of nonadditivity that Mark and Gunsteren (39) have shown definitively, has to do with the geometrical, and as it turns out, topological, properties of the protein structure. As such, once coupling occurs, the problem related to reconstituting the total free energy of a protein, based on knowing the free energy component parts presents itself. In other words, the key ingredient missing is structural information, relating to the available DOF in the system, which directly determines cooperativity found in the protein. The root of nonadditivity lies in mechanics. One way to avoid the nonadditivity problem is to only work with energies directly, and to calculate conformational entropy by sampling over conformations using molecular simulation techniques, such as molecular dynamics or Monte Carlo. A much bolder alternative is to apply FED, but modify the reconstitution process by developing a quantitative way to account for nonadditivity of entropy, as discussed below using a Distance Constraint Model.

3. The Distance Constraint Model

Many models employ a FED, where it is assumed the free energy components can be added to calculate the total free energy of a protein structure. As explained above, unless the generalized coordinates that are used to describe the protein are 100% separable, and independent over all accessible conformations that can take place, this type of approach will fail. An alternative is to use an over-specified coordinate system. In this case, the model applies distinct coordinates for all intramoleculer interactions, thus obtaining an over-specification of the atomic positions within a protein. In this situation, the pertinent question becomes which of these interactions (modeled as a set of distance constraints) are independent or redundant. Using the properties of network rigidity a new paradigm has been formulated that adds entropy contributions only from independent distance constraints.

3.1. Naive Estimate of Conformational Entropy from DOF

Proteins interact with their environment through energy exchange, and therefore statistical mechanics must be employed to predict any kind of measurable property that a protein may exhibit. In equilibrium with a heat bath at temperature T, the probability to find the protein in a given macrostate ν is given by:

$$\text{Pr}\left(v\right)=\Omega \left(v\right)\text{exp}[-E\left(v\right)∕RT]$$ Eq. (1)

where E(ν) is the energy of a macrostate and Ω(ν) is the number of microstates which correspond to the macrostate ν (41). The relevant part of a protein’s energy in a given macrostate, E(ν), is mainly determined by the set of H-bonds present in the structure. The number of microstates, Ω(ν), is proportional to the number of all possible atomic configurations that the protein can explore at the same constant energy, E(ν), which depends on the details of the topological arrangement of all the chemical bonds that defines a macrostate. To first order, a macrostate conserves the same bonding topology. These bonds are modeled as distance constraints that define a distance constraint network. As H-bonds fluctuate, different constraint topologies will be realized and will lead to different set of rigid substructures. In other words, depending on the topology of chemical bonding (covalent bonding plus salt bridges and H-bonding), the protein will be flexible in different regions, and different types of correlated motions will be accessible.

Proteins respond like typical condensed matter systems. Namely, as E(ν) increases, Ω(ν) rapidly increases, and the Boltzmann factor rapidly decreases. Note that as energy increases, this means H-bonds break, and more DOF appear, resulting in greater conformational entropy. As a result, the probability to find the system with a given energy, Pr(E), is a sharply peaked function. The state of a system is decided by the competition between entropy and energy. At room temperature, the folded state of a protein is favorable. As temperature is elevated, the H-bonds break so both energy and entropy increases. At high enough temperatures, the additional DOF compensate the energy increase, and the protein is found predominantly in an unfolded state. It is therefore necessary to know how many microstates contribute to a given macrostate of a protein.

The macrostate, ν, effectively specifies a conformation. The concept of conformation requires some type of coarse-graining procedure, which can vary based on the model used. In the approach considered here, the macrostate, ν, is well defined by specifying a particular set of constraints in the network. Then the macrostate, ν, consists of all atomic configurations that are consistent with the continuous motions of the mechanical network defined by the set of constraints. As a rough estimate, the degeneracy Ω(ν) scales as Ω(ν ) ~ ω ^{N f} , where ω is a typical phase space volume of a single DOF, and N_f is the number of internal DOF. The conformational entropy for macrostate, ν , is given as: S(ν ) = R ln[Ω(ν)] = RN _f ln(ω). Each DOF participates in the continuous deformation of a network. Formally, these DOF are related to the low frequency normal modes of vibration. We also assume that all atomic configurations associated with the same macrostate have approximately the same energy. Thus, macrostate ν has constant energy, E(ν), and conformational entropy that is proportional to N_f. Better estimates will be made below, because one should question why all DOF should be assigned the same phase space factor. Also, as will be discussed below, there will be a question as to when an interaction should be viewed as a constraint or not.

3.3. Network rigidity hierarchically applied to protein structure

To identify the number of DOF within a protein, the constraint network must first be determined based on the H-bond network. To see how this might be done, it is useful to consider the following potential energy (enthalpy) decomposition into terms corresponding to several kinds of interactions:

$$U_{tot}=U_{CF}+U_{BB}+U_{SB}+U_{HB}+U_{DA}+U_{weak}$$ Eq. (2)

where CF, BB, SB, HB and DA correspond respectively to central force, bond bending, salt bridge, H-bond and dihedral angle forces. The U_CF, U_BB and U_DA terms describe covalent bonding. Note that covalent bonds freeze out many DOF at the temperatures of interest. The first two terms are particularly strong, meaning they are modeled well as distance constraints. The dihedral angle term characterizes torsion forces governing the twist motion through a dihedral angle. Torsion forces are weak in most cases, allowing for peptide chains to be flexible. However, torsion forces can be very strong when associated with the partial double bond character of the peptide bond, and in this case, this type of torsion force is also modeled by a distance constraint. Weak torsion force cases are considered to be DOF. In addition to the covalent bond interaction terms, U_SB is the potential energy corresponding to salt-bridges, and U_HB is the potential energy for H-bonds. Finally, there are many other weak interactions present that are related to nonbonding forces (i.e., van der Waals interactions). These weak forces are not modeled as distance constraints. The terms in Eq. (2) are shown in the order of their decreasing magnitude, left to right. The strongest interactions are the covalent bonds making up the primary structure of the protein. The covalent bond interactions are never broken under physiological conditions. Therefore, the role of covalent bonding is mechanical in nature, and do not contribute to energy fluctuations. In particular, the forming and breaking of salt bridges and H-bonds are among the main processes found in protein folding and unfolding.

In order to map chemical interactions described above to a network of distance constraints, one must decide how strong the bond has to be in order to be modeled by a constraint. Since covalent bonds are never broken, the central-force and bond-bending interactions, in addition to strong (double-bond) dihedral angle interactions, are always modeled in terms of quenched constraints. On the other hand, all rotatable dihedral angles are left as free angles of rotation, and thus are defined as DOF. Interestingly, some H-bonds are very weak, while others are very strong. (Note: salt bridges are considered as special types of H-bonds going forward.) For this reason, a threshold energy used to determine when an H-bond should be modeled by a set of distance constraints appears necessary to define. If the threshold binding energy is too high, there will be few H-bonds represented by a constraint and the protein structure will be very flexible. On the contrary, if the threshold binding energy is too small, too many weak H-bonds will also be represented by constraints and the protein structure will be almost completely rigid.

In the attempt to model H-bonds as distance constraints, based on an energy criteria (26), many conceptual problems were created. Although having a sliding energy cut-off allows one to adjust the number of H-bonds, each constraint is treated as being infinitely strong (a true constraint), whereas not having the H-bond present is equivalent to ignoring it completely. However, constraints are used to model interactions that are not actual constraints in the first place. Therefore, it is better to think about a constraint as having a characteristic strength in terms of the curvature of the bottom of a potential well. The flatter the well is (low curvature), the weaker the constraint. Thus, it is not the value of the energy (depth of the well) that determines how effective the constraint is in maintaining a certain fixed distance between two atoms, rather, it is the amount of phase space (wiggle room) associated with that constraint. The energy criteria works reasonably well, but this is due to the high correlation between bonding potentials that are deep (very low energy) have high curvature. Another problem is why should a H-bond with a binding energy of E_c − ε should not be considered as a constraint, while another H-bond with a binding energy of E_c + ε be considered as an infinitely strong constraint, as ε → 0? It is clear that a proper measure for the amount of phase space (wiggle room) must be assigned to all constraints, associated with some sort of interaction. A weak torsion force now becomes one type of constraint with more phase space associated with it, rather than considered a DOF. With these basic problems in mind, a statistical mechanical treatment involving network rigidity has been developed.

3.4. Integrating rigidity and statistical mechanics

Lord Kelvin wrote: “I never satisfy myself until I can make a mechanical model of a thing. If I can make a mechanical model I can understand it!” The DCM is based on formulating a mechanical model to capture the essential elements that govern the properties of protein thermodynamics. That is, we implement a FED scheme by employing network rigidity as an underlying mechanical interaction, which is determined by the topology of distance constraints (4). We assume there are a finite number of constraint types, t, that can be encountered within the structure. These constraint types will be assigned an energy and entropy that will in general depend on the local geometrical details of the atomic configuration in the vicinity of where the constraint is found in the network. The main elements of the DCM are given below:

• For each constraint type, t, assign a molecular free energy contribution given by: G_t = E_t − TS_t

• E_tot = ∑_t N_t E^t, where the total energy is obtained by summing over the energy contributions over all N_t constraints of each type t.

• S_tot = ∑_t I_t S_t, where the total entropy is obtained by summing only over the I_tindependent constraints of type t, as determined by the network rigidity calculation, thus accounting for entropy nonadditivity.

• G_tot = E_tot − TS_tot , which is the free energy of a specified constraint topology.

As described above, rigidity theory allows us to calculate the total number of independent constraints within a given network. Although this number is unique, the identification of which constraint is independent and which is redundant is not unique. As such, different values I_t will be determined based on the ordering of which constraints are place first in the network during the graph-rigidity algorithm (pebble game). Nevertheless, the above expression for S_tot is very useful because it provides a rigorous upper bound estimate for the total conformational entropy. The reason for the upper bound is because the set of independent constraints are not necessarily orthogonal. Only summing over orthogonal components will lead to additivity in entropy. Because of the lack of orthogonality between the constraints that form a linear vector space, there remains some “double counting” in phase space. Nevertheless, any upper bound is better than a straight additivity model (i.e., using N_t instead of I_t). So, simply placing constraints down at random, and using the pebble game algorithm, one can be assured to obtain a better estimate for conformational entropy, albeit this is only an upper bound estimate. The calculated S_tot is dependent on the ordering of constraint placement in the network, because ordering effects how the set of I_t is identified. The best we can do then, is to find the lowest possible upper bound. A greedy algorithm achieves this. Namely, recursively place the constraints in the network in order from those having the lowest entropy parameters, {S_t}, to the highest. Then, by implementing an initial sorting procedure, a rigorous lowest upper bound is obtained with virtually no additional computational cost in the calculations. This procedure is called preferentially placing constraint types with the lowest S_t values first.

Building the free energy function in this way effectively accounts for the nonadditivity of entropy through the mechanical interaction. Because in practice the pebble game performs linearly in the number of atoms, in a tiny fraction of a second for a moderately large protein, the free energy for a fixed constraint topology can be readily calculated. This calculation must be repeated again and again for a large ensemble of diverse constraint topologies (folded to unfolded) to construct the complete thermodynamic response of the protein. In a protein, the free energy, G(F), energy, E(F), and entropy, S(F), of a mechanical framework F (i.e. a constraint network) provide a thermodynamic description of a macrostate of conformations sharing the same free energy. With these definitions, we can formally proceed to construct a full partition function of the protein. We define a dimensionless entropy, γ_t = S_t/R, whose labels are in order from smallest to largest, such that γ₁ < γ₂ < γ₃ < …; note that the ordering of energies is irrelevant. Then,

$$\begin{array}{c}\hfill E=N_1{ϵ}_1+N_2{ϵ}_2+N_3{ϵ}_3+\dots \hfill \\ \hfill S=R\tau \text{where}\tau =I_1{\gamma }_1+I_2{\gamma }_2+I_3{\gamma }_3+\dots \hfill \end{array}$$ Eq. (3)

The full partition function of the protein is then written as: $Q={\sum }_F\text{exp}\left[\tau \left(F\right)\right]\text{exp}[-E\left(F\right)∕RT]$ and the summation is evaluated over all possible topologies, F. The term E(F) gives the total energy at fixed constraint topology, whereas τ(F) is a total pure entropy. Note that exp[τ(F)] is the conformational degeneracy associated with all conformations with a fixed constraint topology.

Once constraints are assigned entropy values that reflect their strength, there is a gray scale --- no longer is there a binary split between infinitely strong or nothing. The entropy can be assigned because we are dealing with a coarse-grained model. This scale allows us to provide a measure for the conformational entropy in a molecular network. In particular, it is important to note that very weak interactions, having potential energy functions with characteristically shallow curvature, are counted as constraints, albeit very feeble. The set of constraint types used to model interactions in the protein need to be complete, such that after all constraints are placed in the network, it is completely rigid. The concept of rigidity used in this context is with respect to the number of independent constraints that will always equal 3N − 6, with precisely no DOF remaining in the network. Paradoxically, once we assign entropy values to constraints, what can be said about the difference between a constraint or a DOF?

The paradox is resolved by noting that flexibility is defined in terms of the set of constraints having very large values of entropy associated with them. Below, we will introduce the notion of native and disordered torsion constraints. A native torsion constraint confines the structure to be near that of the template structure. A disordered torsion means that the entropy value is very high, reflecting a relatively much larger degree of flexibility that allows the structure to deviate far from the template structure. Despite a large entropic contribution, a disordered torsion is regarded as a constraint to adhere to the formulation used to estimate conformational entropy. Concurrently, disordered torsion interactions are interpreted as effectively defining internal DOF when they are independent. This is possible because they facilitate large conformational variations within the coarse-grained description that maintains a constant constraint topology. In other words, DOF have finite measure of entropy, and so do constraints. A native torsion constraint has much lower entropy than a disordered constraint. Thus, the gray scale of characterizing entropy contributions creates this interesting lack of distinction, but well-defined quantification of entropy.

The advantage of employing network rigidity within a DCM is that a good estimate for the conformational entropy can be obtained without moving any atoms. In contrast, most of the computational expense in standard methods is used to simulate motions of protein atoms in order to geometrically sample configurational space. In the DCM, for each particular constraint topology, F, the protein will remain at approximately constant energy, while it wiggles geometrically to different degrees depending on constraint topology. Thus, the DCM shifts the focus from considering all possible geometries that a protein (or macromolecule) can explore to all possible constraint topologies. Since the constraint topologies are generated in terms of graphs, computational times are better than 10¹⁰ times faster than methods that rely on simulation. The constraint types can be of diverse variety, and as a result it is almost trivial to include the effects of hydration, so as to accurately describe cold denaturation [28]. Cold denaturation falls out of the calculation as the most probable constraint topology changes, as the temperature changes.

3.5. Mean-field theory and calculating the free energy landscape

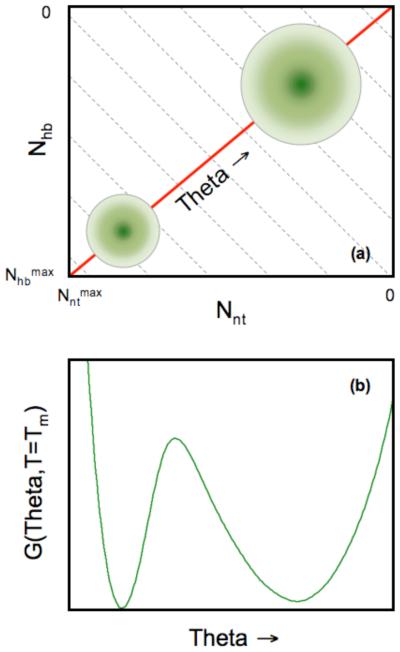
Of course, nothing in life is really for free. In order to evaluate the free energy for a given thermodynamic condition, the sum over an astronomical number of constraint topologies is required. Rather than doing this, we collect all possible microstates corresponding to different constraint topologies into well-defined macrostates. Each macrostate consist of an ensemble of all possible conformations that are consistent with the same number of H-bonds, N_hb, and same number of native torsion constraints, N_nt. Then the partition function can be calculated by performing a double summation over N_hb and N_nt in the two dimensional constraint space shown in Fig. 3a. A grid of nodes is formed within this defined constraint space, where each node specifies a macrostate given by (N_hb, N_nt). We then apply a mean field approximation by assuming the probability for each H-bond and each native torsion constraint is independently distributed. These probabilities are thought of as occupation probabilities, where the constraint is present or not. The occupation probabilities are worked out analytically. In the case of native torsion constraints, a simple probability is assigned to all native torsions, given by Pr(nt) = N_nt/N_max, where N_max is the maximum number of native torsions possible within the protein. All torsion interactions are treated the same, with the probability of being in a native or disordered state is independent, because the mean-field approximation is employed. In reality, we know the probabilities should depend on residue type and its local environment. This drastic approximation is possible because we will introduce effective parameters that are not transferable. Without difficulty, this extreme approximation can be lifted, and furthermore, the DCM is amendable to many generalizations, with only minimal additional cost in computations.

FIGURE 3.

(a) Cartoon of the free energy landscape using the number of hydrogen bonds and native torsions as order parameters. Each point grid defines a macrostate, (N_nt,N_hb), where the free energy, G(N_nt,N_hb), is calculated. The circles identify the native (lower-right) and unfolded (upper-left) basins. (Notice that the axes are decreasing from bottom to top and left to right.) At times it is convenient to express the free energy as a function of a single global flexibility order parameter, θ(N_nt,N_hb). Grey dashed lines represent (approximate) fronts of constant global flexibility due to tradeoff between two constraints types. The red line denotes the shortest path crossing a single saddle from the unfolded to folded basins, which explains why θ is a useful order parameter to consider. (b) An example one dimensional free energy landscape highlights the straddling barrier that must be crossed as the protein transitions between folded and unfolded. This figure is reproduced from Livesay et al., 2008, Chem. Central J. 2:17.

In what we refer to as the minimal DCM (mDCM) (6, 7), torsion interactions are treated the same throughout the protein. However, we do treat H-bonds with more care, where local environmental differences are considered. In other words, the H-bond occupation probabilities will depend on local geometry, which determines the energy of the H-bond. We want to do this in the context of mean field theory to make the problem tractable. Consideration of local variance in a system creates a problem for normal mean field theories because they were developed for homogenous systems. Even a system with disorder that breaks the homogeneity assumption is transformed into an effective medium that represents the average effect of the disorder. However, in the protein, it is not homogeneous. We focus on the H-bond pattern because it is well known that H-bonds govern specificity in the system, and are critical to protein stability and function.

To proceed, we have developed a heterogeneous mean field theory. Since the H-bond occupation probability depends on local environment, we use a Fermi-Dirac distribution function that models a two level system (H- bond present or not) consistent with a global constraint, which is satisfied through a Lagrange multiplier, which is essentially the same thing as a chemical potential. That is, the Lagrange multiplier is adjusted to put precisely N_hb into the network, and thus satisfies the desired global constraint. At this point, we have used mean field theory to efficiently define all occupation probabilities of the constraints while controlling the macroscopic global properties of the protein (system). The ensemble of constraint topologies will depend on the set of these occupation probabilities. Because we require the pebble game algorithm to calculate the long-range interactions that couple entropic contributions of the constraints, we use the a priori known probabilities determined from the heterogeneous mean field theory to generate typical constraint topologies associated with a specified macrostate.

From the precalculated occupation probabilities, we sample over an ensemble of microstates consistent with the specified macrostate. Each macrostate corresponds to a node within a grid that is introduced to define a free energy landscape (in constraint space). Within each node, an astronomical number of distinct constraint topologies remain. To get an estimate of the free energy of a particular node within this grid, we use Monte Carlo sampling to find an average energy and entropy, consistent with the global constraints as dictated by the node. This Monte Carlo sampling is not a simulation; rather, it is a means to estimate averages, given the a priori known probability distribution functions. This hybrid approach is much more efficient than what a normal Monte Carlo simulation would entail, including bias sampling techniques. It turns out that because network rigidity is a long-range interaction, only a small number of Monte Carlo samples are necessary to find reasonably accurate ensemble averages due to self-averaging. We find that one can average over N samples. If N = 200, one obtains averages that are about the same as for N = 10,000. It is quite amazing that a sample of only 200 networks provides good estimates for astronomically large number of constraint topologies, which reveals that the total number of constraints in the network is the most important aspect, rather than the details of what type of constraints there are.

The atomic coordinates for a protein and experimental data for heat capacity, C_p, serve as an input to the mDCM. Three parameters are optimized in order to fit the predicted C_p curves to the experimental data. Two of the parameters, v_nat and δ_nat, respectively correspond to the energy and entropy associated with a native constraint. Note that the energy and entropy values for a disordered constraint are treated as transferable parameters. The energy of a H-bond is calculated using an empirical potential (42), which is linearly related to the H-bond entropy. The third fitting parameter, u_sol, describes the energy of forming a H-bond to solvent when intramolecular H-bonds break. Once these three parameters have been determined, one can easily produce a free energy landscape in the constraint space for a given temperature. For proteins that exhibit two-state thermodynamic behavior, two basins will form corresponding to folded and unfolded states (cf. Fig 3a).

Being that the total number of constraints appear to be of essential importance, rather than the specific types of constraints, it is of interest, therefore, to map the two dimensional constraint space into a one dimensional graph showing the free energy as a function of a single global order parameter. The global flexibility, θ, is defined as the average number of independent DOF per residue. Fig. 3b provides an example of the one dimensional free energy landscape for T = T_m, where the unfolded and folding basin are equally probable. The deepest minimum corresponds to the native state basin characterized by a small value of the global flexibility at T < T_m, whereas the unfolded basin is more stable at T > T_m. Many of the details of the calculations and simulation are found in references (6, 9).

4. DCM Descriptions of Allostery

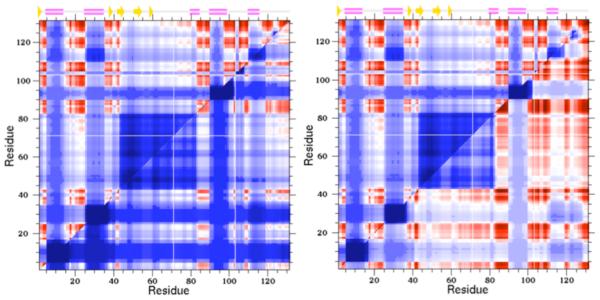
As discussed above, the DCM provides a computationally tractable approach to quantify the give-and-take between thermodynamic and mechanical response. As a consequence, quantified stability/flexibility relationships (QSFR) can be predicted (8-11), which provides a high dimensional characterization of protein stability, flexibility and their interrelationships. Each QSFR metric integrates mechanical and thermodynamic descriptions of structure. For example, the concept of QSFR is best exemplified by the one dimensional free energy landscapes in Fig. 3b that directly relate mechanical and thermodynamic quantities. Other useful QSFR metrics include local descriptions of flexibility, which are based on a thermodynamic average across the ensemble. As such, these flexibility descriptions appropriately adjust with temperature --- a protein is more rigid at low T and more flexible at high T. Two common descriptions of local flexibility are the probability to rotate and the flexibility index, each describing the flexibility within rotatable backbone (PHI and PSI) torsions. The probability to rotate is simply the probability for a given torsion to be disordered (vs. native), whereas the flexibility index quantifies how far from isostatic (marginally rigid) a given torsion is. While providing some orthogonal information, the metrics are highly correlated. Of particular interest here, cooperativity correlation (CC) plots identify mechanical couplings within protein structure, again thermodynamically averaged across the ensemble. That is, CC identifies all pairwise residue-to-residue mechanical couplings within the structure (cf. Fig 4). Therein, blue regions identify residue pairs that are likely to be included within the same rigid cluster, whereas red regions identify residue pairs that are likely to be included within the same correlated motions. White regions identify residue pairs that have no mechanical couplings (e.g. if each residue were within a separate rigid cluster).

FIGURE 4.

Cooperativity correlation plots identify all pairwise residue-to-residue mechanical couplings within a given protein structure as a specified thermodynamic condition. Blue indicates residue pairs likely to be within the same rigid cluster (as averaged across the thermodynamic ensemble), whereas red indicates residue pairs likely to be within the same correlated motion. White indicates that there is no mechanical coupling between the pair. In each example, the upper triangle corresponds to the wild-type human c-type lysozyme, whereas the lower triangles correspond to two different mutants. In the V100A mutant (left), the structure is rigidified with respect to the wild-type, whereas in the Y45F mutant (right) results in increased flexibility.

Our previous work has used the described QSFR metrics to compare stability and flexibility mechanisms across evolutionarily related proteins, and to assess the consequences of ligand-binding. For example, our results (8) on a mesophilic/thermophilic RNase H pair reproduce experimental conclusion (43) that a balance between stability and flexibility is required for function. Moreover, our collective results over several different protein families demonstrate that backbone flexibility is mostly conserved across families, which is not surprising due to fold conservation. Nevertheless, despite qualitative agreement, many quantitative differences in flexibility are observed. Conversely, protein families show surprising diversity and richness. Specifically, our results identify drastic CC differences across datasets of the RNase H pair (8), four bacterial periplasmic binding proteins (10) and nine oxidized thioredoxin mutants (11). In addition, even greater CC changes are observed across pairs of holo/apo binding proteins (10) and oxidized/reduced thioredoxins (11). Taken together, these results highlight the sensitivity within the set of pairwise allosteric couplings present in protein structures.

Ongoing work is attempting to quantify the extent and frequency of changes in QSFR upon minimal perturbation. That is, we are considering a dataset of 13 human c-type lysozyme point mutants, which is the same dataset considered in REF (44). QSFR characterizations of each mutant are compared to the wild-type structure. Across this dataset, our results further underscore the highly sensitive nature of QSFR. For example, while small in scale compared to the changes in CC, changes in backbone flexibility are frequent and occur over long ranges, highlighting the frequency of multiple allosteric pathways within protein structure (45). In addition, increases in flexibility are mostly balanced by increases in rigidity across the dataset. Similar results are observed when considering CC. Because CC plots can be thought of as a snapshot of all pairwise allosteric couplings present in structure, changes in CC upon mutation identify how the set of allosteric mechanisms change. As a typical example, Fig. 4 compares the wild-type (upper triangles) lysozyme CC to two mutants (lower triangles). Myriad changes occur, many at structural locations distal to the mutation site. Interestingly, the V100A mutant tends to rigidify the structure, whereas the Y45F mutant tends to increase its flexibility.

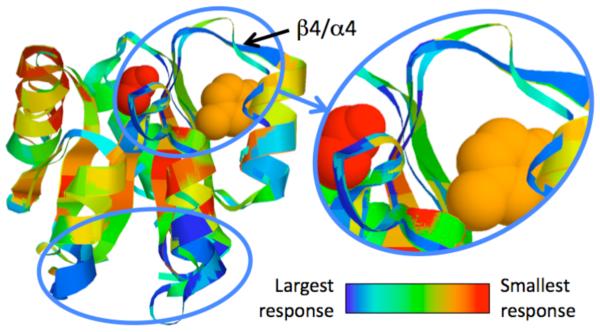
With these results in mind, we have recently developed a mechanical perturbation method (MCM) to identify putative allosteric sites using the mDCM (12). Therein, we introduce a small number of quenched native torsion constraints to mimic the locally rigidifying effect of ligand-binding, and then recalculate all QSFR properties. Thereafter, large changes in the calculated QSFR properties identify sites likely to initiate allostery. While any QSFR metric can be considered, our work thus far has focused on changes to δG_fold, flexibility index and CC (cf. Fig 5). Across three CheY orthologs, our results demonstrate an intriguing mix of conservation and variability. For example, the β4/α4 loop, which has been demonstrated experimentally for relaying the required allosteric signal upon phosphorylation of Asp57 (46, 47), is the only allosteric site conserved in all three orthologs. As expected, similarity within the allosteric responses strongly parallels evolutionary relationships; however, more than 50% of the best scoring putative sites are only identified in a single ortholog. These results suggest that detailed descriptions of intra-protein communication are substantially more variable than structure and function, yet do maintain some evolutionary relationships.

FIGURE 5.

Structure superimposition of 3 CheY orthologs color-coded by changes in cooperativity correlation. Tyr106 (orange) undergoes an allosteric conformational change upon phosphorylation of Asp57 (red) that allows for FliM to bind to CheY, thus relaying the chemotaxis signal. Identified allosteric hotspots are circled, including the β4/α4 loop that is critical to the activation mechanism. Changes in flexibility index are similar, whereas changes in δG_fold identify a mostly orthogonal set of allosteric residues.

5. Conclusions

The motivation behind the DCM is based on the need for computational methods to quickly and accurately characterize protein stability and flexibility, which is a complex problem due to many-body effects where interactions compete with one another simultaneously. As a result, both theoretical and computational methods must balance inclusion of all relevant interactions with computational feasibility. Our ability to maintain this balance has been demonstrated in our early works. Moreover, the DCM is ideally suited to characterize allostery because it robustly characterizes how mechanical and thermodynamic quantities change upon perturbation. Across the various examples presented herein, our collective results advocate that allosteric response is highly sensitive to differences in structure. Finally, it is worth nothing that, while not discussed here, there is also strong experimental evidence for sensitivity within allosteric mechanisms across protein families (the interested reader is referred to the Livesay et al. chapter on correlated mutation algorithms, which is also included in this book).