Principal Component Analysis: A Method for Determining the Essential Dynamics of Proteins

Abstract

It has become commonplace to employ principal component analysis to reveal the most important motions in proteins. This method is more commonly known by its acronym, PCA. While most popular molecular dynamics packages inevitably provide PCA tools to analyze protein trajectories, researchers often make inferences of their results without having insight into how to make interpretations, and they are often unaware of limitations and generalizations of such analysis. Here we review best practices for applying standard PCA, describe useful variants, discuss why one may wish to make comparison studies, and describe a set of metrics that make comparisons possible. In practice, one will be forced to make inferences about the essential dynamics of a protein without having the desired amount of samples. Therefore, considerable time is spent on describing how to judge the significance of results, highlighting pitfalls. The topic of PCA is reviewed from the perspective of many practical considerations, and useful recipes are provided.

1 Introduction

Protein dynamics is manifested as a change in molecular structure, or conformation as a function of time. To describe accessible motions over a broad range of time scales and spatial scales, protein conformations are best represented by a vector space that spans a large number of dimensions equal to the number of degrees of freedom (DOF) selected to characterize the motions. Many molecular simulation techniques are available to generate trajectories to sample the accessible conformational ensemble characterized by those DOF. The interpretation of a trajectory can lead to better understanding of how proteins perform biological functions. To this end, the process of extracting information from sampled conformations over a trajectory, and checking whether the sampling is a robust representation of an ensemble of conformations accessible to the protein, are tasks well suited for statistical analysis. In particular, Principal Component Analysis (PCA) is a multivariate statistical technique (see Note 1) applied to systematically reduce the number of dimensions needed to describe protein dynamics through a decomposition process that filters observed motions from the largest to smallest spatial scales [1–5]. PCA is a linear transform that extracts the most important elements in the data using a covariance matrix or a correlation matrix (normalized PCA) constructed from atomic coordinates that describe the accessible DOF of the protein, such as the Cartesian coordinates that define atomic displacements in each conformation comprising a trajectory [6]. When all of the atomic displacements have similar standard deviations, a covariance matrix is typically used; otherwise it is prudent to employ the correlation matrix, which normalizes the variables to prevent rare but large atomic displacements from skewing the results. In constructing the covariance matrix or correlation matrix (henceforth C-matrix will be generically used for either matrix type), it is often assumed that the amount of sampling is sufficient, but this always requires many more observations than the number of DOF (variables) used in the matrix. An eigenvalue decomposition (EVD) of the C-matrix leads to a complete set of orthogonal collective modes (eigenvectors), each with a corresponding eigenvalue (variance) that characterizes a portion of the motion, where larger eigenvalues describe motions on larger spatial scales (see Note 2). When the original (centered) data is projected onto an eigenvector, the result is called a principal component (PC).

While PCA can be performed on any high dimensional dataset, for the analysis of a protein trajectory, a C-matrix associated with a selected set of atomic positions must be constructed. Often, a coarse grained description of the protein motion is made at the residue level by using the alpha carbon atom as a representative point for the position of a residue. In this case, the C-matrix will be a 3m × 3m real, symmetric matrix, where m is the number of residues. Performing an EVD results in 3m eigenvectors (modes) and 3m − 6 non-zero corresponding eigenvalues, provided that at least 3m observations are used. When the eigenvalues are plotted against mode index that are presorted from highest to lowest variance, a “scree plot” typically appears as a function of mode index. When such a scree plot forms, a large portion of the protein motions can be captured with a remarkably small number of modes that define a low dimensional subspace. The top set of modes typically has a higher degree of collectivity [7], meaning the PCA modes have many appreciable components distributed quite uniformly. Conversely, a low degree of collectivity indicates there are a small number of appreciable components, although they are not necessarily tied to a localized region of space. When analyzing proteins, 20 modes are usually more than enough (even for large proteins) to define an “essential space” that captures the motions governing biological function, thus achieving a tremendous reduction of dimension.

The process of applying PCA to a protein trajectory is called Essential Dynamics (ED) since the “essential” motions are extracted from the set of sampled conformations [8–10]. Of course, a linear combination of the 3m orthogonal PCA modes can be used to describe exact protein motions (at the selected coarse grained level). In practice, the presence of large-scale motions makes it difficult or impossible to resolve small-scale motions because the former has much greater relative amplitude in atomic displacements. Indeed, it is for this reason that the large-scale motions are often the most biologically relevant. Therefore, only a small number of PCA modes having the greatest variances are used to characterize large-scale protein motions. When small-scale motions are of interest, the method of PCA can still be used successfully by applying it to sub-regions of a protein as a way to increase the resolution for describing the dynamics within those sub-regions.

An alternative method to quantify large-scale motions of proteins is to use a Normal Mode Analysis (NMA) [11, 12] derived from an Elastic Network Model (ENM) [13–15]. In the ENM, one typically considers nearby alpha carbon atoms to interact harmonically, where the connectivity is determined from a single structure to extract an elastic network. Typically, the large-scale motions quantified by a small set of lowest frequency modes of vibration are in good agreement with the same corresponding number of PCA modes when direct comparisons of subspaces are made [16–18]. One advantage of performing PCA to obtain the ED of a protein is that information from any selected set of atoms can be used to obtain the PCA modes associated with that subspace. While it is true that ED is often applied to the analysis of alpha carbons, this is not required. The spatial resolution of PCA analysis can be coarser than the resolution of the structures that comprise the trajectory, which, for example, may come from an all-atom based simulation. Another advantage of ED is that statistics from many trajectories may be pooled allowing a great deal of flexibility in the way data from different simulations can be combined. The overall large-scale motions and any number of selected small-scale motions can be determined in a post-simulation phase of research as the nature of the protein motions is being interrogated.

Perhaps the most important difference between NMA and PCA is in the assumption of harmonicity. The premise of NMA requires the molecular motion is confined near the local minimum in the free energy landscape where residues in close proximity (i.e., atomic packing) respond as harmonic pairwise interactions (i.e., springs). Since proteins display a significant amount of anharmonicity in their behavior [19, 20], this assumption is not always suitable [21–23]. PCA makes no assumption of harmonicity, and thus is not limited to harmonic motions. Indeed, because PCA is independent of the model invoked during the simulation to generate the trajectory, the resulting conformational changes that can be explored can deviate far from the harmonic assumption. On the other hand, the limitations of PCA stem from using a linear transform that is based on second moments (covariance), and the fact that subsequent factorization yields eigenvectors that are orthogonal. While a linear transform of the data is always possible, if the variables are not intrinsically linearly related, any nonlinear relationships present will not be properly described. Nonetheless, in practice, standard PCA is similar to the standard ENM approach. In other words, relying on covariance implies higher-order correlated motions related to higher moments are missed.

Nonlinear generalizations of PCA are available such as kernel PCA [24] that can be applied directly, or employed after the most relevant subspace is identified first using standard PCA. A disadvantage of kernel PCA is that the choice of kernel is not obvious because it is problem dependent, although we show below that some common choices work well for protein trajectories. Also problematic is that the reconstruction of data is difficult to interpret because the mapping involves feature space, which is distinctly different than conformational space that has a geometric interpretation despite being of high dimensionality. The reason for employing kernel PCA is to differentiate conformations within an ensemble beyond that possible using standard PCA, which may give insight into structural mechanisms governing protein function. Our work suggests that the simplest PCA, which follows from the C-matrix, offers a validated method to describe the dominate correlations present in atomic motions found in proteins, and it provides an effective dimension reduction scheme that can be used for subsequent analysis to capture nonlinear (or higher order correlations) effects when they are of interest. Nevertheless, in practice it is always important to ensure and test the robustness of the PCA modes.

Keep in mind that individual PCA mode directions are subject to errors related to finite sampling of conformations to construct the empirical C-matrix. The empirical C-matrix should be a good estimate for the actual population C-matrix (infinite samples). In practice, PCA can be strongly influenced by the presence of outliers in a dataset. The main concern is that the outliers may skew the first few mode directions. While there are robust algorithms that are useful in stabilizing PCA in the presence of outliers [25–32], it is often effective to remove identifiable outliers or simply consider a sufficiently long trajectory for which the results are significant. Generating a large number of conformational samples and removal of outliers before the C-matrix is calculated mitigates concerns about robustness of the results. Moreover, this type of intrinsic error does not pose much of a problem as long as biologically relevant motions are described using a superposition of a small set of dominant modes (instead of focusing on one mode). As the mode number increases the core part of this subspace becomes stable against sampling noise. However, only the top several modes tend to be useful.

The choice of which modes to include is often made by examining the scree plot for a visible “kink” (the Cattell criterion) [33, 34], such that all modes up to the kink are important (see Note 3). Although a kink does not have to exist, it typically does in the study of protein dynamics. In fact, a kink will generally appear for any high dimensional dataset. Hence the name scree (geological debris at the bottom of a cliff) plot has been tied to PCA. Other criteria are commonly used for the choice of essential modes. For example, the top set of modes associated with greatest variances when added should reach some fraction (say 80 %) of the total variance possible given by the trace of the C-matrix. The problem with this method is that some a priori set fraction is arbitrary, and for fractions greater than 50 % one tends to end up with many more modes than are truly relevant to the problem. The scree plot provides an objective criterion. Figure 1a shows the scree plots for PCA of two protein simulations and a random process created from independent and identically distributed variables. Notice there is a rapid decrease in the eigenvalues for the proteins that is not present in the random process.

Fig. 1.

(a) Eigenvalue Scree plot for first 100 modes of two example protein simulations (primary y-axis) and a random process (secondary y-axis), each having 225 dimensions. The units are angstrom squared (positional variance). (b) Average RMSIP scores for a random process in different vector space dimensions as a function of subspace dimension. Error bars show plus and minus one standard deviation

When PCA is applied to Cartesian coordinates that describe the positions of atoms, an alignment step is necessary prior to the process of constructing the C-matrix because the intent is to capture the internal motions of a protein. The structural alignment step requires the center of masses to coincide as well as a global rotation to optimally align the structures. The authors implemented a quaternion rotation method to obtain optimal alignment defined by the minimum least-squares error for the displacements between corresponding atoms [35]. PCA is not limited to the analysis of a Cartesian coordinate-based C-matrix. Any set of dynamic variables that describe the protein motion can be used. For example, one may choose to use internal dihedral-angle coordinates such as the (Φ, Ψ) angles or interatomic distances, which eliminates the need to optimally align conformations. However, in the former case, it has been realized there is an intrinsic nonlinear effect that is not well described using standard PCA, suggesting kernel PCA should be employed or an alternative internal coordinate system that is naturally linear should be chosen. In the latter case, internal atomic distances offer the possibility of an all-to-all distance C-matrix for the alpha carbons, which has a row dimension equal to the number of structures in the trajectory and a column dimension equal to m(m − 1)/2, where m is the number of residues considered. A distance based C-matrix can be created, which is a square matrix with dimension m(m − 1)/2, and therefore requires much more sampling. In this case, the PCA modes reveal the coordinated changes in distances between all residue pairs. Despite the advantage of working directly with internal coordinates, performing all-to-all distance PCA quickly becomes computationally prohibitive due to the need to diagonalize very large non-sparse matrices. More importantly, the interpretation of the eigenvectors becomes difficult when the number of residues is greater than ten. Nevertheless, this approach has proven useful when studying a small subset of atoms where the interpretation is clear [36, 37].

The task of applying PCA to a conformational ensemble (CE) requires that a CE be generated. There are multiple ways to create a CE including molecular dynamics (MD) and geometrical simulations such as FIRST/FRODA [38–40]. A CE may be generated by experimental methods such as using protein structures from X-ray crystallography or nuclear magnetic resonance (NMR) techniques. For certain applications it is prudent to combine multiple CEs together that define a single dataset. One reason for combining different CEs is to boost statistics, where each CE has the same characteristics. This is convenient, as the simplest way to apply parallel computing occurs when multiple simulations are run simultaneously and independently. However, the CEs that are combined could represent different conditions, such as different temperatures in MD simulation, fixing a different set of distance constraints in geometric simulation or contrasting mutant structures. Clustering different CEs in the subspace defined by the most relevant PCA modes provides insight into the effect of varying conditions. In some cases, a protein may undergo large-scale (anharmonic) conformational changes that bridge two distinct basins of low free energy. The combined CEs will allow these basins to be clearly identified, as well as the paths connecting them. Similarly, different CEs that represent a set of mutant structures, or apo and holo forms of a protein, possibly with different ligands bound, allow one to differentiate the conformations easily by clustering in a small dimensional subspace.

The most appealing and intuitive way to investigate the nature of protein motions is to project the displacement vectors (DV) defined in the original high dimensional space that characterize different conformations onto a pair of PCA modes. It is even possible to project onto higher dimensions as one visualizes multiple PCA modes simultaneously using specialized software such as R or XL-STAT^™, which is a plug-in for Microsoft Excel developed by Addinsoft^™. Such plots are indispensible for assessing how well certain parts of the subspace are sampled, especially in comparative studies where differentiation in dynamics can have functional consequences. The results of such an analysis show how each state occupies a region of the conformational space defined by the first two PCA modes.

Given that the ED of a protein is characterized using a small vector space defined by PCA modes that reflect different CEs and a combined CE, it becomes necessary to benchmark how similar these subspaces are to one another. When subspaces are sufficiently similar, this implies that the different ensembles capture the same type of protein dynamics. Conversely, when subspaces are dissimilar, different types of motions are being captured, which may have biological consequences tied to the different conditions analyzed. As such, it is necessary to define a measure to quantify the overlap of vector subspaces, as a natural generalization to the concept of a projection (dot product) of one vector onto another. That said, note that a set of n PCA modes forms an orthogonal n dimensional subspace (SS) within the full vector space (VS) defined by the size of the C-matrix (see Note 4). Common metrics that quantify SS similarity include cumulative overlap (CO), root mean square inner product (RMSIP), and principal angles (PA) [12, 41–45]. The CO metric quantifies how well one SS is able to capture the PCA modes of the other SS. The RMSIP metric is a single number that quantifies the SS similarity in terms of multiple inner products between the two. The PA method provides a quantification of the optimal alignment between the two SS that is based on the singular value decomposition (SVD) of a matrix of overlaps (inner products) between the two SS. The result is a sorted (monotonically increasing) set of n angles, where n is the dimension of the compared subspaces, that quantify how well the two SS can be aligned.

A final concern with assessing the PCA output is the significance of the results. While PCA is robust when there is sufficient sampling, the questions that remain are: What constitutes sufficient sampling and how trustworthy are the modes? Since PCA relies on the factorization of the C-matrix, the condition number of the C-matrix indicates the numerical accuracy that can be expected within the solution of the associated set of equations. For a given process, more sampling reduces the condition number. Therefore, if the condition number for a C-matrix is high, this could be in indication there is not enough statistics. If possible, the number of independent samples should be at least ten times the number of variables. Two direct measures for sampling significance are known as the Kaiser-Meyer-Olkin (KMO) score given as:

$$\text{KMO}=\left(\sum _j\sum _{k\ne j}{r}_{jk}^2\right)/\left(\sum _j\sum _{k\ne j}{r}_{jk}^2+\sum _j\sum _{k\ne j}{p}_{jk}^2\right)$$ (1)

and the associated measure of sampling adequacy (MSA) given as:

$${\text{MSA}}_j=\left(\sum _{k\ne j}{r}_{jk}^2\right)/\left(\sum _{k\ne j}{r}_{jk}^2+\sum _{k\ne j}{p}_{jk}^2\right)$$ (2)

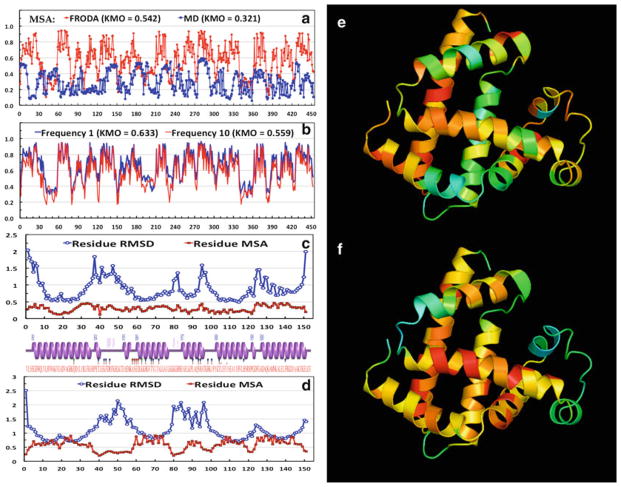
where r is the standard correlation coefficient and p is the standard partial correlation coefficient [46]. These statistics can take values between 0 and 1. If all the partial correlations are zero, then the MSA score is 1. The KMO score indicates the amount of partial correlations between the sampled variables and provides an indicator for when applying PCA is appropriate. The MSA provides a metric for each variable. KMO and MSA should ideally be greater than ½. It is worth noting that the MSA scores for each variable are related in a nontrivial way to the protein environment. Specifically, there tends to be a moderate negative correlation between the MSA scores and the residue RMSD.

When comparing essential subspaces, keep in mind that all of the subspace metrics described above depend on both the dimension of the SS and the dimension of the full VS as shown in Fig. 1b.

One way to assess PCA modes is to compare them to the modes of a random process to obtain a baseline for determining the significance of the subspace comparisons as the dimensions for the SS and full VS change. With these baselines, a Z-score can be calculated to assess the statistical significance of the scores, for example when using RMSIP:

$$Z=\frac{{\text{RMSIP}}_{\text{obs}}-{\text{RMSIP}}_{\text{rand}}}{\text{stdev}({\text{RMSIP}}_{\text{rand}})}$$ (3)

However, the essential SS of a random process has very different characteristics than the essential SS constructed from a protein trajectory as Fig. 1 clearly shows. Randomly shuffling the indices for the components of modes produces a new set of modes that have essentially the same character as the modes determined by PCA on a purely random process. Consequently, any two same-sized proteins share much more in common than would be expected by a random process, making large Z-scores not very useful in practice. This is due to the fact that compared to a completely random process all proteins share much more common dynamics because they share common structural features such as a covalent backbone even if their fold topology is very different. What this means in practice is that any of the metrics described above for any two proteins will show much more overlap compared to a random process. In fact, using two different trajectories under the same conditions, we found that the scores for overlap between two identical proteins can be lower than the overlap between two different proteins when the number of residues is small (<100). This result escalates when using a coarse-grained approach that prunes many discriminating features (to reduce DOF). To obtain a more stringent criterion for Z-score determination, the data presented strongly suggests that a comparison to other proteins, possessing the same number of DOF, that define a decoy set should be used to define the random baseline in (1), rather than a generalized random process. However, to the best of our knowledge, baselines from decoys have not been done.

Figure 2 shows the risks of comparisons made for small proteins using a coarse-grained model. For this analysis, four proteins having distinctly different folds were simulated under the same conditions using geometrical simulation and then subjected to PCA as a combined set, where only the first 75 residues were included in the covariance matrix starting from the N-terminus and always remaining within the N-terminal domain. Figure 2b shows the Z-scores for the comparisons in Fig. 2a. Here it is critical to note the similarity between the random process and the decoy comparisons. When 1WIT is compared to itself (using different simulation conditions), RMSIP saturation suggests that the proper essential subspace dimension is nine modes. However, the random process and the decoy comparisons do not reach a saturation point within the first 30 modes. When working with larger proteins, such comparisons are much safer, as shown in Fig. 2c, d with myosin V (MV). The moral here is that extra care must be taken to claim significance of PCA results on small proteins when coarse-graining is used.

Fig. 2.

(a) RMSIP scores for inter-comparisons between three proteins each having 75 residues and a random process with 225 DOF. Only the true self-comparison yields a curve that saturates rapidly within a small essential space defined by the first nine modes. The decoy plots have much more in common with the protein dynamics of interest compared to the random process up to the first 30 modes. (b) The Z-scores for the RMSIP scores shown in panel a. (c) Comparison of two myosin V (795 residues) CEs run under different simulation conditions and a random process with 2,385 DOF. Again, note the rapid saturation of the RMSIP scores in an essential subspace defined by the first ten modes. (d) The Z-scores for the RMSIP scores in Panel c

Another way to assess how stable the PCA results are can be made by looking for cosine content within the top few PCs. It has been noted that when MD trajectories insufficiently sample conformational space the top few PCs resemble cosine functions with periods equal to half the mode number, which is what occurs for a random diffusion process [47]. The resemblance is determined by finding the correlation between the set of T values of the ith PC and cos(2πt/bT) where 0 < tT <, b = i/2. We note that CEs derived from geometrical simulation do not produce PCs that resemble cosines due to the restriction of conformational space imposed by locking in the distance constraints at the beginning of the simulation. However, when it occurs in MD simulations, this indicates sampling is limited.

Lastly, we note that the contributions of variables to a PC can be assessed to determine if any variables are strongly influencing a particular PC. Additionally, when interpreting the component loadings (eigenvector components multiplied by the square root of the associated eigenvalue), the squared cosine between the variables and a PC can be used to determine if real correlations exist, or if there is only an apparent relation due to the projection onto a low dimensional subspace. To infer a correlation, there should be a clustering on a two-dimensional loading plot, and the squared cosine should be greater than one half. As in all statistical interpretations, the best practice is to examine multiple sources of information. For the case of a single CE analysis, these sources include the KMO scores and the MSA for each variable and/or the condition number of the C-matrix, the scree plot, the collectivity of the PCs, the correlations between the variables and the PCs, RMSD mode plots, two-dimensional scatter plots of observations projected on the PCs, the cosine content of the top few modes, and the squared-cosines for variables. When analyzing multiple CEs, additional sources of information include the PA spectra, the RMSIP scores, and CO scores. Comparisons can be made between each individual CE and a reference CE, constructed by combining all of the CEs together, as well as with an appropriate random process. Each CE may also be directly compared to each other.

2 Methods

2.1 Preliminaries

A dynamic trajectory provides snapshots depicting the protein in multiple configurations called frames (see Note 5). Denote the trajectory as the set A_Raw = {X(t)} where t is a discrete variable referring to a particular frame. The vector X may be composed of a subset of atoms within the protein. Here, we consider the set of alpha carbons. If the protein consists of m residues, then X will be a column vector of dimension 3m. If Acontains n observations, then set A is a matrix of dimension 3m × n, since each alpha carbon has (x, y, z) coordinates in Cartesian space. To study internal motions of the protein, it is essential to set the center of mass of each frame at the origin, and to rotate each frame to its optimally aligned orientation relative to a selected reference structure, defined by X_ref, which also has its center of mass at the origin. Since this translation and rotation process changes the coordinates of each frame, the transformed A matrix is denoted as A_Aligned, which is denoted as A_Aligned = {X_Aligned(t)} (see Note 6). The choice of the reference structure X_ref is not critical, and although it is common to use the initial input structure to the simulation, any frame is as good as any other. It is also possible to use an average structure, but the method of averaging needs to be done with care in an iterative fashion [48]. The data in matrix A_Aligned is then mean centered (here, this means row centering) and we denote this as A′. The covariance matrix Q associated with the 3m variables is then defined as Q = A′A′^T, which is always real and symmetric, and has dimension 3m × 3m. If n ≥ 3m, then the EVD of Q will result in 3m − 6 non-zero eigenvalues, where the six zero eigenvalues correspond to the modes of the trivial degrees of freedom, 3 for translation and 3 for rotation. The same is true for the correlation matrix R, which only differs from Q in that the values of the variances are divided by the associated standard deviations, yielding the value of 1 for each diagonal element. It is prudent to use the correlation matrix when the standard deviations of the variables are strongly skewed. Conversely, correlation based PCA employs normalized variables and this standardization tends to inflate the contribution of variables whose variance is small, and reduce the influence of variables whose dimensions are large. It is therefore not a priori possible to know which approach will provide more insight for any given problem. Both methods should probably be explored (see Note 7).

In order to construct a C-matrix based on the internal coordinates defined by interatomic distances, it is first necessary to construct the all-to-all distance matrix D for the residues of interest. This is a matrix of dimension m(m − 1)/2 × n, where m is the number of residues considered and n is the number of observations (each residue is represented solely by its alpha carbon). Here, the data must be centered so that deviations in all lengths will average out to zero. Therefore, D′ is constructed in which each row is centered. The covariance matrix associated with the m(m − 1)/2 variables is then defined as Q_D = D′D′^T . The correlation matrix R_D is Q_D normalized by the variable standard deviations. This type of PCA, called dPCA is interpretable if one restricts the size of the set of atoms to small numbers. For example, if three residues (alpha carbons) are used, then three modes will result from the EVD of Q_D or R_D and the interpretation of the eigenvectors, which are composed of three components reveals correlations (if any) in the fluctuations in the lengths between the three sets of pairs (see Note 8). This can be useful to interpret fluorescence resonance energy transfer (FRET) experiments [36, 37].

When choosing to work in the sample space, either due to a small number of samples or to implement a non-linear method, one must construct the kernel matrix (K), which is a n × n square symmetric matrix, where n is the number of observations. Each element of K is formed by computing K(i, j), where i and j represent two observations from the centered data set, using the definition for the specific kernel function of interest, k. Essentially, the kernel function maps N dimensional vectors in ℜ^N from the sample space to a new high dimensional (possibly infinite) vector space referred to as feature space. Working in the high dimensional feature space can often detect features that are not apparent in sample space. The “curse of dimensionality” is avoided by constructing the feature space from a collection of inner-products so that the actual mapping function is never calculated. Calculating inner products over the sampled data is not by itself an intensive operation. This method of avoiding the difficulties normally associated with high-dimensional spaces is known as the “kernel trick”. It is worth noting that using this approach, only a subset of feature space is being explored, which is limited by the range of the data of the original sample space.

The kernels that can be employed must yield positive-definite symmetric square matrices [24]. When the kernel is defined simply as the inner product of the input data (linear kernel), then the results of the analysis are identical to the standard PCA. Specifically, one will recover the same set of non-zero eigenvalues as that from the covariance matrix based PCA. In this sense, kernel PCA (kPCA) subsumes standard PCA. Additional features may be detected by using other types of non-linear kernels, such as a Gaussian kernel, a Neural Net kernel (i.e., a tanh function), a kernel that maps the data to a set of degree n polynomials (either homogeneous or inhomogeneous), or a mutual information kernel. There are no rigorous guidelines for which kernel to apply to the data of interest and thus the method of kPCA requires intimate knowledge of one’s data (or based on trial an error) as well as how a particular kernel might or might not affect the resolution of multiple states. Furthermore, most kernel functions have adjustable parameters that need to be set to obtain the best resolving power within feature space. Unfortunately, there is no a priori formula for parameter optimization because this process is highly dependent on the data used. Lastly, unlike standard PCA where the PCs are generated by taking the dot product of the DVs and the appropriate eigenvector, the process for kPCA is more involved. First, the eigenvectors must be normalized in the sample space to reflect the fact that their magnitude in the feature space is unity, and then the PCs (for the training set) are calculated by determining the sum of the inner products of the normalized eigenvectors with the kernel columns. Having used both standard PCA and kPCA, we note that when the parameters are suitably tuned, the ability of kPCA to discriminate multiple states from a trajectory is impressive.

If kPCA is to be used, we note that an ideal approach for computationally intensive kernels is to first use PCA to reduce the dimension of the data and then apply the kernel methods to the top set of PCs. In this approach, we have found that as few as five PCs may be used as input to kPCA with no substantial loss in numerical accuracy. This filtering process greatly reduces the computational intensiveness of the kPCA (see Note 9), although it does not reduce the size of the kernel matrix. Many more properties of kPCA can be found in [24].

For completeness, we briefly consider the method of Independent Component Analysis (ICA) [49]. ICA is a method for performing blind source separation, as when one wishes to decompose a mixed signal into two signals or a signal plus noise. The underpinning mathematics of the method is to detect non-Gaussian processes by looking at higher order correlations than second degree. To achieve this, ICA is typically implemented using either kurtosis or an information theoretic quantity like mutual information (FastICA) as a contrast function [50]. To apply ICA, one must first center the data and then whiten it. Whitening is the process of transforming an observed data vector linearly so that one obtains a new vector, which is white, i.e., its components are uncorrelated and their variances equal unity. In other words, the covariance matrix of a whitened data vector equals the identity matrix. One method for whitening data involves an EVD of the covariance matrix and is given by x̃ = ED^−1/2E^Tx where x is the centered data, E is the matrix of eigenvectors from the EVD of the covariance matrix, with E^T its transpose, and D is the diagonal matrix of eigenvalues from the EVD of the covariance matrix. Once the data has been centered and whitened, the ICA algorithm essentially computes the optimal rotation of the data using higher order statistics (e.g., fourth moments), thereby determining the independent components (ICs). We note that the algorithm can be computationally expensive for high dimensional data when a large number of ICs are to be extracted.

In order to make ICA amenable to large, high-dimensional datasets like protein CEs, PCA is first applied to perform a dimensionality reduction and whitening preprocessing step. Similar results to ICA may be obtained from kPCA by choosing to work with a kernel that maps the data to inner products of degree two polynomials. Such kernels have the property of detecting fourth moments, i.e., kurtosis. Alternatively, we note that one may perform post hoc analyses of the PCs derived from either standard PCA or kPCA to determine which ones have the highest amount of kurtosis. Choosing to examine such PCs will allow the investigator to see if non-Gaussianity, as measured by kurtosis, leads to the detection of a biological signal. The real criterion for assessing the usefulness of ICA is determining if the assumptions of the model are met. We find that for investigating native state dynamics, where proteins are described by a large set of DOF and are not undergoing large conformational shifts, ICA does not provide greater insight than what PCA (or kPCA) provides because most of the variables in the CEs are Gaussian.

PCA is a multivariate statistical approach, and there is almost no limit to the variants available to an investigator. For example, one may perform sparse PCA (SPCA) in which one attempts to form linear combinations that are sparse, meaning that they are combinations of less than all the variables. This is done in an attempt to make the interpretation of the PCA more manageable as is the case of standard PCA the linear combinations include all the variables and in high dimensional data, rendering an interpretation as nontrivial at best. Typically this is done by using a thresh-holding method such as any component less than c is mapped to zero, where c is an ad hoc chosen number between 0 and 1 or by solving an optimization criterion as in the case of SPCA [51]. The effect of such a sparsification is the reduction of complexity in interpretation of correlated motions and often better cluster separation. The problem with the approach is that there is no guarantee that the sparse variables are the important ones. Another approach combines PCA and ICA methodologies in a process called Independent Principal Component Analysis (IPCA) [52], based on the assumption that biologically meaningful components can be obtained if most noise has been removed from the associated loading vectors. In IPCA, PCA is used as a preprocessing step to reduce the dimension of the data and to generate the loading vectors. The FastICA algorithm is then applied to the previously obtained PCA loading vectors to generate the Independent Principal Components (IPCs). In this method, the kurtosis measure of the loading vectors is used to order the IPCs. There is also a sparse variant with a built-in variable selection procedure implemented by applying soft-thresholding on the independent loading vectors (sIPCA). Because of the breath of the topic and the system dependent details that depend on the data itself, it is beyond the scope of this article to provide recipes for ICA, SPCA, IPCA, or sIPCA. The interested reader should refer to the references given for more details on the theory and application of those approaches. One distinct advantage of standard PCA is that recipes can be provided to define protocols and best practices that are largely independent of the specific nature of the data.

Before proceeding to describe the recipes for PCA and kPCA, we note that there are numerical considerations that must be addressed to suit the investigation at hand. Full eigenvector decompositions of large non-sparse matrices scale as (O³) and are thus memory intensive. When the DOF in the covariance matrix are less than 10,000 it is reasonable to perform a full decomposition on a standard computer, however, for larger matrices, one may need to consider numerical approaches such as factoring the C-matrix or kernel matrix or computing only a small number of greatest eigenvalues and corresponding eigenvectors. Additional concerns include the condition number of the C-matrix as this is strongly influenced by the number of observations and is related to the KMO statistic. Typically, the condition number improves as the number of samples increases. If a C-matrix is constructed from a set of observations that is smaller than the number of DOF represented by the matrix, it will almost always be ill-conditioned. Furthermore, in this case, the C-matrix in not invertible and contains many zero eigenvalues. In general, it is good practice to have at least ten times more samples than variables to ensure a reasonable KMO score and that most of the variables will have a MSA score of 0.5 or greater. Another option is to switch the analysis from sample space to feature space by implementing kPCA with an appropriate kernel function.

2.2 Recipe I: Essential Dynamics Using Cartesian Coordinate Based PCA

1. Obtain trajectories (one or more) from dynamic simulation. For illustrative examples, one MD and three geometrical simulation (FRODA) trajectories for myoglobin (PDB ID 1a6n) are considered to explain aspects of PCA. For this purpose, details about the setup of the various simulations are ignored, except when it pertains to methodology. Additional details can be found in [16]. The MD trajectory consists of 2,000 frames after equilibration. One FRODA trajectory has 2,000 frames (100,000 explored conformations), and the other two FRODA trajectories have 10,000 frames. The sampling rate of FRODA is normally set at 1 out of 50 conformations generated. Here, one long trajectory is obtained from sampling every conformation (10,000 explored conformations), meaning it is 10 % as long as the 2,000 frame FRODA trajectory in terms of MC-steps, while the other is obtained from sampling every tenth conformation (100,000 explored conformations), is of equal length.

2. Remove overall translations and rotations by aligning each frame to a reference structure.

   • We use the starting (crystal) structure as our reference, and our quaternion alignment program to optimally align each structure to the reference structure. Only the alpha carbon atoms were included in the alignment process.

3. Choose the set of atoms for the analysis: This forms the data matrix A_Aligned.

   • Protein conformations (observations or frames) define columns, and rows describe the (x, y, z) coordinates of the alpha carbon atoms. In this example, all 151 of the alpha carbons are used, giving 453 total DOF (variables).

4. Examine the descriptive statistics for the variables.

   • Table 1 shows some statistics for three selected coordinates (variables) to highlight the nonuniformity of the standard deviations.

5. Examine the KMO for each CE and MSA scores for each coordinate. The MD and FRODA trajectories each with 2,000 samples are compared in Fig. 3. Most coordinates from (MD, FRODA) simulation (do not, do) meet the recommended KMO cutoff criterion of 0.50. We assess how the KMO statistic changes when the number of FRODA samples is increased from 2,000 to 10,000, and investigate how the sampling frequency affects the sampling adequacy in Fig. 3b. The overall KMO statistic remains about the same, and the individual coordinates that had a low KMO statistic did not improve by increasing the number of samples. Even more surprising, the sample rate of 1 leads to a slight improvement of the KMO. Thus, there exists a trade-off between the amount of conformational space that a simulation explores and the statistical sampling adequacy of those states (see Note 10).

6. Center the variables of A_Aligned (row centering): This forms the centered data matrix A′.

7. Construct the covariance matrix of the {x, y, z} positions for the atoms using A′: Q = A′A′^T

   • For comparisons, construct the correlation matrix R.

8. Diagonalize Q or R using an EVD.

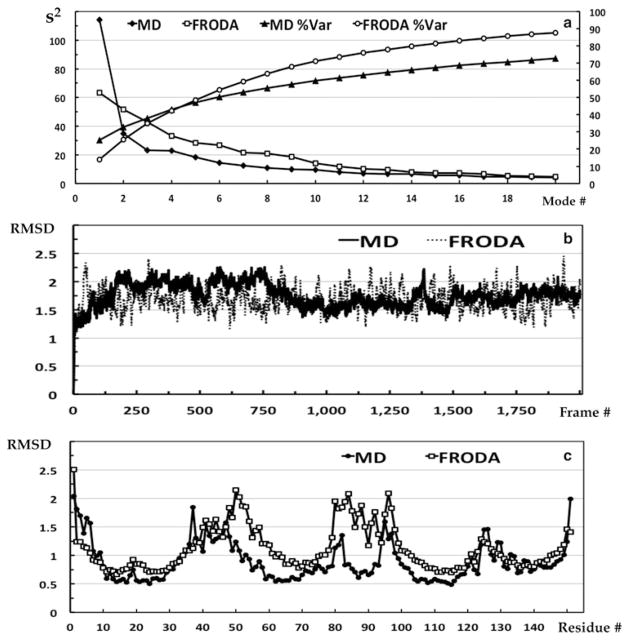
9. Examine the eigenvalue scree plot to determine the number of eigenvectors to include in the reduced vector space that describes the most relevant features. Figure 4 shows these plots in Panel a along with the conformational and residue RMSDs in Panels b and c.

   • It is not advisable to include all modes up to a preset percent of variance cutoff ³. Note that the characteristics of the scree plot depend heavily on whether one is analyzing fluctuations within a single native basin or is analyzing combined trajectories of multiple states. For a single native basin of random motions, many modes will be required to achieve 50 % of the variance. For multiple states/configurations, the first two modes may subsume more than 50 % of the variance. Our example MD plot shows that most of the variance is captured by one mode, because its CE clusters into two conformational states. In contrast, the FRODA plot does not have a dominant mode, but rather shows a monotonically decreasing trend indicative of random fluctuations about the native state of the protein (the input structure).

10. Select the top set of eigenvectors for forming the PCs (Usually 2–20). In our MD example, the top two modes reveal how two distinct states of the protein were sampled. However, at least ten modes are required to define the essential subspaces for a comparison between MD and FRODA CEs (See the RMSIP plots below).

11. Examine the component loadings, which are the product of the square root of the eigenvalue with the eigenvector. When the correlation matrix is used, they are also the correlation coefficients (cosines) between the variables and factors (PCs). Analogous to Pearson’s r, the squared component loading (squared cosine) is the percent of variance in that variable explained by the PC. In Table 2, PC1 is clearly capturing the behavior of the first three variables.

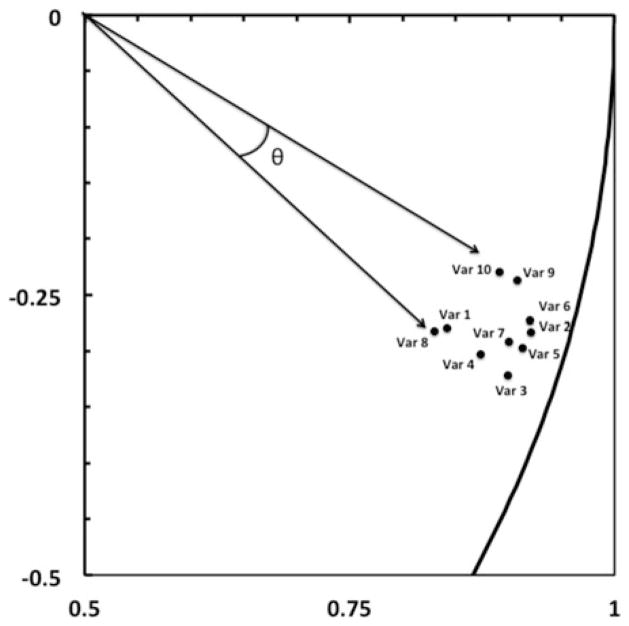
    • Scatterplots of the component loadings for the top two factors should be examined. In Fig. 5 the first ten variables (Var 1 to Var 10) are seen to cluster. The angle between the variables on this scatterplot indicates the level of correlation, with (0, 90, 180) degrees indicating a correlation of (1, 0, −1).

12. Examine the squared cosines of the variables. These values indicate whether a correlation is worthy of interpretation or likely an artifact of projection into a low dimensional subspace. Only the first three are shown in Table 3, and they strongly support the correlations shown in Fig. 5.

13. Examine the contribution of the variables. Here we show only the first three in Table 4, but even from this truncated list, it is clear that the N-terminus residues have a large contribution to the first mode.

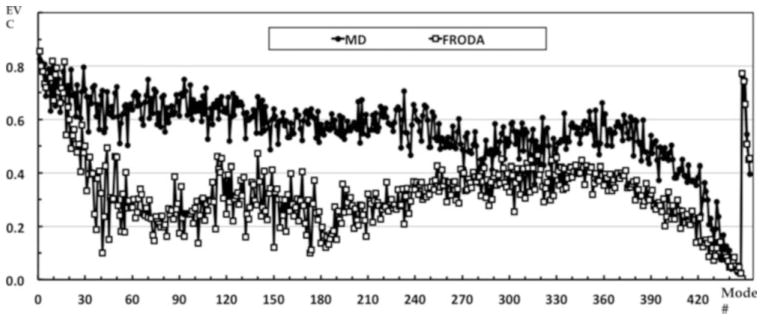
14. Examine the eigenvector collectivity (see Fig. 6). The top modes tend to be more collective than lower modes indicating that many residues are participating in collective motions. For our example, the FRODA eigenvector collectivity drops off rather steeply suggesting that the top 40 or so modes capture most of the collective motions occurring in the native state. This trend of having a set of highly collective modes highlights the fact that real protein motions tend to be captured by a superposition of PC modes, not a single mode. In contrast, the MD collectivity does not drop off rapidly indicating many more modes are required to capture the dynamics that the MD simulation produced. These results also clearly demonstrate that while PCA modes in totality always form a complete basis set, they are derived from statistics, and will be dependent on the sampling. The top PCA modes reflect biasing in the sampling, which may not necessarily be of biological importance. It is therefore important to carefully choose what and how to sample so that biological interpretations can be made.

15. Construct the weighted RMSD modes: Here we map the 3m components of the eigenvectors to m new variables that capture the squared displacements of each residue to visualize which residues contribute most to the fluctuations of each PCA mode. For each eigenvector i, the new mode N_i has m components, with each component defined by the square root of the sum of the squares of the three variables that contribute to the associated residue, scaled by the square root of the corresponding eigenvalue (see Note 11). These results are shown in Fig. 7. The mapping equation is given by:

    $$N_i=\sqrt{{\lambda }_i\left(\begin{array}{c}{x}_1^2+y_1^2+z_1^2\\ ⋮\\ x_m^2+y_m^2+z_m^2\end{array}\right)}$$ (4)

    • Weighting is done by multiplying by the square root of the eigenvalue for the mode, λ_i. This gives units of angstroms.

    • It is often useful to compare the RMSD modes to the overall residue RMSD plot from the entire trajectory. Also, one may use the un-weighted RMSD modes to see relative displacements that are hard to see in the weighted plots due to the typical rapid decrease in the eigenvalues with mode index.

16. Construct the DVs for the trajectory, given by DV_i = X_i − X_ref and construct the PCs.

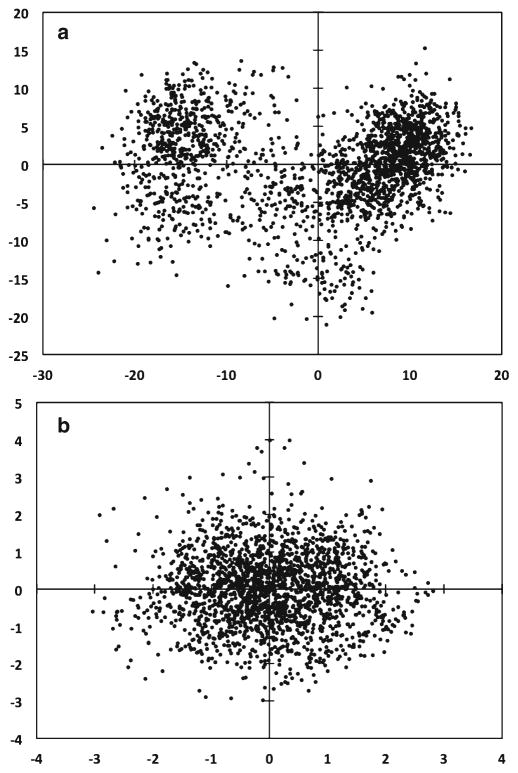
    • PC_i is formed by taking the inner product between eigen-vector i and each DV (Observation) (see Note 12). Projections can be made on singe modes to view as line graphs. Projections on sets of two PCA modes create scatter plots that show how the simulation explored the configuration space defined by the selected set of modes. In Fig. 8, it is evident that the MD trajectory sampled two states of the protein as seen by the two clusters in the scatterplot of PC1 versus PC2. In contrast, the projection of the FRODA trajectory onto the top two modes shows a uniform distribution.

17. Check the contribution of the observations to the PCs to see if there are particular ones that unduly influence the analysis. Here we show only the first three observations in Table 5 and the values are percentages.

18. We also examine the squared cosines of the observations when determining if an observation belongs to a particular cluster or not. In Table 6, we show values for the first three observations. Values in bold are significant at the 0.01 level.

19. Since the sampling in the MD simulation was poor for many variables, we check the cosine content of the top two PCs. Comparing PC1 to a half-period cosine, we find a 0.63 correlation and in comparing PC2 to a full period cosine, we find a 0.16 correlation. The high cosine content in mode one suggests that the MD simulation should be run longer.

20. When examining two or more sets of PCA modes, determination of how similar the trajectories are to each other may be assessed using the CO, RMSIP or PA metrics.

    • In Fig. 9, we compare the vector space of the top modes from the MD trajectory to that of the FRODA trajectory, each with 2,000 frames. Note that the various metrics for SS comparisons depend on the size of the VS and SS (see Note 13). As the SS DIM increases, the ability of that SS to capture a given eigenvector increases. Because all the metrics have dependencies on dimensionality, it is best to have a baseline score for random comparisons as a function of the dim(VS) and dim(SS).

Table 1.

Descriptive statistics for three variables in the MD simulation data

Variable	Minimum	Maximum	Mean	Standard deviation
Var 1	3.456	11.489	7.085	1.610
Var 10	9.568	12.980	11.530	0.707
Var 20	8.390	10.467	9.423	0.301

Fig. 3.

The Kaiser-Meyer-Olkin MSA for (a) the FRODA and MD CEs each with 2,000 frames, and (b) for the FRODA CEs each with 10,000 frames. The overall KMO score is shown parenthetically in the legend. (c) Relationship between residue RMSD and MSA for MD. (d) Relationship between residue RMSD and MSA for FRODA. (e) Ribbon diagram colored by the MSA scores for MD. (f) Ribbon diagram colored by the MSA scores for FRODA

Fig. 4.

(a) Eigenvalue scree plots for the FRODA and MD CEs showing both the correlation explained in each mode and the cumulative correlations (Since the PCA was based on the correlation matrix). (b) The conformation RMSD of the MD and FRODA trajectories. Each value is with respect to the starting structure (crystal structure). (c) The residue RMSD for the MD and FRODA trajectories

Table 2.

Component Loadings for the first three variables in the MD trajectory

Variable	PC1	PC2	PC3
Var 1	0.807	−0.218	−0.056
Var 2	0.890	−0.223	−0.095
Var 3	0.867	−0.254	−0.111

Fig. 5.

The correlations between the first ten variables and the top two PCs. Notice how these variables form a tight cluster with small angles between each, indicating that they are correlated on these PCs. The boundary line on right is an arc of the unit circle to indicate how close the values are to 1

Table 3.

Squared cosines of the variables

Variable	PC1	PC2	PC3
Var 1	0.651	0.048	0.003
Var 2	0.791	0.050	0.009
Var 3	0.752	0.065	0.012

Table 4.

Contribution of the variables to the PCs as percent

Variable	PC1	PC2	PC3
Var 1	0.570	0.137	0.014
Var 2	0.693	0.143	0.039
Var 3	0.659	0.186	0.053

Fig. 6.

The eigenvector collectivity (EVC) for the entire set of eigenvectors from both the MD and FRODA PCA. Note that the mode index is plotted with decreasing size of the eigenvalue, so mode index 1 is the top mode. This plot indicates that the collectivity measure should not be of primary concern

Fig. 7.

The RMSD and the top three RMSD modes are compared from (a) MD and (b) FRODA PCA

Fig. 8.

(a) MD and (b) FRODA displacement vectors are projected onto their respective top two PCs as a scatter plot

Table 5.

Contribution of the observations to the PCs as percent

Observation	PC1	PC2	PC2
Obs 1	0.015	0.529	0.147
Obs 2	0.002	0.329	0.121
Obs 3	0.003	0.485	0.033

Table 6.

Squared cosines of the observations

Observation	PC1	PC2	PC3
Obs 1	0.026	0.285	0.052
Obs 2	0.005	0.222	0.054
Obs 3	0.007	0.351	0.016

Fig. 9.

(a) The cumulative overlap (CO) of each MD eigenvector with the entire set of FRODA eigenvectors defining the subspace of indicated size. We do not show the reverse metric, which is not symmetric, but yields similar values. (b) The RMSIP scores for the comparisons of random processes with 453 DOF, two FRODA simulations using the same conditions, and the MD and FRODA simulations. Error bars on the random process scores indicate plus and minus one standard deviation for 50 iterations. (c) The Z-scores for the RMSIP scores. (d) The PA spectra for the comparisons of the MD and FRODA simulations using the indicated SS DIM

2.3 Recipe II: Essential Dynamics Using Internal Distance Coordinate Based PCA

1. Obtain trajectories (one or more) from dynamic simulation.

2. No need to remove overall translations and rotations as internal coordinates are being used.

3. Choose the set of atoms.

   • For a set of N atoms, there will be N (N − 1)/2 modes. It is recommended that less than ten atoms be selected, because otherwise the interpretation of the resulting modes becomes increasingly difficult.

4. Construct an all-to-all distance matrix D for the residue set chosen for each trajectory.

5. Construct the centered data matrix D′ by centering the variables (row center).

6. Construct the covariance (or correlation) matrix, Q_D (or R_D), from D′.

7. Diagonalize Q_D (or R_D) using an EVD.

   • It is best to implement both methods.

8. Examine the eigenvalue scree plot.

9. Select the top set of modes, typically, this is one or two.

   • Each component of the distance PCA modes indicates how the relative distance between a pair of atoms change. There is no way to map the mode components to individual residues.

10. Construct the weighted distance modes (see Note 14).

    • Weighting is done by multiplying by the square root of the eigenvalue for the mode, λ_i.

11. Construct the DVs for the trajectory, given by DV_i = X_i − X_ref , and construct the PCs.

    • Although there is a physical difference between using internal and Cartesian coordinates, mathematically the same procedures described above in terms of taking inner products and forming projections are identical.

12. When examining two or more sets of PCA modes, determination of how similar the trajectories are to each other may be assessed using the CO, RMSIP or PA metrics.

2.4 Recipe III: Essential Dynamics Using Cartesian Coordinate Based Kernel PCA

1. Obtain trajectories (one or more) from dynamic simulation.

2. Remove overall translations and rotations by aligning each frame to a reference structure.

3. Select the set of atoms for the analysis to define the data matrix, A.

4. Center the variables of A (row center) to define the data matrix A′.

5. Construct the kernel matrix, K, of {x, y, z} positions for the atoms using A′.

   • The matrix K has dim (n × n) where n is the number of observations.

   • Each element (i, j) in the kernel is determined using a chosen kernel function, which has the general form as K_i,j = K(k(x_i, x_j ))_i,j . A linear kernel is given as K(x, y) = (x · y), and a homogeneous polynomial is given by K(x, y) = (x · y)^d = (C_d(x), C_d(y)) where C_D maps x to the vector C_D(x) with entries that are all possible nth degree ordered products of the entries of x. Another kernal type uses a Gaussian weighting function given by $K(x,y)=exp\left(-\frac{{\Vert x-y\Vert }^2}{2{\sigma }^2}\right)$ where the standard deviation, σ, is an adjustable parameter. A neural net kernel is given as K(x, y) = tanh(m(x · y) + b), and a mutual information kernel is given as K(x, y) = MI(x, y) where $\text{MI}(X,\mathit{\Upsilon })={\displaystyle \sum _{y\in \mathit{\Upsilon }}}{\displaystyle \sum _{x\in X}}p(x,y)log\left(\frac{p(x,y)}{p(x)p(y)}\right)$. These are commonly employed kernels in many fields, and are not necessarily particularly useful for protein dynamics. Nevertheless, because higher order correlations in large datasets can be filtered with these kernels, and as such, we have explored all of them.

6. Diagonalize K using an EVD, and ignore the zero eigenvalues.

7. Examine the scree plot, and from where the kink is, select the top modes.

   • The characteristics of this plot depend heavily on whether one is analyzing fluctuations within a single native basin or is analyzing combined trajectories of multiple states. In kPCA, typically that first few eigenvalues are much larger than the remainder.

8. Determine the eigenvector collectivity. When using kPCA with properly tuned parameters, the top eigenvector often has a collectivity of 0.5 or higher.

9. Select the top set of eigenvectors for forming the kernel principal components (kPCs) (Usually 2–5).

10. Scale the top eigenvectors using the condition 1 = λ_n(α_n · α_n) where α_n is the nth eigenvector (a column vector) of K and λ_n is the corresponding nth eigenvalue of K.

    • The eigenvectors are derived from the feature space and usually do not have a meaningful interpretation in the sample space.

11. Construct the DVs for the trajectory given by DV_i = X_i − X_ref, and then construct the kPCs.

    • Calculate kPC_n using ${(\text{kPC})}_n(x)={\displaystyle \sum _{i=1}^M}{\alpha }_i^{n}k(x_i,x)$. Note that x is a test vector, and not a training vector (a vector are used to create the kernel). If only the original centered data is to be used, i.e., the data used to construct K, then all the elements of K are already determined. Projections can be made on singe modes to view as line graphs or on two PCA modes create scatter plots that show how the simulation explored the configuration space defined by the selected set of modes.

    • We applied PCA and kPCA to the set of four 75 residue proteins to assess the ability of the methods to achieve cluster separation. The results are shown in Fig. 10.

12. When examining two or more sets of kPCA modes, determination of how similar the trajectories are to each other may be assessed using the following metrics. We note that the essential subspaces in kPCA are quite small, comprised of usually five or so modes. This is especially true when standard PCA was used as a preprocessing dimensional reduction step. Additionally, subspace comparisons require that the parent vector spaces have the same dimensionality. Therefore, it is possible to compare the essential subspaces derived from different kernels only when the same number of samples is used.

    • In Fig. 10f, we show that the subspaces for the top modes generated from the different kPCA approaches are quite similar using the RMSIP scores and the first PA. The most dissimilar was the SS derived from the MI kernel.

Fig. 10.

Cluster separation for the dynamics of four different proteins using different kernels, but all using the same CE containing trajectories involving 2,000 FRODA frames for each of the four proteins. (a) Linear kernel equivalent to standard PCA. (b) Homogeneous polynomial kernel of degree two, which is sensitive to fourth order statistics. (c) Gaussian kernel with standard deviation set to 50. (d) Neural net kernel with no offset and a slope parameter set to 10⁻⁴. (e) Mutual Information kernel. (f) Subspace comparisons of the four kernels in b–d using the linear kernel essential space as the reference. The SS DIM in all cases was five. The primary y-axis shows RMSIP scores while the secondary y-axis shows the principal angle value in degrees