Requiem for the max rule?

Abstract

In tasks such as visual search and change detection, a key question is how observers integrate noisy measurements from multiple locations to make a decision. Decision rules proposed to model this process haven fallen into two categories: Bayes-optimal (ideal observer) rules and ad-hoc rules. Among the latter, the maximum-of-outputs (max) rule has been most prominent. Reviewing recent work and performing new model comparisons across a range of paradigms, we find that in all cases except for one, the optimal rule describes human data as well as or better than every max rule either previously proposed or newly introduced here. This casts doubt on the utility of the max rule for understanding perceptual decision-making.

INTRODUCTION

Since the dawn of psychophysics, its ambition has been to reveal the workings of the brain’s information-processing machinery by only measuring input-output characteristics. This ambition is normally pursued by conceptualizing the transformation from input to output as a concatenation of an encoding stage, in which the sensory input is internally represented in a noisy fashion, and a decision stage, in which this internal representation is mapped to task-relevant output. In the simplest of models of the simplest of tasks, the internal representation is modeled as a scalar measurement and the decision stage as the application of a criterion to this measurement. Unfortunately, this most basic form of signal detection theory has limited mileage when it comes to bridging the gap between laboratory and real-world tasks. One reason for this is that real-world decisions often involve integrating information from multiple locations – looking for a person in a crowd, detecting an anomaly in an image, or judging a traffic scene. In the laboratory, the essence of such tasks can be mimicked by presenting multiple stimuli and asking for a “global” judgment, i.e. one which requires the observer to take all stimuli into consideration. In such tasks, even if the internal representation of an individual stimulus is modeled as a scalar measurement, the internal representation of the entire stimulus array is a vector, and the decision stage consists of mapping this vector to task-relevant output.

At least for the past sixty years, in multiple-item tasks requiring a global judgment, psychophysicists have been searching for mappings of this kind that are both mathematically cogent and adequately describe human behavior. Rules that have been proposed have mostly come in two types: optimal rules, and simple ad-hoc rules. According to optimal (or Bayes-optimal, or ideal-observer, or likelihood ratio) rules (Green & Swets, 1966; Peterson, Birdsall, & Fox, 1954), observers maximize a utility function by using knowledge of the statistical process that generated the internal representations. When the utility function is overall accuracy, as it often is assumed to be, optimal decision-making reduces to choosing the option that has the highest posterior probability given the current sensory observations (MAP estimation). The notion of an optimal decision rule is general: such a rule can be derived for any task, without having to make task-specific assumptions beyond the formalization of the experimental design.

There are, however, reasons to consider alternatives to optimal decision rules. First, these rules often take a complicated form, meaning that evaluating response probabilities under the optimal model was cumbersome for the digital computers available in the 1960s (Nolte & Jaarsma, 1967); this is much less of a consideration nowadays. Second, observers might not have knowledge of all the task statistics that are needed to compute the optimal rule, or neural implementation of that rule might be infeasible; these are still valid motivations for considering alternative decision rules.

Of all alternatives to optimal decision rules in multiple-item global judgment tasks, the most prominent might be the maximum-of-outputs rule, or max rule. This rule dates back to at least the French-American mathematician Bernard Koopman (Koopman, 1956; Morse, 1982), who considered the problem of making N glimpses to determine whether a signal is present, for example during underwater echo ranging. When time (glimpses) is translated to space (locations), this problem is equivalent to detecting whether a signal is either present at all N locations, or absent at all. Koopman assumed that the observer makes a decision on every glimpse, and makes an overall decision using an “or” operation, which means that the observer reports “present” if any of the individual decisions returns “present”. Assuming that every individual “present” decision is made when an underlying continuous decision variable exceeds one specific criterion, Koopman’s decision model is equivalent to one in which the observer decides that the signal is present if the largest of those decision variables among all locations exceeds that criterion – hence the terminology “max rule”. Since Koopman, the max rule has been considered by many greats of signal detection theory (Graham, Kramer, & Yager, 1987; Green & Swets, 1966; Nolte & Jaarsma, 1967; Palmer, Verghese, & Pavel, 2000; Pelli, 1985; Shaw, 1980; Swensson & Judy, 1981), although predominantly in a different context, namely the problem of detecting one signal among N locations.

When the observer knows the statistics of the sensory observations used to make the decision, the max rule is not the best strategy either in the N-of-N problem Koopman considered or in his successors’ one-of-N problem. Moreover, the max model will need to be modified in ad-hoc ways whenever the task is changes (we will encounter examples of this). Of course, in spite of this suboptimality and lack of generalizability, the max model might be a better description of human behavior than the optimal model in these or other tasks. In this paper, we will argue that this does not seem the case, and that the optimal rule provides an equally good or better account of the data than every max rule in almost every experiment examined.

A note on nomenclature might be helpful. In the classification scheme of (Ma, 2012), we distinguished the notions of Bayesian, optimal, and probabilistic decision rules in perception. Bayesian rules are based on posterior distributions, a rule that is optimal (in a “relative” sense) maximizes performance given sensory noise, and probabilistic rules take into account the quality of sensory evidence on a trial-to-trial basis. An observer can be Bayesian but not optimal, for example when they use previously learned priors rather than the ones appropriate for the experiment. According to this classification, the optimal rules we will consider are both Bayesian and probabilistic, whereas the max rules are suboptimal, non-Bayesian, and in some cases also non-probabilistic.

Scope

In this paper, we consider visual decision-making tasks that meet the following criteria.

1. The observer briefly views either an array of N stimuli, or two arrays of N stimuli separated in space and/or time.

2. The observer makes a single categorical judgment about these stimuli.

3. The categories are defined in terms of a small number of easily parametrizable features.

4. All stimuli are relevant to the category decision.

5. Trials are independent.

We will call these tasks “feature-based global categorization tasks”, although (5) is not captured by that term. This category encompasses many common paradigms, such as

• Visual search: One or more targets are drawn from a target distribution, and the remaining items are drawn from a distractor distribution. Common subparadigms include:

  • ◦
    Detecting the presence of one or more targets among distractors (Palmer, et al., 2000).

    • ▪
      Perhaps the most studied task of this type involves a single target that takes on one fixed value, and distractors that are independently drawn from a distractor distribution.
    • ▪
      Oddity detection: there is a single target whose value varies from trial to trial, and the distractors are identical to each other (homogeneous distractors) but their common value is also variable.
    • ▪
      Sameness judgment: on a target-present trial, all items are targets, and the targets are identical to each other; on a target-absent trial, the distractors are not identical to each other.
  • ◦
    Localizing one or more targets that are present among distractors
  • ◦
    2AFC on which of two arrays contained the target (e.g. (Palmer, Ames, & Lindsey, 1993))
  • ◦
    Categorizing one or more targets that are present among distractors

    • ▪
      Example 1: was the tilted bar among the vertical bars tilted left or right?
    • ▪
      Example 2: all items are targets, the target orientations are drawn independently from the same Gaussian distribution, and the observer reports whether the mean of this distribution was tilted left or right.
• Change detection

  • ◦
    Detecting the occurrence of one or more changes (Eng, Chen, & Jiang, 2005; Pashler, 1988; Phillips, 1974)
  • ◦
    Localizing one or more changes
  • ◦
    Categorizing one or more changes

In this paper, we will not discuss experiments using natural scenes or real-world objects, ones in which only one stimulus is relevant for the decision (such as discrimination at a cued location), ones in which the stimuli are displayed until the subject makes a decision, ones involving crowding, and spatial integration tasks such as judging whether two orientations belong to the same contour (since those rely on categories that are defined not only in terms of the features of the stimuli, but also their spatial locations). We do not imply that the models considered here cannot be generalized to those tasks.

General assumptions and model structure

Human behavior in feature-based global categorization tasks is typically modeled as consisting of two stages: an encoding stage and a decision stage. In the encoding stage, stimuli with task-relevant features s=(s₁,…,s_N) (from here on simply referred to as stimuli) are generated from the category, T. The category would be “target present” or “target absent” in a detection task, a location in a localization task, and a category label in a categorization task. The experimenter controls the joint distribution of stimuli and category, p(T,s). We assume throughout the paper that each stimulus is internally represented as a noisy measurement, giving rise to a measurement vector x=(x₁,…,x_N). We further assume that the noise corrupting the measurements is independent between locations:

$$p(\mathbf{x}|\mathbf{s})=\prod _{i=1}^{N}p(x_i|s_i).$$ (1)

We will sometimes make specific choices for p(x_i|s_i): when s_i is a real-valued variable, that p(x_i|s_i) is Gaussian with mean s_i and variance ${\sigma }_i^2$, and when s_i is a circular variable (such as orientation), that p(x_i|s_i) is Von Mises with circular mean s_i and concentration parameter κ_i. Together, p(T,s) and p(x|s) define the encoding model, also called generative model.

In the decision stage, the observer maps the measurements x to a categorical decision, T̂. This mapping is called a decision rule. The decision rule that is optimal in the sense of maximizing proportion correct is the maximum-a-posteriori decision rule (Green & Swets, 1966). This rule can be considered a “default” decision rule, because it is completely determined by the encoding model; no additional assumptions are needed.

DETECTION OF A SINGLE TARGET

We first discuss a poster child of visual search research, namely the detection of a single target among N stimuli (Peterson, et al., 1954). We denote target presence by T=1 and target absence by T=0. We assume that on every trial, the target is present with probability p₁; thus, p(T=1)=p₁ and p(T=1)=1−p₁. For some function d : x ↦ ℝ, a decision rule (optimal or otherwise) is a rule that states that the observer’s report of T, denoted by T̂, is 1 when d>0 and 0 when d<0. Formulating the decision rule in terms of a single inequality is possible only when T is a binary variable.

Optimal decision rule

The optimal observer has complete knowledge of the statistical structure of the task and reports that the target is present when the probability that T=1 given x exceeds 0.5. This condition is equivalent to d>0, where d is the log posterior ratio of target presence:

$$d=\text{log}\frac{p(T=1|\mathbf{x})}{p(T=0|\mathbf{x})}=\text{log}\frac{p(T=1)p(\mathbf{x}|T=1)}{p(T=0)p(\mathbf{x}|T=0)}=\text{log}\frac{p_1}{1-p_1}+\text{log}\frac{p(\mathbf{x}|T=1)}{p(\mathbf{x}|T=0)}.$$

The two probabilities p(x|T) for T=1 and T=0 are called the likelihoods of the hypotheses T=1 and T=0, respectively. These likelihoods can be evaluated using

$$p(\mathbf{x}|T)=\int p(\mathbf{x}|\mathbf{s})p(\mathbf{s}|T)d\mathbf{s},$$

which holds for both values of T. The N-dimensional integral over the stimulus vector s is an instance of marginalization: the operation of averaging over all unknown variables other than the one of interest (these variables are also called nuisance parameters). The log posterior ratio becomes

$$d=\text{log}\frac{p_1}{1-p_1}+\text{log}\frac{\int p(\mathbf{x}|\mathbf{s})p(\mathbf{s}|T=1)d\mathbf{s}}{\int p(\mathbf{x}|\mathbf{s})p(\mathbf{s}|T=0)d\mathbf{s}}.$$ (2)

All knowledge about the task structure enters the decision variable through the two stimulus distributions p(s|T). Now we can use the knowledge that when the target is present (T=1), it is present in only one location, say the L^th one. If, furthermore, each location has equal probability to contain the target (as we will assume throughout, since the generalization is easy), then Eq. (2) becomes

$$d=\text{log}\frac{p_1}{1-p_1}+\text{log}\frac{\frac{1}{N}\sum _{L=1}^N\int p(\mathbf{x}|\mathbf{s})p(\mathbf{s}|L,T=1)d\mathbf{s}}{\int p(\mathbf{x}|\mathbf{s})p(\mathbf{s}|T=0)d\mathbf{s}}.$$ (3)

The sum over locations is another instance of marginalization, where the summation index L labels the hypothesized target location. Finally, we could substitute Eq. (1) in Eq. (3) to obtain an expression that is valid for all tasks in this section.

Independent distractors

Starting from Eq. (3), we consider the subset of tasks for which the distractors are drawn independently. We introduce the notation T_i to indicate whether the target is present (1) or absent (0) at the i^th location (i=1,…,N). Distractor independence has two aspects, which in most experimental designs are simultaneously realized:

• Target-absent trials: On a target-absent trial, distractor values are independently drawn from distributions p(s_i|T_i=0). In other words,

  $$p(\mathbf{s}|T=0)=\prod _{i=1}^{N}p(s_i|T_i=0).$$ (4)
• Target-present trials: On a target-present trial, the target value is drawn from a distribution p(s_i|T_i=1), and distractor values are again drawn independently from distributions p(s_i|T_i=0). In other words,

  $$p(\mathbf{s}|L,T=1)=p(s_L|T_L=1)\prod _{i\ne L}^{N}p(s_i|T_i=0).$$ (5)

Using Eqs. (4) and (5), and the assumption of independent measurement noise, Eq. (1), the decision variable in Eq. (3) evaluates to

$$d=\text{log}\frac{p_1}{1-p_1}+\text{log}\left(\frac{1}{N}\sum _{i=1}^N{e}^{d_i}\right),$$ (6)

where d_i is the local log likelihood ratio (LLR) of target presence:

$$d_i=\text{log}\frac{p(x_i|T_i=1)}{p(x_i|T_i=0)}=\text{log}\frac{\int p(x_i|s_i)p(s_i|T_i=1)d{s}_i}{\int p(x_i|s_i)p(s_i|T_i=0)d{s}_i}.$$ (7)

To further work out Eq. (7), we will need to make assumptions about p(s_i|T_i=0) and p(s_i|T_i=1).

It is important to keep in mind that expressing the decision variable in terms of local LLRs, Eq. (6), is possible only because of the independence of the distractors. In some single-target detection tasks, distractors are not independent, for instance when they are drawn from a discrete set without replacement, or when they are homogeneous (identical to each other within a display) but variable across trials. We will discuss the latter case later in the paper.

Max decision rule

In this paper, we consider a family of ad-hoc alternatives to the optimal rule, namely maximum-of-output or max rules. Assume that at the i^th location there is a local decision variable d_i, which is a function of the local measurement x_i only. This d_i may or may not be equal to the local log likelihood ratio in Eq. (7). In Koopman’s spirit, a max rule observer can now be defined as one who reports that the target is present if at any of the N locations, d_i exceeds a criterion k. In other words, the max rule observer reports that the target is present only if all d_i are smaller than k:

$$\hat{T}=0\text{ if }{d}_i<k\text{ for all }i\hat{T}=1\text{ otherwise}$$

This is equivalent to reporting that the target is present when

$$\underset{i}{\text{max}}{d}_i>k.$$ (8)

In the max model, the task structure, i.e. the distribution p(s|T), might influence the decision rule through d_i. However, the model does not dictate how d_i depends either on the task structure, if at all, or on the measurements; in these senses, the max model is underdefined.

An important special case of the max rule, Eq. (8), is when d_i is equal to the local LLR for independent distractors, Eq. (7). We will follow the rather unimaginative nomenclature we introduced earlier (Ma, Navalpakkam, Beck, Van den Berg, & Pouget, 2011) and refer to the resulting rule as the max_d rule. This rule combines a Bayesian element (the local LLR) with an ad-hoc operation, and is therefore in a sense a hybrid rule. Most signal detection theory modelers do not consider this form of max rule.

Comparing optimal and max decision rules

Fixed target value, fixed distractor value: Peterson et al. 1954, Palmer 2000, Ma et al. 2011

As a first concrete case, we consider experiments in which the target always has the same value s_T, a distractor always has the same value s_D, and the reliability of the orientation information in the image is equal for all locations. Because of this last condition, the level of measurement noise is assumed equal across locations as well, with value σ. This is a special case of the case of independent distractors, since each distractor can be considered as independently drawn from a delta distribution. Therefore, Eq. (7) is valid. Substituting the expressions for the distributions, the local LLR in Eq. (7) turns out to be monotonic in the measurement x_i:

$$d_i=\frac{s_{\mathrm{T}}-s_{\mathrm{D}}}{{\sigma }^2}(x_i-\frac{s_{\mathrm{T}}+s_{\mathrm{D}}}{2}).$$ (9)

Therefore, the optimal decision rule is to report that the target is present when $\text{log}\frac{p_1}{1-p_1}+\text{log}\frac{1}{N}\sum _{i=1}^N{e}^{\frac{s_{\mathrm{T}}-s_{\mathrm{D}}}{{\sigma }^2}(x_i-\frac{s_{\mathrm{T}}+s_{\mathrm{D}}}{2})}>0$. To our knowledge, this rule was first worked out 60 years ago by Peterson et al. (Peterson, et al., 1954) in a signal processing context. [To be specific: in Eq. (162) of their paper, one can make the substitution n=1 (a single possible target value), and the changes of notation M→N, k→i, N→σ², s_k1→s_T, and $\frac{E}{N_0}\to \frac{s_{\mathrm{T}}^2}{2{\sigma }^2}$ to obtain our likelihood ratio $\frac{1}{N}\sum _{i=1}^N{e}^{\frac{s_{\mathrm{T}}-s_{\mathrm{D}}}{{\sigma }^2}(x_i-\frac{s_{\mathrm{T}}+s_{\mathrm{D}}}{2})}$ with s_D=0.]

• Detection of a single target

• Fixed target value

• Homogeneous distractors with a fixed value

• Equal reliabilities, assume equal precision

• Max_x, max_d, optimal indistinguishable

The optimal decision rule involves a rather complicated inequality in x. A simpler ad-hoc rule is (Nolte & Jaarsma, 1967; P. Verghese, 2001)

$$\underset{i}{\text{max}}{x}_i>k,$$ (10)

which we call the max_x rule. This rule only makes sense when s_T>s_D, but without losing generality, we can choose coordinates such that this is true. For example, when distractors are vertical orientations (say 0º) and the target is tilted 5º, the max observer would report that the target is present when the largest of the N measurements exceeds a criterion.

Eqs. (8) through (10) demonstrate that in the current task, the max_d rule is equivalent to the max_x rule. Moreover, it has long been known that the optimal and the max_x models make very similar predictions in this task (Nolte & Jaarsma, 1967) and both describe human behavior well (Palmer, et al., 2000).

However, it turns out that the three models are highly distinguishable once the experiment is set up such that the equal-noise assumption (σ_i=σ) does not hold, for example by varying contrast across the stimuli within a search array. Then, Eq. (9) for the LLR should be replaced by

$$d_i=\frac{s_{\mathrm{T}}-s_{\mathrm{D}}}{{\sigma }_i^2}(x_i-\frac{s_{\mathrm{T}}+s_{\mathrm{D}}}{2}),$$

which is different in a subtle but important way: σ_i depends on i. In an orientation search task where we varied σ_i randomly across locations and trials by manipulating either contrast or shape, we found that the optimal model outperformed both the max_x and the max_d models ((Ma, et al., 2011); Expts. 1, 1a, 3). The failures of the max_x model were large, both qualitatively and quantitatively. The max_d model fared much better, but its log marginal likelihood was still lower than that of the optimal model by 25.9±2.2, 5.6±0.6, and 5.2±0.8, in different experiments. Typically, log likelihoods larger than 3 to 5 are considered strong evidence (Jeffreys, 1961).

• Detection of a single target

• Fixed target value

• Homogeneous distractors with a fixed value

• Unequal reliabilities

• Optimal wins over max_x and max_d

Fixed target, independent variable distractors: Vincent et al. 2009

We now move away from the case where the distractor value is fixed and consider cases where distractor values are drawn independently from some distribution that is not a delta function. This is also called heterogeneous search. Vincent et al. (Vincent, Baddeley, Troscianko, & Gilchrist, 2009) conducted a single-target detection task with 4 stimuli, where the target was always vertical (which we define as 0), and each distractor was drawn independently from a Gaussian distribution with mean 0 and variance σ_D². Measurement noise level was assumed equal across locations. The dependent measure used was the area under the receiver operating characteristic (AUC).

• Detection of a single target

• Fixed target value

• Independent, normally distributed distractors

• Equal reliabilities, assume equal precision

• Max_x loses; max_d and optimal indistinguishable

In this task, unlike in the previous one, it will often happen that some distractors have smaller values than the target, while others have larger values. Therefore, we do not expect the max_x rule to do well, which is indeed what the authors found. They also claimed that their data supported the optimal decision rule; however, the model that they called optimal is in fact not optimal. To understand this, let us examine their explanation of their model (we modified their notation to make it consistent with ours):

“Rather than calculating the max of sensory percepts, the posterior probability of each display item is calculated, and the maximum of these values is taken (i.e. maximum a posteriori, MAP). MAPs defines a vector of posterior probabilities observed on signal trials, $\mathrm{M}\mathrm{A}{\mathrm{P}}_{\mathrm{s}}=\underset{i}{\text{max}}p(T_i=1|x_i)$, and similarly MAP_n for noise trials, $\mathrm{M}\mathrm{A}{\mathrm{P}}_{\mathrm{n}}=\underset{i}{\text{max}}p(T_i=0|x_i)$.” (Vincent, et al., 2009)

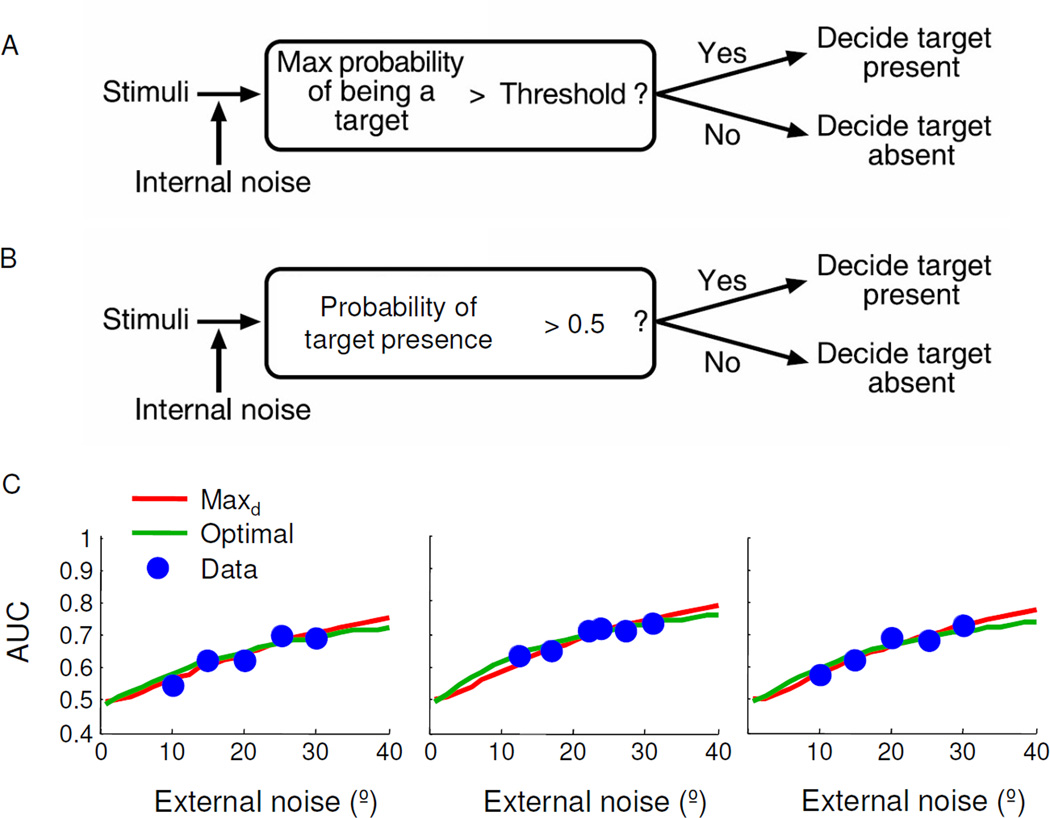
This process is depicted in Figure 1A.

Figure 1. Detection of a single target among heterogeneous distractors.

(A) Model schematic from Figure 2 of Vincent et al. (2009), describing what they call the optimal MAP model. (B) Correct schematic of the optimal MAP model. (C) Comparison of max_d and optimal decision rules based on the data extracted from Vincent et al. (2009). External noise is the value of σ_D. AUC is the area under the receiver operating characteristic. Each plot represents one subject.

In other words, the authors defined the decision variable d_Vincent,i = p(T_i = 1|x_i), and used the decision rule of reporting target present when $\underset{i}{\text{max}}{d}_{\text{Vincent},i}>k$ for some criterion k. This is wrong in an instructive way: what they call the optimal decision variable is the maximum over locations of the local posterior probabilities of target presence. In reality, the optimal decision rule is to pick the value of the global target presence variable, T, that has the highest posterior probability (Figure 1B). The maximum in “MAP” is always over the world state of interest (here T), not over a nuisance parameter such as location.

Incidentally, Vincent et al.’s decision rule reduces to a rule we already encountered. To see this, we rewrite the local LLR of target presence, d_i in Eq. (7), as

$$d_i=\text{log}\frac{p(T_i=1|x_i)p(T_i=0)}{p(T_i=0|x_i)p(T_i=1)}=\text{log}\frac{d_{\text{Vincent},i}}{1-d_{\text{Vincent},i}}+\text{log}\frac{1-\frac{1}{2N}}{\frac{1}{2N}}.$$

Since this is a monotonically increasing function of d_Vincent,i, the decision rule $\underset{i}{\text{max}}{d}_{\text{Vincent},i}>k$ is equivalent to max $\underset{i}{\text{max}}{d}_i>\tilde{k}$, for some other criterion k̃. Thus, at least in terms of AUC, Vincent’s rule is equivalent to the max_d rule. Hence, what their paper showed is that max_d is superior to max_x and fits human data well.

Since Vincent et al. did not test the actual optimal decision rule, the question remains whether that rule can also account for their data. The local LLR is, starting From Eq. (7),

$$d_i=\text{log}\frac{p(x_i|s_i=0)}{\int p(x_i|s_i)p(s_i|T_i=0)d{s}_i}=\text{log}\frac{\frac{1}{\sqrt{2\pi {\sigma }^2}}{e}^{-\frac{x_i^2}{2{\sigma }^2}}}{\int \frac{1}{\sqrt{2\pi {\sigma }^2}}{e}^{-\frac{{(x_i-s_i)}^2}{2{\sigma }^2}}\frac{1}{\sqrt{2\pi {\sigma }_{\mathrm{D}}^2}}{e}^{-\frac{s_i^2}{2{\sigma }_{\mathrm{D}}^2}}d{s}_i}=-\frac{x_i^2}{2}(\frac{1}{{\sigma }^2}-\frac{1}{{\sigma }^2+{\sigma }_{\mathrm{D}}^2})+\frac{1}{2}\text{log}(1+\frac{{\sigma }_{\mathrm{D}}^2}{{\sigma }^2}).$$ (11)

Substituting this in Eq. (6) together with p₁=0.5, we obtain the optimal decision variable.

To obtain the AUC, we simulated the left-hand side of either decision rule ($\text{log}\left(\frac{1}{N}\sum _{i=1}^N{e}^{d_i}\right)$ for the optimal model, and $\underset{i}{\text{max}}{d}_i$ for the max_d model) over many trials, both for T=0 and T=1. This resulted in two distributions of the decision variable. We then computed hit and false-alarm rates for a running criterion on the decision variable, thus producing a receiver-operating characteristic and an area under it. We then fitted the measurement noise level σ in each model by minimizing the sum of squares between the empirical and predicted AUC as a function of external noise level (σ_D). The optimal model accounts equally well for the empirical AUCs as Vincent’s model (Figure 1C). Thus, at least at the level of the AUCs, the optimal and max_d decision rules are both good descriptors of human behavior in this experiment.

Fixed target, independent variable distractors: Navalpakkam and Itti 2007, Rosenholtz 2001

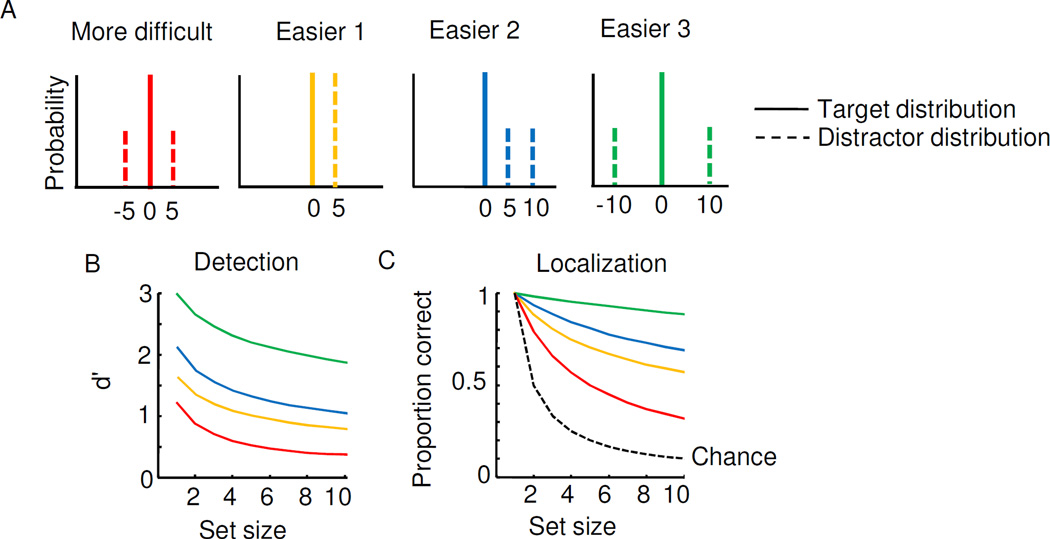
Navalpakkam and Itti (Navalpakkam & Itti, 2007) attempted to predict the relative difficulties of several orientation search conditions (Fig. 2A). The target orientation was always 0°. In the “difficult” condition, a distractor orientation was randomly chosen to be either +5° or −5° (Fig. 2A). The authors compared this condition to three others known to be easier for human subjects (Bauer, Jolicoeur, & W.B., 1996; D'Zmura, 1991; Duncan & Humphreys, 1989; Hodsoll & Humphreys, 2001; Rosenholtz, 2001). In the first, a distractor is always at +5°. In the second, a distractor is at either +5° or +10°. In the third, a distractor is randomly at either +10° or −10°.

• Detection of a single target

• Fixed target value

• Independent distractors drawn from a set of discrete values

• Equal reliabilities, assume equal precision

• Max_d and optimal qualitatively consistent

Figure 2. Heterogeneous search conditions considered by Navalpakkam and Itti.

(A) Distribution of the target and distractor features. The first panel depicts a task in which the target is always vertical, but each distractor is tilted 5° to the right or 5° to the left, with equal probability. According to previous studies, this task is more difficult for than for any of the other three. (B) Predictions of a optimal model for d′ in each of these four search conditions, for single-target detection and for a fixed level of measurement noise (σ=3). No effects of distributed attention were taken into account. (C) Same as (B), but for proportion correct in single-target localization.

One metric of task difficulty that Navalpakkam and Itti tested is the signal detection measure of discriminability, d′, between the measurement distributions in the target-absent and target-present conditions – the difference between their means divided by the square root of the average variance. Navalpakkam and Itti rejected d′ as a suitable metric for task difficulty because of its supposed failure to predict that any of the three easier conditions is in fact easier; they instead proposed a different, salience-based metric.

We argue, however, that this failure lies in the choice of a linear decision variable that is implicit in their definition of d′, and that d′ based on the log posterior ratio of target presence, Eq. (6), accounts well for the relative difficulties of the search conditions. We take the target to have value 0, denote the M possible distractor values by s_Dj, and consider the case that all distractor values are equally probable. Then the local LLR from Eq. (7) becomes

$$d_i=\text{log}\frac{p(x_i|s_i)}{\int p(x_i|s_i)\frac{1}{M}\sum _{j=1}^M\delta (s_i-s_{\mathrm{D}j})d{s}_i}=-\frac{x_i^2}{2{\sigma }^2}-\text{log}\left(\frac{1}{M}\sum _{j=1}^M{e}^{-\frac{{(x_i-s_{\mathrm{D}j})}^2}{2{\sigma }^2}}\right).$$

When M=1 (“Easier 1” in Fig. 2A), this simplifies to Eq. (9). From d_i, we can compute the optimal decision variable d using Eq. (6), again taking p₁=0.5. This decision variable is highly nonlinear in x and thus, its T-conditioned distributions are very different than the T-conditioned distributions of x_i used by Navalpakkam and Itti. By simulating the decision rule d>0, we obtained hit rates H and false-alarm rates F, and then computed discriminability, d′=Φ⁻¹(H)−Φ⁻¹(F), where Φ is the cumulative standard normal distribution. Doing so for each of the four search tasks in Fig. 2A, we found that optimal model predicts higher d′ for each of the tasks that are easier for humans than the “difficult” task (Fig. 2B). (So will the max_d rule; to our knowledge, the rules have not been compared in these search tasks.) The same holds for a localization task (Fig. 2C). Thus, the search conditions considered by Navalpakkam and Itti, at least at a qualitative level, do not pose any qualitative problems for the optimal decision rule. A realistic model for set size effects in heterogeneous search likely also requires incorporating an increase of measurement noise with set size (Mazyar, van den Berg, & Ma, 2012; Mazyar, van den Berg, Seilheimer, & Ma, 2013), for example due to the distribution of attention, but such an increase will leave the ranking of task difficulty in Fig. 2B–C intact.

Although human behavior is qualitatively consistent with both the max_d and the optimal rule, the jury is still out on which model provides the best quantitative fit to human data under the distractor distributions in Fig. 2A. A meticulous model comparison attempt was made by Rosenholtz (2001), who tested subjects, in a 2AFC paradigm, not only on these distributions but also more complex ones (complex in terms of the number of defining parameters). She reported deviations between the optimal model and the data. It is difficult to determine whether these deviations were systematic, because few subjects were tested in each experiment. Moreover, it is not clear how well subjects learned the distractor distributions and what assumptions they might have made to compensate for incomplete knowledge of the distributions. Nevertheless, the deviations from optimality are puzzling and deserve further examination.

Duncan and Humphreys (1989) proposed, in the context of reaction time experiments, that increasing target-distractor similarity and decreasing distractor-distractor similarity both hurt search performance. These trends are consistent with the predictions from the optimal model (Fig. 2B–C). For example, in “More Difficult”, the distractors are less similar to each other than in “Easier 1”, while target-distractor similarity is the same. It might be interesting to try to express the performance of the optimal observer in terms of Duncan and Humphreys’ two main explanatory variables.

Fixed target, independent variable distractors: Ma et al. 2011

We investigated whether observers take into account variations in measurement noise both across items and across trials, during single-target detection with distractors drawn independently from a uniform distribution ((Ma, et al., 2011); Expts. 2, 2a, 4). Like Vincent et al. (2009), we found that the max_x model could easily be ruled out. Computing the log likelihood of each model by summing over model parameters, we found that the max_d model also lost to the optimal model, by log likelihood differences of 8.6±0.8, 56±20, and 60±11 in different experiments. The optimal model was found to be best among 8 models. In particular, this suggests that observers weight evidence by uncertainty in this form of heterogeneous visual search.

• Detection of a single target

• Fixed target value

• Independent, uniformly distributed distractors

• Equal reliabilities, allow for variable precision

• Optimal wins over max_x and max_d

Fixed target, independent variable distractors: Mazyar et al. 2013

We recently performed an experiment similar to Vincent et al. (2009), but with the difference that distractors were drawn from narrower or wider distributions in different conditions (Mazyar, et al., 2013). The feature of interest was orientation, the target was always vertical, and the distractor distribution was a Von Mises distribution with concentration parameter κ_D, which could take values 0 (uniform distribution), 1, and 8. We compared the max_d and optimal decision rules. When we assume the measurement at the i^th location, x_i, to follow a Von Mises distribution around the corresponding orientation s_i with concentration parameter κ_i, then the local LLR takes the following form:

$$d_i=\frac{I_0({\kappa }_{\mathrm{D}})e^{{\kappa }_i\text{cos}2x_i}}{I_0\left(\sqrt{{\kappa }_i^2+{\kappa }_{\mathrm{D}}^2+2{\kappa }_i{\kappa }_{\mathrm{D}}\text{cos}2x_i}\right)}$$

(Mazyar, et al., 2013), where I₀ is the modified Bessel function of the first kind of order 0 (it arises as the normalization of a Von Mises distribution). We modeled κ_i as a random variable. This is a form of the variable-precision model (Van den Berg, Shin, Chou, George, & Ma, 2012), in which the precision of the measurement of a stimulus varies across locations and trials, in part due to fluctuations in attention. In our implementation, we drew precision J_i from a gamma distribution, and used a monotonic mapping from J_i to κ_i. We found that the max_d and optimal decision rules were indistinguishable.

• Detection of a single target

• Fixed target value

• Independent, Von Mises-distributed distractors

• Equal reliabilities, allow for variable precision

• Max_d and optimal indistinguishable

Fixed target, homogeneous variable distractors: Mazyar et al. 2013

In the same paper, we studied a search condition in which the distractors were not independent ((Mazyar, et al., 2013); Expt. 2). Instead, distractors were all identical to each other on a given trial (homogeneous), but we randomly drew the common distractor value on each trial from a Von Mises distribution with mean the target value, s_T, and concentration parameter κ_D.

• Detection of a single target

• Fixed target value

• Homogeneous distractors

• Distractor value Von Mises-distributed

• Equal reliabilities, allow for variable precision

• Optimal wins over max_x and max_d

In view of the dependence between the distractors, Eqs. (4) and (5) do not apply in this task and the expression for the optimal decision variable in terms of local LLRs, Eq. (6), is therefore not valid. Instead, we have to start over from Eq. (2). On a given trial, the observer does not know either the location of the target nor the distractor orientation s_D. Therefore, they have to marginalize (average) over both variables – this is why a sum over locations and an integral over s_D appear:

$$d=\text{log}\frac{p_1}{1-p_1}+\text{log}\frac{\int (\prod _{i=1}^{N}p(x_i|s_i))p(\mathbf{s}|T=1)d\mathbf{s}}{\int (\prod _{i=1}^{N}p(x_i|s_i))p(\mathbf{s}|T=0)d\mathbf{s}}=\text{log}\frac{p_1}{1-p_1}+\text{log}\frac{\int \int (\prod _{i=1}^{N}p(x_i|s_i))p(\mathbf{s}|T=1,s_{\mathrm{D}})p(s_{\mathrm{D}})d\mathbf{s}d{s}_{\mathrm{D}}}{\int \int (\prod _{i=1}^{N}p(x_i|s_i))p(\mathbf{s}|T=0,s_{\mathrm{D}})p(s_{\mathrm{D}})d\mathbf{s}d{s}_{\mathrm{D}}}=\text{log}\frac{p_1}{1-p_1}+\text{log}\frac{\frac{1}{N}\sum _{i=1}^{N}p(x_i|s_i=s_{\mathrm{T}})\int (\prod _{j\ne i}p(x_j|s_j=s_{\mathrm{D}}))p(s_{\mathrm{D}})d{s}_{\mathrm{D}}}{\int (\prod _{i}p(x_j|s_j=s_{\mathrm{D}}))p(s_{\mathrm{D}})d{s}_{\mathrm{D}}}$$

Because of the integral over the shared distractor orientation, s_D, this expression cannot be simplified much further.

To our knowledge, the max model has never been generalized to this task. One possible choice of max rule is the max_d rule for the Vincent et al. task, namely to report “target present” when $\underset{i}{\text{max}}{d}_i>k$, with d_i given by the equivalent of Eq. (11) for Von Mises-distributed measurements and variable precision,

$$d_i={\kappa }_i\text{cos}2(x_i-s_{\mathrm{T}})+\frac{I_0\left({\kappa }_{C=1,i}\right)}{I_0\left({\kappa }_{C=0}\right)},$$

with

$${\kappa }_{C=1,i}=\sqrt{{\left(\sum _{j\ne i}{\kappa }_j\text{cos}2x_j\right)}^2+{\left(\sum _{j\ne i}{\kappa }_j\text{sin}2x_j\right)}^2}$$ (12)

$${\kappa }_{C=0}=\sqrt{{\left(\sum _{j=0}^N{\kappa }_j\text{cos}2x_j\right)}^2+{\left(\sum _{j=0}^N{\kappa }_j\text{sin}2x_j\right)}^2}$$

(Mazyar, et al., 2013). The factors of 2 are due to the nature of orientation space, which has period π instead of 2π. In Eq. (12), all four sums start at j=0, and we have defined x₀=s_T and κ₀=κ_D. A simpler max rule is to report “target present” when $\underset{i}{\text{max}}\text{cos}2(x_i-s_{\mathrm{T}})>k$, i.e. when any of the measurements is sufficiently close to the target orientation; we call this the max_x model. We compared the optimal rule to both versions of the max rule using the data of the homogeneous condition in Mazyar et al. (2013). We found that the optimal model provides a much better fit than max_d and the max_x models, with log marginal likelihood differences of 54.0±6.4 and 31±10, respectively.

LOCALIZATION OF A SINGLE TARGET

Localization of a target among N stimuli has received little attention compared to target detection, in spite of or perhaps because of the fact that the optimal decision rules for localization tasks are very similar to those for detection. We denote by L the location of the target (L=1,…,N), and by p(s|L) the distribution of stimuli given target location. The likelihood of target location L is the probability of the measurements x given the hypothesis that the target is at that location. The posterior over location is

$$p(L|\mathbf{x})\propto p(\mathbf{x}|L)p(L)=p(L)\int p(\mathbf{x}|\mathbf{s})p(\mathbf{s}|L)d\mathbf{s}.$$ (13)

In a detection task, the optimal strategy involves marginalizing over L (see Eq. (3)). In a localization task, however, it is to report the location L for which p(L|x) is highest. If the distractors are independent, then the distribution of stimulus sets s given target location L is

$$p(\mathbf{s}|L)=p(s_L|T_L=1)\prod _{i\ne L}^{N}p(s_i|T_i=0).$$

and Eq. (13) becomes

$$p(L|\mathbf{x})\propto p(L)\int (\prod _{i=1}^{N}p(x_i|s_i))p(s_L|T_L=1)(\prod _{i\ne L}^{N}p(s_i|T_i=0))d\mathbf{s}=p(L)(\int p(x_L|s_L)p(s_L|T_L=1)d{s}_L)\prod _{i\ne L}^N(\int p(x_i|s_i)p(s_i|T_i=0)d{s}_i).\propto p(L)\frac{\int p(x_L|s_L)p(s_L|T_L=1)d{s}_L}{\int p(x_L|s_L)p(s_L|T_L=0)d{s}_L},$$ (14)

where L-independent factors have been absorbed into the proportionality sign. The optimal decision rule is now to report the location for which this quantity is highest:

$$\hat{L}=\underset{L}{\text{argmax}}p(L|\mathbf{x}).$$ (15)

Two studies that tested this rule (Eckstein, Abbey, Pham, & Shimozaki, 2004; Vincent, 2011) both found that the optimal rule described the data well, but neither compared it to alternative rules.

Alternative decision rules for the target localization task would most naturally take the form $\hat{L}=\underset{i}{\text{argmax}}{d}_i$, for some alternative decision variable d_i. We are particularly interested in max models, but the generalization of max models from target detection to target localization can be approached from at least three views, which differ in what one considers the essence of a max model:

• The first view is to call the optimal MAP rule Eq. (15) a form of max rule, since it contains an “argmax” operation. However, according to that logic, the optimal MAP model is a max model for any task, since the argmax of the posterior is always taken. Therefore, we reject this view.

• The second view is that the max_d model is characterized by maximizing the local LLR of target presence over locations. When p(L) is uniform and the distractors are independent, Eq. (14) states that p(L|x) is proportional to the local LLR, and therefore, the max_d model for this task coincides with the optimal model.

• The third view starts from the basic premise of the max model for target detection, which is that the observer makes N independent decisions d_i>k, where i=1,…,N. In localization, the vector of Booleans produced by N independent decisions could be converted into a location report by randomly choosing a location for which “true” was returned.

We leave the comparison of these models to further work but emphasize that the ambiguity in the definition of the max rule argues against this rule serving as the basis of a general account of perceptual decision-making.

CATEGORIZATION OF A SINGLE TARGET

We now consider tasks in which exactly one target is present on each trial, and the observer categorizes its feature value. For example, the target might be the only tilted stimulus among vertical distractors, and the observer decides whether the tilt is clockwise or counterclockwise with respect to vertical (Baldassi & Burr, 2000). We cannot think of a naturalistic example of such tasks, but if that is not of concern, then they are at least as suitable to study decision rules as target detection or localization tasks. As an aside, we use the term “categorization” instead of “discrimination” because the number of possible responses will typically be smaller (namely 2) than the number of stimulus values.

Variable target, variable distractors: Baldassi and Verghese (2002)

Baldassi and Verghese (Baldassi & Verghese, 2002) extended the Baldassi and Burr task by including a second condition, in which orientation noise (drawn from a zero-mean Gaussian distribution with standard deviation σ_s) was added to every stimulus, including the target. The target orientation itself was drawn from a different distribution, which we here approximate as a Gaussian distribution with mean vertical and standard deviation σ_T. We denote by C the direction of tilt of the target: C=−1 means tilted counterclockwise, and C=1 clockwise. The relevant distributions are in the box, where 1_A indicates the indicator function on the domain specified by the condition A.

• Left-right categorization of a single target

• Independent, normally distributed distractors

• In EN condition, orientation noise added to each stimulus.

• Equal reliabilities, allow for variable precision

• Optimal and four max models indistinguishable, except that one max_d model wins in EN condition

The optimal decision variable is the log posterior ratio of target category,

$$d=\text{log}\frac{p(C=1|\mathbf{x})}{p(C=-1|\mathbf{x})}=\text{log}\frac{p(\mathbf{x}|C=1)}{p(\mathbf{x}|C=-1)},$$

where we have chosen a prior of 0.5 so as to not give the optimal model an unfair advantage over the max model, which we discuss below. The log posterior ratio becomes

$$d=\text{log}\left(\frac{1}{N}\sum _{i=1}^N{e}^{d_i^{(1)}}\right)-\text{log}\left(\frac{1}{N}\sum _{i=1}^N{e}^{d_i^{(-1)}}\right),$$ (16)

where

$$d_i^{(C)}=\text{log}\frac{\int p(x_i|s_i)p(s_i|T_i=1,C)d{s}_i}{\int p(x_i|s_i)p(s_i|T_i=0)d{s}_i}$$ (17)

is the LLR of the hypothesis that the target is present at the i^th location and is of class C, versus the hypothesis that the target is absent at that location. Eqs. (16) and (17) parallel Eqs. (6) and (7) for single-target detection; in particular, Eq. (16) contains marginalizations over target location, reflecting that the observer does not commit to a single possible target location. The optimal decision rule is to report “clockwise” when d>0, or equivalently, when

$$\sum _{i=1}^N{e}^{d_i^{(1)}}>\sum _{i=1}^N{e}^{d_i^{(-1)}}.$$

Substituting the expressions for the distributions, we find

$$d_i^{(C)}=\frac{1}{2}\text{log}\frac{a_i{b}_i}{{\sigma }_{\mathrm{T}}^2}+\frac{b_i}{2a_i}{x}_i^2+\text{log}(\frac{1}{2}+\frac{C}{2}\text{erf}(x_i\sqrt{\frac{b_i}{2a_i}}\left)\right)$$ (18)

where $a_i={\sigma }_{\mathrm{s}}^2+{\sigma }_i^2,b_i=\frac{{\sigma }_{\mathrm{T}}^2}{{\sigma }_{\mathrm{s}}^2+{\sigma }_i^2+{\sigma }_{\mathrm{T}}^2}$, and erf is the error function. The optimal decision rule becomes $\sum _{i=1}^N\sqrt{a_i{b}_i}{e}^{\frac{b_i{x}_i^2}{2a_i}}\text{erf}\left(x_i\sqrt{\frac{b_i}{2a_i}}\right)>0$, which is analogous to a decision rule that Ma and Huang (2009; Eq. (18)) derived for single-change categorization.

Max_x model

Baldassi and Verghese (2002) proposed a max_x rule for single-target categorization, which they called the “signed-max rule”. It is to report “rightward” when the measurement x_i that is largest in absolute value is positive, in other words, when

$$\underset{L}{\text{max}}{x}_L>\underset{L}{\text{max}}(-x_L).$$ (19)

This condition is equivalent to the average of the largest and the smallest measurement being positive. When N=1, the max_x rule is equivalent to the optimal rule: they both reduce to x₁>0. When N=2, the max rule is equivalent to the optimal rule when σ₁=σ₂.

Max_d model

For single-target detection, we discussed a more principled type of max rule, the max_d rule, which compares the maximum of local LLRs to a criterion. A max_d rule can also be formulated for single-target categorization, and has the advantage over the max_x rule that it is also applicable when categories are not mirror images of each other. However, because a stimulus can belong to at least two categories (e.g., target tilted left, target tilted right, distractor), there are multiple ways to construct a max_d rule. First, by analogy to single-target detection, a max_d rule can be obtained by replacing the averaging of evidence over locations in the optimal decision rule (Eq. (16)) by a maximum operation:

$$d=\text{log}\left(\underset{i}{\text{max}}{e}^{d_i^{(1)}}\right)-\text{log}\left(\underset{i}{\text{max}}{e}^{d_i^{(-1)}}\right),$$

and then evaluating d>0, which amounts to reporting C=1 when

$$\underset{i}{\text{max}}{d}_i^{(1)}>\underset{i}{\text{max}}{d}_i^{(-1)},$$

where $d_i^{(C)}$ is given by Eq. (18). We call this the max_d1 model. A second construction would be to locally compute the LLR for C=1 versus C=−1 as if the item at that location were the only item in the display (this is $d_i^{(1)}-d_i^{(-1)}$), and then choose the hypothesis with the largest-magnitude LLR anywhere in the display. This amounts to reporting C=1 when

$$\underset{i}{\text{max}}(d_i^{(1)}-d_i^{(-1)})>\underset{i}{\text{max}}(d_i^{(-1)}-d_i^{(1)}).$$

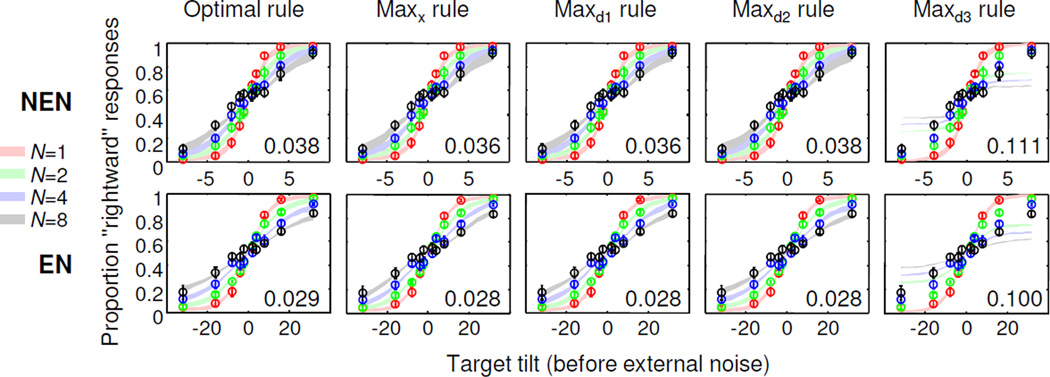
This is like the signed-max rule, Eq. (19), but applied to local posterior ratios rather than to measurements. We call this the max_d2 model. A third view would prescribe to make an independent decision at each location, namely to count for how many locations $d_i^{(1)}>d_i^{(-1)}$, and decide on the category that receives the most “votes”, using a coin flip as a tiebreaker. We call this the max_d3 model. Of these four max models, Baldassi and Verghese (2002) only fitted the max_x model. Therefore, we conducted our own experiment and fitted the optimal, max_x, and three max_d models.

Replication of Baldassi and Verghese’s variable-target, variable-distractor experiment

We followed the experimental design introduced by Baldassi and Verghese (2002). Subjects were presented with one or multiple items, one of which was always the target. The task was to report whether the target stimulus was oriented to the right or left of vertical.

Stimuli

Stimuli were displayed on a 21" LCD monitor. Subjects were seated at a viewing distance of approximately 60 cm. Each of the stimuli was a Gabor patch with a spatial frequency of 2.9 cycles per degree of visual angle, a Gaussian standard deviation of 0.25 degrees, and a peak luminance of 64 cd/m². Background luminance was 28 cd/m². Stimuli were presented on an imaginary circle of radius 5 degrees around the fixation point. First, the target. was placed at a random angle. In trials with distractors (N>1), the distractors were placed such that any two adjacent items were separated by the same angle (180° at N=2, 90° at N=4, and 45° at N=8).

Conditions

On each trial, set size was 1, 2, 4, or 8, randomly chosen with equal probabilities. In the No External Noise (NEN) condition, all distractors (non-target items) were vertical (0°), and the target orientation was drawn with equal probabilities from the set ±{0.5, 1, 2, 4, 8}°. In the External Noise (EN) condition, mean target orientation was drawn with equal probabilities from a different set, to approximately match the overall difficulty of the NEN condition: ±{2, 4, 8, 16, 32}°. In addition, in the EN condition, orientation noise was added to every item, drawn independently from a normal distribution with mean 0° and standard deviation σ_s=8°. (Baldassi and Verghese used multiple EN conditions, but we restrict ourselves to one.)

Procedure

Subjects were asked to fixate at the cross in the center of the screen. Stimuli were presented for 100 ms. Subjects pressed a key to report whether the target was tilted to the left or right from the vertical. Trial-to-trial feedback was given by changing the color of the fixation point to green or red.

Subjects and sessions

Eight subjects participated (3 authors and 5 naïve). All subjects had normal or corrected-to-normal vision. Each subject completed a total of 3840 trials over 3 sessions. Each session consisted of 4 blocks of NEN trials, followed by 4 blocks of EN trials. Overall, a subject completed 96 trials in each combination of external noise condition (NEN/EN), set size, and target orientation. Informed consent was obtained. The work was carried out in accordance with the Declaration of Helsinki.

Models

As an encoding model, we used the variable-precision model (Van den Berg, Shin, et al., 2012), in which inverse variance J is drawn from a gamma distribution with mean decreasing with set size in power law fashion: J̅ = J̅₁N^−α, and scale parameter τ. (Neither the gamma distribution nor the power law have normative underpinnings.) We tested the max_x, max_d, and optimal decision rules. The optimal and max_d decision rules all use Eq. (18), but in the NEN condition with σ_s = 0. The max_x decision rule is always Eq. (19). The models had three free parameters: J̅₁, α, and τ. We fitted parameters by maximizing the parameter likelihood (computed from all individual trials) using a customized genetic algorithm, separately for the NEN and EN conditions.

Results

Fig. 3 shows the fits of the five models. Besides the max_d3 model, all provide reasonably good fits to the summary statistics. The maximum log likelihood of the optimal model minus that of the max_x, max_d1, max_d2, and max_d3 models is −1.6±2.4, −1.0±1.4, −6.8±1.7, and 200±32, respectively; each model has the same number of parameters so no corrections are needed. This means that the max_d3 model is a very poor model, the max_d2 model fits best, and the remaining three models are approximately equally good.

Figure 3. Replication of Baldassi and Verghese’ s target categorization task, with model fits.

We used two search conditions: without (NEN) and with external noise (EN). Circles and error bars: mean and s.e.m. of data. Shaded areas: mean and s.e.m. of model fit. The first four models all fit qualitatively well. Numbers: root-mean-square differences between data and model, averaged over subjects.

The performance advantage of the max_d2 model, which turns out to come exclusively from the EN condition, is an anomaly among the results reported in this paper, which generally point to max models fitting no better than the optimal model. We can think of three possible sources of this discrepancy:

• Stochastic variation. While a log likelihood difference of 6.8 is not small, it should be kept in mind that we have been looking for any instance among many experiments in which any max model can outperform the optimal model. Thus, a multiple-comparisons correction of some sort might be necessary.

• Inadequacy of the optimal model for this task. In order to be optimal in this task, an observer needs to learn both the target distribution and the external noise distribution. All other tasks discussed in this paper required learning a single stimulus distribution. Learning two distributions might be difficult based on the samples provided.

• Our conclusion does not hold as generally as we claim, and the EN condition in this task is one case in which people do prefer a particular max rule over being optimal.

Further work is needed to distinguish these possibilities. This could include a replication in which observers are trained better on the two noise distributions.

Variable target, homogeneous variable distractors: Shen and Ma (2015)

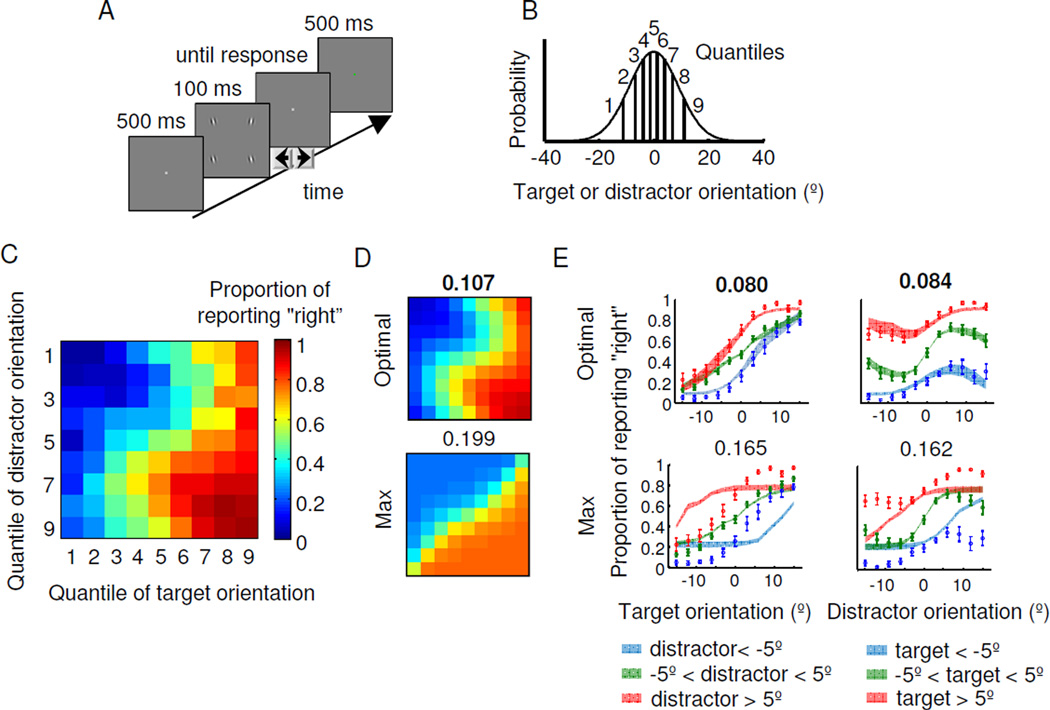
In a recent study, we attempted to qualitatively distinguish the optimal rule from several suboptimal rules (Shen & Ma, 2015). In this experiment, the observer viewed four orientations, three of which were identical to each other (the distractors); the fourth item was defined as the target (Fig. 4A). The target orientation and the common distractor orientation were drawn from the same Gaussian distribution around vertical (Fig. 4B). The psychometric surface as a function of target and distractor quantile shows an interesting pattern (Fig. 4C).

• Left-right categorization of single target

• Homogeneous distractors

• Normally distributed distractor value

• Equal reliabilities, assume equal precision

• Optimal wins over max_x

Figure 4. Single-target categorization task by Shen and Ma.

(A) Trial procedure. Each display contains four items, of which three have a common orientation; these are the distractors. Subjects report whether the fourth item (the target) is tilted to the left or to the right with respect to vertical. (B) On each trial, the target orientation and the common distractor orientation are independently drawn from the same Gaussian distribution with a mean of 0° (vertical) and a standard deviation of 9.06°. For plotting, we divide orientations into 9 quantiles. (C) Proportion of reporting “right” as a function of target and distractor orientation, averaged over 10 subjects. (D) Model fits to the data in (C). (E) Proportion of reporting “right” as a function of target orientation (left column) and distractor orientation (right column). Circles and error bars: mean and s.e.m. of data. Shaded areas: mean and s.e.m. of model fit. Numbers above plots in (D) and (E) represent root-mean-square differences between data and model, averaged over subjects. The model fits are based on the stimuli actually presented in the experiment; therefore, apparent discontinuities are due to stimulus variability, rather than simulation noise.

We derived the optimal decision rule along the same lines as for Mazyar et al.’s homogeneous-distractor task. The only difference is that in the earlier task, the target orientation was always vertical, whereas here, it was drawn from the same distribution as the distractor orientation. We denote by C the direction of tilt of the target (±1). We obtained the likelihood of C by marginalizing over target location, target orientation, and distractor orientation. For C=1,

$$p(\mathbf{x}|C=1)=\sum _{i=1}^N{\int }_0^{\infty }{\int }_{-\infty }^{\infty }p(x_i|s_{\mathrm{T}})p(s_{\mathrm{T}})(\prod _{j\ne i}p(x_j|s_{\mathrm{D}}))p(s_{\mathrm{D}})d{s}_{\mathrm{T}}d{s}_{\mathrm{D}}.$$

Like in Mazyar et al.’s homogeneous-distractor task, because the distractors are linked to each other, the decision rule is not defined in terms of local LLRs, and therefore it is difficult to define the max_d model. However, Baldassi and Verghese’s signed max rule (a max_x model), which would return the sign of the most tilted stimulus, is reasonable in this task and will perform above chance: the observer would tend to be correct when target and distractor have the same sign (50% of trials), and when the target is more tilted than the distractor (another 25% of trials). Both the optimal and the signed-max model had two free parameters: measurement noise σ and a lapse rate. (Strictly speaking, in the optimal model, a nonzero lapse rate violates optimality; however, we can think of the model as a two-process model: either the observer guesses, or is optimal.)

We found that the max_x model provided a qualitatively poor fit to the data, while the optimal model provided an excellent fit (Fig. 4D–E).

DETECTING, LOCALIZING, OR DISCRIMINATING A SINGLE CHANGE

Change detection, localization, and categorization are very similar to target detection, localization, and categorization. There are two displays, a sample display and a test display, and the observer detects, localizes, or categorizes a change of one or more stimuli between the two displays. The changing item plays the role of the target in a single-target search task, and the non-changing items play the role of homogeneous distractors. In change detection and categorization with a single change, when the sample display contains N stimuli, the test display can in principle contain any number of stimuli, but in practice, experimenters have used 1, 2, or N stimuli. In change localization, of course, the number of stimuli has to be greater than 1, and in practice it is either 2 or N.

We will first consider a paradigm in which the test display contains N items, and the non-changing items (which we will call distractors) are drawn independently of each other. This task is common in studies of working memory (Luck & Vogel, 1997; Pashler, 1988). In earlier work, we proposed the maximum-absolute-differences rule to describe human decision-making in this task (Wilken & Ma, 2004): the observer would make N noisy measurements x₁,…,x_N in the sample display, N noisy measurements y₁,…,y_N in the test display, take at each location the distance (absolute difference) between the sample measurement and the test measurement, then report that a change occurred if the largest of these absolute differences across the display exceeds a criterion. This is equivalent to

$$\underset{i}{\text{max}}|y_i-x_i|>k.$$ (20)

This rule, which is the change detection equivalent of the max_x rule encountered for fixed-target, fixed-distractor target detection, Eq. (10), fitted human receiver-operating characteristics well, in color, orientation, and spatial frequency change detection (Wilken & Ma, 2004). In that study however, we fitted aggregate rather than individual data, and did not test the optimal rule.

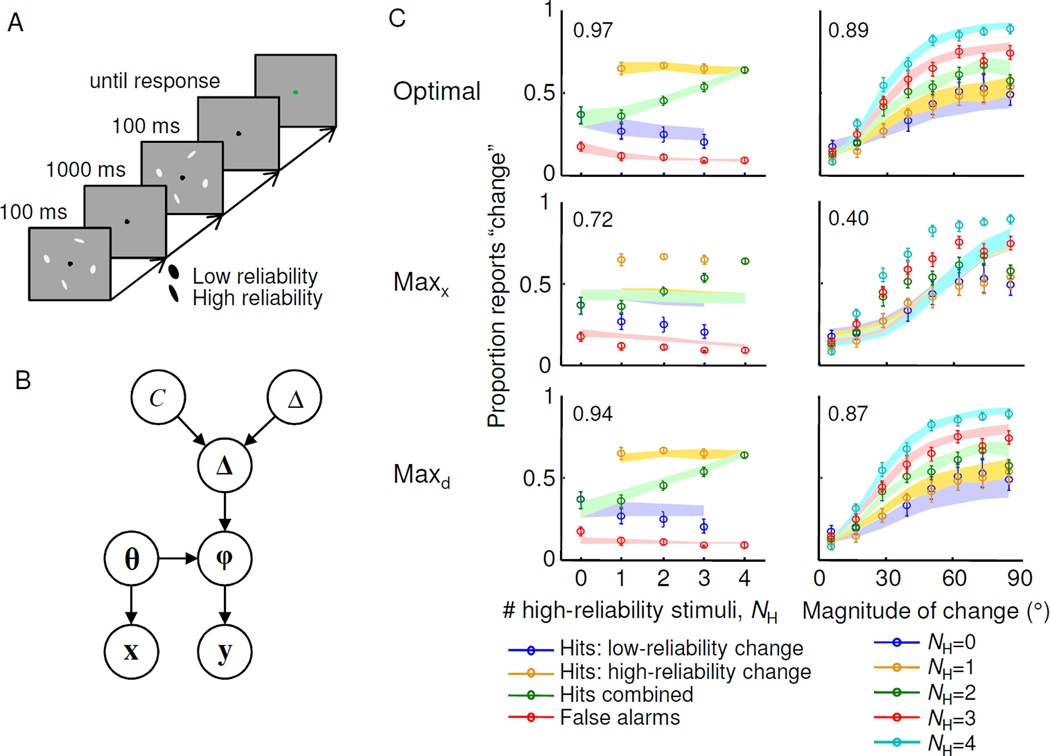
In a more detailed and rigorous study, we compared the optimal rule and the max rule in Eq. (20), while also considering model variants along different dimensions: we tested equal versus variable precision, and considered different assumptions that observers might be making about precision (Keshvari, Van den Berg, & Ma, 2012). We systematically varied the magnitude of change, so as to have a richer data set to fit. Analogous to the search study discussed earlier (Ma, et al., 2011), we also varied stimulus reliability through shape, unpredictably across locations and trials (Fig. 5A). The generative model (Fig. 5B) shows the statistical dependencies between variables. The relevant variables are change occurrence, T (0 or 1), magnitude of change, Δ, the vector of change magnitudes at all locations, Δ, the vectors of stimulus orientations in the first and second displays, θ and φ=θ+Δ, and the vectors of corresponding measurements, x and y. The optimal decision variable is

$$d=\text{log}\frac{p_{\text{change}}}{1-p_{\text{change}}}+\text{log}\left(\frac{1}{N}\sum _{i=1}^N{e}^{d_i}\right),$$

where p_change is the prior probability of a change. This is equivalent to Eq. (6) for search. The local LLR is (Keshvari, et al., 2012)

$$d_i=\text{log}\frac{\int p(x_i,y_i|{\mathrm{\Delta }}_i=\mathrm{\Delta })p(\mathrm{\Delta })d\mathrm{\Delta }}{p(x_i,y_i|{\mathrm{\Delta }}_i=0)},$$ (20)

which would be analogous to a search task in which the target value is variable from trial to trial. The max_d rule is $\underset{i}{\text{max}}{d}_i>k$. It turns out that the max_x rule, Eq. (20), can be obtained by taking the max_d rule and assuming that the observer does not use any knowledge of sensory/memory noise but instead assumes a single level of noise.

• Detection of a single change

• Independent, uniformly distributed distractors

• Unequal reliabilities

• Optimal wins over max_x and max_d

Figure 5. Detection of a single change.

(A) Trial procedure. Stimuli were ellipses, and the reliability of their orientation information was controlled by elongation. Set size was always 4. (B) Generative model (see text). (C) Model comparison for proportion of “change” reports as a function of the number of high-certainty stimuli, N_H (left column), and as a function of the magnitude of change, for different values of N_H. Circles and error bars: mean and s.e.m. of data. Shaded areas: mean and s.e.m. of model fit. The number in each plot is the R² of the fit. All panels were adapted from Keshvari et al. (2012).

Fig. 5C shows a comparison between the three models. The max_x rule fares very poorly. The max_d model fits the data subtly worse than the optimal model (compare the top and bottom panels in the left column of Fig. 5C), and formal model comparison shows that the log marginal likelihood of the max_d model is 15.4±7.3 lower than that of the optimal model (Keshvari, et al., 2012).

In localization tasks, there is always at least one change, and observers report the locations of the perceived changes. When we otherwise keep the same assumptions as above, the optimal rule is to report the location i for which d_i in Eq. (20) is largest. This is the analogue of Eq. (15) for visual search. We found that the optimal rule could well describe human change localization judgments (Van den Berg, Shin, et al., 2012), but we did not test alternative rules.

MULTIPLE TARGETS

So far, we have discussed global, feature-based categorization for a single target. What if there are multiple targets? For concreteness, we consider detection: the observer reports whether or not any targets were present. Just like the optimal observer in a single-target task marginalized over all possible target locations (sum over i in Eq. (6)), the optimal observer in a multiple-target task would marginalize over possible configurations of targets. For example, when the observer knows that on a target-present trial, 3 of 6 stimuli are targets, they will have to consider for every subset of 3 of 6 measurements the possibility that this subset was the target set. To model such scenarios, we introduce the target configuration vector T, which indicates for each location whether a target is present (entry is 1) or absent (entry is 0) at that location. We assume independent targets and independent distractors. The optimal decision variable is then

$$d=\text{log}\frac{p_1}{1-p_1}+\text{log}\frac{p(\mathbf{x}|T=1)}{p(\mathbf{x}|T=0)}=\text{log}\frac{p_1}{1-p_1}+\text{log}\frac{\sum _{\mathbf{T}}p(\mathbf{T}|T=1)p(\mathbf{x}|\mathbf{T})}{p(\mathbf{x}|\mathbf{T}=\mathbf{0})}=\text{log}\frac{p_1}{1-p_1}+\text{log}\frac{\sum _{\mathbf{T}}p(\mathbf{T}|T=1)(\prod _{i:T_i=1}p(x_i|T_i=1))(\prod _{i:T_i=0}p(x_i|T_i=0))}{\prod _{i}p(x_i|T_i=0)}=\text{log}\frac{p_1}{1-p_1}+\text{log}(\sum _{\mathbf{T}}p(\mathbf{T}|T=1)\prod _{i:T_i=1}\frac{p(x_i|T_i=1)}{p(x_i|T_i=0)})$$

Here, p(T|T=1) indicates how often each target configuration occurs on a target-present trial. When the number of targets is N_targets, the number of configurations that must be considered is $\left(\begin{array}{c}\hfill N\hfill \\ \hfill N_{\text{targets}}\hfill \end{array}\right)$; in other words, a combinatorial explosion might occur. It is unknown whether the brain can effectively approximate a sum of potentially so many terms.

Change detection with multiple targets and multiple distractors was examined by Wilken and Ma (Wilken & Ma, 2004). We found that a model in which the decision variable is the sum of local absolute differences fitted the data well, but we did not test the optimal model.

A special case of change detection with multiple targets is when all items are targets. Then, the optimal decision variable when targets are independent of each other and distractors are independent of each other becomes

$$d=\text{log}\frac{p_1}{1-p_1}+\sum _{i=1}^N\text{log}\frac{p(x_i|T_i=1)}{p(x_i|T_i=0)}.$$

In other words, the optimal decision variable is expressed as a sum of local LLRs. This is an example of a sum rule (Graham, et al., 1987; Green & Swets, 1966). Verghese and Stone conducted a speed change discrimination task in which all stimuli on target-present trials were targets (N_targets=N) (P Verghese & Stone, 1995); a careful re-analysis revealed that the sum rule (hence the optimal rule) described their data better than a max_x rule (Palmer, et al., 2000).

• Detection of all items changing

• Identical changes

• Equal reliabilities, assume equal precision

• Optimal wins over max_x

Finally, we consider another example of N_targets=N, but with targets not independent of each other and distractors not independent of each other. On a target-present trial, all targets are identical to each other and the target value is drawn from a distribution p(s_T). On a target-absent trial, distractors are drawn from a multivariate distribution p(s_D). The task has now become a sameness judgment task: are all stimuli the same (targets present) or are they all different (targets absent)? The optimal decision variable becomes

$$d=\text{log}\frac{p_1}{1-p_1}+\text{log}\frac{\int (\prod _{i=1}^{N}p(x_i|s_i=s_{\mathrm{T}}))p(s_{\mathrm{T}})d{s}_{\mathrm{T}}}{\int (\prod _{i=1}^{N}p(x_i|s_i=s_{\mathrm{D},i}))p({\mathbf{s}}_{\mathrm{D}})d{\mathbf{s}}_{\mathrm{D}}}.$$

A max_x model might prescribe that the observer responds that the stimuli are the same when the largest absolute difference between any two measurements is smaller than a criterion k,

$$\underset{i,j}{\text{max}}|x_i-x_j|<k$$

(Van den Berg, Vogel, Josic, & Ma, 2012). We tested the optimal model against this max_x model in an orientation sameness judgment task where noise level was varied randomly across stimuli. We found that the log likelihood of the optimal model was higher by 24.7±4.6.

• Target detection when all items are targets

• Homogeneous targets

• Target value uniformly distributed

• Independent distractors normally distributed

• around a uniformly distributed mean

• Equal reliabilities, assume equal precision

• Optimal wins over max_x

NEURAL IMPLEMENTATION

So far, we have only considered psychophysical evidence. Of course, a behavioral model also needs a neural implementation. One has been suggested for the max model, in the task of detecting a target of fixed value among homogeneous distractors also of fixed value (P. Verghese, 2001). In its simplest form, this implementation relies on N neurons, each with their receptive field at the location of one of the stimuli in the search display. The activity of one of these neurons is meant to signal the amount of evidence that a target is present in its receptive field. In the decision stage, an output neuron takes the maximum of the activities of these N neurons, and produces a “target present” decision when this maximum exceeds a threshold level.

At first glance, this model seems to be supported by the presence of neurons in inferotemporal cortex whose response to multiple stimuli can be described as the maximum of their responses to the individual stimuli (M Riesenhuber & Poggio, 1999). Upon closer look however, this support is tenuous. First, the maximum of responses to individual stimuli is not the same as the maximum of the activity of the afferent neurons. Second, the task was a passive fixation task, so the only relevance to the neural implementation of global categorization might be that a max operation might exist in cortex. Third, other studies have argued instead for linear (Zoccolan, Cox, & DiCarlo, 2005) or other nonlinear (Britten & Heuer, 1999) functions for describing the response to multiple stimuli. Thus, neural evidence in support of the max model for visual search is scarce.

Another problem with the proposal outlined in Verghese (2001) is its lack of generality. Identifying neural activity at a location with the amount of evidence for target presence at that location only makes sense in very specific cases, such as a target of fixed value among homogeneous distractors also of fixed value, with equal and constant sensory noise levels. For heterogeneous distractors, variable targets, or unequal sensory noise levels, the relation between evidence and activity is much more complicated (Ma, 2010).

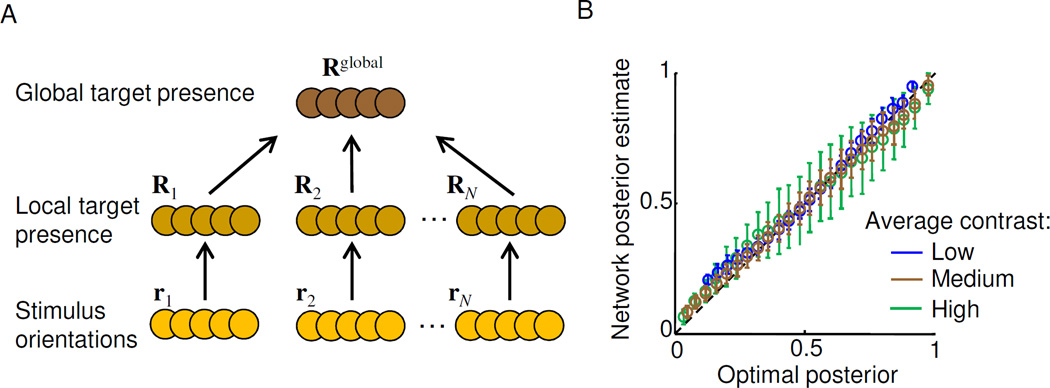
This leaves the question of whether the optimal rule can be computed by neural circuits using plausible operations. This question was explored for single-target detection in the presence of fixed distractors or variable distractors (Ma, et al., 2011). We used a neural coding framework known as probabilistic population coding, according to which a sensory neural population encodes a likelihood function over a stimulus on each trial. We used this form of code to construct a neural network whose output can, on each trial, represent a good approximation the posterior probability of target presence, and therefore can also behave in a near-optimal manner (Fig. 6). The resulting network contained linear, quadratic, and divisive normalization operations, all of which have been widely observed in cortex. This is a first indication that the apparent complexity of optimal decision rules does not preclude a plausible neural implementation. In particular, these types of networks could be an alternative to max-based networks such as those proposed by Riesenhuber and Poggio (M. Riesenhuber & Poggio, 2000).

Figure 6. Network for optimal visual search (Ma et al., 2011).

(A) A three-layer feedforward firing-rate network. In each layer, a population of neurons encodes the likelihood function over a variable: r over stimulus orientation, R over local target presence, and R^global over global target presence. Operations can be linear, quadratic, and divisive normalization. (B) After training, this network can accurately estimate the posterior probability that a target is present in a scene, even when sensory noise (here contrast) varies unpredictably across items and trials. Removing the divisive normalization does not allow for accurate estimation, even after relearning. Adapted from Ma et al., 2011.

CONCLUSION

Although it has generally proven difficult to distinguish the optimal decision rule from max decision rules, in cases where a clear winner emerged, that winner was the optimal rule – with one exception, in which the generative model was the most complex of all tasks examined here. Varying reliability across the stimuli within a display seems to be a useful manipulation for distinguishing the models. This is because those variations affect the optimal and max decision rules in different ways. Reliability is also expected to vary in natural vision, due to variations in depth, eccentricity, occluder transparency, etc.

We can conclude that there is, at present, little or no evidence for idea that the brain makes global decisions by combining the results of local decisions. More broadly, our results can construed as a rebuke of the common preference of signal detection theory modelers for simple ad-hoc rules over – usually more complex – optimal rules. We believe that any future study involving a feature-based global categorization task should test the optimal decision rule in addition to ad-hoc decision rules. In doing so, researchers should take care to derive the correct form of the optimal rule.

Our conclusions do come with some caveats. Their generality can be questioned given that some subparadigms within the domain of feature-based global categorization remain largely unexplored. In particular, more psychophysics and model comparison are needed for single-target localization, multiple-target search of any kind (detection, localization, or categorization), and oddity detection. Furthermore, recall that Koopman (1954) was concerned with multiple glimpses over time, not multiple stimuli within a single display; this might change the conclusion.

An epistemological argument can be made in support of optimal models. The optimal decision rule can always be derived directly from the generative model of a task, based on the goal of maximizing accuracy. By contrast, there are often multiple choices for how to construct a max model for a given task; this ambiguity could be considered an argument against max models.

Finally, we have argued that at present, the plausibility of neural implementation cannot be used as an argument to arbitrate between decision rules. Instead, we believe that the outcome of model comparison at the behavioral level should guide the investigation of the neural basis of decision rules, and therefore that optimal, not max models, should be used as the starting point to create neural models.

• -We derive optimal decision rules for many multiple-item perceptual tasks.
• -“Max” rules almost never describe human data better than the optimal rule.
• -There is no evidence for people combining local decisions into a global decision.
• -The optimal rule should be taken as the basis for neural models.

Biography

Bernard Osgood Koopman (image from (Morse, 1982)