Transmission Heterogeneity and Autoinoculation in a Multisite Infection Model of HPV

Abstract

The human papillomavirus (HPV) is sexually transmitted and can infect oral, genital, and anal sites in the human epithelium. Here, we develop a multisite transmission model that includes autoinoculation, to study HPV and other multisite diseases. Under a homogeneous-contacts assumption, we analyze the basic reproduction number R₀, as well as type and target reproduction numbers, for a two-site model. In particular, we find that R₀ occupies a space between taking the maximum of next generation matrix terms for same site transmission and taking the geometric average of cross-site transmission terms in such a way that heterogeneity in the same-site transmission rates increases R₀ while heterogeneity in the cross-site transmission decreases it. Additionally, autoinoculation adds considerable complexity to the form of R₀. We extend this analysis to a heterosexual population, which additionally yields dynamics analogous to those of vector–host models. We also examine how these issues of heterogeneity may affect disease control, using type and target reproduction numbers.

1. Introduction

The basic reproduction number R₀ is an important quantity in infectious disease epidemiology, defined as the average number of secondary cases arising from a typical primary case in an entirely susceptible population [1, 2, 3]. Equivalently, it is often defined as a threshold parameter that controls the stability of the disease-free equilibrium: if R₀ < 1, an emergent disease will die off quickly, while if R₀ > 1, the disease will become epidemic [3, 4]. The values of R₀ vary greatly by disease [2], ranging from close to 1 for seasonal influenza to 5–7 for smallpox and polio to 12–18 for measles and pertussis. Mathematical modeling is used to estimate the basic reproduction number and other relevant quantities. In practice, R₀ is calculated as a threshold parameter that may not precisely correspond to the number of secondary cases per infection, especially in the case of an environmentally transmitted disease [4]. For example, virus shed into the environment may contribute to additional infections not directly attributable to a specific infected person. In practice, R₀ is typically calculated as the spectral radius of the next generation matrix [4].

The basic reproduction number also has implications for infection control. If a fraction of the population greater than $1-\frac{1}{R_0}$ is permanently protected from infection, such as through immunization at birth, the infection cannot become epidemic [2, 3, 5]. The concept of the basic reproduction number, at least in these infection control terms, can be extended to the type and target reproduction numbers [5, 6, 7]. If there are multiple host types, the type reproduction number for host type i is denoted T_i, and the infection can be controlled by protecting a greater fraction than $1-\frac{1}{T_i}$ of host type i, provided no other host acts as a reservoir for the infection. The type reproduction number is especially of interest for vector-borne and other multiple-species infections, and it can be extend to consider any subset of host types [5, 6]. The target reproduction number is a further generalization, in which specific pathways are targeted for control. This corresponds to considering only certain entries of the next generation matrix, instead of whole rows as is the case of the type reproduction number [7].

Here, we consider a class of diseases that may infect multiple sites in a host. Our motivating example is the human papillomavirus (HPV); it is well documented that oral and anogenital sites, although not completely independent, can become infected or clear the virus whether or not the other sites are infected and that autoinoculation may be an important pathway [8, 9, 10]. However, this model is also relevant to other sexually transmitted infections that affect multiple sites. Autoinoculation of the herpes simplex virus (HSV), which can infect genital, oral, anal and other epithelial sites, can occur, especially during the primary outbreak [11, 12, 13]. Chlamydia trachomatis is a bacterium that can infect the genital, gastrointestinal tract, pharynx, and the eyes. Transmission between sites can be direct (usually sexual) or through autoinoculation [14, 15, 16]. Infections by Candida species of yeast, Candida albicans in particular, can infect many sites, particularly oral and genital [17]. The model can also be used to consider multisite infections not typically spread by sexual interaction, such as Trichophyton (athlete’s foot) or conjunctivitis, and may possibly be extended to infections, such as molluscum and warts, that infect multiple, though not distinctly delineated, sites on the epithelium [18].

Deviation from the average, or heterogeneity, in various aspects of infectious disease models is important to the study of the basic reproduction number. Heterogeneity of populations, whether in terms of behavior, spatial distribution, or other characteristics, has been widely studied [19, 20, 3, 21] and has led to the development of such tools as mulitgroup modeling. Although the contexts are quite different, like Robertson et al. [22] we will consider heterogeneity among multiple transmission pathways. While Robertson et al. [22] considered heterogeneity in the direct and indirect pathways of waterborne cholera transmission, we consider differences within same-site and cross-site transmission of a multisite infectious agent.

In this paper we first develop and explore the dynamics of a multisite model with homogeneous contacts (homo- or pansexual population or a nonsexual infection), including analysis of the reproduction numbers and the effects of heterogeneity in the transmission pathways. We then extend this multisite model to one with heterogeneous contacts (heterosexual population) and see how the additional complexity translates into the reproduction numbers.

2. Two-site model with homogeneous contacts

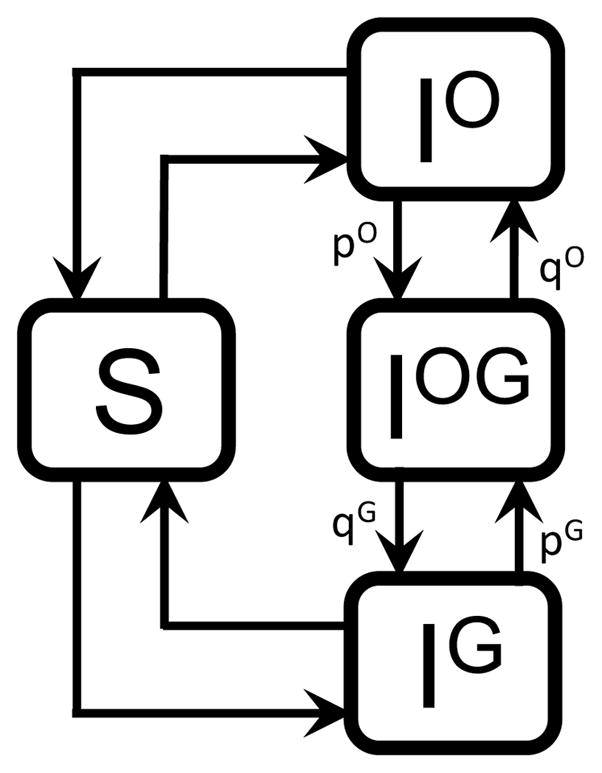
We first consider a model of a two-site sexually transmitted infection assuming that contacts are homogeneous in order to explore the dynamics of a two-site system without the complication of heterosexual contact. We assume that clearance of the infection does not induce immunity (SIS framework). We denote, without loss of generality, the infection sites as oral and genital. Denote the fraction of the population that is uninfected by S, the fraction infected at site X by I^X for X ∈{O, G}, and the fraction infected at both sites by I^OG. Let μ be the birth/death rate, γ^X the recovery rate of infection at site X, ν^XY the rate of autoinoculation from site X to site Y, and β^XY the transmission rate from site X on one individual to site Y on a second individual. As most of the diseases we consider here (including HPV) result in negligible mortality on transmission timescales (e.g. mortality due to HPV is typically on the longer timescale of cancer development later in life), we neglect death due to disease. All parameters are also assumed to be non-negative. The probability of two simultaneous events is assumed to be zero. A model schematic is presented in Figure 1, a summary of model parameters may be found in Table 1, and the following equations define our system:

$$\begin{array}{ll}\hfill \stackrel{.}{S}& =\mu +{\gamma }^G{I}^G+{\gamma }^O{I}^O-S\mu -S(({\beta }^{OO}+{\beta }^{OG})(I^O+I^{OG})+({\beta }^{GO}+{\beta }^{GG})(I^G+I^{OG})),\\ \hfill {\stackrel{.}{I}}^O& =S({\beta }^{OO}(I^O+I^{OG})+{\beta }^{GO}(I^G+I^{OG}))+{\gamma }^G{I}^{OG}-I^O({\nu }^{OG}+{\gamma }^O+\mu +{\beta }^{OG}(I^O+I^{OG})+{\beta }^{GG}(I^G+I^{OG}))\\ \hfill {\stackrel{.}{I}}^G& =S({\beta }^{OG}(I^O+I^{OG})+{\beta }^{GG}(I^G+I^{OG}))+{\gamma }^O{I}^{OG}-I^G({\nu }^{GO}+{\gamma }^G+\mu +{\beta }^{OO}(I^O+I^{OG})+{\beta }^{GO}(I^G+I^{OG}))\\ \hfill {\stackrel{.}{I}}^{OG}& =I^O({\nu }^{OG}+{\beta }^{OG}(I^O+I^{OG})+{\beta }^{GG}(I^G+I^{OG}))+I^G({\nu }^{GO}+{\beta }^{OO}(I^O+I^{OG})+{\beta }^{GO}(I^G+I^{OG}))-I^{OG}({\gamma }^O+{\gamma }^G+\mu ).\end{array}$$ (1)

Figure 1.

Multisite model schematic with rates.

Table 1.

List of parameters in the two-site infectious disease model with homogeneous contacts.

Symbol	Parameter
μ	Population birth/death rate
βOG	Transmission from oral site to genital site on another person
βGO	Transmission from genital site to oral site on another person
βOO	Transmission from oral site to oral site on another person
βGG	Transmission from genital site to genital site on another person
γO	Clearance of an oral infection
γG	Clearance of a genital infection
νOG	Autoinoculation of a genital site from the oral site
νGO	Autoinoculation of an oral site from the genital site

As written, the region {0 ≤ S ≤ 1, 0 ≤ I^O ≤ 1, 0 ≤ I^G ≤ 1, 0 ≤ I^OG ≤ 1} is positive invariant for the system, and all trajectories are subject to S + I^O + I^G + I^OG = 1. Some terms, such as I^Oβ^OGI^O, which reflects a sexual contact between two people with an oral infection that results in one person becoming infected genitally, are not typical in disease models but rather arise because of the multisite nature of the infection modeled.

A key feature of this class of models is autoinoculation. Here, we consider autoinoculation to be the infection of a new site on a host who currently has at least one infected site in the absence of contact with another infected individual. As noted in van den Driessche and Watmough [4], it is not always mathematically fixed whether particular terms—in this case, autoinoculation—should be considered new infections in the context of the next generation matrix. However, we argue that it is epidemiologically correct to consider autoinoculation to be a stage progression (incorporated in the V matrix) rather than a new infection (reflected in the F matrix). Consider an arbitrary individual, patient zero, with single-site infection who is introduced into a fully susceptible population. The basic reproduction number quantifies the number of secondary people infected by this initial infection over patient zero’s whole infective period. If we consider autoinoculation to be a new infection, autoinoculation might cause one secondary infection (at patient zero’s second site) but result in no new infected people. If we consider it to be a stage transfer, the infection at the new site may also contribute to secondary infections. The second interpretation gives a more epidemiologically meaningful R₀.

It is useful to note that this model is in some ways similar to other models that include more than one type of infectious class, e.g. multi-strain or multi-stage infectious disease models, in that there are multiple infected classes between which individuals can move, and some structural similarities in the terms for transmission and autoinoculation. However, there are several important differences. In this model, an infected of one type can generate an infection of either type (e.g. an oral infection can generate an oral or genital infection, unlike in a typical multi-strain model), and new infections do not all begin in a particular stage (as would be the case for a typical stage-progression model). In particular, the cross-transmission and autoinnoculation features of the model yield that, generically, there are no single-site equilibria (e.g. in which we have genital but not oral prevalence of disease), as there often are for multi-strain models [4]. This can be seen by setting I^O or I^G to 0 and observing that the only solution is the disease-free equilibrium.

2.1. Basic reproduction number

We begin with a derivation and analysis of the reproduction number for this model (eq. 1). The disease-free equilibrium is trivially (1, 0, 0, 0). We construct the next generation matrix K = FV⁻¹ as in van den Driessche and Watmough [4]. The rows of the F and V matrices correspond to the three infected compartments, namely I^O, I^G, and I^OG. The F matrix of new infections is

$$F=\left[\begin{array}{ccc}{\beta }^{OO}& {\beta }^{GO}& {\beta }^{OO}+{\beta }^{GO}\\ {\beta }^{OG}& {\beta }^{GG}& {\beta }^{OG}+{\beta }^{GG}\\ 0& 0& 0\end{array}\right],$$ (2)

and the V matrix of compartment transfer is

$$V=\left[\begin{array}{ccc}{\nu }^{OG}+{\gamma }^O+\mu & 0& -{\gamma }^G\\ 0& {\nu }^{GO}+{\gamma }^G+\mu & -{\gamma }^O\\ -{\nu }^{OG}& -{\nu }^{GO}& {\gamma }^O+{\gamma }^G+\mu \end{array}\right].$$ (3)

Then it is easy to show that V⁻¹ has the form

$$V^{-1}=\frac{1}{1-p^O{q}^O-p^G{q}^G}\left[\begin{array}{ccc}{\tau }^O(1-p^G{q}^G)& {\tau }^O{p}^G{q}^O& {\tau }^O{q}^O\\ {\tau }^G{p}^O{q}^G& {\tau }^G(1-p^O{q}^O)& {\tau }^G{q}^G\\ {\tau }^{OG}{p}^O& {\tau }^{OG}{p}^G& {\tau }^{OG}\end{array}\right],$$ (4)

where the τ are average waiting times in the compartments, neglecting further infection as we are considering behavior near the disease-free equilibrium, i.e.

$$\begin{array}{ll}\hfill {\tau }^O& =\frac{1}{{\gamma }^O+{\nu }^{OG}+\mu },\\ \hfill {\tau }^G& =\frac{1}{{\gamma }^G+{\nu }^{GO}+\mu },\\ \hfill {\tau }^{OG}& =\frac{1}{{\gamma }^O+{\gamma }^G+\mu },\end{array}$$ (5)

and the p and q are probabilities that the next compartment transfer will be to I^OG or from I^OG, respectively, i.e.

$$\begin{array}{l}{p}^O=\frac{{\nu }^{OG}}{{\gamma }^O+{\nu }^{OG}+\mu }={\nu }^{OG}{\tau }^O,\\ p^G=\frac{{\nu }^{GO}}{{\gamma }^G+{\nu }^{GO}+\mu }={\nu }^{GO}{\tau }^G,\\ q^O=\frac{{\gamma }^G}{{\gamma }^O+{\gamma }^G+\mu }={\gamma }^G{\tau }^{OG},\\ q^G=\frac{{\gamma }^O}{{\gamma }^O+{\gamma }^G+\mu }={\gamma }^O{\tau }^{OG}.\end{array}$$ (6)

It should be noted that 1–p^Oq^O –p^Gq^G > 0. We can heuristically understand the form of V⁻¹ in the following way (as in van den Driessche and Watmough [4]). In compartment I^OG, the probability of returning to that compartment in two moves is p^Oq^O + p^Gq^G by going either to I^O and back or I^G and back. The average amount of time spent in I^OG, assuming we start in, say, I^O, is

$${\tau }^{OG}[p^O+p^O(p^O{q}^O+p^G{q}^G)+p^O{(p^O{q}^O+p^G{q}^G)}^2+\cdots ]=\frac{{\tau }^{OG}{p}^O}{1-(p^O{q}^O+p^G{q}^G)}.$$ (7)

We can put this heuristic approach in more formal terms: consider the adjacency matrix A of the infected components of the directed graph depicted in Figure 2, where entry a_m,n is probability of entering component m from component n, for m, n ∈{I^O, I^G, I^OG}. Thus

Figure 2.

Multisite model graph.

$$A=\left[\begin{array}{ccc}0& 0& q^O\\ 0& 0& q^G\\ p^O& p^G& 0\end{array}\right].$$ (8)

Then

$$I+A+A^2+\cdots ={(I-A)}^{-1}=\frac{1}{1-p^O{q}^O-p^G{q}^G}\left[\begin{array}{ccc}1-p^G{q}^G& p^G{q}^O& q^O\\ p^O{q}^G& 1-p^O{g}^O& q^G\\ p^O& p^G& 1\end{array}\right].$$ (9)

This expression, with the inclusion of the τ parameters, leads directly to V⁻¹.

The next generation matrix K = F V⁻¹ thus has the form

$$K=\left[\begin{array}{ccc}{K}^{O\mid O}& K^{G\mid O}& K^{OG\mid O}\\ K^{O\mid G}& K^{G\mid G}& K^{OG\mid G}\\ 0& 0& 0\end{array}\right],$$ (10)

where

$$\begin{array}{l}{K}^{O\mid O}=\frac{{\beta }^{OO}{\tau }^O(1-p^G{q}^G)+{\beta }^{GO}{\tau }^G{p}^O{q}^G+({\beta }^{OO}+{\beta }^{GO}){\tau }^{OG}{p}^O}{1-p^O{q}^O-p^G{q}^G},\\ K^{G\mid O}=\frac{{\beta }^{OO}{\tau }^O{p}^G{q}^O+{\beta }^{GO}{\tau }^G(1-p^O{q}^O)+({\beta }^{OO}+{\beta }^{GO}){\tau }^{OG}{p}^G}{1-p^O{q}^O-p^G{q}^G},\\ K^{OG\mid O}=\frac{{\beta }^{OO}{\tau }^O{q}^O+{\beta }^{GO}{\tau }^G{q}^G+({\beta }^{OO}+{\beta }^{GO}){\tau }^{OG}}{1-p^O{q}^O-p^G{q}^G},\\ K^{O\mid G}=\frac{{\beta }^{OG}{\tau }^O(1-p^G{q}^G)+{\beta }^{GG}{\tau }^G{p}^O{q}^G+({\beta }^{OG}+{\beta }^{GG}){\tau }^{OG}{p}^O}{1-p^O{q}^O-p^G{q}^G},\\ K^{G\mid G}=\frac{{\beta }^{OG}{\tau }^O{p}^G{q}^O+{\beta }^{GG}{\tau }^G(1-p^O{q}^O)+({\beta }^{OG}+{\beta }^{GG}){\tau }^{OG}{p}^G}{1-p^O{q}^O-p^G{q}^G},\\ K^{OG\mid G}=\frac{{\beta }^{OG}{\tau }^O{q}^O+{\beta }^{GG}{\tau }^G{q}^G+({\beta }^{OG}+{\beta }^{GG}){\tau }^{OG}}{1-p^O{q}^O-p^G{q}^G}.\end{array}$$ (11)

The elements of the next generation matrix have a straightforward biological interpretation: K^X|Y is the expected number of secondary cases of infection at site Y produced by one individual originally infected at site X, assuming an otherwise susceptible population. Because two events cannot happen simultaneously, trajectories near the disease-free equilibrium have I^OG = 0, and so all terms of the form K^X|OG are zero. It is important to note here that $K^{O\mid O}\ne R_0^O$and $K^{G\mid G}\ne R_0^G$, where $R_0^O={\beta }^{OO}{\tau }^O$ and $R_0^G={\beta }^{GG}{\tau }^G$ are the basic reproduction numbers of the single site SIS models, except in the case of no autoinoculation. In this model, without loss of generality, an individual with only a genital infection originally can autoinoculate their oral site and spread infection from either, which adds significant complexity to the terms of the next generation matrix.

It is also useful to note here that from the form of the elements of the next generation matrix, we see it is possible to have $R_0^O<1$ and $R_0^G<1$, and yet have the overall R₀ > 1, depending on the rates of autoinoculation and cross transmission. This can happen for biologically reasonable ranges of parameters. Consider β^OO = β^OG = β^GO = β^GG = 1, ν^OG = ν^GO = 1, γ^O = γ^G = 2, and μ = 0; then $R_0^O=R_0^G=\frac{1}{2}$ while $R_0=\frac{3}{2}$.

We find that the spectral radius of the next generation matrix (eq. 10) is

$$R_0=\frac{1}{2}\left(K^{O\mid O}+K^{G\mid G}\right)+\frac{1}{2}\sqrt{{(K^{O\mid O}+K^{G\mid G})}^2+4(K^{G\mid O}{K}^{O\mid G}-K^{O\mid O}{K}^{G\mid G})}.$$ (12)

It is helpful here to think of K^O|O + K^G|G as the R₀ of the system under the balance condition that K^O|OK^G|G = K^O|GK^G|O, that is when the product of the same-site transmission terms of the next generation matrix is equal to the product of the analogous cross-site terms. Hence, more generally, R₀ is K^O|O + K^G|G modified by a term that accounts for how balanced same-site and cross-site infections are, which naturally leads us to the question of heterogeneity. The balance term is, in fact, a measure of balance in same-site and cross-site transmission rates, not just in the expectations of number of infected as a cursory inspection of eq. 12 would suggest:

$$\begin{array}{l}{K}^{O\mid G}{K}^{G\mid O}-K^{O\mid O}{K}^{G\mid G}=\frac{({\beta }^{OG}{\beta }^{GO}-{\beta }^{OO}{\beta }^{GG})({\tau }^O{\tau }^G+p^O{\tau }^G{\tau }^{OG}+p^G{\tau }^O{\tau }^{OG})}{1-p^O{q}^O-p^G{q}^G}\\ =\frac{({\beta }^{OG}{\beta }^{GO}-{\beta }^{OO}{\beta }^{GG}){\tau }^O{\tau }^G(1+({\nu }^{OG}+{\nu }^{GO}){\tau }^{OG})}{1-p^O{q}^O-p^G{q}^G}.\end{array}$$ (13)

Although all parameters affect the value of R₀, it is the relationship between the transmission parameters that affects the structure of R₀, e.g. whether R₀ is taking the maximum of the same-site terms, the geometric average of the cross-site terms, or some sort of intermediate behavior. Hence, understanding the effects of heterogeneity in the transmission parameters is necessary to understand the dynamics of the model.

In the next sections, we explore the how the two major unique features of this model—(i) the interplay of same- and cross-site transmission and (ii) autoinoculation—each affect R₀, focusing first on how heterogeneity in same-site and cross-site transmission affects R₀ and related threshold parameters. We then explore how the added complexity derived from autoinoculation may affect estimates of R₀ in practice.

2.2. Limiting cases and transmission heterogeneity

The basic reproduction number displays some interesting limiting behavior. As either K^G|O or K^O|G, but not necessarily both, go to 0, R₀ goes to max(K^O|O, K^G|G). As both K^O|O and K^G|G go to 0, R₀ goes to $\sqrt{K^{G\mid O}{K}^{O\mid G}}$. Hence, the basic reproduction number can be thought of as occupying a space between taking the maximum and taking a geometric average, displaying behavior more similar to one or the other depending on the type and strength of transmission pathways. Note that these limiting cases are already suggestive of the effect of heterogeneity on the same-site and cross-site terms, which we will explore further below. Considering a different limiting case, we note that as the autoinoculation parameters ν^GO and ν^OG go to zero, the basic reproduction number becomes

$$\frac{1}{2}({\beta }^{OO}{\tau }^O+{\beta }^{GG}{\tau }^G)+\frac{1}{2}\sqrt{{({\beta }^{OO}{\tau }^O+{\beta }^{GG}{\tau }^G)}^2+4{\tau }^O{\tau }^G({\beta }^{GO}{\beta }^{OG}-{\beta }^{OO}{\beta }^{GG})},$$ (14)

which is a significant reduction in complexity.

Without making these significantly simplifying assumptions, we can still consider heterogeneity, as noted above, in the same-site and cross-site terms of the next generation matrix. Heterogeneity can be seen as a kind of weakly limiting case.

Proposition 2.1

For a fixed total K^O|G + K^G|O, R₀ is largest when K^O|G = K^G|O. For a fixed total K^O|O + K^G|G, R₀ is smallest when K^O|O = K^G|G.

This proposition is clear by basic calculus on eq. 12. For a fixed sum K^O|G + K^G|O, the product K^O|GK^G|O is largest when K^O|G = K^G|O, meaning that R₀ is largest when the two sites have the same expected number of secondary cross-site infections. So, R₀ is large when the cross-site terms are similar and is small when they are different. Similarly, in the formula for R₀ (eq. 12), the product K^O|OK^G|G has the opposite sign from K^O|GK^G|O, meaning that, for a fixed sum K^O|O + K^G|G, heterogeneity in the terms increase R₀. That is, R₀ is large when the expected number of same-site infections is very different for the oral and genital sites and small when they are similar. Heterogeneity in the expected site-specific secondary infections, i.e. elements of the next generation matrix, thus, has a very different effect for same-site than for cross-site infection.

To better understand the effect of heterogeneity in the biological transmission parameters, we derive some analytic results for a special limiting case—identical sites—and then consider, through simulation, how the general model deviates from the limiting case.

2.2.1. Identical site model

In order to simplify the analysis, consider the scenario in which the two sites, although they may have different transmission parameters, have identical clearance and autoinoculation parameters. While a simplification for many diseases, this one is biologically realistic for infections such as athlete’s foot or conjunctivitis.

For this section, γ^O = γ^G and ν^OG = ν^GO. Hence, τ^O = τ^G, p^O = p^G, and q^O = q^G. We drop the superscripts for the rest of this section, except from τ^OG, which is distinct from τ^O = τ^G = τ. Here

$$K^{O\mid O}+K^{G\mid G}=\frac{1}{1-2pq}[({\beta }^{OO}+{\beta }^{OG}+{\beta }^{GO}+{\beta }^{GG})p{\tau }^{OG}+({\beta }^{OO}+{\beta }^{GG})\tau (1-pq)+({\beta }^{GO}+{\beta }^{OG})\tau pq]$$ (15)

and

$$K^{O\mid G}{K}^{G\mid O}-K^{O\mid O}{K}^{G\mid G}=\frac{({\beta }^{OG}{\beta }^{GO}-{\beta }^{OO}{\beta }^{GG})\tau (\tau +2p{\tau }^{OG})}{1-2pq}$$ (16)

Proposition 2.2

For a fixed total transmission β^OO + β^GO + β^OG + β^GG = k, the extrema of R₀ of the identical site model are on the boundary of {β^OO ≥ 0, β^GG ≥ 0, β^OG ≥ 0, β^GO ≥ 0}. Moreover, R₀ is constant on the planes described by { ${\beta }^{OG}+{\beta }^{GG}=\frac{k}{2}$} and { ${\beta }^{OG}+{\beta }^{OO}=\frac{k}{2}$}. These planes partition the constrained parameter space into two regions of higher and two regions of lower R₀.

The proof uses the method of Lagrange multipliers and is left to the appendix. These partitioning planes contain three lines of interest: {β^OO = β^GG, β^OG = β^GO}, {β^OO = β^GO, β^GG = β^OG}, and {β^OO = β^OG, β^GG = β^GO}. Along these lines the following are true respectively: K^O|O = K^G|G and K^O|G = K^G|O; K^O|O = K^G|O and K^G|G = K^O|G; and K^O|O = K^O|G and K^G|G = K^G|O.

We wish to visualize the values of R₀ on the surface β^OO + β^GO + β^OG + β^GG = k in the four dimensional transmission parameter space. In Figure 3, we plot slices of two three-dimensional projections of this surface, with and without the partitioning planes. In this case, the values of R₀ are symmetric in the β^OG and β^GO coordinates as well as in the β^OO and β^GG coordinates. Simulations were coded in MATLAB [23]. For the purposes of illustration, clearance (γ) and autoinoculation (ν) parameters were set to 1 (matching realistic HPV clearance times of about 1 year [24, 25] and assuming relatively rare autoinoculation events), and transmission rates are as given in the axes of Figure 3.

Figure 3.

Heat map of R₀ under the identical site assumptions.

We see that, in the (β^OO, β^GG)-plane (the lower boundary of the figure), R₀ has a minimum, and, in the (β^OG, β^GO)-plane (the z-axis in the figure) R₀ has a maximum. These results are consistent with our analysis above of the impact of heterogeneity of the same-site and cross-site terms of the next generation matrix, highlighting the fact that R₀ is maximized by heterogeneity in same-site transmission and homogeneity in cross-site transmission.

In fact, the planes partition the space into four regions, two of which have larger R₀ (toward primarily same-site transmission) and two of which have smaller R₀ (toward primarily cross-site transmission). The global extrema of R₀ are achieved when there is only one transmission pathway. Indeed, if all transmission is in one pathway with rate k, then eq 12 simplifies (via eqs 15 and 16) to

$$R_0=\frac{k(p{\tau }^{OG}+(1-pq)\tau )}{1-2pq}$$ (17)

if that pathway is same-site and

$$R_0=\frac{k(p{\tau }^{OG}+pq\tau )}{1-2pq}$$ (18)

if that pathway is cross-site. On the partitioning planes of Proposition 2.2, we have

$$R_0=\frac{k(p{\tau }^{OG}+\tau /2)}{1-2pq}.$$ (19)

2.2.2. Deviations from the identical site model

The equations to solve for the partitioning planes in the general case are intractable. However, numerical simulation gives a reasonably clear picture as to how R₀ behaves under deviations from the identical site model. We examine the effect that changing the autoinoculation and recovery parameters has on the values of R₀ in the constrained transmission parameter space.

Increasing $\frac{{\gamma }^G}{{\gamma }^O}$ from 1 (increasing γ_G to 1.2 while keeping γ^O and ν^OG = ν^GO constant) moves the intersection of the three lines of partitioning planes so that β^OO < β^OG = β^GO < β^GG as seen in Figure 4, which has the same parameters as Figure 3 except for a larger γ^G. Here, the values of R₀ are symmetric in the β^OG and β^GO coordinates, but, unlike the identical site model, the values are not symmetric in β^OO and β^GG. The planes move to balance the faster clearance in the compartment with a higher transmission rate. Note that by increasing one clearance parameter relative to Figure 3, R₀ is reduced overall. Increasing both parameters but not changing their ratio would have rescaled the values of R₀ in Figure 3 but not broken its symmetries.

Figure 4.

Heat map of R₀ for γ_G > γ_O.

Increasing $\frac{{\nu }^{OG}}{{\nu }^{GO}}$ from 1 (increasing ν^OG to 1.2) and keeping the recovery parameters constant, moves moves the intersection of the three lines of the partitioning planes so that β^OG < β^GG = β^OO < β^GO as in Figure 5. Now, the values of R₀ are symmetric in β^OO and β^GG but no longer in β^OG and β^GO. Here, the surface moves to balance the movement in either direction along the infection cycles; that is, we compensate for an increased ν^OG by also increasing its complement in the cycle, β^GO, and similarly for the other direction. In Figure 5, we see that, as we have only increased one autoinoculation parameter relative to Figure 3, autoinoculation acts like transmission to increase R₀ overall, which is as expected.

Figure 5.

Heat map of R₀ for ν_OG > ν_GO.

In the identical site model, the three lines of the partitioning planes corresponded to equality of pairs of next generation matrix terms. These equalities do not hold along the corresponding lines of the partitioning planes when γ^O ≠ γ^G or ν^OG ≠ ν^GO.

Although the position and orientation of the partitioning planes change, the overall qualitative behavior does not. That is, regardless of the values of the recovery and autoinoculation parameters, the extrema of R₀ lie on the boundaries of the positive parameter space, and moving off the partitioning plane increases or decreases R₀ depending on which of the four regions the movement is into. Moving toward primarily same-site transmission increases R₀ while moving toward primarily cross-site transmission decreases it.

2.3. Type and target reproduction numbers

Let us next consider the type reproduction number for, without loss of generality, the genital site in the full two-site model (eq. 1), calculated as in Shuai et al. [7]. The type reproduction number for genital infections is, provided K_OO < 1,

$$\begin{array}{l}{T}_G=\frac{K^{O\mid G}{K}^{G\mid O}+K^{G\mid G}(1-K^{O\mid O})}{1-K^{O\mid O}}\\ =K^{G\mid G}+\frac{K^{O\mid G}{K}^{G\mid O}}{1-K^{O\mid O}}.\end{array}$$ (20)

That is, if the oral site is not an infection reservoir, here meaning that the expected number of oral infections from an oral infection is less than one, then the infection can be controlled by permanently preventing genital infection in a fraction of the population greater than

$$1-\frac{1}{T_G}=\frac{(K^{G\mid G}+K^{O\mid O}-1)+(K^{G\mid O}{K}^{O\mid G}-K^{O\mid O}{K}^{G\mid G})}{K^{G\mid G}+(K^{G\mid O}{K}^{O\mid G}-K^{O\mid O}{K}^{G\mid G})}.$$ (21)

Note the reappearance of the balance term. Further, the possible deleterious effects of model misspecification can be seen here. If one is using a model with only genital infection, one will estimate the fraction of the population in which need to prevent genital infections as $\frac{{\beta }^{GG}{\tau }^G-1}{{\beta }^{GG}{\tau }^G}$, which may differ significantly from the true fraction. We should be careful to realize, however, that the estimates of β^GG here may be biased as another result of misspecification, which makes direct comparison of the fractions under the two models difficult.

Returning to the two-site model, if we seek to control only genital-to-genital infections, perhaps through condom use, the target reproduction number is

$$T_{GG}=\frac{(1-K^{O\mid O})K^{G\mid G}}{1-K^{O\mid O}-K^{O\mid G}{K}^{G\mid O}},$$ (22)

provided K^O|O + K^O|GK^G|O < 1. That is, the infection will be controlled if we prevent genital to genital infection by a fraction of more than

$$1-\frac{1}{T_{GG}}=\frac{(K^{G\mid G}+K^{O\mid O}-1)+(K^{G\mid O}{K}^{O\mid G}-K^{O\mid O}{K}^{G\mid G})}{K^{G\mid G}-K^{O\mid O}{K}^{G\mid G}}.$$ (23)

That this latter endeavor is more challenging is seen in the reduction in the denominator between the type and target reproduction numbers described here. The two numbers are the same only if either K^O|G or K^G|O is zero. That these fractions are the same when K^G|O is zero is sensible, since all genital transmission in that case will be same-site transmission. It is not so obviously true, heuristically, in the case that K^O|G is zero.

We also include the target reproduction number for either of the cross-site transmissions solely. The target reproduction number, provided both K^O|O and K^G|G are less than 1, is

$$T_{GO}=\frac{K^{G\mid O}{K}^{O\mid G}}{(1-K^{O\mid O})(1-K^{G\mid G})},$$ (24)

so that the infection will be controlled if we prevent genital to oral transmission by more than

$$1-\frac{T}{T_{GO}}=\frac{(K^{G\mid G}+K^{O\mid O}-1)+(K^{G\mid O}{K}^{O\mid G}-K^{O\mid O}{K}^{G\mid G})}{K^{G\mid O}{K}^{O\mid G}}.$$ (25)

Again, to control only genital to oral transmission is easier than controlling all genital infections, and we see that the denominators of eqs. 23 and 25 add up to the denominator of eq. 21. The latter fact is a nice way of expressing that, in this case,

$$T_G=\frac{T_{GO}(T_{GG}-1)+T_{GG}(T_{GO}-1)}{T_{GO}{T}_{GG}-1}.$$ (26)

In each of T_G, T_GG, and T_OG, K^O|G and K^G|O only appear as a product. That each depends upon the product instead of the sum or some other function of K^O|G and K^G|O cannot be easily understood without this analysis. This result has implications for disease control. For instance, a product can more effectively be reduced by reducing only one of the terms than a sum can be. Further, the trade-off structure, if one were able to reduce one term at the expense of another, is very different. That K^O|G and K^G|O only appear as a product also has implications for the impact of heterogeneity in the terms as it did with the basic reproduction number. In each case, heterogeneity in the cross-site terms decreases the reproduction number. The impact of heterogeneity in K^O|O and K^G|G is less clear for T_G and T_GG, though heterogeneity in these same-site terms, unlike for the basic reproduction number, decreases T_GO.

2.4. Effects of autoinoculation

In addition to the effects of transmission pathway heterogeneity, we noted in eqs. 1 and 11 that autoinoculation is a key feature of the model, adding significant complexity to both the model equations and R₀. Autoinoculation has been noted to be a potentially important pathway for cervical and oral infections [10], and, indeed, a history of warts at different sites (including a range of non-genital sites) has been shown to be associated with increased risk of genital HPV infections [26]. However, the role of autoinculation in oral and genital infections is not yet fully understood. The added complexity that autoinoculation brings to R₀ also brings the potential for significant misestimation of R₀ if the underlying disease process includes autoinoculation but a model neglecting the autoinoculation pathway is used for fitting the data. In eq. 11 in particular, we see that when the autoinoculation terms are nonzero, the actual total same-site cases generated has the potential to be significantly higher than would be expected based on the single-site R₀s that do not consider autoinoculation, i.e. we are in general likely to have $K^{O\mid O}\ne R_0^O$ and $K^{G\mid G}\ne R_0^G$.

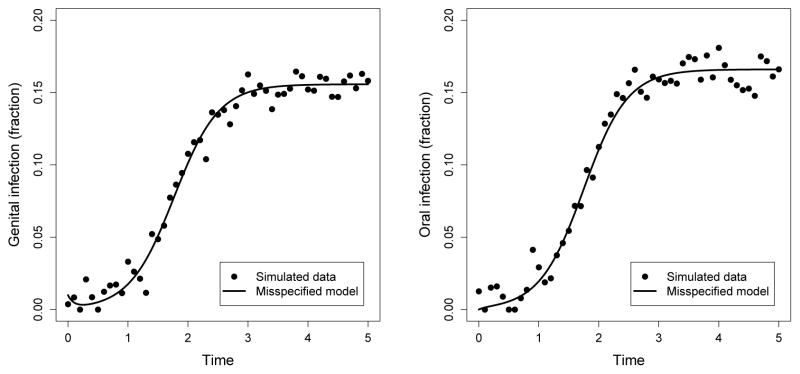
To illustrate the potential for errors in R₀ estimates due to model misspecification, we generated simulated data using the full model (including autoinoculation) and normally distrbuted error, and then fitted this data using least squares, assuming a reduced model with ν^OG = ν^GO = 0. For all model simulations we assumed background birth/deaths in the population were negligible (μ = 0) for simplicity. As shown in Figure 6, both models yield quite similar trajectories for both genital and oral prevalence, however the R₀ of the model underlying the data was 4.0 while the estimate of the misspecified (no autoinoculation) model was only 1.25. In general, we found that simulations for a range of parameter values underestimated R₀ when autoinoculation was not included in the model. The full model parameters in Figure 6, which were not based on data but rather were chosen to illustrate the potential for mispecification within biologically reasonable bounds, were: β^OO = 3, β^OG = 1, β^GO = 0, β^GG = 1, γ^O = 2, γ^G = 2, ν^OG = 5, ν^GO = 4). While values for the transmission and autoinoculation parameters are largely unknown, these reflect what information there is on clearance times [27, 28, 29]. The resulting estimates for the reduced model when fitted to the data from the full model were β^OO = 11.5, β^OG = 9.9, β^GO = 2.0, β^GG = 0, γ^O = 10.6, γ^G = 8.4. To be sure this effect was a result of misspecification rather than of fitting, we also fit the full model to the data, yielding nearly identical fits as for the misspecified model and the following parameter estimates: β^OO = 2.5, β^OG = 1.3, β^GO = 0.3, β^GG = 0.9, γ^O = 2.0, γ^G = 1.9, ν_OG = 4.3, ν^GO = 4.4. While we do not recover the original parameters exactly, the R₀ estimate of 4.1 is a good approximation.

Figure 6.

Fits of a misspecified model assuming ν^OG = ν^GO = 0 (lines) to simulated genital and oral prevalence data generated from the full model (dots). Genital infections (left) and oral infections (right) over time (years) match closely for both the full model and misspecified model. The true R₀ = 4 for the full model used to generate the data. However, the estimate for R₀ using the full model (not shown) was 4.1, while the estimate using the misspecified model was 1.25.

3. Two-site model with heterogeneous contacts

Here we extend the two-site model with homogeneous contacts (homo- or pansexual population or nonsexual infection) to one with heterogeneous contacts (in particular, a heterosexual population). This model has many analogous features to the model homogeneous contacts, but also has an added layer of complexity from the vector–host-like dynamics (since new infections can only occur from a member of the opposite sex). For sex i ∈ {M, F} with oral (O) and genital (G) sites and i ≠ j, we have the following equations:

$$\begin{array}{ll}\hfill {\stackrel{.}{S}}_i& =\frac{\mu }{2}+{\gamma }_i^G{I}_i^G+{\gamma }_i^O{I}_i^O-S_i\mu -S_i({\beta }_{ji}^{OO}(I_j^O+I_j^{OG})+{\beta }_{ji}^{GO}(I_j^G+I_j^{OG}))-S_i({\beta }_{ji}^{OG}(I_j^O+I_j^{OG})+{\beta }_{ji}^{GG}(I_j^G+I_j^{OG})),\\ \hfill {\stackrel{.}{I}}_i^O& =S_i({\beta }_{ji}^{OO}(I_j^O+I_j^{OG})+{\beta }_{ji}^{GO}(I_j^G+I_j^{OG}))+{\gamma }_i^G{I}_i^{OG}-I_i^O({\nu }_i^{OG}+{\gamma }_i^O+\mu +{\beta }_{ji}^{OG}(I_j^O+I_j^{OG})+{\beta }_{ji}^{GG}(I_j^G+I_j^{OG})),\\ \hfill {\stackrel{.}{I}}_i^G& =S_i({\beta }_{ji}^{OG}(I_j^O+I_j^{OG})+{\beta }_{ji}^{GG}(I_j^G+I_j^{OG}))+{\gamma }_i^O{I}_i^{OG}-I_i^G({\nu }_i^{GO}+{\gamma }_j^G+\mu +{\beta }_{ji}^{OO}(I_j^O+I_j^{OG})+{\beta }_{ji}^{GO}(I_j^G+I_j^{OG})),\\ \hfill {\stackrel{.}{I}}_i^{OG}& =I_i^O({\nu }_i^{OG}+{\beta }_{ji}^{OG}(I_j^O+I_j^{OG})+{\beta }_{ji}^{GG}(I_j^G+I_j^{OG}))+I_i^G({\nu }_i^{GO}+{\beta }_{ji}^{OO}(I_j^O+I_j^{OG})+{\beta }_{ji}^{GO}(I_j^G+I_j^{OG}))-I_i^{OG}({\gamma }_i^O+{\gamma }_i^G+\mu ).\end{array}$$ (27)

Here, the parameters are the same as in Table 1 except that we additional need to denote that transmission as originating with one of the sexes. In particular, ${\beta }_{ij}^{XY}$ are transmission rates from site X in sex i to site Y in sex j and, as before, ${\gamma }_i^X$ are clearance rates for sex i and site X and ${\nu }_i^{XY}$ are autoinoculation rates in sex i from site X to site Y. The disease free-equilibrium is $S_F=S_M=\frac{1}{2}$. Then the matrix F has the form

$$F=\left[\begin{array}{cc}0& F_{ji}\\ F_{ij}& 0\end{array}\right],$$ (28)

where

$$F_{ji}=\frac{1}{2}\left[\begin{array}{ccc}{\beta }_{ji}^{OO}& {\beta }_{ji}^{GO}& {\beta }_{ji}^{OO}+{\beta }_{ji}^{GO}\\ {\beta }_{ji}^{OG}& {\beta }_{ji}^{GG}& {\beta }_{ji}^{OG}+{\beta }_{ji}^{GG}\\ 0& 0& 0\end{array}\right].$$ (29)

The V matrix has the form

$$V=\left[\begin{array}{cc}{V}_i& 0\\ 0& V_j\end{array}\right],$$ (30)

where

$$V_i=\left[\begin{array}{ccc}{\nu }_i^{OG}+{\gamma }_i^O+\mu & 0& -{\gamma }_i^G\\ 0& {\nu }_i^{GO}+{\gamma }_i^G+\mu & -{\gamma }_i^O\\ -{\nu }_i^{OG}& -{\nu }_i^{GO}& {\gamma }_i^O+{\gamma }_i^G+\mu \end{array}\right].$$ (31)

Then V ⁻¹ has the form

$$V^{-1}=\left[\begin{array}{cc}{V}_i^{-1}& 0\\ 0& V_j^{-1}\end{array}\right],$$ (32)

where

$$V_i^{-1}=\frac{1}{1-p_i^O{q}_i^O-p_i^G{q}_i^G}\left[\begin{array}{ccc}{\tau }_i^O(1-p_i^G{q}_i^G)& {\tau }_i^O{p}_i^G{q}_i^O& {\tau }_i^O{q}_i^O\\ {\tau }_G{p}_i^O{q}_i^G& {\tau }_i^G(1-p_i^O{q}_i^O)& {\tau }_G{q}_i^G\\ {\tau }_i^{OG}{p}_i^O& {\tau }_i^{OG}{p}_i^G& {\tau }_i^{OG}\end{array}\right]$$ (33)

and the τ are average waiting times, neglecting further infection, in the compartments (as in eq. 5), and the p_i and q_i are probabilities for sex i that the next compartment transfer will be to go to $I_i^{OG}$ or from $I_i^{OG}$, respectively (as in eq. 6).

The next generation matrix K = FV ⁻¹ thus has the form

$$F{V}^{-1}=\left[\begin{array}{cc}0& F_{ji}{V}_j^{-1}\\ F_{ji}{V}_i^{-1}& 0\end{array}\right],$$ (34)

where

$$F_{ij}{V}_i^{-1}=\left[\begin{array}{ccc}{K}_{ij}^{O\mid O}& K_{ij}^{G\mid O}& K_{ij}^{OG\mid O}\\ K_{ij}^{O\mid G}& K_{ij}^{G\mid G}& K_{ij}^{OG\mid G}\\ 0& 0& 0\end{array}\right]$$ (35)

and

$$K_{ij}^{O\mid O}=\frac{{\beta }_{ij}^{OO}{\tau }_i^O(1-p_i^G{q}_i^G)+{\beta }_{ij}^{GO}{\tau }_i^G{p}_i^O{q}_i^G+({\beta }_{ij}^{OO}+{\beta }_{ij}^{GO}){\tau }_i^{OG}{p}_i^O}{2(1-p_i^O{q}_i^O-p_i^G{q}_i^G)},$$ (36)

$$K_{ij}^{G\mid O}=\frac{{\beta }_{ij}^{OO}{\tau }_i^O{p}_i^G{q}_i^O+{\beta }_{ij}^{GO}{\tau }_i^G(1-p_i^O{q}_i^O)+({\beta }_{ij}^{OO}+{\beta }_{ij}^{GO}){\tau }_i^{OG}{p}_i^G}{2(1-p_i^O{q}_i^O-p_i^G{q}_i^G)},$$ (37)

$$K_{ij}^{OG\mid O}=\frac{{\beta }_{ij}^{OO}{\tau }_i^O{q}_i^O+{\beta }_{ij}^{GO}{\tau }_i^G{q}_i^G+({\beta }_{ij}^{OO}+{\beta }_{ij}^{GO}){\tau }_i^{OG}}{2(1-p_i^O{q}_i^O-p_i^G{q}_i^G)},$$ (38)

$$K_{ij}^{O\mid G}=\frac{{\beta }_{ij}^{OG}{\tau }_i^O(1-p_i^G{q}_i^G)+{\beta }_{ij}^{GG}{\tau }_i^G{p}_i^O{q}_i^G+({\beta }_{ij}^{OG}+{\beta }_{ij}^{GG}){\tau }_i^{OG}{p}_i^O}{2(1-p_i^O{q}_i^O-p_i^G{q}_i^G)},$$ (39)

$$K_{ij}^{G\mid G}=\frac{{\beta }_{ij}^{OG}{\tau }_i^O{p}_i^G{q}_i^O+{\beta }_{ij}^{GG}{\tau }_i^G(1-p_i^O{q}_i^O)+({\beta }_{ij}^{OG}+{\beta }_{ij}^{GG}){\tau }_i^{OG}{p}_i^G}{2(1-p_i^O{q}_i^O-p_i^G{q}_i^G)},$$ (40)

$$K_{ij}^{OG\mid G}=\frac{{\beta }_{ij}^{OG}{\tau }_i^O{q}_i^O+{\beta }_{ij}^{GG}{\tau }_i^G{q}_i^G+({\beta }_{ij}^{OG}+{\beta }_{ij}^{GG}){\tau }_i^{OG}}{2(1-p_i^O{q}_i^O-p_i^G{q}_i^G)}.$$ (41)

Hence, we find the basic reproduction number is

$$R_0=\sqrt{\frac{1}{2}{R}^2+\frac{1}{2}\sqrt{R^4-4\left(K_{FM}^{O\mid O}{K}_{FM}^{G\mid G}-K_{FM}^{O\mid G}{K}_{FM}^{G\mid O}\right)\left(K_{MF}^{O\mid O}{K}_{MF}^{G\mid G}-K_{MF}^{O\mid G}{K}_{MF}^{G\mid O}\right)}},$$ (42)

where

$$R^2=K_{FM}^{O\mid O}{K}_{MF}^{O\mid O}+K_{FM}^{G\mid G}{K}_{MF}^{G\mid G}+K_{FM}^{O\mid G}{F}_{MF}^{G\mid O}+K_{FM}^{G\mid O}{F}_{MF}^{O\mid G}.$$ (43)

We see that the quantity R is the R₀ of the system under the either (or both) of the balance conditions $K_{FM}^{O\mid O}{K}_{FM}^{G\mid G}=K_{FM}^{O\mid G}{K}_{FM}^{G\mid O}$ and $K_{MF}^{O\mid O}{K}_{MF}^{G\mid G}=K_{MF}^{O\mid G}{K}_{MF}^{G\mid O}$. The balance terms appearing in the form of R₀ are analogous to the one we saw in the pansexual model above, but we now have one term for each sex instead of one for the whole population.

The influence of the two-site and the heterosexual aspects of the heterosexual two-site model can be clearly seen in the form of R₀ here. The hallmark of the one-site heterosexual transmission model, similarly to vector–host models, is the geometric average of the cross-sex elements of the next generation matrix: for the the model

$$\begin{array}{ll}\hfill {\stackrel{.}{S}}_i& =\frac{\mu }{2}-\mu S_i+{\gamma }_i{I}_i-S_i{\beta }_{ji}{I}_j,\\ \hfill {\stackrel{.}{I}}_i& =S_i{\beta }_{ji}{I}_j-({\gamma }_i+{\mu }_i)I_i,\end{array}$$ (44)

we find

$$R_0=\sqrt{K_{MF}{K}_{FM}}=\frac{1}{2}\sqrt{({\beta }_{FM}{\tau }_F)({\beta }_{MF}{\tau }_M)},$$ (45)

where ${\tau }_i=\frac{1}{{\gamma }_i+\mu }$. In the two-site heterosexual model, although we do not have direct geometric averaging, some patterns are preserved: in eq. 42, products (cycles) of the cross-sex elements replace the terms of the homogeneous-contacts model (eq. 12) and a square root is taken at the end, as with geometric averaging. In fact, we recover geometric averaging under certain limiting cases, as shown below.

3.1. Limiting cases

Here we consider two limiting cases: i) independence of sites and ii) one site is a “dead-end” infection. In the first case, we assume that there is no cross-transmission (β^OG = β^GO = 0) and no autoinoculation (ν^OG = ν^GO = 0). Under these assumptions, the two sites are essentially independent as K^O|G = K^G|O = 0, and the basic reproduction number is

$$R_0=max\left(\sqrt{K_{FM}^{O\mid O}{K}_{MF}^{O\mid O}},\sqrt{K_{FM}^{G\mid G}{K}_{MF}^{G\mid G}}\right)=max(R_0^O,R_0^G).$$ (46)

That is, since there is no autoinoculation, R₀ is the maximum of the of the basic reproduction number for the model with a heterosexual population and only oral sites $R_0^O$ and the basic reproduction number of the model with only genital sites $R_0^G$.

In the second case, we assume, without loss of generality, that the oral sites are a “dead-end” infection, that is, oral sites do not transmit the infection (β^OG = β^OO = ν^OG = 0). Then K^O|O = K^O|G = 0, and, letting ${\tau }_i=\frac{1}{{\gamma }_i+\mu }$,

$$R_0=\sqrt{K_{FM}^{G\mid G}{K}_{MF}^{G\mid G}}=\frac{1}{2}\sqrt{({\beta }_{FM}^{GG}{\tau }_F)({\beta }_{MF}^{GG}{\tau }_M)}$$ (47)

under these assumptions. Thus, despite ν_GO ≡ 0, R₀ is the same (c.f. eq. 45) as the basic reproduction number of the model with only genital sites, $R_0^G$. This result is intuitive, as additional time spent in compartments I^O or I^OG over the infective lifetime will not produce any additional infections.

3.2. Type reproduction number

The type reproduction number for either gender, assuming the other is not a reservoir, is the square of the basic reproduction number. This result is sensible because the system is similar to vector–host models for which similar results hold [5]. The type reproduction number for, without loss of generality, the genital site, as long as the oral sites are not a reservoir, that is, as long as $\sqrt{K_{FM}^{O\mid O}{K}_{MF}^{O\mid O}}<1$, is

$$T_G=\frac{A}{2B}+\frac{1}{2B}\sqrt{A^2-4B\left(K_{FM}^{O\mid O}{K}_{FM}^{G\mid G}-K_{FM}^{O\mid G}{K}_{FM}^{G\mid O}\right)\left(K_{MF}^{O\mid O}{K}_{MF}^{G\mid G}-K_{MF}^{O\mid G}{K}_{MF}^{G\mid O}\right)},$$ (48)

where

$$A=K_{FM}^{O\mid G}{K}_{MF}^{G\mid O}+K_{FM}^{G\mid O}{K}_{MF}^{O\mid G},$$ (49)

$$B=1-K_{FM}^{O\mid O}{K}_{MF}^{O\mid O}$$ (50)

Although the form is similar to that of the basic reproduction number (eq. 42), there is no final square root because the type reproduction number considers cycles in the transmission graph (which is bipartite for a heterosexual population) rather than geometrically averaging over both transmission directions, and there is a term, $1-K_{FM}^{O\mid O}{K}_{MF}^{O\mid O}$, which takes into account the strength of the infection at the other site.

4. Conclusions

In this work, we developed a model of a multisite infectious disease and derived expressions for the basic reproduction number under a number of different assumptions and limiting cases. To the best of our knowledge, it is the first analysis of such a model. Although developed with HPV in mind, it may also be relevant to other infections such as HSV and chlamydia, among others.

We find that autoinoculation adds considerable complexity to the analysis of two-site models, as shown in eqs. 1 and 11. Thus, there is a possibility that neglecting autoinoculation may potentially result in severe model misspecification, that is, making incorrect estimations and conclusions as a direct result of using a model that does not fully capture the dynamics. Fortunately, the analysis of the two-site model with homogeneous contacts gives a reasonably clear picture of how the relative magnitudes of the autoinoculation parameters (and, similarly, the clearance parameters) change the impact of heterogeneity in the same-site and in the cross-site transmission parameters (Figures 4 and 5), with heterogeneity in autoinoculation and clearance breaking the symmetry of the identical site model to alter the high- and low-risk regions defined by the partitioning planes. In general, increasing overall autoinoculation rates also increased R₀ while increasing clearance decreased it (also shown in Figures 4 and 5). Figure 6 shows the potential for significant error in estimating R₀ if the underlying disease process includes autoinoculation but this pathway is neglected in the model. While both the full model and the model lacking autoinoculation generate quite similar oral and genital prevalence trajectories, the true R₀ for the simulated data using the full model was 4, while the estimated R₀ with the reduced, misspecified model was 1.2. Indeed, the individual transmission and clearance parameters for the misspecified model were quite different from the true values, including altering the relative balance of the transmission pathways. This highlights the strong importance of further work uncovering the potential role of autoinoculation between oral and genital HPV infections, and more generally examining the relative balance of autoinoculation and person-to-person transmission in generating new infections at different sites, particularly as autoinoculation via warts at distal sites has been shown to play a role in increasing genital HPV infection risk [26]. This example also more generally highlights problems that are likely to arise when fitting an incomplete or mispecified model to data, particularly if not all transmission routes are accounted for in the model, as in this case.

Regardless of the magnitudes of the autoinoculation and clearance parameters, heterogeneity in the cross-site next generation matrix terms decreases R₀ while heterogeneity in the same-site next generation matrix terms increases it. For a fixed total transmission rate, the extrema of R₀ occur when transmission is predominantly through one transmission pathway: the extremum is a maximum when that transmission pathway is same-site and a minimum when it is cross-site. Moreover, the constrained transmission parameter space is partitioned by two planes into four regions in which R₀ is either larger or smaller than its value on the partition.

That heterogeneity affects the pathways differently is a departure from the classical association between increasing heterogeneity and larger R₀ [30, 3]. Robertson et al. [22] investigated the effect of heterogeneity in transmission pathways for a waterborne disease model, considering heterogeneity in the direct (person-to-person) and indirect (person-to-water-to-person) pathways among different communities as well as their relative contributions. They found that although it was possible to have high heterogeneity and a low R₀ by minimizing the connectendess of communities (i.e. a low indirect transmission), their measure of heterogeneity, namely the variance of the direct transmission plus twice the covariance of the direct and indirect transmission, was predictive of and increased with R₀. Our results, then, suggest that the effects of heterogeneity in transmission pathways can be very dependent on the structure of the transmission pathways and, thus, should be investigated more broadly.

We are able to comment on the effects of heterogeneity in the clearance and autoinoculation parameters as well. Heterogeneity in the clearance parameters breaks the symmetry between the two same-site transmission terms when considering R₀ on the plane β_OO + β_GG + β_OG + β_GO = k, and heterogeneity in the autoinoculation parameters breaks the symmetry in the cross-site transmission terms. In particular, increasing γ^G relative to γ^O (genital sites clear faster) moves the intersection of the three lines of the partitioning planes so that β^OO < β^OG = β^GO < β^GG. That is, for a fixed sum β^OO + β^GG, R₀ achieves its minimum at a point where β^OO < β^GG. Increasing ν^OG relative to ν^GO moves the intersection point so that β^OG < β^OO = β^GG < β^GO. Thus for a fixed total β^OG + β^GO, R₀ achieves its maximum at a point where β^GO is greater than β^OG.

One interesting feature of the effects of heterogeneity on R₀ is that we found partitioning planes both for the identical sites model (Figure 3) and general model (Figures 4 and 5), which break the parameter space into two high-R₀ regions and two low-R₀ regions. This suggests that in general we may not need precise estimates of the different transmission parameters in order to know the rough level of risk for a particular community. These high and low risk regions can give us approximate information about R₀ based only on the overall balance and relative strength or dominance of the different transmission pathways. As exact estimates of the transmission parameters are often difficult to determine empirically (compared to estimates of clearance times for example), this sort of relative understanding of the transmission pathways may be easier to determine in practice. This could also potentially help in guiding interventions, by informing which alternative behaviors or intervention strategies are most likely to shift the balance of transmission towards a lower-risk region (for example by promoting oral sex over genital sex to shift from the right high-risk region to the top low-risk region in Figures 3 – 5).

The analysis of the type and target reproduction numbers for the model with homogeneous contacts gives a quantitative way to describe how much more difficult it is to control an infection by targeting a specific pathway rather than a whole site. This may be relevant in the context of HPV, when considering condom use and vaccination as controls. Further, we note the importance of the product of the cross-site infection terms to the basic, type, and target reproduction numbers. In the pansexual model, K^O|G and K^G|O never appear anywhere but as the product K^O|GK^G|O. This structure drives the results about cross-site heterogeneity. It may also have implications for the efficacy of different control methods, since a product and a sum are affected by their terms differently and have different trade-off structures.

Although extending the pansexual two-site model to a heterosexual one adds even more complexity, we can see the contributions of the two-site aspect, which balances between taking a maximum and taking a geometric average, and the heterosexual aspect, which incorporates vector–host-like dynamics by taking a square root of transmission cycles between the two sexes. Further, the behavior of the model near limiting cases is clear. However, further analysis is needed to fully flesh out the dynamics of the model more generally.

These results could be generalized to models with more than two sites, such as oral/genital/anal sites for HPV, oral/genital/ocular sites for chlamydia, or more broadly for warts/viral papillomas at a range of epithelial sites. Because of the shape of the F matrix, the R₀ of an n-site model will be the largest eigenvalue of the n × n submatrix of K = FV⁻¹ containing only those rows and columns corresponding to infection at a single site. Thus, combinatorial tools might be helpful to study R₀ for multisite models in this generalized context. In general, we conjecture that the distinct effects of same-site vs. cross-site transmission heterogeneity will persist as we expand to multiple sites, as may analogs of our results regarding partitioning planes making general regions of high and low risk depending on the balance of the transmission terms. More generally, there are several useful directions for future work with this or similar multi-site models, both in understanding the dynamics and connecting the model to data. Once relevant parameter values have been reported clinically (or data sufficient for parameter estimation recorded), this model will be useful for understand the evolution of disease prevalence in time. Sensitivity of the model to the parameters, then, will become an important consideration in future work. In the meantime, a comprehensive global sensitivity analysis would be a useful first step. Additionally, while we focused on analysis of R₀ here, future contributions may include a broader dynamical analysis of multi-site disease models.

Highlights.

• We analyze the basic reproduction number R0 of a multisite infection model.

• Heterogeneity between same site transmission rates increases R0.

• Heterogeneity between cross site transmission rates decreases R0.

• Neglecting autoinoculation may result in severe misestimation of R0.