Multiscale mechanobiology: computational models for integrating molecules to multicellular systems

Abstract

Mechanical signals exist throughout the biological landscape. Across all scales, these signals, in the form of force, stiffness, and deformations, are generated and processed, resulting in an active mechanobiological circuit that controls many fundamental aspects of life, from protein unfolding and cytoskeletal remodeling to collective cell motions. The multiple scales and complex feedback involved present a challenge for fully understanding the nature of this circuit, particularly in development and disease in which it has been implicated. Computational models that accurately predict and are based on experimental data enable a means to integrate basic principles and explore fine details of mechanosensing and mechanotransduction in and across all levels of biological systems. Here we review recent advances in these models along with supporting and emerging experimental findings.

Introduction

Biological systems are comprised of mechanical components at all scales, from molecules to organisms. Fundamental biological capabilities, including protein unfolding, cell migration, and tissue morphogenesis, are mechanical in nature, involving structural reorganization, force generation, and coordinated motions. Our understanding of mechanobiology – the spatial and temporal convolution of mechanics with biological complexes – however is incomplete, mainly due to challenges in elucidating multiscale interactions and reciprocity, especially in large systems. The integrated mechanobiological circuit, which encompasses force transmission and transduction pathways, consists of several basic functional components – (1) polymers, such as actin and collagen, that provide structural support and a wiring system to propagate mechanical signals, (2) network modifying proteins, such as α-actinin and filamin, that enhance structural integrity and are mechanosensitive to activate biochemical signaling cascades, (3) interfacial complexes, such as focal adhesions, adherens junctions, and the LINC-complex, that mechanically link the extracellular matrix (ECM), neighboring cells, the cytoskeleton, and the nucleus, in addition to activating signaling pathways, and (4) molecular motors that generate forces and spatial distortions – the basic signals in the mechanobiological circuit – that are subsequently propagated throughout the intra- and extracellular space. Through evolutionary large-scaled integration, these basic components are assembled into mechano-sensing active networks, dynamic self-organizing systems, and tissues that are governed by multiscale regulation, exhibit collective behavior, and perform vital functions.

Rigorous computational models that implicitly or explicitly incorporate multiscale mechanisms and system coordination, closely coupled with empirical support, provide a means to accurately simulate and capture phenomena of complex, multibody systems. Here, we review recent progress in computational approaches in mechanobiology at different scales along with support from experimental evidence and empirically based principles. Table 1 shows typical strategies used to model phenomena at various biological scales together with examples, limitations, and strengths. We first review the basic molecular building blocks and their functional mechanisms. Subsequently, we discuss system-level integration and the emergence of global phenomena. Several computational studies, along with brief descriptions, from the molecular to multicellular scales are shown in Fig. 1, demonstrating some important and experimentally unwieldy insights that are possible to obtain through modeling.

Table 1.

Different methods are used to model biological phenomena, typically depending on the length and time scales of interest, types of interactions involved, and nature of the system

Model type	Scale	Examples	Limitations	Advantages
Molecular Dynamics	Atoms and molecules	1–3	-Small spatiotemporal domain size -No resolution of long-term biological behavior -Computationally costly -Equilibrium system information approximated from nonequilibrium processes in steered molecular dynamics simulations1	High resolution, physics based down to the atomistic level
Coarse-grained agent-based	Large molecular complexes, cytoskeletal and extracellular networks, single and collective cells	4–7	May not produce all biologically relevant phenomena at either small or large scales	Can simulate many interacting components at the scale of interest
Continuum-Based	Single cells and small tissues	8–10	Limited resolution of discrete biological components	-Large physical domain size – Underlying physical principles can be directly experimentally tested
Rule-based	Collective cells and large tissues	11–13	-Mostly phenomenological -Underlying assumptions are difficult to reconcile with physical principles	-Simple rules can produce complex biologically mimicking patterns -Can simulate emergent behaviors not easily attainable by other methods

Fig. 1.

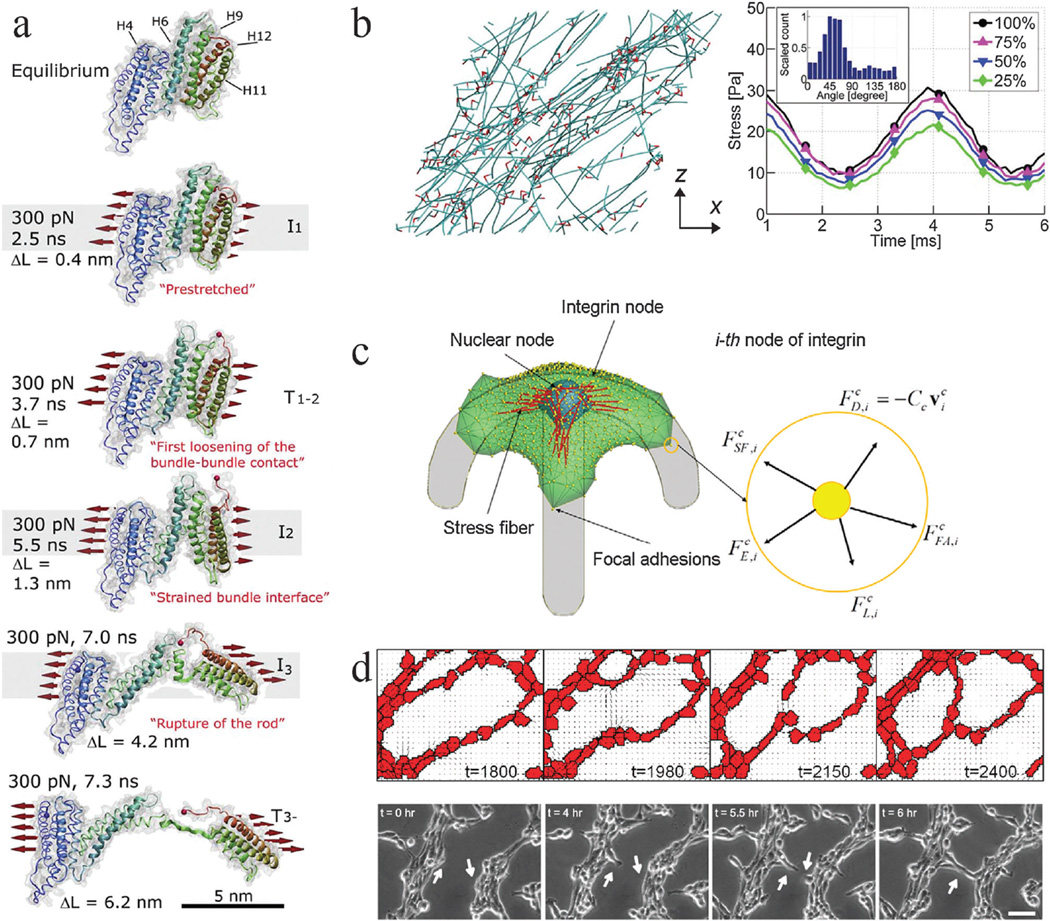
Mechanobiology simulations from molecular to multicellular scales. Coarse graining of simulation elements or reduction in system interactions is required to simulate larger scales due to computational cost. (a) Steered molecular dynamics simulation of a stretching force applied to the H1–H12 rod of talin, adapted from ref. 2. Talin has five vinculin binding helices (H4, H6, H9, H11, H12) in its rod domain. As the molecule is stretched by a 300 pN force distributed across its cross section (as indicated), the amount of buried surface area of the vinculin binding sites is reduced, suggesting increased binding affinity for vinculin. ΔL corresponds to the increase in length of the domain as compared to its equilibrium length, which is 3.2 nm. (b) Brownian dynamics simulations of actin (teal) networks connected via actin crosslinking proteins ACPs (red), adapted from ref. 4. (left) A prestrain is applied to this network in the x direction, inducing stress on ACPs and actin. This model predicts that a supportive framework emerges in this network that bears the majority of the stress, such that removal of large fractions of ACPs and actin still enables most of the stress to be sustained when identical oscillatory strain is applied (right). Simulation results provide insights that different mechanisms, such as ACP and actin bending and extension, dictate network viscoelasticity depending on prestrain. (c) A single-cell migration model with focal adhesions, stress fibers, protrusions, and a nucleus, adapted from ref. 110. The cell can adhere to a micropatterned surface and generate spatial profiles of traction forces comparable to experimental studies. Focal adhesions adhere to the substrate and stress fibers can connect to adhesion sites and the nucleus. 3D force balance calculations are performed at each integrin node. This model provides a platform for investigating how prominent intracellular components interact with each other and respond to environmental constraints to generate an integrated cell response. It also implicates the nucleus as a cause for asymmetry in leading and trailing edge adhesion dynamics. (d) Hybrid Potts and finite element model of endothelial networks, adapted from ref. 13. (top) Endothelial cells generate forces and deform a soft substrate. Neighboring cells respond to substrate strains and undergo durotaxis, leading to the formation of networks from single cells that resemble experimental observations (bottom). This model provides indications of how force signals can lead to endothelial morphogenesis.

Atomistic scale: forces and structure

Biomolecules constitute the most basic components in biology. Fundamentally, molecular complexes have structure and mechanical properties. They may exist in several energetically favorable states, and mechanical force can induce a transition between states, as demonstrated by single-molecule experimental studies with optical or magnetic tweezers^14,15 and molecular dynamics or atomistic Monte Carlo simulations.¹⁶ A number of studies have elucidated the working principles and mechanisms for mechanosensing functions of proteins that play an important role in mechanobiology. Actin, actin binding and crosslinking proteins, adhesion complexes, and ECM proteins are some of the most basic molecular structures that confer mechanical integrity and functionality to cells.¹⁷ The responses of these components to mechanical stimuli may therefore provide underlying mechanisms that enable larger biological entities, such as whole cells, to sense and react to mechanical signals.

Signaling molecules in the cytoskeleton, such as actin cross-linking proteins (ACPs), may activate in response to mechanical stimuli. Molecular dynamics simulations coupled with empirical evidence from single-molecule studies using optical tweezers revealed that filamin A, a prominent ACP, can assume a longer, unfolded mechanical state when subject to physiological tension. Simulations revealed fine details about the unfolding of the rod domain of filamin A, including conformations of each immunoglobulin-like tandem repeat.³ Altered conformations of the tandem repeats may trigger downstream signaling cascades, for instance by modulating binding to filamin interacting protein and downstream pathways.³ Furthermore, phosphorylation of filamin A at Ser^21,52 appears to promote force-induced unfolding and affinity for integrin.¹⁸ A recent single-molecule experiment with optical tweezers on filamin A showed another potential mechanism for mechanosensing based on force-induced cis–trans proline isomerization of the force sensing domain pair 20–21 in filamin A.¹⁹ Under stretching forces above 4 pN, domain 20 becomes unfolded and accessible for proline isomerization, which stabilizes the unfolded state under lower forces. This conformation is conducive toward receptor binding (e.g. integrin) in domain 21.

In addition to directly responding to force, actin filaments and ACPs bind to adhesion complexes near the cell membrane, connecting with the extracellular environment. Recent studies investigated the mechanics of these membrane-linked complexes, particularly focal adhesions, which are aggregates of adhesion and associated proteins. These studies demonstrated a mechanism for mechanosensing at focal adhesions via talin. Single-molecule and molecular dynamics studies showed that talin can undergo conformational changes under tension, resulting in elongation and exposing cryptic binding sites, thereby enhancing the binding affinity to vinculin, another cytoskeletal protein.^15,20,21 The binding of vinculin to talin at focal adhesions reinforces the link between the cytoskeleton and the ECM²⁰ and also keeps talin in an unfolded state.²² Recent experimental work in live cells, using two different fluorescent labels each tagging one end of talin, showed that active myosin II motors pulling on actin filaments can stretch talin, anchored to the cell surface, up to several hundred nm. This stretching phenomenon is dynamic and can be stabilized by vinculin.²³ Interestingly, the deformation dynamics of adhesion proteins is suggested to confer the ability of focal adhesions to grow or shrink in certain directions along the cell in response to applied forces.²⁴ Future integrated experimental and computational methods are required to fully explore not only the static configuration changes of proteins due to force but also the impact of dynamic force fluctuations on the temporal nature of the transduced biochemical signal. Innovative approaches that incorporate rigorous signal processing and analysis techniques from other fields will likely be required to interpret complex mechanobiological signals.

Other prominent adhesion associated and crosslinking proteins, such as α-actinin,²⁵ and certain ion channels²⁶ have also been shown to be mechanosensitive and may respond to force by conformational change. Overall, molecular dynamics simulations coupled with single-molecule experimental techniques have provided tremendous insight into the molecular origins of mechanobiology. ACPs and adhesion proteins can have altered functionality via conformational changes induced by tension. This leads to downstream biochemical or biomechanical responses, including altered molecular binding kinetics for different bond structures (slip bonds, catch bonds),^27,28 thus transducing mechanical stimuli (e.g. force and stretch) into an integrated cell response. Fig. 2 illustrates molecular-level examples of coordinated mechanochemical signaling across the cell membrane.

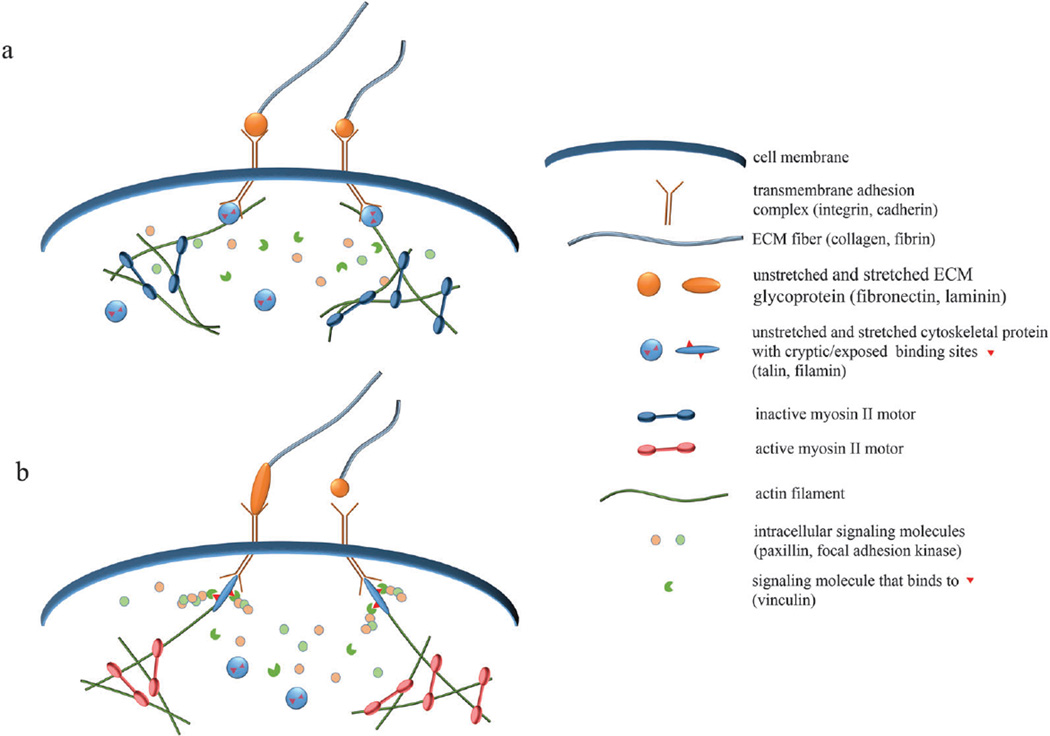
Fig. 2.

Schematics of molecular-level mechanotransduction. (a) When myosin II motors are inactive, cells exhibit reduced tension, causing mechanosensitive protein complexes to assume inactive forms. Inactive talin and filamin have cryptic binding sites, which are unavailable for binding with affiliated molecules. (b) When myosin motors are active or external tension is applied, mechanosensitive proteins become stretched, making accessible previously hidden binding sites. Downstream signaling proteins, such as vinculin, can then bind and activate signaling cascades that promote adhesion, migration, and other physiological functions. Increased force can also alter the binding kinetics and adhesion dynamics of mechanosensitive complexes.

Moreover, tunability of the properties of individual cytoskeletal proteins can confer diversity in mechanochemical states in the overall cytoskeletal network. Cytoskeletal constituents can change their inherent stiffness in a variety of ways, which may modulate mechanical signal propagation. Actin filaments and gels stiffen under strain.²⁹ Their bending rigidities and molecular conformations can be tuned by cation and nucleotide binding, leading to altered strain-stiffening behavior, as shown by Bidone et al. in a multiscale modeling approach coupling molecular to Brownian dynamics simulations of F-actin.³⁰ Actin crosslinking proteins (ACPs) further enhance the stiffness of actin networks^31,32 and may bind to other proteins for signaling.³³

Actin cytoskeleton: active, dynamic scaffolding networks

The structure of the cell is conferred primarily by the actin cytoskeleton formed via kinetic and mechanical integration of molecular complexes. The actin cytoskeleton provides a force-generating, load-bearing, and shape-changing network in mammalian cells.³⁴ It plays an important role in transmission and transduction of forces between intracellular and extracellular environments as well as for distribution of mechanical forces within cells.³⁵ As mentioned earlier, many of the proteins constituting the actin cytoskeleton show force sensitivity, exhibiting changes in binding affinity and unbinding rates. As a result, the actin cytoskeleton also shows highly dynamic rheological behaviors in response to the time-dependence, spatial orientation, and magnitude of mechanical loads.³⁶ For illuminating how forces are transmitted and distributed within the cells, it is crucial to elucidate the complicated, force-sensitive rheological behaviors of the actin cytoskeleton. However, since the cytoskeleton is a complex system involved with numerous biochemical signals and accessory proteins, a simplified system using either reconstituted actin networks formed of purified cytoskeletal proteins or computer simulations can be useful in understanding the rheology of the actin cytoskeleton.^37,38 Several rheological studies have shown that reconstituted actin networks are viscoelastic with the relative importance of viscous and elastic properties depending on frequency of mechanical loads and how well the actin filaments are crosslinked with each other by ACPs.^39,40 Transmission of forces can be more effective in an elastic network than a viscoelastic one because the viscous aspect of the networks dissipates energy. It has been shown that application of moderate external tensile strain or stress can significantly stiffen networks so that the networks become highly elastic regardless of the frequency of the mechanical loads, leading to effective force transmission.^31,39–42 Computational models have demonstrated the stiffening behavior of actin networks is attributed to the transition from a regime dominated by bending of the actin filaments to one dominated by extension.^4,32,43 Interestingly, very large tensile strain or stress induces softening of reconstituted actin networks and cells,^44–46 fluidizing the material reversibly and potentially disturbing mechanotransduction. Simulations have shown that viscoelastic behaviors observed in the actin networks subject to force or stress, such as the softening, creep, stress relaxation, and plastic deformation, are governed mainly by transient crosslinks formed by ACPs that turn over more frequently with higher applied forces.^47–50 In addition, connectivity and percolation of actin networks have been investigated in various computational studies because of their importance for mechanotransduction.^51,52 These features, together with ACP binding mechanics and geometries, may promote different morphological phases of actin networks, resembling bundles, clusters, and other cytoskeletal structures.⁵³

The actin cytoskeleton within active cells is in a stiffened state primarily due to tensile forces generated by molecular motors, myosin II, walking on actin filaments.^54,55 Although previous studies without consideration of motors provided insight into actin rheology under externally applied strain or stress, it is more physiological to probe how local interactions between actin filaments, ACPs, and motors affect viscoelasticity and connectivity of networks. Addition of myosin II motors to reconstituted actin networks with ATP could lead to stiffening of the networks to an extent depending on densities of motors and crosslinking level,^56,57 studies which were further explored by computer simulations.^58,59 Another computational study demonstrated that active networks with motors can undergo a phase transition from a percolated state to a disconnected state depending on the ratio of motors to ACPs.^60–62 It was also shown that actomyosin networks can facilitate mechanosensing observed in cells – a complex interaction between substrate stiffness and cell force generation – by dependence of motor activity on stiffness of external environments.^63–65

The richness in the mechanical properties of cytoskeletal networks revealed in both experiments and computer simulations demonstrates that modulation of microscopic parameters, such as motor activity or crosslinker density, can dramatically modulate the stiffness and connectivity of the cytoskeleton, potentially altering how forces are transmitted and transduced within cells, as illustrated in Fig. 3. Furthermore, there are emergent features associated with biopolymer networks that are not fully understood or integrated into existing models. A recent study showed that two bundled actin filaments exhibit complex interfilament sliding dynamics that can undergo a transition from solid to hydrodynamic frictional characteristics depending on added polymeric brushes (from polyethylene glycol treatment).⁶⁶ This suggests that actin filament bundles, which are common throughout cells and serve as important components of force generation and structural integrity, may have altered dynamics and tunability than previously considered, although system level biological implications are not clear. Future computational models of the cytoskeleton that incorporate these additional physical principles of interfilament interactions may provide more comprehensive insights toward their impact on the distribution and dissipation of force signals within cells.

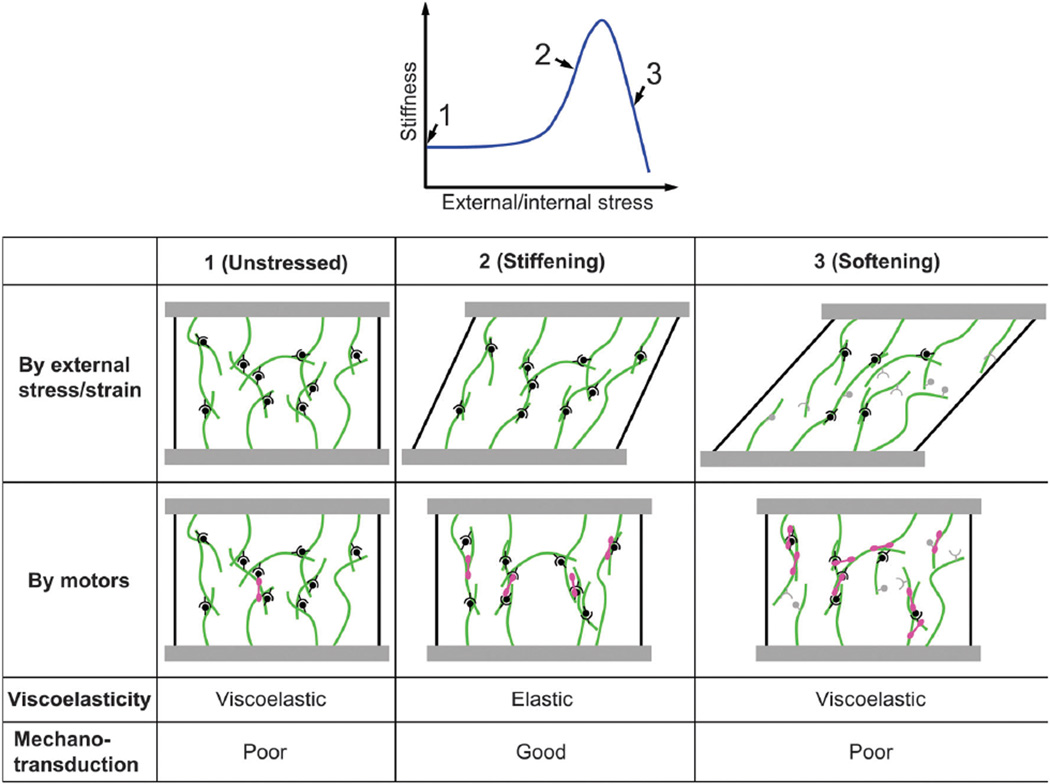
Fig. 3.

Schematic illustrating mechanical properties of crosslinked filament networks and the impact on mechanotransduction. Crosslinked actin networks exhibit stiffening and enhanced elasticity under an appropriate, intermediate level of strain or stress, which can be induced by external application or internal motors. Crosslinker and filament kinetics and mechanics determine the appropriate range. Elastic networks, where forces are not rapidly dissipated, that exhibit fibrillar alignment enable longer range transmission and transduction of mechanical signals.

The cell–environment interface

Interfacing the cytoskeletal matrix with the ECM and other cells are the cell membrane and associated membrane-bound or transmembrane proteins. Mechanical signals are transferred between the two separated environments via adhesion complexes, particularly involving integrins and cadherins, which physically link the inside and outside of the cell. This physical connection can therefore directly transfer force between the two sides. A key phenomenon that occurs is the clustering of adhesion complexes, which is associated with biochemical signal transduction and tensile forces.^67–71 However, the dynamics and principles that drive this process are unclear.

Recent computational studies have provided insights into the mechanisms that drive integrin clustering. Paszek et al.⁷² developed a model of integrin receptors and ligands distributed on the cell membrane and ECM, respectively. Additionally, the glycocalyx was modeled as an elastic buffer between the cell and the ECM. By considering these components as springs with various stiffnesses and stochastically modeling the force-dependent binding kinetics between integrins and ligands, Paszek and co-workers showed that cluster formation can be induced in a mechanics (deformations and force) and binding kinetics dependent way, suggesting simple underlying mechanochemical mechanisms that may regulate cell–ECM mechanosensation. Of note, the mechanics of the glycocalyx in this model can modulate cluster formation. In particular, integrin–ligand bonds bring the cell membrane and ECM closer together by inducing local spatial deformations. Proximity enhances binding rates, and glycocalyx mechanical properties modulate local displacements, energy requirements for reactions, and cooperativity in integrin–ligand binding. A relatively thick and stiff glycocalyx, up to a certain extent, leads to high cooperativity and thus enhanced cluster formation.⁷² This feature has recently gained experimental support and implicates the upregulation of glyco-proteins in cancer as a means of promoting integrin mediated signals for growth and metastasis.⁷³

In other computational studies, Jamali et al.⁷⁴ recently developed an agent based model of integrin clustering that includes additional factors, such as ligand clustering and mobility, integrin homo-oligomerization, and membrane crowdedness. Some key results show that the affinity between integrin homo-subunits plays a role in determining the size of integrin clusters, especially when ligand concentrations are low and integrin concentrations are high, membrane crowdedness influences integrin clustering more for randomly distributed rather than clustered ligands, and integrin–integrin interactions are critical in conditions where there exists only low concentrations of mobile ligands.

These detailed simulation results provide insights that may guide future experiments and present in numerical detail phenomena that would be difficult to elucidate empirically. In the context of cluster formation, mechanics of the environment and spatial distributions of binding partners, in addition to intrinsic chemical affinities, appear critical, and computational methods are crucial toward revealing underlying principles. Through these interfacial adhesion complexes, the cytoskeleton can communicate bidirectionally with the extracellular environment, leading to migratory patterns and guiding cell fate.

Extracellular matrix mechanics

Migration and shape change are fundamentally mechanical functions. In addition, cells must communicate with their neighbors, and this communication occurs via both chemical and mechanical signals. In order for cells to perform these functions, they must mechanically engage, via adhesions, protrusions, and contractions, their local environments, which are often a fibrous network of proteins called the extracellular matrix (ECM). Therefore, the mechanical properties of the ECM are critical in determining how and if these phenomena proceed in time and space.

Like the cytoskeleton, the ECM is a matrix of deformable fibers. Collagen I is a common component, and purified collagen I gels have been used extensively as model ECM scaffolds to culture cells.⁷⁵ Fibrin is another common material, particularly for forming in vitro vascular networks.⁷⁶ The ECM is a complex, nonlinear mechanical network, consisting of both viscous and elastic features. It is porous, consisting of voids that cells may migrate through, and filaments that can be degraded via proteolytic factors^77,78

Recent studies have focused on the fibrillar nature of the ECM, since it gives rise to characteristics not captured by usual viscoelastic or poroelastic continuum models. Computational efforts have modeled the ECM as a discrete network of cross-linked fibers to examine how these networks respond to deformations or contractile stresses. From Wang et al.,⁷⁹ as the ECM is deformed, two families of fibers emerge – one that is aligned along the direction of principle stretch and the other that remains isotropic. By constitutively modeling the isotropic component as a hyperelastic material and the aligned component as a nonlinear anisotropic material that contributes in a directional manner dependent on principle stretches, they demonstrated that long range anisotropic tensions are generated, consistent with experimental results with cells pulling on fibrous matrices.^79,80 A related study from Ma et al. 2013⁸¹ also demonstrated that strain hardening of a homogenous material is not sufficient to propagate long range stresses and that a fibrous material with aligned fibers is required. Recent experimental findings further revealed the consequences of the fibrillar nature of the ECM, including the strain history dependence of uncrosslinked networks⁸² and compression-induced softening-to-hardening transition,⁸³ due to events such as fiber stretching, buckling, and in the latter case densification.

In addition to stiffening and aligning under tension and strain, which promote rapid, long range force transmission, certain ECM proteins, such as fibronectin, undergo conformational and functional changes under tension. Steered molecular dynamics simulations showed that fibronectin affinity for integrin is reduced when unfolded,⁸⁴ thus modulating cell–matrix adhesion. Furthermore, extension of fibronectin exposes cryptic binding sites, which promotes fibril assembly⁸⁵ and can lead to downstream biochemical signaling.^86,87 Traction force experiments corroborate that fibronectin fibril assembly by adherent cells depends on well-coordinated contractile forces.⁸⁸

The ECM is mechanosensitive and its mechanical properties govern how forces are propagated over long distances in the cell microenvironment. These forces may then serve to activate intracellular mechanosensors, such as integrin, talin, and filamin in distant cells, leading to long-range cell–cell communication, as well as ECM proteins, promoting matrix assembly and dynamic cell–matrix signaling. Furthermore, ECM properties, including stiffness, pore size, and architecture, can change depending on gel concentrations, the presence of proteolytic factors, pH, and temperature.^89,90 These changes can directly impact cell behavior, including adhesion and migration, which we discuss in more detail later. Coupled experimental and computational approaches can unveil underlying properties of the ECM that may otherwise be difficult to predict a priori, e.g. the important consequences of a fibrillar architecture. Comprehensive computational models that integrate physiological ECM architecture and mechanics with chemical kinetics and molecular signaling can help provide dynamic, spatial maps of biological signals in the extracellular landscape.

Holistic cell systems and cell–environment interactions

The existence of cells in soft, elastic, 3D matrices immediately implicates the generation of spatial distortions in the environment, which are related via network elasticity to forces. The fibrillar architecture of the ECM serves to propagate these distortions over long distances. Spatial distortions provide an immediate means for stimulated symmetry breaking and environmental heterogeneities for local and distant cells. The remaining question is – are these distortions sufficient to induce a specific cell response (as opposed to being insignificant background noise)? From experimental studies, the answer is a resounding yes. Cell behavior is highly biased by substrate stiffness,^69,91 directional cues⁹² and alignment of local fibers,^93,94 local forces,^95,96 nanotopography,^97–99 geometry,^100,101 and dimensionality.^102–106 Multicellular aggregates can generate large distortions over even longer distances.¹⁰⁷ Local tension can lead to accumulation and activation of various force sensitive proteins and downstream signaling cascades, as discussed in previous sections. The fact that the nature of cells and biological systems is clearly and substantially impacted by mechanics proves that mechanics cannot be ignored in biology, for otherwise an entire dimension of possibilities is artificially fixed. As a direct consequence of taking mechanics into account, factors such as geometry and boundary conditions are critical in regulating complex biological phenomena.

There are two critical problems to consider: (1) how are forces (and deformations) propagated in the intracellular and extracellular environments and (2) how are forces transduced into biochemical responses? The first question requires consideration of the mechanical properties and kinetics of the force propagating medium, including compliance, porosity, dimensionality, fibrillarity, geometry, topography, plasticity, and boundary conditions. The second problem requires the coupling between biochemistry, mechanics, and molecular and systems biology. Simulations, particularly molecular dynamics and systems biology approaches, are critical towards connecting conformational changes of proteins to binding affinity changes and pathway (de)activation. Integrating these two problems can reveal critical details about the nature of the mechanical signaling circuit and provide insights into how modulating the physical microenvironment of cells, including and beyond substrate stiffness, can lead to emergent biological behaviors, such as single and collective cell migration, stem cell differentiation, angiogenesis, and organogenesis. Furthermore, the mechanical signaling circuit may overlap with canonical pathways, including but not limited to integrin mediated pathways, thus enabling modulation of cell biochemistry through mechanics and vice versa.

A key advantage of computational methods is that they can simulate and extract precise information from large, interacting parameter spaces that are often out of the reach of experimental studies, including explicit control of individual cell components such as adhesion sites and stress fibers. Recent work has produced multicomponent integrated single cell models. Borau et al. devised a voxel based scheme, where each voxel corresponds to a subcellular mechanical element.¹⁰⁸ The contractile force generated by each voxel depends on substrate stiffness, based on another computational mechano-sensing model⁶³ qualitatively consistent with experimental findings, which show that cell stress scales with substrate rigidity up to a certain point before plateauing.^91,109 The contractile force, in addition to chemokine and flow effects, is factored into the probability of each cell voxel moving, thus simulating in a stochastic manner the migratory behavior of the cell under various physiological conditions at subcellular resolution. In a different approach, Kim et al. developed a single cell model with subcellular components including lamel-lipodial protrusions, contractile stress fibers, and focal adhesions.¹¹⁰ The model is based on force balance between stress fibers and adhesion sites, and adhesions are kinetic with ligand concentration-dependent binding and force-dependent unbinding probabilities. Simulations reproduce experimentally consistent cell shapes and traction force maps under geometric constraints as well as cell spreading dynamics^111,112 and suggest that the position of the nucleus relative to the leading and trailing edges of the cell plays a role in determining cell polarity. The rear of the cell, due to the position of the nucleus, exhibits larger normal stresses at adhesion sites, leading to faster adhesion and stress fiber turnover and forward motion. Cell migratory behavior in confined channels¹¹³ is also accurately simulated with this model.¹¹⁴

As modeling efforts for integrated single cells advance so more physiological phenomena can be captured, more details of the internal cell machinery need to be accounted for. In the same basic way that cells propagate forces through the ECM, molecular motors propagate forces inside the cell through the cytoskeletal matrix. Individual motor activity leads to forces and spatial distortions transmitted throughout the cell, including at adhesion complexes where forces are then propagated outside the cell and at the nucleus where forces may impact the morphology of the nucleus and transcription dynamics. Similarly, forces outside the cell propagate through adhesion complexes and can lead to spatial distortions and force propagation inside the cell, leading to signal activation and/or spatial redistribution of stress and molecular concentrations in the cytoskeleton and nucleoskeleton. Experimental studies have demonstrated that substrate stiffness impacts cell tension, biochemical signaling, and stem cell differentiation.^{69,91,115,116} In addition to the direct impact on adhesion mediated signaling, tension in the cell may propagate to the nucleus to alter conformation and transcription, which may lead to cell differentiation.^117,118 Recent integrated theoretical and experimental work shows that matrix rigidity can regulate cellular forces and stress fiber orientation in a non-monotonic manner.¹¹⁹ The findings suggest that the elastic microenvironment can induce intracellular structural and force distribution polarization in a tunable way with different sensitivity levels, potentially leading to different stem cell differentiation signals. Next generation computational models with explicit consideration of force generating and bearing components in the cell and nucleus as well as realistic biomolecular architecture of sub-nucleus components such as chromosomes, histones, and DNA, and transcription kinetics may elucidate fundamental mechanisms of mechanically induced differentiation and gene expression. A schematic of the overall propagation of mechanical signals across intra- and extracellular matrices is illustrated in Fig. 4. Forces and material distortions generated by actuators in the form of cells and molecules are transported through an internal and external mechanical network linked by a mechanosensitive interface.

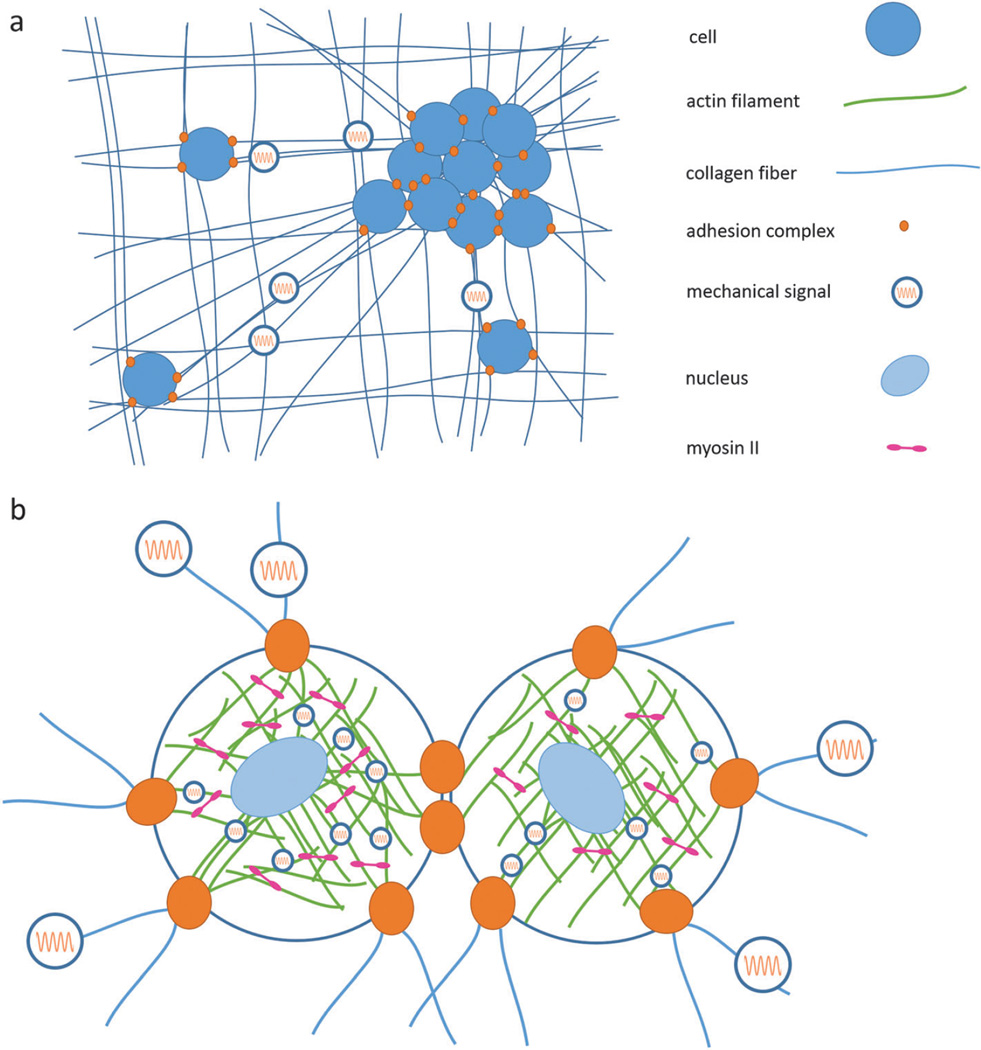
Fig. 4.

Mechanical signals, in the form of force and spatial distortions, are generated by cells and molecular motors. The soft, fibrillar ECM and cytoskeleton are the mechanical wiring networks in which these signals are transmitted, and adhesion complexes enable bidirectional transduction between the two environments. The cell nucleus is also directly connected to this mechanical circuit. (a) Single cells and cell aggregates exert contractile forces on the ECM, propagating signals to distant cells and generating matrix alignment. (b) Expanded view of two connected cells illustrates the connections between a cell and its neighbor and the ECM via adhesion complexes, which act to transmit mechanical signals both inside-out and outside-in. Inside the cell, molecular motors such as myosin II contract the intracellular matrix made of crosslinked actin filaments. The actin cytoskeleton is further connected to the nucleus via the LINC-complex, enabling direct force transmission to the nucleus.

Multicellular models: emergent collective behaviors

Multiple cells interact to form more complex structures, like vascular networks, mammary acini, tumor spheroids, organoids, and tissues. The process, dynamics, and interactions in these multicellular structures are complex, with numerous parameters which may not all be fully elucidated to date. Nonetheless, computational methods based on empirical data have revealed some global trends and apparent rules. The cellular Potts model (CPM), a lattice based model based on minimizing an effective energy, has emerged as a popular approach capable of producing various biological phenomena at multiple scales according to user-defined rules such as cell– cell adhesion, cell elongation, migration, and proliferation.^11,120 The self-propelled particles model and related constructs, based on imposing correlations of migratory directions and velocities of cells with their neighbors, have been demonstrated to capture collective cell motions and general flocking behaviors.^5,121

Kabla demonstrated with the CPM that by considering volume exclusion, membrane tension, and motile force generation, a variety of migratory modes within dense cell populations can be recovered.¹²² An imposed relation between cell–cell interactions via adhesions and membrane tension and directed motile forces controls transitions between three collective states – epithelium (relatively static), sheet migration, and uncoordinated. In an alternative approach based on stochastic interacting particles, Sepúlveda et al. showed that by explicitly correlating the velocity between neighboring cells, experimentally consistent velocity fields of epithelial sheets can be generated.⁶ These studies also explicitly tested for the impact of leader cells, which are subpopulations that have different properties such as directional persistence and velocity profiles, and showed that the existence of these cells are important for determining biased trends, such as preferred directions¹²² and fingers at the boundaries of the epithelium.⁶ Other models based on experimentally supported principles and rules at the cell scale, including substrate stiffness and strain response,¹³ cell adhesions at the discrete receptor level,¹²³ and stochastic interacting pseudopod dynamics,¹²⁴ are starting to recover system level features, such as cell-pair dynamics,^13,123,124 endothelial sprouting,¹³ and complex social behaviors.¹²⁴ Furthermore, multicellular models taking tissue morphologies into account can be applied to simulate disease progression and provide potential medically relevant insights. A recent study applied the CPM to simulate breast cancer progression in Ductal carcinoma in situ (DCIS). Boghaert et al. simulated two cell types representing myoepithelial and luminal epithelial cells placed in a 2D circular or cylindrical geometry mimicking mammary ducts.¹² By considering the relative magnitude of key parameters that include proliferation, apoptosis, necrosis, contractility, and adhesion into the effective Hamiltonian of the CPM, four different DCIS morphologies can emerge, consistent with clinical histology data, and geometry dependent invasion mimicking experiments with 3D micropatterned ducts¹²⁵ can be reproduced.

It is noteworthy that most simulations to date focus on 2D motile modes, mimicking cell sheet dynamics, or ignore complex geometric boundaries of the cell microenvironment. Formulating these models in 3D with consideration of the ECM and its rich and dynamic mechanical features would be useful in recovering the underlying physical principles in more physiologically relevant systems.

Current models provide a means to explore how different parameters can impact the overall behavior of multicellular systems. However, further integrated experimental and computational studies are required to fully identify the underlying biological phenomena, including key molecular species, interaction potentials, and fundamental physics and biology-based mechanisms at all scales, that drive the emergence of these macroscale biological trends and rules. Without directly linking overall biophysical behaviors to underlying biochemical origins, there will be a divide that limits our ability to leverage huge genomics and proteomics databases and drug discovery infrastructures to understand and control emergent features of complex biological systems for medically practicable and desired purposes.

Recent experimental evidence implicates several key physical parameters, along with underlying molecular origins, in governing multicellular behavior. In monolayers, cell migration appears to follow the principal stresses.¹²⁶ RhoA signaling and actomyosin cables that bridge across multiple cells regulate cell monolayer boundaries and locations of new finger formation.¹²⁷ Long-range force propagation driven partially by Rho-ROCK signaling drives migration patterns and interactions between multiple multicellular spheroids.¹⁰⁷ The interactions are stalled and dissemination from spheroids is stopped when tension is relieved via optical ablation.¹⁰⁷ Advances in measurement techniques, such as injectable, functionalized, and deformable micro-oil droplets, further enable mechanical forces of more complex, physiologically important 3D multicellular systems (e.g. embryonic tissues) to be quantified.¹²⁸ This study also showed via inhibitor treatments that actomyosin activity, implicated in single-cell contractility, is indeed the driver of cell compaction in 3D multicellular aggregates. Taken together, these experimental tools and findings and the underlying mechanisms, both physical and biochemical, that are revealed can provide the basis for more realistic multicellular models that follow rules based on fundamental principles within a concrete biological framework. Improved and experimentally consistent models can then be used to simulate larger parameter spaces more accurately in order to investigate and predict more complex mechanobiological phenomena, such as embryogenesis and organogenesis.

Discussion and conclusion

As systems become more complex and parameter spaces expand, detailed experimental studies become more challenging. Computational models can serve as invaluable tools to guide new experimental studies as well as product design and development. They also serve as a useful means of capturing complex experimental observations and revealing resultant emergent behaviors. Recently, synthetic and systems biology has adopted the use of computer aided design based on frameworks from computer logic and electronic circuits to develop new synthetic gene networks,^129,130 a task that would be much more challenging otherwise. Similarly, computational models, with well-defined, concrete, physical, and biological inputs, simulating multiscale dynamics, mechanics, and mechanochemistry can be leveraged to design mechanobiology circuits, which may serve to guide the development of scaffolds for tissue regeneration and stem cell differentiation and mechanotargeting therapeutics.

Although they are versatile and invaluable tools, all modeling strategies have inherent limitations that restrict their applicability to specific ranges of phenomena or spatiotemporal scales (Table 1). For instance molecular dynamics models, while providing detailed molecular structural changes and interactions, are currently too computationally intensive to simulate networks of biomolecules and whole cells. Thus, it is often difficult to extract information of high interest, such as mechanisms of morphogenesis and diseases. Coarse graining of model components is required to reduce computational cost, but comes at the expense of reduced information content. At the other spatiotemporal limit, larger-scaled models currently have limited predictive capabilities for reconciling with empirical studies in which specific biological parameters and molecular species are modulated and complex downstream output signals are produced. For instance, many rule-based models that simulate complex, emergent behaviors in multicellular systems and tissues only take into account general physical features, such as adhesion and force generation. They often do not incorporate specific mechanical properties of multiple molecular species, biochemical signal transduction cascades, and complex, multiscale mechano-chemical feedback mechanisms – which are key areas of interest in many experimental studies. Thus, careful coordination between models of different scales is required to ensure that critical information is not lost. This will be an important component of future models, where modelers will need to be familiar with multiple modeling techniques and synthesize information from different approaches to build fully integrated models that feed data between scales and platforms.

Finally, the influence of mechanics in biological phenomena span additional domains currently not well explored. There are several emerging areas of interest – (1) stochastic mechanical signals and (2) deformations and mechanotransduction at the nucleus and chromatin. These are among important areas in mechanobiology where there are existing and impending experimental data but less conceptual synthesis, elucidated implications, and rigorously quantified mechanisms of action. The intracellular space is crowded with a dense fibrous matrix filled with macromolecules and organelles, which may be effectively compartmentalized rather than freely diffusing.¹³¹ Stochastic stress fluctuations and non-thermal motions in the cytoskeletal network due to active molecular motors, as shown in intracellular particle tracking experiments,^{103,132–134} may enhance large-scale random motions and transport, which are forms of mechanical signaling, characterized by mechanical perturbations with a processivity time on the order of 10 seconds.¹³² These mechanical signals may serve to stochastically activate and deactivate mechanosensitive proteins and actively redistribute macromolecules. Modeling frequency modulated and stochastic mechanotransduction and mechanotransmission in a spatially resolved manner can help elucidate physiologically relevant signaling dynamics.

Furthermore, for gene regulation to occur in response to force, the nucleus must be involved. Recent experimental work demonstrated that nano-Newton forces applied at the cell membrane lead to chromatin decondensation within several seconds in an actin polymerization and myosin contraction dependent manner along with translocation of transcription cofactor megakaryoblastic acute leukemia factor-1 (MKL).¹³⁵ This connection of external forces applied to cells and intranucleus modulation suggests direct gene regulatory mechanisms. In addition, forces applied directly to isolated nuclei at the LINC-complex induce nuclear stiffening in a manner dependent on emerin tyrosine phosphorylation,¹³⁶ suggesting that mechanical responses and biochemical signal activation due to force can occur in the nucleus. Future computational models incorporating integrated mechanochemical signaling at the nucleus can help bridge gene expression dynamics and cell fate commitment mechanisms with mechanics.

Future work will require innovative ways to bridge different modeling strategies to simulate multiscale phenomena and to connect experiments with models to ensure valid results. The experimental challenge is to extract parameter values, such as mechanosensitivity, from a multitude of molecular species and cell types. High throughput microfluidic techniques that can parallelize single-molecule experiments¹³⁷ may be useful, particularly when integrated with scalable, high resolution mechanical manipulation techniques such as nanophotonic tweezers.¹³⁸ Additional complexities to consider include physiologically accurate experimental conditions, such as molecular crowding and multiple interacting species, which may be very different from in vitro studies in dilute buffer solutions. Computational challenges include reconciling disparate modeling methods, from molecular dynamics to rule-based tissue dynamics, in order to capture multiscale reciprocity – as shown in ref. 30 and 139. Force-induced unfolded protein configurations can be programmed into agent based Brownian dynamics models to simulate local cytoskeletal behavior. Network results can be inserted into a cell migration model to simulate boundary movements, shape change, and force redistribution, which can be fed back into molecular dynamics simulation databases to extract molecular configurations for the next computational step. Uncovering multiscale constitutive relations, with experimentally testable molecular details, in mechanobiology can provide important insights toward the role of mechanics in development and disease.

Insight, innovation, integration.

Mechanics is proving to be a prominent aspect of biological phenomena across multiple scales. Mechanical signals are generated, propagated, and transduced at each scale, from molecules to collections of cells, leading to complex behavior and functions that are often difficult to fully understand and predict a priori. Computational models are critical in providing a framework to assess the principles of mechanobiology and connect multiscale phenomena. In this review we illustrate how computational models, especially when supported by empirical data, can capture and provide conceptual and quantitative insights to the role of mechanics in biology. We also indicate directions and emerging areas in mechanobiology that will require next generation computational and experimental integration.

Biographies

Michael Mak

Michael Mak is a postdoctoral fellow at the Massachusetts Institute of Technology and Boston University. He obtained his BS in Engineering-Physics at Brown University in 2008 and his PhD in Biomedical Engineering at Cornell University in 2013, during which he was an NSF Graduate Research Fellow. His research interests focus on integrating computational modeling and novel experimental techniques to elucidate the mechanobiological features of disease and development across multiple scales.

Taeyoon Kim

Dr Taeyoon Kim received his BS in Mechanical Engineering from Seoul National University in 2004. He received his SM and PhD degrees in Mechanical Engineering from the Massachusetts Institute of Technology in 2007 and 2010, respectively. Then, he held a postdoctoral position in the Institute for Biophysical Dynamics at the University of Chicago until 2013. At Purdue University, Dr Kim is the principal investigator of the Molecular, Cellular, and Tissue (MCT) Biomechanics Laboratory, which studies diverse mechanical behaviors of biological matters, using cutting-edge computational models that span subcellular levels to the cell and tissue levels.

Muhammad H. Zaman

Muhammad H. Zaman is the Howard Hughes Medical Institute Professor of Biomedical Engineering and International Health at Boston University. Dr Zaman received his PhD from the University of Chicago in Physical Chemistry in 2003, where he was Burroughs-Wellcome Interdisciplinary Research Fellow. He then moved to MIT as a postdoc where he worked in the Department of Bioengineering as a Herman and Margaret Sokol Foundation Postdoctoral Fellow in Cancer Research. Prof. Zaman’s lab focuses on two main areas of research, namely developing computational and experimental models to study tumor progression and developing novel technologies for high impact global health problems.

Roger D. Kamm

Roger D. Kamm is the Cecil and Ida Green Distinguished Professor of Biological and Mechanical Engineering and Director of the NSF Science and Technology Center for Emergent Behaviors of Integrated Cellular Systems. A primary objective of Kamm’s research group has been the application of fundamental concepts in fluid and solid mechanics to better understand essential biological and physiological phenomena. His lab focuses on the molecular mechanisms of cellular force sensation, and the development of new microfluidic technologies for vascularized engineered tissues and models of metastatic cancer.