Bolus Estimation—Rethinking the Effect of Meal Fat Content

Abstract

Background: Traditionally, insulin bolus calculations for managing postprandial glucose levels in individuals with type 1 diabetes rely solely on the carbohydrate content of a meal. However, recent studies have reported that other macronutrients in a meal can alter the insulin required for good postprandial control. Specifically, studies have shown that high-fat (HF) meals require more insulin than low-fat (LF) meals with identical carbohydrate content. Our objective was to assess the mechanisms underlying the higher insulin requirement observed in one of these studies.

Materials and Methods: We used a combination of previously validated metabolic models to fit data from a study comparing HF and LF dinners with identical carbohydrate content in seven subjects with type 1 diabetes. For each subject and dinner type, we estimated the model parameters representing the time of peak meal-glucose appearance (τ_m), insulin sensitivity (S_I), the net hepatic glucose balance, and the glucose effect at zero insulin in four time windows (dinner, early night, late night, and breakfast) and assessed the differences in model parameters via paired Wilcoxon signed-rank tests.

Results: During the HF meal, the τ_m was significantly delayed (mean and standard error [SE]: 102 [14] min vs. 71 [4] min; P = 0.02), and S_I was significantly lower (7.25 × 10⁻⁴ [1.29 × 10⁻⁴] mL/μU/min vs. 8.72 × 10⁻⁴ [1.08 × 10⁻⁴] mL/μU/min; P = 0.02).

Conclusions: In addition to considering the putative delay in gastric emptying associated with HF meals, we suggest that clinicians reviewing patient records consider that the fat content of these meals may alter S_I.

Introduction

Continuous glucose monitors (CGMs) combined with subcutaneous insulin infusion pumps provide individuals with type 1 diabetes convenience and flexibility in managing their blood glucose levels.^1,2 However, there has been little guidance on how to use the CGM data to optimize insulin delivery. Retrospective analysis of CGM data can identify periods of hypo- or hyperglycemia indicating that too much or too little insulin was given. However, there is no method by which the CGM data can be used to directly infer how the insulin pump settings should be modified to correct these problems. Interpretation of the CGM data is confounded by factors that may have affected the subject's insulin sensitivity (S_I) on any given day, such as prior exercise and stress. Hypo- or hyperglycemia following meals with unusually low or high glycemic indices, respectively, may be due to an inappropriate bolus pattern (square wave, dual wave, etc.)³ or an inappropriate duration of insulin delivery,⁴ rather than an error in the carbohydrate-to-insulin ratio per se. Additionally, all bolus estimators assume the background basal rate to be correct, which may not always be true. Furthermore, analysis of CGM data is confounded by the emerging body of evidence suggesting that macronutrients other than carbohydrate may require adjustments to the insulin dosing.⁵

Traditionally, high-fat (HF) meals have been thought to delay gastric emptying,⁵ thus motivating the use of extended or dual-wave boluses to cover these meals. However, it is not commonly believed that HF content requires an increased amount of insulin. Nonetheless, a prospective randomized controlled trial (RCT) using an artificial pancreas system to control low-fat (LF) and HF dinner meals with identical carbohydrate content showed that even with 42% more insulin being delivered, the glucose levels during the HF meal remained elevated.⁶

To better understand this finding and to possibly develop an improved method of adjusting the bolus recommendations covering HF meals, we sought to identify the mechanism responsible for the increased insulin requirement observed in the original RCT.⁶ In this study, we hypothesized that in addition to the putative effect of fat to delay gastric emptying, it may also limit insulin's ability to increase glucose uptake into peripheral tissues and suppress endogenous glucose production. We tested this hypothesis by fitting the plasma insulin and glucose data obtained from the RCT study⁶ to previously validated metabolic models describing the time of peak meal-glucose appearance (τ_m) that represents the time constant of gastric emptying,⁷ the pharmacokinetic profile of insulin following subcutaneous delivery,⁸ the delay in the effect of insulin to enhance glucose uptake into cells, the S_I of the cells, and the glucose effect at zero insulin (GEZI) to suppress endogenous glucose production and increase glucose uptake into cells.⁹

Materials and Methods

Subject characteristics, meal composition, and study design of the RCT quantifying the increase in insulin required to cover HF versus LF meals are provided in the original publication⁶ (for complete meal description, see comments made by Wolever¹⁰ in a Letter to the Editor and the author's response¹¹).

In brief, seven adult subjects (five men and two women) 55 years of age (standard deviation [SD] = 12), with a diabetes duration of 42 years (SD = 6; range, 15–60), hemoglobin A1c of 7.2% (SD = 0.8), total daily insulin dose of 0.50 U/kg (SD = 0.14; range, 0.28–0.73), and body mass index of 26.3 kg/m² (SD = 3.6; range, 21.5–30.6) were studied on two occasions, each lasting 18 h on consecutive days. During each occasion, subjects were admitted to a clinical research center on the afternoon of the first study day. At 6 p.m. on the day of admission, subjects consumed either an HF (60 g) or LF (10 g) dinner meal with identical carbohydrate (96.7 g [SD = 19.1]) and were monitored until noon on the following day. Breakfast (102.8 g [SD = 16.3] of carbohydrate), served at 8 a.m., was identical in all respects on both days. Beginning at 6 p.m. and ending at 12 p.m. (noon) the subsequent day, each subject's insulin requirement was obtained via a closed-loop artificial pancreas algorithm¹² together with blood samples obtained approximately every 15 min during meals and approximately every 60 min during the night. Blood samples were assessed for plasma glucose using a YSI 2300 glucose analyzer (YSI Life Sciences, Yellow Springs, OH) and for plasma insulin using a chemiluminescent immunoassay (Beckman Coulter, Fullerton, CA). During the night, supplementary meals consisting of juices with carbohydrate content between 7 g and 15 g were given to subjects with glucose levels nearing 70 mg/dL to avoid the risk of hypoglycemia (glucose <60 mg/dL).

Metabolic model parameter estimation

Using the data (carbohydrate [in g], insulin delivery rate [in U/h], plasma insulin concentration [in μU/mL], and plasma glucose concentration [in mg/dL]), we estimated the parameters of previously validated metabolic models that represent the τ_m,⁷ insulin clearance (C_INS) and delays associated with insulin appearance in plasma following subcutaneous delivery (τ₁ and τ₂) and its subsequent effect (1/p₂) to increase glucose uptake in cells,⁸ S_I of the cells, net hepatic glucose balance at zero insulin and zero glucose (NHGB₀), the GEZI, and the ratio of the glucose distribution volume to the bioavailability of meal carbohydrate (V_G/A_G).⁹ We provide the model equations in the Appendix.

As in previous studies assessing time-varying metabolic parameters,¹³ we defined discrete time intervals in which we assumed the metabolic model parameters to be approximately constant: dinner interval (6 p.m.–11 p.m.), early nighttime interval with a transition time (T_N) (11 p.m.–T_N), late night/early morning (T_N–8 a.m.), and breakfast (8 a.m.–12 p.m.). We incorporated a 20-min transition phase to allow a piecewise smooth transition in parameter values from one interval to the next and identified T_N separately for each subject. We estimated the pharmacodynamic model parameters S_I, GEZI, and NHGB₀ separately in each interval, allowing the values to differ between HF and LF meal glucose profiles. We estimated τ_m separately for the LF dinner, HF dinner, breakfast, and all supplementary meals. Pharmacokinetic model parameters describing insulin transport within the body (subcutaneous depot [C_INS and τ₁], plasma [τ₂], and remote interstitial fluid surrounding insulin-sensitive tissue [p₂]) and V_G/A_G were assumed to be the same in each interval and to be unaffected by meal fat content. We assessed the quality of the estimated parameters by computing the fractional SD (FSD) of each parameter (details are provided in the Appendix).

We report plasma glucose and insulin concentrations and the associated model fits as mean and standard error (SE). Goodness of fit (R²; coefficient of determination)¹⁴ are reported as median and range. We report the estimated parameters as the mean and SE values and assess parameter differences during and following closed-loop LF and HF dinners using two-sided paired Wilcoxon signed-rank tests,¹⁴ with P < 0.05 considered significant. We performed parameter identification, model simulations, and statistical comparisons using MATLAB version 7.14 software (The Mathworks Inc., Natick, MA).

Results

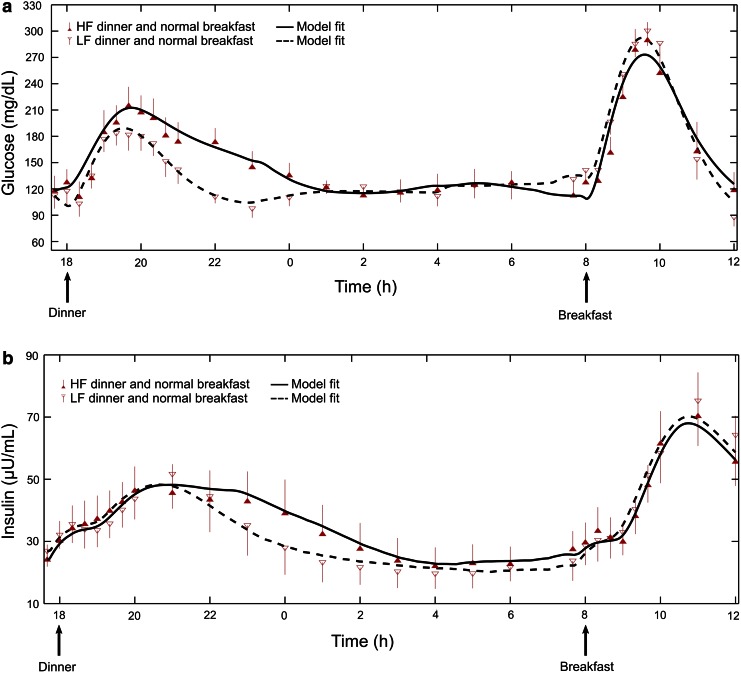
Plasma glucose (Fig. 1a) and insulin (Fig. 1b) were well fit by the model for both the LF dinner (median R² of 0.88 [range, 0.40–0.94] and 0.91 [range, 0.81–0.97] for plasma insulin and glucose, respectively) and the HF dinner (0.74 [range, 0.31–0.96] and 0.90 [range, 0.71–0.94] for plasma insulin and glucose, respectively).

FIG. 1.

Plasma (a) glucose and (b) insulin levels from seven subjects consuming a low-fat (LF) or high-fat (HF) dinner with identical carbohydrate content at 6 p.m., followed by identical breakfasts at 8 a.m. Symbols indicate measured concentration levels (mean and SE). Lines indicate the mean curves of the metabolic model fits across the seven subjects, with the mean LF fit represented by a dashed curve and the mean HF fit represented by a solid curve.

Model parameters for all subjects were generally well estimated (e.g., median FSD for S_I = 17% [range, 11–37%] except for subject 4, whose FSD was 92% for the HF meal). Supplementary Tables S1–S4 (Supplementary Data are available online at www.liebertonline.com/dia) provide the estimated model parameters, their corresponding FSDs, and meal information for each subject for both LF and HF meal conditions.

Average S_I (Table 1) was significantly lower during the HF versus LF dinner (7.25 × 10⁻⁴ mL/μU/min [SE = 1.29 × 10⁻⁴] vs. 8.72 × 10⁻⁴ mL/μU/min [SE = 1.08 × 10^–4]; P = 0.02), and average τ_m was significantly delayed (102 min [SE = 14] vs. 71 min [SE = 4]; P = 0.02). We did not observe any statistically significant differences in NHGB₀ or GEZI during the LF and HF meals or during the two nighttime intervals (11 p.m.–approximately 4:34 a.m. and approximately 4:34 a.m.–8 a.m.) (Table 1). Parameters assumed not to be affected by dinner fat content or to vary during the day (C_INS, V_G/A_G, τ₁, τ₂, and p₂) were estimated to be 894 mL/min (SE = 150), 133 dL (SE = 19), 176 min (SE = 44), 51 min (SE = 12), and 0.016 min⁻¹ (SE = 0.005), respectively. We noted that the parameter values for the LF meal condition were statistically similar to the parameter values reported by Kanderian et al.¹³

Table 1.

Mean Values of the Variable Parameters Insulin Sensitivity, Net Hepatic Glucose Balance at Zero Insulin and Zero Glucose, and Glucose Effect at Zero Insulin and the Time of Peak Meal-Glucose Appearance Across the Seven Study Subjects

Parameter, meal type	Dinner (6 p.m.–11 p.m.)	Pvalue	Early night (11 p.m.–TN)	P value	Late night (TN–8 a.m.)	Pvalue	Breakfast (8 a.m.–12 p.m.)	Pvalue
SI × 10−4 (mL/μU/min)
LF	8.72 (1.08)	0.02a	7.89 (1.01)	0.16	7.08 (1.86)	0.99	6.72 (1.29)	0.69
HF	7.25 (1.29)		10.94 (1.36)		7.04 (1.97)		6.41 (1.50)
NHGB0 (mg/dL/min)
LF	2.55 (0.69)	0.81	2.41 (0.54)	0.58	3.13 (0.51)	0.58	1.56 (0.03)	0.44
HF	3.07 (0.68)		3.23 (0.52)		2.54 (0.42)		1.55 (0.03)
GEZI × 10−2 (min−1)
LF	0.81 (0.24)	0.69	0.71 (0.18)	0.84	1.02 (0.17)	0.06	0.50 (0.01)	0.38
HF	0.89 (0.25)		0.64 (0.06)		0.59 (0.05)		0.51 (0.01)
τm (min)
LF	71(4)	0.02a	—				60 (7)	0.30
HF	102 (14)						57 (5)

Values in parentheses are SEs.

^aIndicates statistically significant differences between low-fat (LF) and high-fat (HF) values (P < 0.05).

τ_m, time of peak meal-glucose appearance; GEZI, glucose effect at zero insulin; NHGB₀, net hepatic glucose balance at zero insulin and zero glucose; S_I, insulin sensitivity; T_N, transition time.

Discussion

Adjusting insulin doses for meal fat content remains controversial, with patients typically being advised that fat only affects the rate of gastric emptying and that they should consider using an extended or dual-wave bolus.³ However, several studies have emerged challenging this belief.⁵ Model analysis confirmed the well-established belief that HF meals are associated with delayed gastric emptying (here estimated to be approximately 30 min) but also pointed to a significant decrease in S_I (here approximately 17%), and a possible decrease in GEZI later in the night, albeit this effect did not achieve statistical significance (P = 0.06).

Although the 17% decrease in S_I identified here for the HF meal was statistically significant, it was not sufficient to explain the approximately 42% increase in the insulin requirement observed in the original study.⁶ The observed decrease in S_I is consistent with clamp studies showing that when levels of free fatty acids are prevented from falling by a concomitant infusion of intralipid heparin, S_I is lower.^15–17 However, in those studies the decrease was largely attributed to a decrease in insulin's ability to suppress endogenous glucose production.

In the present study, we did not observe differences in NHGB₀ (the hepatic glucose balance that would be expected at zero insulin), but this does not preclude the possibility that insulin's ability to alter the balance was impaired in the HF meal. Our analysis does not allow the time course of insulin's effect to alter NHGB₀ to be separated from the time course of its effect to increase peripheral glucose uptake, as this would require the use of glucose tracers.^18,19 It is also possible that the decrease in GEZI, observed later in the night, contributed to the increased insulin level, although this effect did not achieve statistical significance in this study (P = 0.06) and occurred at a time when plasma insulin levels and S_I were well matched. Thus, we attribute the difference between the observed increase in insulin requirement (42%) and the amount that can be explained by the decrease in S_I (17%) to the mismatch between the delay in insulin effect (1/p₂) and the peak meal absorption time τ_m. In the present study, 1/p₂ was 62 min, whereas τ_m was 102 min for the HF meal, as opposed to 71 min for the LF meal. Such a mismatch reduces insulin's ability to increase glucose disposal, thus increasing the insulin requirement.

The present study design included only one level of meal carbohydrate content (96 g) with two levels of meal fat content (10 g vs. 60 g) and is therefore not sufficient to infer the insulin dosing for a moderate amount of fat (10–20 g) or to determine if further increases in the amount of fat would increase the insulin requirement. Although the effect of fat on insulin requirement was possibly enhanced due to the substantially increased meal-fat content in this study (60 g), other controlled studies have found this effect for meal-fat content ranging from 6.6 to 52.0 g.⁵ In particular, at least one study showed that 35 g of meal-fat content increased postprandial glucose concentrations by approximately 40 mg/dL at 5 h.²⁰ Thus, there is an emerging body of evidence suggesting that meal-fat content alters the dose of insulin required for those meals.

However, whether the insulin dosing should be obtained via an adjustment to the carbohydrate-to-insulin ratio (consistent with fat decreasing insulin's ability to dispose of carbohydrate) or via an additional factor proportional to the grams of fat per se (consistent with carbohydrate and fat having independent effects) is unclear. Equally unclear is how to factor the effects of the amount of protein or the glycemic index of a meal into the insulin dosing calculation. Nonetheless, our results showing a metabolic model to be capable of fitting observed glucose profiles for a specific meal, be it LF or HF (Fig. 1), suggests that model analysis could potentially be used to calculate the optimal insulin dosing and delivery pattern (dose amount and duration) for any meal.

The metabolic model used in the present study was composed entirely of submodels developed and validated by other investigators for reasons unrelated to the characterization of meal responses in subjects with type 1 diabetes. The pharmacokinetic/pharmacodynamic models are identical to those proposed by Sherwin et al.⁸ in 1974. Model components describing the effects of insulin and glucose at zero insulin to increase glucose uptake and decrease endogenous glucose production are derived from the minimal model equations of Bergman et al.⁹ and the model describing the rate of meal glucose appearance follows from work by Wilinska et al.⁷ The combined model (Appendix, Eqs. 1–5) has been used to characterize interday variability in metabolic parameters in adult subjects with type 1 diabetes studied under closed-loop control,¹² with the results subsequently used to predict closed-loop study results obtained in an independent population of pediatric subjects.²¹ We note here that Eq. 3 of the combined model that describes the insulin effect on glucose was the same in the model reported by Sherwin et al.⁸ and the minimal model of Bergman et al.⁹

Independently, Schiavon et al.²² have recently shown that the minimal model subcomponent can be used to derive an index of S_I using only CGM data and subcutaneous insulin delivery and that this estimate is well correlated with the traditional oral minimal model estimate of S_I. This suggests that plasma insulin concentration data per se are not needed when identifying the model. However, without these data S_I can only be identified in combination with C_INS (see Appendix). Having at least some insulin data also improves the precision (FSD) of the estimated parameters, which, while being generally acceptable (FSD <37% in 13 of the 14 estimates of S_I obtained in this study), was higher than desired in some cases (e.g., Supplementary Table S1, 92% in subject 4 for HF meal). Furthermore, although the models used in the present analysis are well established, with reports on their use dating back more than 40 years,⁸ the ability to fit or characterize a specific meal at a specific point in time, as previously shown¹³ and reconfirmed here (Fig. 1), or to predict average results that could be obtained in a population of subjects not used to derive the model²¹ does not imply that the model will be able to predict the response to a different meal consumed on the same day or the same meal consumed on a different day by a subject. Factors affecting inter- and intraday changes in metabolic parameters remain unknown.

In summary, the results of the present study suggest that previously validated models can be combined to describe complex meal response profiles. The ability to model these responses may ultimately serve to improve existing open-loop bolus estimators and possibly optimize a closed-loop, artificial pancreas system. The analysis presented in this study adds to the findings reported in the original study,⁶ showing that HF meals require more insulin than LF meals with identical carbohydrate content. Specifically, parameters identified here indicate that increased insulin requirement was due to both delayed gastric emptying and an effect of fat to decrease S_I. We suggest that clinicians and dieticians reviewing patient records consider the fat content of meals with unexpectedly high glucose levels when considering the insulin requirements for those meals.

Appendix

Metabolic model equations

Insulin subsystem (pharmacokinetic model).

where τ₁ and τ₂ represent the insulin time constants for subcutaneous insulin concentration (I_SC) and plasma insulin concentration (I_P), respectively, ID denotes the delivered insulin, and C_INS denotes the insulin clearance rate.

Glucose subsystem (pharmacodynamic model).

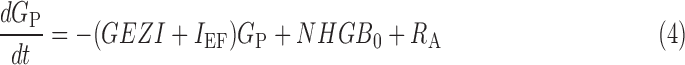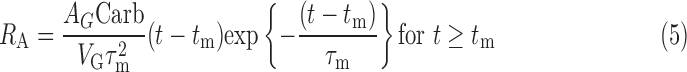where I_EF denotes the effect of insulin on glucose, 1/p₂ is the time constant for the insulin effect, S_I denotes the insulin sensitivity, G_P denotes the plasma glucose concentration, GEZI denotes the glucose effect at zero insulin, NHGB₀ represents the net hepatic glucose balance, R_A denotes the rate of glucose appearance due to meal carbohydrates (Carb), V_G denotes the glucose distribution volume, A_G is a number between 0 and 1 indicating the bioavailability of meal carbohydrates, τ_m is the time of peak meal-glucose appearance, and t_m denotes the mealtime. Parameters (τ₁, τ₂, p₂, GEZI, NHGB₀, τ_m, and ratios V_G/A_G and S_I/C_INS) are identifiable from pump insulin data (ID, Eq. 1), glucose concentration (G_P, Eq. 4), and meal carbohydrate (Carb, Eq. 5). If plasma insulin data are available, as in the present study, S_I and C_INS can be separately identified.

Model parameter identification procedure

We estimated the insulin subsystem parameters using the measured plasma insulin data. For the glucose subsystem, initially, we estimated a different T_N for each of the two meal types. However, the T_N estimates for both meal types were within 15 min of each other. We found that constraining T_N to be the same for both meal types yielded model fits similar to the unconstrained fits. Hence, we used the following procedure for model estimation.

• Step 1. Estimated the parameters of the insulin subsystem (τ₁, τ₂, and C_INS) by driving it with the insulin delivery data (ID) and minimizing the squared error between the predicted I_P and the measured insulin data during the 18-h study period for the LF/HF meal types.

• Step 2. Fixed T_N and the insulin subsystem parameters and estimated the parameters of the glucose subsystem (V_G/A_G, p₂, S_I, GEZI, NHGB₀, and τ_m) by minimizing the squared error between the predicted G_P and the measured glucose data during the 18-h study period for both meal types. We estimated the parameters S_I, GEZI, and NHGB₀ separately in four time windows. For example, S_I was estimated as S_I(D) during dinner, S_I(N1) during early night, S_I(N2) during late night, and S_I(B) during breakfast. For each meal, including supplementary meals, we estimated a separate τ_m. We weighted the squared error by 2 for glucose values above 180 mg/dL and below 70 mg/dL to better capture the peak and nadir glucose levels.

• Step 3. Fixed the parameters of the glucose and insulin subsystems and estimated T_N by minimizing the squared error of the glucose subsystem.

• Step 4. Repeated Steps 2 and 3 until convergence, which was assessed by determining whether the difference between the squared error in the present iteration and the previous one was <10^–3.

After the convergence criterion was met, we confirmed that the parameter values did not change when Steps 2 and 3 were repeated once again.

Parameter fractional standard deviations

We assessed the parameter uncertainties that provide information about the quality of model fit by computing their fractional standard deviations (FSDs; the percentage of the ratio between the SD and the estimated value). There are two methods for computing the parameter SDs: (1) the Jacobian approximation of the metabolic model and (2) the Monte Carlo sampling method.²³ The Jacobian method is straightforward but approximate; the Monte Carlo method provides accurate estimates of the FSDs if the estimated parameters remain within the specified bounds, but it is computationally expensive.^{23,sect. 15.6} We used the Monte Carlo method in three out of the seven subjects to verify the correctness of the FSDs estimated from the Jacobian method.

The Monte Carlo method involves generating virtual data, fitting the model on the virtual data to obtain model parameter distributions, estimating the parameter SDs, and, lastly, computing the FSDs. We generated 1,000 realizations of the glucose and insulin data for each subject using the formula y^S = y^T + ω, where y^S denotes the simulated data, y^T is the measured data, and ω ∼ N (0, σ), with σ set to the root mean squared error between y^T and the best-fit model. Fitting the model to each virtual data sample, we obtained the parameter distributions and estimated their FSDs. To assess the reliability of the computed FSDs, we recomputed them using 500 of the 1,000 realizations and found the values obtained to be similar to those yielded by using all 1,000 realizations. Furthermore, for the parameters that did not hit the bounds, we found that the FSDs obtained via the Monte Carlo method yielded values similar to those obtained by the Jacobian approximation of the metabolic model. We noted that in cases where parameters consistently hit the bounds in the 1,000 realizations, the parameter distributions were skewed toward those bounds, yielding unreliable estimates of the SDs. In those cases, the Jacobian method offers the only means of estimating the FSDs. After verifying the similarity between the FSDs obtained by the Jacobian and Monte Carlo methods for three subjects, we used only the Jacobian method to compute the FSDs for the other subjects. Supplementary Tables S1–S4 provide the parameter estimates and their FSDs estimated for each subject using the Jacobian method.

Acknowledgments

The study was supported by U.S. Department of Defense grant W81XWH-11-1-0421 to G.M.S. and by the Military Operational Medicine Research Area Directorate of the U.S. Army Medical Research and Materiel Command, Fort Detrick, MD, to S.L. and J.R.

Author Disclosure Statement

No competing financial interests exist.