Abstract
In recent years, electronic health records (EHRs) have been widely adapted at many healthcare facilities in an attempt to improve the quality of patient care and increase the productivity and efficiency of healthcare delivery. These EHRs can accurately diagnose diseases if utilized appropriately. While the EHRs can potentially resolve many of the existing problems associated with disease diagnosis, one of the main obstacles in effectively using them is the patient privacy and sensitivity of the medical information available in the EHR. Due to these concerns, even if the EHRs are available for storage and retrieval purposes, sharing of the patient records between different healthcare facilities has become a major concern and has hampered some of the effective advantages of using EHRs. Due to this lack of data sharing, most of the facilities aim at building clinical decision support systems using limited amount of patient data from their own EHR systems to provide important diagnosis related decisions. It becomes quite infeasible for a newly established healthcare facility to build a robust decision making system due to the lack of sufficient patient records. However, to make effective decisions from clinical data, it is indispensable to have large amounts of data to train the decision models. In this regard, there are conflicting objectives of preserving patient privacy and having sufficient data for modeling and decision making. To handle such disparate goals, we develop two adaptive distributed privacy-preserving algorithms based on a distributed ensemble strategy. The basic idea of our approach is to build an elegant model for each participating facility to accurately learn the data distribution, and then can transfer the useful healthcare knowledge acquired on their data from these participators in the form of their own decision models without revealing and sharing the patient-level sensitive data, thus protecting patient privacy. We demonstrate that our approach can successfully build accurate and robust prediction models, under privacy constraints, using the healthcare data collected from different geographical locations. We demonstrate the performance of our method using the Type-2 diabetes EHRs accumulated from multiple sources from all fifty states in the U.S. Our method was evaluated on diagnosing diabetes in the presence of insufficient number of patient records from certain regions without revealing the actual patient data from other regions. Using the proposed approach, we also discovered the important biomarkers, both universal and region-specific, and validated the selected biomarkers using the biomedical literature.
Keywords: Privacy-preserving data mining, Ensemble learning, Electronic health records, Boosting, Machine learning, Healthcare
1. Introduction
In recent years, electronic health records (EHRs) have been widely adapted at many healthcare facilities in an attempt to improve the quality of patient care and increase the productivity and efficiency of healthcare delivery. Typically, EHRs are generated and maintained within a particular healthcare facility, such as a hospital, clinic or physician’s office. These EHRs can not only aid in various daily healthcare operations but can also help in accurately diagnosing diseases, if utilized appropriately [32].
While the EHRs can resolve many of the existing problems associated with disease diagnosis, one of the main obstacles in effectively using them is the patient privacy and sensitivity of the medical information available in the EHR. EHRs generally contain patient information about demographics, diagnostics, medications, living habits and other health-related information. It is needless to say that most of these information is extremely sensitive [31]. EHR systems must abide the Health Insurance Portability and Accountability Act (HIPAA) [6] to preserve the privacy of patient information. Thus, the public EHR products must be certified by certain institutes such as Certification Commission for Healthcare Information Technology (CCHIT), and Office of the National Coordination for Health Information Technology (ONC) [38]. Due to these legal concerns and medical ethics [19, 4], physicians are always keen about maintaining the highest possible standards while protecting patient privacy [36].
Due to these concerns, even if the EHRs are available for storage and retrieval purposes, sharing of patient records between different healthcare facilities has become a major concern and has hampered some of the effective advantages of using EHRs. Due to this lack of data sharing, most of the facilities do not have any other option but to build their own clinical decision support systems with limited amount of patient data available in their own EHRs for important diagnosis related decisions. In addition, it becomes quite infeasible for a newly established healthcare facility, small hospital, or rural hospital to build a robust decision making system due to lack of sufficient patient records. However, to make effective decisions from clinical data, it is indispensable to have large amounts of data to train the decision making models. As a result, these small and/or rural hospitals are less motivated, and in 2011, only 20.8% of them were using EHR systems [12]. In this regard, it is clear that there is a conflicting objective of maintaining patient privacy and having sufficient data for modeling and decision making.
The problem statement of the work that is being developed in this paper is as follows. Given healthcare data collected from multiple facilities, how do we obtain a decision model that leverages the knowledge from all the facilities without revealing any patient specific information from any of the individual facilities. In other words, the goal is to develop a knowledge based data integration mechanism in a privacy-preserving context.
To deal with these challenges, we propose a privacy-preserving data mining framework based on horizontally distributed healthcare data. The goal of our work is to build an effective decision making system that can utilize the knowledge from multiple facilities (or geographical locations) without revealing any patient-level information [24]. In our approach, an elegant model for each participating facility to accurately learnt for approximating the local data distribution, and the useful healthcare knowledge acquired on such local data is then transferred in the form of their own decision models without revealing and sharing the sensitive data, thus, protecting the patient privacy. Transferring knowledge between multiple locations is a common practice with the goal of improving the prediction power [22]. Our approach can successfully build accurate and robust prediction models, under privacy constraints, with healthcare data collected from different geographical locations. Each participator shares its own local model with others and builds a specific integrated model based on its own specifications.
Merely trying to acquire the entire knowledge available from all the participators without carefully accounting for the distribution differences can potentially degrade the performance of the classifier [33]. While the overall data distribution for a particular disease must be similar within different hospitals since we are dealing with the same disease, there will still be certain significant differences that arise due to the differences in the demographics of the patient population. Such distribution differences will play a vital role in building robust integrated decision making models that are specific to the population group. However, in the horizontal distribution privacy-preserving problem, there is no access to the original EHR data, one can not directly measure the data distribution differences among participators but can only approximately say how large the difference might be by analyzing the difference between the models trained by each participator.
Most of the state-of-the-art privacy-preserving data mining methods for horizontally distributed data are built based on a star network, where an untrusted third-party is needed [40, 11]. Each participator shares their statistical data distribution with a centralized agent, and this central agent is responsible for building the integrated decision model [24]. However, this framework suffers from two important issues: 1) participators need frequent information exchange with the central agent and hence the communication cost is high; 2) the decision model is built on the central agent whose aim is to provide a decision support for all participators, but it ignores the data distribution differences between the participators.
In addition, in the horizontal distributed privacy preserving data mining literature, there is no prior work on preventing “negative impact during integration”. In our work, as each participator will build a specific integrated model based on their own specifications, they can selectively decide which of the models from other participators can be used to build the integrated model. We build local prediction models to represent data, detect the data distribution difference, and transfer knowledge. In our work, the AdaBoost algorithm is chosen to be the local learner for each participator because it is a simple yet effective classifier which is extensively studied in the literature.
The main contributions of our work are summarized as follows:
Propose an adaptive distributed privacy-preserving data mining technique based on an ensemble strategy which can successfully acquire knowledge from multiple healthcare facilities without gaining access to the sensitive patient data.
Propose a new integration scheme which does not require a third-party agent, and each participator can build its own integrated model based on its particular needs and can selectively prevent the “negative impact” during the integration process.
Demonstrate the performance of the proposed distributed privacy-preserving ensemble method using type-2 diabetes patient records gathered from multiple sources from all the fifty states in the U.S. Evaluate our method on diagnosing diabetes in the presence of insufficient number of patient records from certain regions without revealing the actual patient data from other regions.
Identify the important global and region-specific biomarkers for Type-2 diabetes and validate the selected biomarkers using the biomedical literature.
The rest of this paper is organized as follows: In section 2, we provide important relevant works on privacy-preserving data mining and also information about the Type-2 diabetes disease. In Section 3, we propose our adaptive distributed privacy-preserving ensemble method. Our experimental results along with the important biomarkers discovered using the proposed work are presented in Section 4. Finally, Section 5 concludes our discussion with some future research directions.
2. Related Work
In this section, we will provide the related literature in the field of privacy-preserving data mining and then discuss more about the Type-2 diabetes disease.
2.1. Privacy-Preserving Data Analysis
Recently, health data privacy has become an important area of research. As a result, privacy-preserving data mining has gained much more attention especially in the context of healthcare data analysis. The state-of-the-art methods for privacy-preserving data mining can be categorized under three types, namely, randomization, k-anonymization, and distributed privacy-preserving data mining [1]. In randomization approach, some techniques are used during the data collection process to induce perturbation in the selected attributes of the original data records for concealing certain sensitive information [3]. These techniques include swapping attribute values [14], principal component analysis (PCA) based techniques [18], adding random components which follow a known probability distribution [2], etc. However, in some applications such as healthcare, randomization methods are not sufficient. It has been shown that by incorporating certain publicly available data, the hidden sensitive information in the processed records can be recovered and hence the privacy will be compromised. The k-anonymity procedure [34] was proposed as a solution for this indirect de-identification issue. By using generalization and suppression techniques, the k-anonymity method guarantees that any attribute value can be indistinguishably backtracked to at least k records. In [7], k-Optimize algorithm has been developed to efficiently solve the problem of optimal k-anonymization in most cases.
The third category, which is the distributed privacy preservation, is closely related to secure distributed computation which is a research topic in cryptography [30]. In this scenario, non-fully trusting collaborators can jointly compute useful aggregate statistics over the entire dataset without sharing the original data. Thus the privacy of the individual dataset can be protected from various other participators. Based on the partitioning mechanism, distributed privacy-preserving data analysis can be grouped into two sub-categories: vertically partitioned distributed privacy preservation and horizontally partitioned distributed privacy preservation [10]. In the vertically partitioned distributed privacy preservation problem, each participant has a different set of attributes for the same group of data objects and the primary goal is to build a robust model that can leverage the entire set of attributes without revealing the individual details of the features to other participators. More detailed work about this approach can be found in [13]. In the horizontally partitioned distributed privacy preservation, each participator has different subset of records with the same set of attributes. The work proposed in this paper falls into this horizontally partitioned category where the patient data is being collected at multiple facilities and each patient record will consist of the same set of attributes. One of the first works in this category presented a strategy that extends the popular ID3 algorithm to two-party privacy preservation [23]. Then, there were a number of approaches proposed for horizontally partitioned distributed privacy preservation using various machine learning algorithms such as naive Bayes classifier [21], support vector machine [40], and ensemble based classifiers [16]. Amongst these methods, the ensemble-based approaches have demonstrated good performance in terms of simultaneously preserving privacy and having good accuracy.
Gambs et al. [16] proposed MultBoost algorithm which is a boosting-based privacy-preserving data mining method. However, the main problem with these above-mentioned models is that they need a third-party (central agent) that participates in the protocol to revise and aggregate the integrated final models. This also leads to an extra cost in processing. In addition, as each participator must have frequent contact with the third-party, a significant portion of the time is spent on the communication between the participators rather than the actual computation itself. Most importantly, those methods are not adaptable, i.e., a new integrated model has to be learned from scratch by repeating the entire learning process every time when a new participator is added. In this paper, we propose a distributed ensemble based horizontally partitioned privacy preservation algorithm which overcomes these limitations by making each participator compute their own local models independently from each other. Therefore, each participator can take advantage of the aggregate statistics (or a basic prediction model) without compromising their own privacy. Also the communication cost is substantially reduced because a third-party is not needed in our model, and the participators will have to only recompute the models for the newly integrated components once a new participator is added.
2.2. Type-2 Diabetes
Diabetes is the 7th leading cause of death in the United States [17] and the 8th leading cause of death in the world [39]. Around 29.1 million Americans (or 9.3% of the U.S. population) have diabetes [9]. In adults, type-2 diabetes (or insulin-dependent diabetes mellitus) accounts for approximately 90% to 95% of all diagnosed cases of diabetes. The risk for developing type-2 diabetes is mostly associated with older age, obesity, family history of diabetes, history of gestational diabetes, impaired glucose metabolism, physical inactivity, and race/ethnicity (African American, Alaska Native, American Indian, Asian American, Hispanic/Latino, or Pacific Islander American have a high prevalence of diabetes) [26, 9, 5].
There are several medical tests that can be performed to check if a person has diabetes or not. Currently, the American Diabetes Association (ADA) recommends four kinds of testing methods for diagnosing type-2 diabetes: 1) A1C test [27] which measures a person’s average levels of blood glucose over a period of 3 months. 2) Fasting Plasma Glucose (FPG) test [28] which measures the blood glucose in a person who has fasted for more than 8 hours. 3) Oral Glucose Tolerance Test (OGTT) [25] measures the blood glucose after a person fasts for at least 8 hours and 2 hours after the person drinks a liquid containing 75 grams of glucose dissolved in water. 4) Random Plasma Glucose (RPG) test [28] which is performed during a regular health checkup.
Though these medical diagnoses tests are relatively accurate (patients really have diabetes when these tests are positive), they typically have poor sensitivity (will miss a lot of cases). In 2012, 8.1 million (27.8% of 29.1 million) people with diabetes were undiagnosed [9]. In addition, in the data that we used in our study, only 1/8th of the patients suffering from diabetes were diagnosed by those medical tests. In addition, such tests cause inconvenience to the patients. Hence, it is an important problem to diagnose these patients at early stages through their electronic health records (EHR) using data-driven methods.
To improve the diagnosis of type-2 diabetes, a machine learning community hosted a “Practice Fusion Diabetes Classification” challenge [20] in 2012 which aims at developing some advanced EHR based type-2 diabetes diagnostic support system. There were a total of 9,948 patients, and amongst them 1,904 patients suffer from diabetes. These patients come from all the 50 states and the District of Columbia in the U.S. and the Commonwealth of Puerto Rico. For each patient, the EHRs were comprehensively collected from the following primary sources of information [22]:
Demographic information such as year of birth, gender, weight, and geographical location of each patient.
Diagnosis information consists of the ICD9 Codes.
Allergy and immunization consists of a list of allergies and vaccination records.
Laboratory information consists of lab test observations for lab panels, and the lab test results received from lab facilities.
Medication and Prescription consists of the medication history, where each medicine is identified by National Drug Code (NDC), and prescription records.
Patient smoking status is an ordinal status variable maintained on a yearly basis.
Transcripts consist of visited document records including allergy, medication, and diagnosis information.
We integrated all the information from 17 different sources and constructed a consolidated repository of diabetes EHR which contained 536 variables in total after combining all the data from multiple sources. It should be noted that, amongst all these features, only the gender and location are categorical in nature; the lab test results and personal information are real-valued attributes; certain status attributes such as smoking status, and emergency status have ordinal values. A significant majority of the remaining features are count variables.
3. Proposed work
In this section, we will explain the proposed framework for privacy-preserving data mining. Before describing the details of our proposed distributed ensemble based approach, we will first review the working of the standard AdaBoost algorithm [15]. The AdaBoost algorithm will be used as our local learner for each participator along with the decision stump which will be used as the weak learner. In our approach, we choose the AdaBoost algorithm because it is a simple, flexible and effective classifier, and it is constructed using a weighted combination of weak classifiers. Before going to the details of the proposed methods, we will first introduce the notations used in this paper in Table 1.
Table 1.
Notations used in this paper.
| Notation | Description |
|---|---|
| n (p) | sampling size of pth participator |
| Dp | dataset of pth participator |
| X n(p) | data matrix |
| Y | corresponding labels ∈ {+1, −1} |
| fn | name of the attribute |
| θ | test threshold |
| δ | sign of the test ∈ {+1, −1} |
| hp(t)(·) | the weak classifier trained at tth iteration in pth participator |
| α p(t) | the weight of hp(t)(·) |
| Hp(·) | the classifier trained in the pth participator |
| ϵ p | training error rate of pth participator |
| testing error rate of qth model in the pth participator’s training data | |
| S (p) | the index set of selected models for pth participator |
| λ p | instance proportion of pth participator |
| σ | a factor of the integrated weight |
AdaBoost is a well-known high-performance ensemble learning method which iteratively generates a strong classifier from a pool of weak hypotheses. In each iteration, a base classifier is learned, and based on the correctness of the prediction in each iteration, the weights of the training examples are updated. Thus, in the subsequent iteration, the base classifiers will focus on the misclassified samples in the previous iteration. The final ensemble classifier is a weighted combination of these base classifiers, where for each base classifier, the weight depends on the corresponding error rate. In other words, a classifier with lower error rate gets higher weight. Simple learners such as decision stumps (decision trees with only two leaf nodes) often perform well for AdaBoost [8]. Typically, a decision stump can be expressed using three parameters: (i)the name of the attribute to be tested (fn), (ii) the test threshold (θ), and (iii) the sign of the test (δ ∈ {+1, −1}). Note that a decision stump can only handle one attribute (feature) at a time and hence the weights of weak classifiers can also be used to measure the ability to distinguish the corresponding features conditional on the learning task. The final boosted model will be a linear combination of these independent decision stumps, and this independence would not require each participator to have exactly the same set of features which is another primary advantage of our proposed model. Finally, this will allow us to select the common important features among all participators, and each participator can take advantage of the useful aggregate model statistics without sharing the original data.
3.1. Adaptive Distributed Privacy Preserving using Boosting
In this section, we will discuss the proposed boosting based adaptive model for privacy-preserving data mining with horizontally partitioned data. In this case, each participant has different set of records with both common features and local unique attributes. Let denote the datasets of M participators, the dataset of pth participator contains a total of n(p) samples, and it can be represented as
where each example is a covariate vector with K(p) components and each label for the binary decision making that is being considered here. In our model, we employ AdaBoost algorithm to build an ensemble classifier for each participator, and these ensemble classifiers can be used to represent the data distribution of each participator. By sharing these local models with each other, all the participators can build their individual integrated model which takes advantage of other participators’ knowledge without direct access to the datasets. Hence, the privacy of the individual datasets can be preserved.
Firstly, the standard AdaBoost algorithm is applied to each participator for T boosting iterations, and set of T weak classifiers will be learned. In the decision stump case, each weak classifier can be represented by the variable set (fn, θ, δ), where fn denotes the name of the selected attribute, θ is the decision threshold of the attribute fn, and δ is the sign of the decision. For any instance Xi, the hypothesis h(Xi), which is made by decision stump, is either +1 or −1. For the pth participator, the ensemble classifier Hp(·) is a set of T weak classifiers:
where hp(t)(·) is the weak classifier at tth iteration and αp(t) is the corresponding weight of that weak classifier. For a particular test instance Xi, the binary prediction made by the pth participator’s local model can be defined as:
| (1) |
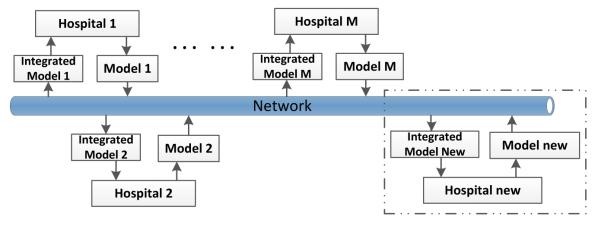
where sign {·} is the signum function. Once the local models are built, all the participators share their own models and sample sizes with each other, and hence each participator will receive M − 1 models from other participators. Then, each participator will build an integrated model independently based on their specific requirements. For example, some facilities might want to maximize the sensitivity of their models instead of the area under curve (AUC) value for their clinical decision support system. Using our ensemble based approach, they can use their own cost matrix to select the decision threshold for the integrated model that is being built in their own facility. The P2P network based distributed framework of the proposed ensemble system is shown in Figure 1, and we can see that no third-party (central agent) is needed to build an integrated model in our proposed framework.
Figure 1.
Block diagram representing various participators, the local and the integrated models built at each participator.
As each participator will build their local model independently, when a new participator is added, it will learn a local model by itself and share this trained model with other participators. Then, each existing participator will decide whether it needs to update the integrated model based on the new local model’s performance on their own data. We can see that this P2P network based framework is more adaptable and can provide more autonomy for participators than the star network based distributed privacy-preserving framework. Each participator integrates the final model independently, and hence the integrated model will take care of the specific needs of their own local data. In summary, having an individualized integrated model separately at each participator will tailor the model to their own local data. Only the integration component will have to be selectively computed again when a new participator is added, rather than re-training the entire model from scratch.
Each participator receives M − 1 models and another important issue needs to be resolved for a specific participator. That is, how to integrate those local models and its own model in an appropriate manner so that the integrated model performs better than the local model. Also, there is a slight risk that by integrating various unwanted (or poor) models, the performance of the integrated model might deteriorate. To prevent such “negative impact” during integration, when the model integration is performed for the pth participator, first one has to decide which of the other local models can be used to build the final integrated model.
The basic idea here is to not include the models from the other participators whose data distribution is very different from the data distribution of this pth participator. Since looking into the original data distribution of the other participators is infeasible due to patient privacy, we resort to applying all the other local models on the training set of pth participator, , and compare the error rate of each local model with the training error rate of pth participator’s trained model. Note that the models received from the other participators might include some decision stumps for their own unique local features. Hence, before using those models, the pth participator should select a suitable subset of common decision stumps based on fn. For the pth participator, the error rate of qth participator’s model is given by
| (2) |
where is the selected subset of decision stumps from Hq(·), the model trained by qth participator, I(·) is the indicator function. The training error rate of the pth participator’s trained model is given by
| (3) |
For every local model, we compute the difference between and ϵp. If is less than a certain threshold τ, then we can assume that the data distribution in pth participator and qth participator are similar, and we can use qth participator’s trained model to build the integrated model for pth participator. The integrated model only uses other local models (not the other participators’ data) and selects the ones with similar data distribution to that of the local data; thus, it indirectly strengthens the data distribution. By doing this, it avoids the overfitting problem in the presence of only a few samples in the local data. For our experiments, we set τ = 0.2 which is a relatively a large threshold. This is because ϵp (the training error rate of AdaBoost) is very small; thus, (ϵp + 0.2) is a reasonable threshold for (the testing error rate of qth model in the pth participator’s training data) as the qth model is not trained from the training data of pth participator.
Now that the model selection is complete, for pth participator we get a index set of selected models (S(p)) which will be used in the model integration. It should be noted that p also belongs to S(p). We will now explain the actual integration of the selected models. The model integration should not only take advantage of the aggregate statistics from other selected local models but also consider the specificity of the participator. To achieve this goal, we establish the following three criteria for the proposed ensemble based model integration in the pth participator:
More weight should be assigned to the participator’s own local model compared to any other local model with same sample size. This is because of the fact that the data from other participators might follow a slightly different distribution and hence one cannot give more importance to the other local models. The assumption here is that by adding other local models, one can strengthen the local data distribution. This is important especially since the participator weights suffer from insufficient data.
The weight of the pth participator’s own local model is positively related to n(p). This is because the more the number of samples, the fewer the mistakes that are caused by insufficient sampling.
The weight of the pth participator’s own local model should have an upper bound. Otherwise, the weight of selected participator’s model will become insignificant, and the final integrated model will be the same as pth participator’s own model and integration becomes unnecessary.
Considering these guidelines, the weight of each participator will be updated when building the integrated model for each participator. To illustrate this concept, let denote the weight assigned to the qth participator’s model when we compute the integrated model for pth participator, where p ∈ {1, 2, ··· ,M}, q ∈ S(p), and is the instance proportion of qth participator. is updated as follows:
| (4) |
where λmin = min(λq) is the minimum proportion among all the selected participators, λmax = max(λq) is the maximum proportion, and ⌈·⌉ denotes the ceiling function. We will now prove that the proposed weight update mechanism will satisfy all the three criteria mentioned earlier.
Theorem 1
The weight update mechanism will assign more weight to pth participator’s own model compared to any other local models if they have the same sample size (criterion 1).
Proof
If q ≠ p then ; that is to say the weight of other participator’s local model is λq. Now let us consider the value of , the weight of pth participator’s own model, i.e., when q = p. We note that the λq is bounded as follows. λmin ≤ λq ≤ λmax. We can see that the minimum possible value for is obtained when λp = λmin. Now, this value . Thus, if λp = λq, we have This means that for any participator, in the model integration procedure, its own model will have more weight compared to any of the other selected participators once they have the same sample size.
Theorem 2
The weight update mechanism will ensure that the weight of pth participator’s own model is positively related to n(p) (criterion 2).
Proof
For pth participator, since S(p) will be a constant set after model selection, λmin and λmax are also constant values. When is the weight of pth participator’s own model and contains only one variable , which is proportional to n(p) since the denominator is just a normalization factor. So, is positively related to n(p).
Theorem 3
The weight update mechanism will ensure that the weight of other participator’s local model will not become insignificant thus making the model integration unnecessary (criterion 3).
Proof
When , is the weight of pth participator’s own local model. We note that the λp is bounded as follows: λmin ≤ λp ≤ λmax. We observe that the maximum possible value for is obtained when λp = λmax. This limitation ensures that the weight of other participators’ high-performance weak learner will not become insignificant.
Algorithm 1 outlines our proposed BOPPID (BOosting-based Privacy-Preserving Integration of Distributed data) algorithm. First, each participator employs standard AdaBoost algorithm to train their own local model and obtain the training error (lines 2-3). Then, they share their trained models with other participators (line 4). After the model sharing process, each participator will independently build its own integration model. In lines 7-13, each participator applies all the other local models to its own training data and selects a subset of “good” models from other participators for the subsequent integration process. The sample size proportion of the selected local models is calculated in line 14. Finally, the integration model is built using Eq. (4) (lines 16-23).
3.2. Complexity Analysis
The computational complexity of proposed BOPPID depends on the AdaBoost algorithm in line 2. For pth participator, the overall cost of AdaBoost in all T iterations is Θ(K(p)(T + log n(p))) if the weak learner is a decision stump, and the training error rate can be calculated in Θ(n(p)). In the integration procedure for each participator, the cost of selecting a subset of the beneficial local models is Θ(Mn(p)). In the worst case scenario, where all M participators are selected, the computational cost of updating the weights for all participators is Θ(M) and generating the final classifier Hq*(·) takes Θ(MT) time. Thus, the total computational complexity of the pth participator is Θ(K(p)(T + log n(p)) + MT + Mn(p)). As each participator trains its local model and does the final integration independent from other participators, it is possible to perform these computations in parallel. In addition, note that the model integration can only start after all the participators complete the computation of their own local models, so the computational complexity of the proposed model depends on the participator with the largest number of samples. Hence, the total computational cost of BOPPID is Θ(Kmax(T+log nmax)+MT+Mnmax), here nmax and Kmax stands for the largest sample size and largest feature dimensions among all the M participators, respectively.
For the communication cost, let the network latency for transferring a model is f and the communication cost for sending and receiving a model are g and h respectively. For M participators, each of them will send their own model to M − 1 other participators, and receive M − 1 models from other participators. Hence, the total communication cost for BOPPID is (M − 1)(f + g + h).
Now let us consider the scenario where a new participator is added, and the number of participators grows from M to M + 1. In our model, only the integration part has to be recomputed, and hence the computational cost for the existing M participators is Θ((M + 1)T + (M + 1)nmax), and for the new participator, the computation cost is Θ(Kmax(T + log nnew) + MT + Mnmax). Here nnew and Kmax corresponds to the sample size and feature dimension of the new participator, respectively. Because all of the existing M participators will send their own models to the new participatorand receive a new model from the new participator, the communication cost for the existing M participators is (f + g + h) and for the new participator, the communication cost is M(f + g + h). However, if a new participator is added in the existing methods such as MultBoost, a new integrated model has to be retrained from the beginning. Therefore, the computation cost for all M + 1 participators is [16] and communication cost becomes 2T(f + g + h). Hence, we can clearly observe that our proposed model is more efficient when a new participator is added (which is a more practical scenario).
| ALGORITHM 1: BOosting-based Privacy-Preserving Integration of Distributed data (BOPPID) | |
|---|---|
| Input: The training sets of M participators , | |
| Number of boosting iterations (T), and | |
| Threshold for error rate increase (τ). | |
| Output: The set of M final classifiers {H1*(·), · · · , HM*(·)}. | |
| 1 | foreach p in M participators parallel do |
| 2 | Hp(·) ← AdaBoost; |
| 3 | ; |
| 4 | Share Hp(·) with all other participators |
| 5 | end |
| 6 | foreach p in M participators parallel do |
| 7 | Initialize the Index set of selected participators S ← {p}; |
| 8 | for q ← 1 to M do |
| 9 | ; |
| 10 | if then |
| 11 | Add q in S(p) |
| 12 | end |
| 13 | end |
| 14 | ; |
| 15 | Find λmax, λmin; |
| 16 | foreach q in S do |
| 17 | if p = q then |
| 18 | ; |
| 19 | else |
| 20 | ; |
| 21 | end |
| 22 | end |
| 23 | return |
| 24 | end |
3.3. Adaptive Variant of Parallel Boosting
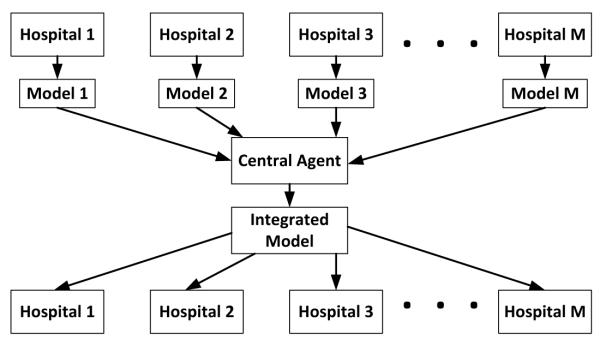
To strengthen our work, we also propose a new variant of an existing parallel boosting algorithm and make it applicable to the context of mining EHR data. In our previous work on parallel boosting [29], we developed a parallel variant of the boosting algorithm called AdaBoost.PL. Though originally designed for improving the computational efficiency, the overall layout of AdaBoost.PL can fit into the distributed privacy-preserving setting as it does not directly communicate the data from one participator to the others. The AdaBoost.PL algorithm follows the MapReduce workflows, where the original dataset is equally partitioned into M parts and mapped into M workers to learn M models which will then be reduced (integrated) into a final model. For each worker, its weak classifiers will be sorted with increasing order of αp(t) values (line 3 in Algorithm 2). The basic intuition of sorting the workers’ weak classifiers with respect to their weights is to place the classifiers with similar correctness at the same sorted level. This is a critical component of the AdaBoost.PL since this will ensure that like-minded classifiers will be merged during each boosting iteration. After sorting, hp*(t)(·) is the weak learner of pth participator at the tth iteration, and αp*(t) denotes the corresponding weight. In this paper, we generalize the idea of AdaBoost.PL and propose a new variant, AdaBoost.PL.V2, which can handle the diversity of sample size of each participator in the privacy-preserving context. It should be noted that similar to AdaBoost.PL, the proposed AdaBoost.PL.V2 is also built on a star network, which is shown in Figure 2. Most of state-of-the-art horizontally distributed privacy-preserving methods are also built on this star network, so that we can see to it that there is only one integration model that is being built for all hospitals.
Figure 2.
The framework of star network based horizontal distributed privacy-preserving method.
Thus, compared with BOPPID, AdaBoost.PL.V2 is less adaptive and cannot preserve the data characteristics of each participator. AdaBoost.PL.V2 discards the “map” part of the AdaBoost.PL because the datasets are distributed and stored by each participator, and αt is the weighted average, (instead of the standard average used in AdaBoost.PL) of αp*(t) for all possible p. The weights are based on the sample size proportion (line 9 in Algorithm 2).
The merged classifier, h(t)(·) is a ternary classifier, a variant of weak classifier, which can return ‘+1’, ‘−1’, and ‘0’ as a way of abstaining from answering [35]. It is built by taking a simple majority vote among weak classifiers of the worker as follows:
| (5) |
The ternary classifier will answer ‘0’ if equal number of positive and negative predictions are made by the workers’ weak classifiers. Otherwise, it will answer the majority prediction. In line 8, the weight of the ternary classifier are obtained by the weighted average of the corresponding classifier weights. Once all the ternary classifiers for T rounds are generated, the algorithm returns their weighted combination as the final classifier.
4. Experimental Results
In this section, we demonstrate the performance of the proposed approach using real-world EHRs of diabetes patients. We first present the clinical feature transformation performed on the EHR data. We will then compare the performance of our proposed model against the state-of-the-art distributed privacy preserving ensemble prediction models. In addition, we also perform a detailed study on the biomarkers selected by the proposed algorithm on this data. It shows that our proposed model can successfully select some important ‘universal’ and ‘region-specific’ biomarkers which can be used in the medical domain to improve the diagnosis of type-2 diabetes.
| ALGORITHM 2: AdaBoost.PL.V2 | |
|---|---|
| Input: Training sets of M participators | |
| , and | |
| Number of boosting iterations (T). | |
| Output: The final classifiers H(·) | |
| 1 | foreach p in M participators parallel do |
| 2 | Hp(·) ← AdaBoost; |
| 3 | Hp*(·) ← the weak classifiers in Hp(·) sorted w.r.t. αp(t); |
| 4 | Send Hp*(·) to central agent; |
| 5 | end |
| 6 | Initialize ; |
| 7 | for t ← 1 to T do |
| 8 | h(t)(·) ← Merge (h1*(t)(·), …, hM*(t)(·)); |
| 9 | ; |
| 10 | end |
| 11 | return |
4.1. Clinical Feature Pre-Processing
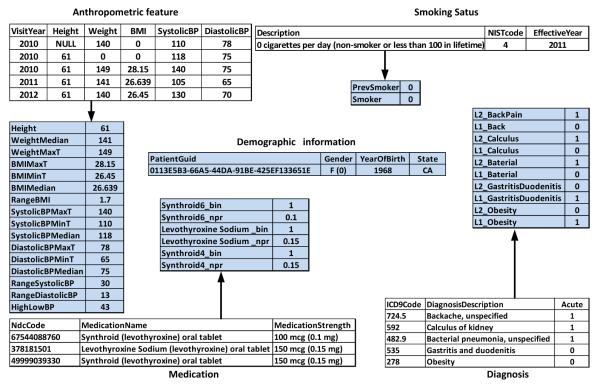
We now explain the clinical feature transformation procedure which transforms the raw EHR data to a format that is more suitable for data analysis. The original data contains patient records for a total of 9,948 patients, and each patient can be identified using a specific serial number. In Figure 3, we show the feature creation procedure from EHR data by considering a sample patient. In this example, we use several records from different categories for a particular patient (with PatientGuid “0113E5B3-66A5-44DA-91BE-425EF133651E”).
Figure 3.
Clinical feature transformation for a single patient.
We extracted all the features for distinct anthropometric variables present in the data. In this example, we consider height, weight, Body Mass Index (BMI), systolic blood pressure (SystolicBP), and diastolic blood pressure (DiastolicBP). To tackle the problem of multiple anthropometric values for the same patient, we represent each anthropometric feature using a set of summary statistics (maximum, minimum, and median). Note that, in this example, some anthropometric features are missing. It should be noted that certain missing values (like height in this example) are easy to fill. For example, we can confidently replace ‘NULL’ by 61 and calculate the corresponding BMI by using . However, other missing values like weight cannot be filled-in, and hence we leave them empty. “HighLowBP” is the difference between the median of systolic blood pressure and the median of diastolic blood pressure. Lab variables are also generated using a similar approach. In addition, we also created a variable which counts the number of times the lab was conducted for the patient. ICD-9 code is a list code for International Statistical Classification of Diseases, and each code presents a disease description. With the acute indicator, two binary variables can be created to reflect whether the patient has a special disease or not, and if the disease is present, whether it is acute or not (“L2_” represents acute and “L1_” represents not acute). In this example, the codes 278 and 724.5 represent obesity and backache, respectively. Because this patient suffered from serious backache only once, we give the value of 1 to “L2_ BackPain” feature. For the medication information, we created two variables for each distinct medication (according to NDC) given to the patient; one feature represents the number of times the individual medication was given to the patient, and the other feature represents the dose. There are several states corresponding to smoking status which can be represented using ordinal numbers, and we build two new features, one for the current smoking state and another for the smoking history. When the patient has never smoked in the past, the status of “0 cigarettes per day” is denoted by 0.
In summary, based on the generated features which are listed in tables with pale blue color, one can observe that following our transformation procedure not only helps in immensely reducing the dimensionality and complexity of the raw EHR data, but also summarizes the complex EHRs into a succinct representation which is then used for building prediction models.
4.2. Experimental Setup
We will demonstrate the performance of the proposed algorithms on improving the diagnosis of the diabetes condition. Hence, for our experiments, we selected the top 14 states based on the total patient population in each state (which will be considered as a participator). Table 2 shows the demographic statistics of these 14 selected states.
Table 2.
Demographic statistics of the top 14 states based on patient population.
| State | Total No. of patients |
No. of Diabetes Patients |
No. of Non-diabetes Patients |
Prevalence Rate (%) |
|---|---|---|---|---|
| Arizona (AZ) | 295 | 56 | 239 | 18.98% |
| California (CA) | 1917 | 258 | 1659 | 13.46% |
| Florida (FL) | 804 | 158 | 646 | 19.65% |
| Illinois (IL) | 412 | 75 | 337 | 18.20% |
| Michigan (MI) | 344 | 61 | 283 | 17.73% |
| Missouri (MO) | 702 | 104 | 598 | 14.81% |
| New Jersey (NJ) | 575 | 119 | 456 | 20.70% |
| Nevada (NV) | 495 | 135 | 360 | 27.27% |
| New York (NY) | 557 | 167 | 390 | 29.98% |
| Ohio (OH) | 515 | 111 | 404 | 21.55% |
| Pennsylvania (PA) | 250 | 67 | 183 | 26.80% |
| South Dakota (SD) | 325 | 40 | 285 | 12.31% |
| Texas (TX) | 897 | 243 | 654 | 27.09% |
| Virginia (VA) | 484 | 79 | 405 | 16.32% |
We compare our proposed adaptive distributed privacy-preserving ensemble system with the MultBoost [16] and local Adaboost (LOCAL_Ada) algorithms. LOCAL_Ada algorithm is a local model obtained by applying the standard Adaboost on each participator independently. For all the algorithms, the number of boosting iterations is set to 100. In Table 3, we provide the performance results of AUC values from different algorithms using 10-fold cross validation.
Table 3.
Performance comparison of different algorithms based on the AUC values (along with their standard deviation)
| State | LOCAL_Ada | Multboost | AdaBoost.PL.V2 | BOPPID |
|---|---|---|---|---|
| AZ | 0.799 ± 0.103 | 0.831 ± 0.085 | 0.845 ± 0.096 | 0.865 ± 0.088 |
| CA | 0.895 ± 0.046 | 0.844 ± 0.060 | 0.870 ± 0.064 | 0.902 ± 0.049 |
| FL | 0.882 ± 0.065 | 0.861 ± 0.059 | 0.878 ± 0.056 | 0.899 ± 0.053 |
| IL | 0.849 ± 0.071 | 0.876 ± 0.076 | 0.885 ± 0.053 | 0.896 ± 0.046 |
| MI | 0.881 ± 0.065 | 0.926 ± 0.038 | 0.923 ± 0.037 | 0.934 ± 0.038 |
| MO | 0.914 ± 0.034 | 0.886 ± 0.052 | 0.902 ± 0.048 | 0.921 ± 0.040 |
| NJ | 0.802 ± 0.040 | 0.835 ± 0.051 | 0.847 ± 0.042 | 0.857 ± 0.048 |
| NV | 0.863 ± 0.045 | 0.877 ± 0.033 | 0.891 ± 0.029 | 0.901 ± 0.019 |
| NY | 0.858 ± 0.060 | 0.857 ± 0.038 | 0.873 ± 0.061 | 0.891 ± 0.056 |
| OH | 0.885 ± 0.041 | 0.879 ± 0.066 | 0.892 ± 0.053 | 0.900 ± 0.050 |
| PA | 0.816 ± 0.082 | 0.809 ± 0.117 | 0.873 ± 0.071 | 0.885 ± 0.071 |
| SD | 0.892 ± 0.072 | 0.920 ± 0.067 | 0.929 ± 0.056 | 0.937 ± 0.047 |
| TX | 0.854 ± 0.040 | 0.838 ± 0.038 | 0.845 ± 0.027 | 0.871 ± 0.027 |
| VA | 0.789 ± 0.056 | 0.827 ± 0.045 | 0.838 ± 0.072 | 0.863 ± 0.059 |
In Table 4, we present the comparison of F-measure values which is calculated as follows:
| (6) |
where , and ; therefore, a high value of F-measure indicates that both precision and sensitivity are reasonably high. It should be noted that the positive individuals are diabetics and the negative individuals are non-diabetics. Thus, here TP corresponds to the number of diabetics correctly predicted by the classifier, FN corresponds to the number of diabetics wrongly predicted as non-diabetics, and FP is the number of nondiabetics wrongly predicted as diabetics.
Table 4.
Performance comparison of different algorithms based on the F-measure values (along with their standard deviation)
| State | LOCAL_Ada | Multboost | AdaBoost.PL.V2 | BOPPID |
|---|---|---|---|---|
| AZ | 0.541 ± 0.141 | 0.592 ± 0.084 | 0.612 ± 0.148 | 0.631 ± 0.151 |
| CA | 0.592 ± 0.092 | 0.498 ± 0.049 | 0.562 ± 0.079 | 0.608 ± 0.090 |
| FL | 0.664 ± 0.098 | 0.615 ± 0.085 | 0.643 ± 0.083 | 0.679 ± 0.092 |
| IL | 0.572 ± 0.102 | 0.643 ± 0.136 | 0.630 ± 0.110 | 0.659 ± 0.088 |
| MI | 0.619 ± 0.110 | 0.708 ± 0.087 | 0.707 ± 0.087 | 0.720 ± 0.091 |
| MO | 0.654 ± 0.069 | 0.608 ± 0.097 | 0.646 ± 0.094 | 0.667 ± 0.103 |
| NJ | 0.534 ± 0.059 | 0.583 ± 0.058 | 0.585 ± 0.056 | 0.589 ± 0.063 |
| NV | 0.668 ± 0.049 | 0.691 ± 0.058 | 0.705 ± 0.058 | 0.715 ± 0.043 |
| NY | 0.699 ± 0.086 | 0.682 ± 0.054 | 0.709 ± 0.099 | 0.731 ± 0.093 |
| OH | 0.657 ± 0.074 | 0.639 ± 0.104 | 0.688 ± 0.080 | 0.701 ± 0.084 |
| PA | 0.637 ± 0.090 | 0.623 ± 0.128 | 0.693 ± 0.092 | 0.721 ± 0.112 |
| SD | 0.666 ± 0.190 | 0.696 ± 0.159 | 0.691 ± 0.140 | 0.732 ± 0.107 |
| TX | 0.661 ± 0.065 | 0.628 ± 0.050 | 0.639 ± 0.035 | 0.675 ± 0.042 |
| VA | 0.493 ± 0.088 | 0.512 ± 0.075 | 0.560 ± 0.096 | 0.566 ± 0.079 |
We observe that for all the 14 states, our proposed algorithm can diagnose type-2 diabetes more accurately compared with the other algorithms. This demonstrates that we have successfully transferred useful medical knowledge and clinical information within all the participators under the privacy constraints without revealing the data itself from each participator. This also means that those participators can take advantage of the aggregated global models without compromising the privacy of individual patients.
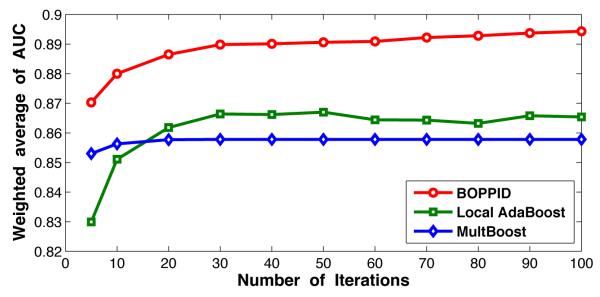
Figure 4 shows the 10-fold cross validation result of weighted average AUC values at different iterations of the algorithm. The weighted average AUC is defined as:
| (7) |
where AUC(p) is the AUC value of pth participator, n(p) is the number of patients in the pth participator. The figure shows that the proposed algorithm always works better than MultBoost and Local AdaBoost, and only a few selected important features (or iterations) can provide a good prediction model.
Figure 4.
Comparison of weighted average AUC values of Local AdaBoost, MultBoost, and BOPPID algorithms on the diabetes dataset for 100 iterations.
4.3. Biomarker Discovery
Biomarkers are important indicators used to diagnose a particular disease in a clinical setting. From Figure 4, we can see that the weighted average AUC of our proposed model achieves 0.88 after 10 iterations and approximately 0.89 after 20 iterations. This indicates that the top selected features in each state can well represent the corresponding data distribution. It should be mentioned that since the weak classifier used in our algorithm is a decision stump, each iteration will correspond to the usage of only one feature with a simple split. In Figure 5, we show the selected biomarkers for each state after 10 iterations (in the left) and 20 iterations (in the right). In the 10 iterations scenario, we find 39 important biomarkers, and in the 20 iterations case, this number becomes 60. For comparison, we present these two settings under a same coordinate system, where the vertical axis is the index of selected features and the horizontal axis corresponds to the list of states that contain this attribute in their top feature list. Figure 5 clearly shows the selected important features and the corresponding state.
Figure 5.
Selected biomarkers for each state.
From Figure 5, we can conclude that there are a total of 6 universal biomarkers: “YearOfBirth” which represents the age of patient, “High-LowBP” measures the difference between systolic blood pressure and diastolic blood pressure, “L2_HypertensionEssential” is a biomarker that reflects whether the patient has been diagnosed with hypertension or not, “L2_MixedHyperlipidemia” is an indicator that tells whether the patient has suffered with mixed hyperlipidemia or not, “TotDiagPerVisit” indicates the number of complications the patient had, and “medication_diag_NA” indicates whether the patient was previously diagnosed with type-2 diabetes through medical tests. These 6 selected features meet the well known common knowledge in the clinical domain. The clinical study suggests that hypertensive persons are more predisposed to the development of diabetes than normotensive persons. Moreover, up to 75% of cardiovascular disease (CVD) in diabetes is attributed to hypertension [37] and older people are more likely to suffer from type-2 diabetes [26]. Medical diagnoses tests are relatively accurate, i.e., most of the patients who were diagnosed with diabetes by the medical tests actually have diabetes. However, the sensitivity of these tests is low, i.e., a lot of diabetic patients remain undetected through these tests.
Our results can also reflect that overweight or obese is closely related to type-2 diabetes [26], but for different states it is represented in different ways. For most of the states the body mass index (BMI) (related to features 6-9) is more important than the direct body weight, while for few other states direct body weight plays an important role as well. It can be seen from our results, that our approach can provide a more accurate set of “region-specific” biomarkers in addition to the global markers. Such analysis on region-specific biomarkers in comparison to the overall biomarkers (which are typically known in the medical literature) can provide new medical insights into specific regional patient data which can thus lead to new discoveries in the clinical domain.
5. Conclusions and future work
Healthcare in the United States is currently undergoing a revolutionary transformation and EHRs are playing a vital role in improving the quality of patient care. However, due to the patient privacy and the sensitivity of the patient information that is being stored in the EHRs, there are considerable barriers to EHR proliferation. In this paper, we developed a novel distributed privacy-preserving integration method based on an ensemble based strategy for building robust prediction models from EHR data. Using our approach, each participator will need to reveal only limited model information built using the local data without revealing any patient-specific information. The local models built from each participator will be effectively combined to build an integrated model that is specific to each participator. This integrated model is built by taking advantage of aggregate knowledge from all the participators instead of the local participator’s data alone. Compared to other existing works, our proposed framework can prevent the “negative impact” during integration from multiple sources, which typically happens when the data distribution differences amongst the participators are very large, by building a specific integration model for each participator with only a few selected local models instead of taking all the local models. We demonstrated the performance of our proposed method using the Type-2 diabetes EHR data and have shown that constructing a global model which utilizes other local models performs better compared to the original local models built on each participator’s data separately. In addition, we also successfully identified some important universal/global and region-specific biomarkers.
In the future, we will try to find more accurate ways to measure the difference of data distributions among multiple participators under privacy constraints. We also plan to extend our work with the idea of k-anonymity, so that we can measure the data distributions more accurately without compromising on patient privacy.
Acknowledgements
This work was supported in part by the National Science Foundation grants IIS-1242304, IIS-1231742, IIS-1527827 and the National Institutes of Health grant R21CA175974.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- [1].Aggarwal CC, Philip SY. A general survey of privacy-preserving data mining models and algorithms. Springer; 2008. [Google Scholar]
- [2].Agrawal D, Aggarwal CC. Proceedings of the twentieth ACM SIGMOD-SIGACT-SIGART symposium on Principles of database systems. ACM; 2001. On the design and quantification of privacy preserving data mining algorithms; pp. 247–255. [Google Scholar]
- [3].Agrawal R, Srikant R. Privacy-preserving data mining. ACM Sigmod Record. 2000;29(2):439–450. [Google Scholar]
- [4].Alther M, Reddy CK. Clinical decision support systems. In: Reddy CK, Aggarwal CC, editors. Healthcare Data Analytics. Chapman and Hall/CRC Press; 2015. [Google Scholar]
- [5].American Diabetes Association and others Diagnosis and classification of diabetes mellitus. Diabetes care. 2008;31(Supplement 1):S55–S60. doi: 10.2337/dc08-S055. [DOI] [PubMed] [Google Scholar]
- [6].An Act Health insurance portability and accountability act of 1996. Public Law. 1996;104:191. [PubMed] [Google Scholar]
- [7].Bayardo RJ, Agrawal R. Data privacy through optimal k-anonymization. Data Engineering, 2005. ICDE 2005. Proceedings. 21st International Conference on; IEEE; 2005. pp. 217–228. [Google Scholar]
- [8].Caruana R, Niculescu-Mizil A. Data mining in metric space: an empirical analysis of supervised learning performance criteria. Proceedings of the tenth ACM SIGKDD international conference on Knowledge discovery and data mining; ACM; 2004. pp. 69–78. [Google Scholar]
- [9].Centers for Disease Control and Prevention and others . National diabetes statistics report: estimates of diabetes and its burden in the united states, 2014. US Department of Health and Human Services; Atlanta, GA: 2014. [Google Scholar]
- [10].Clifton C, Kantarcioglu M, Vaidya J, Lin X, Zhu MY. Tools for privacy preserving distributed data mining. ACM SIGKDD Explorations Newsletter. 2002;4(2):28–34. [Google Scholar]
- [11].Clifton C, Kantarciolu M, Doan A, Schadow G, Vaidya J, Elmagarmid A, Suciu D. Privacy-preserving data integration and sharing. Proceedings of the 9th ACM SIGMOD workshop on Research issues in data mining and knowledge discovery; ACM; 2004. pp. 19–26. [Google Scholar]
- [12].DesRoches CM, Worzala C, Joshi MS, Kralovec PD, Jha AK. Small, nonteaching, and rural hospitals continue to be slow in adopting electronic health record systems. Health Affairs. 2012;31(5):1092–1099. doi: 10.1377/hlthaff.2012.0153. [DOI] [PubMed] [Google Scholar]
- [13].Dwork C, Nissim K. Advances in Cryptology–CRYPTO 2004. Springer; 2004. Privacy-preserving datamining on vertically partitioned databases; pp. 528–544. [Google Scholar]
- [14].Fienberg SE, McIntyre J. Privacy in statistical databases. Springer; 2004. Data swapping: Variations on a theme by dalenius and reiss; pp. 14–29. [Google Scholar]
- [15].Freund Y, Schapire RE. A decision-theoretic generalization of on-line learning and an application to boosting. Journal of computer and system sciences. 1997;55(1):119–139. [Google Scholar]
- [16].Gambs S, Kégl B, Aïmeur E. Privacy-preserving boosting. Data Mining and Knowledge Discovery. 2007;14(1):131–170. [Google Scholar]
- [17].Hoyert DL, Xu J, et al. Deaths: preliminary data for 2011. National vital statistics reports. 2012;61(6):1–51. [PubMed] [Google Scholar]
- [18].Huang Z, Du W, Chen B. Deriving private information from randomized data. Proceedings of the 2005 ACM SIGMOD international conference on Management of data; ACM; 2005. pp. 37–48. [Google Scholar]
- [19].Jha AK, DesRoches CM, Campbell EG, Donelan K, Rao SR, Ferris TG, Shields A, Rosenbaum S, Blumenthal D. Use of electronic health records in us hospitals. New England Journal of Medicine. 2009;360(16):1628–1638. doi: 10.1056/NEJMsa0900592. [DOI] [PubMed] [Google Scholar]
- [20].kaggle.com Practice Fusion Diabetes Classification: Identify patients diagnosed with Type 2 Diabetes. 2012 https://www.kaggle.com/c/pf2012-diabetes.
- [21].Kantarcıoglu M, Vaidya J, Clifton C. Privacy preserving naive bayes classifier for horizontally partitioned data. IEEE ICDM workshop on privacy preserving data mining.2003. pp. 3–9. [Google Scholar]
- [22].Li Y, Vinzamuri B, Reddy CK. Constrained elastic net based knowledge transfer for healthcare information exchange. Data Mining and Knowledge Discovery. 2015;29(4):1094–1112. [Google Scholar]
- [23].Lindell Y, Pinkas B. Advances in Cryptology-CRYPTO 2000. Springer; 2000. Privacy preserving data mining; pp. 36–54. [Google Scholar]
- [24].Mathew G, Obradovic Z. Distributed privacy-preserving decision support system for highly imbalanced clinical data. ACM Transactions on Management Information Systems (TMIS) 2013;4(3):12. [Google Scholar]
- [25].Matsuda M, DeFronzo RA. Insulin sensitivity indices obtained from oral glucose tolerance testing: comparison with the euglycemic insulin clamp. Diabetes care. 1999;22(9):1462–1470. doi: 10.2337/diacare.22.9.1462. [DOI] [PubMed] [Google Scholar]
- [26].National Diabeties Information Clearinghouse Am I at risk for type 2 diabetes? taking steps to lower your risk of getting diabetes. Jun, 2012. NIH Publication No. 12-4805.
- [27].National Diabeties Information Clearinghouse The A1C test and diabetes. Mar, 2014. NIH Publication No. 147816.
- [28].National Diabeties Information Clearinghouse Diagnosis of diabetes and prediabetes. Jun, 2014. NIH Publication No. 144642.
- [29].Palit I, Reddy CK. Scalable and parallel boosting with mapreduce. Knowledge and Data Engineering, IEEE Transactions on. 2012;24(10):1904–1916. [Google Scholar]
- [30].Pinkas B. Cryptographic techniques for privacy-preserving data mining. ACM SIGKDD Explorations Newsletter. 2002;4(2):12–19. [Google Scholar]
- [31].Rahman R, Reddy CK. Electronic health records: A survey. In: Reddy CK, Aggarwal CC, editors. Healthcare Data Analytics. Chapman and Hall/CRC Press; 2015. [Google Scholar]
- [32].Reddy CK, Aggarwal CC. HealtHcare Data analytics. CRC Press; 2015. [Google Scholar]
- [33].Reddy CK, Li Y. A review of clinical prediction models. In: Reddy CK, Aggarwal CC, editors. Healthcare Data Analytics. Chapman and Hall/CRC Press; 2015. [Google Scholar]
- [34].Samarati P. Protecting respondents identities in microdata release. Knowledge and Data Engineering, IEEE Transactions on. 2001;13(6):1010–1027. [Google Scholar]
- [35].Schapire RE, Singer Y. Improved boosting algorithms using confidence-rated predictions. Machine learning. 1999;37(3):297–336. [Google Scholar]
- [36].Simon SR, Kaushal R, Cleary PD, Jenter CA, Volk LA, Orav EJ, Burdick E, Poon EG, Bates DW. Physicians and electronic health records: a statewide survey. Archives of Internal Medicine. 2007;167(5):507–512. doi: 10.1001/archinte.167.5.507. [DOI] [PubMed] [Google Scholar]
- [37].Sowers JR, Epstein M, Frohlich ED. Diabetes, hypertension, and cardiovascular disease an update. Hypertension. 2001;37(4):1053–1059. doi: 10.1161/01.hyp.37.4.1053. [DOI] [PubMed] [Google Scholar]
- [38].US Department of Health, Human Services and others Health information technology: Initial set of standards, implementation specifications, and certification criteria for electronic health record technology. Federal Register. 2010;75(8):13. [PubMed] [Google Scholar]
- [39].World Health Organization The top 10 causes of death. 2012 http://www.who.int/mediacentre/factsheets/fs310/en/
- [40].Yu H, Jiang X, Vaidya J. Privacy-preserving svm using nonlinear kernels on horizontally partitioned data. Proceedings of the 2006 ACM symposium on Applied computing; ACM; 2006. pp. 603–610. [Google Scholar]