Abstract
An automated noise-robust premature ventricular contraction (PVC) detection method is proposed based on the sparse signal decomposition, temporal features, and decision rules. In this Letter, the authors exploit sparse expansion of electrocardiogram (ECG) signals on mixed dictionaries for simultaneously enhancing the QRS complex and reducing the influence of tall P and T waves, baseline wanders, and muscle artefacts. They further investigate a set of ten generalised temporal features combined with decision-rule-based detection algorithm for discriminating PVC beats from non-PVC beats. The accuracy and robustness of the proposed method is evaluated using 47 ECG recordings from the MIT/BIH arrhythmia database. Evaluation results show that the proposed method achieves an average sensitivity of 89.69%, and specificity 99.63%. Results further show that the proposed decision-rule-based algorithm with ten generalised features can accurately detect different patterns of PVC beats (uniform and multiform, couplets, triplets, and ventricular tachycardia) in presence of other normal and abnormal heartbeats.
Keywords: electrocardiography, medical signal detection, medical signal processing, knowledge based systems, decision trees
Keywords: sparse signal decomposition, temporal features, automated PVC detection, noise robust PVC detection, premature ventricular contraction, decision rules, ECG signal sparse expansion, electrocardiogram, mixed dictionaries, QRS complex, P waves, T waves, baseline wanders, muscle artefacts, decision rule based detection algorithm, MIT-BIH arrhythmia database
1. Introduction
Accurate detection of premature ventricular contraction (PVC) beats in electrocardiogram (ECG) signal is essential for predicting life-threatening ventricular arrhythmias [1–3]. Many methods were presented based on spline wavelet [1], Gaussian process classifiers (GPCs) and support vector machines (SVMs) [2], wave-based Bayesian framework [4], fuzzy neural network (FNN) [5], wavelet transform (WT) and timing interval (TI) features [6], Haar wavelet coefficients [7], Gaussian process and S-transform [8], WT and discrete cosine transform (DCT) [9], SVM and particle swarm optimisation (PSO) [10], principal component analysis (PCA) and feed-forward artificial neuron network (ANN) using the multi-dimensional PSO scheme [11], high-order statistics (HOS) and GPC [12], 26 features and Kth nearest-neighbours (KNN) rule [13], and the quadratic spline wavelet and FNN [14].
In this section, we briefly summarise signal features and classifiers used for discriminating PVC beats from non-PVC beats. In [1], Chang et al. presented a PVC detection based on the biorthogonal spline wavelet-based R-peak detection and two features including the sum of the trough, and the sum of the R-peak with minimum. In [4], Omid Sayadi et al. presented a detection of PVCs using a wave-based Bayesian framework with an extended Kalman filter. In [5], Joon S. Lim presented a set of eight generalised coefficient features for PVC classification using the Haar WT and the neuro-fuzzy system with the bounded sum of weighted fuzzy membership functions. In [6], Inan et al. presented a robust neural network (NN)-based PVC classification using quadratic spline WT and TI features. In [7], Adnane and Belouchrani presented a PVC detection based on the Haar coefficients and fixed feature thresholding rule. The product of the third detail and fourth detail coefficients is used to discriminate between normal and PVC beats. In [8], Ya Bazi et al. presented a PVC detection and classification using Gaussian process and S-transform.
In [9], Khorrami and Moavenian presented a comparative study of discrete wavelet transform (DWT), continuous wavelet transform (CWT), and DCT transforms for classifying ECG arrhythmias. In [10], the effectiveness of different approaches based on the KNN classifier, radial basis function (RBF) NN, three SVM classifiers (SVM-linear, SVM-poly and SVM-rbf), PCA-KNN, PCA-RBF, PCA-SVM-rbf, and PSO-SVM classifiers was studied for ECG beats. In [13], Christov et al. presented PVC and normal beat classification using the KNN rule and 26 parameters (including, 11 × 2 for two ECG leads, QRS width and three parameters derived from a single vectorcardiogram plane). In [14], Shyu et al. presented a wavelet-based ventricular premature contraction (VPC) detection approach with the QRS duration and QRS area features that are obtained from the three and four scales, respectively, and the FNN classifier.
The results of the previous studies showed that the methods could not distinguish between PVCs and left bundle branch block (LBBB) beats [4, 6, 14]. Based on the classification results reported in [4] for normal, PVC and other beat classes, it is noted that the method had PVC beat class detection rates of below 95% for a few ECG records 116, 201, 202, 213, 215, and 219 but it had other beat classification rates of below 75% for the records 100, 105, 114, 200, 202, 203, 205, 208, 213, 220, 223, and 234. In most methods, the database annotation is used to locate R-peaks in ECG signals and to perform ECG wave boundary recognition [2, 6]. In practice, a good performance of PVC detection method depends heavily on the accurate and reliable detection of the R-wave peaks under varying PQRST morphologies and noisy conditions. Most studies have shown that large datasets greatly reduces classification accuracy due to the significant variations in ECG beat morphologies [2, 4, 6]. Existing methods had poor detection accuracy for the ECG signals with LBBB, right bundle branch block (RBBB), atrial premature (AP) beats, aberrated AP beats, atrial flutter, and paced beats. Results further showed that most methods had poor tradeoff between the sensitivity (Se) and specificity (Sp). Thus, automatic PVC beat detection is still a challenging problem under different kinds of PQRST morphologies and background noises.
In this Letter, an automated noise-robust PVC detection method is presented based on the sparse signal decomposition, R-peak determination, temporal feature extraction, and decision-rule-based PVC detection algorithm. The rest of the Letter is organised as follows. Section 2 describes the sparse expansions of ECG signals and background noises on mixed dictionaries. The proposed temporal features and decision-rule-based PVC detection algorithm are explained in detail. In Section 3, accuracy and robustness of the proposed method is validated using different types of clean and noisy ECG signals. Finally, conclusions are drawn in Section 4.
2. Proposed PVC detection method
In this section, we first introduce sparse representation of ECG signals on mixed dictionaries for simultaneously enhancing the QRS complex and reducing the influence of P and T waves, baseline wander (BW), power line interference (PLI), and muscle artefact (MA).
2.1. ECG signal decomposition on mixed dictionaries
In this Letter, we assume that the composite ECG signal x is compactly represented on hybrid dictionary matrix , M > N, including time-localised and frequency-localised elementary waveforms. For a predefined mixed dictionary with M > N, a discrete-time signal x can be expressed as
| (1) |
where α = [α1, α2, α3, …, αM] is the sparse transformed coefficient vector [15–17]. The representation overcomplete dictionary matrix can either be designed using analytical basis functions or constructed using the beat patterns extracted from the reference ECG signals. The frequency-domain localised components such as BW and PLI noises and low-frequency (LF) components of an ECG beat can be effectively modelled using sinusoidal waveforms. The spike-like components of MA may be modelled as impulsive elementary waveforms. As compared with transform matrix constructed using a single basis function, the additive components of the ECG signal and background noise can be well approximated with a mixed dictionary matrix including both time-localised and frequency-localised elementary waveforms derived from different basis functions. Thus, the sinusoidal and impulse basis functions are used for compact representations of ECG signals and background noise. In this Letter, the ECG signal is decomposed using the predefined overcomplete hybrid dictionary matrix with a size of N × M as
| (2) |
where N denotes the length of discrete-time ECG sequence x, M denotes the number of elementary waveforms (or columns) of hybrid dictionary , denotes the BW dictionary designed for capturing the BW components, ΨLF denotes the LF dictionary designed for capturing the P-wave, T-wave, and LF components of QRS complexes, ΨPLI denotes the PLI dictionary for capturing the PLI components and ΨHF denotes the high-frequency (HF) dictionary for capturing the high-slope portions of the QRS complexes and muscle spikes in the ECG signal. The HF dictionary ΨHF contains the elementary impulse waveforms that are well localised in the time domain. The HF dictionary is constructed as
| (3) |
The BW dictionary ΨBW, LF dictionary ΨLF, and PLI dictionary ΨPLI matrices are constructed using the elementary sine and cosine waveforms computed from the discrete sine and cosine basis functions, which can adequately capture the noise components including the BW, PLI, and local ECG waves including the P-wave, T-wave, and wide QRS complexes. For a given frequency bin range of each aforementioned dictionary, a set of elementary sine waveforms is computed as
| (4) |
where for i = N–1, otherwise and a set of elementary cosine waveforms is computed as
| (5) |
where for i = 0, otherwise εi = 1. In this Letter, we use both discrete cosine and sine elementary waveforms in order to reduce the waveform discontinuities at the block boundaries. The computational complexity of the sparse coefficient estimation algorithm depends upon the size of the dictionary matrix and the number of iterations performed by the algorithm [16, 18]. Depending on specific-event detection, feature parameter estimation, compression and denoising problems, the sizes of the cosine and sine dictionaries can be adopted based on the frequency characteristics of the signals of interests [16]. Since this Letter mainly focuses on the detection of the PVC beats, the sizes of the above sinusoidal dictionary matrices such as ΨBW, ΨPLI, and ΨLF are determined based on the dominant frequency ranges of the BW, the PLI, and the ECG local waves (including P-wave, wide QRS complex, and T-wave). The frequency of BW noise is typically below 0.8 Hz, extending up to 1 Hz during stress tests [19]. The PLI signals fall within a grid operating frequency range of 57–63 (or 47–53) Hz for the fundamental of 60/50 Hz. The dominant frequencies of the P and T waves lie in the range of 2–6 Hz [20]. The dominant frequencies of the wide QRS complexes generally fall within a range of 3–10 Hz. The variations of dominant frequencies of wide and narrow QRS complexes are observed in the range of 3–40 Hz [21]. In this Letter, the frequency bin ranges for capturing the BW, PLI, and LF components are chosen as: [0–1], [47–53], and [1–6] Hz. For a given frequency F1, the column number is computed as , where Fs is the sampling rate and N is the length of the signal. Then, the elementary sine and cosine waveforms are obtained using mathematical expressions in (4) and (5) for each of the desired frequency bin ranges. The LF dictionary matrix ΨLF is constructed for adequately capturing the P and T waves and the wide QRS complexes of the ECG signal.
For a predefined overcomplete dictionary matrix Ψ and ECG signal x, the sparse coefficients vector α is estimated by using the ℓ1-norm-regularised least squares algorithm [17, 18]
| (6) |
where and are known as the reconstruction error term and the sparsity term, respectively, x is a signal to be decomposed, and λ is a regularisation parameter for sparsity that controls the relative importance of the fidelity and the sparsity of vector α. The ℓ1-norm and ℓ2-norm of the vector α are defined as and , respectively. The estimated sparse coefficients vector is represented as
| (7) |
where αB is the sine and cosine coefficients obtained for the BW dictionary ΨBW, αL is the sine and cosine coefficients obtained for the LF dictionary ΨLF, αP is the sine and cosine coefficients obtained for the PLI dictionary ΨPLI, and αH is the impulsive coefficients obtained for the HF dictionary ΨHF. By using equations (1), (2), and (7), the input ECG signal x can be represented as a linear combination of weighted elementary waveforms from columns of overcomplete hybrid dictionary (OHD) matrix Ψ
| (8) |
| (9) |
Finally, the input ECG signal can be approximately expressed as
| (10) |
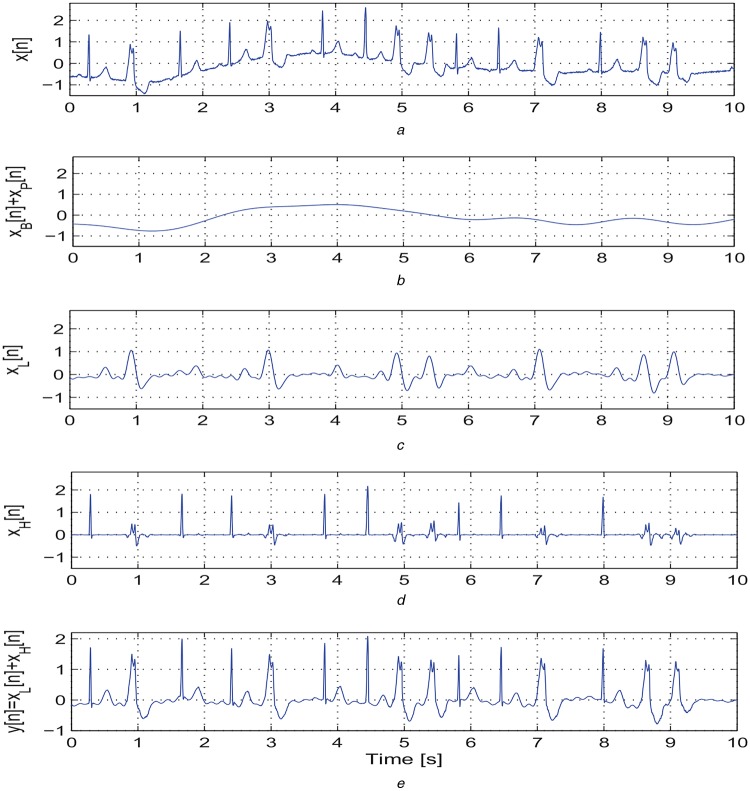
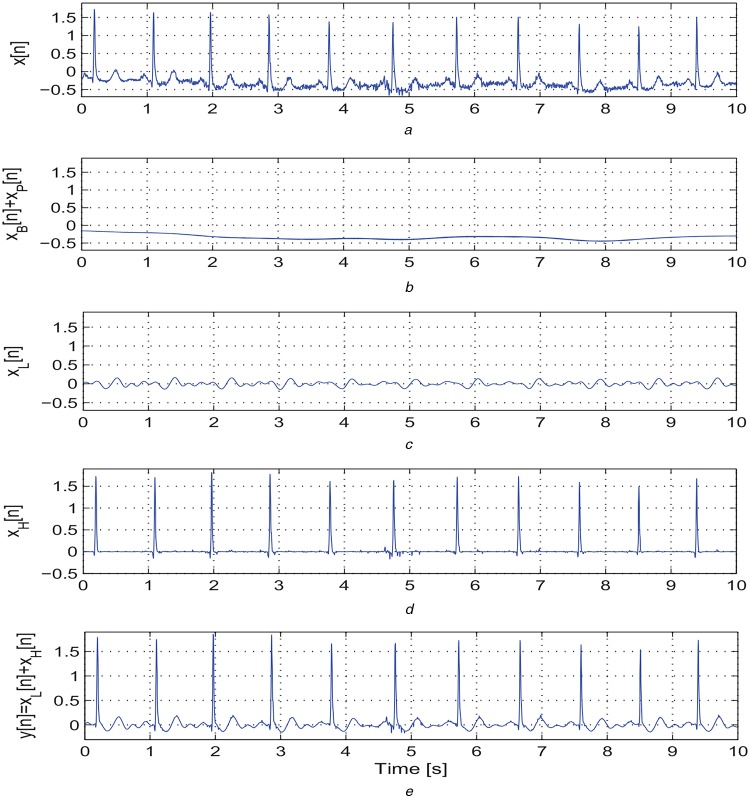
By using the above mentioned decomposition algorithm, the ECG signal is decomposed into four sub-signals: the BW signal xB[n]; the LF signal xL[n] including the P-wave, LF components of QRS complex, and T-wave; the PLI signal xP[n]; and the HF signal xH[n] including the high-slope portions of QRS complex and spike components. The effectiveness of the proposed decomposition approach is illustrated in Figs. 1 and 2. Based on our decomposition results, it is noted that the proposed method significantly suppresses the BW and background noises. The LF signal xL[n] contains the LF components of wide QRS complex, P and T waves. The HF signal xH[n] contains only high-slope portions of QRS complexes for clean normal and abnormal ECG signals. Thus, the HF signal xH[n] is further processed to locate R-peaks in the ECG signal. From the LF signals as shown in Figs. 1c and 2c, it is noted that the maximum and minimum amplitudes for an ECG signal with narrow QRS complexes (−0.2–0.2 mV) are much smaller as compared with that of an ECG signal with wide QRS complexes. Therefore, at the first stage of PVC detection, the absolute maximum value of the LF signal is used to detect the ECG signals with narrow QRS complexes (<100 ms) and P/T waves with absolute amplitude <0.2 mV. Results further show that the proposed decomposition approach adequately preserves the morphological content including amplitude, duration, timing, and polarity of the P-wave, QRS complex, and T-wave in LF and HF signals (xL[n] and xH[n]) and filtered signal y[n]. Thus, we investigate the temporal features extracted from the subsignals and filtered signal for detection of PVC beats.
Fig. 1.
Outputs of the proposed sparse decomposition approach
a Original ECG signal taken from a mitbiha record 208 containing BW, narrow and wide QRS complexes
b Extracted BW xB[n] plus PLI signal xP[n]
c Extracted LF signal xL[n] including the P-wave, LF components of QRS complex, and T-wave
d Extracted HF xH[n] including the high-slope portions of QRS complex and spike components
e Filtered signal y[n] = xL[n] + xH[n] after discarding the xB[n] and xP[n]
Fig. 2.
Outputs of the proposed sparse decomposition approach
a Original ECG signal taken from a mitbiha record 101 containing narrow QRS complexes, BW, and background noises
b Extracted BW xB[n] plus PLI signal xP[n]
c Extracted LF signal xL[n] including the P-wave, LF components of QRS complex, and T-wave
d Extracted HF xH[n] including the high-slope portions of QRS complex and spike components
e Filtered signal y[n] = xL[n] + xH[n] after discarding the xB[n] and xP[n]
2.2. Decision-rule-based PVC detection algorithm
In this section, we present the components of R-wave peak detection, a set of ten generalised features extracted from the LF signal xL[n] and filtered signal y[n], and the significance of each of the proposed features for discriminating PVC beats from non-PVC beats.
2.2.1. R-peak detection
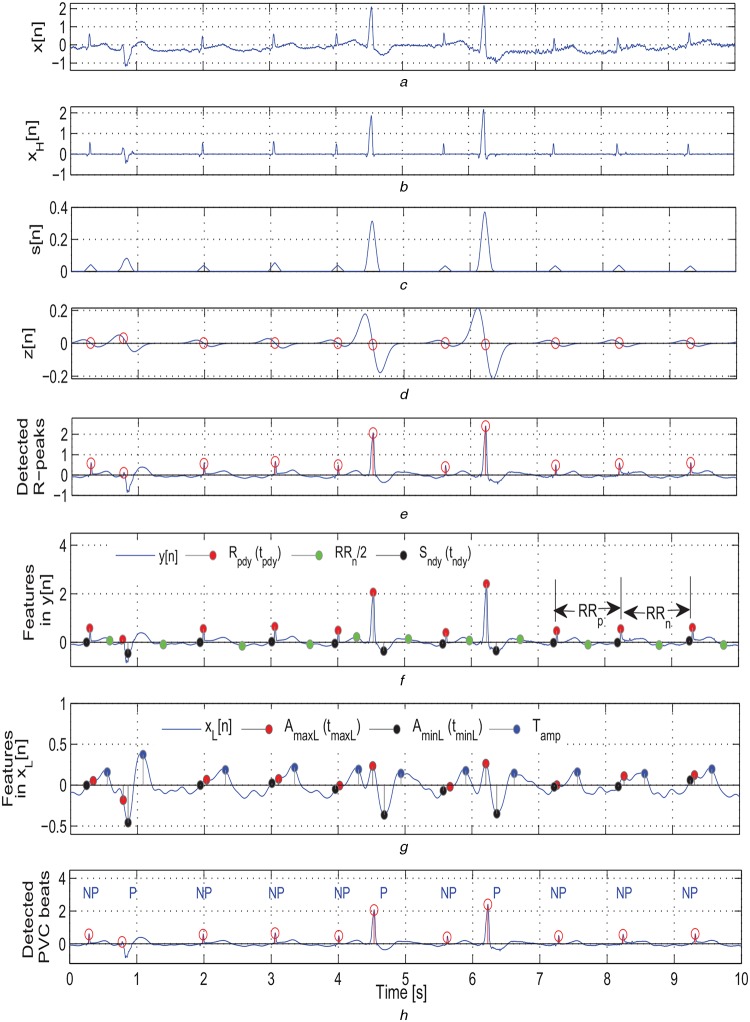
In the R-wave peak detection stage, the HF signal xH[n] is processed using the detection algorithm presented in Fig. 3 for determining locations of R-peaks in the ECG signal. The outputs of different stages of the proposed algorithm are shown in Figs. 4a–e. The detection results show the effectiveness of the proposed algorithm for the ECG signal containing narrow and wide QRS complexes, negative QRS complexes, BW, and background noises. The comprehensive results of the R-peak detection algorithm on the MIT/BIH arrhythmia database are summarised in Table 1.
Fig. 3.

Proposed detection algorithm for determining R-peaks
Fig. 4.
Outputs of the proposed PVC detection method
a Original ECG signal taken from a mitbiha record 208 containing narrow and wide QRS complexes, BW, and background noises
b Extracted HF signal xH[n]
c Output of the smoothing filter
d Output of the Gaussian derivative based peak finding logic
e Output of the peak correction step
f Features extracted from the filtered signal y[n]
g Features extracted from the LF signal xL[n]
h Detection results of the proposed method (NP, non-PVC beat; P, PVC beat)
Table 1.
Detection results on MIT/BIH arrhythmia database
| ECG type | Test ECG signals | Results of our method | Results of [2] | ||||||
|---|---|---|---|---|---|---|---|---|---|
| R-peak | PVC | PVC | |||||||
| Rec. no. | Total beats | PVC beats | MDR, % | FDR, % | Se, % | Sp, % | Se, % | Sp, % | |
| A | 115 | 1952 | 0 | 0.31 | 0.10 | – | 100 | – | 99.97 |
| 122 | 2474 | 0 | 0 | 0 | – | 100 | – | 99.97 | |
| B | 106 | 2027 | 520 | 0.30 | 0.10 | 97.88 | 100 | 99.89 | 99.95 |
| 119 | 1987 | 444 | 0 | 0 | 98.65 | 100 | 99.64 | 100 | |
| 123 | 1517 | 3 | 0 | 0 | 100 | 100 | 100 | 99.79 | |
| 221 | 2427 | 396 | 0 | 0 | 97.98 | 100 | 98.59 | 93.04 | |
| 230 | 2255 | 1 | 0 | 0 | 100 | 100 | 100 | 99.14 | |
| C | 101 | 1864 | 0 | 0.16 | 0.16 | – | 100 | – | 99.63 |
| 103 | 2083 | 0 | 0 | 0 | – | 100 | – | 99.96 | |
| 112 | 2537 | 0 | 0 | 0 | – | 100 | – | 99.98 | |
| 113 | 1794 | 0 | 0.33 | 0.22 | – | 100 | – | 99.41 | |
| 117 | 1534 | 0 | 0 | 0 | – | 100 | – | 99.81 | |
| 212 | 2747 | 0 | 0.51 | 0 | – | 99.49 | – | 99.91 | |
| 220 | 2046 | 0 | 0.20 | 0 | – | 99.32 | – | 97.19 | |
| 222 | 2483 | 0 | 0.16 | 0 | – | 99.84 | – | 77.62 | |
| D | 107 | 2136 | 59 | 0 | 0 | 94.92 | 99.13 | 82.37 | 96.98 |
| 109 | 2530 | 38 | 0 | 0 | 92.10 | 99.36 | 23.16 | 99.86 | |
| 118 | 2277 | 16 | 0.13 | 0.09 | 100 | 99.38 | 100 | 97.91 | |
| 214 | 2260 | 256 | 0.35 | 0.13 | 97.66 | 99.60 | 99.61 | 98.31 | |
| 111 | 2123 | 1 | 0 | 0 | 100 | 99.62 | 40 | 99.85 | |
| 124 | 1618 | 47 | 0 | 0 | 91.49 | 99.24 | 62.13 | 99.91 | |
| 232 | 1779 | 0 | 0 | 0.17 | – | 99.38 | – | 97.32 | |
| E | 100 | 2271 | 1 | 0 | 0 | 100 | 100 | 100 | 99.69 |
| 102 | 2185 | 4 | 0 | 0 | 75.00 | 99.17 | 60 | 100 | |
| 105 | 2572 | 41 | 0.23 | 0.31 | 92.68 | 100 | 97.07 | 95.58 | |
| 114 | 1879 | 43 | 0 | 0 | 90.70 | 99.78 | 85.12 | 99.50 | |
| 116 | 2411 | 109 | 1.00 | 0 | 90.83 | 99.65 | 99.08 | 99.63 | |
| 121 | 1862 | 1 | 0 | 0 | 0 | 100 | 100 | 99.65 | |
| 200 | 2600 | 826 | 0.15 | 0.12 | 98.06 | 99.77 | 96.47 | 98.83 | |
| 201 | 1963 | 198 | 0.31 | 0 | 95.96 | 98.98 | 81.92 | 92.88 | |
| 202 | 2135 | 19 | 0.23 | 0 | 94.74 | 99.81 | 66.32 | 83.99 | |
| 203 | 2979 | 444 | 0.74 | 0 | 86.94 | 94.95 | 91.48 | 71.99 | |
| 205 | 2655 | 71 | 0.30 | 0 | 100 | 99.69 | 80.86 | 99.96 | |
| 208 | 2953 | 992 | 0.68 | 0 | 96.47 | 100 | 99.13 | 89.56 | |
| 210 | 2648 | 194 | 0.72 | 0 | 93.81 | 99.43 | 80.72 | 93.55 | |
| 213 | 3249 | 220 | 0.06 | 0 | 96.36 | 99.97 | 96 | 97.05 | |
| 215 | 3361 | 164 | 0 | 0 | 92.68 | 100 | 92.93 | 99.62 | |
| 217 | 2208 | 162 | 0.32 | 0 | 95.06 | 99.46 | 98.89 | 95.51 | |
| 219 | 2154 | 64 | 0.09 | 0.09 | 92.19 | 99.90 | 98.13 | 57.51 | |
| 223 | 2604 | 473 | 0.15 | 0 | 98.10 | 100 | 68.16 | 96.26 | |
| 228 | 2053 | 362 | 0.78 | 0.25 | 98.34 | 100 | 97.62 | 99.12 | |
| 231 | 1570 | 2 | 0.51 | 0.19 | 50 | 99.62 | 70.00 | 75.88 | |
| 233 | 3077 | 830 | 0.26 | 0 | 99.52 | 99.87 | 86.36 | 99.11 | |
| 234 | 2752 | 3 | 0.07 | 0 | 33.33 | 100 | 100 | 99.86 | |
| 104 | 2227 | 2 | 0.18 | 0.40 | 100 | 99.28 | 30 | 99.88 | |
| 108 | 1761 | 16 | 0.45 | 0.40 | 87.50 | 99.31 | 96.25 | 98.83 | |
| 209 | 3003 | 1 | 0.13 | 0 | 100 | 99.73 | 60 | 97.76 | |
2.2.2. Temporal feature extraction
The normal ECG signals typically exhibit the narrow QRS complexes and regular RR intervals. The PVC beats have the following main characteristics [1, 3]: (i) broad QRS complex (at least > 0.12 s, but often very broad at around 0.16–0.20 s) with abnormal morphology, (ii) ST depression and large T-wave inversion in leads with a dominant R-wave (or ST elevation with upright large T waves in leads with a dominant S wave), and (iii) full compensatory pause (the PVC beats have a shorter RR interval preceding the PVC with a longer RR interval after the PVC) [4]. The PVCs often occur in repeating patterns [22]: bigeminy, trigeminy, and quadrigeminy. The PVCs may occur as isolated single beat or as couplets, triplets, and consecutive of more than four beats. Ventricular tachycardia (VT) is a fast heart rhythm, with at least three or more ventricular premature beats in a row. A few such repeating wide complexes can produce VT event with fast normal rhythm at rate of about 120–250 beats/min. It is noted that the local RR interval ratio (IR) feature may fail to detect the PVC beats occurred in couplets, triplets, and consecutive of more than four beats (or VT event), wherein the detection rule is based on estimated IR value: normal beats (IR ≃ 1) and PVC beats (IR <1) [4, 6].
Based on the above mentioned ECG characteristics, the temporal features are extracted from the filtered signal y[n] and the LF signal xL[n] for discriminating PVC beats from non-PVC beats: (i) local maximum QRS complex peak amplitude (Rpdy), which corresponds to an amplitude of y[n] at the location of detected R-peak, denoted as tpdy; and local minimum ST segment amplitude (Sndy) and its location (tndy), which is computed by selecting a window of samples from the filtered signal y[n], starting from the R-peak location to half of the next RR interval after the current R-peak; (ii) the local maximum amplitude (AmaxL) and local minimum amplitude (AminL) that are extracted from the LF signal xL[n] by selecting a window of −50 ms to half of the next RR interval around the R-peak; (iii) the peak locations (tmaxL and tminL) of the AmaxL and AminL values, respectively; (iv) the global absolute maximum amplitude AagmL from the LF signal xL[n]; (v) the maximum T-wave amplitude (Tamp), which is computed by selecting a window of samples from the LF signal xL[n], starting from the minimum ST segment amplitude location (tndy) to half of the next RR interval after the current R-peak; and (vi) the preceding RR interval (RRp) and the next RR interval (RRn) features for the current R-peak. The decision-rule-based PVC detection algorithm is presented in Fig. 5. Here, the detection threshold parameters are chosen based on the nominal values of amplitude and duration of QRS and T-waves, RR intervals measured for the consecutive of more than two PVC beats (couplets, triplets, VT), and refractory period. The extracted features are marked in Figs. 4f and g. The effectiveness of the proposed detection approach is shown in Fig. 4h for the ECG signal containing narrow and wide QRS complexes, BW, and background noises.
Fig. 5.

Proposed decision-rule-based PVC detection algorithm
3. Results and discussion
In this section, we evaluate robustness and accuracy of the proposed PVC detection method using the well-known MIT/BIH arrhythmia (mitbiha) database, which contains 48 half-hour of two-channel ECG recordings digitised at sampling rate of 360 Hz with 11-bit resolution over a 10 mV range [22]. The ECG recordings are categorised into five groups [4]: group A (records only with normal beats); group B (records including only normal beats and PVCs); group C (records with no PVCs); group D (records with no normal beats); group E (records containing normal beats and abnormal beats such as AP beats, aberrated AP beats, supraventricular premature beats, fusion beats, junctional premature beats, paced beats). It is noted that the ECG signals include sharp and tall P and T waves, sudden changes in QRS amplitudes and QRS morphologies, BWs, muscle noise, and long pauses. The primary annotations of the 48 ECG recordings are available in [22].
In this Letter, the performance of proposed method is tested and validated using complete duration of 47 mitbiha ECG recordings. The proposed method is implemented using MATLAB software on a 1.6 GHz AMD E-350 Processor with 2 GB RAM. For each ECG recording, the detection performance of our method is compared with the existing methods such as wave-based Bayesian filtering (WBF) [4], NN with WT and TI features (NN+WT+TI) [6]. The performance of the R-peak detection approach is evaluated in terms of missed detection rate (MDR), which is defined as the fraction of missed R-peaks over the total number of R-peaks in the record; and false detection rate (FDR), which is defined as the fraction of false detections over the total number of peaks by the method. The performance of the PVC detection method is evaluated in terms of three metrics [2, 4, 6, 14]: the Se = TN/(TN+FP), where true negative (TN) denotes PVC beat being classified as PVC and false positive (FP) denotes PVC beat being miss-classified as non-PVC beat; and the Sp = TP/(TP+ FN), where true positive (TP) denotes non-PVC beat being classified as non-PVC beat and false negative (FN) denotes non-PVC beat being miss-classified as PVC beat.
Based on our comprehensive results in Table 1, it is noted that the proposed R-wave peak detector achieves an average MDR of 0.216% with 233 missed beats for a total of 107582 beats and FDR of 0.06%. The results further show that the proposed R-peak detection approach can effectively determine R-peaks in normal and abnormal ECG signals under influence of BW and MA noises. Unlike existing R-peak detection approaches, the proposed approach does not use search back algorithm with sets of amplitude-dependent, timing-dependent, and duration-dependent thresholds for rejecting noise peaks and including missed peaks.
The comprehensive PVC detection results of the proposed method and the HOS+GP-RBF-ARD method [2] are summarised in Table 1. In [2], the HOS+ GP-RBF-ARD method had a poor PVC detection rate of below Se = 87% for the ECG records: 107 (Npvc = 59, 82.37%), 109 (Npvc = 38, 23.16%), 114 (Npvc = 43, 85.12%), 124 (Npvc = 47, 62.13%), 201 (Npvc = 198, 81.92%), 205 (Npvc = 70, 80.86%), 210 (Npvc = 194, 80.72%), 223 (Npvc = 473, 68.16%), and 233 (Npvc = 830, 86.36%) and had a poor non-PVC detection rate of below Sp = 90% for the ECG records: 202 (Nnpvc = 2116, 83.99%), 203 (Nnpvc = 2532, 71.99%), 208 (Nnpvc = 1692, 89.56%), 219 (Nnpvc = 2088, 57.51%), 222 (Nnpvc = 2579, 77.62%), and 231 (Nnpvc = 1564, 75.88%). The WT-NN-based method with RR IR achieved a Se of 3.05% and Pp of 83.33% for record 215 with a total of 164 PVCs [6]. In [6], the WT-NN-based method had a Se of below 83% for the ECG records 105 (4.88%), 109 (65.79%), 116 (77.98%), 118 (43.75%), 213 (43.18%), 214 (47.66%), 215 (3.05%), 219 (75%), 223 (40.38%), and 233 (82.77%) that include runs of more than two PVC beats, longest pauses of VT events, multiform PVCs, and sudden changes in RR intervals.
For the above mentioned ECG record numbers, the proposed method achieves a Se ranging from 91.41 to 100% and a Sp ranging from 99.62 to 100%. For most test ECG records, the method had better overall detection rates as compared with the rates of the HOS+ GP-RBF-ARD method [2], except for the ECG records: 102 (Npvc = 4, Se = 75%), 203 (Npvc = 444, Se = 86.94%), 231 (Npvc = 02, Se = 50%), 234 (Npvc = 3, Se = 33.33%), and 108 (Npvc = 16, Se = 87.50%). The proposed method had poor detection rates for the record 203 (Se = 86.94% and Sp = 94.95%) which includes low-amplitude QRS complexes and wide QRS complexes that look like PVC events, but these beats are annotated as non-PVC beats in the database. For the record 102 with a total of 4 PVC beats, the proposed method detects 03 PVC beats. By visually inspecting the detection results, it is noted that the ECG beat (at sample number 207743 in the original record) is labelled as a PVC beat but it has narrow QRS (<120 ms) and also the amplitudes of R and S waves are nearly equal. In most cases, the detection results show that the proposed method is capable of discriminating PVC beats from different types of abnormal beats under the influence of BWs and MA.
Based on our results, it is noted that the transition interval (Dti) measured between the R-peak location (tpdy) and minimum ST segment amplitude location (tndy), and the maximum T-wave amplitude (Tamp) features significantly improve overall detection rates for the ECG signals including LBBB and RBBB, paced and AP beats. Further, the method yields better detection rates for the ECG signals with the isolated single PVC beats and the runs of more than two PVC beats by using the proposed three decision rules that are constructed based on the interval features (RRp and RRn) and the local amplitude features (AmaxL and AminL), and the local amplitude timing features (tmaxL and tminL). It is found, in this Letter, that the proposed global absolute maximum amplitude AagmL feature can effectively distinguish the ECG signals with narrow QRS complexes (<120 ms) from the ECG signals with wide QRS complexes. The results of PVC detection methods are summarised in Table 2. The proposed method achieves an average Se of 89.69% and an Sp of 99.63%. These results demonstrate that the proposed method significantly outperforms the detection rates of the existing methods. Based on the results, it is noted that the computation time of the sparse decomposition technique is high as compared with the other decomposition techniques. As compared with other existing methods, the proposed method has the following advantages: (i) the sparse signal decomposition technique adequately preserves the essential morphological features (including amplitude, duration, polarity, and shape of QRS complex) and effectively reduces the influence of the P/T waves and the BW, PLI, and MA, (ii) does not require feature dimensionality reduction approach, (iii) does not require learning phase to obtain detection thresholds based on the past detected R-peaks, and (iv) does not demand collection of different types of ECG beats for generating heartbeat models.
Table 2.
Comparison of PVC detection results
| PVC detection methods | Rec. no. | Total beats | PVC beats | Se, % | +P/Sp*, % |
|---|---|---|---|---|---|
| NN+WT+TI [6] | 40 | 100239 | 6958 | 82.57 | 93.42 |
| WT-PCA+multi-dimensional (MD)-PSO [11] | 40 | 100239 | 6958 | 93.4 | 93.3 |
| 26 features+KNN [13]* | 44 | 100225 | 6996 | 97.2 | 96.7 |
| WBF [4] | 40 | 92588 | 6956 | 98.77 | 97.47 |
| HOS+GP-RBF-ARD [2]* | 48 | 109887 | 7117 | 92.19 | 95.15 |
| HOS+GP [12]* | 27 | – | 4080 | 84.7 | 97.5 |
| Haar WT+neural network with weighted fuzzy membership functions (NEWFMs) [5]* | 6 | – | 935 | 99.21 | 99.93 |
| WT+FNN [14]* | 7 | – | 943 | 99.02 | 96.67 |
| proposed method* | 47 | 107582 | 7023 | 89.69 | 99.63 |
4. Conclusion
An automated noise-robust PVC detection method is presented based on the sparse signal decomposition, R-peak determination, temporal feature extraction, and decision-rule-based PVC detection algorithm. The decomposition results demonstrate that the proposed sparse signal decomposition technique adequately preserves the essential morphological features (including amplitude, duration, polarity, and shape of QRS complex) and effectively reduces the influence of the P/T waves, BWs, powerline interference, and MA. Evaluation results show that the proposed method can effectively discriminate PVC beats from different types of non-PVC beats, providing an average Se of 89.69%, and Sp of 99.63% on 47 ECG recordings of the MIT/BIH arrhythmia database. Results further show that the proposed PVC detection algorithm with ten generalised temporal features extracted from the decomposed signals is capable of accurately detecting PVC beats in presence of other normal and abnormal beats such as LBBB, RBBB, fusion, junctional, paced, and AP beats.
5. Conflict of interest
The author declare that they have no conflict of interest.
6 References
- 1.Chang R.C.H., Lin C.H., Wei M.F., et al. : ‘High-precision real-time premature ventricular contraction (PVC) detection system based on wavelet transform’, J. Signal Process. Syst., 2014, 77, (3), pp. 289–296 (doi: ) [Google Scholar]
- 2.Naif Alajlan Y., Bazi F., Malek M.S., et al. : ‘Detection of premature ventricular contraction arrhythmias in electrocardiogram signals with kernel methods’, Signal Image Video Process., 2014, 8, pp. 931–942 (doi: ) [Google Scholar]
- 3.Morris F., Brady W.J., Camm J.: ‘ABC of clinical electrocardiography’, (BMJ Books, London, 2nd edn.) [Google Scholar]
- 4.Sayadi O., Shamsollahi M.B., Clifford G.D.: ‘Robust detection of premature ventricular contractions using a wave-based Bayesian framework’, IEEE Trans. Biomed. Eng., 2010, 57, (2), pp. 353–362 (doi: ) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Lim J.S.: ‘Finding features for real-time premature ventricular contraction detection using a fuzzy neural network system’, IEEE Trans. Neural Netw., 2009, 20, pp. 522–527 (doi: ) [DOI] [PubMed] [Google Scholar]
- 6.Inan O.T., Giovangrandi L., Kovacs G.T.A.: ‘Robust neural-network based classification of premature ventricular contractions using wavelet transform and timing interval features’, IEEE Trans. Biomed. Eng., 2006, 53, (12), pp. 2507–2515 (doi: ) [DOI] [PubMed] [Google Scholar]
- 7.Adnane M., Belouchrani A.: ‘Premature ventricular contraction arrhythmia detection using wavelet coefficients’. Eighth Int. Workshop on Systems, Signal Processing and their Applications (WoSSPA), 2013, pp. 170–173 [Google Scholar]
- 8.Bazi Y., Hichri H., Alajlan N., et al. : ‘Premature ventricular contraction arrhythmia detection and classification with Gaussian process and S transform’. Fifth Int. Conf. on Computational Intelligence, Communication Systems and Networks (CICSyN), 2013, pp. 36–41 [Google Scholar]
- 9.Khorrami H., Moavenian M.: ‘A comparative study of DWT, CWT and DCT transformations in ECG arrhythmias classification’, Expert Syst. Appl., 2010, 37, pp. 5751–5757 (doi: ) [Google Scholar]
- 10.Melgani F., Bazi Y.: ‘Classification of electrocardiogram signals with support vector machines and swarm particle optimization’, IEEE Trans. Inf. Technol. Biomed., 2008, 12, pp. 667–677 (doi: ) [DOI] [PubMed] [Google Scholar]
- 11.Ince T., Kiranyaz S., Gabbouj M.: ‘Automated patient-specific classification of premature ventricular contractions’. Proc. of 30th Int. Conf. on IEEE EMBS, 2008, pp. 5474–5477 [DOI] [PubMed] [Google Scholar]
- 12.Melgani F., Bazi Y.: ‘Detecting premature ventricular contractions in ECG signals with Gaussian processes’, Proc. Comput. Cardiol., 2008, 35, pp. 237–240 [Google Scholar]
- 13.Christov I., Jekova I., Bortolan G.: ‘Premature ventricular contraction classification by the Kth nearest-neighbours rule’, Physiol. Meas., 2005, 26, pp. 123–130 (doi: ) [DOI] [PubMed] [Google Scholar]
- 14.Shyu L.Y., Wu Y.H., Hu W.: ‘Using wavelet transform and fuzzy neural network for VPC detection from the Holter ECG’, IEEE Trans. Biomed. Eng., 2004, 51, (7), pp. 1269–1273 (doi: ) [DOI] [PubMed] [Google Scholar]
- 15.Manikandan M.S., Ramkumar B.: ‘Straightforward and robust QRS detection algorithm for wearable cardiac monitor’, Healthc. Technol. Lett., 2014, 1, (1), pp. 40–44 (doi: ) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Manikandan M.S., Samantaray S.R., Kamwa I.: ‘Detection and classification of power quality disturbances using sparse signal decomposition on hybrid dictionaries’, IEEE Trans. Instrum. Meas., 2015, 64, (1), pp. 27–38 (doi: ) [Google Scholar]
- 17.Aharon M., Elad M., Bruckstein A.: ‘K-SVD: an algorithm for designing overcomplete dictionaries for sparse representation’, IEEE Trans. Signal Process., 2006, 54, (11), pp. 4311–4322 (doi: ) [Google Scholar]
- 18.Yang A.Y., Zhou Z., Balasubramanian A.G., et al. : ‘Fast l1-minimization algorithms for robust face recognition’, IEEE Trans. Image Process., 2013, 22, (08), pp. 3234–46 (doi: ) [DOI] [PubMed] [Google Scholar]
- 19.Kligfield P., et al. : ‘Recommendations for the standardization and interpretation of the electrocardiogram: part I: the electrocardiogram and its technology’, J. Am. Coll. Cardiol., 2007, 49, (10), pp. 1109–1127 (doi: ) [DOI] [PubMed] [Google Scholar]
- 20.Li C., Zheng C., Tai C.: ‘Detection of ECG characteristic points using wavelet transforms’, IEEE Trans. Biomed. Eng., 1995, 42, pp. 21–28 (doi: ) [DOI] [PubMed] [Google Scholar]
- 21.Friesen G.M., Jannett T.C., Jadallah M.A., et al. : ‘A comparison of the noise sensitivity of nine QRS detection algorithms’, IEEE Trans. Biomed. Eng., 1990, 37, (1), pp. 85–98 (doi: ) [DOI] [PubMed] [Google Scholar]
- 22.Mark R., Moody G.: ‘The MIT-BIH arrhythmia database’. Available at http://physionet.org/physiobank/database/mitdb/ [DOI] [PubMed]
- 23.Martis R.J., Acharya U.R., Min L.C.: ‘ECG beat classification using PCA, LDA, ICA and discrete wavelet transform’, Biomed. Signal Process. Control, 2013, 8, (5), pp. 437–448 (doi: ) [Google Scholar]
- 24.Martis R.J., Acharya U.R., Mandana K.M., et al. : ‘Application of principal component analysis to ECG signals for automated diagnosis of cardiac health’, Expert Syst. Appl., 2012, 39, (14), pp. 11792–11800 (doi: ) [Google Scholar]