Fractionation of a galacto-oligosaccharides solution at low and high temperature using nanofiltration

Abstract

Like in many applications, solutions of high sugar content can cause serious problems due to microorganism contaminations. Hence, the main aim of this work was to study a nanofiltration process for GOS purification at 5 °C and 60 °C that may circumvent or reduce potential microbial growth. Process performances and rejection behaviors of monosaccharide as well as individual GOS components were compared. Operating at 5 °C is more advantageous especially with respect to the oligosaccharide (OS) recovery yield. Using a NF membrane (NP030) at 45 bar, a product purity of 85% (based on monosaccharide content) and an OS recovery yield of 82% could be achieved. However, a low average permeate flux of 3 L/m² h had to be accepted. A diafiltration step improved product purity to 90% with 30% losses of OS. A qualitative theoretical discussion shows that a possible change of the pore radius distribution depending on temperature could play a role in solute rejection as well as selectivity.

1. Introduction

In a huge number of membrane applications like in the present case, the purification of oligosaccharides, microorganism growth is a serious problem. The degree of severity is different from case to case. For example, biofouling (biofilm formation), one of the main operating problems, has been discussed in numerous studies [1–3]. The difficulties are not only to be considered from a practical point of view. Also in some experimental or theoretical studies conducted in the room temperature region, the microbial problems need to be taken into account when results are interpreted.

Galacto-oligosaccharides (GOS), classified as prebiotic, have gained considerable attention in the last two decades [4,5]. A prebiotic is defined as a substance that is resistant to acids and enzymes in the gastrointestinal tract of the host, and is selectively utilized by certain beneficial members (mainly lactobacilli and bifidobacteria) of the gastrointestinal microbiota, leading to health benefits in the human host [4,6,7]. GOS are usually composed of two to ten molecules of galactose and a single glucose moiety at the reducing end of the oligosaccharides [5]. Typically, a GOS solution consists of glucose, galactose, lactose and a mixture of other di- and oligosaccharides of different structures.

The application of GOS products depends on GOS purity and the production cost. The removal of non-prebiotic sugars (glucose and galactose) is in general advantageous and could expand the application possibilities into pharmaceutical and food industry for diabetic people [5,8]. Currently, commercial GOS products are produced by the enzymatic reaction of concentrated lactose solutions at 200–400 g/L with β-galactosidase from different sources. Several purification techniques have been investigated such as precipitation by ethanol [9], adsorption by activated charcoal [10–12], separation by ion exchange chromatography [13] and membrane fractionation [14–19]. Nanofiltration is of particular interest because of its selectivity properties for the present application, thus, some studies have already been published [14–19]. In general, these reported investigations have been carried out using different membranes at more or less standard operating conditions (15–50 °C, 6–40 bar). However, as indicated under these conditions, it would be hardly possible to operate the process in a commercial scale due to the above mentioned microbial contamination. Besides sterilization, sterile filtration and UV irradiation [20], operating at higher or lower temperatures can be helpful to reduce microbial growth. However, the process performance of the filtration system will change noticeable.

Therefore, the objectives of this study were to investigate the nanofiltration performance for GOS purification at low and high temperature and also to optimize the separation process. In addition, some theoretical aspects regarding rejections were discussed qualitatively.

2. Materials and methods

2.1. Chemicals

All chemicals used were analytical grade and purchased from either Sigma (Sigma, St. Louis, MO, USA) or Merck (Darmstadt, Germany). All solutions were prepared with demineralized water.

2.2. GOS synthesis – feed preparation

Recombinant β-galactosidase from Lactobacillus delbrueckii subsp. bulgaricus was produced and purified according to the method of Nguyen et al. [21]. Synthesis of GOS was performed in a discontinuous process at 50 °C for 5 h using 1.5 lactase U of β-galactosidase per mL of reaction mixture containing 600 mM initial lactose concentration (216 g/L) in 50 mM sodium phosphate buffer (pH4.5) and 10 mM MgCl₂. After completion of the reaction the enzyme was inactivated by heating in boiling water for 5 min. The GOS mixture (a total feed sugar concentration of 216 g/L) thus produced contained 58.5% of oligosaccharides (2.7% β-1,6-galactobiose (M_m 342 g/mol), 1.1% β-1,3-galactobiose (M_m 342 g/mol), 13.7% 3′-galactosyllactose (M_m 504 g/mol), 5.9% β-1,3-galactosylglucose (M_m 342 g/mol), 0.3% 4′-galactosyllactose (M_m 504 g/mol), 11.4% 6′-galactosyllactose (M_m 504 g/mol), 23.5% of lactose (M_m 342 g/mol)), 25.0% of glucose (M_m 180 g/mol) and 16.5% of galactose (M_m 180 g/mol).

2.3. Membranes

Two flat sheet NF membranes, NP030 from Microdyn-Nadir (Wiesbaden, Germany) and Desal-5 DL from GE Water & Process Technologies (Pennsylvania, USA), were used in this study. The NP030 membrane is a polyethersulphone-based membrane with a nominal MWCO of 400 Dalton, whereas Desal-5 DL consists of aromatic polyamides with a nominal MWCO ranging from 150 to 300 Dalton [17,19].

2.4. Nanofiltration experiments

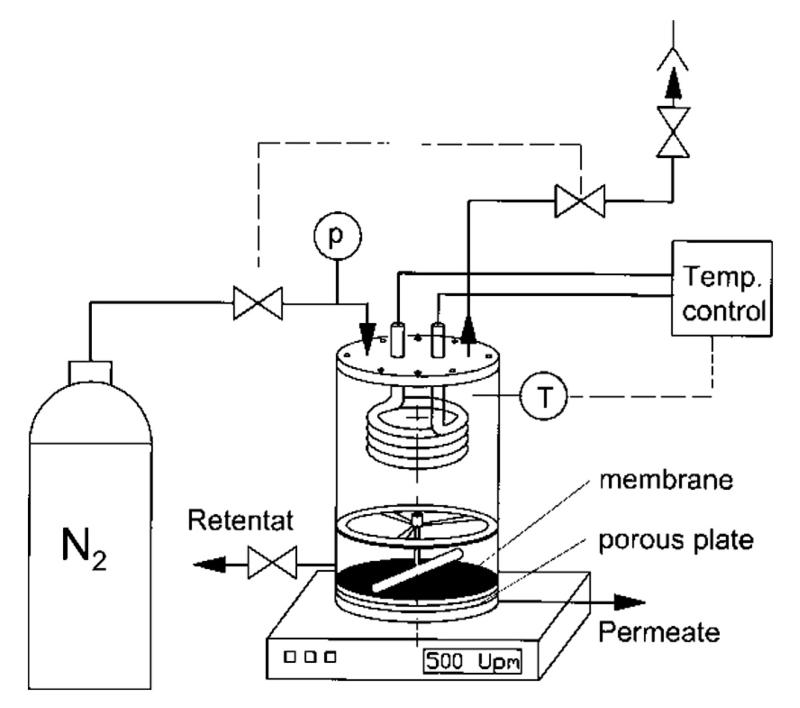
A high pressure stirred cell test unit with an effective membrane area of 152 cm² was used for the NF process. A schematic diagram of the experimental set-up is shown in Fig. 1. The solution temperature was controlled and monitored by a cooling/heating coil connected to a temperature-controlled water bath (Julabo F12-ED, Germany). Unless otherwise stated, the magnetic stirrer speed was fixed at 500 rpm. The initial volume of feed solution was 1000 mL. The experiments were stopped at a volume reduction factor (VRF) of 4. VRF is defined as the ratio between initial feed volume and the volume of the retentate. Both permeate and retentate samples were collected for subsequent sugar and dry mass quantifications. Initial water flux measurements were performed at different operating pressures (5–15 bar) at 25 °C and compared with the data provided by the membrane manufacturer. In order to avoid significant changes in sugar compositions in each experiment, both concentrates and permeates were pooled together and used as a feed solution for the next experiment. The same flat sheet membranes were used in all experiments. The effects of operating temperature (5, 25 and 60 °C) and pressure (25, 35 and 45 bar) on membrane performance were determined. The diafiltration technique was also applied.

Fig. 1.

Schematic diagram of the experimental set up (stirred NF cell).

2.5. Analytical methods

Quantification of the concentration of sugars (glucose, galactose, lactose and galacto-oligosaccharides) was carried out by using high-performance anion exchange chromatography with pulse amperometric detection (HPAEC-PAD) according to a method previously described [22]. The term monosaccharides (MS) is used to refer to glucose and galactose present in the mixture, while the term oligosaccharides (OS) stands for both di- and trisaccharides present in the sugar mixture with lactose, β-1,6-galactobiose, β-1,3-galactobiose, β-1,3-galactosylglucose, 3′-galactosyllactose, 4′-galactosyllactose and 6′-galactosyllactose identified by using authentic standard sugars and quantitated.

The dry matter or solid contents were determined by the Moisture Analyzer AnD MX-50 (Tokyo, Japan). These data were used to express the total mass of the sugar solution assuming that total solids in the solution constitute mainly sugars. Therefore, the total mass of OS was calculated from the difference between a total mass of dry matters and MS mass. The total OS concentration was then calculated by dividing the total mass by the total volume of the solution. These concentrations were subsequently used for the calculations of the respective sugar rejection.

The permeate flux was measured gravimetrically using a Kern KB 3600-2N laboratory scale (Balingen, Germany), which was connected to and monitored by a computer.

2.6. Calculations

The observed rejection in % for a given solute was calculated from the equation:

$$R=\left(1-\frac{C_p}{C_f}\right)\times 100$$ (1)

where C_P and C_f are the solute concentration in the permeate and the feed, respectively.

The yield value of the OS was calculated from the equation:

$$Y=\left(\frac{m_{\mathit{OS},R}}{m_{\mathit{OS},F}}\right)\times 100$$ (2)

where m_OS,F and m_OS,R are the mass of OS in the feed and retentate, respectively.

The OS purity was determined by

$$P=\left(\frac{m_{\mathit{OS},R}}{m_{\mathit{DM},R}}\right)\times 100$$ (3)

where m_DM,R is the total mass of dry matter in the retentate.

Apart from GOS preparation, all results were obtained in duplicate and the accuracy is ±5%.

3. Results and discussion

3.1. Membrane selection

For the membrane selection, two types of NF membranes (NP030 and Desal-5 DL) were used. The initial experiments were performed at an operating pressure of 25 bar and a temperature of 25 °C. Table 1 presents rejection values, yields, and OS purities. Due to somewhat better results (rejection value 49.0% and yield 62.3%), the NP030 membrane was chosen for further studies.

Table 1.

Comparison of NP030 and Desal-5 DL performances in terms of rejection value, yield and purity of OS in a stirred cell (25 °C, 25 bar).

	NP030	Desal-5DL
RMS (%)	8.1	2.7
ROS (%)	49.0	36.2
Yield (%)	62.3	53.4
Purity (%)	86.0	86.5

3.2. Effect of temperature – practical considerations

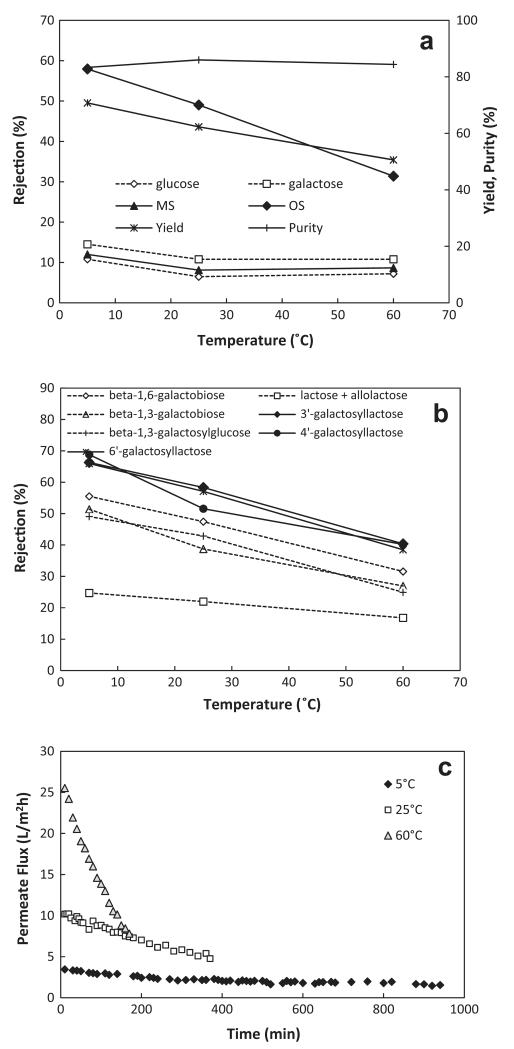
Fig. 2a shows the rejection values of the sugars at different operating temperatures (5, 25 and 60 °C). In general, this membrane showed acceptable selectivity properties at 5 °C with regard to MS and OS, which means, in contrast to MS, rejection values of OS markedly increased with decreasing temperature. Simultaneously, this resulted in a noticeable increase of yield. However, the purity remained more or less constant due to higher MS rejections. On the other hand, the MS rejection is practically temperature independent from around 25–60 °C. The results indicated that the process can only be operated at around 5 °C. As already mentioned, at room temperature, the microorganism problem is difficult to manage, and at 60 °C, the obtained yield was unacceptable due to the low rejections of OS.

Fig. 2.

Nanofiltration of an OS product solution. Effect of temperature on rejection values of each sugar; (a) OS purity and yield; (b) the individual oligosaccharides and (c) the permeate flux (NP030 membrane, 25 bar).

In order to have a better understanding of the behavior of individual OS in the GOS mixture, the rejections of lactose, β-1,6-galactobiose, β-1,3-galactobiose, β-1,3-galactosylglucose, 3′-galactosyllactose, 4′-galactosyllactose and 6′-galactosyllactose were investigated as well (Fig. 2b). As expected, differences in the rejections between di- and trisaccharides were obtained. However, the values of all compounds considered individually showed some interesting points. At first, the rejections are linearly dependent on temperature, and apart from lactose, the slopes of the lines were similar. Secondly, while the rejections at each temperature were more or less equal for all trisaccharides (3′-galactosyllactose, 4′-galactosyllactose and 6′-galactosyllactose), significant differences for disaccharides (equal molecular mass) were observed. Especially the relatively low rejection of lactose (allolactose; these two components could not be separated by HPEAC-PAD with the applied gradient) is worth noting. Possible explanations are for example discussed in Santos et al. [23]. In their study, model simulations suggest that the target solute rejection depends on its preferential orientation especially for elongated molecules. In the case of lactose, the relatively high concentration in the feed seems to be an additional influencing factor.

In general, the different rejection behaviors can be mainly attributed to the temperature-dependent variation in the ratios of molecular size to pore size, and to the influence of temperature on pore size, solution viscosity and diffusion coefficient. Sharma et al. [24] investigated the effect of temperature on pore sizes in more details and they showed that the average pore size of a DL membrane increased by ~21% when the temperature increased from 5 °C to 41 °C.

Finally, Fig. 2c shows the permeate fluxes over time at different temperatures. The average values were 2.5, 7.5 and 16.6 L/m² h at a pressure of 25 bar and at 5, 25 and 60 °C, respectively. While the flux decreased considerable over time especially at 60 °C, a rather slow flux decline over approx. 1000 min was observed at 5 °C. In this case, it is to be expected that practically no concentration polarization occurs. The observed fluxes (time dependent) are influenced by the differences in membrane resistance (R_m), concentration polarization as well as osmotic pressure (Δπ).

3.3. Effect of pressure

To improve the process performance especially with respect to the permeate flux, the effect of operating pressures ranging from 25 to 45 bar at 5 °C was studied. Firstly, the rejection values of each compound increased expectedly with increasing pressure and the progression was practically linear in all cases (Fig. 3a and b). Increasing pressure causes higher solvent fluxes while the solute diffusive transport through the membranes remains relatively constant [14]. Fig. 3a also presents the course of the OS recovery yield and purity. The pressure did not have a significant effect on OS purity. However, OS recovery yields could be improved considerably. Under optimized conditions (5 °C and 45 bar), a purity of 84.5% and a recovery yield of 81.6% could be achieved. Fig. 3c shows the permeate fluxes, and the average values at 25, 35 and 45 bar were 2.5, 2.9 and 3.3 L/m² h respectively.

Fig. 3.

Nanofiltration of an OS product solution. Effect of pressure on rejection values of each sugar; (a) OS purity and yield; (b) the individual oligosaccharides and (c) the permeate flux (NP030 membrane, 5 °C).

Finally, a diafiltration step was performed (5 °C, 45 bar). The retentate from the first filtration (200 mL) was mixed with deionized water (200 mL), which was subsequently removed. The purity of OS increased to 88.2% while the yield decreased to 72.5%.

3.4. Some qualitative theoretical considerations

Based on chosen models, theoretical investigations regarding mass transfer in nanofiltration usually are conducted under specific conditions such as low solute concentration and a constant feed parameter. In the present case, a real application was investigated in which a mixture of different compounds with different and partially high concentrations (total sugar content around 200 g/L) was separated into two fractions. Moreover, some further requirements were necessary to be fulfilled, for example, high product concentration, high purity, etc. Since a very high number of factors (mostly dependent on each other) changes during such a process operation, it is not easy to develop a corresponding model. Nevertheless, e.g. the extended Nernst–Planck transport equation including further aspects (hindered nature of diffusion and convection of transported molecules inside the membrane) can be used to discuss the nature of mass transfer qualitatively [25,26]. The flux of a solute (j_i) can be given by

$$j_i=-K_{i,d}{D}_{i,\infty }\frac{{\mathit{dc}}_i}{\mathit{dx}}-\frac{z_i{c}_i{D}_{i,p}}{\mathit{RT}}F\frac{d\psi }{\mathit{dx}}+K_{i,c}{c}_{i}V$$ (4)

where K_i,d and K_i,c are the hindrance factor for diffusion and convection; D_i,∞ and D_i,p are the bulk and hindered diffusivity respectively; c_i is the concentration in membrane; x is the distance normal to the membrane; z_i is the valence of ion; R is the gas constant; T is temperature; F is the Faraday constant; ψ is the electric potential in an axial direction and V is the velocity of solute. Although charged species were also in the present solution (buffer salts for the enzymatic reaction), the transport of the ions will not be considered. Thus, the electrodynamic term in Eq. (4) is not taken into account. As discussed in many publications [25–30], firstly, the hindrance factors (K_i,d and K_i,c) need to be considered. Both are defined as functions of the ratio between the solute and the pore radius (r_p):

$$\lambda =\frac{r_s}{r_p}$$ (5)

The effective solute radius in the pore (r_s) can be expressed for example by the Stokes–Einstein equation:

$$r_s=\frac{\mathit{kT}}{6\pi \eta D_{i,\infty }}$$ (6)

where k is Boltzman’s constant and η is the viscosity of the bulk solution. In this context, a relation between r_s and molecular mass (M_m) is helpful to obtain the size of molecules.

In defined classes of compounds, r_s can be expressed in the form:

$$\log r_s=-a+b\log M_m$$ (7)

For example in case of glycerine, glucose, sucrose, raffinose, α-cyclodextrin and vitamin B₁₂, the factor a is 1.3 and b is 0.4 [25].

Under specific assumptions (steric compounds and cylindrical pores) and if r_p is known, the hindrance factors can be expressed through Eqs. (8) and (9) (validity: 0 < λ < 0.95) [28,31].

$$K_{i,d}=1-2.3\lambda +1.154{\lambda }^2+0.224{\lambda }^3$$ (8)

$$K_{i,c}=(2-\Phi )(1+0.054\lambda -0.988{\lambda }^2+0.441{\lambda }^3)$$ (9)

The steric partition factor (Φ) is related physically to the concentration ratios at the membrane interfaces (c_i,x=0/C_i,m and c_i,x=Δx/C_i,p) and can, in case of a parabolic profile of the velocity in the pores and purely steric interactions, be expressed through Eq. (10):

$$\Phi ={(1-\lambda )}^2$$ (10)

When (theoretically) dealing with mass transfers and membrane structures, the experimentally observed and so called real (based on concentration polarization) rejections are helpful. An expression for the real rejection of a neutral solute can be developed with Eq. (4):

$$R_{\mathit{real}}=1-\frac{C_{i,p}}{C_{i,m}}=1-\frac{\Phi K_{i,c}}{1-\exp (-\mathit{Pe})[1-\Phi K_{i,c}]}$$ (11)

where Pe is the Peclet number which can be defined as

$$\mathit{Pe}=\frac{K_{i,c}}{K_{i,d}}\frac{V\Delta x}{D_{i,\infty }{A}_k}$$ (12)

A_k is the membrane porosity and Δx is the membrane thickness.

The membrane surface solute concentration, C_i,m (or relation between C_i,p/C_i,m) can be obtained based on the film theory model and can be given as

$$\frac{C_{i,m}-C_{i,p}}{C_{i,b}-C_{i,p}}=\exp \frac{J_v}{k_m}$$ (13)

where C_i,p and C_i,b are the permeate and bulk concentration, respectively; k_m is the mass transfer coefficient and J_v is the volume flux. Finally, using the rejection fraction instead of concentrations, a relationship between observed rejection (R_obs) and real rejection (R_real) can be expressed as:

$$\ln \frac{1-R_{\mathit{real}}}{R_{\mathit{real}}}=\ln \frac{1-R_{\mathit{obs}}}{R_{\mathit{obs}}}-\frac{J_v}{k}$$ (14)

where R_obs is defined as

$$R_{\mathit{obs}}=1-\frac{C_{i,p}}{C_{i,b}}$$ (15)

In a cross flow system, the mass transfer coefficient (k_m) can be calculated with the equation:

$$\mathit{Sh}=\frac{k_m{d}_h}{D}={\alpha }_1{\mathit{Re}}^{{\alpha }_2}{\mathit{Sc}}^{{\alpha }_3}$$ (16)

where Sh is the Sherwood number, Re the Reynolds number, Sc the Schmidt number, d_h the hydraulic diameter and D the diffusion coefficient. The factors α_i are filtration system related factors. Based on similar physical background, in a stirred cell, k_m can be expressed as [32]:

$$k_m={\beta }_1{\omega }^{{\beta }_2}$$ (17)

where β₁ and β₂ are constant and dependent on the filtration geometry and ω is the stirring speed. The factor β₂ is assumed to be 0.567 for a stirred cell [26].

The solution volume flux (J_v) can be expressed based on irreversible thermodynamics considerations [33]:

$$J_v=L_p(\Delta P-\sigma \Delta \pi )$$ (18)

where ΔP is the applied pressure and σ is the reflection coefficient.

The pure water permeability (L_p) can be defined as:

$$L_p=\frac{r_p^2}{8\eta }\frac{A_k}{\Delta x}$$ (19)

In case of the pure water flux (J_w), the Hagen–Poiseuille equation can be used:

$$J_w=\frac{r_p^2\Delta P}{8\eta (\Delta x∕A_k)}$$ (20)

If r_p is known, the value for Δx/A_k can be calculated.

When combining the theoretical models with experimental measurements, structure parameters of the membrane as well as mass transfer properties can be evaluated. As in the present work, the temperature effects on mass transfer were of special interest, published studies dealing with the influences of temperature on membrane structures as well as mass transfer were considered in particular for the following discussion. In order to assess the change of r_p with temperature of the present NP030 membrane, firstly, data regarding the relation between r_p and temperature were taken from Ben Amar [34] and Sharma and Chellam [35]. It should be noted that the used membrane in their studies and the present one were not identical. However, all considered are organic based nanofiltration membranes, thus analyzing the results of the above studies, the following approach should be acceptable. Within a temperature range between 5 and 60 °C, the change in r_p is assumed to be linear and the slope is estimated to be around 0.0036. For the theoretical discussion in the present work, it is not of major importance if the slope differs to a certain extent. Also instead of a linear, a power function approach is possible. Simultaneously in Wang and Chung [36], the NADIR^® N30F nanofiltration membrane (identical with the NP030 membrane) was characterized based on both irreversible thermodynamic and steric-hindrance pore (SHP) models. The average pore radius at 18 °C was estimated to be 0.74 nm. Hence, the following relationship between pore radius and temperature for the present membrane can be given as:

$$r_p\cong 0.0036T+0.68$$ (21)

where r_p is the pore radius (nm) and T the temperature (°C).

In Wang and Chung [36], also values for A_k/Δx are presented and were in the range of 20,377–41,936 in relation to glycerol, glucose (monosaccharide), saccharose (disaccharide), raffinose and (trisaccharide). The most important aspect at this point is that it can be assumed that the pore radius increases with increasing temperature. Now, with different r_p, for example different hindrance factors could be estimated, however as already mentioned in the present case, the solution does not fulfill all model requirements e.g. solute concentrations, etc. Nevertheless, the above information about the pore radius is helpful to discuss the obtained experimental results in relation to the pore size distribution of the membrane. The pore size distribution is an important aspect with regard to mass transfer considerations as discussed in various studies [37,38]. Taking specific aspects into account, a log normal distribution in the form of Eq. (22) is useful and can be expressed as [38]:

$$f_R\left(r_p\right)=\frac{1}{r_p\sqrt{2\pi b}}\exp \left[-\frac{{\left\{\log \left(\frac{r_p}{r_{\mathit{pm}}}\right)+b∕2\right\}}^2}{2b}\right]$$ (22)

$$\text{where}b=\log \left[1.0+{\left(\frac{{\sigma }_{\log }}{r_{\mathit{pm}}}\right)}^2\right]$$ (23)

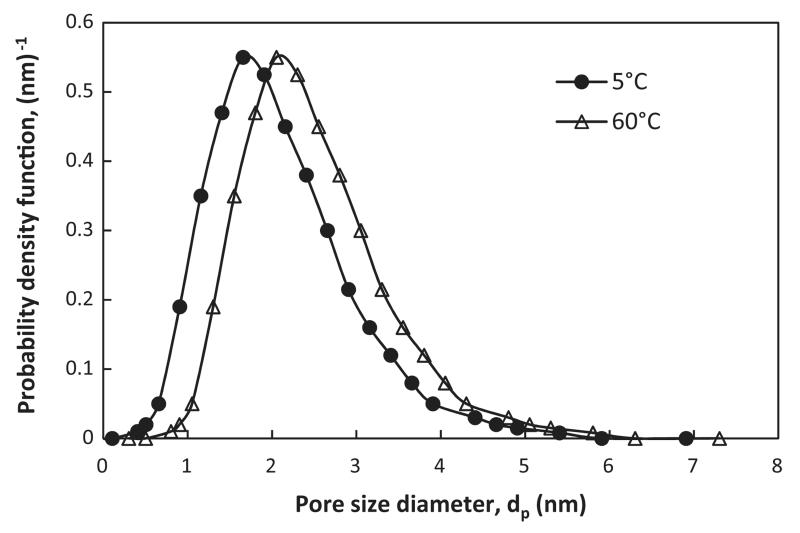
This probability density function (f_R) is expressed in terms of the distribution mean pore radius (r_pm) and standard deviation (σ_log). Like in Van der Bruggen and Vandecasteele [37], reflection coefficients depending on molecular weight or effective diameter (Eq. (7)) as well as retentions can in principal be calculated. On the other hand, in Wang and Chung [36], also probability density function curves for the two membranes (N30F and NF PES10) at 18 °C, 10 and 20 bar were investigated and determined. Again, since the N30F is identical with the used one in this work, the change in pore size distribution was estimated by applying the relation (Eq. (21)). Assuming that this relation is valid for a relatively narrow pore radius range, the new distributions corresponding to 5 and 60 °C were calculated and shown in Fig. 4.

Fig. 4.

Estimated probability density function curves for the NP030 membrane at 5 and 60 °C, based on the experimental data from [34–36].

Based on the above discussion, especially based on the possible noticeable change of the membrane pore size distribution with temperature, the increase of the rejection with decreasing temperature (Fig. 2) can be expected. The practically linear correlation between rejection and temperature for all compounds is partially surprised. On the other hand, considering the change of the mean pore radius with temperature (r_pm ~ 0.975 nm at 5 °C and ~1.2 nm at 60 °C calculated using Eq. (22)) and a fixed solute size, an approximate linear behavior can partially be expected based on the hindrance model within a λ range. Similar behavior was also shown for example in Dang [27]. In their work, changes in real rejection of idealized spherical solutes as a function of membrane pore radius, when feed temperature increases from 20 to 40 °C, were shown to be practically linear.

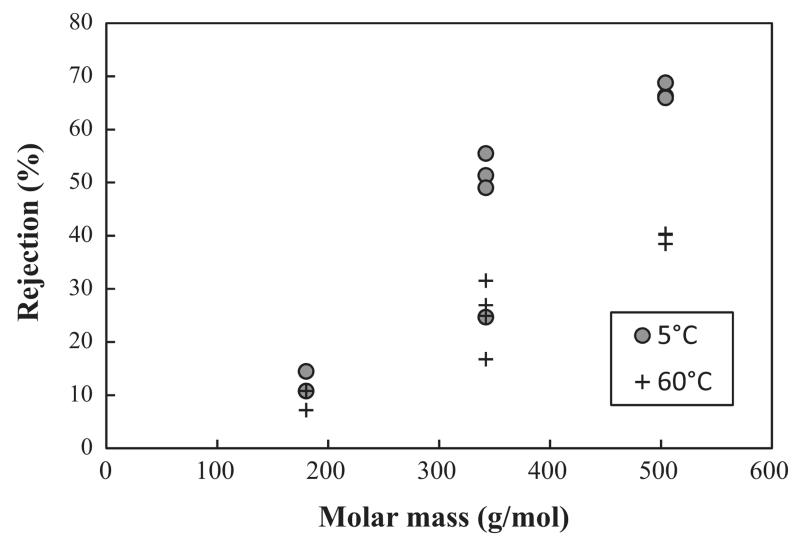
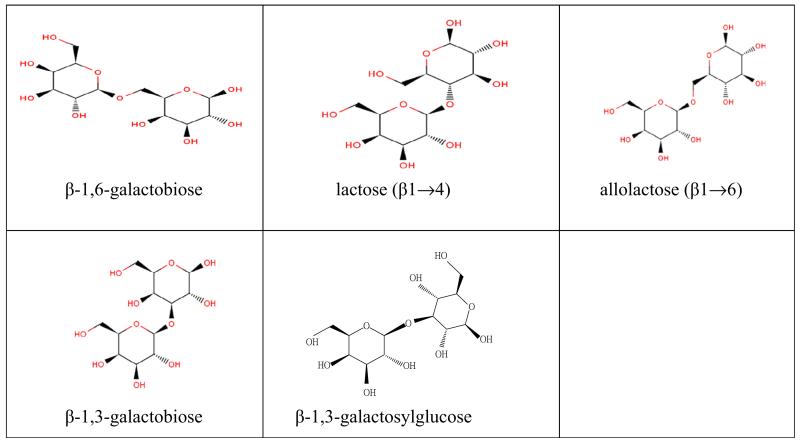
As shown in the results, the rejections are noticeable depending on molecular structure and concentration of the solute, besides the dependence on molecular mass (see Fig. 5). The rejections for disaccharides (same molecular mass) vary considerably. For better orientation, the chemical structures of the disaccharides are presented in Fig. 6. In this context, the possible influence of the molecule geometry was already mentioned above [23].

Fig. 5.

Rejections of mono-, di- and tri-saccharides (MM: 180, 342 and 504 g/mol) as a function of molecular mass at different temperature (NP030 membrane, 25 bar, 500 rpm).

Fig. 6.

The different structures of disaccharides.

The rejection is dependent on volume flux as well (see Fig. 3, however, presented depending on pressure). In the end, apart from the pore radius and membrane thickness, other parameters like viscosity, diffusivity change with temperature too, which, of course, need to be taken into account. A number of further experiments are of interest in order to better discuss the mass transfer properties under real practical conditions. However, these were out of the scope of the present work.

4. Conclusions

Due to its simplicity, NF is of interest for the purification of OS (separation of monosaccharides from di-and oligosaccharides), if very high purity degrees are not required. However, microbial growth during the operation under standard conditions (room temperature region) may represent a serious problem. By reducing or increasing the temperature, this problem can be solved to a certain extent. A comparison between 5 °C and 60 °C shows that 5 °C is more advantageous for the filtration process especially with regard to product yield. Using the membrane type NP030 at 45 bar, a purity of 85% and an OS recovery yield of 82% could be reached. With diafiltration, purities around 90% are achievable; however, about 30% of product loss has to be taken into account. From an economical point of view, higher production costs need to be accepted due to the low permeate flux which in the present case was around 3 L/m² h.

Regarding solute rejections as well as selectivities, a qualitative theoretical discussion shows that a possible change of the pore radius distribution with temperature may play a role, besides the diffusivity, chemical structure and concentration of individual compounds.