Composite Measures of Health Care Provider Performance: A Description of Approaches

Abstract

Context

Since the Institute of Medicine’s 2001 report Crossing the Quality Chasm, there has been a rapid proliferation of quality measures used in quality-monitoring, provider-profiling, and pay-for-performance (P4P) programs. Although individual performance measures are useful for identifying specific processes and outcomes for improvement and tracking progress, they do not easily provide an accessible overview of performance. Composite measures aggregate individual performance measures into a summary score. By reducing the amount of data that must be processed, they facilitate (1) benchmarking of an organization’s performance, encouraging quality improvement initiatives to match performance against high-performing organizations, and (2) profiling and P4P programs based on an organization’s overall performance.

Methods

We describe different approaches to creating composite measures, discuss their advantages and disadvantages, and provide examples of their use.

Findings

The major issues in creating composite measures are (1) whether to aggregate measures at the patient level through all-or-none approaches or the facility level, using one of the several possible weighting schemes; (2) when combining measures on different scales, how to rescale measures (using z scores, range percentages, ranks, or 5-star categorizations); and (3) whether to use shrinkage estimators, which increase precision by smoothing rates from smaller facilities but also decrease transparency.

Conclusions

Because provider rankings and rewards under P4P programs may be sensitive to both context and the data, careful analysis is warranted before deciding to implement a particular method. A better understanding of both when and where to use composite measures and the incentives created by composite measures are likely to be important areas of research as the use of composite measures grows.

Policy Points.

• Composite measures of health care provider performance aggregate individual performance measures into an overall score, thus providing a useful summary of performance.

• Numerous federal, state, and private organizations are adopting composite measures for provider profiling and pay-for-performance programs.

• This article makes an important contribution to the literature by highlighting the advantages and disadvantages of different approaches to creating composite measures and also by summarizing key issues related to the use of the various methods.

• Composite measures are a useful complement to individual measures when profiling and creating incentives for improvement, but because of the sensitivity of results to the methods used to create composite measures, careful analysis is necessary before they are implemented.

The performance of US health care organizations has received increasing attention since the publication of the Institute of Medicine (IOM) report To Err Is Human, which described a health care system replete with both quality and efficiency problems.1 The IOM’s companion report, Crossing the Quality Chasm, called for major health care system reforms in order to achieve safe, effective, efficient, timely, patient-centered, and equitable health care.2 Since 2001, there has been a rapid proliferation of quality measures put forth by both federal and private organizations for hospital-profiling and pay-for-performance (P4P) programs. For example, in 2002, the Hospital Quality Alliance, a public-private consortium, advocated the development of a national public database of condition-specific hospital performance measures that would serve as measures of hospital quality. Since the establishment of the Hospital Compare website in 2005, the Centers for Medicare and Medicaid Services (CMS) has added a large number of process and outcome measures.

Although individual performance measures are useful for identifying specific processes and outcomes for improvement and tracking progress, they do not provide an easily accessible overview of performance. Further, the plethora of recently developed quality measures may contribute to confusion and add to the burden of managers and potential users who may want (and need) simple ways to understand whether and by how much an organization is improving. Composite measures, which aggregate individual performance measures into summary scores, reduce the amount of data that must be processed and provide a clearer picture of overall performance.3 Composite measures also can serve multiple purposes and stakeholders. Macro-level composite measures, such as the total performance score calculated as part of the CMS Hospital Value-Based Purchasing (VBP) Program4 (discussed in more detail later), provide a useful summary of the extent to which management has created a “culture of excellence” and designed processes to ensure high performance in delivering services throughout the organization. For senior leaders, composite measures allow them to benchmark their organization’s performance against high-performing organizations and to monitor changes over time. For mid-level managers, composite measures allow them to track a particular service or unit’s performance. For patients selecting a provider for their care, a composite measure that combines different dimensions of performance into a single number is more easily understood than a large number of individual performance measures. For policymakers, composite measures provide performance criteria to use in selecting high-performing providers to include in health care delivery networks. For health care payers, a composite measure can facilitate the creation of P4P programs that differentially pay providers on the basis of overall performance. Finally, for researchers, composite measures can help identify high-performing organizations, which can then be studied to identify characteristics that distinguish them from lower-performing organizations.

Despite these multiple purposes, composite measures are not useful for targeting specific areas of improvement. Instead, the individual measures comprising the composite must be examined in order to determine and prioritize where specific improvement efforts should be concentrated. Thus, it is important that the individual measures be of high quality. In discussing its most recent criteria for endorsing composite measures, the National Quality Forum (NQF) noted that although “NQF endorsement is not necessary for the component measures unless they are intended to be used independently to make judgments about performance . . . the individual component measures should meet specific subcriteria, such as for clinical evidence and performance gap.”5

Specific criteria also are used to assess the measurement properties and performance of composite measures. For example, the NQF’s criteria include the following: (1) evidence, performance gap, and priority—importance to measure and report; (2) reliability and validity—scientific acceptability of measure properties; (3) feasibility; and (4) usability and use. The American College of Cardiology Foundation / American Heart Association Task Force on Performance Measures 2010 Position Statement on Composite Measures for Healthcare Performance Assessment also provides a concise review of many issues related to composite measures.6

Recent experience with the Agency for Healthcare Research and Quality (AHRQ) Patient Safety Indicator (PSI)-90 composite, used by CMS as a component of the Hospital-Acquired Condition Reduction Program and the Hospital VBP Program, reinforces the need for specific evaluation criteria for composite measures and also illustrates some of the challenges in developing and implementing composite measures. This composite, created from 8 individual PSIs identified from administrative data, has not yet been endorsed by the NQF because of the controversy surrounding its use in the Hospital VBP Program.7 Specifically, these concerns relate to the reliability and validity of specific individual measures (eg, postoperative venous thromboembolism is vulnerable to surveillance bias, so event rates can be higher when there is increased surveillance); accuracy of the adverse events identified (eg, diagnostic codes for unintentional injury are used to identify adverse events like accidental puncture or laceration, even though studies have shown that they often are not meaningful or clinically relevant unintentional injuries); inadequate risk adjustment because of reliance on administrative data; and the use of weights to create the composite that assume that the level of harm associated with each component measure is the same.

The purpose of our article is to describe and illustrate, through examples, the different approaches to creating composite measures and the advantages and limitations of each approach. The article is divided into 8 sections. After this introduction, we discuss the 2 alternative ways in which a composite measure can be conceptualized, as either a reflective or a formative construct.8 We then illustrate the implications of different weighting schemes for composite measures conceptualized as formative constructs and the major ways in which individual measures comprising the composite might be rescaled before being combined into a composite. The next section gives specific examples of composite measures conceptualized as reflective constructs, with a particular emphasis on the Hospital Consumer Assessment of Healthcare Providers and Systems (HCAHPS) survey (also referred to as the CAHPS Hospital Survey). Following this, we discuss improvements in measure precision and reliability that result from using composite measures, and we briefly consider issues of validity. Next we describe shrinkage estimators that, by taking into account differences in the precision of individual measures from providers of different sizes, can lead to better estimates of both individual measures and composite measures. We briefly examine the different perspectives of composite measures when used in profiling and P4P programs. Finally, we offer conclusions about key issues when developing composite measures and look at the relevant policy implications of different approaches. Throughout the article, we use the general term “provider” or “facility” to refer to the organizations delivering health care services. Specific examples of composite measures are from different types of providers: hospitals, service units within hospitals (eg, surgery), health plans, nursing homes, family practices, and individual clinicians.

Two Alternative Ways to Conceptualize a Composite Measure

Reflective Constructs

To illustrate the alternative conceptualizations, consider a composite measure representing an organization’s quality of care. Quality may be conceptualized as an inherent or latent characteristic of the organization that is “reflected” in specific quality measures. For example, similar to a student who is good in mathematics (an underlying characteristic of the person) and does well on mathematics tests, an organization that provides high-quality care also does well on empirical measures of quality. When conceptualized in this way, quality is a “reflective” construct. A reflective construct exists independently of the specific measures used to measure it, and thus specific measures can be added or taken away without changing the meaning of the construct. The distinguishing feature of a reflective construct is that the direction of causality is from the construct to the empirical measures; that is, the empirical measures are high or low because the construct is high or low. Therefore, to improve quality, interventions should focus on the construct rather than on the specific measures. An organization might want to focus interventions on one or more of its underlying characteristics, such as culture (is there a culture of quality?), resources (are sufficient resources allocated to quality improvement?), or training (do employees have sufficient job knowledge and skills?). Because the empirical measures reflect the underlying construct, they generally are highly correlated. Statistical approaches like principal components analysis and factor analysis are widely used to find sets of correlated measures that are hypothesized to reflect underlying latent constructs.

Formative Constructs

Alternatively, a construct can be conceptualized as “formative”; that is, it is formed from the empirical measures used to measure the phenomena of interest. In this case, the construct does not exist independently of the empirical measures, and the meaning of the construct will change if there are any changes in the measures associated with the construct. The goal in defining a formative construct is to identify a range of measures that capture the different dimensions of the performance in which one is interested, rather than different measures that reflect the same characteristic or trait, as in the case of a reflective construct. Thus, in contrast to a reflective construct, the measures defining a formative construct are not necessarily highly correlated, as they are selected purposefully to measure different dimensions of performance.

To illustrate, consider a person’s socioeconomic status, which might be measured by a combination of education, income, occupation, and residence. These empirical measures define what is meant by socioeconomic status; they are not reflections of some underlying characteristic of a person. If one changes the measures that define socioeconomic status, then one changes the meaning of the term. If one wants to intervene to improve socioeconomic status, one needs to focus an intervention on improving the individual measures used to define the construct, such as an individual’s opportunity for additional education. Similarly, if one wants to improve quality conceptualized as a formative construct, one has to target the specific measures used to define the construct.

Because sets of quality measures are typically not highly correlated, particularly when the measures are selected from different domains of care (eg, processes, outcomes, patient satisfaction, efficiency), formative constructs are used much more widely for composite measures than reflective constructs. Next we look at a number of important issues associated with formative constructs and then briefly consider reflective constructs.

Formative Constructs

Weighting

Since a formative construct is not based on the hypothesis that the measures are correlated, the correlation structure of the data cannot be used to determine the construct. Rather, the construct is estimated by taking a weighted average of the measures that comprise the construct. To illustrate the different weighting schemes commonly used, consider a single facility and 3 types of adverse events. Table 1 shows, for each type of adverse event, the number of patients “eligible” to experience the event and the number of events.

Table 1.

How Weights Are Calculated

Type of		Number of	Adverse		Opportunity-	Numerator-
Adverse	Number	Adverse	Event Rate	Equal	Based	Based
Event	Eligible	Events	by Type	Weights	Weights	Weights
A	100	20	20/100 = .20	.333	100/200 = .50	20/80 = .25
B	60	40	40/60 = .667	.333	60/200 = .30	40/80 = .50
C	40	20	20/40 = .50	.333	40/200 = .20	20/80 = .25
Total	200	80

Equal Weights

Equal weights assign a weight of one-third to each type of adverse event, which results in a composite score of 0.456, as shown in Table 2. This approach has strong intuitive appeal when there is no basis for distinguishing differences in the seriousness of impact on patients from the 3 types of adverse events. As Babbie9 notes, without strong justification for differential weights, equal weighting should be the norm. It is not clear, however, that the intent of equal weighting is actually best achieved by using equal weights. To illustrate, consider reducing each type of adverse events by 10 events. As shown in Table 2, the resulting composite scores are not the same. Equal weighting creates an incentive to focus on Type C events, since this will lead to the greatest reduction in the composite score. It is straightforward to show that the same composite score will result by reducing Type A events by 10, Type B events by 6, or Type C events by 4. Assuming it costs the same to achieve a reduction of 1 adverse event for each of the 3 types of events, equal weighting of event rates creates unequal incentives for reducing the 3 types of events. This example demonstrates how one can be misled if the weight is used as the basis for prioritizing interventions rather than the impact on the composite measure.

Table 2.

Effects of Different Weighting Systems on the Composite Score When Event Rates Are Reduced

Weighting System	Calculation of the Composite Score
Equal weights	(1/3)∗(20/100) + (1/3)∗(40/60) + (1/3)∗(20/40) = 0.456
Reduce A by 10	(1/3)∗(10/100) + (1/3)∗(40/60) + (1/3)∗(20/40) = 0.422
Reduce B by 10	(1/3)∗(20/100) + (1/3)∗(30/60) + (1/3)∗(20/40) = 0.400
Reduce C by 10	(1/3)∗(20/100) + (1/3)∗(40/60) + (1/3)∗(10/40) = 0.372
Opportunity-based weights	(100/200)∗(20/100) + (60/200)∗(40/60) + (40/200)∗(20/40) =
	(20 + 40 + 20)/200 = 0.400
Reduce A by 10	(10 + 40 + 20)/200 = 0.350
Reduce B by 10	(20 + 30 + 20)/200 = 0.350
Reduce C by 10	(20 + 40 + 10)/200 = 0.350
Numerator-based weights	(20/80)∗(20/100) + (40/80)∗(40/60) + (20/80)∗(20/40) = 0.508
Reduce A by 10	(10/70)∗(10/100) + (40/70)∗(40/60) + (20/70)∗(20/40) = 0.538
Reduce B by 10	(20/70)∗(20/100) + (30/70)∗(30/60) + (20/70)∗(20/40) = 0.414
Reduce C by 10	(20/70)∗(20/100) + (40/70)∗(40/60) + (10/70)∗(10/40) = 0.474

Opportunity-Based Weights

Opportunity-based weights (also called denominator-based weights) are calculated as the number of people eligible for each type of adverse event (ie, the number of opportunities for an adverse event) divided by the sum of the numbers eligible for each type of event (Table 1), resulting in a composite score of 0.400 (Table 2). As Table 2 shows, the composite score can be calculated most directly as the sum of the number of adverse events across types divided by the sum of the number eligible for each type of adverse event. Thus, a 10-person reduction in each type of adverse event has exactly the same impact on the composite measure. Opportunity-based weights result in the same incentive to focus on each type of adverse event. In addition, opportunity-based weights take into account the differences in the types of patients that a provider might care for, to the extent these differences are reflected in the number of people eligible for each measure (eg, the number eligible for diabetes-related measures compared with the number eligible for measures related to breast cancer screening).

Numerator-Based Weights

Numerator-based weights are calculated as the number of people who experience each type of adverse event divided by the sum of the number of people who experience each of the adverse events, resulting in a composite score of 0.508. As Table 2 illustrates, numerator-based weights can lead to counterintuitive incentives. When Type A events are reduced by 10, the composite score actually increases. The reason is because of the much larger weight associated with Type B events (the weight increases from 0.50 to 0.57) and the relatively higher rate associated with Type C events. Also, even though the numerator-based weight is the same for Type A and Type C events, the impact of a reduction in each type of event on the composite is not the same. Numerator-based weights can create disincentives to focus on the less prevalent types of events and very strong incentives to focus on the more prevalent types of events. Contrast this approach with opportunity-based weights, which encourage interventions in those types of adverse events that are most easily reduced (since each reduction of an adverse event, regardless of type, has the same effect on the composite).

The important assumption in these examples is that the cost to reduce each type of adverse event by one is similar. This may be a reasonable assumption if the method by which the adverse events are reduced relates to the performance of a specific set of activities for each individual patient. But if the way in which adverse events are reduced is by a process redesign, it might be more reasonable to assume an equal percentage reduction for each of the types of adverse events. Under this assumption, there are strong incentives to focus on the most prevalent types of adverse events, incentives that will be strongly reinforced if numerator-based weights are used.

Both numerator- and opportunity-based weights are most useful when calculated separately for each hospital. From a policy perspective, however, it often is useful to have a common set of weights that apply to all hospitals. In this case, the number of events (numerators) and the number of eligible cases (denominators) are aggregated across hospitals, resulting in a total number of events and a total number eligible for each type of event in the population. The composite is then calculated from these totals using one of the approaches just described. For example, AHRQ uses numerator-based weights calculated from this type of aggregation across all hospitals for the PSI-90 composite measure.10

Although our focus in this discussion has been on measures that can be expressed as proportions, these same approaches work for outcome measures expressed as the ratio of observed events to expected events (O/E ratios), where the expected events are derived from a risk-adjustment model. In this case, the composite measure using opportunity-based weights is calculated as the sum of the Os (across all conditions being studied) divided by the sum of the Es. CMS often uses a random effects model for risk adjustment. In this case, the numerator is the predicted risk for a specific hospital (calculated by adding a hospital-level factor to the risk-adjustment model), and the denominator is the predicted risk for an average hospital (ie, the hospital-level effect equals zero). P/E ratios (hospital-specific predicted divided by average-hospital predicted) can be similarly combined into a composite.

All-or-None Measures

All-or-none measures11 use equal weighting of the individual measures but aggregate results at the patient level rather than at the hospital level, as in the preceding examples. To illustrate, consider a specific medical condition for which there are 6 evidence-based processes associated with high-quality care. Rather than using as a performance measure the proportion of individuals eligible for each process measure who receive the intervention, one might take the patients’ perspective and ask, “What proportion of patients received all 6 interventions for which they were eligible?” The composite measure is the proportion of patient “successes,” that is, the proportion of patients who receive all the interventions for which they are eligible. This is equivalent to assigning to each measure a 1 (if the patient received the intervention) or a 0, averaging the results, and calling the patient a success if the average equals 1. In introducing the all-or-none measure, Nolan and Berwick wrote: “It raises the bar and illuminates excellence in a societal enterprise that should not be satisfied with partial credit or incomplete execution and should have widespread adoption.”11^(p1170)

We should distinguish an all-or-none measure from the more general term, “a bundle.” Whereas the former term focuses on specific process of care measures delivered to the patient, the latter is a grouping of “best practices with respect to a disease process that individually improve care, but when applied together result in substantially greater improvement.”12 For example, hand decontamination immediately before and after each episode of patient contact would be considered part of a bundle rather than an all-or-none measure, since no process intervention was directly delivered to the patient.

As noted, all-or-none measures implicitly assume that each process component is equally important. One might modify the set of “required” processes by identifying a core set for which there is the strongest evidence of benefit and then restrict the all-or-none measure to this core set. Alternatively, one might count as a success a patient who receives 4 or 5 of the specified 6 required processes, an approach that again counts each measure as equally important. For adverse events, it is straightforward to extrapolate an “all-or-none” measure to an “any-or-none” measure. That is, patients are successes if they do not experience any adverse events. Similar to the all-or-none measure, this approach treats all adverse events as equally harmful. In developing a composite measure of performance for coronary artery bypass grafting (CABG), the Society of Thoracic Surgeons (STS) Quality Management Task Force (QMTF) used an all-or-none approach to calculate a composite measure from 4 measures of perioperative care and an any-or-none approach to calculate a composite from 5 measures of postoperative risk-adjusted major morbidity.13 A number of states, including Minnesota and Wisconsin, also use all-or-none composite measures for profiling and in P4P programs. For example, Minnesota uses all-or-none composite measures for clinic patients needing specific types of care: diabetes care (5 component measures), vascular care (4 component measures), and asthma care (3 component measures); for hospital patients, all-or-none measures are used for heart failure (3 component measures) and pneumonia (2 component measures).14

Weighting Based on Expert Judgment

Weights based on expert judgment are sometimes used to calculate a composite measure. The Leapfrog Composite Safety Score illustrates a thoughtful approach to developing a judgment-based weighting system.15 The weights were determined by a 9-member expert panel in a multistage process. First, “discussion and repeated voting to maximize consensus” were used to select 26 measures from an initial list of 45 candidate measures. Weights were developed for each measure by assigning points based on the following criteria: strength of evidence (1 or 2 points), opportunity for improvement (a score between 1 and 3 based on the coefficient of variation), and impact, which was measured by summing the points associated with the percentage of patients affected (1 to 3 points) and “severity of harm” (1 to 3 points). Because all the individual measures had already met a high standard of evidence, opportunity and impact were weighted more heavily in the weight score, which was calculated as

evidence score + (opportunity score*impact score).

To convert the weight score to a percentage weight, the weight scores for each measure in each domain (structure/process and outcome) were summed, and the final weight for each measure was calculated as

final weight = [weight score/sum(weight scores in the domain)] * 0.50.

Multiplying by 0.50 in the equation enables the process/structure measures and the outcome measures each to contribute 50% to the composite measure. Finally, before the composite score was calculated, all measures were standardized by subtracting the overall mean and then dividing by the standard deviation (explained later).

Consumer Judgment

Consumer judgment can also be used to set weights, for example, by designing a system that allows potential consumers the flexibility to enter their own set of weights. A news item in Significance describes LineUp as an

open-source application that allows ordinary citizens to make quick, easy judgments about rankings that are based on multiple attributes. LineUp allows users to assign weights to different parameters to create a custom ranking . . . [they] can change the weightings of different attributes and see how that affects the rankings.16^(p3⁾

Adding this feature to websites would allow consumers to rate their provider’s performance based on their judgment about the relative importance of different measures or domains. If users of the website were asked to indicate their preferred weights, over time a database could be built from which weights reflecting the average views of consumers could be derived. For example, in the Quality Rating System and Qualified Health Plan Enrollee Experience Survey (currently in beta testing), which will be used to evaluate Qualified Health Plans offering coverage through the Health Insurance Marketplaces, 3 broad domain scores (clinical quality management; enrollee experience; and plan efficiency, affordability, and management) are combined into a final global rating.17 Consumers could be offered the option of specifying their own weights for the 3 broad domains, as well as weights for the subdomain scores that are aggregated to calculate the broad domain scores.

In summary, the main advantages of each approach are that equal weighting is the most intuitive; opportunity-based weights create an equal incentive to focus on each measure and adjust for case-mix differences; numerator-based weights create a strong incentive to focus on the most prevalent measures; all-or-none measures are patient focused and the most consistent with a commitment to the highest quality; expert panels can make judgments about dimensions such as the level of harm associated with each measure (a dimension missing from all the other approaches); and consumer-based weighting aligns mostly closely with consumer-/patient-centered care.

Impact of Alternative Methods on Provider Profiles

A number of authors have examined the impact of the different methods for creating composites on provider profiles. Reeves and colleagues18 compared the following 5 methods: (1) all-or-none; (2) 70% standard, a modification of all-or-none in which a patient is considered a success if 70% or more of the process measures for which a patient is eligible are delivered; (3) overall percentage, in which the composite is calculated using opportunity-based weights; (4) measure average, in which the composite is calculated by averaging the proportion of times each process measure was delivered to eligible patients (this is equivalent to using equal weights); and (5) patient average, a composite that is the percentage of measures for which the patient was eligible that were delivered. In one analysis that used data on 200 measures covering 23 conditions from 16 family practices in the United Kingdom the rank of practices “varied considerably” by method. For example, when the measure average and the patient average were compared, 56% of the practices changed places by more than a quarter of all rank positions. In another analysis, which considered 3 conditions (coronary heart disease, asthma, and type 2 diabetes) from 60 family practices, there were fewer large changes in the ranks, and many of the correlations between approaches were above 0.90. However, there were large differences between the all-or-none ranks and those ranks using the other methods (correlations were around 0.80). Reeves and colleagues concluded that “different methods of computing composite quality scores can lead to different conclusions being drawn about both relative and absolute quality among health care providers. Different methods are suited to different types of applications.”18^(p489)

Reeves and colleagues also offer a useful summary of the strengths and weaknesses of each approach. For example, for the following criteria, the all-or-none approach has either some or considerable advantage: It assesses quality with respect to the care given to each patient; it is appropriate when the desired outcome depends on completing a full set of tasks; it is suitable when individual patient scores are required; and it allows standard errors to be estimated using standard distributional methods. Similarly, opportunity-based weights have some or considerable advantage for the following: They assess quality with respect to each opportunity to provide care; the composite scores are not affected by the number of measures; and they can be used with a smaller sample of patients (ie, smaller standard errors).

Eapen and colleagues19 used both opportunity-based weights and the all-or-none approach to calculate a composite measure from 6 process measures, using data from more than 194,000 acute myocardial infarction (AMI) patients from 334 hospitals. They found that although there was greater dispersion in the all-or-none scores (interquartile range = 14.7% vs. 7.4%), the 2 scoring methods resulted in both composites and hospital rankings that were highly correlated with each other (r = 0.98 and r = 0.93, respectively), as well as similar rankings of the top and bottom hospital quintiles. Interestingly, they also found that when more process measures were added, the 2 methods produced similar changes in hospital rankings.

The conclusions that Jacobs, Goddard, and Smith20 reached were similar to those of Reeves and colleagues with respect to the impact of different methods on hospital profiling. Jacobs and colleagues raised another important issue: when decision rules are used to place providers into categories based on performance on individual measures (eg, providers might be assigned 1 to 5 stars, depending on the proportion of measures above some threshold), the ranking of organizations can be particularly sensitive to thresholds on individual measures. If providers are placed into a category based on a composite measure, the category assignments can be quite unstable.

To summarize these studies, it appears that the sensitivity of the results to the weighting methods used to calculate the composite score is dependent on the data set used and the context in which the composite is applied. When increasingly large numbers of performance measures from different domains are used, the results are more sensitive to the weighting approach. Nevertheless, in any given situation, it is necessary to evaluate alternative approaches in order to understand the implications of using one or another of the approaches.

Rescaling the Individual Measures Before Creating a Composite Score

Different types of measures are sometimes combined into a composite measure, for example, patient satisfaction, which might be measured on a scale of 1 to 10; adherence to a process measure, which varies from 0% to 100%; and an O/E (observed/expected) ratio, which might vary from 0.2 to 5.0 or more. Before combining such measures, it is important to rescale the individual measures.

The 2 most widely used methods of rescaling are (1) using z scores and (2) using a proportion of the range scores. As Table 3 illustrates, a z score is calculated as

(observed performance − mean performance) / standard deviation of performance,

where the mean and standard deviation (SD) are calculated across all facilities. Then as shown in Table 4, the proportion of the range score is calculated as

(observed value − minimum value)/(maximum value − minimum value),

where the maximum and minimum values represent the performance of the highest and lowest performing facilities. The denominator is referred to as the “range of the data.”

Tables3 and 4 present examples of the 2 different methods of rescaling for 2 process measures with different amounts of variation. They give the calculation of rescaled scores using both the z score (Table 3) and the proportion of the range score (Table 4), as well as the calculation of the composite score by averaging the rescaled scores (ie, using equal weights). They also show the impact of improving each of the process measures by one rescaled unit. Note that although the scores have been rescaled so that the 2 process measures’ differences in variation do not affect the composite score, an improvement of one rescaled unit is harder to achieve in the original units for the process measure with the larger variation. For example, in Table 3, to improve the composite score by 0.5, one could increase either process 1 or process 2 by one rescaled unit. Increasing process 1 by one rescaled unit requires an improvement in adherence from the current level of 86% to 94%; however, increasing process 2 by one rescaled unit requires an improvement in adherence from 76% to 92%. In its development of the CABG composite, the STS QMTF considered both methods of rescaling before combining the scores from each of the 4 domains comprising the composite. The correlation between the 2 sets of rescaled scores was 0.99. The QMTF thus decided to use the z score approach to rescaling.13

Table 3.

Rescaling Approach Using the Z Score

		Observed		Improvement	New %
Process	Mean (SD)	% Adherence	Z Score	(Z Scale)	Adherence
1	70% (8%)	86	(86 − 70)/8 = 2	1a	94
2	60% (16%)	76	(76 − 60)/16 = 1	1b	92
Composite score			(2 + 1)/2 = 1.5	a: (3 + 1)/2 = 2
				b: (2 + 2)/2 = 2

In this table, z score = (observed value – mean)/standard deviation (SD).

Table 4.

Rescaling Approach Using the Range Score

	Maximum	Observed %	Rescaled	Improvement	New %
Process	(Minimum)	Adherence	Score*	(Range Scale)	Adherence
1	50% (40%)	45	(45 − 40)/(50 − 40) = .5	.1a	46
2	60% (40%)	50	(50 − 40)/(60 − 40) = .5	.1b	52
Composite score			(.5 + .5)/2 = .5	a: (.6 + .5)/2 = .55
				b: (.5 + .6)/2 = .55

In this table, rescaled value = (observed – minimum)/(range), where range = maximum – minimum.

A third approach sometimes used for rescaling is to convert each measure into a rank and then to average the ranks. The performance of 2 providers that differ by one rank on a particular measure may be either slightly or very different. This is because information about their relative differences in performance is lost when conversion to ranks is used for rescaling. As a result, it is unclear how much an improvement on a measure will contribute to a change in ranks. In its scorecard on state health system performance, the Commonwealth Fund averages ranks in order to determine composite measures by domain and across all domains.21

In some cases, scores within different domains are categorized, usually into 1 of 5 categories, and then are given 1 to 5 stars. These categorical scores are then combined into an overall composite categorization. For example, in the CMS’s Nursing Home Compare Five-Star Quality Rating System,22 the following 3 domains are considered: health inspection ratings, staffing measures, and performance on 11 quality measures. The health inspection score is calculated based on points assigned to health deficiencies identified in inspections and complaint investigations, and then in each state, facilities are assigned 1 to 5 stars. The top 10% of nursing homes in a state receive 5 stars; the next 3 groups, each with 23.3% of the homes, receive 4 to 2 stars, respectively; and the worst 20% receive 1 star. The staffing measure is based on the total number of nursing hours per resident day and the number of RN hours per resident day. A nursing home is assigned 1 to 5 stars based on each staffing measure, and these in turn are combined into a 1- to 5-star categorization for staffing. For most of the quality measures (there are slight adjustments for low prevalence measures), facilities are grouped into quintiles based on the national distribution of facilities and are assigned points based on their quintile. The points are summed across measures, and then the facilities are mapped into a star category. A complicated algorithm is then used to combine the star categorizations across the 3 domains. To give a flavor of this approach, the first 2 steps are as follows: (1) start with the health inspection 5-star rating; and (2) add 1 star to the Step 1 result if the staffing rating is 4 or 5 stars and greater than the health inspection rating, but subtract 1 star if staffing is 1 star. At this step, the overall rating must be between 1 and 5 stars.

The Quality Rating System developed by CMS for Qualified Health Plans issuing coverage through the Health Insurance Marketplace17 also maps measure scores into 5 categories, which are then rolled up into a 5-category global score. Much of the transparency of the 5-star systems is lost when 5-star category assignments are rolled up into increasingly broad domains and then a final 5-star classification. In addition, the star systems’ ease of interpretation comes at a real cost for some facilities, that is, arbitrary classification of facilities with scores near thresholds that define each category. Shwartz and colleagues23 illustrate this using a composite measure based on the probability that a facility is in different quantiles. They classified 112 US Veterans Affairs (VA) nursing homes into star categories and then showed that 4 of the 5 facilities ranked in the bottom 5 in the 4-star category based on the point estimate of their composite score had more than a 40% chance of really being 3-star or lower facilities. Four of the top 5 facilities in the 3-star category had more than a 39% chance of being a 4-star or higher facility.

Spiegelhalter and colleagues24 discussed several thoughtful approaches to rating organizations, deciding which to inspect, and monitoring them in order to identify problems as they arise. Among their suggestions are the following: (1) transform individual measures so their distribution follows a normal (bell-shaped) distribution (they suggest a number of transformations for different types of measures); (2) rescale the measures using the z score approach; (3) make adjustments to avoid the impact of extreme values, the easiest of which is to “winsorize” the rescaled scores, that is, to reset scores above and below some specified threshold (eg, 3 standard deviations from the mean) to the high or low threshold, at which point the standard deviation is recalculated and new rescaled scores are determined; and (4) combine the rescaled scores into a composite using an approach that down-weights sets of highly correlated scores (since they provide the same information).

Reflective Constructs

Surveys

Surveys are one of the most important areas in which reflective constructs are used and in which psychometrics predominates. In many cases, the goal of a survey is to assess respondents’ attitudes toward specific domains. Associated with each domain is an underlying latent construct that is reflected in questions related to the domain. One would expect the answers to these questions to be highly correlated, since they are reflecting the same underlying latent construct, and to have a lower correlation with responses to questions reflecting other domains. The challenge in survey development is to identify a series of questions related to each domain but unrelated to other domains. Much of the psychometric analysis of pilot survey data involves using various statistical analyses (principal components analysis or factor analysis predominates) to demonstrate that sets of questions related to specific domains are highly correlated and that questions related to different domains have relatively lower correlations.

To combine domain-specific questions into a domain-specific composite score, one could weight each question by the component or factor loadings (if principal components analysis or factor analysis were used to identify sets of correlated questions). This is rarely done, however. Rather, a composite measure for each domain is usually calculated by averaging the responses to questions associated with that domain; that is, equal weighting is used. Assuming multiple domains, there will then be multiple composite measures, one for each domain. If an overall summary measure is desired, the same challenge will exist as in a formative construct: weighting the various domain composite scores in order to arrive at the summary measure.

We use the Hospital Consumer Assessment of Healthcare Providers and Systems (HCAHPS) survey, developed through a rigorous, multistep process, to illustrate survey-based composite measures.25 A variety of psychometric analyses were conducted using HCAHPS data.26 The 2013 version of the survey contains 25 substantive questions grouped into major domains reflecting patients’ experiences: care from nurses, care from doctors, the hospital environment, experiences in the hospital, experiences related to discharge, extent of understanding of postdischarge care at the time of discharge, and the overall rating of the hospital. For example, the 4 questions under care from nurses (which are answered “never,” “sometimes,” “usually,” and “always” and scored 1 to 4 points, respectively) are (1) “During this hospital stay, how often did nurses treat you with courtesy and respect?” (2) “During this hospital stay, how often did nurses listen carefully to you?” (3) “During this hospital stay, how often did nurses explain things in a way you could understand?” and (4) “During this hospital stay, after you pressed the call button, how often did you get help as soon as you wanted it?” The score for the nursing domain is calculated by averaging the responses to these 4 questions.

Instead of calculating an overall composite reflecting consumers’ attitudes toward their hospital experience by averaging domain-specific composite scores across the domains, HCAHPS asks 2 broad questions to capture the “gestalt” of the hospital stay: (1) “Using any number from 0 to 10, where 0 is the worst hospital possible and 10 is the best hospital possible, what number would you use to rate this hospital?” and (2) “Would you recommend this hospital to your friends and family?” (Responses are on a 4-point scale of “definitely no,” “probably no,” “probably yes,” and “definitely yes.”) Because the consumer has first been motivated to think about and score the different dimensions of hospital care, it is not unreasonable to then ask, “Pulling all of this together, what is your overall assessment of the hospital stay?” The major advantage of this approach is that the implicit weighting needed to go from the domain scores to an overall assessment reflects consumers’ preferences and is thus patient centered. But it also has a disadvantage: Because the hospital does not know how the consumer felt about the relative importance of the different dimensions of hospital care, this type of implicit composite provides little guidance on which major areas to target for improvement.

Other Examples of Reflective Constructs

Because reflective constructs require correlation among subsets of measures, they are more widely used when the measures reflect specific domains of care. For example, Glickman and colleagues27 considered the 8 process measures for acute myocardial infarction (AMI) and 4 for heart failure from 4,226 acute care hospitals on the Hospital Compare database (though they combined 2 of the AMI measures into a single measure). They found that 2 principal components adequately represented the correlations in the data. One component was conceptualized as “clinical” (ie, pharmacologic interventions) and the second as “administrative” (ie, patient instructions or counseling activities). These 2 areas better reflect how hospitals organize the delivery of cardiac care than does a distinction based on therapeutic area (AMI or heart failure). The authors demonstrated that the 2 composite scores were better able to predict AMI mortality in the next year than was a single score calculated using opportunity-based weights.

Shwartz and colleagues28 described the use of a Bayesian latent variable model to estimate an underlying construct “process quality” that is reflected in the 15 process measures originally monitored by CMS on the Hospital Compare website (6 measures for AMI, 4 for congestive heart failure, and 5 for pneumonia). Using data available from more than 3,200 hospitals, they were able to demonstrate a statistically significant link between the underlying construct process quality and the 15 process measures. The authors compared rankings of hospitals based on the latent variable process quality with rankings based on a composite created using opportunity-based weights. Even though the ranks were highly correlated (0.92), about 20% of the hospitals ranked in the top decile by one method were ranked in a lower decile (usually the second decile) by the other method.

Using Composite Measures to Increase Precision and Reliability and Considerations of Validity

Precision is a measure of how close an estimate calculated from a sample is to the “true” level of the variable if it were calculated from all patients in the population. The population may be “hypothetical,” for example, all potential users of a particular hospital if they need hospital care. The precision of an average calculated from a sample depends on the amount of variation in the variable, which is usually estimated by the standard deviation of the variable in the sample, and the size of the sample. It is measured by the standard error, which for an average is the standard deviation divided by the square root of the sample size.

To ensure some minimum level of precision and to reduce large fluctuations in rates over time due to random variation, policymakers frequently include a particular performance measure from a facility in profiling and P4P only if it has some minimum number of cases over a specified time period. For example, when publicly reporting risk-adjusted mortality and risk-adjusted readmission rates for AMI, heart failure, and pneumonia, CMS reports only the rates for those facilities that have at least 25 cases over a 3-year period. By considering a longer time period than the typical 1 year, CMS is able to include more facilities and increase the precision of reported rates. But this makes it more difficult to detect a significant change in performance in any 1 year, since prechange rates are included in the calculation of performance measures. For less frequently performed procedures or rarer conditions, smaller sample sizes might be used. For example, in its composite measure to evaluate adult cardiac surgery, the Society of Thoracic Surgeons Quality Management Task Force uses all facilities that performed at least 10 isolated coronary artery bypass graft (CABG) surgeries in a year.13 As we explain later, shrinkage estimators are an approach to “smooth” rates based on small sample sizes.

When individual rates are aggregated into composite measures, which measures to include and minimum sample sizes become more complex. In the CMS Hospital VBP Program, hospitals receive a clinical Process of Care Domain score if they had at least 10 cases during the 1-year performance period for at least 4 of the 12 process of care measures in the domain. Scores for each measure in the domain are summed and then “normalized” by calculating the percentage that the summed score is of the total possible score given the number of process measures included. The Outcome Domain consists of 3 mortality measures (AMI, heart failure, and pneumonia), each of which requires a minimum of 25 cases; the AHRQ PSI-90 (Patient Safety Indicator-90), which requires at least 3 cases on at least 1 of the 8 PSIs comprising the measure; and a central line–associated bloodstream infection (CLABSI) measure, which requires at least 1 predicted infection. The Outcome Domain is calculated for only those hospitals in which the case minimum is met for 2 of the 5 measures. The final total performance score (TPS) is calculated as the weighted average of 4 domain scores: clinical processes (20%), patient experience (30%), outcome (30%), and efficiency (20%).4 Hospitals need scores for at least 2 of the 4 domains in order for the TPS to be calculated. The weights associated with any excluded domains are distributed proportionally to the remaining domains. Similar to the way in which many performance measurement systems are operationalized, little justification is provided for the minimum sample sizes. Nonetheless, they likely reflect the best judgment of the policymakers and methodologists who helped develop the rules.

Missing data from facilities on processes of care or certain outcomes usually indicate that the facility does not provide the relevant services. Sometimes, however, missing data may result from a conscious decision by the facility to withhold unfavorable information. Accordingly, composite measures can be structured to reduce incentives to withhold information. To illustrate, 1 of the 2 domains in the CMS Hospital-Acquired Condition (HAC) Reduction Program is composed of the standardized infection rates (SIRs) for central line–associated bloodstream infection (CLABSI) and catheter-associated urinary tract infection (CAUTI). These data come from the Centers for Disease Control and Prevention (CDC) National Healthcare Safety Network (NHSN), which collects self-reported data from hospitals. The current methodology assigns 10 points (worst score) for each measure in the domain when hospitals do not report NHSN data. If a hospital reports one NHSN measure but not the other, the hospital’s score is based solely on the single NHSN measure reported. CMS is considering a modification in the scoring, as follows: If a hospital does not submit data for either of the measures (and does not have a waiver or exemption), then 10 points will be assigned to both of the hospital’s measures. This change removes any incentive to submit data only for the infection with the lowest rate.

The use of composite scores may increase the level of precision compared with that of individual measures. This was examined by Van Doorn-Klomberg and colleagues29 using data from 455 Dutch family practices. They considered 12 clinical process measures for diabetes from 350 of these practices, 9 for cardiovascular disease and risk management (CVD/RM) from 342 practices, and 4 for chronic obstructive pulmonary disease (COPD) from 286 practices. Individual measures were the proportion of eligible patients receiving the indicated intervention, and composite measures were calculated for each condition by averaging the proportions across measures. Precision was measured as 1.96*standard error, which is the distance on each side of the mean of a 95% confidence interval. For most of the measures, a sample of about 100 cases was needed to attain 10% precision (ie, to be 95% certain of being within plus or minus 10% of the population average) for many of the practices. Through the use of composite scores, the same level of precision could be achieved for most practices with much smaller samples than required for a single measure. If higher levels of precision are needed (eg, under 5%), however, it would still be necessary to have a large number of cases for some conditions. The authors note that a composite score’s precision depends on performance on the individual measures (high or low performance scores have lower standard errors) and on the correlations among the measures (measures with lower correlations contribute additional unique information).

Whereas precision measures how close to the “true” population value that an estimator from a sample is likely to be, reliability measures how well an estimator can distinguish between high- and low-performing providers. Total variation in a performance measure is due to both random variation of the measure among a provider’s patients (within-provider variation) and variation in the measure across sets of patients seen by different providers (across-provider variation). The reliability of a performance measure is the ratio of variation across providers to the sum of variation across providers and variation within providers. If reliability is low, it will be difficult to detect a “signal” in a performance measure (ie, information to distinguish among providers) because of the large amount of “noise” in the data (ie, the random variation within a provider). In general, a reliability of 0.70 or higher is considered acceptable for psychometric purposes.30

Scholle and colleagues31 examined the reliability of individual and composite quality measures using administrative data from 9 health plans in different regions of the United States. They considered 27 HEDIS (Health Effectiveness Data and Information Set) quality measures, which are process measures for preventive care and for both chronic and acute care conditions. For each quality measure, they examined reliability as a function of the number of eligible patients seen by individual providers. Composite scores were calculated for the preventive, chronic, and acute measures as well as overall by first standardizing each measure (ie, calculating a z score) and then using opportunity-based weights for aggregation. When a standard of 0.70 or higher was used, only a small percentage of physicians could be reliably evaluated on a single quality measure; the largest percentages were 8% for colorectal cancer screening and 2% for nephropathy screening. When the overall composite measure was used, 15% to 20% of physicians could be reliably evaluated.

Kaplan and colleagues32 examined 11 diabetes process and intermediate outcome quality measures for 7,574 patients from 210 physicians. They calculated a composite score from an aggregation of 5 of the 6 process measures (those with sufficient variation) and 4 of the 5 intermediate outcome measures (those that contributed to variation in the composite measure). The reliability of the composite score was greater than 0.80. Kaplan and colleagues showed that after case-mix adjustment, the composite score could differentiate those physicians scoring in the highest quartile from those in the lowest.

The validity of measures of health care quality is difficult to evaluate both because quality is multidimensional and because there are few gold standards. NQF’s criteria5 state that “validity testing demonstrates that measure data elements are correct and/or the measure score correctly reflects the quality of care provided, adequately identifying differences in quality.” When gold standards are lacking, operationalizing these criteria is a challenge. In part, validity of a composite measure rests on the validity of the component measures. But NQF also requires direct validity testing of the composite, though it recognizes that such tests are likely to focus on construct validity (usually measured by correlating the composite measure with other measures of quality or by showing that the composite score differs among groups known to differ in quality measured by some other means). The problem is that there are likely to be concerns about the “other measures of quality.” Eapen and colleagues19 examined the correlation between composite measures of processes of care relevant to AMI patients (calculated using both opportunity-based weights and an all-or-none approach) and risk-standardized all-cause mortality and readmission rates. Both composite measures had a relatively low but statistically significant relationship with mortality (r = −0.25 and r = −0.24, p < 0.001, respectively) but no relationship with readmissions. Is this a reflection of the construct validity of the composite measures or of the comparison measures? As Shwartz and colleagues have shown,33 the low correlation between composite measures from different domains of care makes it difficult to identify high-performing hospitals, as well as to evaluate the construct validity of composite measures.

Shrinkage Estimators

When considering a particular performance measure calculated from all eligible patients at a facility (or treated by a provider), one cannot increase the precision of estimated performance by increasing the sample size. One can, however, modify the way in which estimated performance is calculated. Instead of relying on data from just the specific facility, one “borrows strength” by also considering performance in a set of facilities that can be assumed to be roughly similar to the specific facility. Consider a facility that is planning to implement a new program. Without any information about how well the program will work at the facility, one might well guess that the success rate will be the same as it is at other similar facilities that have implemented the program. But once the program has been implemented at the specific facility, its success might be estimated by placing some weight on the facility-specific success rate and some on the success rate at other similar facilities. As more data become available at the specific facility, more weight will be placed on the facility-specific estimate and less weight on the estimate from other facilities.

This approach takes into account 3 main factors when attempting to estimate the “true” value of a performance measure at a facility: the overall value of the measure from all facilities (considered to be the population value), the value of the measure at a specific facility, and the number of cases on which the specific facility experience is based. When estimating the “true” (long-run) value at a facility, less weight should be given to the population value and more weight to the value at the facility as the sample size increases. Or said another way, with a small sample size, the best guess of the “true” value at a facility is “pulled” or “shrunken” from the observed value at the facility toward the average value across all facilities. As the sample size increases, there is less and less pulling or shrinkage away from the facility-specific value. These types of estimators are called shrinkage estimates (or smoothed estimates)34 because they adjust for the greater uncertainty associated with smaller sample sizes.

Simple shrinkage estimators for a facility are calculated by taking a weighted average of the observed value of the measures at a facility and the overall values of the measures from all facilities. The weight w given to the observed value of a particular measure at a facility is larger when there are more cases for that measure at the facility (the remaining weight [1-w] is given to the value from all facilities). For a fixed sample size, when there is more variation in the performance measure across facilities, more weight is given to the facility-specific value and less to the population value (since the population value is a less reliable measure of performance at any specific facility). Various authors have discussed the advantages of these types of estimates.13,35–43

A composite measure can be calculated by aggregating shrunken estimates of performance on the individual measures rather than observed performance. The AHRQ PSI-90 Composite uses this approach.10 In the Hospital Readmission Reduction Program,44 CMS uses a sophisticated random effects model (ie, a model that assumes that facility effects come from a common probability distribution) that results in shrunken estimates of a hospital’s effect on readmission after adjusting for patient risk factors. The ratio of the hospital’s predicted readmission rate, given its case mix, to the expected readmission rate if there was no hospital effect is called the “risk-standardized readmission ratio” (RSRR). To calculate an all-condition hospital-wide readmission measure (ie, a readmission composite measure), CMS calculates RSRRs for 5 cohorts of patients (comprising most hospital discharges), takes the log of the RSRRs (because these types of ratios are skewed to the right), creates a composite using denominator-based weights, then exponentiates the result (to get the composite back to a scale on the original units), and finally multiplies the exponentiated number by the overall national readmission rate for the cohorts. The result is the risk-standardized hospital-wide readmission rate.

In more complex situations, shrinkage can depend not only on the relationship of a hospital-specific measure to the overall population average of that measure but also on the relationship between hospital-specific measures and population averages of other measures with which the particular measure is correlated. Shwartz and colleagues43 illustrated this using data on the 28 quality measures calculated from the Minimum Data Set (derived from an assessment instrument used in nursing homes). When this is done, the estimate of the individual performance measure of interest is a composite measure (ie, it is calculated by combining information about several different performance measures). This type of composite measure does not provide a more comprehensive view of performance, however, but can be a more precise view of performance on a single measure.

Birkmeyer, Dimick, Staiger, and colleagues have been in the forefront of advancing the use of these types of composite measures to better estimate a single performance measure.42,45–47 To illustrate, in a 2009 paper, Staiger and colleagues42 developed an improved measure of aortic valve replacement (AVR) mortality that considered a number of hospital structural characteristics (volume, teaching status, and nurse staffing levels), operative mortality (death before discharge or within 30 days of surgery) and nonfatal complications for AVR, and operative mortality and nonfatal complications for 7 other procedures. Their shrunken estimate of operative mortality for AVR at each hospital took into account both hospital-specific rates and overall population rates for AVR, the correlation of AVR with the other measures, and the reliability of each of the measures. The composite measure explained more of the variation in next year’s AVR mortality rates than did a shrunken measure of AVR mortality that did not include correlated variables (70% vs 32%). It also was better able to forecast differences in mortality across quintiles that were created based on this year’s AVR mortality rates.

Shrinkage estimators improve the precision of point estimates, particularly for smaller facilities whose observed performance levels are imprecise, and underscore that one is not able to learn much about small facilities from their observed performance level to distinguish their performance from average. As Silber and colleagues48 pointed out, in some situations (they use the example of AMI), it is known from the literature that facilities with lower volumes for certain procedures or conditions have a lower quality. In this case, shrinkage to an overall average can be misleading. As an alternative, smaller facilities can be shrunk toward a different target rate, for example, the average of all small facilities. This highlights the fact that on average, smaller facilities do not perform as well as larger facilities do on certain measures, but it may be unfair to the high-performing small facility that sees its estimated performance shrunk toward the lower average rate of all small facilities. How to handle estimates from small facilities therefore has been a matter of debate.34

Composite Measures Can Provide a Different Perspective in Profiling and P4P Programs

Very little research with regard to profiling facilities or P4P programs has compared the use of composite measures with individual measures. Shwartz and colleagues33 demonstrated that hospitals that do best on a composite measure are often not among the best on most of the individual measures. They examined 5 performance measures (processes of care, readmissions, mortality, efficiency, and patient satisfaction) from 577 hospitals. For each of the measures, each hospital was assigned to a quintile based on its performance on the measure. The composite measure was calculated as the sum of the quintiles. The top 5% of hospitals had a composite score of 9 or less. The top-ranked hospital (sum of quintiles = 6) was in the first quintile on 4 of 5 measures and in the second quintile on the last. There seems little doubt that this hospital should be considered a high performer. Among the 7 hospitals for which the sum of the quintiles was 7, there were 2 patterns: (1) the hospital was in the top quintile on 4 of 5 measures and in the third quintile on the fifth; and (2) the hospital was in the top quintile on 3 measures and in the second quintile on the other 2. These seem like reasonable patterns for a high-performing hospital. The situation is less clear, though, when considering the 20 hospitals for which the sum of the quintiles was 8 or 9. Many of these hospitals were in the top quintile on only 2 of the 5 performance measures. One might be hesitant to call these hospitals high performers. The next 5% of sample hospitals had a sum of quintiles that equaled 10, indicating that they were in the second quintile, on average, across all 5 measures. This pattern does not seem consistent with what one would expect for a high-performing hospital.

As part of an evaluation of a new performance measure (the probability that a facility is in the top quintile) using data from 28 quality measures from 112 VA nursing homes, Shwartz and colleagues23 compared how each facility would fare under a P4P program that rewarded each facility bonus payments based on its performance on individual measures versus bonus payments based on its performance on a composite measure. When allocations were based on a composite score, the payment bonuses ranged from 4.3% of the pool for the highest performers to almost nothing, but when allocations were based on aggregating bonuses for individual quality indicators, the bonuses ranged from 1.7% of the pool to 0.3%. The facilities ranked the highest when using the composite score often were ranked much lower when rewards were based on performance on the individual measures. For example, of the 23 facilities receiving the largest bonuses based on the composite score, only 3 were in the top 23 based on individual score bonus payments; 13 were ranked below the median. Overall, there was no relationship between the rankings based on the composite and the rankings based on the individual quality measures (r = −0.11, p = 0.25).

Both of these examples suggest that composite measures are identifying certain types of facilities as high performers that would not be picked out by looking at just the individual measures comprising the composite. We suspect that composite measures are identifying as high performers some facilities that do “reasonably well” across most of the component measures but not “well enough” to be high performers on those measures. More research to examine this hypothesis would thus be useful.

Conclusions

Composite measures are relatively new arrivals on the performance measure scene, reflected in part by NQF’s evolving criteria for formal endorsement. Composite measures provide a useful summary of both current performance and improvement, but they must be used in conjunction with the component individual performance measures to find opportunities for improvement and to guide specific improvement activities.

As we explained, each of the approaches to developing composite measures has advantages and disadvantages. No one approach is clearly superior, and the impact of using one or another approach is likely to be dependent on the data set and the context in which the composite measure is being used. Also, there is much to learn about how different types of composites might differentially affect the behavior of key stakeholders, such as senior leaders of hospitals and health plans, payers, providers, researchers, and consumers/patients.

Recognizing the trade-offs necessary when selecting an approach and the gaps in knowledge, we offer the following conclusions:

• • Of the different approaches to aggregating facility-level measures, we prefer opportunity-based weights. They create equal incentives for targeting each of the component measures in the composite and adjust for major case-mix differences across providers.

• • Numerator-based weights are useful for creating strong incentives to focus on high-prevalence measures.

• • All-or-none approaches, which aggregate measures at the patient level, are most consistent with person-centered care and with a commitment to provide the highest levels of quality to each individual.

• • Weights based on the level of harm associated with the events being measured are desired by many users of composite measures, but to date, such weights have not been widely used because estimates of harm are based on expert judgment rather than explicit analyses. Given the need for harm-based weights, research in this area is likely to increase.

• • Reflective measures continue to be the mainstay of survey development, but as broad-based composite measures are increasingly implemented, the role of reflective measures is likely to diminish.

• • Both z scores and range scores are useful approaches to rescaling measures.

• • Five-star categorizations are easily communicated and reduce users’ cognitive burden. However, they can be unfair to facilities whose scores are near the category thresholds. Also, in a system in which individual measure scores are rolled up into increasingly broad hierarchies of composites, it is preferable to base the categorization at each level on the actual scores rather than on categories created at lower levels.

• • Shrinkage estimators are a useful way to stabilize or smooth estimates, either before creating composites or while creating composites, particularly when the size of the facilities varies greatly. But shrinkage estimators come at the cost of some loss in transparency. Moreover, when there is evidence linking quality to facility size, the target rates (the rates to which estimates are shrunk) for different sizes and types of facilities are controversial.

Our goal in this article was to describe the major issues associated with the creation and use of composite measures and to pull them together into one place. In Figure 1, we highlight these issues and summarize our conclusions. A better understanding of both when and where to use composite measures and the effect of their use are certain to be important areas of research as the application of composite measures to assess providers’ performance increases.

Figure 1.

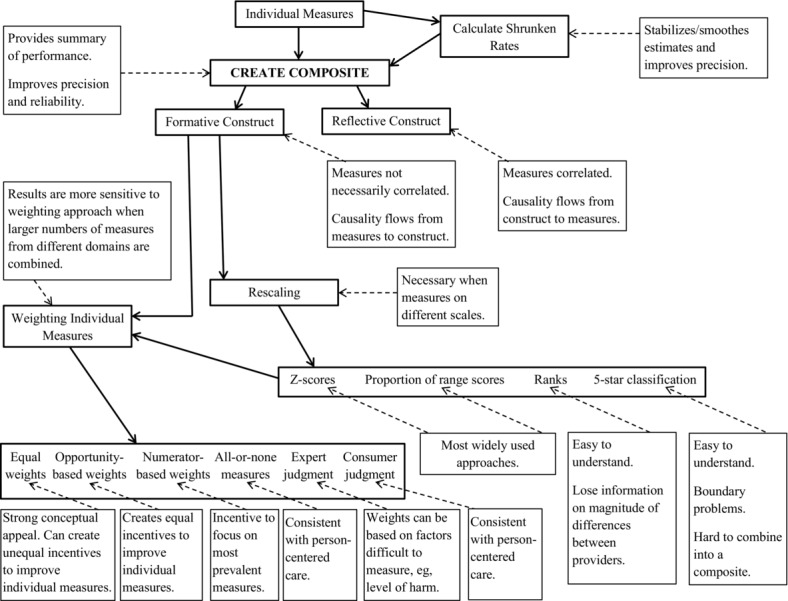
Issues in Creating Composite Measures: Summary Flow Diagram

Funding/Support: The work reported here was supported by the Jayne Koskinas and Ted Giovanis Foundation for Health and Policy. The views expressed in this article are those of the authors and do not necessarily represent the views of the foundation.

Conflict of Interest Disclosures: All authors have completed and submitted the ICMJE Form for Disclosure of Potential Conflicts of Interest. No disclosures were reported.

Acknowledgments: We would like to acknowledge the Department of Veterans Affairs, Veterans Health Administration, Office of Research and Development, which supported much of our original work on composite measures.