Low-cost solution to the grid reliability problem with 100% penetration of intermittent wind, water, and solar for all purposes

Significance

The large-scale conversion to 100% wind, water, and solar (WWS) power for all purposes (electricity, transportation, heating/cooling, and industry) is currently inhibited by a fear of grid instability and high cost due to the variability and uncertainty of wind and solar. This paper couples numerical simulation of time- and space-dependent weather with simulation of time-dependent power demand, storage, and demand response to provide low-cost solutions to the grid reliability problem with 100% penetration of WWS across all energy sectors in the continental United States between 2050 and 2055. Solutions are obtained without higher-cost stationary battery storage by prioritizing storage of heat in soil and water; cold in water and ice; and electricity in phase-change materials, pumped hydro, hydropower, and hydrogen.

Abstract

This study addresses the greatest concern facing the large-scale integration of wind, water, and solar (WWS) into a power grid: the high cost of avoiding load loss caused by WWS variability and uncertainty. It uses a new grid integration model and finds low-cost, no-load-loss, nonunique solutions to this problem on electrification of all US energy sectors (electricity, transportation, heating/cooling, and industry) while accounting for wind and solar time series data from a 3D global weather model that simulates extreme events and competition among wind turbines for available kinetic energy. Solutions are obtained by prioritizing storage for heat (in soil and water); cold (in ice and water); and electricity (in phase-change materials, pumped hydro, hydropower, and hydrogen), and using demand response. No natural gas, biofuels, nuclear power, or stationary batteries are needed. The resulting 2050–2055 US electricity social cost for a full system is much less than for fossil fuels. These results hold for many conditions, suggesting that low-cost, reliable 100% WWS systems should work many places worldwide.

Worldwide, the development of wind, water, and solar (WWS) energy is expanding rapidly because it is sustainable, clean, safe, widely available, and, in many cases, already economical. However, utilities and grid operators often argue that today’s power systems cannot accommodate significant variable wind and solar supplies without failure (1). Several studies have addressed some of the grid reliability issues with high WWS penetrations (2–21), but no study has analyzed a system that provides the maximum possible long-term environmental and social benefits, namely supplying all energy end uses with only WWS power (no natural gas, biofuels, or nuclear power), with no load loss at reasonable cost. This paper fills this gap. It describes the ability of WWS installations, determined consistently over each of the 48 contiguous United States (CONUS) and with wind and solar power output predicted in time and space with a 3D climate/weather model, accounting for extreme variability, to provide time-dependent load reliably and at low cost when combined with storage and demand response (DR) for the period 2050–2055, when a 100% WWS world may exist.

Materials and Methods

The key to this study is the development of a grid integration model (LOADMATCH). Inputs include time-dependent loads (every 30 s for 6 y); time-dependent intermittent wind and solar resources (every 30 s for 6 y) predicted with a 3D global climate/weather model; time-dependent hydropower, geothermal, tidal, and wave resources; capacities and maximum charge/discharge rates of several types of storage technologies, including hydrogen (H₂); specifications of losses from storage, transmission, distribution, and maintenance; and specifications of a DR system.

Loads and Storage.

CONUS loads for 2050–2055 for use in LOADMATCH are derived as follows. Annual CONUS loads are first estimated for 2050 assuming each end-use energy sector (residential, transportation, commercial, industrial) is converted to electricity and some electrolytic hydrogen after accounting for modest improvements in end-use energy efficiency (22). Annual loads in each sector are next separated into cooling and heating loads that can be met with thermal energy storage (TES), loads that can be met with hydrogen production and storage, flexible loads that can be met with DR, and inflexible loads (Table 1).

Table 1.

Projected 2050 CONUS load by sector and use in sector and projected percent and quantity of load for each use that is flexible and/or can be coupled with storage

(1) End-use sector	(2) 2050 total load (GW)*	(3) Percent of sector load (%)†	(4) Percent of load that is flexible (F) or coupled with TES (S) or used for H2 (H) (%)‡	(5) 2050 load that is flexible or coupled with TES (GW)§	(6) 2050 load used for H2 production and compression (GW)¶
Residential
Air conditioning	17.44	6.2	85 (S)	14.82	0
Air heating	116.7	41.5	85 (S, H)	99.23	0
Water heating	49.79	17.7	85 (S)	42.32	0
Other	97.33	34.6	15 (S, H)	14.60	0
Total residential	281.3	100	60.78	171.0	0
Commercial
Air conditioning	23.19	7.91	95 (S)	22.02	0
Refrigeration	17.12	5.84	50 (S)	8.56	0
Air heating	106.3	36.26	95 (S, H)	100.95	0
Water heating	22.51	7.68	95 (S)	21.39	0
Other	124.0	42.31	5 (S, H)	6.20	0
Total commercial	293.1	100	54.29	159.1	0
Transportation	292.6	100	85.0 (F, S, H)	108.9	139.8
Industry
Air conditioning	6.61	0.936	95 (S)	6.28	0
Refrigeration	16.92	2.40	50 (S)	8.46	0
Air heating	37.44	5.304	95 (S)	35.57	0
On-site transport	5.07	0.72	85 (F)	4.31	0
Hi-T/chem/elec procs	615.4	87.19	70 (F, H)	390.44	40.35
Other	24.35	3.45	0	0	0
Total industry	705.8	100	68.77	445.05	40.35
All sectors	1,572.8		67.66	884.03	180.2

Bold indicates a total amount.

^*Total 2050 loads for each sector are from ref. 22 and include inflexible and flexible loads and loads coupled with storage. Column 2 minus columns 5 and 6 is inflexible load. Loads by category in each sector are obtained by multiplying the percent loads in column 3 by the total load in column 2.

^†Percent load is estimated from refs. 33, 34, and 35 for the residential, commercial, and industrial sectors, respectively.

^‡A percent of load that is flexible is applied only to categories for which 100% of the load could theoretically be supplied from storage (air and water heating, water cooling, refrigeration, some transportation, and some industrial processes) or shifted in time (some transportation, some industrial processes). The percentages are then reduced to <100% to account for some on-demand energy (SI Appendix, Section S1.J).

^§Obtained by multiplying column 2 by column 4 then subtracting column 6.

^¶From ref. 22.

Most (50–95%) air conditioning and refrigeration and most (85–95%) air heating and water heating are coupled with TES (Table 1). Cooling coupled with storage is tied to chilled water (sensible-heat) TES (STES) and ice production and melting [phase-change material (PCM)-ice] (SI Appendix, Table S1). All building air- and water-heating coupled with storage uses underground TES (UTES) in soil. UTES storage is patterned after the seasonal and short-term district heating UTES system at the Drake Landing Community, Canada (23). The fluid (e.g., glycol solution) that heats water that heats the soil and rocks is itself heated by sunlight or excess electricity.

Overall, 85% of the transportation load and 70% of the loads for industrial high temperature, chemical, and electrical processes are assumed to be flexible or produced from H₂ (Table 1).

Six types of storage are treated (SI Appendix, Table S1): three for air and water heating/cooling (STES, UTES, and PCM-ice); two for electric power generation [pumped hydropower storage (PHS) and phase-change materials coupled with concentrated solar power plants (PCM-CSP)]; and one for transport or high-temperature processes (hydrogen). Hydropower (with reservoirs) is treated as an electricity source on demand, but because reservoirs can be recharged only naturally they are not treated as artificially rechargeable storage. Lithium-ion batteries are used to power battery-electric vehicles but to avoid battery degradation, not to feed power from vehicles to the grid. Batteries for stationary power storage work well in this system too. However, because they currently cost more than the other storage technologies used (24), they are prioritized lower and are found not to be necessary for a reliable system. Nevertheless, they could still be incorporated, but at higher cost, in this system.

PHS is limited to its present penetration plus preliminary and pending permits as of 2015. CSP is coupled with a PCM rather than molten salt because of the greater efficiency and lower cost of the PCM (25). The maximum charge rate of CSP storage (thus mirror collector size) can be up to a factor of 5 the maximum discharge rate of CSP steam turbines to increase CSP’s capacity factor (26). Here, the maximum CSP charge rate is ∼2.6 times the maximum discharge rate (SI Appendix, Tables S1 and S2), but more CSP turbines are used than needed solely to provide annual CONUS power to increase the discharge rate of stored CSP power during times of peak power demand.

The 2050 annual cooling and heating loads (Table 1) are distributed in LOADMATCH each 30-s time step during each month of 2050–2055 in proportion to the number of cooling- and heating-degree days, respectively, each month averaged over the United States from 1949 to 2011 (27). Hydrogen loads and flexible loads are initially spread evenly over each year. Annual 2050 and 2051 inflexible loads are scaled by the ratio of hourly to annual 2006 and 2007 CONUS-aggregated loads, respectively (SI Appendix, Figs. S2 and S3) (28) to give hourly 2050 and 2051 inflexible loads, which are then applied alternately between 2052 and 2055 and distributed evenly each 30-s time step each hour. DR allows initial flexible loads to be pushed forward in 30-s increments but by no more than 8 h in the base case, at which point they are made inflexible loads. However, sensitivity tests indicate that the system is also stable with no DR (SI Appendix, Fig. S14).

Electric Power and Heat Supplies.

To maximize the environmental and social benefits of energy production and use, all 2050 loads are supplied only with WWS technologies: onshore and offshore wind turbines, rooftop photovoltaic (PV) systems, utility PV plants, CSP plants, geothermal plants, hydropower plants, tidal devices, wave devices, and solar collectors for heating fluid. SI Appendix, Table S2 provides the proposed CONUS 2050 installed capacities and capital costs of each generator type, both of which are preestimated state-by-state based on resource and load constraints, to provide 2050 all-purpose end-use power in each state (22).

The state-by-state wind and solar installations are input here into the Gas, Aerosol, Transport, Radiation-General Circulation, Mesoscale, and Ocean Model (GATOR-GCMOM), a 3D global climate/weather model (29, 30) (SI Appendix, Section S1). Wind turbines are placed near each of 42,000 existing US turbines (31, 32). Utility PV and CSP (SI Appendix, Section S1.I) are sited in deserts or low-latitude regions of states where they exist. Rooftop PV is placed in urban areas. The model predicts time-dependent winds, accounting for competition among wind turbines for limited kinetic energy at the 100-m hub height of turbines (SI Appendix, Section S1.H). It also calculates direct and diffuse solar and infrared radiation accounting for time-varying gases, aerosols, and clouds and the cooling of underlying surfaces by all PV and CSP during energy extraction. It further calculates heat release to the air during electricity use. Modeled solar and wind resources are aggregated spatially to obtain CONUS totals each 30-s time step from 2050 to 2055.

Priorities for Satisfying Load in Grid Integration Model.

The 2050–2055 loads and intermittent resources described above are input into LOADMATCH, which prioritizes load matching, to determine whether and at what cost supply can match load.

When more instantaneous WWS electricity supply is available than needed for current inflexible plus flexible electricity loads during a time step, both loads are met immediately with the supply. Excess supply then goes first to fill non-UTES storage up to the storage limit, then to produce H₂ up to its storage limit, then to fill UTES storage up to its storage limit, and last to shedding.

When instantaneous WWS electricity supply exceeds inflexible load (including H₂ load not met from storage) but is less than inflexible plus flexible load during a time step, inflexible plus flexible load up to WWS supply is first satisfied with supply, and the remaining flexible load is pushed to the next 30-s time step. Any flexible load not satisfied during the previous 8 h is converted to inflexible load that is immediately satisfied first with current instantaneous supply, then with stored electricity, and last with hydropower.

When instantaneous WWS electricity supply is lower than inflexible load for a given time step, the difference is made up first from stored electricity and then from hydropower, which is used only as a last resort.

All instantaneous heat from non-CSP solar-thermal collectors first satisfies instantaneous heat load. Any excess then goes into UTES. WWS electricity can also increase UTES, but only when all of the following constraints are met: instantaneous WWS electricity supply exceeds inflexible plus flexible electricity load; all non-UTES storage is filled; and H₂ storage is filled. Although UTES is not an efficient way to store excess electricity, it is more efficient than simply shedding the excess.

When instantaneous heat load exceeds instantaneous solar-thermal collector heat, the excess load is drawn from UTES. If UTES is depleted, the energy for meeting the heat load is drawn first from current WWS electricity, then in order from stored PCM-CSP electricity, PHS, and hydropower.

Hydrogen demand each time step is first met with stored hydrogen. If hydrogen storage is depleted, the remaining demand is met with electrolysis using current electricity. Hydrogen is produced, compressed, and added to storage when more electricity is available than can be put into non-UTES storage.

The model assumes a short- and long-distance transmission (T&D) system that carries power from distributed and centralized WWS generators to storage and load centers. Costs of and power losses during T&D are accounted for (Table 2, footnote), but power flows through individual lines or substations are not explicitly modeled. The model also accounts for storage costs and power losses during charging/discharging (SI Appendix, Table S1).

Table 2.

Summary of energy loads met, losses, energy supplies, changes in storage, and costs during the base 6-y (52,548-h) simulation

Energy load, supply, or loss	Energy (TWh) or cost
Total load met over 6 y	82,695
Electricity load for H2 production/compression	9,469
Electricity load not for H2	67,170
Heat load from solar collectors and UTES	6,056
Total lossesa	10,189
Transmission, distribution, maintenance losses	6,334
Losses CSP storage	52.7
Losses non-CSP, non-UTES storage	238.9
Losses UTES storage	2,365
Losses from shedding heat	1,198
Total load plus losses (energy required)	92,884
Total WWS supply before T&D losses	92,979
Onshore + offshore wind electricityb	43,509
Rooftop + utility PV + CSP electricityc	39,901
Hydropower electricityd	2,413
Wave electricitye	320.8
Geothermal electricityf	1003.8
Tidal electricityg	113.0
Solar heath	5,718
Net energy taken from (+) or added to (−) storage	−95.4
Net energy taken from (+) CSP storage	0
Net energy taken from (+) non-UTES storage	0
Net energy taken from (+) UTES storage	205.8
Net energy taken from (+) H2 storage	−301.2
Total energy supplied plus taken from storage	92,884
Capital cost ($ trillion) new generators + storagei	14.6 (12.0–17.2)
Capital cost ($ trillion) new generators	13.9 (11.8–16.0)
2050 total LCOE (¢/kWh-to-load) in 2013 dollars	11.37 (8.5–15.4)
Electricity + heat + short-distance T&D (¢/kWh)j	10.26 (8.12–13.1)
Long-distance transmission (¢/kWh)k	0.32 (0.081–0.86)
All storage except H2 (¢/kWh)l	0.33 (0.062–0.75)
H2 prod/compress/stor. (excl. elec. cost) (¢/kWh)m	0.46 (0.22–0.69)

All units are TWh over the CONUS, except costs, which are either $ trillion or ¢/kWh-delivered-to-load. Bold indicates a total amount. Bold italics indicates a sum of totals. T&D, transmission and distribution.

^aTransmission/distribution/maintenance losses are 5–10% of electricity generation for all generators except rooftop PV (1–2%) and solar thermal (2–4%). Transmission losses are averaged over short and long-distance (with high-voltage direct current) lines. Maintenance downtime is discussed in SI Appendix, Section S1.L. Storage efficiencies are given in SI Appendix, Table S1. Excess electricity is either stored or used to produce H₂, so is not shed. Only excess heat is shed if heat storage is saturated.

^bOnshore and offshore wind turbines, installed in the climate model, are REpower 5-MW turbines with 126-m-diameter rotors, 100-m hub heights, a cut-in wind speed of 3.5 m/s, and a cut-out wind speed of 30 m/s.

^cEach solar PV panel for rooftop and utility solar, installed in the climate model is a SunPower E20 435 W panel with panel area of 2.1621 m², which gives a panel efficiency (Watts of power output per Watt of solar radiation incident on the panel) of 20.1%. The cell efficiency (power out per watt incident on each cell) is 22.5%. Each CSP plant before storage is assumed to have the characteristics of the Ivanpah solar plant, which has 646,457 m² of mirrors and 2.17 km² of land per 100 MW installed power and a CSP efficiency (fraction of incident solar radiation that is converted to electricity) of 15.796%, calculated as the product of the reflection efficiency of 55% and the steam plant efficiency of 28.72% (36).

^dThe capacity factor for hydropower from the simulation is 52.5%, which also equals that from ref. 22.

^eThe assumed capacity factor for wave power is 23.3% (22).

^fThe assumed capacity factor for geothermal is 92.1% (22).

^gThe assumed capacity factor for tidal power is 26.1% (22).

^hThe efficiency of the solar hot fluid collection (energy in fluid divided by incident radiation) is 34% (23).

ⁱCapital costs for new generators are derived from SI Appendix, Table S2 and for storage are derived from SI Appendix, Table S1.

^jThe electricity plus heat plus local transmission costs here are derived from capital costs in SI Appendix, Table S2 assuming a discount rate of 3.0 (1.5–4.5)%, a facility lifetime/amortization time of 30 (35–25) y for all technologies except geothermal [35 (30–40) y] and hydropower [55 (50–60) y], an annual O&M cost that varies by technology as in ref. 22, a short-distance transmission cost of 1.15 (1.1–1.2) ¢/kWh (22), a distribution cost of 2.57 (2.5–2.64) ¢/kWh (22), decommissioning costs of 1.125 (0.75–1.5)% of capital costs (22), and the annualized load met in Table 2.

^kLong-distance transmission costs are 1.2 (0.3–3.2) ¢/kWh for 1,200- to 2,000-km lines (37). The base case assumes that 30% of all wind and solar electric power generated are subject to long-distance transmission lines. This percent is varied in sensitivity tests in SI Appendix, Fig. S13.

^lStorage costs are the product of the storage capacity and the capital cost per unit of storage capacity of each storage technology (SI Appendix, Table S1), summed over all technologies, annualized with the same discount rates and annual O&M percentages as for power generators, and divided by the annual-average load met in Table 2 (i.e., the total load met over 6 y divided by 6 y).

^mH₂ costs are 4.0 (1.96–6.05) ¢/kWh-to-H₂ for the electrolyzer, compressor, storage equipment, and water. This cost equals 2.36 (1.16–3.57) $/kg-H₂ divided by 59.01 kWh/kg-H₂ required to electrolyze (53.37 kWh/kg-H₂) and compress (5.64 kWh/kg-H₂) H₂ (38). These costs exclude electricity costs, which are included elsewhere in the table. The overall cost of H₂ in ¢/all-kWh-delivered is equal to the cost in ¢/kWh-to-H₂ multiplied by the fraction of delivered power used for hydrogen (11.46% = Table 1, column 6 divided by column 2).

Results

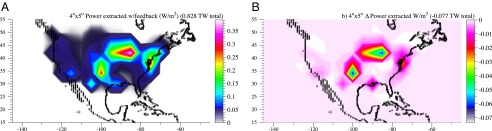
LOADMATCH is run first with a 30-s time step for 6 y, using the parameters in Table 1 and SI Appendix, Tables S1 and S2 and time-dependent wind and solar resources derived from GATOR-GCMOM. An ensemble of 19 additional simulations with different time series of wind, solar, and load inputs is also run to test the model’s robustness (SI Appendix, Sections S1.K and S1.M). The GATOR-GCMOM simulations account for extraction of and competition for kinetic energy by wind turbines (Fig. 1). The power extracted among all onshore plus offshore turbines when accounting for competition among ∼489,809 5-MW onshore plus offshore CONUS turbines (SI Appendix, Table S2) is ∼0.828 TW (Fig. 1A), giving a wind capacity factor of ∼33.81%, vs. ∼36.95% when competition is ignored. Thus, competition among turbines reduces aggregate power output by ∼0.0769 TW (Fig. 1B), or ∼8.5%, and peak wind speeds averaged over 400- × 400-km regions by up to ∼1 m/s.

Fig. 1.

(A) Difference in GATOR-GCMOM modeled (at 4° × 5° horizontal resolution) 100-m wind speed, averaged over 6 y, due to extracting kinetic energy from the wind by ∼335,400 onshore and ∼154,400 offshore 5-MW wind turbines placed state by state in the CONUS. (B) Loss in total power extracted by the turbines due to the competition for kinetic energy among them in A.

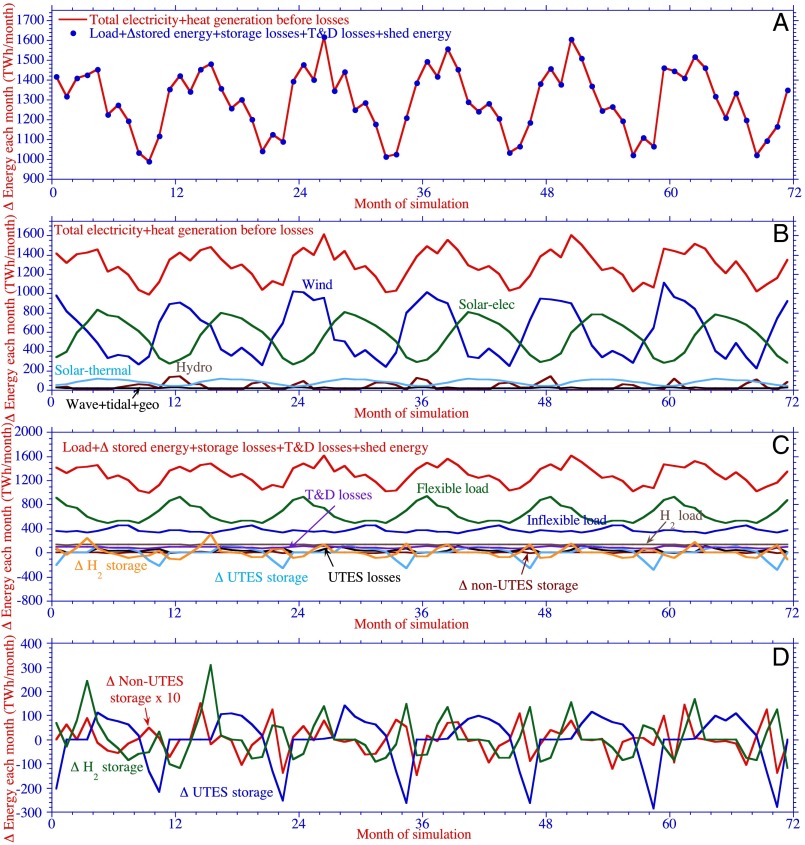
Table 2, Figs. 2–4, and SI Appendix, Figs. S4–S6 summarize results from the baseline LOADMATCH simulation. Zero load loss occurs for the base case (Table 2 and Fig. 2) and all sensitivity cases (SI Appendix, Table S3 and Figs. S7–S19). For the base case, ∼11% of all WWS energy potentially available is lost during transmission, distribution, maintenance downtime, and storage. Zero electricity shedding occurs because all excess electricity goes into either hydrogen production or storage. Some excess solar heat is shed when UTES storage is full (Table 2). Energy summed over all storage at the end of the simulation slightly exceeds that at the beginning (Table 2).

Fig. 2.

(A) Six-year (72-mo) time series comparison of modeled CONUS-aggregated power generation vs. load plus losses plus changes in storage plus shedding. (B) Breakdown of power generation for the same period. (C) Breakdown of load plus losses plus changes in storage plus shedding. (D) Breakdown of changes in storage.

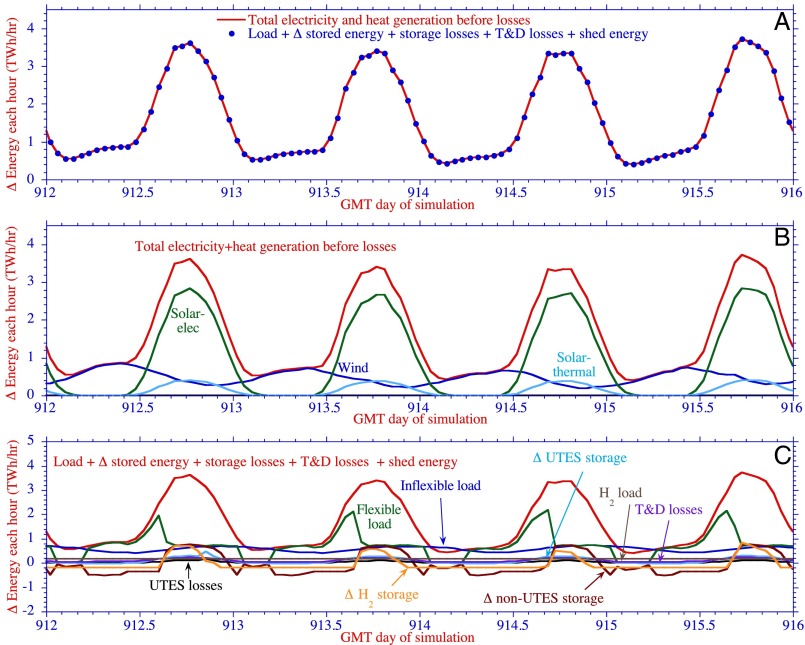
Fig. 4.

(A) Time series comparison each hour of modeled CONUS-aggregated power generation vs. load plus losses plus changes in storage plus shedding for January 14–17, 2055. (B) Breakdown of power generation for the same period. (C) Breakdown of load plus losses plus changes in storage plus shedding.

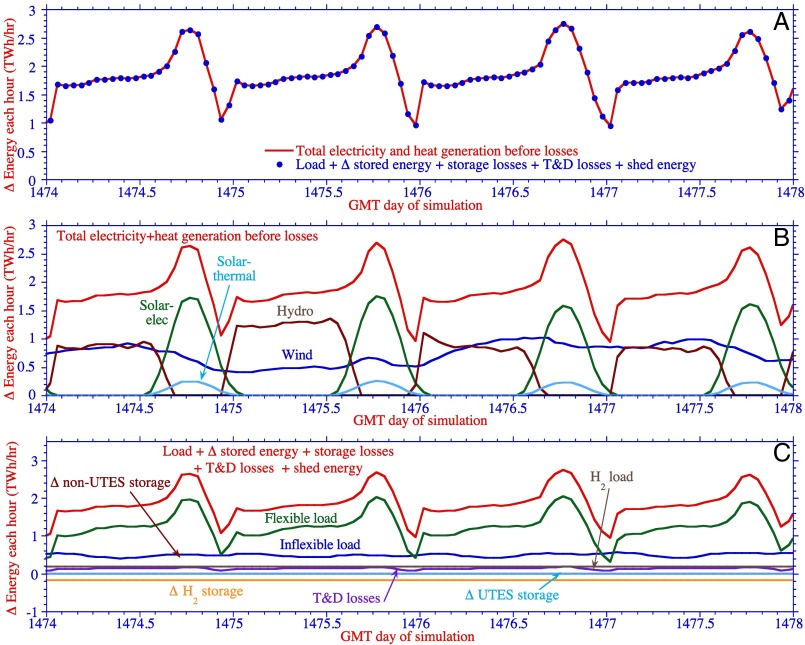
Figs. 2–4 and SI Appendix, Figs. S4–S6 indicate supply exactly matches load plus losses and changes in storage at all times. Solar and wind are complementary seasonally (Fig. 2) and diurnally (Figs. 3 and 4 and SI Appendix, Figs. S4–S6). Seasonally, CONUS-aggregated wind peaks during winter; solar peaks during summer. Daily, wind peaks at night and is often lowest when solar is greatest during the day.

Fig. 3.

(A) Time series comparison each hour of modeled CONUS-aggregated power generation vs. load plus losses plus changes in storage plus shedding for July 1–4, 2052. (B) Breakdown of power generation for the same period. (C) Breakdown of load plus losses plus changes in storage plus shedding.

Collected solar heat is added to UTES during summers and removed primarily during winters. Conversely, electricity is drawn from storage other than UTES during summers to provide peaking electricity. Hydropower is used only sporadically and only when other storage is depleted.

Discussion and Conclusions

The 2050 delivered social (business plus health and climate) cost of all WWS including grid integration (electricity and heat generation, long-distance transmission, storage, and H₂) to power all energy sectors of CONUS is ∼11.37 (8.5–15.4) ¢/kWh in 2013 dollars (Table 2). This social cost is not directly comparable with the future conventional electricity cost, which does not integrate transportation, heating/cooling, or industry energy costs. However, subtracting the costs of H₂ used in transportation and industry, transmission of electricity producing hydrogen, and UTES (used for thermal loads) gives a rough WWS electric system cost of ∼10.6 (8.25–14.1) ¢/kWh. This cost is lower than the projected social (business plus externality) cost of electricity in a conventional CONUS grid in 2050 of 27.6 (17.2–54.4) ¢/kWh, where 10.6 (8.73–13.4) ¢/kWh is the business cost and ∼17.0 (8.5–41) ¢/kWh is the 2050 health and climate cost, all in 2013 dollars (22). Thus, whereas the 2050 business costs of WWS and conventional electricity are similar, the social (overall) cost of WWS is 40% that of conventional electricity. Because WWS requires zero fuel cost, whereas conventional fuel costs rise over time, long-term WWS costs should stay less than conventional fuel costs.

In sum, an all-sector WWS energy economy can run with no load loss over at least 6 y, at low cost. As discussed in SI Appendix, Section S1.L, this zero load loss exceeds electric-utility-industry standards for reliability. The key elements are as follows: (i) UTES to store heat and electricity converted to heat; (ii) PCM-CSP to store heat for later electricity use; (iii) pumped hydropower to store electricity for later use; (iv) H₂ to convert electricity to motion and heat; (v) ice and water to convert electricity to later cooling or heating; (vi) hydropower as last-resort electricity storage; and (vii) DR. These results hold over a wide range of conditions (e.g., storage charge/discharge rates, capacities, and efficiencies; long-distance transmission need; hours of DR; quantity of solar thermal) (SI Appendix, Table S3 and Figs. S7–S19), suggesting that this approach can lead to low-cost, reliable, 100% WWS systems many places worldwide.