New class of turbulence in active fluids

Significance

It is widely appreciated that turbulence is one of the main challenges of modern theoretical physics. Whereas up to now, most work in this area has been dedicated to the study of Navier–Stokes flows, numerous examples exist of systems that exhibit similar types of spatiotemporal chaos but are described by more complex nonlinear equations. One such problem of quickly growing scientific interest is turbulence in active fluids. We find that such systems can exhibit power-law energy spectra with nonuniversal exponents as a result of nonlinear self-organization, defining a new class of turbulent flows.

Abstract

Turbulence is a fundamental and ubiquitous phenomenon in nature, occurring from astrophysical to biophysical scales. At the same time, it is widely recognized as one of the key unsolved problems in modern physics, representing a paradigmatic example of nonlinear dynamics far from thermodynamic equilibrium. Whereas in the past, most theoretical work in this area has been devoted to Navier–Stokes flows, there is now a growing awareness of the need to extend the research focus to systems with more general patterns of energy injection and dissipation. These include various types of complex fluids and plasmas, as well as active systems consisting of self-propelled particles, like dense bacterial suspensions. Recently, a continuum model has been proposed for such “living fluids” that is based on the Navier–Stokes equations, but extends them to include some of the most general terms admitted by the symmetry of the problem [Wensink HH, et al. (2012) Proc Natl Acad Sci USA 109:14308–14313]. This introduces a cubic nonlinearity, related to the Toner–Tu theory of flocking, which can interact with the quadratic Navier–Stokes nonlinearity. We show that as a result of the subtle interaction between these two terms, the energy spectra at large spatial scales exhibit power laws that are not universal, but depend on both finite-size effects and physical parameters. Our combined numerical and analytical analysis reveals the origin of this effect and even provides a way to understand it quantitatively. Turbulence in active fluids, characterized by this kind of nonlinear self-organization, defines a new class of turbulent flows.

Despite several decades of intensive research, turbulence—the irregular motion of a fluid or plasma—still defies a thorough understanding. It is a paradigmatic example of nonlinear dynamics and self-organization far from thermodynamic equilibrium also closely linked to fundamental questions about irreversibility (1) and mixing (2). The classical example of a turbulent system is a Navier–Stokes flow, with a single quadratic nonlinearity, well-separated drive and dissipation ranges, and an extended intermediate range of purely conservative scale-to-scale energy transfer (3). However, many turbulent systems of scientific interest involve more general patterns of energy injection, transfer, and dissipation. A fascinating example of these kinds of generalized turbulent dynamics can be observed in dense bacterial suspensions (4). Although the motion of the individual swimmers in the background fluid takes place at Reynolds numbers well below unity, the coarse-grained dynamics of these self-propelled particles display spatiotemporal chaos, i.e., turbulence (5–7). Nevertheless, the correlation functions of the velocity and vorticity fields display some essential differences compared with their counterparts in classical fluid turbulence (8, 9). Moreover, the collective motion of bacteria in such suspensions exhibits long-range correlations (10), appears to be driven by internal instabilities (11), and depends strongly also on physical parameters like large-scale friction (12). Such results challenge the orthodox understanding of turbulent motion and call for a detailed theoretical investigation. There also exist many other systems with similar characteristics, including flows generated by space-filling fractal square grids (13) , turbulent astrophysical (14) and laboratory (15, 16) plasmas, and chemical reaction–diffusion processes (17).

In the present work, we study—numerically as well as analytically—the spectral properties of a continuum model that has recently been suggested as a minimal phenomenological model to describe the collective dynamics of dense bacterial suspensions (4, 18, 19). A basic assumption of the model is that at high concentrations the dynamics of bacterial flow may be described as an incompressible fluid obeying the following equation of motion for the velocity field $\mathbf{v}\left(\mathbf{x},t\right)$,

$$\frac{\partial \mathbf{v}}{\partial t}+{\lambda }_0\left(\mathbf{v}\cdot \nabla \right)\mathbf{v}+\nabla p=-{\mathrm{\Gamma }}_0\mathrm{\Delta }\mathbf{v}-{\mathrm{\Gamma }}_2{\mathrm{\Delta }}^2\mathbf{v}-\mu \left(v\right)\mathbf{v}\hspace{0.17em},$$ [1]

where $\mu \left(v\right)=\alpha +\beta {\left|\mathbf{v}\right|}^2$. In addition to the advective nonlinearity, $\left(\mathbf{v}\cdot \nabla \right)\mathbf{v}$, and pressure term, $\nabla p$, familiar from the Navier–Stokes model, the equation also accounts for internal drive and dissipation processes. Apart from the last term on the right-hand side and the pressure term, Eq. 1 amounts to a straightforward multidimensional generalization of the Kuramoto–Sivashinsky (KS) equation that has found application in describing magnetized plasmas (20, 21), chemical reaction–diffusion processes (22, 23), and flame front propagation (24, 25). It is widely regarded as a prototypical example of “phase turbulence.” (26) As a hallmark, if both kinetic parameters are positive (${\mathrm{\Gamma }}_0,\hspace{0.17em}{\mathrm{\Gamma }}_2>0$), the KS equation is linearly unstable for a band of wave vectors k, similar to other paradigmatic models of nonlinear dynamics, e.g., the Swift–Hohenberg model (27). For active systems this feature emulates energy input into the bacterial system through stress-induced instabilities (11). The growth of these linearly unstable modes is limited by nonlinear and dissipative terms. The main dissipation mechanism in Eq. 1 is mediated through the cubic nonlinearity on the right-hand side, $-\mu \left(v\right)\mathbf{v}$. Such a term was originally introduced by Toner and Tu to account for a propensity of self-propelled rod-like objects to exhibit local polar order (“flocking”) (28, 29). This hydrodynamic model comprises some of the key features common to systems exhibiting mesoscale turbulence: interplay of energy input due to a band of linearly unstable modes with the advective Navier–Stokes nonlinearity as well as with terms modeling flocking behavior and dissipation. These generic features are shared by more elaborate hydrodynamic models of active matter recently reviewed in ref. 30. Thus, Eq. 1 serves as a simple but generic test case to address some of the fundamental questions in the field of active turbulence. Via an appropriate choice of parameters, one can describe several different physical systems as explained in more detail in Table S1.

Table S1.

Classification of the different limit cases for Eq. 1, depending on the choice of parameters

${\lambda }_0$	α	β	${\mathrm{\Gamma }}_0$	${\mathrm{\Gamma }}_2$	Limit case
1	0	0	${\mathrm{\Gamma }}_0<0$	0	Classical Navier–Stokes equation
1	0	0	0	${\mathrm{\Gamma }}_2>0$	Navier–Stokes equation with hyperviscosity of the second order
1	α > 0	0	${\mathrm{\Gamma }}_0<0$	0	Navier–Stokes equation with large-scale friction, i.e., Ekman damping
1	0	0	$\mathrm{\Gamma }>0$	${\mathrm{\Gamma }}_2>0$	Straightforward multidimensional generalization of the Kuramoto–Sivashinsky equation for incompressible velocity fields

First and foremost, the similarities and differences between low and high Reynolds number turbulence remain to be elucidated. In particular, there is still a lack of understanding of the energy flow between different length scales. Here, we address the above questions by a systematic analysis of the turbulent features of Eq. 1, combining numerical and analytical approaches, and we give a comprehensive picture of the spectral energy balance facilitating the understanding of the interactions among different spatial scales. Furthermore, extensive numerical simulations confirm the existence of a spectral power law at the largest scales of the system with its steepness depending on the parameters of the system (both of the linear and of the nonlinear terms in Eq. 1). The form of the turbulent energy spectrum is an important quantity related to the frictional drag between the system and the surrounding walls (31, 32). In the present work, insight into the remarkable feature of a variable spectral exponent is gained by analyzing the role of the different terms in the equation for the spectral energy balance. As expected for a 2D incompressible fluid, there exists an inverse flow of energy from intermediate to large scales (33). Nevertheless, in contrast to classical, fully developed 2D Navier–Stokes turbulence, there is no inertial range characterized by a constant energy flux. Instead, we find that at large scales the nonlinear frequency corresponding to the Navier–Stokes energy flux is constant for the whole range characterized by spectral self-similarity. This differs fundamentally from the classical Navier–Stokes case, where this nonlinear frequency, the inverse of the nonlinear eddy turnover time, is a function of wave number and energy. In the model at hand, this energy flux is balanced by a linear dissipation/injection and a cubic dissipation term. For the latter, we derive an analytic approximation that compares very favorably with the numerical results and allows for an analytic closure predicting the type of dependence of the power law on the model parameters that is also confirmed numerically.

Results

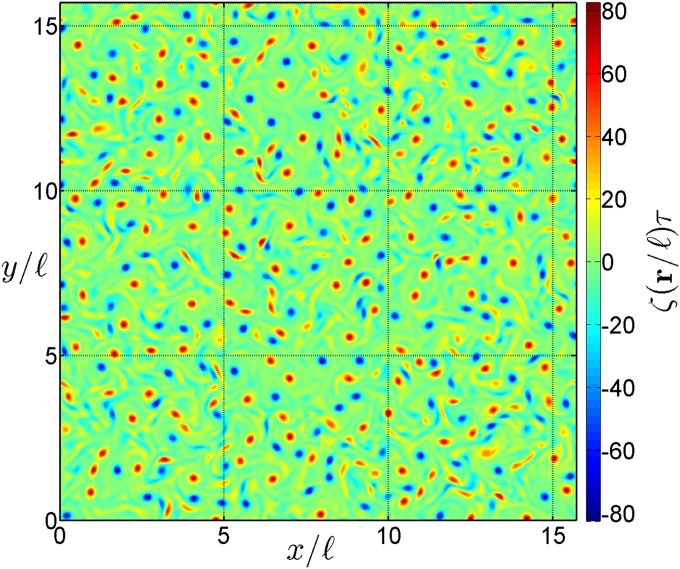
We have studied the 2D version of the continuum model defined by Eq. 1 both analytically and numerically. Our computational approach relies on a pseudospectral code where the linear terms are computed in Fourier space and the nonlinearities in real space. The details of this procedure and the necessary normalization are described in SI Text, section S1. All numerical results reported in this paper use a resolution of 1,024 effective Fourier modes in each direction, unless stated otherwise. A typical velocity is given by $v_0:=\sqrt{{\mathrm{\Gamma }}_0^3/{\mathrm{\Gamma }}_2}$. From the spectral representation $\gamma \left(k\right):=-\alpha +{\mathrm{\Gamma }}_0{k}^2-{\mathrm{\Gamma }}_2{k}^4$ of the linear part of Eq. 1, one reads off the wave number of the fastest growing mode, $k_{\max }=\sqrt{{\mathrm{\Gamma }}_0/\left(2{\mathrm{\Gamma }}_2\right)}$, which suggests characteristic length and time scales as $\ell =5\pi /k_{\max }$ and $\tau =\ell /v_0$, respectively. Accordingly, the normalized form of the parameters ${\mathrm{\Gamma }}_0$ and ${\mathrm{\Gamma }}_2$ reduces to fixed numbers; i.e., ${\mathrm{\Gamma }}_0\tau /{\ell }^2=1/\left(5\sqrt{2}\pi \right)$ and ${\mathrm{\Gamma }}_2/\left(\ell v_0^3\right)\approx 9\cdot {10}^{-5}$. The parameters β and ${\lambda }_0$ can still be chosen freely and here they are set to $\beta \tau v_0=0.5$ and ${\lambda }_0=3.5$. The normalization units used here are the same as the ones in ref. 4, meaning that our parameters (with $\alpha =-1$ and up to the different sign of ${\mathrm{\Gamma }}_0$) correspond to the bacterial suspension described therein. A typical snapshot of the real-space vorticity field in the turbulent regime is shown in Fig. 1. It makes evident the random distribution of vortices across the simulation domain. Moreover, the time evolution of the vortex configuration turns out to be strongly incoherent. Due to this highly nonlinear behavior, associated with spatiotemporal chaos, exhibited by the system, we refer to its dynamics as turbulent.

Fig. 1.

Snapshot of the 2D vorticity field $\zeta ={\partial }_x{v}_y-{\partial }_y{v}_x$ right after the onset of the turbulent regime as obtained from a numerical solution of Eq. 1, using a pseudospectral code. The computation has been performed with 1,024 (effective) points in each direction under the constraint of periodic boundary conditions. The Ekman parameter equals $\alpha \tau =-1$, implying that there are two energy sources acting at large scales—the two positive terms in the expression for $\gamma \left(k\right)$. The strength of the cubic nonlinearity is set to $\beta \tau v_0=0.5$ and for the advective term we have used ${\lambda }_0=3.5$. One can clearly see the highly disordered distribution of vortices justifying the classification of the regime as turbulent.

Spectral Analysis.

For the analysis of the flow of energy between different spatial scales mediated by the various terms in Eq. 1 we use a Fourier decomposition of $\mathbf{v}$ (SI Text, section S1). $E_{\mathbf{k}}:=\langle {\left|{\mathbf{v}}_{\mathbf{k}}\left(t\right)\right|}^2\rangle /2$ is referred to as the energy of Fourier mode $\mathbf{k}$, where $\langle \cdot \rangle$ denotes an ensemble average, equivalent to a time average for a statistically stationary state as discussed in SI Text, section S1. The ensuing spectral energy balance equation reads

$${\partial }_t{E}_{\mathbf{k}}=2\gamma \left(k\right)E_{\mathbf{k}}+T_{\mathbf{k}}^{\mathrm{adv}}+T_{\mathbf{k}}^{\mathrm{cub}},$$ [2]

with the advective and cubic nonlinear terms given by

$$T_{\mathbf{k}}^{\mathrm{adv}}=+{\lambda }_0\hspace{0.17em}\mathrm{Re}\left[{\displaystyle \sum _{\mathbf{p}}{M}_{ijl}\left(\mathbf{k}\right)\langle v_{-\mathbf{k}}^i{v}_{\mathbf{k}-\mathbf{p}}^l{v}_{\mathbf{p}}^j\rangle }\right],$$ [3a]

$$T_{\mathbf{k}}^{\mathrm{cub}}=-\beta \hspace{0.17em}\mathrm{Re}\left[{\displaystyle \sum _{\mathbf{p},\mathbf{q}}{D}_{ij}\left(\mathbf{k}\right)\langle v_{-\mathbf{k}}^i{v}_{\mathbf{k}-\mathbf{p}-\mathbf{q}}^l{v}_{\mathbf{q}}^l{v}_{\mathbf{p}}^j\rangle }\right],$$ [3b]

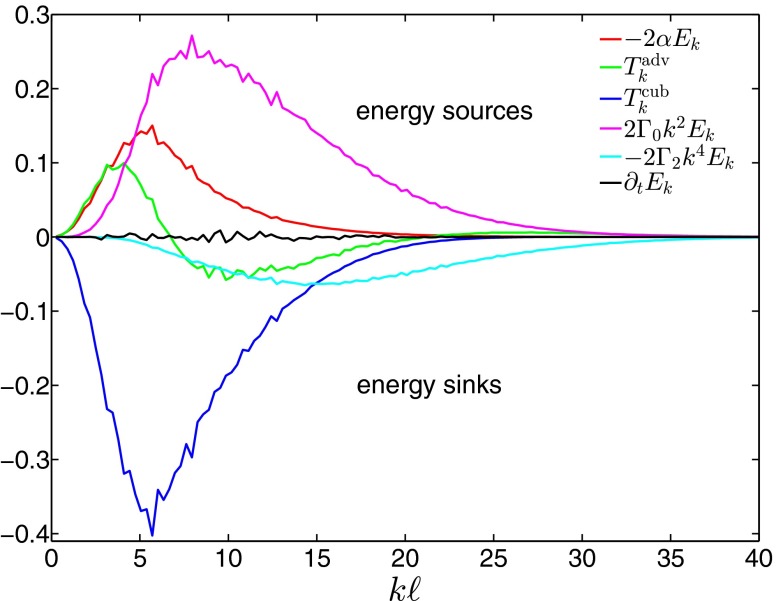
where we have used sum convention for Cartesian indexes, $D_{ij}\left(\mathbf{k}\right):={\delta }_{ij}-k_i{k}_j/k^2$ are the components of the projection tensor, $M_{njl}\left(\mathbf{k}\right):=-\left(\text{i}/2\right)\left(k_j{D}_{nl}\left(\mathbf{k}\right)+k_l{D}_{nj}\left(\mathbf{k}\right)\right)$, and we have omitted all time arguments for simplicity. The Ekman term (proportional to α) either injects ($\alpha <0$) or dissipates ($\alpha >0$) energy into/from the system with a rate proportional to $E_{\mathbf{k}}$. The other linear terms are also responsible for either local energy injection (${\mathrm{\Gamma }}_0$ term) or dissipation (${\mathrm{\Gamma }}_2$ term). The nontrivial dynamics of Eq. 1 result from the nonlinear terms, i.e., advection term and cubic nonlinearity. They couple different wave numbers and provide a flow of energy in spectral space that (on average) balances the local injection or dissipation. The different terms in Eq. 2, obtained from a numerical solution of Eq. 1, are shown in Fig. 2. We have averaged over nearly $10,\hspace{0.17em}000$ time steps and (using spherical symmetry) summed over modes with the same absolute value (hence the scalar form of the index k). Note that the advective nonlinearity (green curve) is positive for small k but negative for intermediate k and, thus, transports energy from small to large scales. This inverse energy flow is characteristic of 2D turbulent systems and is due to the constraint of enstrophy conservation (34). In the present context, it takes energy from the intermediate wave numbers where the ${\mathrm{\Gamma }}_0$ injection (magenta) is particularly active and transports it to larger scales where it acts as an energy source together with the Ekman term (red) for $\alpha <0$. At large length scales, those two sources are balanced by the cubic nonlinearity (dark blue) acting as an energy sink for most wave numbers. This energy sink, however, has a nonlinear character that allows it to dynamically adjust its magnitude to the sources for a balance to be reached. Additionally, at large scales the contribution of the cubic interaction is roughly proportional to the energy spectrum $E_k$. Later, we show that those two features can be derived from a closure approximation for small k.

Fig. 2.

Spectral form of the different terms in Eq. 2 in the statistically stationary state (time averaged): red, Ekman term; green, advective nonlinearity $T_k^{\mathrm{adv}}$; dark blue, cubic interaction $T_k^{\mathrm{cub}}$; magenta, $k^2$ injection; light blue, $k^4$ dissipation; black, time average of the left-hand side. A positive contribution means that at these wave numbers the corresponding term acts as an energy source, and a negative value indicates an energy sink. We see that the nonlinear terms change their character, depending on the scale under consideration. At large and intermediate scales, however, the cubic nonlinearity is always dissipative. Additionally, the Ekman term can provide energy injection or dissipation, depending on the sign of α. For the simulation presented here the latter was set to $\alpha \tau =-1$; i.e., it represents an additional energy source.

Spectral Shell Decomposition.

To further assess the energy transfer among different length scales, we divide the spectral space into circular shells $S_J$, $J=\mathrm{1,2,3},\dots$ centered at $k=0$ and complementary to each other. (Details on the shell decomposition are given in SI Text, section S2). Moreover, we introduce the projection operator $P_J$ defined as

$$\left(P_{J}f\right)\left(\mathbf{r}\right):={\langle f\left(\mathbf{r}\right)\rangle }_J:={\displaystyle \sum _{\mathbf{k}\in S_J}{f}_{\mathbf{k}}{\text{e}}^{\text{i}\mathbf{k}\cdot \mathbf{r}}}.$$ [4]

Such a decomposition will prove useful for analyzing the nonlinear terms. The latter terms represent interactions between different spatial scales and computing the contributions arising from different shells will help us gain physical insights into those interactions, e.g., the degree of locality of the energy transfer. Additionally, examining the symmetry of the shell-to-shell coupling corresponding to the quadratic and cubic nonlinearity will reveal their completely different physical character.

Applying $P_J$ to Eq. 1 leads to an evolution equation for the energy $E_J:={\displaystyle \int {\left|{\langle \mathbf{v}\rangle }_J\right|}^2\text{d}\mathrm{\Omega }/\left(2V\right)}$ of shell $S_J$, which reads

$$\frac{\partial E_J}{\partial t}={\displaystyle \sum _{\mathbf{k}\in S_J}\gamma \left(k\right)\hspace{0.17em}{\left|{\mathbf{v}}_{\mathbf{k}}\right|}^2}+{\displaystyle \sum _I\left(T_{IJ}^{\mathrm{adv}}+T_{IJ}^{\mathrm{cub}}\right)},$$ [5]

with the advective and cubic nonlinear terms

$$T_{IJ}^{\mathrm{adv}}=-{\lambda }_0{\displaystyle \sum _{\mathbf{k}}\overline{{\langle {\mathbf{v}}_{\mathbf{k}}\rangle }_J}\cdot \mathrm{ℱ}\left\{\left(\mathbf{v}\cdot \nabla \right){\langle \mathbf{v}\rangle }_I\right\}\left(\mathbf{k}\right)}\hspace{0.17em},$$ [6a]

$$T_{IJ}^{\mathrm{cub}}=-\beta {\displaystyle \sum _{\mathbf{k}}\overline{{\langle {\mathbf{v}}_{\mathbf{k}}\rangle }_J}\cdot \mathrm{ℱ}\left\{{\left|\mathbf{v}\right|}^2{\langle \mathbf{v}\rangle }_I\right\}\left(\mathbf{k}\right)}\hspace{0.17em},$$ [6b]

where $\mathrm{ℱ}$ denotes the Fourier transform (SI Text, section S1).

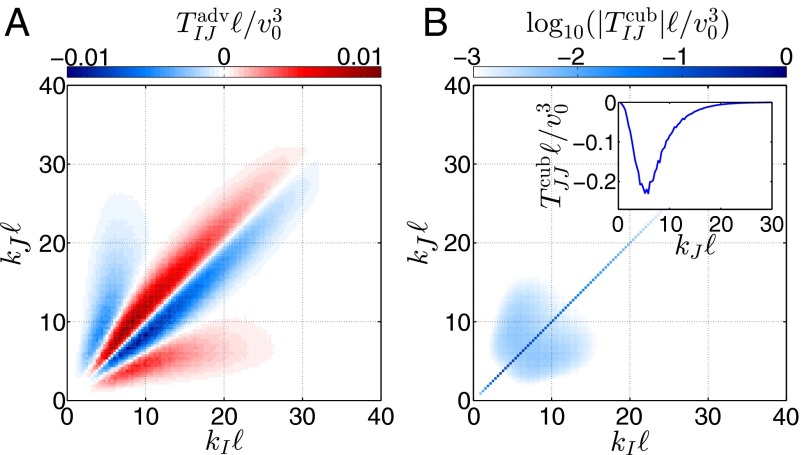
The terms $T_{IJ}^{\mathrm{adv}}$ and $T_{IJ}^{\mathrm{cub}}$ characterize the transfer of energy between shells $S_I$ and $S_J$. Due to the incompressibility constraint, $T_{IJ}^{\mathrm{adv}}$ is antisymmetric with respect to the shell indexes I and J (SI Text, section S2); i.e., summing over both indexes gives zero. This shows that (in an incompressible system) the Navier–Stokes nonlinearity neither injects nor dissipates energy but only redistributes it among the different shells $S_J$. A numerical computation of $T_{IJ}^{\mathrm{adv}}$ is shown in Fig. 3A. In addition to verifying the antisymmetry, this also illustrates the direction of energy transfer in spectral space. There is a combination of forward and inverse energy flows. At intermediate wave numbers, there is mainly a local forward energy flux; see the areas next to the diagonal in Fig. 3A, where red above the diagonal and blue below it indicate a flow from smaller to larger k. Additionally, there is also a nonlocal inverse energy flow dominating at small wave numbers, represented by the smaller side branches in Fig. 3A. The green curve in Fig. 2 represents the cumulative effect of the 2D structures seen in Fig. 3A. The Navier–Stokes nonlinearity extracts energy from the intermediate wave numbers (negative contribution) and supplies it to both smaller (inverse cascade) and larger (forward cascade) wave numbers. The contribution of the cubic nonlinearity, on the other hand, is symmetric ($T_{IJ}^{\mathrm{cub}}=T_{JI}^{\mathrm{cub}}$) and, therefore, cannot be viewed as a term that simply transfers energy from one shell to another in a conservative manner (SI Text, section S2). Because every second-rank tensor can be uniquely decomposed into a symmetric and an antisymmetric part, $T_{IJ}^{\mathrm{cub}}$ represents physical processes that are fundamentally distinct from a Navier–Stokes-like energy transfer. It does not redistribute energy between different shells. Instead, it couples different shells, say $S_I$ and $S_J$, in such a way that the same amount of energy is either produced in both shells or extracted from them. The numerical results displayed in Fig. 3B clearly show that the entries of $T_{IJ}^{\mathrm{cub}}$ are dominated by the diagonal terms whereas the off-diagonal terms are negligibly small. Note that the curve in Fig. 3B, Inset resembles closely the blue line in Fig. 2. Moreover, the diagonal entries are negative, indicating the dissipative nature of the cubic nonlinearity. This feature together with the different physical interpretation of the cubic term represents the central result that the shell-to-shell decomposition yields. Both aspects are essential for the cubic interaction and should be captured by a successful closure approximation.

Fig. 3.

Numerical computation of the shell-to-shell couplings $T_{IJ}^{\mathrm{adv}}$ and $T_{IJ}^{\mathrm{cub}}$ as given in Eqs. 6a and 6b; all shells have the same width of three times the minimal wave number $\mathrm{\Delta }k$ and a time average over the statistically stationary state has been performed. (A) The coupling term $T_{IJ}^{\mathrm{adv}}$ due to the advective Navier–Stokes nonlinearity in units of $v_0^3/\ell$. It exhibits both forward and backward energy flow in spectral space. At intermediate and large wave numbers there is a local forward flux; see the lobes close to the diagonal. In contrast, for small k, there is an inverse flux nonlocal in spectral space; see the side branches. (B) The coupling term $T_{IJ}^{\mathrm{cub}}$ due to the cubic nonlinearity in units of $v_0^3/\ell$. Note the logarithmic scale. In contrast to the Navier–Stokes term, $T_{IJ}^{\mathrm{cub}}$ is symmetric in the shell indexes. In addition, it is almost diagonal, indicating that coupling between different shells is negligible. This shows that at large scales the cubic interaction can be well approximated as a local dissipation term. Inset displays only the diagonal entries on a linear scale.

Cubic Damping Term.

To make progress beyond a numerical analysis, we seek an approximate solution for the stationary state of the energy spectrum. The analysis is complicated by the fact that the right-hand side of Eq. 2 involves third- and fourth-order velocity correlation functions, $T_{\mathbf{k}}^{\mathrm{adv}}$ and $T_{\mathbf{k}}^{\mathrm{cub}}$. Formulating evolution equations for those gives rise to even higher-order velocity correlations. One way to deal with this “hierarchy” problem is to make approximations at some level (via a “closure relation”), leading to a closed set of equations. Guided by the observation that the statistics of the velocity field at large spatial separations in classical 2D Navier–Stokes turbulence are very close to Gaussian (which we also confirmed numerically for Eq. 1 as explained in SI Text, section S3), a natural way to approach the cubic damping term in Eq. 2 is via the quasi-normal approximation (35), also known as the Millionshchikov hypothesis (36). According to it, third-order correlations, e.g., $\langle v_{-\mathbf{k}}^i{v}_{\mathbf{k}-\mathbf{p}}^l{v}_{\mathbf{p}}^j\rangle$, are nonzero, and the even-order correlations are approximately sums of products of all possible combinations of second-order correlations (as in Wick’s theorem). Defining the scalar correlation function $Q_k\left(t\right)$ via $D_{ij}\left(\mathbf{k}\right)Q_k\left(t\right):=\langle v_{-\mathbf{k}}^i\left(t\right)v_{\mathbf{k}}^j\left(t\right)\rangle$ and using spatial homogeneity and isotropy, one arrives (for a 2D setting) at

$$T_{\mathbf{k}}^{\mathrm{cub}}\approx -\beta Q_k{\displaystyle \sum _{\mathbf{p}}\left(2\frac{{\left(\mathbf{k}\cdot \mathbf{p}\right)}^2}{k^2{p}^2}+1\right)Q_p\approx -8\beta \hspace{0.17em}{E}_{\mathrm{tot}}\hspace{0.17em}{E}_k},$$ [7]

where $E_{\mathrm{tot}}$ denotes the total energy of the system; for details of the derivation see SI Text, section S3. Hence, the approximation of the cubic damping term in Eq. 2 is directly proportional to the energy spectrum $E_k$. This resonates with Fig. 3B, showing that the diagonal terms are the dominant ones in $T_{IJ}^{\mathrm{cub}}$. Hence, the cubic damping term is of the same form as the linear Ekman damping, however, with a damping rate that is not constant but proportional to the total energy $E_{\mathrm{tot}}$ of the system. This captures the nonlinear character of the cubic damping term: It provides a dynamical response at large spatial scales, where an increase of the total energy of the system leads to a stronger dissipation that, in turn, decreases $E_k$. This nonlinear feature helps to maintain the spectral energy balance and achieve a statistically stationary state. The latter cannot always be attained if $\beta =0$. Our investigations revealed that in this case there is a critical value for α (necessarily positive) below which the dissipation due to friction is insufficient and cannot balance the energy that accumulates at the large scales as a result of the inverse energy flow in 2D Navier–Stokes systems.

Advective Nonlinearity.

In contrast to the cubic damping term, the advective nonlinearity in Eq. 2 produces an expression that involves third-order correlations, meaning that the quasi-normal approximation is not directly applicable. Formulating an evolution equation for the third-order correlation leads to the known hierarchy problem, which here, due to the presence of the cubic term, would be even more convoluted. Such a hierarchical scheme can, nevertheless, lead to a closed system of equations after applying the Millionshchikov hypothesis, but the resulting system of equations is highly complicated and tractable only numerically.

Because our goal here is to arrive at an analytical approximation for the energy spectrum at small wave numbers, we choose a more heuristic approach. As already discussed, the advective nonlinearity redistributes energy only among the different modes. This implies an energy flux in spectral space, defined as ${\mathrm{\Pi }}_k^{\mathrm{adv}}=-{\displaystyle {\int }_0^k{T}_p^{\mathrm{adv}}\text{d}p}$, which is taken to be proportional to the energy $E_k$ at any given scale. The energy corresponding to an eddy of size $\sim 1/k$ scales as $k\hspace{0.17em}{E}_k$, which suggests the relation

$$\mathrm{\prod }_k^{\mathrm{adv}}\propto {\omega }_k\hspace{0.17em}k\hspace{0.17em}{E}_k,$$ [8]

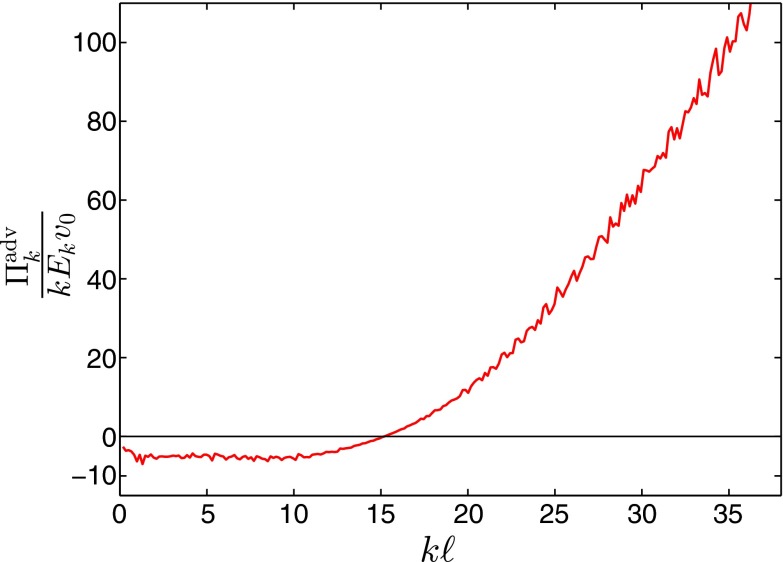
where ${\omega }_k$ is a characteristic frequency that may vary with k. Because ${\omega }_k$ is still undetermined, the above relation merely shifts the challenge to finding the function ${\omega }_k$. However, it suggests a physical interpretation for it. In 2D and 3D Navier–Stokes turbulence this frequency is determined by ${\omega }_k^2\sim {\displaystyle {\int }_0^k{p}^2{E}_p\text{d}p}$ (35). Physically, $1/{\omega }_k$ can be viewed as the characteristic distortion time at length scale $1/k$. For the energy cascade in classical turbulence ${\omega }_k$ scales as $k^{2/3}$. Thus, larger eddies have longer eddy turnover times whereas smaller eddies have shorter ones. This implies that over a time period of the order of the eddy turnover time at scale $1/k$ the effects of the larger wave numbers average out due to their faster dynamics. On the other hand, due to their comparatively slower dynamics, the larger length scales (compared with $1/k$) provide a coherent contribution to the average shear rate acting at the scale $1/k$. Given the decrease of $E_k$ with k in the cascade range of Navier–Stokes turbulence, the main contribution to the integral comes from the part of the integrand around $p\sim k$. Thus, most of the shear stems from wave numbers of a magnitude similar to k, which relates to the locality of the classical energy cascade. Eq. 8 together with the integral expression for ${\omega }_k$ given above simplifies the equations and provides a closure that, in the limit of an energy/enstrophy cascade, i.e., constant energy/enstrophy flux, yields the Kraichnan solution for the energy spectrum in the energy/enstrophy inertial range (37). As evident from Fig. 2, however, at large scales there is no range of wave numbers for which the advective nonlinearity is zero; i.e., there is no inertial range. Furthermore, as shown in Fig. 4, the spectral form of the ratio ${\mathrm{\Pi }}_k^{\mathrm{adv}}/\left(k{E}_k\right)$ is constant at large scales, i.e., ${\omega }_k={\omega }_c=\mathrm{const}$, implying that the physics in our case are qualitatively different from what we have in classical Navier–Stokes turbulence, both 2D and 3D. The result that the characteristic frequency is not a function of the local wave number but instead a constant over a wide range in spectral space implies a kind of synchronization of the large-scale structures. Such a synchronization deviates considerably from the classical ${\omega }_k\propto k^{2/3}$ scaling and requires nonlocal interactions involved in the inverse energy cascade at small k as seen in Fig. 3A. In addition, in classical turbulence models large spatial scales are more energetic than smaller ones, giving the former the potential to shear and distort the latter. For Eq. 1, however, the energy spectrum $E_k$ first increases with k up to some maximum and then decreases again; see the red curve in Fig. 2. Hence, for the spectral region we are interested in, the larger scales are not able to shear the smaller ones. In summary, our investigation of the advective nonlinearity in this model shows that at small wave numbers there is a distinct constant frequency ${\omega }_c$ that controls the energy transfer at large scales. Incorporating this insight into our analysis will provide us with an approximate solution for the energy spectrum at those scales.

Fig. 4.

Numerical computation of the frequency ${\omega }_k$ as a function of k as defined by Eq. 8. Owing to the positive definiteness of the denominator $k{E}_k$, the sign of the function agrees with the sign of the energy flux arising from the advective nonlinearity. Thus, there is evidently an inverse energy flow (negative flux) at large length scales and a forward energy flow (positive flux) at small length scales. Additionally, ${\omega }_k$ is approximately constant at small wave numbers. The numerical simulation was performed with $\alpha \tau =1$.

Variable Spectral Exponent.

In the statistically stationary state, time-averaging Eq. 2 yields zero on the left-hand side,

$$-2\left(\alpha +4\beta E_{\mathrm{tot}}+{\mathrm{\Gamma }}_0{k}^2-{\mathrm{\Gamma }}_2{k}^4\right)E_k-\frac{\text{d}{\mathrm{\Pi }}_k^{\mathrm{adv}}}{\text{d}k}=0,$$ [9]

where we have already incorporated the result of the quasi-normal approximation for the cubic damping term. Discarding the term proportional to ${\mathrm{\Gamma }}_2$ that is negligible at small wave numbers and using Eq. 8 with constant ${\omega }_k$, we arrive at a differential equation for the energy spectrum $E_k$, the solution of which reads

$$E_k={\tilde{E}}_0{k}^{\delta }\exp \left(-\frac{{\mathrm{\Gamma }}_0}{{\lambda }_0{\omega }_c}{k}^2\right),$$ [10]

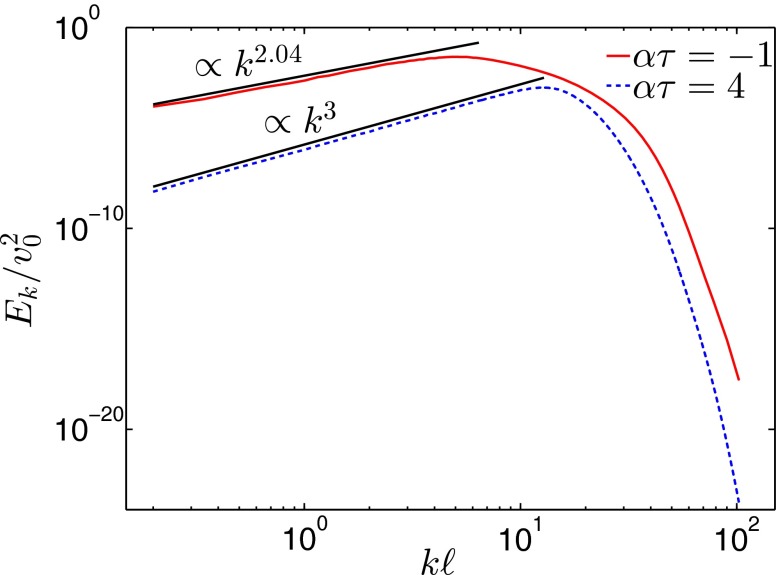
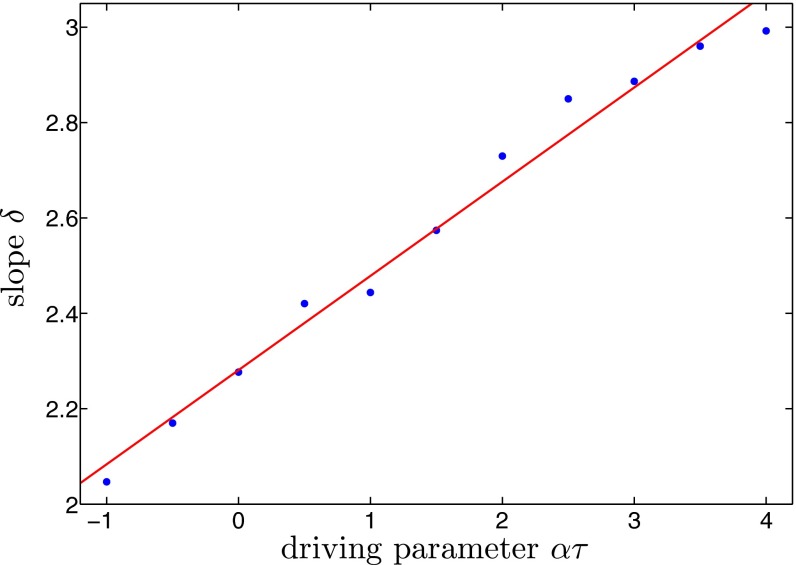
where ${\tilde{E}}_0$ is a constant of integration and the exponent is given by $\delta =\left(2\alpha +8\beta E_{\mathrm{tot}}\right)/\left({\lambda }_0{\omega }_c\right)-1$. Eq. 10 shows that at small wave numbers ($k\to 0$) the energy spectrum behaves as a power law. However, the exponent δ of this power law is not universal but depends (directly and indirectly) on various system parameters. Qualitatively, a stronger dissipation, i.e., a positive α and a higher factor of $\beta E_{\mathrm{tot}}$, will induce a steeper power law. An example is shown in Fig. 5, where the numerical solution of Eq. 1 is presented for two different values of α. In both cases, the system exhibits clear power-law spectra over more than one order of magnitude in wave-number space, and it is evident that our model predicts the correct qualitative dependence of the spectral exponents. A quantitative test of our semianalytical result can be undertaken by carrying out numerical simulations for different values of α. We note in passing that such a parameter scan requires that there are always enough instabilities to drive the turbulence and that statistical homogeneity and isotropy are ensured. The linear growth rate of the most unstable mode equals $-\alpha +{\mathrm{\Gamma }}_0^2/\left(4{\mathrm{\Gamma }}_2\right)$, which gives an upper bound on the variation of α once ${\mathrm{\Gamma }}_0$ and ${\mathrm{\Gamma }}_2$ have been set. On the other hand, the term $-\alpha \mathbf{v}$ in Eq. 1 tries to destroy the statistical isotropy of the system. Thus, the energy injected by the α term must be considerably smaller than that injected by the ${\mathrm{\Gamma }}_2$ term, which imposes a lower bound on α. The result from such a parameter scan of the numerical solution of Eq. 1 is displayed in Fig. 6, where every point is obtained by fitting a power law on the left end of the energy spectrum. The data from our investigation show a linear dependence of the slope δ on the parameter α, which agrees with the expression for δ provided by our model. Further numerical simulations indicate that the dependence of the slope on the strength of the cubic interaction β is qualitatively the same but quantitatively much weaker. This can be due to the factor $\beta E_{\mathrm{tot}}$ appearing in δ. Stability analysis shows that for ${\lambda }_0={\mathrm{\Gamma }}_0={\mathrm{\Gamma }}_2=0$ and $\alpha <0$ an ordered state arises with a constant velocity field and total system energy $E_{\mathrm{tot}}\propto 1/\beta$. If a similar scaling applies also in the presence of the advective nonlinearity and the other linear terms, then the product $\beta E_{\mathrm{tot}}$ should exhibit only weak dependence on β.

Fig. 5.

Time-averaged energy spectrum $E_k$ for two different values of $\alpha \tau$ at the two ends of the parameter domain supporting the turbulent regime, $\alpha \tau =-1$ and $\alpha \tau =4$. There is a clear power law at large scales and the effect of varying the strength of the Ekman term manifests as a variation of its slope. In general, more intensive energy injection (via the parameter α) leads to a less steep slope of the power law, more energy at each scale, and a peak of the energy spectrum that occurs at smaller wave numbers.

Fig. 6.

Variation of the slope of the energy spectrum at small wave numbers with respect to α. The steepness of the power law at large scales varies continuously with the driving parameter in a nearly linear fashion as long as there is a statistically isotropic turbulent regime. The parameter range where this applies derives from the condition that there are enough linear instabilities to sustain the turbulence: i.e., α should not be too large, and the energy injection from the Ekman term should not dominate over the ${\mathrm{\Gamma }}_0$ term; i.e., α should not be too negative.

Summary and Conclusions

In the present work, we investigated the properties of a continuum model describing the turbulent motion of active fluids driven by internal instabilities. In addition to the convective nonlinearity of Navier–Stokes type, the model contains a cubic nonlinearity. Analytical and numerical considerations revealed that at large scales, the latter behaves like an Ekman damping with a frequency that is set by the system self-consistently. The system displays power-law energy spectra even in the absence of an inertial range, but the spectral exponents depend on the system parameters. These properties should be observable in laboratory experiments.

How do these findings fit into a broader perspective on turbulence? In Navier–Stokes turbulence, the dynamics are characterized by an inertial range that is dominated by a single nonlinear term and free of energy sources/sinks, displaying universal properties. Several turbulence models in the literature deviate from this standard picture in that they introduce multiscale forcing and/or damping with a power-law spectrum, thereby removing the inertial range (in a strict sense) (38–40). It can be shown, however, that, in general, this modification really affects the system only at very small or very large scales, i.e., in the asymptotic limit (41). If and only if the power-law exponent is such that the linear forcing/damping rates scale exactly like the nonlinear energy transfer rates, does the forcing/damping affect the entire scale range, inducing nonuniversal behavior (16, 42, 43).

The physical system discussed in this paper is fundamentally different, however. Here, the existence of a second nonlinearity provides additional freedom, such that the system is able to self-organize into such a critical state (characterized by a scale-by-scale balance between linear forcing/damping rates and nonlinear transfer rates), without the need for external fine-tuning. The observed nonuniversal behavior is a natural consequence of this feature. These properties define a new class of turbulence.

S1. Normalization and Numerical Methods

Normalization.

For the sake of completeness, we discuss here briefly the normalization of the quantities used and describe the numerical implementation of the continuum model. Written in dimensional units, Eq. 1 reads

$$\frac{\partial \mathbf{v}}{\partial t}+{\lambda }_0\left(\mathbf{v}\cdot \nabla \right)\mathbf{v}=-\frac{1}{\rho }\nabla p-\left(\alpha +\beta {\left|\mathbf{v}\right|}^2\right)\mathbf{v}-{\mathrm{\Gamma }}_0\mathrm{\Delta }\mathbf{v}-{\mathrm{\Gamma }}_2{\mathrm{\Delta }}^2\mathbf{v},$$ [S1]

where ρ denotes density of the fluid and is considered constant. In contrast to ref. 4, we have omitted the term ${\lambda }_1\nabla {\left|\mathbf{v}\right|}^2$ because, for constant ${\lambda }_1$, it is obsolete. Being a gradient of a scalar function, it is of the same type as the pressure term and can be absorbed in it. Additionally, our definition for ${\mathrm{\Gamma }}_0$ is such that positive values correspond to linear instabilities. Due to the nature of the problem, we need only to specify a velocity and a length scale, $v_0$ and $\ell$, respectively, with the resulting time scale being $\tau =\ell /v_0$. The parameters ${\mathrm{\Gamma }}_0$ and ${\mathrm{\Gamma }}_2$ controlling the linear instability and dissipation give rise to a velocity scale defined as $v_0=\sqrt{{\mathrm{\Gamma }}_0^3/{\mathrm{\Gamma }}_2}$. For the determination of the length scale, we consider the linear growth rate γ of the spectral modes given by $\gamma \left(k\right)=-\alpha +{\mathrm{\Gamma }}_0{k}^2-{\mathrm{\Gamma }}_2{k}^4$. It has a maximum located at $k_{\max }=\sqrt{{\mathrm{\Gamma }}_0/\left(2{\mathrm{\Gamma }}_2\right)}$ after which it decreases and eventually becomes negative, meaning that the short wavelength modes are linearly stable. Thus, the linear instability is most prominent at the spatial scale of $\pi /k_{\max }$. Proper resolution of the physical processes involved demands that the size of the system is much larger than $\pi /k_{\max }$. Hence, we define our normalization length scale as $\ell =5\pi /k_{\max }=5\pi \sqrt{2{\mathrm{\Gamma }}_2/{\mathrm{\Gamma }}_0}$. The physical quantities and operators map to their dimensionless forms as

$$v\to v{v}_0\hspace{0.17em};\hspace{1em}t\to t\tau ;\hspace{1em}p\to p{v}_0^2\rho ;\hspace{1em}\alpha \to \alpha /\tau ;$$ [S2]

$$\beta \to \frac{\beta }{\ell v_0};\hspace{1em}{\mathrm{\Gamma }}_0\to {\mathrm{\Gamma }}_0\ell v_0;\hspace{1em}{\mathrm{\Gamma }}_2\to {\mathrm{\Gamma }}_2{\ell }^3{v}_0;\hspace{1em}\mathrm{and}\hspace{1em}\nabla \to \frac{1}{\ell }\nabla .$$ [S3]

Using the velocities and length scales defined above sets the normalized values of the parameters ${\mathrm{\Gamma }}_0$ and ${\mathrm{\Gamma }}_2$ as ${\mathrm{\Gamma }}_0=1/\left(5\sqrt{2}\pi \right)\approx 0.045$ and ${\mathrm{\Gamma }}_2={\mathrm{\Gamma }}_0^3\approx 9\cdot {10}^{-5}$. The normalization units chosen above are the same as those used in ref. 4, which facilitates comparison. All of the numerical results presented here were obtained with ${\lambda }_0=3.5$ and a normalized value for β of $\beta =0.5$. Given that $\alpha =-1$ and the different sign convention for ${\mathrm{\Gamma }}_0$, the parameters used in this paper correspond to the experimental values characterizing the bacterial suspension described in ref. 4.

Eq. 1 possesses five different parameters, which makes a thorough investigation of its complete parameter space a very tedious task. To bring some structure into this highly dimensional parameter space, we present some limit cases in Table S1. It is important to note that for $\beta <0$ the dynamics represented by Eq. 1 do not reach a stationary state and the kinetic energy of the velocity field grows without a limit. Thus, this case is of no physical relevance.

Numerical Methods.

Numerical solutions of Eq. 1 have been obtained via the pseudospectral approach (44), which is common in computational fluid dynamics. According to it spatial derivatives are computed in Fourier space where they reduce to simple multiplication. The nonlinear terms, on the other hand, are computed in real space because they correspond to a convolution in Fourier space, which is a computationally expensive procedure. The time evolution is computed numerically by the exponential time differencing scheme first developed in ref. 45 and later improved in ref. 46, where a fourth-order Runge–Kutta method has been used. The underdetermined system of Eq. 1 is completed by the incompressibility condition $\nabla \cdot \mathbf{v}=0$ and solved on the quadratic domain $\left[0,L_x\right]\times \left[0,L_y\right]$ with $L_x=L_y=L$ and periodic boundary conditions. The decomposition in Fourier series is achieved as

$$\mathbf{v}\left(\mathbf{r},t\right)={\displaystyle \sum _{\mathbf{k}}{\mathbf{v}}_{\mathbf{k}}\left(t\right){\text{e}}^{\text{i}\mathbf{k}\cdot \mathbf{r}}},$$ [S4]

where the components of the wave number vector $\mathbf{k}=\left(k_x,k_y\right)$ are related to the system size by $k_{x,y}=n2\pi /L_{x,y}$ with $n\in {\mathrm{\mathbb{Z}}}_0$. For the ease of notation we omit the traditional ^{^} symbol. It should be clear from the corresponding argument whether we mean the real-space function or the Fourier component. According to the definition given above, the Fourier coefficients are determined as

$${\mathbf{v}}_{\mathbf{k}}\left(t\right)=\frac{1}{L_x{L}_y}{\displaystyle \underset{0}{\overset{L_y}{\int }}{\displaystyle \underset{0}{\overset{L_x}{\int }}\mathbf{v}\left(\mathbf{r},t\right){\text{e}}^{-\text{i}\mathbf{k}\cdot \mathbf{r}}\text{d}x}\text{d}y}=:\mathrm{ℱ}\left\{\mathbf{v}\right\}\left(\mathbf{k},t\right),$$ [S5]

where the real-space coordinate vector is given by $\mathbf{r}=\left(x,y\right)$. Note that the pseudospectral approach introduces the so-called aliasing errors when computing the nonlinear term. To avoid that in numerical simulations of Navier–Stokes flows, we use the $3/2$ dealiasing rule. It consists of neglecting the higher $1/3$ of the Fourier modes; i.e., the “effective” Fourier modes are only $2/3$ of the numerical ones. However, such a $3/2$ rule can be applied only in the case of quadratic nonlinearities. For a cubic nonlinearity as in Eq. 1 the $3/2$ dealiasing rule, standard in Navier–Stokes simulations, is insufficient. Instead, we should set to zero the upper half of the Fourier components (47).

The solution of Eq. 1 in the part of parameter space we are interested in exhibits rapid fluctuations typical for turbulent systems. The same applies also for quantities like the energy of a given mode or the total energy of the system. In the turbulence literature the so-called “ensemble average” is defined, which corresponds to an average over many possible realizations of the flow due to different initial conditions. However, such an average procedure is computationally extremely demanding. In the case of a system that reaches a statistically stationary regime, we use a time average instead, denoted by $\langle \cdot \rangle$, which is performed over a time window that starts after the onset of the statistically stationary state. In mathematical terms, for an arbitrary function $f\left(t\right)$ we have that

$$\langle f\rangle =\frac{1}{T}{\displaystyle \underset{t_1}{\overset{t_1+T}{\int }}f\left(t\right)\text{d}t}.$$ [S6]

For a discrete time variable t the integral becomes a sum. Under the assumption of ergodicity the definition above yields the same result as an ensemble average.

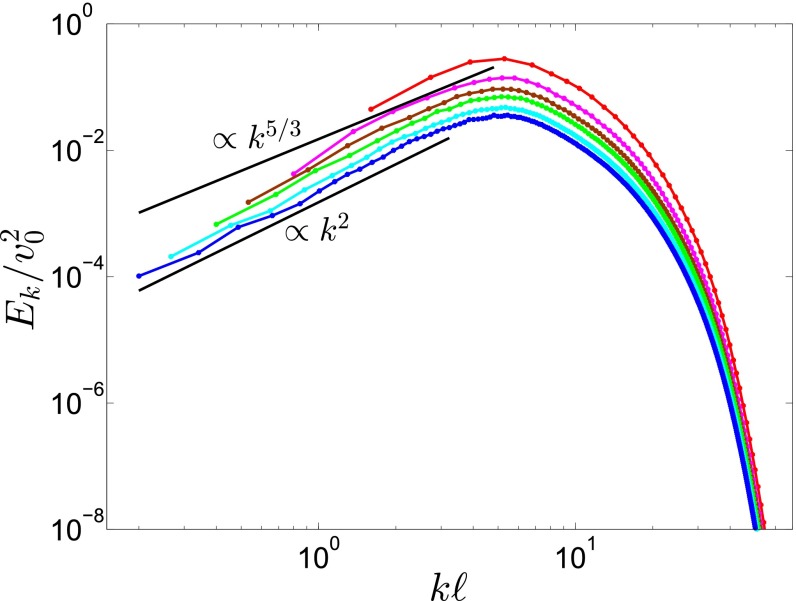
In ref. 4, where the continuous model we study here has been introduced, the main goal has been to compare its results with experimental measurements and with the findings based on more basic self-propelled rods (SPR) models. This determined the size of the real-space domain used in the simulations. In this article, however, we aim for a more fundamental examination of the turbulent dynamics produced by Eq. 1. Because we are interested in the spectral range at small wave numbers, we investigate the convergence of the numerical results when the box size becomes larger. The latter is inversely proportional to the smallest nonzero wave number we have, meaning that a larger real-space domain allows for a better representation of the small-k part of the energy spectrum. Numerical simulations of Eq. 1 for different domain sizes yield the energy spectra displayed in Fig. S1. The box size and number of points representing numerically the real-space domain that have been used for obtaining the red curve are nearly the same as those used in ref. 4 and the slope of $k^{5/3}$ given by the upper black line is the one reported there. Due to the parameters of the simulation the smallest wave number is still rather large and close to the peak of the spectrum. Considering that there are only three points before the peak, it is hard to justify a power law in that region. Note that for obtaining a one-dimensional spectrum from a 2D spectral representation one has to group together modes with similar $\left|\mathbf{k}\right|$. For the first few k points such a grouping can lead to notable ambiguity in the value of k assigned to the whole group and, thereby, influence the form of the curve. Therefore, the slope of a power law calculated by using only the first few points will be very sensitive to such numerical details. The blue curve, on the other hand, has been obtained with a much larger domain size and number of points (effectively $\mathrm{1,024}\times \mathrm{1,024}$ or $\mathrm{2,048}\times \mathrm{2,048}$ including dealiasing) and represents the simulation parameters used for all of the numerical results reported here. It is evident that, in this case, there is a much larger (over one order of magnitude) domain at small k with a prominent power law of nearly $E\left(k\right)\propto k^2$ for this set of parameters (given by the lower black line), which, in addition, is also more robust. Thus, our analysis shows that the form of the power law is sensitive to finite-size effects of the simulation domain. With increasing the box size and keeping all physical parameters constant, it converges to a value that is different from the one presented in ref. 4.

Fig. S1.

Numerical computation of the energy spectrum for different domain sizes: red, $\mathrm{\Omega }=\left[\mathrm{0,1.25}\pi \ell \right]\times \left[\mathrm{0,1.25}\pi \ell \right]$; magenta, $\mathrm{\Omega }=\left[\mathrm{0,2.5}\pi \ell \right]\times \left[\mathrm{0,2.5}\pi \ell \right]$; brown, $\mathrm{\Omega }=\left[\mathrm{0,3.75}\pi \ell \right]\times \left[\mathrm{0,3.75}\pi \ell \right]$; green, $\mathrm{\Omega }=\left[\mathrm{0,5.0}\pi \ell \right]\times \left[\mathrm{0,5.0}\pi \ell \right]$; cyan, $\mathrm{\Omega }=\left[\mathrm{0,7.5}\pi \ell \right]\times \left[\mathrm{0,7.5}\pi \ell \right]$; and blue, $\mathrm{\Omega }=\left[\mathrm{0,10.0}\pi \ell \right]\times \left[\mathrm{0,10.0}\pi \ell \right]$. The numerical resolution was kept constant in all simulations. A rather large box size is needed for the manifestation of an unambiguous power law at small wave numbers. The numerical simulations were performed with $\alpha \tau =-1$.

S2. Symmetry of the Nonlinear Transfer Terms

Generally speaking, nonlinear terms tend to play a key role in determining the behavior of complex systems. This is also true here. In the main part of the paper, these terms were studied quantitatively by introducing specific projection operators in spectral space as defined in Eq. 4. One can easily verify that $P_J$ is idempotent and, thus, indeed a projection operator. In addition, $P_J$ is self-adjoint with respect to the usual scalar product in $L^2\left(\mathrm{\Omega }\right)$ and commutes with temporal and spatial derivatives. This definition of $P_J$ is still rather general and we have the freedom to choose the boundaries $k_J$ of the individual shells. In the turbulence literature the shells are usually chosen such that $k_{J+1}/k_J=\mathrm{const}>1$. For analyzing the spectral region of small wave numbers, however, this is rather inconvenient, because we want to have as many shells as possible in this spectral range. Thus, we construct the shells to be of equal width, which will not change the results of our analysis. The numerical results reported in this work are obtained with the width of the circular bands being $3\mathrm{\Delta }k$, where $\mathrm{\Delta }k$ is the difference between two adjacent modes along the x or the y axis. This ensures that every shell contains an appreciable number of modes and thereby reduces statistical fluctuations.

Applying $P_J$ on Eq. 1 gives us an evolution equation for the filtered velocity field ${\langle \mathbf{v}\rangle }_J$. Multiplying with ${\langle \mathbf{v}\rangle }_J$, integrating over space, and taking into account that the energy of each spectral shell is given by $E_J={\displaystyle \int {\left|{\langle \mathbf{v}\rangle }_J\right|}^2\text{d}\mathrm{\Omega }}/\left(2V\right)$, we arrive at

$$\frac{\partial E_J}{\partial t}=-2\alpha E_J-{\lambda }_0\frac{1}{V}{\displaystyle \underset{\mathrm{\Omega }}{\int }{\langle \mathbf{v}\rangle }_J\cdot {\langle \left(\mathbf{v}\cdot \nabla \right)\mathbf{v}\rangle }_J\text{d}\mathrm{\Omega }}-\hspace{0.17em}\beta \frac{1}{V}{\displaystyle \underset{\mathrm{\Omega }}{\int }{\langle \mathbf{v}\rangle }_J\cdot {\langle {\left|\mathbf{v}\right|}^2\mathbf{v}\rangle }_J\text{d}\mathrm{\Omega }}-{\mathrm{\Gamma }}_0\frac{1}{V}{\displaystyle \underset{\mathrm{\Omega }}{\int }{\langle \mathbf{v}\rangle }_J\cdot \mathrm{\Delta }{\langle \mathbf{v}\rangle }_J\text{d}\mathrm{\Omega }}-{\mathrm{\Gamma }}_2\frac{1}{V}{\displaystyle \underset{\mathrm{\Omega }}{\int }{\langle \mathbf{v}\rangle }_J\cdot {\mathrm{\Delta }}^2{\langle \mathbf{v}\rangle }_J\text{d}\mathrm{\Omega }}.$$ [S7]

Due to the periodic boundary conditions and the incompressibility constraint, the contribution of the pressure term vanishes; i.e.,

$${\displaystyle \underset{\mathrm{\Omega }}{\int }{\langle \mathbf{v}\rangle }_J\cdot \nabla {\langle p\rangle }_J\text{d}\mathrm{\Omega }}={{\langle p\rangle }_J{\langle \mathbf{v}\rangle }_J\cdot \text{d}\mathit{\sigma }|}_{\partial \mathrm{\Omega }}-{\displaystyle \underset{\mathrm{\Omega }}{\int }{\langle p\rangle }_J{\langle \nabla \cdot \mathbf{v}\rangle }_J\text{d}\mathrm{\Omega }}=0,$$ [S8]

where $\text{d}\mathit{\sigma }$ is an infinitesimal oriented surface element on the boundary of the domain $\mathrm{\Omega }$ with a direction normal to the boundary and pointing outward. In a similar way integration by parts leads to

$${\displaystyle \underset{\mathrm{\Omega }}{\int }{\langle \mathbf{v}\rangle }_J\cdot \mathrm{\Delta }{\langle \mathbf{v}\rangle }_J\text{d}\mathrm{\Omega }}=-{\displaystyle \underset{\mathrm{\Omega }}{\int }\left(\nabla {\langle v_x\rangle }_J\cdot \nabla {\langle v_x\rangle }_J+\nabla {\langle v_y\rangle }_J\cdot \nabla {\langle v_y\rangle }_J\right)\text{d}\mathrm{\Omega }}$$ [S9]

and

$${\displaystyle \underset{\mathrm{\Omega }}{\int }{\langle \mathbf{v}\rangle }_J\cdot {\mathrm{\Delta }}^2{\langle \mathbf{v}\rangle }_J\text{d}\mathrm{\Omega }}={\displaystyle \underset{\mathrm{\Omega }}{\int }\mathrm{\Delta }{\langle \mathbf{v}\rangle }_J\cdot \mathrm{\Delta }{\langle \mathbf{v}\rangle }_J\text{d}\mathrm{\Omega }}.$$ [S10]

The self-adjointness of $P_J$ allows us to drop the filter operator in the second factor in the scalar products representing the nonlinear contributions in Eq. S7; i.e.,

$${\displaystyle \underset{\mathrm{\Omega }}{\int }{\langle \mathbf{v}\rangle }_J\cdot {\langle \left(\mathbf{v}\cdot \nabla \right)\mathbf{v}\rangle }_J\text{d}\mathrm{\Omega }}={\displaystyle \underset{\mathrm{\Omega }}{\int }{\langle \mathbf{v}\rangle }_J\cdot \left(\mathbf{v}\cdot \nabla \right)\mathbf{v}\text{d}\mathrm{\Omega }},$$ [S11]

$${\displaystyle \underset{\mathrm{\Omega }}{\int }{\langle \mathbf{v}\rangle }_J\cdot {\langle {\left|\mathbf{v}\right|}^2\mathbf{v}\rangle }_J\text{d}\mathrm{\Omega }}={\displaystyle \underset{\mathrm{\Omega }}{\int }{\langle \mathbf{v}\rangle }_J\cdot \left({\left|\mathbf{v}\right|}^2\mathbf{v}\right)\text{d}\mathrm{\Omega }}.$$ [S12]

With the aid of the decomposition of the velocity field into contributions from different spectral shells the nonlinear terms can be rewritten even further with the goal to facilitate interpretation. The Navier–Stokes nonlinearity can be represented as

$$\frac{1}{V}{\displaystyle \underset{\mathrm{\Omega }}{\int }{\langle \mathbf{v}\rangle }_J\cdot \left(\mathbf{v}\cdot \nabla \right)\mathbf{v}\text{d}\mathrm{\Omega }}={\displaystyle \sum }_I\frac{1}{V}{\displaystyle \underset{\mathrm{\Omega }}{\int }{\langle \mathbf{v}\rangle }_J\cdot \left(\mathbf{v}\cdot \nabla \right){\langle \mathbf{v}\rangle }_I\text{d}\mathrm{\Omega }}=:\frac{1}{{\lambda }_0}{\displaystyle \sum _I{T}_{JI}^{\mathrm{avd}}}.$$ [S13]

The summand in the equation above contains the contribution from two shells, $S_I$ and $S_J$, and can be interpreted as the interaction between shell $S_I$ and shell $S_J$. The picture of the Navier–Stokes term that arises in Fourier space is that of a three-wave coupling, i.e., a triadic interaction. The third mode/shell comes from the advective term $\mathbf{v}\cdot \nabla$. Here, we have not introduced a third index for it; i.e., we compute the interaction between the shells $S_I$ and $S_J$ mediated by all possible shells.

Applying the velocity decomposition on the term stemming from the cubic nonlinearity in Eq. 1 leads to

$$\frac{1}{V}{\displaystyle \underset{\mathrm{\Omega }}{\int }{\left|\mathbf{v}\right|}^2{\langle \mathbf{v}\rangle }_J\cdot \mathbf{v}\text{d}\mathrm{\Omega }}={\displaystyle \sum }_I\frac{1}{V}{\displaystyle \underset{\mathrm{\Omega }}{\int }{\left|\mathbf{v}\right|}^2{\langle \mathbf{v}\rangle }_J\cdot {\langle \mathbf{v}\rangle }_I\text{d}\mathrm{\Omega }}=:\frac{1}{\beta }{\displaystyle \sum _I{T}_{JI}^{\mathrm{cub}}},$$ [S14]

which, in analogy to the Navier–Stokes nonlinearity, can be interpreted as the interaction between shells $S_I$ and $S_J$ due to the cubic term. In this case the third “leg” mediating the interaction is ${\left|\mathbf{v}\right|}^2$, i.e., the local energy density in real space. We can also look at it as two legs, namely one for each velocity field $\mathbf{v}$. In this case we have summed over two legs to obtain a shell-to-shell interaction. From the summands in Eqs. S13 and S14 we can read off the corresponding the shell-to-shell coupling terms; namely

$$T_{IJ}^{\mathrm{adv}}=-{\lambda }_0\frac{1}{V}{\displaystyle \underset{\mathrm{\Omega }}{\int }{\langle \mathbf{v}\rangle }_J\cdot \left(\mathbf{v}\cdot \nabla \right){\langle \mathbf{v}\rangle }_I\text{d}\mathrm{\Omega }}$$ [S15a]

and

$$T_{IJ}^{\mathrm{cub}}=-\beta \frac{1}{V}{\displaystyle \underset{\mathrm{\Omega }}{\int }{\left|\mathbf{v}\right|}^2{\langle \mathbf{v}\rangle }_J\cdot {\langle \mathbf{v}\rangle }_I\text{d}\mathrm{\Omega }}\hspace{0.17em}.$$ [S15b]

The equations above are equivalent to Eqs. 6a and 6b in the main text, representing merely their real-space formulation.

Due to the symmetry of the scalar product ${\langle \mathbf{v}\rangle }_J\cdot {\langle \mathbf{v}\rangle }_I$, it is clear that $T_{IJ}^{\mathrm{cub}}$ is also symmetric with respect to the interchange of I and J; i.e., $T_{IJ}^{\mathrm{cub}}=T_{JI}^{\mathrm{cub}}$. On the other hand, for an incompressible velocity field and periodic boundary conditions $T_{IJ}^{\mathrm{avd}}$ is antisymmetric with respect to I and J. Denoting for brevity ${\langle \mathbf{v}\rangle }_I$ by $\mathbf{a}$ and ${\langle \mathbf{v}\rangle }_J$ by $\mathbf{b}$ and setting ${\lambda }_0=1$, we have after integration by parts

$$T_{IJ}^{\mathrm{avd}}=\frac{1}{V}{\displaystyle \underset{\mathrm{\Omega }}{\int }\mathbf{a}\cdot \left(\mathbf{v}\cdot \nabla \right)\mathbf{b}\text{d}\mathrm{\Omega }}=\frac{1}{V}{\displaystyle \underset{\mathrm{\Omega }}{\int }\left(a_x{v}_x\frac{\partial b_x}{\partial x}+a_x{v}_y\frac{\partial b_x}{\partial y}+a_y{v}_x\frac{\partial b_y}{\partial x}+a_y{v}_y\frac{\partial b_y}{\partial y}\right)\text{d}\mathrm{\Omega }}=\underset{=0}{\underbrace{\mathrm{boundary}\hspace{0.17em}\mathrm{terms}}}-\frac{1}{V}{\displaystyle \underset{\mathrm{\Omega }}{\int }\left(b_x\frac{\partial \left(a_x{v}_x\right)}{\partial x}+b_x\frac{\partial \left(a_x{v}_y\right)}{\partial y}+b_y\frac{\partial \left(a_y{v}_x\right)}{\partial x}+b_y\frac{\partial \left(a_y{v}_y\right)}{\partial y}\right)\text{d}\mathrm{\Omega }}=-\frac{1}{V}{\displaystyle \underset{\mathrm{\Omega }}{\int }\mathbf{b}\cdot \left(\mathbf{v}\cdot \nabla \right)\mathbf{a}\text{d}\mathrm{\Omega }}-\frac{1}{V}{\displaystyle \underset{\mathrm{\Omega }}{\int }\left(\mathbf{a}\cdot \mathbf{b}\right)\underset{=0}{\underbrace{\left(\nabla \cdot \mathbf{v}\right)}}\text{d}\mathrm{\Omega }}=-T_{JI}^{\mathrm{adv}}.$$ [S16]

S3. Derivation of Eq. 7 from the Millionshchikov Hypothesis

As discussed in the main text, the quasi-normal approximation rests on the Millionshchikov hypothesis (36) according to which the velocity correlations of odd order are still nonzero, but the even-order correlations can be expressed approximately as the sum of all possible products of second-order correlations. Thus, for the fourth-order correlation in Eq. 2 we can write

$$\langle v_{-\mathbf{k}}^i\left(t\right)v_{\mathbf{k}-\mathbf{p}-\mathbf{q}}^l\left(t\right)v_{\mathbf{q}}^l\left(t\right)v_{\mathbf{p}}^j\left(t\right)\rangle =\langle v_{-\mathbf{k}}^i\left(t\right)v_{\mathbf{k}-\mathbf{p}-\mathbf{q}}^l\left(t\right)\rangle \langle v_{\mathbf{q}}^l\left(t\right)v_{\mathbf{p}}^j\left(t\right)\rangle +\langle v_{-\mathbf{k}}^i\left(t\right)v_{\mathbf{q}}^l\left(t\right)\rangle \langle v_{\mathbf{k}-\mathbf{p}-\mathbf{q}}^l\left(t\right)v_{\mathbf{p}}^j\left(t\right)\rangle +\langle v_{-\mathbf{k}}^i\left(t\right)v_{\mathbf{p}}^j\left(t\right)\rangle \langle v_{\mathbf{k}-\mathbf{p}-\mathbf{q}}^l\left(t\right)v_{\mathbf{q}}^l\left(t\right)\rangle .$$ [S17]

Assuming that the system is statistically homogeneous and isotropic, the three terms on the right-hand side of the above equation can be further simplified as

$$\begin{array}{l}\langle v_{-\mathbf{k}}^i\left(t\right)v_{\mathbf{k}-\mathbf{p}-\mathbf{q}}^l\left(t\right)\rangle \langle v_{\mathbf{q}}^l\left(t\right)v_{\mathbf{p}}^j\left(t\right)\rangle =D_{il}\left(\mathbf{k}\right)D_{jl}\left(\mathbf{p}\right)Q_k\left(t\right)Q_p\left(t\right){\delta }_{\mathbf{q},-\mathbf{p}}\\ \langle v_{-\mathbf{k}}^i\left(t\right)v_{\mathbf{q}}^l\left(t\right)\rangle \langle v_{\mathbf{k}-\mathbf{p}-\mathbf{q}}^l\left(t\right)v_{\mathbf{p}}^j\left(t\right)\rangle =D_{il}\left(\mathbf{k}\right)D_{jl}\left(\mathbf{p}\right)Q_k\left(t\right)Q_p\left(t\right){\delta }_{\mathbf{q},\mathbf{k}}\\ \langle v_{-\mathbf{k}}^i\left(t\right)v_{\mathbf{p}}^j\left(t\right)\rangle \langle v_{\mathbf{k}-\mathbf{p}-\mathbf{q}}^l\left(t\right)v_{\mathbf{q}}^l\left(t\right)\rangle =D_{ij}\left(\mathbf{k}\right)D_{ll}\left(\mathbf{q}\right)Q_k\left(t\right)Q_q\left(t\right){\delta }_{\mathbf{p},\mathbf{k}},\end{array}$$ [S18]

where ${\delta }_{\mathbf{k},\mathbf{p}}$ equals one if $\mathbf{k}=\mathbf{p}$ and zero otherwise. The equal-time scalar correlation function $Q_k\left(t\right)$ is defined as $\langle v_{\mathbf{k}}^i\left(t\right)v_{-\mathbf{k}}^j\left(t\right)\rangle =:D_{ij}\left(\mathbf{k}\right)Q_k\left(t\right)$, which also requires statistical isotropy. Substituting the above expressions into the term in the energy balance equation that arises from the cubic nonlinearity, we can now perform the summation over the Cartesian indexes i, j, and ł. A preliminary computation that proves to be useful in this regard yields

$${\displaystyle \sum _j{D}_{jj}\left(\mathbf{k}\right)}=1,$$ [S19a]

$${\displaystyle \sum _i{D}_{ij}\left(\mathbf{k}\right)D_{il}\left(\mathbf{k}\right)}=D_{jl}\left(\mathbf{k}\right),$$ [S19b]

$${\displaystyle \sum _{i,j}{D}_{ij}\left(\mathbf{k}\right)D_{ij}\left(\mathbf{k}\right)}=1,$$ [S19c]

$${\displaystyle \sum _{j,l}{D}_{jl}\left(\mathbf{k}\right)D_{jl}\left(\mathbf{p}\right)}=\frac{{\left(\mathbf{k}\cdot \mathbf{p}\right)}^2}{k^2{p}^2}$$ [S19d]

for a 2D setting. With the aid of the above results one can easily derive the first part of Eq. 7. For the second part of Eq. 7, one needs to relate the scalar correlation function $Q_k\left(t\right)$ to the energy spectrum $E_{\mathbf{k}}\left(t\right)$ and perform the summation over the wave number $\mathbf{p}$. The former follows directly from the definition of the quantities and in two dimensions gives $E_{\mathbf{k}}\left(t\right)=Q_k\left(t\right)/2$. Note that, despite the vector notation of the argument, in the isotropic case $E_{\mathbf{k}}\left(t\right)$ depends only on the absolute value of the wave number. Analogously, one derives that ${\displaystyle {\sum }_{\mathbf{k}}{Q}_k\left(t\right)}=2E_0\left(t\right)$. The contribution involving the scalar product $\mathbf{k}\cdot \mathbf{p}$ can be computed analytically in the limit of an infinitely large system, i.e., $L\to \infty$, in which the wave number becomes a continuous variable. Denoting the angle between $\mathbf{k}$ and $\mathbf{p}$ as θ, we can write

$${\displaystyle \sum _{\mathbf{p}}\frac{{\left(\mathbf{k}\cdot \mathbf{p}\right)}^2}{k^2{p}^2}{Q}_p\left(t\right)}={\displaystyle \sum _{\mathbf{p}}{\cos }^2\left(\theta \right)Q_p\left(t\right)}\approx {\displaystyle \underset{0}{\overset{2\pi }{\int }}{\displaystyle \underset{0}{\overset{\infty }{\int }}{\cos }^2\left(\theta \right)Q_p\left(t\right)p\text{d}p}\text{d}\theta }=\frac{1}{2}2\pi {\displaystyle \underset{0}{\overset{\infty }{\int }}p{Q}_p\left(t\right)\text{d}p}=\frac{1}{2}{\displaystyle \underset{0}{\overset{2\pi }{\int }}{\displaystyle \underset{0}{\overset{\infty }{\int }}{Q}_p\left(t\right)p\text{d}p}\text{d}\varphi }=\frac{1}{2}{\displaystyle \sum _{\mathbf{p}}{Q}_p\left(t\right)}=E_0.$$ [S20]

Taking this into account, one can easily derive the end result in Eq. 2.

In the turbulence literature it is often tested how close the statistics of the velocity field are to the Gauss distribution by means of the two-point velocity increments $\delta \mathbf{v}$. The latter represent the difference in velocity at two different points separated by the vector $\mathbf{r}$. We distinguish between longitudinal ($\parallel$) and transverse ($\perp$) velocity increments that are given by the projection of $\delta \mathbf{v}$ on the separation vector $\mathbf{r}$ and on its orthogonal complement, respectively. In mathematical terms we have that

$$\delta v_{\parallel }\left(\mathbf{x},\mathbf{r},t\right)=\delta \mathbf{v}\cdot \frac{\mathbf{r}}{r}=\left(\mathbf{v}\left(\mathbf{x},t\right)-\mathbf{v}\left(\mathbf{x}+\mathbf{r},t\right)\right)\cdot \frac{\mathbf{r}}{r}$$ [S21]

$$\delta v_{\perp }\left(\mathbf{x},\mathbf{r},t\right)=\delta \mathbf{v}\cdot {\mathbf{e}}_T=\left(\mathbf{v}\left(\mathbf{x},t\right)-\mathbf{v}\left(\mathbf{x}+\mathbf{r},t\right)\right)\cdot {\mathbf{e}}_T,$$ [S22]

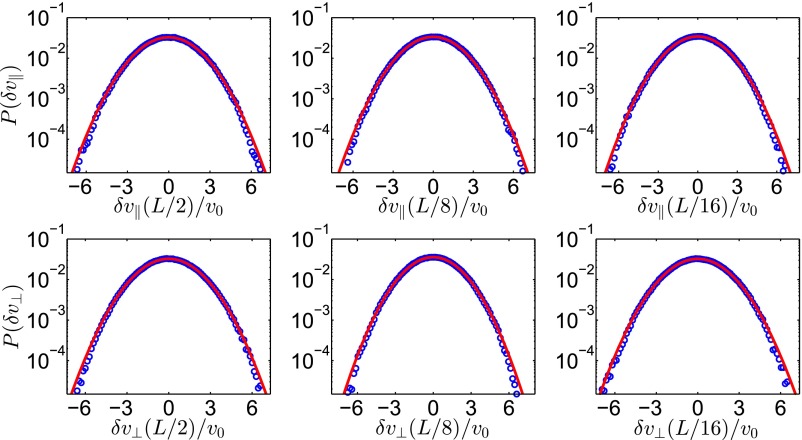
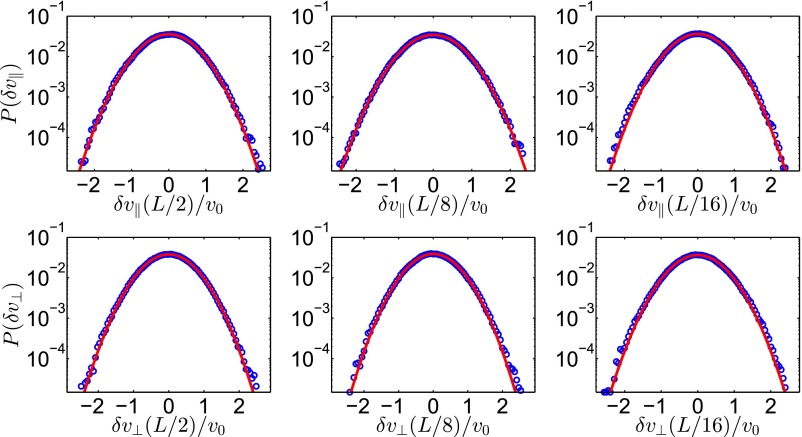
where ${\mathbf{e}}_T$ is a unit vector that is perpendicular to the separation vector $\mathbf{r}$ and in terms of the unit vectors in the plane, i.e., ${\mathbf{e}}_1$ and ${\mathbf{e}}_2$, it is given by ${\mathbf{e}}_T=\left(\left(\mathbf{r}\cdot {\mathbf{e}}_2\right){\mathbf{e}}_1-\left(\mathbf{r}\cdot {\mathbf{e}}_1\right){\mathbf{e}}_2\right)/r$. For statistically homogeneous systems the statistical properties of the velocity increments do not depend on the particular choice of the reference point $\mathbf{x}$. In addition, in the case of statistical isotropy $\delta \mathbf{v}$ will depend only on the distance r between the two points; i.e., $\delta \mathbf{v}=\delta \mathbf{v}\left(r,t\right)$. In the time series of $\delta v_{\parallel }\left(r,t\right)$ and $\delta v_{\perp }\left(r,t\right)$ some values will be obtained more often than others, which gives us the probability distribution P of the velocity increments. (Strictly speaking, this gives us the probability density function.) A numerical computation of P (blue circles) for the case of $\alpha \tau =-1$ is shown in Fig. S2 in a semilogarithmic representation for three different separation vectors with Fig. S2, Upper Row displaying $P\left(\delta v_{\parallel }\right)$ and Fig. S2, Lower Row displaying $P\left(\delta v_{\perp }\right)$. The red line gives the closest fit to a Gauss distribution $P\left(\delta v_{\parallel ,\perp }\right)=A\exp \left(-\delta v_{\parallel ,\perp }^2/{\sigma }^2\right)$ with A and σ being the fit parameters. As seen in Fig. S2, the distribution of velocity increments is very close to a Gaussian at large scales, which supports the use of the quasi-normal approximation. In addition, note that all of the distributions in Fig. S2 have nearly the same parameters A and σ. To connect the results shown here to the energy spectra in wave-number space let us remark that the separations displayed in Fig. S2 correspond to $k\ell \approx 0.2$, $k\ell \approx 0.8$, and $k\ell \approx 1.6$, respectively. They all belong to the low-k range studied in this work, because, for comparison, the peak of the energy spectrum lies around $k\ell \approx 7$ for $\alpha \tau =-1$ and $k\ell \approx 15$ for $\alpha \tau =4$. Fig. S3 displays the same probability distributions but for a different value of the constant in front of the Ekman term: $\alpha \tau =3$, which lies close to the other end of the parameter range considered here. The data lead to the same conclusion regarding the statistics of the velocity field as in the previous case for $\alpha \tau =-1$. The only difference appears to be the corresponding value of σ. Here it is considerably lower, meaning that the width of the distribution is smaller. The reason for this lies in the fact that for $\alpha \tau =-1$ the Ekman term acts as an energy source whereas for $\alpha \tau =3$ it dissipates energy. Thus, in the first case the total energy of the system, proportional to the integral of ${\left|\mathbf{v}\right|}^2$ over the whole domain, is considerably higher, making larger velocity increments more probable. In conclusion, the data represented in Figs. S2 and S3 support the quasi-normal approximation we used in our analysis.

Fig. S2.

Numerically computed probability density function (blue circles) for the longitudinal (Upper Row) and transverse (Lower Row) velocity increments for three different separations: $L/2$ (Left Column), $L/8$ (Center Column), and $L/16$ (Right Column), where L denotes the box size of $10\pi \ell$ and the Ekman parameter is set to $\alpha \tau =-1$. The red line gives the closest fit of a Gauss distribution. Hence, the statistics of the velocity field at large scales are indeed very close to Gaussian.

Fig. S3.

Numerically computed probability density function (blue circles) for the longitudinal (Upper Row) and transverse (Lower Row) velocity increments for three different separations: $L/2$ (Left Column), $L/8$ (Center Column), and $L/16$ (Right Column), where L denotes the box size of $10\pi \ell$. Here the Ekman parameter equals $\alpha \tau =3$. The red line gives the closest fit of a Gauss distribution. The statistics of the velocity field at large scales are again very close to Gaussian.